Propagation of Surface Waves in a Rotating Coated Viscoelastic Half-Space under the Influence of Magnetic Field and Gravitational Forces
Abstract
:1. Introduction
2. Basic Equations
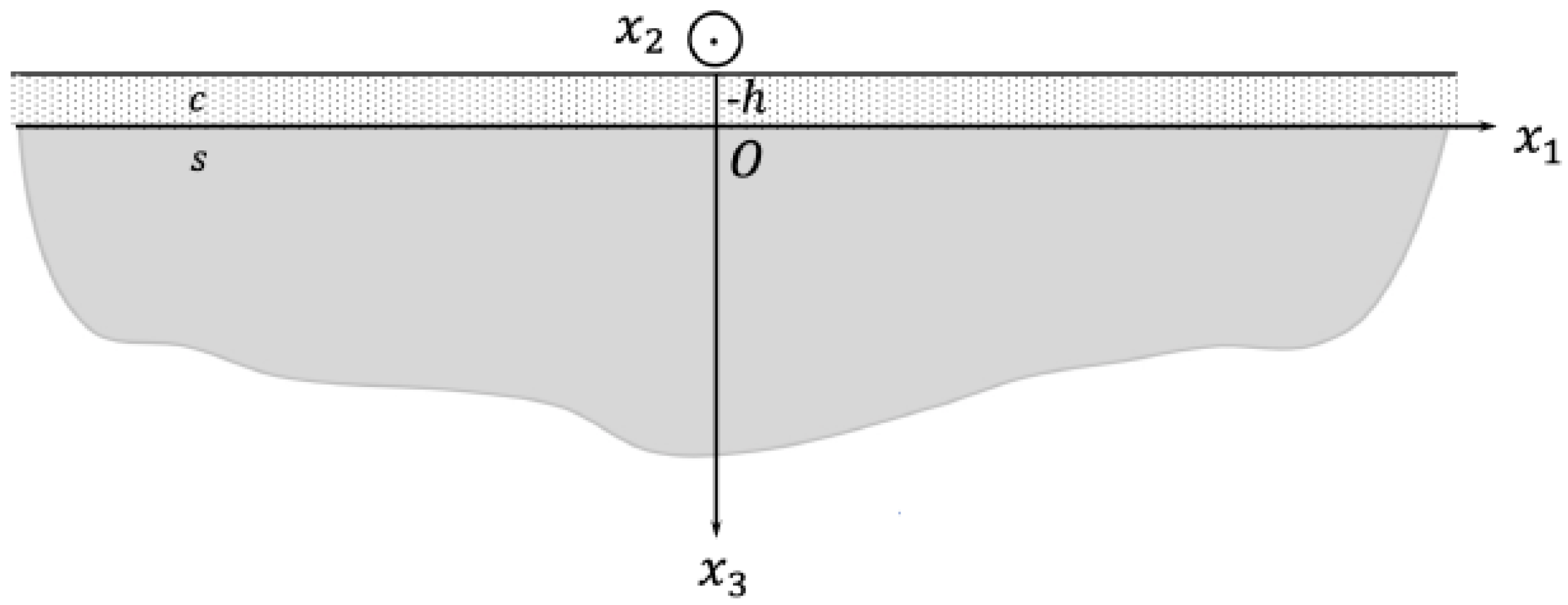
3. Problem Formulation
4. Problem Solution
5. Frequency Equation
Special Cases of the Frequency Equation
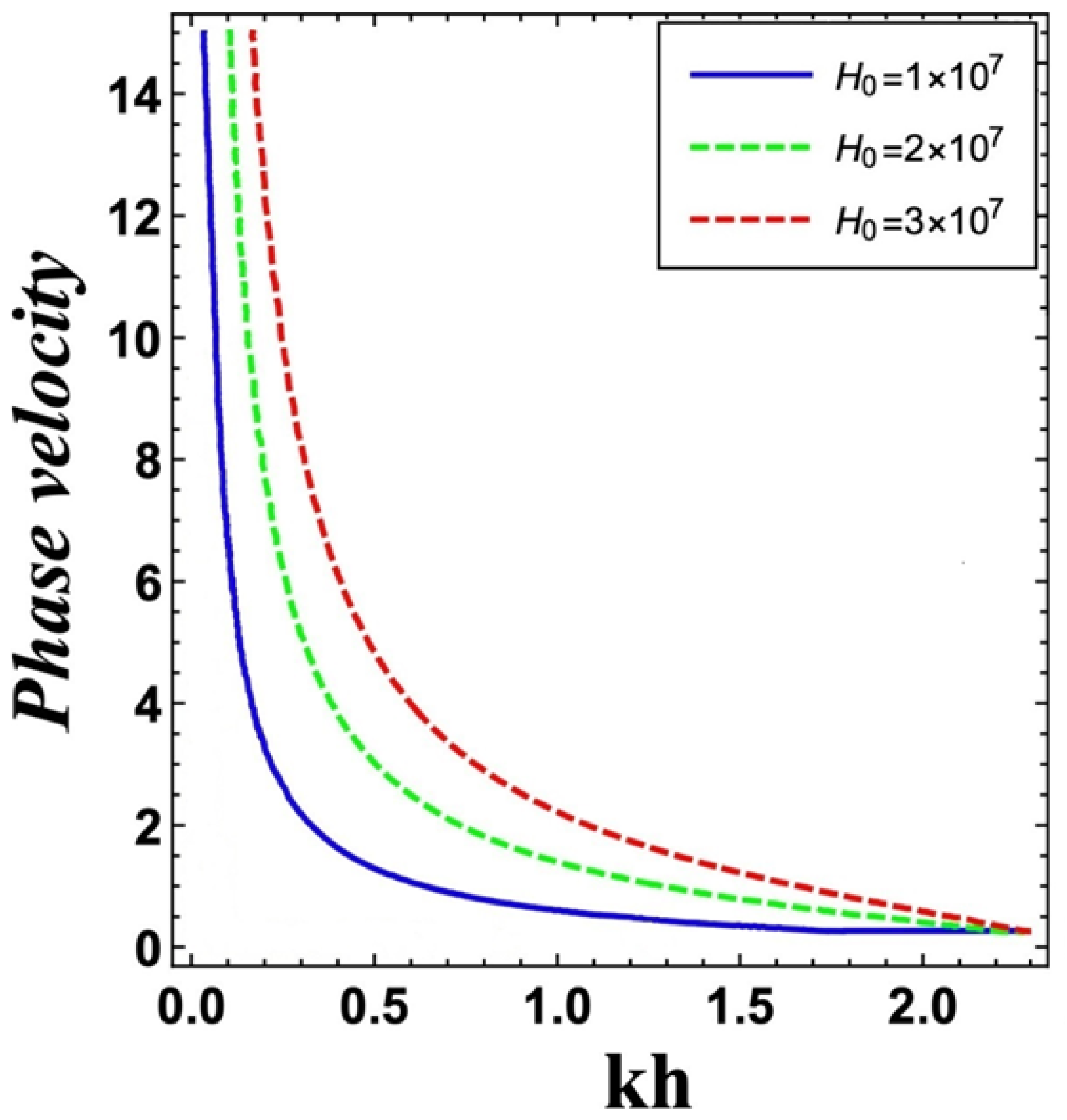
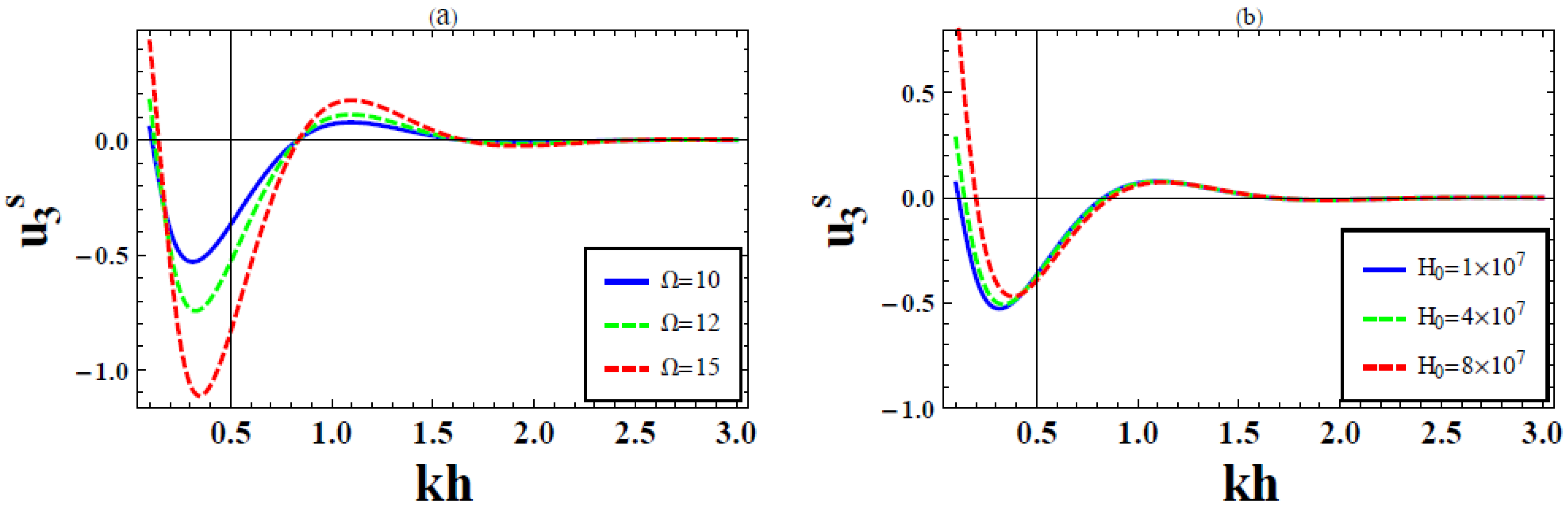
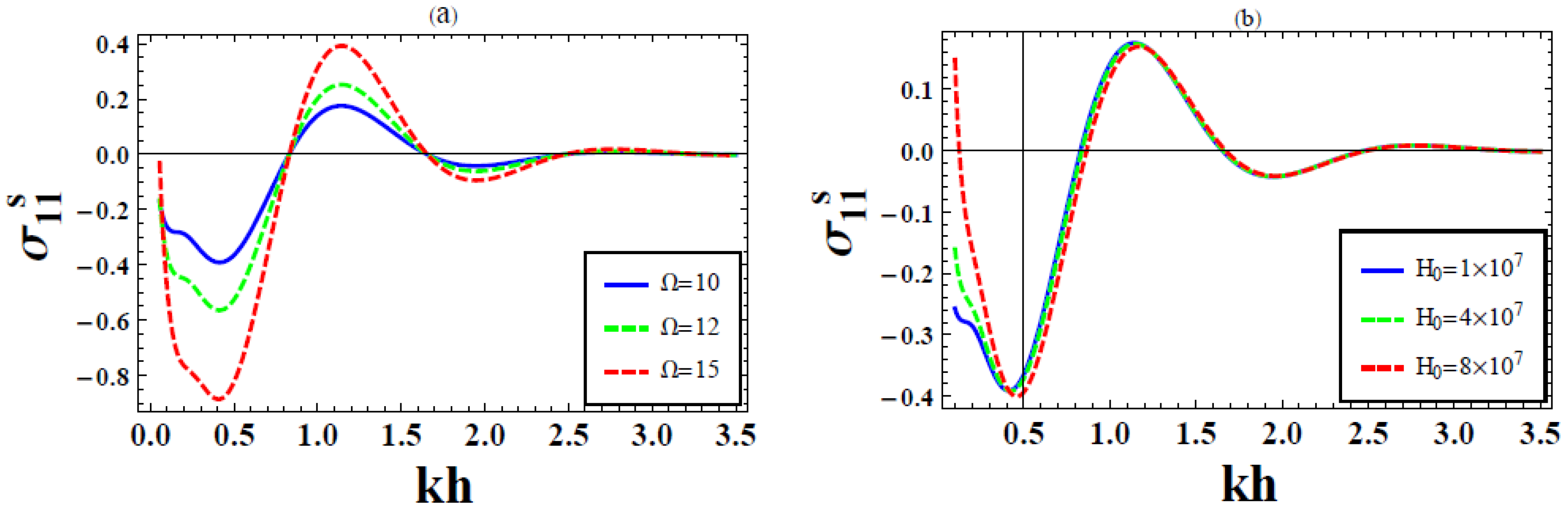
6. Numerical Results and Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
Appendix C
Appendix D
References
- Achenbach, J. Wave Propagation in Elastic Solids; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Brigatti, M.F.; Mottana, A. Layered Mineral Structures and Their Application in Advanced Technologies; The Mineralogical Society of Great Britain and Ireland: Twickenham, UK, 2011; Volume 11. [Google Scholar] [CrossRef]
- Ewing, W.M.; Jardetzky, W.S.; Press, F.; Beiser, A. Elastic Waves in Layered Media. Phy. Today 1957, 10, 27. [Google Scholar] [CrossRef]
- Kaplunov, J.D.; Kossovitch, L.Y.; Nolde, E.V. Dynamics of Thin Walled Elastic Bodies; Academic Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Nuruddeen, R.I.; Nawaz, R.; Zia, Q.M.Z. Asymptotic approach to anti-plane dynamic problem of asymmetric three-layered composite plate. Math. Methods Appl. Sci. 2021, 44, 10933–10947. [Google Scholar] [CrossRef]
- Nuruddeen, R.I.; Nawaz, R.; Zia, Q.M.Z. Investigating the viscous damping effects on the propagation of Rayleigh waves in a three-layered inhomogeneous plate. Phy. Scr. 2020, 95, 065224. [Google Scholar] [CrossRef]
- Bose, S. High Temperature Coatings; Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Chattopadhyay, D.K.; Raju, K.V.S.N. Structural engineering of polyurethane coatings for high performance applications. Prog. Polym. Sci. 2007, 32, 352–418. [Google Scholar] [CrossRef]
- Datta, P.K. Surface Engineering: Engineering Applications; Royal Society of Chemistry: London, UK, 1993. [Google Scholar]
- Padture, N.P.; Gell, M.; Jordan, E.H. Thermal barrier coatings for gas-turbine engine applications. Science 2002, 296, 280–284. [Google Scholar] [CrossRef] [PubMed]
- Dai, H.-H.; Kaplunov, J.; Prikachikov, D.A. A long-wave model for the surface wave in a coated half-space. Proc. R. Soc. A Math. Phy. Eng. Sci. 2010, 466, 3097–3116. [Google Scholar] [CrossRef] [Green Version]
- Li, M.; Liu, Q.; Jia, Z.; Xu, X.; Cheng, Y.; Zheng, Y.; Xi, T.; Wei, S. Graphene oxide/hydroxyapatite composite coatings fabricated by electrophoretic nanotechnology for biological applications. Carbon 2014, 67, 185–197. [Google Scholar] [CrossRef]
- Tiainen, V.M. Amorphous carbon as a bio-mechanical coating-mechanical properties and biological applications. Diamond Rel. Mat. 2001, 10, 153–160. [Google Scholar] [CrossRef]
- Qian, Z.; Jin, F.; Kishimoto, K.; Wang, Z. Effect of initial stress on the propagationn behavior of SH-waves in multilayered piezoelectric composite structures. Sens. Actuators A Phys. 2004, 112, 368–375. [Google Scholar] [CrossRef]
- Biot, M.A. Thermoelasticity and irreversible thermodynamics. J. Appl. Phy. 1956, 27, 240–253. [Google Scholar] [CrossRef]
- Lord, H.W.; Shulman, Y. A generalized dynamical theory of thermoelasticity. J. Mech. Phy. Solids. 1967, 15, 299–309. [Google Scholar] [CrossRef]
- Green, A.E.; Lindsay, K.A. Thermoelasticity. J. Elast. 1972, 2, 1–7. [Google Scholar] [CrossRef]
- Green, A.E.; Naghdi, P.M. Thermoelasticity without energy dissipation. J. Elast. 1993, 31, 189–208. [Google Scholar] [CrossRef]
- Chandrasekharaih, D.S. Thermoelasticity with second sound: A review. Appl. Mech. Rev. 1986, 39, 355–376. [Google Scholar] [CrossRef]
- Chandrasekharaih, D.S. Hyperbolic thermoelasticity: A review of recent literature. Appl. Mech. Rev. 1998, 51, 705–729. [Google Scholar] [CrossRef]
- Yu, J.; Ma, Q.; Su, S. Wave propagation in non-homogeneous magneto-electro-elastic hollow cylinders. Ultras 2008, 48, 664–677. [Google Scholar] [CrossRef] [PubMed]
- Ebrahimi, F.; Barati, M.R.; Dabbagh, A. Wave propagation in embedded inhomogeneous nanoscale plates incorporating thermal effects. Waves Random Complex Media 2018, 28, 215–235. [Google Scholar] [CrossRef]
- Abo-Dahab, S.M.; Lotfy, K.; Gohaly, K.A. Rotation and magnetic field effect on surface waves propagation in an elastic layer lying over a generalized thermoelastic diffusive half-space with imperfect boundary. Math. Probl. Eng. 2015, 2015, 671783. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.Z.; Li, F.M.; Kishimoto, K. Thermal effects on vibration properties of double-layered nanoplates at small scales. Compos. Part B Eng. 2011, 42, 1311–1317. [Google Scholar] [CrossRef]
- Selim, M.M. Effect of thermal stress and magnetic field on propagation of transverse wave in an anisotropic incompressible dissipative initially stressed plate. Appl. Math. Inf. Sci. 2017, 11, 195–200. [Google Scholar] [CrossRef]
- Erbaş, B.; Kaplunov, J.; Nobili, A.; Kılıç, G. Dispersion of elastic waves in a layer interacting with a Winkler foundation. J. Acoust Soc. Am. 2018, 144, 2918–2925. [Google Scholar] [CrossRef] [Green Version]
- Abd-Alla, A.M.; Abo-Dahab, S.M.; Khan, A. Rotational effects on magneto-thermoelastic Stoneley, Love, and Rayleigh waves in fibre-reinforced anisotropic general viscoelastic media of higher order. Comp. Mat. Continua. 2017, 53, 49–72. [Google Scholar]
- Farhan, A.M.; Abd-Alla, A.M. Effect of rotation on the surface wave propagation in magneto-thermoelastic materials with voids. J. Ocean Engr. Sci. 2018, 3, 334–342. [Google Scholar] [CrossRef]
- Nuruddeen, R.I.; Nawaz, R.; Zia, Q.M.Z. Dispersion of elastic waves in an asymmetric three-layered structure in the presence of magnetic and rotational effects. Prog. Electr. R. 2020, 91, 165–177. [Google Scholar] [CrossRef]
- Abbas, I.A. Eigenvalue approach in a three-dimensional generalized thermoelastic interactions with temperature-dependent material properties. Comp. Math. Appl. 2014, 68, 2036–2056. [Google Scholar] [CrossRef]
- Zennir, K.; Allahem, A.; Cherif, B. Quantitative studies for a magneto-visco-elastic system and its applications. Int. J. Appl. Math. Stat. 2018, 57, 1–15. [Google Scholar]
- Nuruddeen, R.I.; Nawaz, R.; Zia, Z.Q.M. Effects of thermal stress, magnetic field and rotation on the dispersion of elastic waves in an inhomogeneous five-layered plate with alternating components. Sci. Prog. 2020, 103, 0036850420940469. [Google Scholar] [CrossRef]
- Zennir, K.; Allahem, A.; Boulaaras, S.; Cherif, B. New mathematical studies for surface waves on multi-layered liquid films. Int. J. Eng. Res. Tech. 2019, 12, 269–275. [Google Scholar] [CrossRef]
- Gholami, A.; Ganji, D.D.; Rezazadeh, H.; Adel, W.; Bekir, A. Application of modified Mickens iteration procedure to a pendulum and the motion of a mass attached to a stretched elastic wire. Int. J. Nonlinear Sci. Num. Simul. 2021. [Google Scholar] [CrossRef]
- Al-Duhaim, H.R.; Yilbas, B.S.; Zaman, F.D. Determination of temperature distribution and thermal stress for the hyperbolic heat conduction equation due to laser short pulse heating. Lasers Eng. 2016, 35, 275–301. [Google Scholar]
- Nawaz, R.; Nuruddeen, R.I.; Zia, Q.M.Z. An asymptotic investigation of the dynamics and dispersion of an elastic five-layered plate for anti-plane shear vibration. J. Eng. Math. 2021, 128, 1–12. [Google Scholar] [CrossRef]
- Davodi, A.G.; Rezazadeh, H.; Adel, W.; Bekir, A.; Ganji, D.D. Fluctuation and frequency of the oscillators with exponential spring using accurate approximate analytical solutions. Fluct. Noise Lett. 2021, 20, 2150036. [Google Scholar] [CrossRef]
- Miyasita, T.; Zennir, K. Finite time blow-up for a viscoelastic wave equation with weak-strong damping and power nonlinearity. Osaka J. Math. 2021, 58, 661–669. [Google Scholar]
- Dridi, H.; Zennir, K. New class of Kirchhoff type equations with Kelvin-Voigt damping and general nonlinearity: Local existence and blow-up in solutions. J. Partial. Diff. Equ. 2021, 34, 313–347. [Google Scholar]
- Biot, M.A. Mechanics of Incremental Deformations; Wiley: New York, NY, USA, 1965. [Google Scholar]
- Ting, T.C.T. Surface waves in an exponentially graded, general anisotropic elastic material under the influence of gravity. Wave Motion 2011, 48, 335–344. [Google Scholar]
- Mubaraki, A.M.A. Asymptotic Models for Surface Waves in Coated Elastic Solids. Ph.D. Thesis, Keel University, Keele, UK, 2021. [Google Scholar]
- Abo-Dahab, S.M.; Abd-Alla, A.M.; Khan, A. Rotational effect on Rayleigh, Love and Stoneley waves in non-homogeneous fibre-reinforced anisotropic general viscoelastic media of higher order. Struc. Eng. Mech. 2016, 58, 181–197. [Google Scholar] [CrossRef]
- Younesian, D.; Hosseinkhani, A.; Askari, H.; Esmailzadeh, E. Elastic and viscoelastic foundations: A review on linear and nonlinear vibration modeling and applications. Nonlinear Dyn. 2019, 97, 1–43. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mubaraki, A.; Althobaiti, S.; Nuruddeen, R.I. Propagation of Surface Waves in a Rotating Coated Viscoelastic Half-Space under the Influence of Magnetic Field and Gravitational Forces. Fractal Fract. 2021, 5, 250. https://doi.org/10.3390/fractalfract5040250
Mubaraki A, Althobaiti S, Nuruddeen RI. Propagation of Surface Waves in a Rotating Coated Viscoelastic Half-Space under the Influence of Magnetic Field and Gravitational Forces. Fractal and Fractional. 2021; 5(4):250. https://doi.org/10.3390/fractalfract5040250
Chicago/Turabian StyleMubaraki, Ali, Saad Althobaiti, and Rahmatullah Ibrahim Nuruddeen. 2021. "Propagation of Surface Waves in a Rotating Coated Viscoelastic Half-Space under the Influence of Magnetic Field and Gravitational Forces" Fractal and Fractional 5, no. 4: 250. https://doi.org/10.3390/fractalfract5040250
APA StyleMubaraki, A., Althobaiti, S., & Nuruddeen, R. I. (2021). Propagation of Surface Waves in a Rotating Coated Viscoelastic Half-Space under the Influence of Magnetic Field and Gravitational Forces. Fractal and Fractional, 5(4), 250. https://doi.org/10.3390/fractalfract5040250





