Fractal–Fractional Michaelis–Menten Enzymatic Reaction Model via Different Kernels
Abstract
:1. Introduction
2. Numerical Schemes of Fractal–Fractional Michaelis–Menten Enzymatic Reaction Model
2.1. Preliminaries and Notation
2.2. FFMMER Scheme via the Power-Law Kernel
2.3. FFMMER Scheme via the Exponential Decay Kernel
2.4. FFMMER Scheme via the Mittag-Leffler Kernel
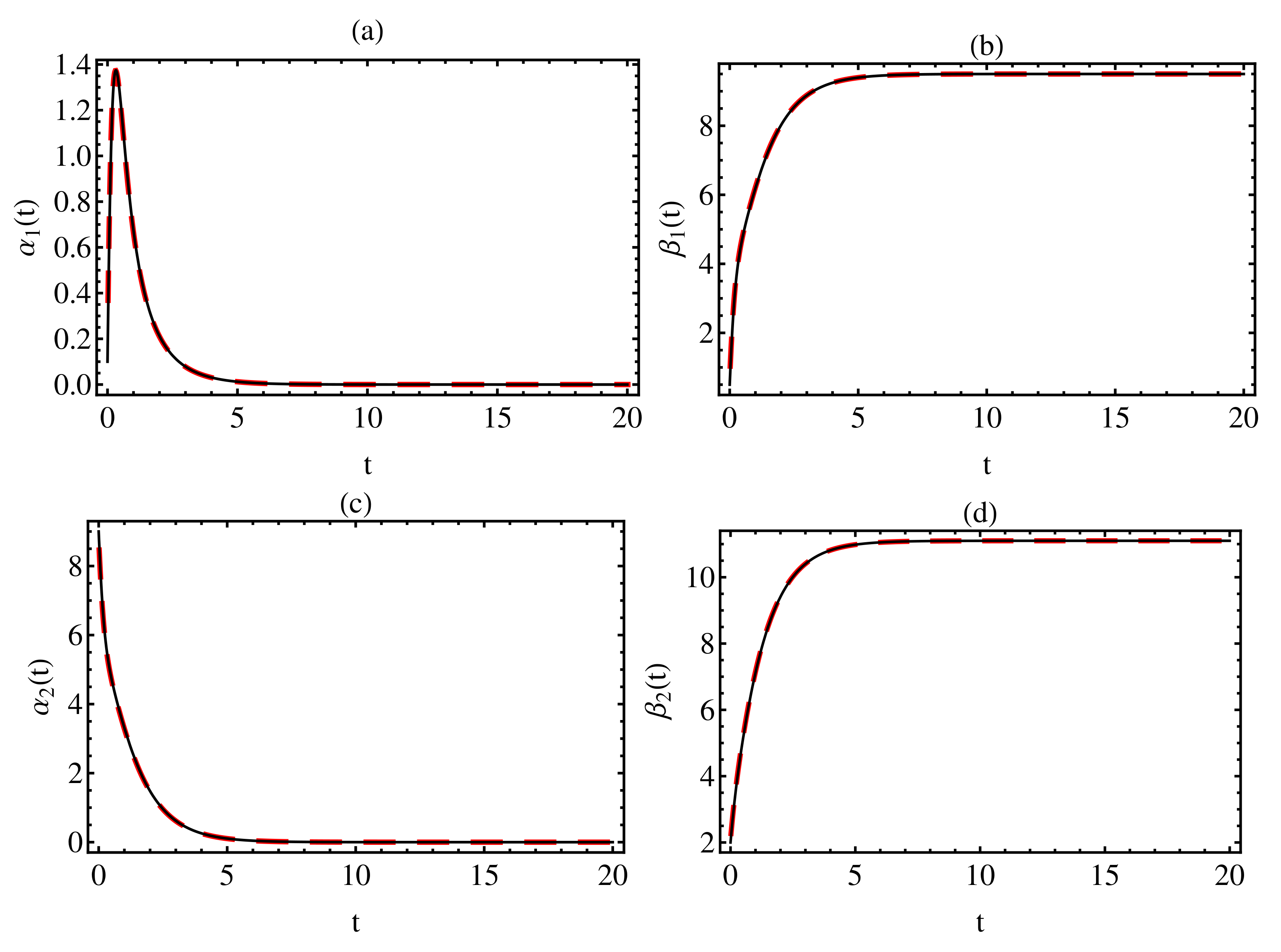
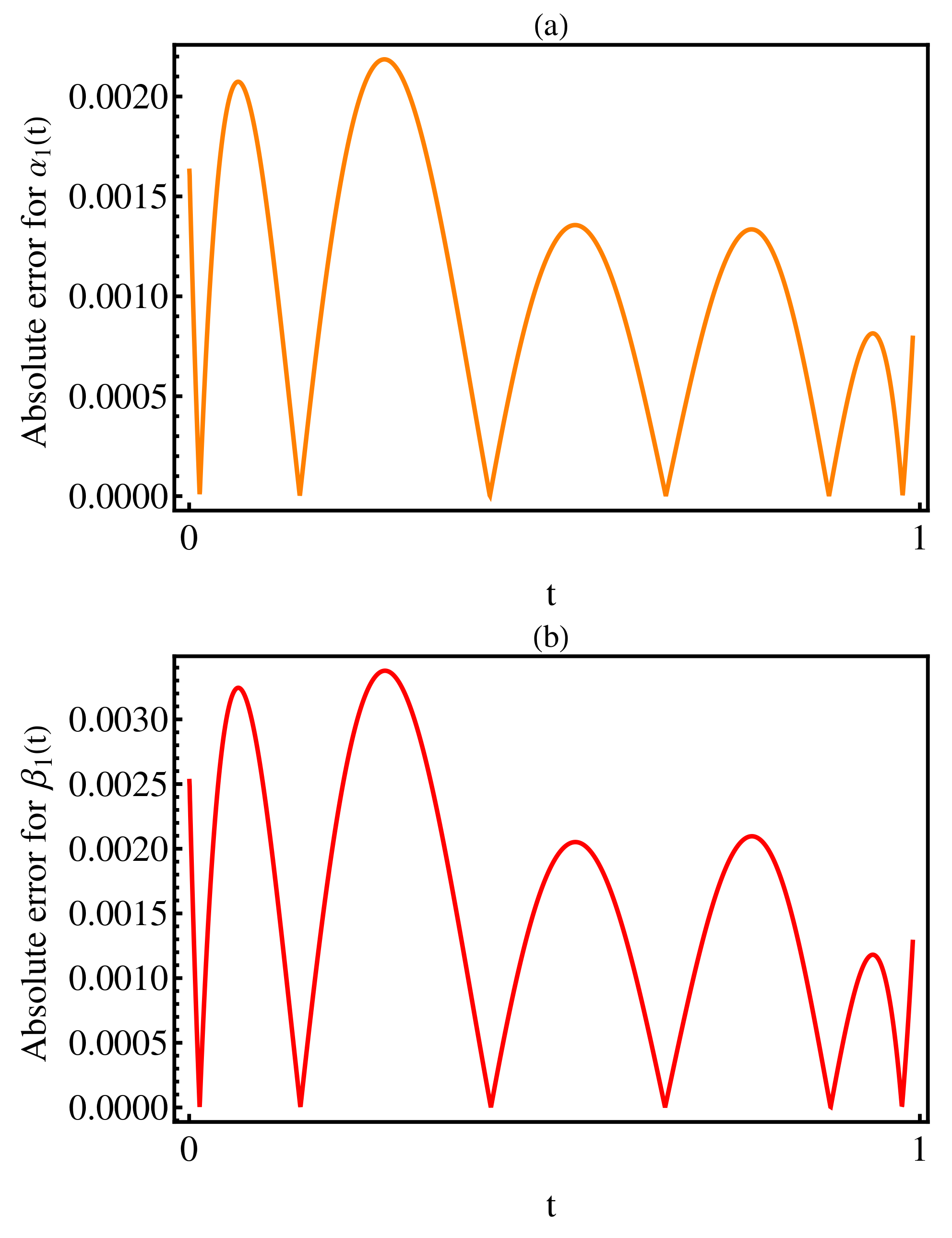
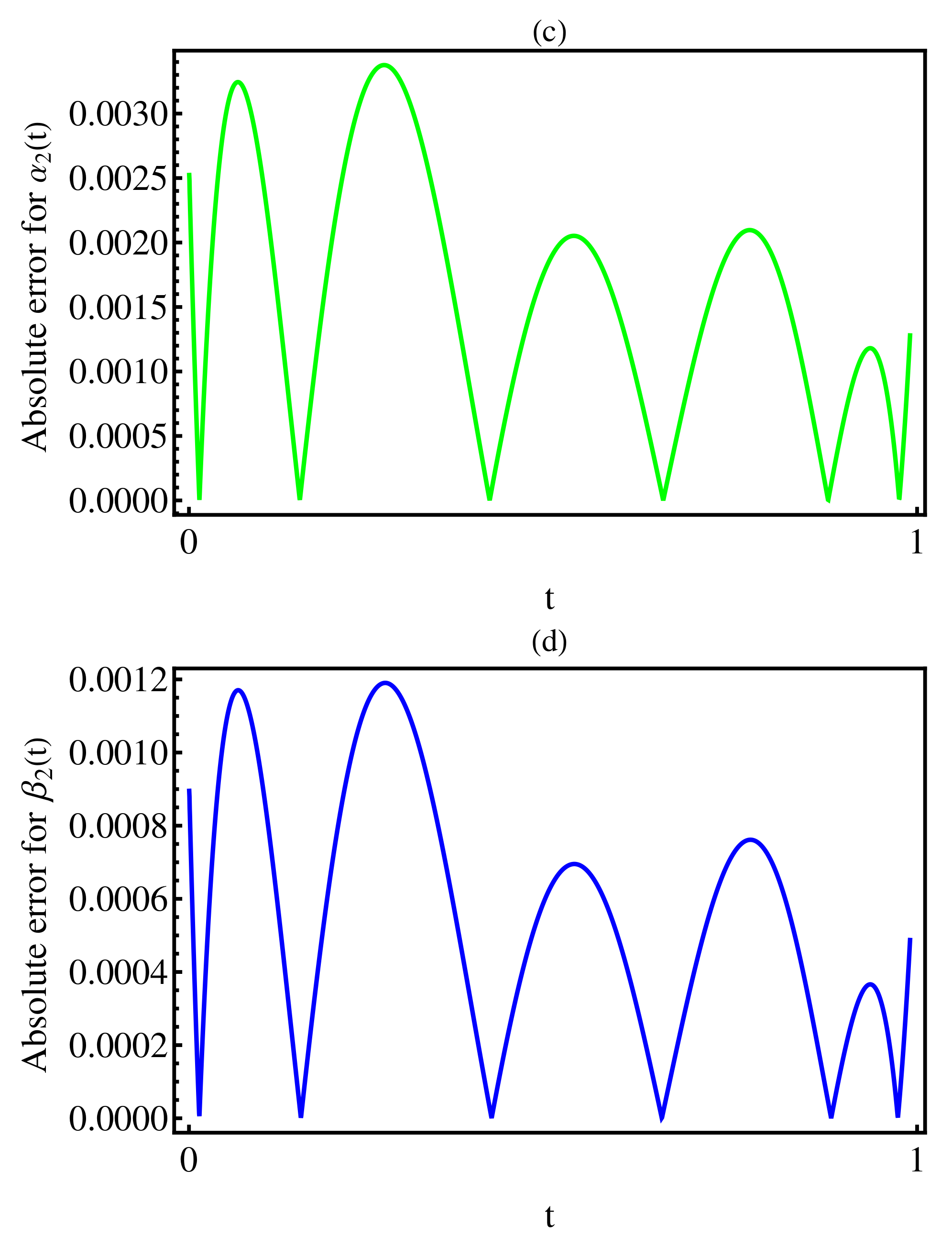
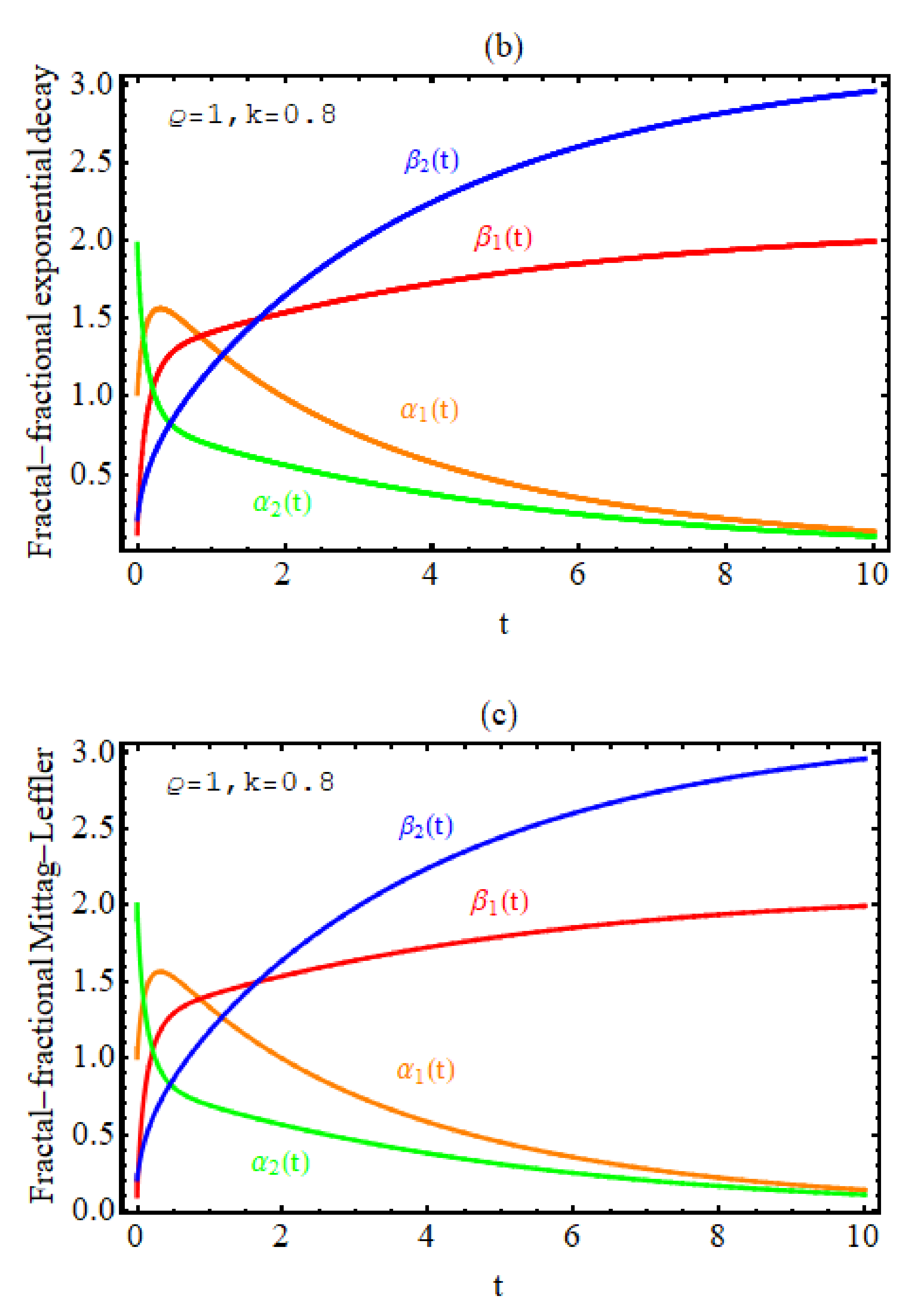
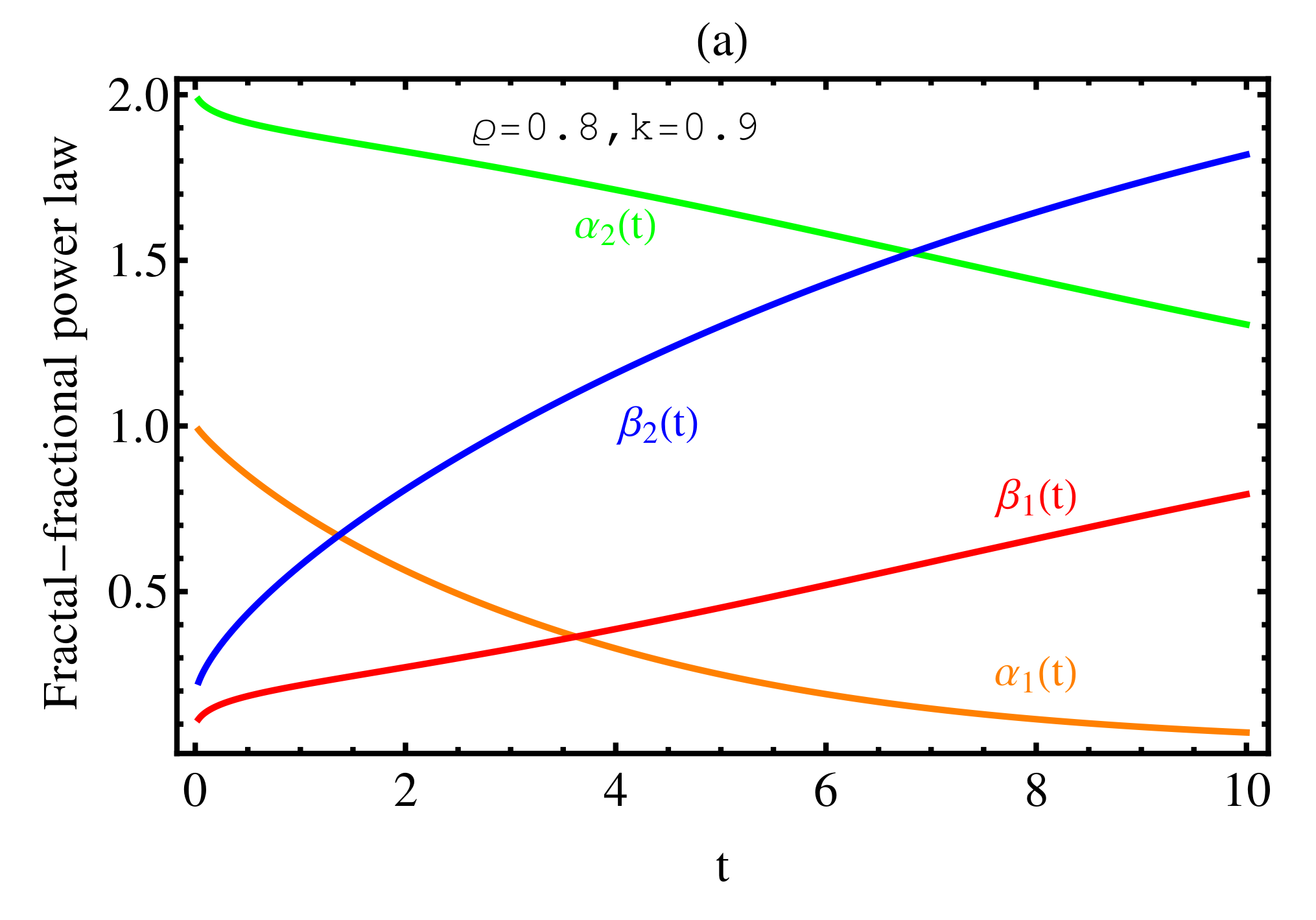
3. Numerical Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shatey, S.; Motsa, S.S.; Khan, Y. A new piecewise spectral homotopy analysis of the Michaelis-Menten enzymatic reactions model. Numer. Algor. 2014, 66, 495–510. [Google Scholar] [CrossRef]
- Abu-Reesh, I.M. Optimal design of continuously stirred membrane reactors in series using Michaelis-Menten kinetics with competitive product inhibition: Theoretical analysis. Desalination 2005, 180, 119–132. [Google Scholar] [CrossRef]
- Golicnik, M. Explicit reformulations of time-dependent solution for a Michaelis-Menten enzyme reaction model. Anal. Biochem. 2010, 406, 94–96. [Google Scholar] [CrossRef] [PubMed]
- Golicnik, M. Evaluation of enzyme kinetic parameters using explicit analytic approximations to the Michaelis-Menten equation. Biochem. Eng. J. 2011, 53, 234–238. [Google Scholar] [CrossRef]
- Uma Maheswari, M.; Rajendran, L. Analytical solution of non-linear enzyme reaction equations arising in mathematical chemistry. J. Math. Chem. 2011, 49, 1713–1726. [Google Scholar] [CrossRef]
- Vogt, D. On approximate analytical solutions of differential equations in enzyme kinetics using homotopy perturbation method. J. Math. Chem. 2013, 51, 826–842. [Google Scholar] [CrossRef]
- Liang, S.; Jeffrey, D.J. Comparison of homotopy analysis method and homotopy perturbation method through an evolution equation. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 4057–4064. [Google Scholar] [CrossRef]
- Li, R.; Van Gorder, R.A.; Mallory, K.; Vajravelu, K. Solution method for the transformed time-dependent Michaelis–Menten enzymatic reaction model. J. Math. Chem. 2014, 52, 2494–2506. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Some issues on HPM and HAM methods: A convergence scheme. Math. Comput. Model. 2011, 53, 1929–1936. [Google Scholar] [CrossRef]
- Alrabaiah, H.; Ali, A.; Haq, F.; Shah, K. Existence of fractional order semianalytical results for enzyme kinetics model. Adv. Differ. Equ. 2020, 2020, 443. [Google Scholar] [CrossRef]
- Liao, S.-J. On the homotopy analysis method for nonlinear problems. Appl. Math. Comput. 2004, 147, 499–513. [Google Scholar] [CrossRef]
- Saad, K.M.; AL-Shareef, E.H.F.; Alomari, A.K.; Baleanu, D.; Gómez-Aguilar, J.F. On exact solutions for timefractional Korteweg-de Vries and Korteweg-de Vries-Burgers equations using homotopy analysis transform method. Chin. J. Phys. 2020, 63, 149–162. [Google Scholar] [CrossRef]
- He, J.H. Variational iteration method-a kind of nonlinear analytical technique: Some examples. Int. J. Non-Linear Mech. 1999, 34, 699–708. [Google Scholar] [CrossRef]
- Shi, X.C.; Huang, L.L.; Zeng, Y. Fast Adomian decomposition method for the Cauchy problem of the time-fractional reaction diffusion equation. Adv. Mech. Eng. 2016, 8, 1–5. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Saad, K.M. Some new and modified fractional analysis of the time-fractional Drinfeld–Sokolov–Wilson system. Chaos Interdiscip. J. Nonlinear Sci. 2020, 30, 113104. [Google Scholar] [CrossRef]
- Bueno-Orovio, A.; Kay, D.; Burrage, K. Fourier spectral methods for fractional-in-space reaction-diffusion equations. BIT Numer. Math. 2014, 54, 937–954. [Google Scholar] [CrossRef]
- Takeuchi, Y.; Yoshimoto, Y.; Suda, R. Second order accuracy fnite difference methods for space-fractional partial differential equations. J. Comput. Appl. Math. 2017, 320, 101–119. [Google Scholar] [CrossRef]
- Yildiray, Y.K.; Aydin, K. The solution of the Bagley Torvik equation with the generalized Taylor collocation method. J. Frankl. Inst. 2010, 347, 452–466. [Google Scholar]
- Saad, K.M.; Srivastava, H.M.; Gómez-Aguilar, J.F. A fractional quadratic autocatalysis associated with chemical clock reactions involving linear inhibition. Chaos Solitons Fractals 2020, 132, 109557. [Google Scholar] [CrossRef]
- Saad, K.M. Fractal-fractional Brusselator chemical reaction. Chaos Solitons Fractals 2021, 150, 111087. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; NorthHolland Mathematical Studies; Elsevier (North-Holland) Science Publishers: Amsterdam, The Netherlands; London, UK; New York, NY, USA, 2006; Volume 204. [Google Scholar]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Mathematics in Science and Engineering; Academic Press: New York, NY, USA; London, UK; Sydney, Australia; Tokyo, Japan; Toronto, ON, Canada, 1999; Volume 198. [Google Scholar]
- Atangana, A. Fractal-fractional differentiation and integration: Connecting fractal calculus and fractional calculus to predict complex system. Chaos Solitons Fractals 2017, 102, 396–406. [Google Scholar] [CrossRef]
- Heydari, M.H.; Atangana, A.; Avazzadeh, Z.; Yang, Y. Numerical treatment of the strongly coupled nonlinear fractal-fractional Schr-dinger equations through the shifted Chebyshev cardinal functions. Alex. Eng. J. 2020, 59, 2037–2052. [Google Scholar] [CrossRef]
- Saad, K.M.; Alqhtania, M.; Gómez-Aguilarc, J.F. Fractal-fractional study of the hepatitis C virus infection model. Results Phys. 2020, 19, 103555. [Google Scholar] [CrossRef]
- Arfan, M.; Shah, K.; Ullah, A. Fractal-fractional mathematical model of four species comprising of prey-predation. Phys. Scr. 2021, 96, 124053. [Google Scholar] [CrossRef]
- LI, Z.; Liu, Z.; Khan, M.A. Fractional investigation of bank data with fractal-fractional Caputo derivative. Chaos Solitons Fractals 2020, 131, 109528. [Google Scholar] [CrossRef]
- Caputo, M. Linear models of dissipation whose Q is almost frequency independent: II. Geophys. J. Roy. Astron. Soc. 1967, 13, 529539. [Google Scholar] [CrossRef]
- Caputo, M.; Fabrizio, M. A new defnition of fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2015, 2, 73–85. [Google Scholar]
- Atangana, A.; Baleanu, D. New fractional derivative with nonlocal and non-singular kernel. Chaos Solitons Fractls Therm. Sci. 2016, 20, 757–763. [Google Scholar]
- Michaelis, L.; Menten, M.L. Die kinetik der invertinwirkung. Biochem. Z 1913, 49, 333–369. [Google Scholar]
- Agarwal, P.; Nieto, J.J.; Ruzhansky, M.; Torres, D.F.M. Analysis of Infectious Disease Problems (COVID-19) and Their Global Impact; Springer: Singapore, 2021. [Google Scholar]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alqhtani, M.; Saad, K.M. Fractal–Fractional Michaelis–Menten Enzymatic Reaction Model via Different Kernels. Fractal Fract. 2022, 6, 13. https://doi.org/10.3390/fractalfract6010013
Alqhtani M, Saad KM. Fractal–Fractional Michaelis–Menten Enzymatic Reaction Model via Different Kernels. Fractal and Fractional. 2022; 6(1):13. https://doi.org/10.3390/fractalfract6010013
Chicago/Turabian StyleAlqhtani, Manal, and Khaled M. Saad. 2022. "Fractal–Fractional Michaelis–Menten Enzymatic Reaction Model via Different Kernels" Fractal and Fractional 6, no. 1: 13. https://doi.org/10.3390/fractalfract6010013
APA StyleAlqhtani, M., & Saad, K. M. (2022). Fractal–Fractional Michaelis–Menten Enzymatic Reaction Model via Different Kernels. Fractal and Fractional, 6(1), 13. https://doi.org/10.3390/fractalfract6010013





