Flow of a Self-Similar Non-Newtonian Fluid Using Fractal Dimensions
Abstract
:1. Introduction
2. Laminar Flow of an Incompressible Non-Newtonian Fluid
2.1. The Rheological Behavior of Fluids
2.2. Momentum Conservation Equation
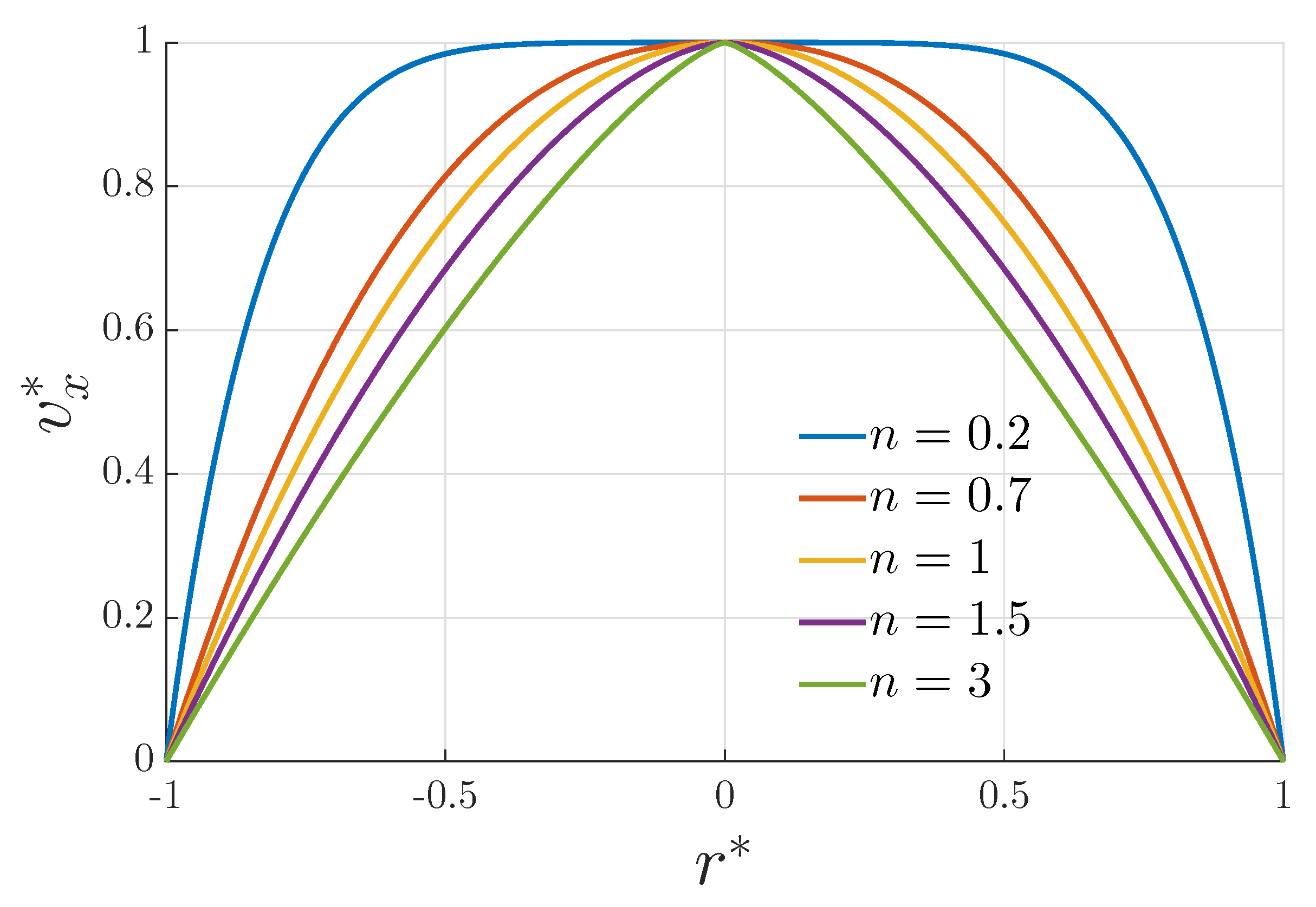
3. Laminar Flow of an Incompressible Fractal Non-Newtonian Fluid
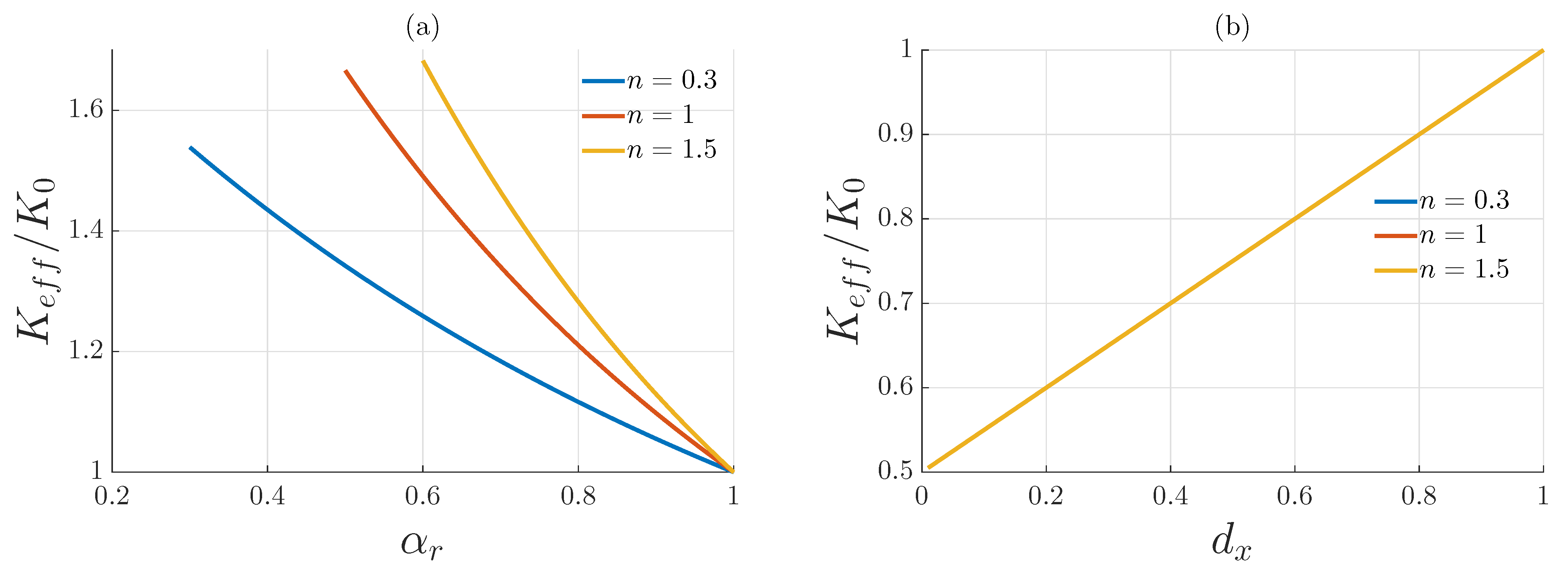
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pandey, V.; Holm, S. Linking the fractional derivative and the lomnitz creep law to non-Newtonian time-varying viscosity. Phys. Rev. E 2016, 94, 032606. [Google Scholar] [CrossRef] [Green Version]
- Bird, R.B.; Dai, G.; Yarusso, B.J. The rheology and flow of viscoplastic materials. Rev. Chem. Eng. 1983, 1, 1–70. [Google Scholar] [CrossRef]
- Mahmood, A.; Parveen, S.; Ara, A.; Khan, N. Exact analytic solutions for the unsteady flow of a non-Newtonian fluid between two cylinders with fractional derivative model. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 3309–3319. [Google Scholar] [CrossRef]
- Tapadia, P.; Wang, S.Q. Direct visualization of continuous simple shear in non-Newtonian polymeric fluids. Phys. Rev. Lett. 2006, 96, 016001. [Google Scholar] [CrossRef]
- Balmforth, N.J.; Frigaard, I.A.; Ovarlez, G. Yielding to stress: Recent devel- opments in viscoplastic fluid mechanics. Annu. Rev. Fluid Mech. 2014, 46, 121–146. [Google Scholar] [CrossRef]
- Pimenta, T.A.; Campos, A. Friction losses of newtonian and non-Newtonian fluids flowing in laminar regime in a helical coil. Exp. Therm. And Fluid Sci. 2012, 36, 194–204. [Google Scholar] [CrossRef] [Green Version]
- Liao, S.J. On the analytic solution of magnetohydrodynamic flows of non- Newtonian fluids over a stretching sheet. J. Fluid Mech. 2003, 488, 189–212. [Google Scholar] [CrossRef] [Green Version]
- Luikov, A.; Shulman, Z.; Puris, B. External convective mass transfer in non- Newtonian fluid: Part i. Int. J. Heat Mass Transf. 1969, 12, 377–391. [Google Scholar] [CrossRef]
- Li, B.; Zheng, L.; Zhang, X. Heat transfer in pseudo-plastic non-Newtonian fluids with variable thermal conductivity. Energy Convers. Manag. 2011, 52, 355–358. [Google Scholar] [CrossRef]
- Matsuhisa, S.; Bird, R.B. Analytical and numerical solutions for laminar flow of the non-Newtonian ellis fluid. AIChE J. 1965, 11, 588–595. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. The Fractal Geometry of Nature; WH Freeman: New York, NY, USA, 1982; p. 486. [Google Scholar]
- Falconer, K.J. The Geometry of Fractal Sets; Cambridge University Press: Cambridge, MA, USA, 1986. [Google Scholar]
- Feder, J. Fractals; Springer Science & Business Media: New York, NY, USA, 2013. [Google Scholar]
- Mainardi, F. Fractional calculus. In Fractals and Fractional Calculus in Continuum Mechanics; Springer: Berlin/Heidelberg, Germany, 1997; pp. 291–348. [Google Scholar]
- Addison, P.S. Fractals and Chaos: An illustrated Course; CRC Press: Boca Raton, FL, USA, 1997. [Google Scholar]
- Shui, H.; Zhou, H. Viscosity and fractal dimension of coal soluble con- stituents in solution. Fuel Process. Technol. 2004, 85, 1529–1538. [Google Scholar] [CrossRef]
- Hills, B.; Manoj, P.; Destruel, C. Nmr q-space microscopy of concentrated oil-in-water emulsions. Magn. Reson. Imaging 2000, 18, 319–333. [Google Scholar] [CrossRef]
- Shiyan, A. Viscosity for fractal suspensions: Dependence on fractal dimen- sionality. Phys. Lett. A 1996, 220, 117–119. [Google Scholar] [CrossRef]
- Haider, L.; Snabre, P.; Boynard, M. Rheology and ultrasound scattering from aggregated red cell suspensions in shear flow. Biophys. J. 2004, 87, 2322–2334. [Google Scholar] [CrossRef] [Green Version]
- Heinen, M.; Schnyder, S.K.; Brady, J.F.; Löwen, H. Classical liquids in fractal dimension. Phys. Rev. Lett. 2015, 115, 097801. [Google Scholar] [CrossRef] [Green Version]
- Tarasov, V.E. Flow of fractal fluid in pipes: Non-integer dimensional space approach. Chaos Solitons Fractals 2014, 67, 26–37. [Google Scholar] [CrossRef] [Green Version]
- Tarasov, V.E. Anisotropic fractal media by vector calculus in non-integer dimensional space. J. Math. Phys. 2014, 55, 083510. [Google Scholar] [CrossRef] [Green Version]
- Kigami, J. Analysis on Fractals; Cambridge University Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Strichartz, R.S. Analysis on fractals. Not. AMS 1999, 46, 1199–1208. [Google Scholar]
- Strichartz, R.S. Differential equations on fractals. In Differential Equations on Fractals; Princeton University Press: Princeton, NJ, USA, 2018. [Google Scholar]
- Carpinteri, A.; Cornetti, P.; Kolwankar, K.M. Calculation of the tensile and flexural strength of disordered materials using fractional calculus. Chaos Solitons Fractals 2004, 21, 623–632. [Google Scholar] [CrossRef]
- Carpinteri, A.; Chiaia, B.; Cornetti, P. A disordered microstructure material model based on fractal geometry and fractional calculus. ZAMM-J. Appl. Math. Mech. Angew. Math. Mech. Appl. Math. Mech. 2004, 84, 128–135. [Google Scholar] [CrossRef]
- Yang, X.J.; Srivastava, H.; He, J.H.; Baleanu, D. Cantor-type cylindrical-coordinate method for differential equations with local fractional derivatives. Phys. Lett. A 2013, 377, 1696–1700. [Google Scholar] [CrossRef]
- Yang, X.J.; Baleanu, D.; Tenreiro Machado, J. Systems of navier-stokes equations on cantor sets. Math. Probl. Eng. 2013, 2013. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.J. Advanced Local Fractional Calculus and Its Applications; World Science Publisher: Singapore, 2012. [Google Scholar]
- Ostoja-Starzewski, M.; Li, J. Fractal materials, beams, and fracture mechanics. Z. Angew. Math. Phys. 2009, 60, 1194–1205. [Google Scholar] [CrossRef]
- Li, J.; Ostoja-Starzewski, M. Fractal solids, product measures and fractional wave equations. Proc. R. Soc. A Math. Phys. Eng. Sci. 2009, 465, 2521–2536. [Google Scholar] [CrossRef]
- Li, J.; Ostoja-Starzewski, M. Micropolar continuum mechanics of fractal media. Int. J. Eng. Sci. 2011, 49, 1302–1310. [Google Scholar] [CrossRef]
- Tarasov, V.E. Continuous medium model for fractal media. Phys. Lett. A 2005, 336, 167–174. [Google Scholar] [CrossRef] [Green Version]
- Tarasov, V.E. Fractional hydrodynamic equations for fractal media. Ann. Phys. 2005, 318, 286–307. [Google Scholar] [CrossRef] [Green Version]
- Collins, J.C. Renormalization: An Introduction to Renormalization, the Renormalization Group and the Operator-Product Expansion; Cambridge University Press: Cambridge, MA, USA, 1985. [Google Scholar]
- Stillinger, F.H. Axiomatic basis for spaces with noninteger dimension. J. Math. Phys. 1977, 18, 1224–1234. [Google Scholar] [CrossRef]
- Palmer, C.; Starvinou, P.N. Equations of motion in a non-integer dimensional space. J. Phys. A Math. Gen. 2004, 37, 6987. [Google Scholar] [CrossRef]
- Tarasov, V.E. Vector calculus in non-integer dimensional space and its applications to fractal media. Commun. Nonlinear Sci. And Numerical Simul. 2015, 20, 360–374. [Google Scholar] [CrossRef] [Green Version]
- Tarasov, V.E. Poiseuille equation for steady flow of fractal fluid. Int. J. Mod. Phys. B 2016, 30, 1650128. [Google Scholar] [CrossRef]
- Balankin, A.S.; Mena, B.; Susarrey, O.; Samayoa, D. Steady laminar flow of fractal fluids. Phys. Lett. A 2017, 381, 623–628. [Google Scholar] [CrossRef]
- Bouchendouka, A.; Fellah, Z.E.A.; Larbi, Z.; Louna, Z.; Ogam, E.; Fellah, M.; Depollier, C. Fractal analysis of a non-Newtonian fluid flow in a rough-walled pipe. Materials 2022, 15, 3700. [Google Scholar] [CrossRef]
- Shapovalov, V. On the applicability of the ostwald?de waele model in solving applied problems. J. Eng. Phys. Thermophys. 2017, 90, 1213–1218. [Google Scholar] [CrossRef]
- Gabrys, E.; Rybaczuk, M.; Kedzia, A. Blood flow simulation through fractal models of circulatory system. Chaos Solitons Fractals 2006, 27, 1–7. [Google Scholar] [CrossRef]
- Jayalalitha, G.; Deviha, V.S.; Uthayakumar, R. Fractal model for blood flow in cardiovascular system. Comput. Biol. Med. 2008, 38, 684–693. [Google Scholar] [CrossRef]
- Stieger, M. The rheology handbook-for users of rotational and oscillatory rheometers. Appl. Rheol. 2002, 12, 232. [Google Scholar] [CrossRef]
- Singh, R.P.; Heldman, D.R. Introduction to Food Engineering; Gulf Professional Publishing: Burlington, MA, USA, 2001. [Google Scholar]
- Barnes, H.A.; Hutton, J.F.; Walters, K. An Introduction to Rheology; Elsevier: Amsterdam, The Netherlands, 1989. [Google Scholar]
- Painter, P.C.; Coleman, M.M. Fundamentals of Polymer Science: An Introductory Text; Routledge: London, UK, 2019. [Google Scholar]
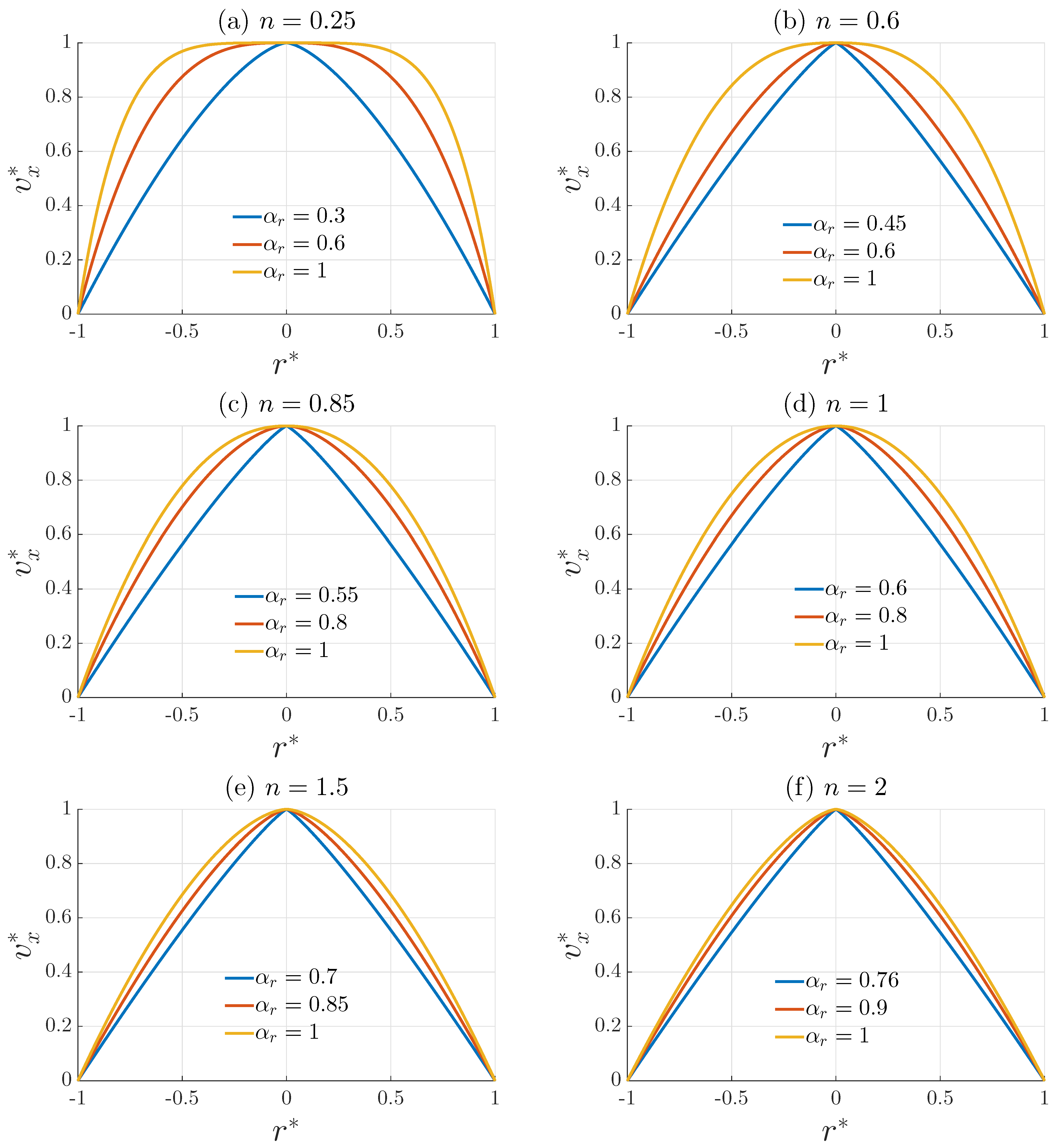
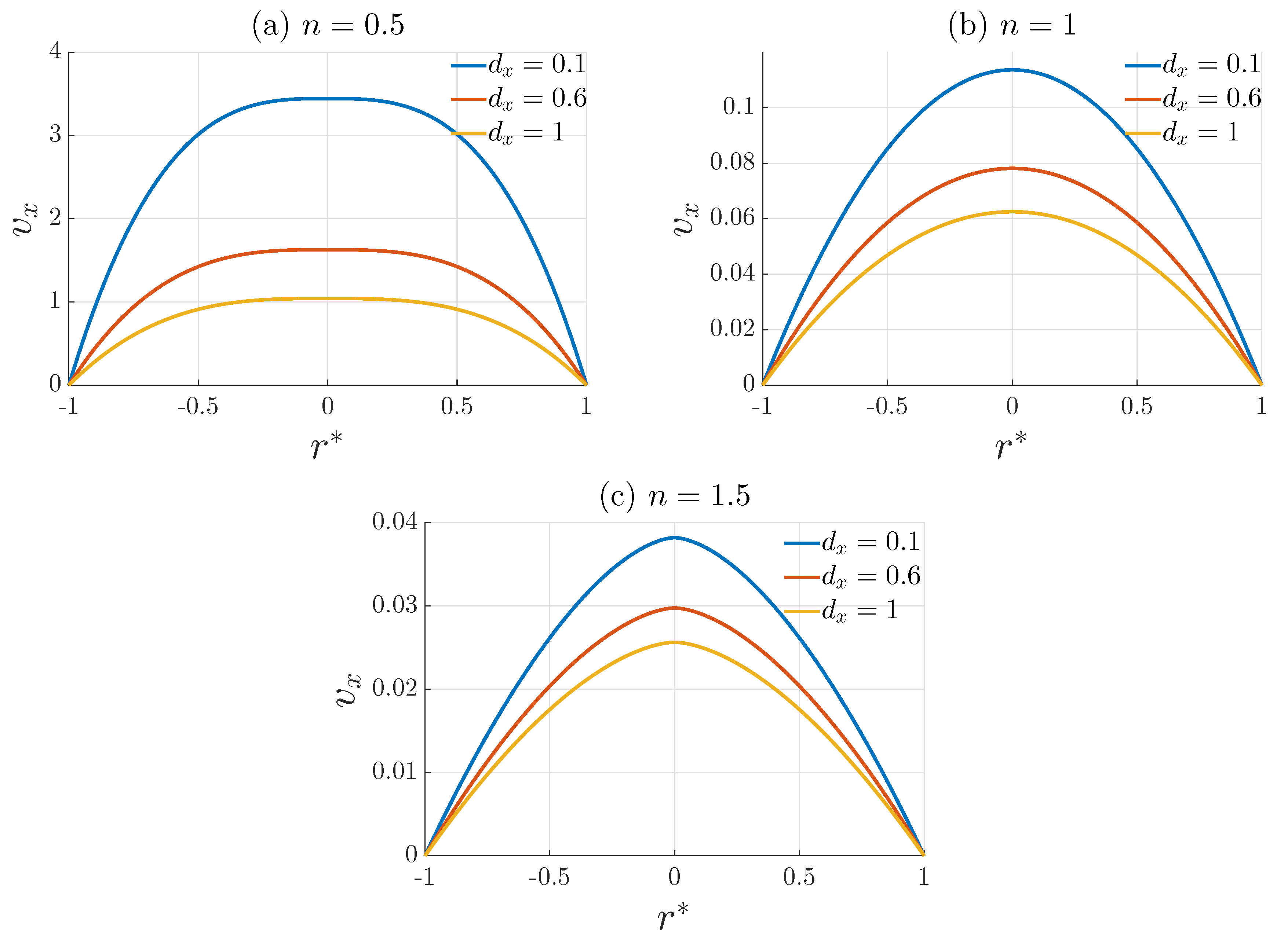
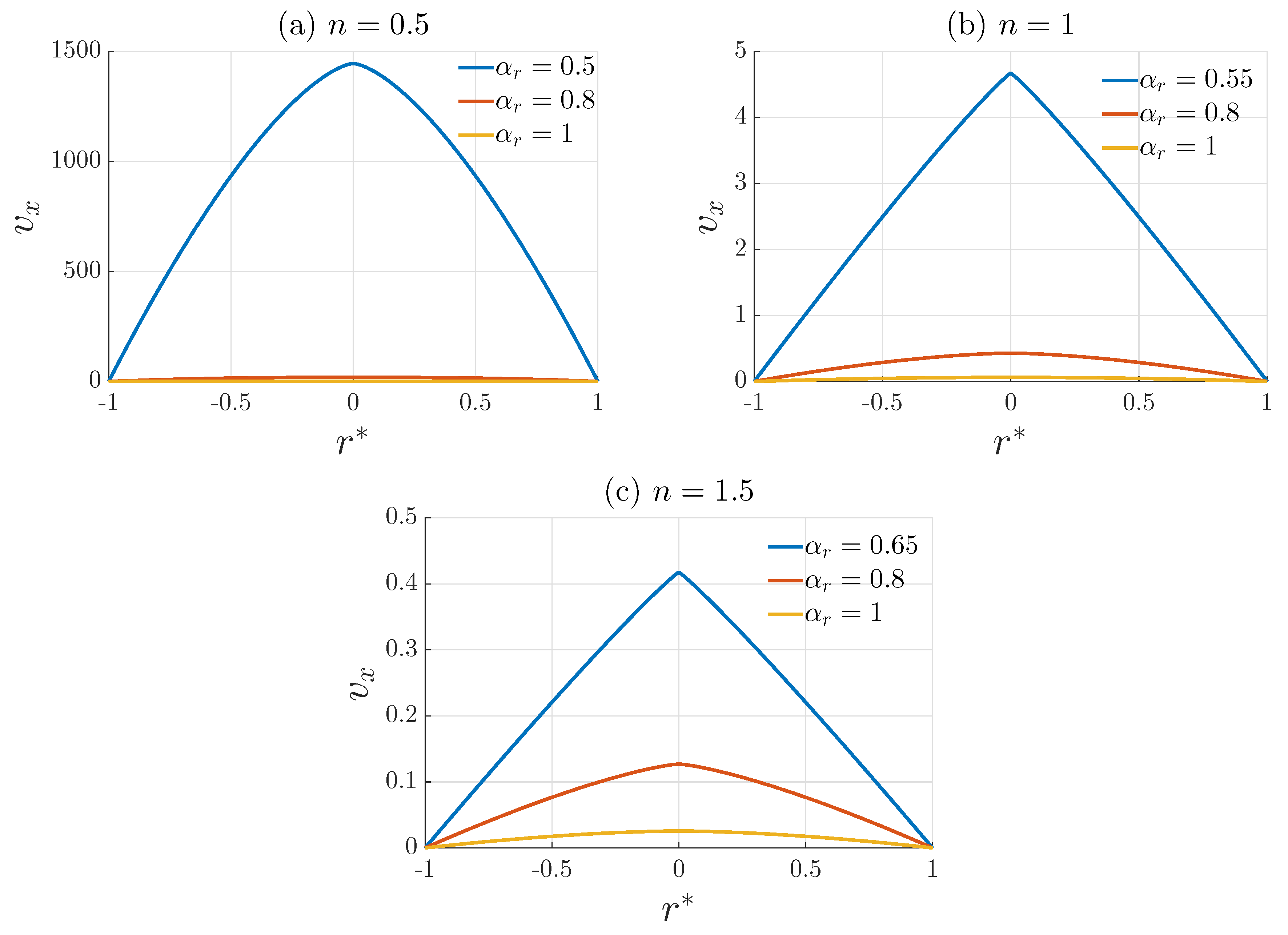
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bouchendouka, A.; Fellah, Z.E.A.; Larbi, Z.; Ongwen, N.O.; Ogam, E.; Fellah, M.; Depollier, C. Flow of a Self-Similar Non-Newtonian Fluid Using Fractal Dimensions. Fractal Fract. 2022, 6, 582. https://doi.org/10.3390/fractalfract6100582
Bouchendouka A, Fellah ZEA, Larbi Z, Ongwen NO, Ogam E, Fellah M, Depollier C. Flow of a Self-Similar Non-Newtonian Fluid Using Fractal Dimensions. Fractal and Fractional. 2022; 6(10):582. https://doi.org/10.3390/fractalfract6100582
Chicago/Turabian StyleBouchendouka, Abdellah, Zine El Abiddine Fellah, Zakaria Larbi, Nicholas O. Ongwen, Erick Ogam, Mohamed Fellah, and Claude Depollier. 2022. "Flow of a Self-Similar Non-Newtonian Fluid Using Fractal Dimensions" Fractal and Fractional 6, no. 10: 582. https://doi.org/10.3390/fractalfract6100582
APA StyleBouchendouka, A., Fellah, Z. E. A., Larbi, Z., Ongwen, N. O., Ogam, E., Fellah, M., & Depollier, C. (2022). Flow of a Self-Similar Non-Newtonian Fluid Using Fractal Dimensions. Fractal and Fractional, 6(10), 582. https://doi.org/10.3390/fractalfract6100582









