A Novel Nonlinear Pseudorandom Sequence Generator for the Fractal Function
Abstract
1. Introduction
- All chaotic-based cryptographic algorithms use dynamic systems defined on the set of real numbers and are therefore difficult to implement;
- The security and performance of chaos-based methods are rarely tested by researchers using standard tools of cryptography.
- We propose a pseudo-random sequence generator based on the non-linear chaotic systems with the lambda fractal function.
- Sequences generated by PRSG pass 16 rigorous tests from the National Institute of Standards and Technology (NIST), which has developed the most authoritative pseudo-random sequence standard detection tool [38].
- We propose a data processor based on the matrix operations for the secondary encryption, which reduces the data characteristics of the ciphertext sequences, producing a more balanced distribution of 0 s and 1 s.
2. Related Work
2.1. Random Sequence Generator
2.2. Typical Nonlinear Sequence Generators
2.3. Generators Based on the Non-Linear Chaotic Systems
3. Method
3.1. Nonlinear Generator
3.1.1. Theoretical Foundations
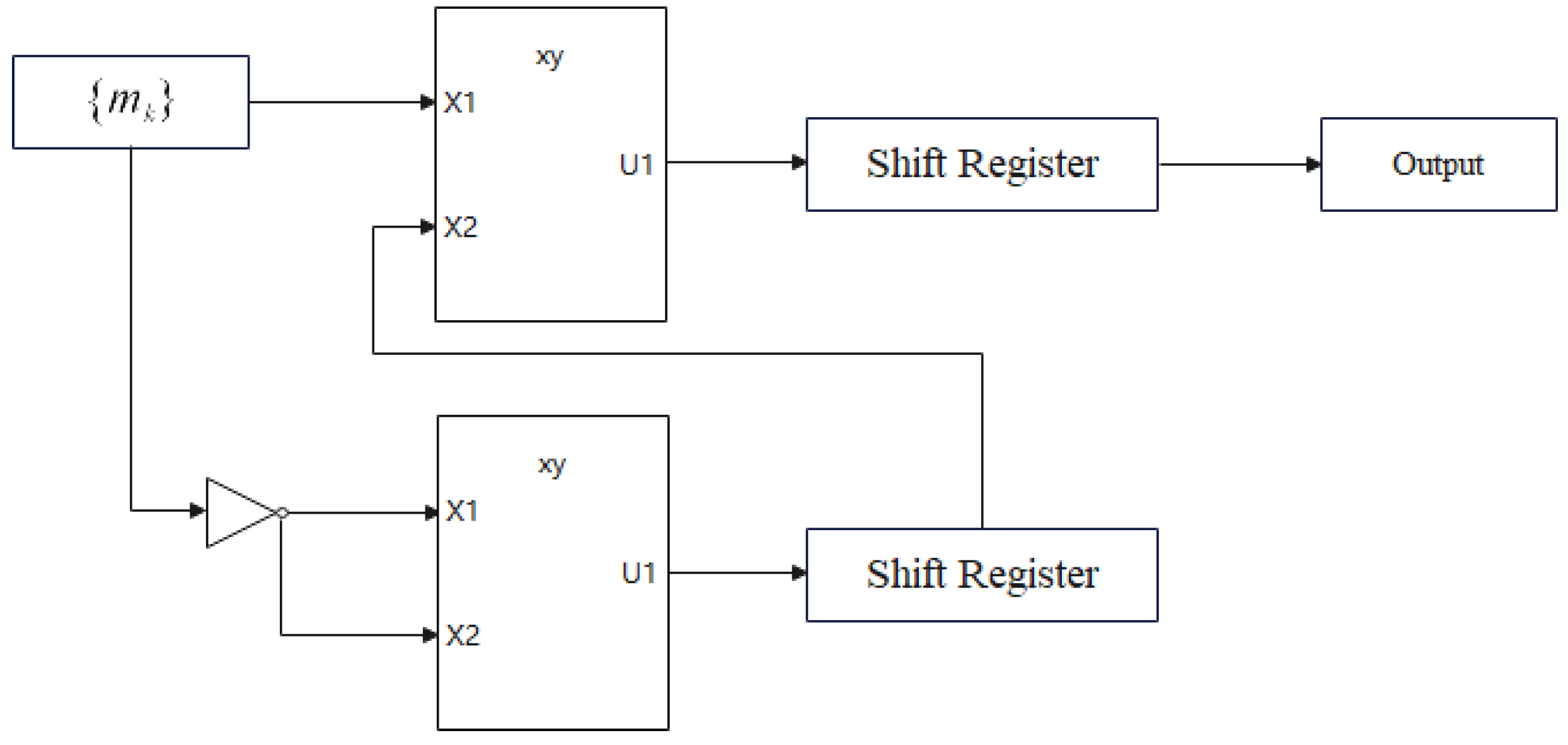
3.1.2. Implementation
- The m-LFSR reads the and generates the new state sequence ;
- Input the to the lambda fractal function and output sequence ;
- The shift register reads and generates the new state sequence ;
- Output the state sequence and perform bitwise AND operation ; then, store in the register;
- Read the register state sequence and perform a bit-by-bit XOR operation to generate the new element ;
- The shift register is shifted to the left by one bit, and is used as the return value of the feedback function to enter the rightmost end;
- Output as the pseudorandom number.
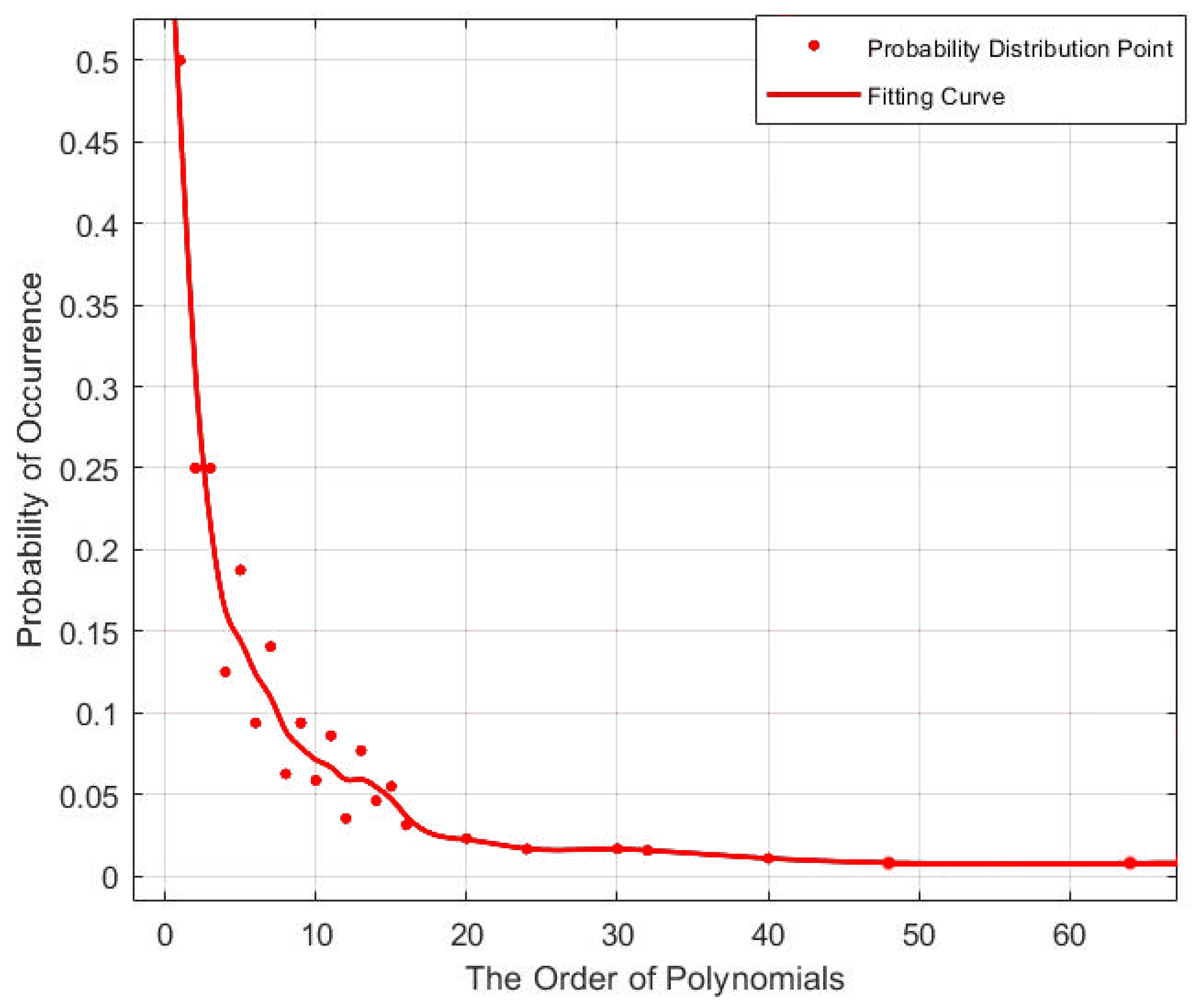
3.1.3. Period Estimation
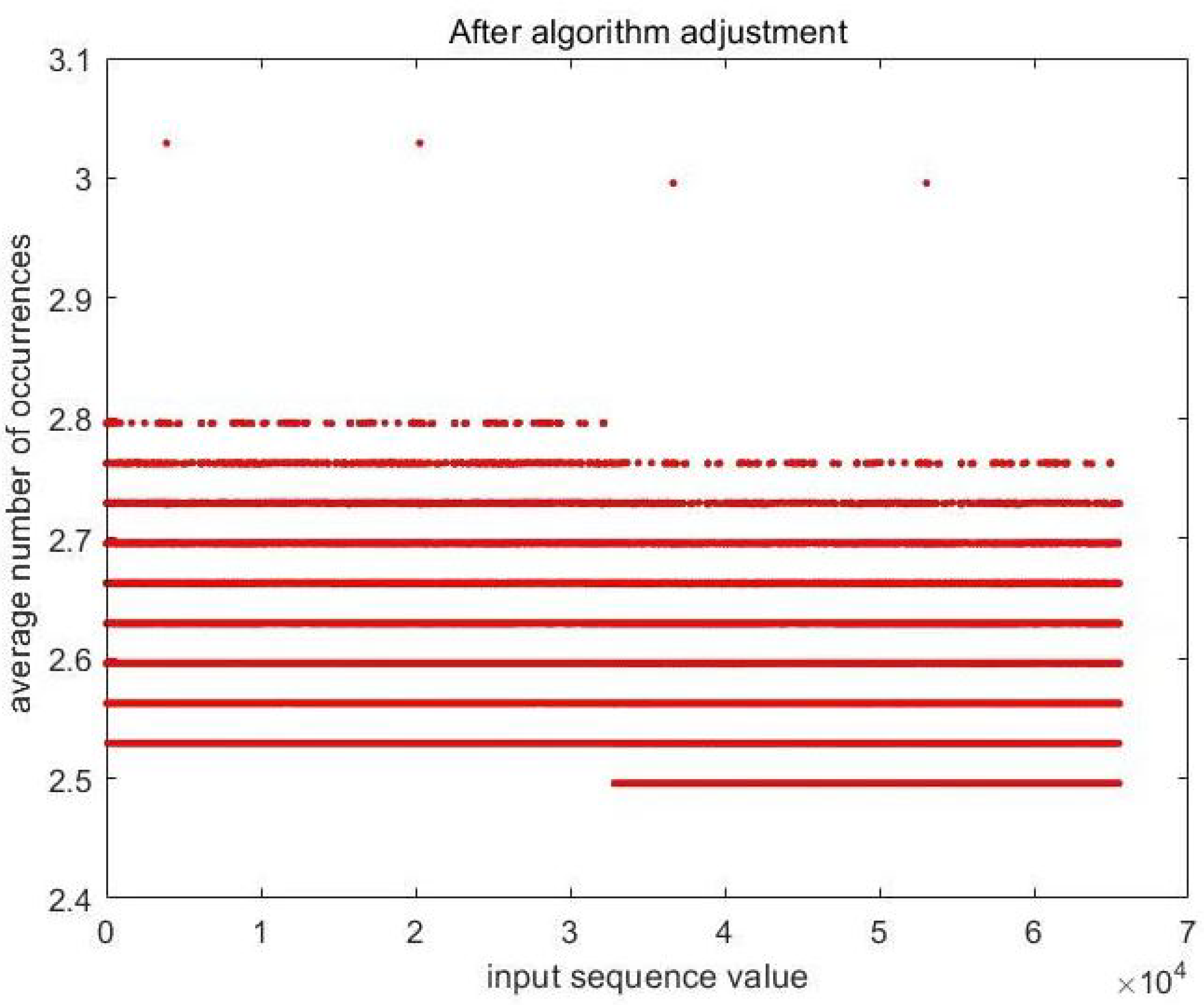
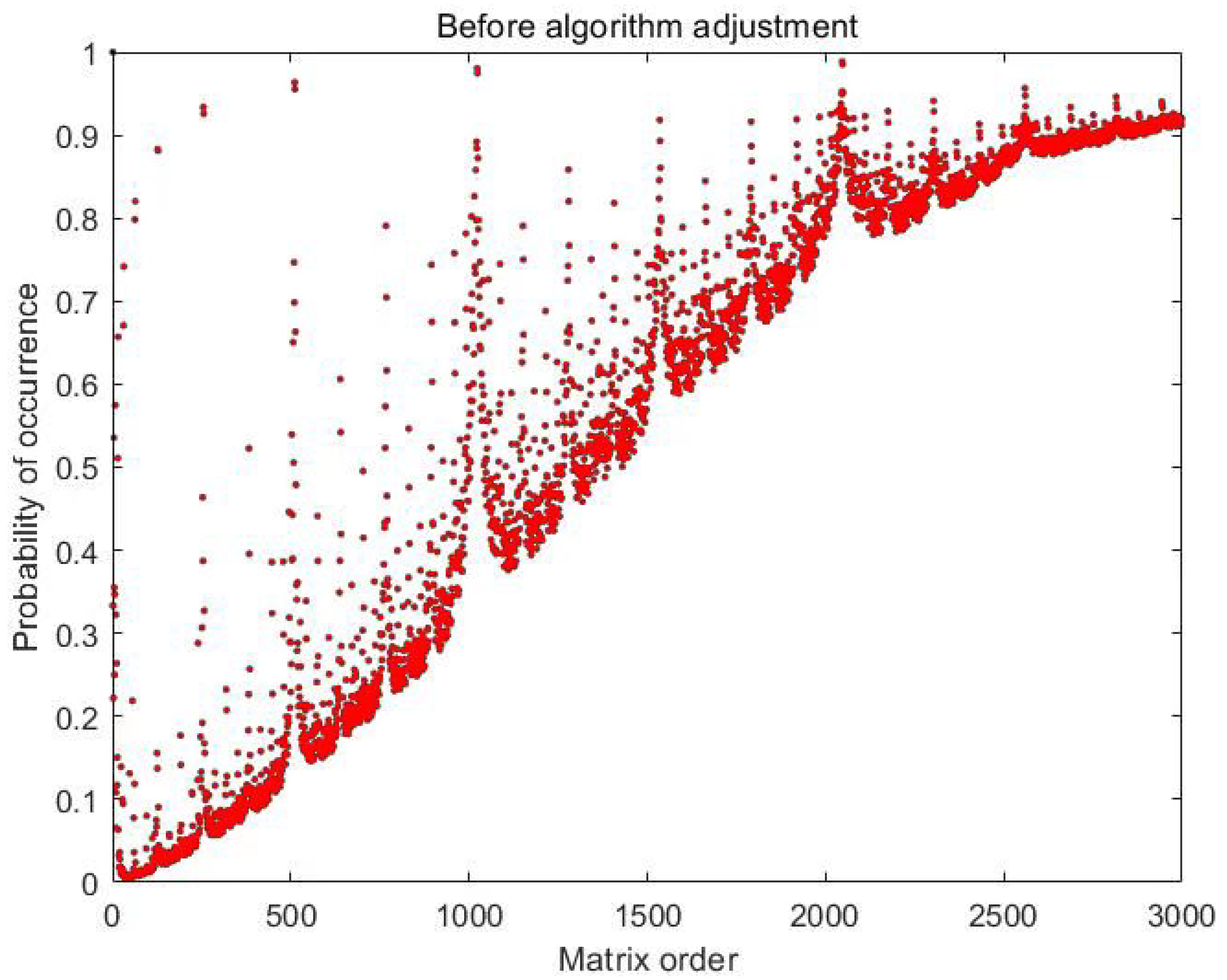
3.2. Data Processor
3.2.1. Theoretical Foundations
3.2.2. Implementation
3.3. Security
- Record the identifier of the communication object;
- Record the state of the nonlinear generator at the beginning and end of the communication, which are the seeds of this and the next loop, respectively;
- The nonlinear generator starts to work when it receives the communication requests and if the verification of the communication object fails, record the state of the linear generator and the object identifier sending the communication request.
- S records the device identifier of the device requesting communication and then checks whether the device is legal;
- If R is not in the list of objects that are allowed to communicate, S does not respond to the communication request and then records the state of the nonlinear generator and the identifier of R;
- If R is in the list of objects allowed to communicate, S responds to the communication request and then updates the seeds with F (we cannot rule out that R is masquerading as the legitimate device F).
4. Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Initial input to the generator, which are the sequences of booleans | |
| Characteristic polynomial of the linear feedback shift register | |
| The feedback state of i-stage | |
| The greatest common factor of a and b | |
| Complex parameters | |
| Sequence | |
| Mathematical expectations for X | |
| The plaintext suspicion degree | |
| Space of plaintext and ciphertext | |
| Sequences of plaintext and ciphertext | |
| The mathematical expectation of traversing the sequence entropy | |
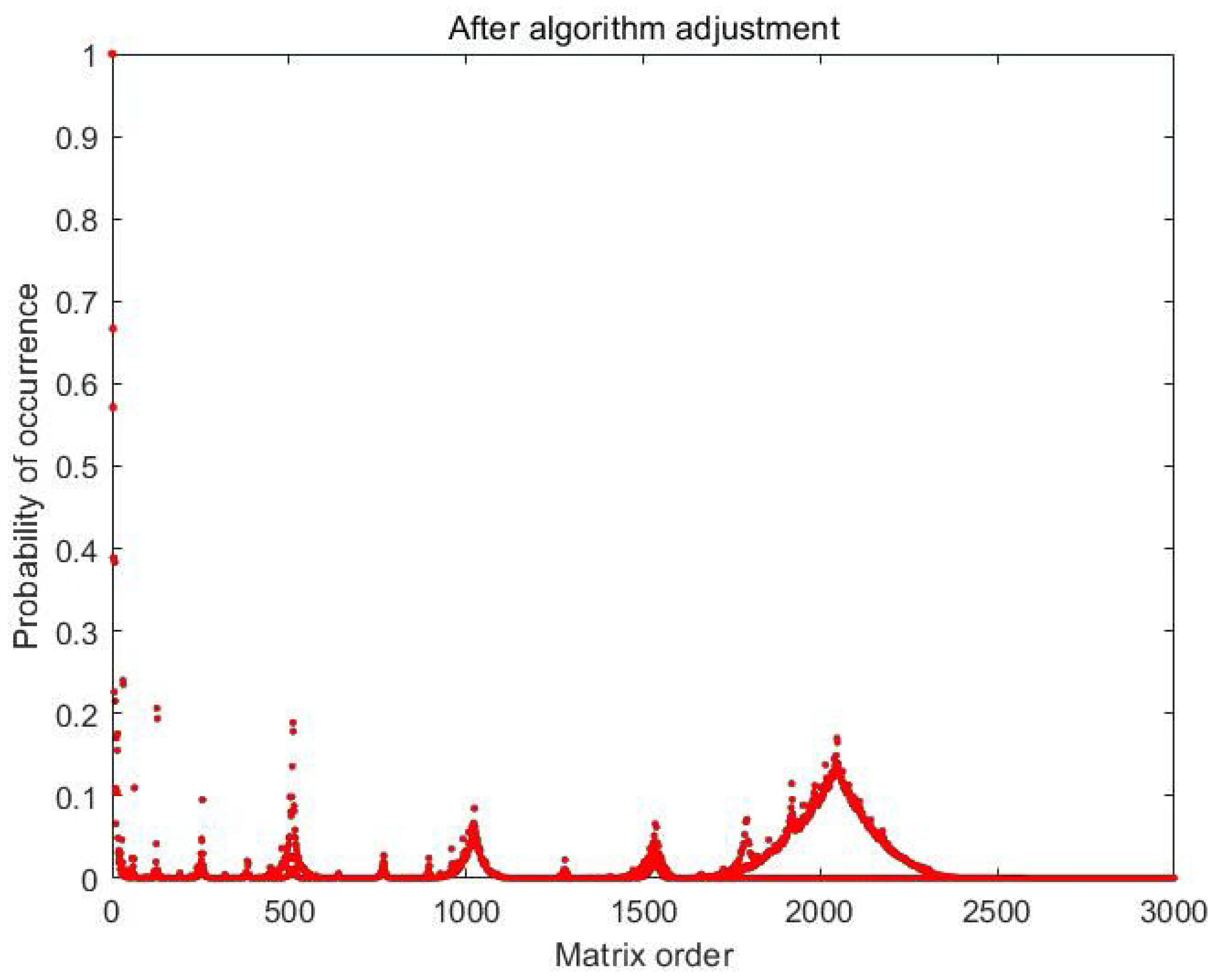
| The position and width of the peak |
Appendix A. Algorithm
| Algorithm A1: The Fractal Function |
 |
| Algorithm A2: The Nonlinear Pseudorandom Sequence Generator |
 |
| Algorithm A3: Data Processor |
 |
Appendix B. Code
References
- Topuzoğlu, A.; Winterhof, A. Pseudorandom sequences. In Topics in Geometry, Coding Theory and Cryptography; Springer: Berlin/Heidelberg, Germany, 2006; pp. 135–166. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Shannon, C.E. Communication theory of secrecy systems. Bell Syst. Tech. J. 1949, 28, 656–715. [Google Scholar] [CrossRef]
- Sarwate, D.V.; Pursley, M.B. Crosscorrelation properties of pseudorandom and related sequences. Proc. IEEE 1980, 68, 593–619. [Google Scholar] [CrossRef]
- Shamir, A. On the generation of cryptographically strong pseudorandom sequences. ACM Trans. Comput. Syst. (TOCS) 1983, 1, 38–44. [Google Scholar] [CrossRef]
- Blum, M.; Micali, S. How to generate cryptographically strong sequences of pseudorandom bits. SIAM J. Comput. 1984, 13, 850–864. [Google Scholar] [CrossRef]
- Ko, K.I. On the notion of infinite pseudorandom sequences. Theor. Comput. Sci. 1986, 48, 9–33. [Google Scholar] [CrossRef]
- Bardell, P.H. Analysis of cellular automata used as pseudorandom pattern generators. In Proceedings of the International Test Conference, Washington, DC, USA, 10–14 September 1990; pp. 762–768. [Google Scholar]
- Gong, G.; Berson, T.A.; Stinson, D.R. Elliptic curve pseudorandom sequence generators. In Proceedings of the International Workshop on Selected Areas in Cryptography, Kingston, ON, Canada, 9–10 August 1999; pp. 34–48. [Google Scholar]
- Zierler, N. Linear recurring sequences. J. Soc. Ind. Appl. Math. 1959, 7, 31–48. [Google Scholar] [CrossRef]
- Massey, J. Shift-register synthesis and BCH decoding. IEEE Trans. Inf. Theory 1969, 15, 122–127. [Google Scholar] [CrossRef]
- Key, E. An analysis of the structure and complexity of nonlinear binary sequence generators. IEEE Trans. Inf. Theory 1976, 22, 732–736. [Google Scholar] [CrossRef]
- Persons, C.; Brandon, M. Linear and Nonlinear Correlators for Pseudorandom Signal Detection: A Theoretical and Experimental Study of the Output Characteristics of Correlators for Active Sonar Systems; Technical Report; Navy Electronics Lab: San Diego, CA, USA, 1963. [Google Scholar]
- Simpson, H. A sampled-data nonlinear filter. In Proceedings of the Institution of Electrical Engineers; IET Digital Library: London, UK, 1965; Volume 112, pp. 1187–1196. [Google Scholar]
- Lewis, T.G.; Payne, W.H. Generalized feedback shift register pseudorandom number algorithm. J. ACM 1973, 20, 456–468. [Google Scholar] [CrossRef]
- Zeng, K.; Yang, C.H.; Wei, D.Y.; Rao, T. Pseudorandom bit generators in stream-cipher cryptography. Computer 1991, 24, 8–17. [Google Scholar] [CrossRef]
- Bensikaddour, E.H.; Bentoutou, Y.; Taleb, N. Satellite image encryption method based on AES-CTR algorithm and GEFFE generator. In Proceedings of the 2017 8th International Conference on Recent Advances in Space Technologies (RAST), Istanbul, Turkey, 19–22 June 2017; pp. 247–252. [Google Scholar]
- Salman, Z.I. Attacking of Geffe Generator by Solving Linear Equations System of the Generated Sequence. J. Univ. Babylon 2014, 22, 1516–1524. [Google Scholar]
- Din, M.; Bhateja, A.K.; Ratan, R. Cryptanalysis of geffe generator using genetic algorithm. In Proceedings of the Third International Conference on Soft Computing for Problem Solving, New Delhi, India, 17–24 October 2014; pp. 509–515. [Google Scholar]
- Khader, A.S.; Lai, D. Preventing man-in-the-middle attack in Diffie-Hellman key exchange protocol. In Proceedings of the 2015 22nd International Conference on Telecommunications (ICT), Sydney, Australia, 27–29 April 2015; pp. 204–208. [Google Scholar]
- Elineau, G.; Wiesbeck, W. A new JK flip-flop for synchronizers. IEEE Trans. Comput. 1977, 26, 1277–1279. [Google Scholar] [CrossRef]
- Hirota, K.; Pedrycz, W. Designing sequential systems with fuzzy JK flip-flops. Fuzzy Sets Syst. 1991, 39, 261–278. [Google Scholar] [CrossRef]
- Law, F.K.; Uddin, M.R.; Chen, A.T.C.; Nakarmi, B. Positive edge-triggered JK flip-flop using silicon-based micro-ring resonator. Opt. Quantum Electron. 2020, 52, 1–12. [Google Scholar] [CrossRef]
- Zenner, E. On the efficiency of the clock control guessing attack. In Proceedings of the International Conference on Information Security and Cryptology, Melbourne, Australia, 3–5 July 2002; pp. 200–212. [Google Scholar]
- Sadkhan, S.B.; Hamza, R.M. A study of Algebraic Attack and proposed developed clock control stream cipher. J. Babylon Univ. Appl. Sci. 2014, 22, 622–633. [Google Scholar]
- Sadkhan, S.B. A proposed Development of Clock Control Stream Cipher based on Suitable Attack. In Proceedings of the 2020 1st. Information Technology to Enhance e-Learning and Other Application (IT-ELA), Baghdad, Iraq, 12–13 July 2020; pp. 165–170. [Google Scholar]
- Agarwal, S. Designing a pseudo-random bit generator using generalized cascade fractal function. Chaos Theory Appl. 2021, 3, 11–19. [Google Scholar] [CrossRef]
- Teh, J.S.; Alawida, M.; Sii, Y.C. Implementation and practical problems of chaos-based cryptography revisited. J. Inf. Secur. Appl. 2020, 50, 102421. [Google Scholar] [CrossRef]
- Yang, T.; Wu, C.W.; Chua, L.O. Cryptography based on chaotic systems. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 1997, 44, 469–472. [Google Scholar] [CrossRef]
- Baptista, M. Cryptography with chaos. Phys. Lett. A 1998, 240, 50–54. [Google Scholar] [CrossRef]
- Dachselt, F.; Schwarz, W. Chaos and cryptography. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2001, 48, 1498–1509. [Google Scholar] [CrossRef]
- Muthukumar, P.; Balasubramaniam, P. Feedback synchronization of the fractional order reverse butterfly-shaped chaotic system and its application to digital cryptography. Nonlinear Dyn. 2013, 74, 1169–1181. [Google Scholar] [CrossRef]
- Hsiao, H.I.; Lee, J. Fingerprint image cryptography based on multiple chaotic systems. Signal Process. 2015, 113, 169–181. [Google Scholar] [CrossRef]
- Akgul, A.; Arslan, C.; Aricioglu, B. Design of an interface for random number generators based on integer and fractional order chaotic systems. Chaos Theory Appl. 2019, 1, 1–18. [Google Scholar]
- Kocarev, L. Chaos-based cryptography: A brief overview. IEEE Circuits Syst. Mag. 2001, 1, 6–21. [Google Scholar] [CrossRef]
- Li, S.; Liu, Y.; Ren, F.; Yang, Z. Design of a high throughput pseudo-random number generator based on discrete hyper-chaotic system. IEEE Trans. Circuits Syst. II Express Briefs 2022. [Google Scholar] [CrossRef]
- Nardo, L.G.; Nepomuceno, E.G.; Bastos, G.T.; Santos, T.A.; Butusov, D.N.; Arias-Garcia, J. A reliable chaos-based cryptography using Galois field. Chaos Interdiscip. J. Nonlinear Sci. 2021, 31, 091101. [Google Scholar] [CrossRef]
- Olver, F.W.; Lozier, D.W.; Boisvert, R.F.; Clark, C.W. NIST Handbook of Mathematical Functions Hardback and CD-ROM; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Fischer, V.; Drutarovskỳ, M. True random number generator embedded in reconfigurable hardware. In Proceedings of the International Workshop on Cryptographic Hardware and Embedded Systems, Redwood Shores, CA, USA, 13–15 August 2002; pp. 415–430. [Google Scholar]
- Holman, W.T.; Connelly, J.A.; Dowlatabadi, A.B. An integrated analog/digital random noise source. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 1997, 44, 521–528. [Google Scholar] [CrossRef]
- Park, K.H.; Park, S.M.; Choi, B.G.; Kim, J.B.; Son, K.J. High rate true random number generator using beta radiation. AIP Conf. Proc. 2020, 2295, 020020. [Google Scholar]
- Huo, J.; Xu, Y.; Chen, Y.; Cui, W.; Li, W.; Zhang, Z.; Han, D.; Wang, Y.; Wang, J. An X-ray CCD signal generator with true random arrival time. Nucl. Electron. Detect. Technol. 2011, 31, 174–177. [Google Scholar]
- Zheng, Z.; Zhang, Y.; Huang, W.; Yu, S.; Guo, H. 6 Gbps real-time optical quantum random number generator based on vacuum fluctuation. Rev. Sci. Instrum. 2019, 90, 043105. [Google Scholar] [CrossRef] [PubMed]
- Shi, Y.; Chng, B.; Kurtsiefer, C. Random numbers from vacuum fluctuations. Appl. Phys. Lett. 2016, 109, 041101. [Google Scholar] [CrossRef]
- Cusick, T.W.; Stanica, P. Chapter 2—Fourier Analysis of Boolean Functions. In Cryptographic Boolean Functions and Applications, 2nd ed.; Cusick, T.W., Stanica, P., Eds.; Academic Press: Cambridge, MA, USA, 2017; pp. 7–29. [Google Scholar] [CrossRef]
- Lei, T. Similarity between the Mandelbrot set and Julia sets. Commun. Math. Phys. 1990, 134, 587–617. [Google Scholar] [CrossRef]
- Peitgen, H.O.; Jürgens, H.; Saupe, D. Chaos and Fractals: New Frontiers of Science; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Shand, M.; Vuillemin, J. Fast implementations of RSA cryptography. In Proceedings of the IEEE 11th Symposium on Computer Arithmetic, Windsor, ON, Canada, 29 June–2 July 1993; pp. 252–259. [Google Scholar]
- Wiener, M.J. Cryptanalysis of short RSA secret exponents. IEEE Trans. Inf. Theory 1990, 36, 553–558. [Google Scholar] [CrossRef]
- Boneh, D. Twenty years of attacks on the RSA cryptosystem. Not. AMS 1999, 46, 203–213. [Google Scholar]
- Kocher, P.C. Timing attacks on implementations of Diffie-Hellman, RSA, DSS, and other systems. In Proceedings of the Annual International Cryptology Conference, Santa Barbara, CA, USA, 18–22 August 1996; pp. 104–113. [Google Scholar]
- Zhang, Z. Fundamentals of Modern Cryptography; Beijing University of Posts and Telecommunications Press: Beijing, China, 2004. [Google Scholar]
- Yan, S.Y. Computational Number Theory and Modern Cryptography; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Courtois, N.T.; Meier, W. Algebraic attacks on stream ciphers with linear feedback. In Proceedings of the International Conference on the Theory and Applications of Cryptographic Techniques, Warsaw, Poland, 4–8 May 2003; pp. 345–359. [Google Scholar]
- Courtois, N.T.; O’Neil, S.; Quisquater, J.J. Practical algebraic attacks on the Hitag2 stream cipher. In Proceedings of the International Conference on Information Security, Orlando, FL, USA, 13–16 July 2009; pp. 167–176. [Google Scholar]
- Meier, W.; Staffelbach, O. Fast correlation attacks on certain stream ciphers. J. Cryptol. 1989, 1, 159–176. [Google Scholar] [CrossRef]
- Chose, P.; Joux, A.; Mitton, M. Fast correlation attacks: An algorithmic point of view. In Proceedings of the International Conference on the Theory and Applications of Cryptographic Techniques, Amsterdam, The Netherlands, 28 April–2 May 2002; pp. 209–221. [Google Scholar]
- Biham, E.; Kocher, P.C. A known plaintext attack on the PKZIP stream cipher. In Proceedings of the International Workshop on Fast Software Encryption, Leuven, Belgium, 14–16 December 1994; pp. 144–153. [Google Scholar]
- Klapper, A.; Goresky, M. Cryptanalysis based on 2-adic rational approximation. In Proceedings of the Annual International Cryptology Conference, Santa Barbara, CA, USA, 27–31 August 1995; pp. 262–273. [Google Scholar]
- Carlet, C.; Feng, K. An infinite class of balanced functions with optimal algebraic immunity, good immunity to fast algebraic attacks and good nonlinearity. In Proceedings of the International Conference on the Theory and Application of Cryptology and Information Security, Melbourne, Australia, 7–11 December 2008; pp. 425–440. [Google Scholar]
- Aqel, M.J.; Alqadi, Z.A.; El Emary, I.M. Analysis of stream cipher security algorithm. J. Inf. Comput. Sci. 2007, 2, 288–298. [Google Scholar]
- Jiang, H.; Li, C.; Fan, J. Research on Pseudo-Random Characteristics of New Random Components. In Proceedings of the 2019 International Conference on Artificial Intelligence and Advanced Manufacturing (AIAM), Dublin, Ireland, 17–19 October 2019; pp. 163–167. [Google Scholar] [CrossRef]
- Siswanto, M.; Witjaksono, G.; Soeheila, M.; Hamdan, Z. Study on the effects of characteristic polynomial in LFSR for randomness quality. In Proceedings of the International Conference on Advanced Science, Engineering and Information Technology (ICASEIT 2011), Daegu, Korea, 20–22 April 2011. [Google Scholar]





| Test Items | p-Value | p-Value | p-Value |
|---|---|---|---|
| Frequency Test | 0.364718 | 0.214125 | 0.446560 |
| Frequency Test within a Block | 0.716768 | 0.633599 | 0.729238 |
| Cumulative Sums Test | 0.528209 | 0.446560 | 0.550851 |
| Runs Test | 0.164068 | 0.265407 | 0.355647 |
| Test for the Longest Run of Ones in a Block | 0.323647 | 0.280352 | 0.393501 |
| Binary Matrix Rank Test | 0.122371 | 0.222959 | 0.114587 |
| Discrete Fourier Transform (Spectral) Test | 0.876181 | 0.723175 | 0.638315 |
| Non-overlapping Template Matching Test | 0.509980 | 0.645031 | 0.407472 |
| Overlapping Template Matching Test | 0.630870 | 0.693978 | 0.784372 |
| Maurer’s Universal Statistical Test | 0.513756 | 0.501741 | 0.489264 |
| Approximate Entropy Test | 0.135386 | 0.254827 | 0.221754 |
| Random Excursions Test | 0.429587 | 0.578509 | 0.318043 |
| Random Excursions Variant Test | 0.395772 | 0.355201 | 0.451801 |
| Serial Test | 0.791572 | 0.666109 | 0.519752 |
| Linear Complexity Test | 0.204319 | 0.249184 | 0.218881 |
| Lempel–Ziv Compression Test | 0.199323 | 0.161428 | 0.173379 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, Y.; Wang, H.; Chang, C.; Lu, H.; Yang, F.; Wang, C. A Novel Nonlinear Pseudorandom Sequence Generator for the Fractal Function. Fractal Fract. 2022, 6, 589. https://doi.org/10.3390/fractalfract6100589
Feng Y, Wang H, Chang C, Lu H, Yang F, Wang C. A Novel Nonlinear Pseudorandom Sequence Generator for the Fractal Function. Fractal and Fractional. 2022; 6(10):589. https://doi.org/10.3390/fractalfract6100589
Chicago/Turabian StyleFeng, Yelai, Huaixi Wang, Chao Chang, Hongyi Lu, Fang Yang, and Chenyang Wang. 2022. "A Novel Nonlinear Pseudorandom Sequence Generator for the Fractal Function" Fractal and Fractional 6, no. 10: 589. https://doi.org/10.3390/fractalfract6100589
APA StyleFeng, Y., Wang, H., Chang, C., Lu, H., Yang, F., & Wang, C. (2022). A Novel Nonlinear Pseudorandom Sequence Generator for the Fractal Function. Fractal and Fractional, 6(10), 589. https://doi.org/10.3390/fractalfract6100589









