A Second-Order Adaptive Grid Method for a Singularly Perturbed Volterra Integrodifferential Equation
Abstract
1. Introduction
2. Preliminary Results
3. Truncation Error Analysis
4. Adaptive Grid and Convergence Analysis
5. Numerical Results and Discussion
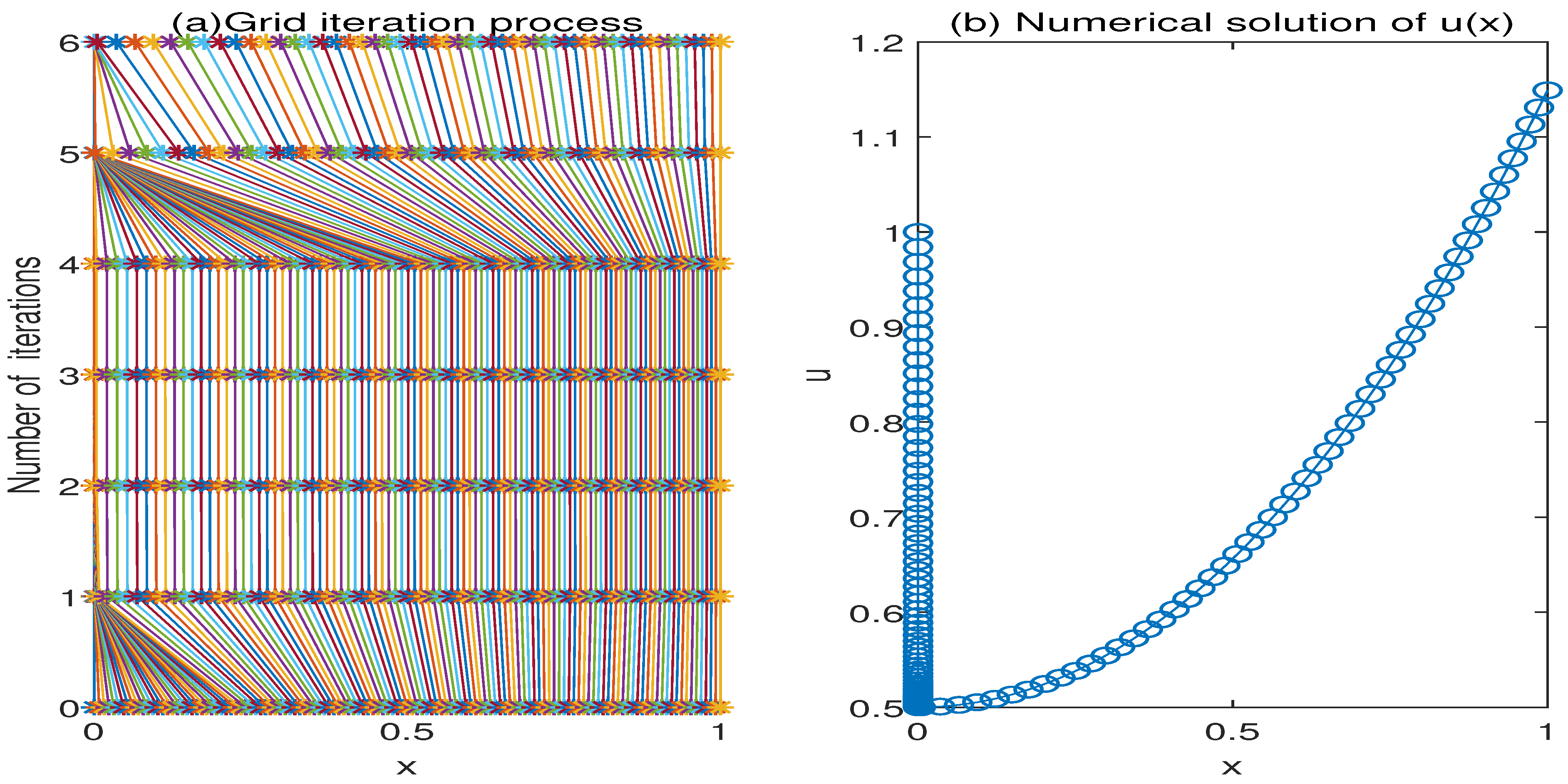
5.1. Mesh Generation Algorithm
| Algorithm 1: Adaptive grid algorithm |
Step 1. Provide an initial uniform mesh with N mesh intervals. Choose a constant that controls the algorithm terminates. Step 2. For a given grid , and the corresponding computed solution , set for each i and and for . Step 3. Define . If holds true, then go to Step 5. Otherwise go to Step 4. Step 4. For , let and be a linear interpolation function through knots . Then, generate a new mesh by for . Let and return to Step 2. Step 5. Take as the final calculation mesh and as the corresponding numerical solution. Then, stop iteration process. |
5.2. Numerical Experiments and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yapman, M.; Amiraliyev, G.M. A novel second-order fitted computational method for a singularly perturbed Volterra integro-differential equation. Int. J. Comput. Math. 2020, 97, 1293–1302. [Google Scholar] [CrossRef]
- Brunner, H. Collocation Methods for Volterra Integral and Related Functional Equations; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Rudenko, O.V. Nonlinear integro-differential models for intense waves in media like biological tissues and geostructures with complex internal relaxation-type dynamics. Acouset. Phys. 2014, 60, 398–404. [Google Scholar] [CrossRef]
- Bouchra, A. Qualitative analysis and simulation of a nonlinear integro-differential system modelling tumor-immune cells competition. Int. J. Biomath. 2018, 11, 1850104. [Google Scholar]
- de Gaetano, A.; Arino, O. Mathematical modelling of the intravenous glucose tolerance test. J. Math. Biol. 2000, 40, 136–168. [Google Scholar] [CrossRef] [PubMed]
- Abdul, I. Introduction to Integral Equations with Application; Wiley: New York, NY, USA, 1999. [Google Scholar]
- Amiraliyev, G.M.; Şevgin, S. Uniform difference method for singularly perturbed Volterra integro-differential equations. Appl. Math. Comput. 2005, 179, 731–741. [Google Scholar] [CrossRef]
- Salama, A.A.; Bakr, S.A. Difference schemes of exponential type for singularly perturbed Volterra integro-differential problems. Appl. Math. Model. 2007, 31, 866–879. [Google Scholar] [CrossRef]
- Ramos, J.I. Exponential techniques and implicit Runge-Kutta method for singularly-perturbed Volterra integro-differential equations. Neural Parallel. 2008, 16, 387–404. [Google Scholar]
- Şevgin, S. Numerical solution of a singularly perturbed Volterra integro-differential equation. Adv. Differ. Equations 2014, 2014, 171–196. [Google Scholar] [CrossRef]
- Iragi, B.C.; Munyakazi, J.B. A uniformly convergent numerical method for a singularly perturbed Volterra integro-differential equation. Int. J. Comput. Math. 2020, 97, 759–771. [Google Scholar] [CrossRef]
- Huang, J.; Cen, Z.; Xu, A.; Liu, L.-B. A posteriori error estimation for a singularly perturbed Volterra integro-differential equation. Numer. Algorthms 2020, 83, 549–563. [Google Scholar] [CrossRef]
- Kauthen, J.P. Implicit Runge-Kutta methods for some singularly perturbed Volterra integro-differential-algebraic equation. Appl. Numer. Math. 1993, 13, 125–134. [Google Scholar] [CrossRef]
- Kauthen, J.P. Implicit Runge-Kutta methods for singularly perturbed integro-differential systems. Appl. Numer. Math. 1995, 18, 201–210. [Google Scholar] [CrossRef]
- Kopteva, N.; Stynes, M. A robust adaptive method for a quasilinear one-dimensional convection-diffusion problem. SIAM J. Numer. Anal. 2001, 39, 1446–1467. [Google Scholar] [CrossRef]
- Linß, T. Analysis of a system of singularly perturbed convection-diffusion equations with strong coupling. SIAM J. Numer. Anal. 2009, 47, 1847–1862. [Google Scholar] [CrossRef]
- Roos, H.-G.; Stynes, M.; Tobiska, L. Robust Methods for Singularly Perturbed Differential Equations, 2nd ed.; Springer Series in Computational Mathematics; Springer: Berlin/Heidelberg, Germany, 2008; Volume 24. [Google Scholar]
- Kumar, S.S.; Vigo-Aguiar, J. Analysis of a nonlinear singularly perturbed Volterra integro-differential equation. J. Comput. Appl. Math. 2021, 404, 113410. [Google Scholar]
- Long, G.; Liu, L.-B.; Huang, Z. Richardson extrapolation method on an adaptive grid for singularly perturbed Volterra integro-differential equations. Numer. Funct. Anal. Optim. 2021, 42, 739–757. [Google Scholar] [CrossRef]
- Luo, X.; Yang, N.; Tong, Q. A Novel Second-Order Adaptive Grid Method for Singularly Perturbed Convection-Diffusion Equations. J. Uncertain Syst. 2021, 14, 2150026. [Google Scholar] [CrossRef]
- Amiraliyev, G.M.; Yilmaz, B. Fitted difference method for a singularly perturbed initial value problem. Int. J. Math. Comput. 2014, 22, 1–10. [Google Scholar]
- Kudu, M.; Amirali, I.; Amiraliyev, G.M. A finite-difference method for a singularly perturbed delay integro-differential equation. J. Comput. Appl. Math. 2016, 308, 379–390. [Google Scholar] [CrossRef]
- Mackenzie, J. Uniform convergence analysis of an upwind finite-difference approximation of a convection-diffusion boundary value problem on an adaptive grid. IMA J. Numer. Anal. 1999, 19, 233–249. [Google Scholar] [CrossRef]
- Beckett, G.; Mackenzie, J.A. Convergence analysis of finite difference approximations to a singularly perturbed boundary value problem. Appl. Numer. Math 2000, 35, 87–109. [Google Scholar] [CrossRef]
- Kopteva, N.; Madden, N.; Stynes, M. Grid equidistribution for reaction-diffusion problems in one dimension. Numer. Algorthms 2005, 40, 305–322. [Google Scholar] [CrossRef]
- Qiu, Y.; Sloan, D.M.; Tang, T. Numerical solution of a singularly perturbed two point boundary value problem using equidistribution: Analysis of convergence. J. Comput. Appl. Math. 2000, 116, 121–143. [Google Scholar] [CrossRef]
- Chen, Y. Uniform pointwise convergence for a singularly perturbed problem using arc-length equidistribution. J. Comput. Appl. Math. 2003, 159, 25–34. [Google Scholar] [CrossRef][Green Version]

| 1.95 | 1.98 | 1.99 | 1.99 | 2.00 | - | ||
| 1 | 1 | 1 | 1 | 1 | 1 | ||
| 1.60 | 1.78 | 1.96 | 1.93 | 1.97 | - | ||
| 2 | 2 | 1 | 1 | 1 | 1 | ||
| 1.79 | 1.78 | 1.69 | 1.64 | 1.75 | - | ||
| 3 | 2 | 2 | 2 | 2 | 1 | ||
| 1.80 | 1.89 | 1.99 | 1.87 | 1.85 | - | ||
| 3 | 3 | 2 | 2 | 3 | 2 | ||
| 1.75 | 1.99 | 1.94 | 1.99 | 1.99 | - | ||
| 4 | 4 | 3 | 3 | 2 | 2 | ||
| 1.97 | 1.85 | 2.01 | 1.96 | 1.99 | - | ||
| 5 | 4 | 4 | 3 | 3 | 3 |
| N | ||||||
|---|---|---|---|---|---|---|
| S-Mesh [1] | Method [20] | Our Method | S-Mesh [1] | Method [20] | Our Method | |
| 64 | ||||||
| 1.81 | 1.92 | 1.74 | 1.82 | 2.03 | 1.95 | |
| 128 | ||||||
| 1.84 | 1.87 | 2.01 | 1.86 | 1.97 | 1.95 | |
| 256 | ||||||
| 1.93 | 1.79 | 1.84 | 1.93 | 2.04 | 1.88 | |
| 512 | ||||||
| 1.98 | 1.65 | 1.81 | 1.99 | 1.99 | 2.07 | |
| 1024 | ||||||
| 1.51 | 1.75 | 1.93 | 1.92 | 1.96 | - | ||
| 2 | 2 | 2 | 1 | 1 | 1 | ||
| 2.01 | 2.05 | 2.00 | 1.69 | 1.07 | - | ||
| 3 | 3 | 3 | 2 | 2 | 3 | ||
| 1.74 | 2.21 | 1.99 | 2.02 | 1.99 | - | ||
| 5 | 8 | 4 | 3 | 3 | 3 | ||
| 2.01 | 2.20 | 2.01 | 1.99 | 2.02 | - | ||
| 7 | 9 | 5 | 5 | 4 | 3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Liang, Y.; Zhang, Y. A Second-Order Adaptive Grid Method for a Singularly Perturbed Volterra Integrodifferential Equation. Fractal Fract. 2022, 6, 636. https://doi.org/10.3390/fractalfract6110636
Liu L, Liang Y, Zhang Y. A Second-Order Adaptive Grid Method for a Singularly Perturbed Volterra Integrodifferential Equation. Fractal and Fractional. 2022; 6(11):636. https://doi.org/10.3390/fractalfract6110636
Chicago/Turabian StyleLiu, Libin, Ying Liang, and Yong Zhang. 2022. "A Second-Order Adaptive Grid Method for a Singularly Perturbed Volterra Integrodifferential Equation" Fractal and Fractional 6, no. 11: 636. https://doi.org/10.3390/fractalfract6110636
APA StyleLiu, L., Liang, Y., & Zhang, Y. (2022). A Second-Order Adaptive Grid Method for a Singularly Perturbed Volterra Integrodifferential Equation. Fractal and Fractional, 6(11), 636. https://doi.org/10.3390/fractalfract6110636










