Study on the Complex Dynamical Behavior of the Fractional-Order Hopfield Neural Network System and Its Implementation
Abstract
:1. Introduction
2. FOHNN System with Four Neurons
2.1. Principle of the Fractional Calculus
2.2. Solution of the FOHNN-Based System
3. Study of the Dynamical Characteristics of the FOHNN System
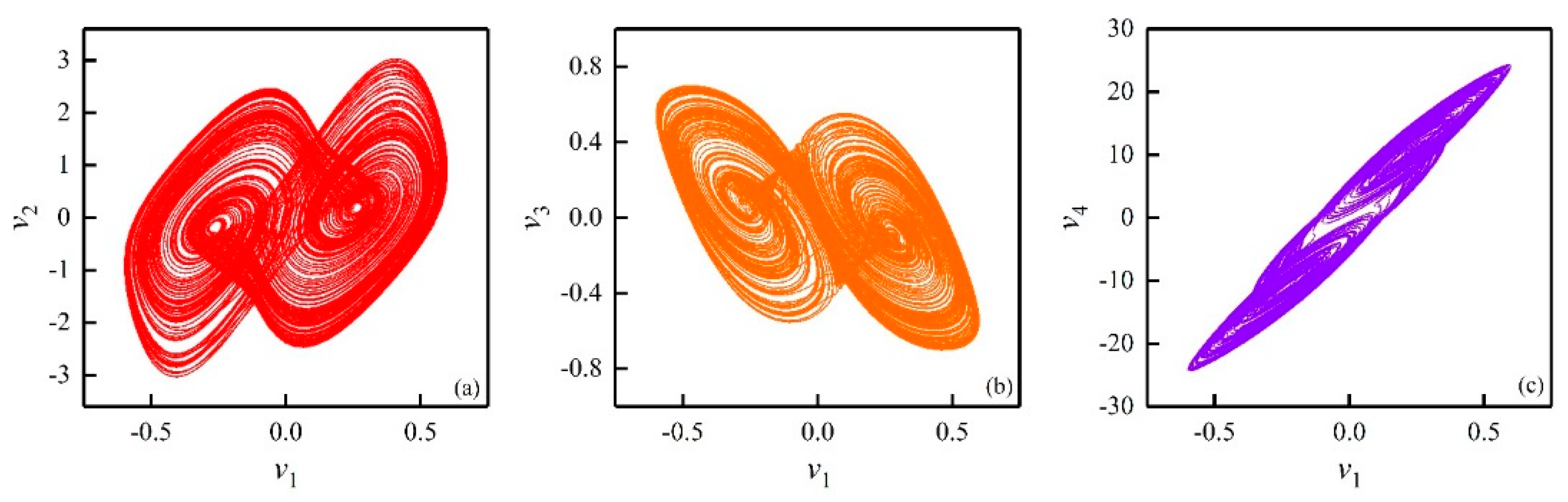
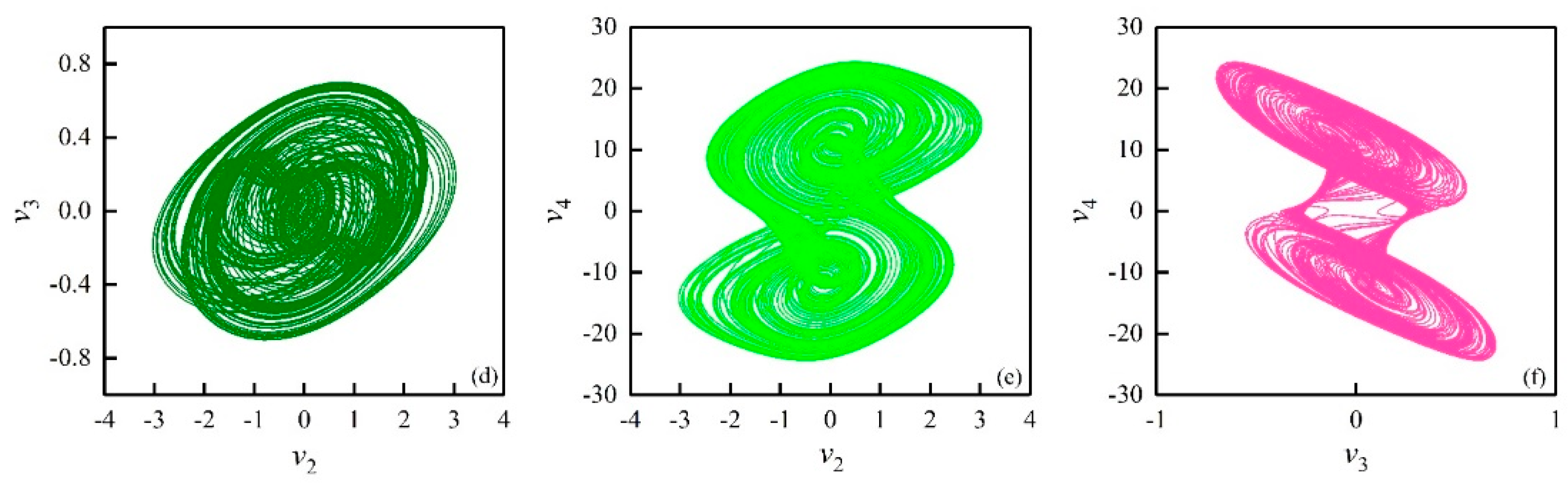
3.1. Dissipation of the FOHNN System with the Existence of Attractors
3.2. Stability Analysis of the Equilibrium Point of the FOHNN System
3.3. Stability Analysis of the Equilibrium Point of the FOHNN System
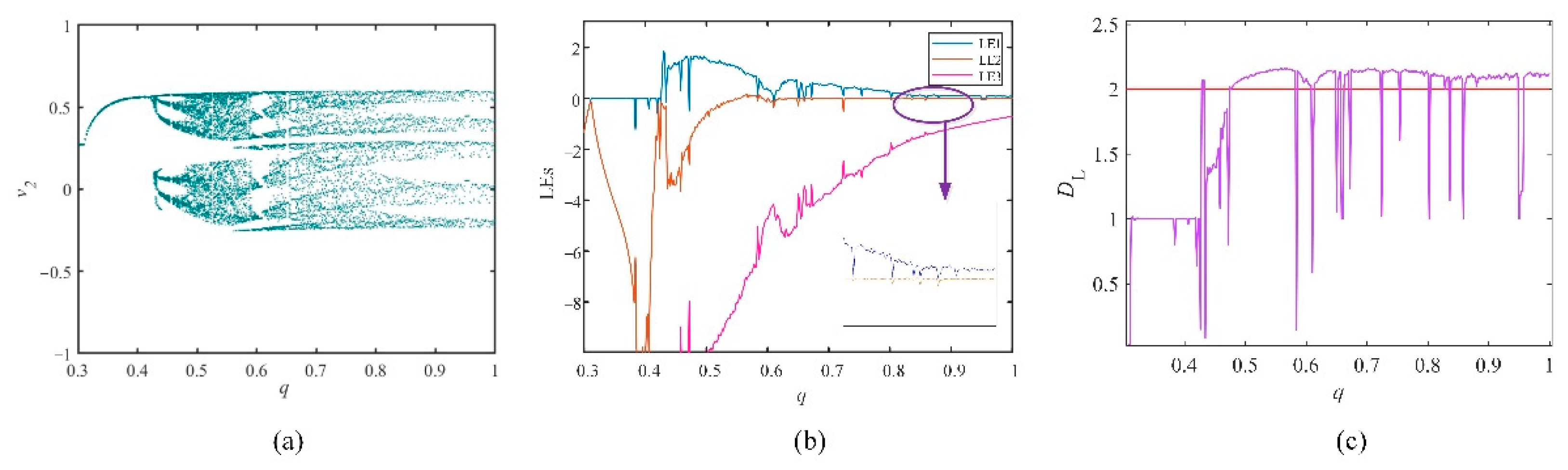
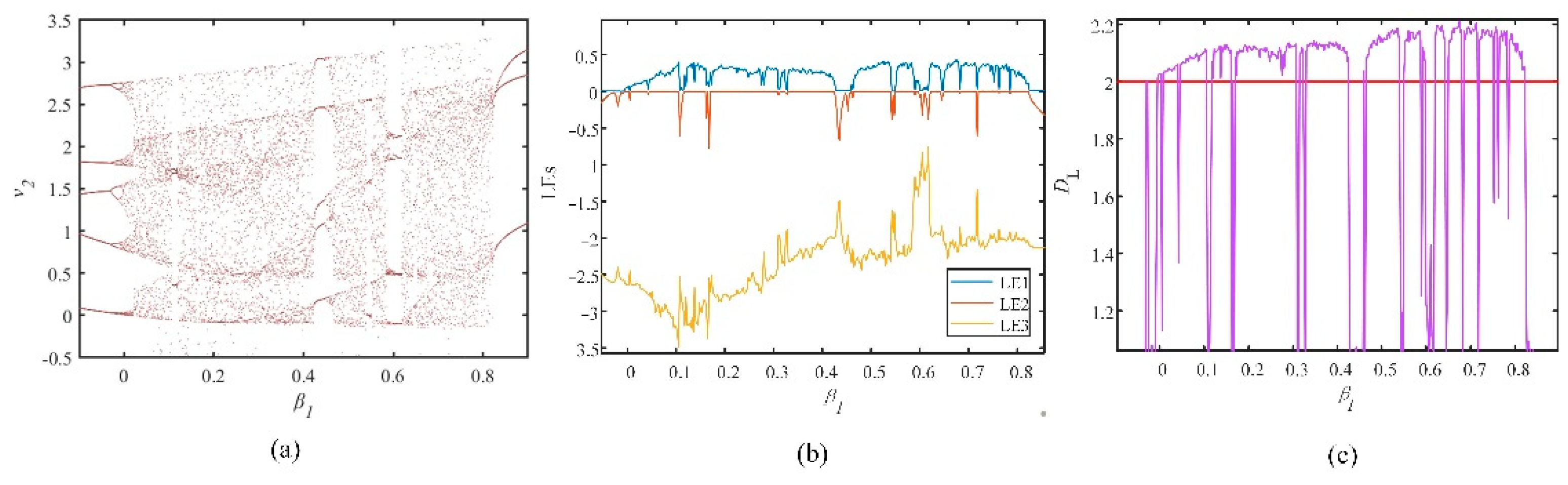
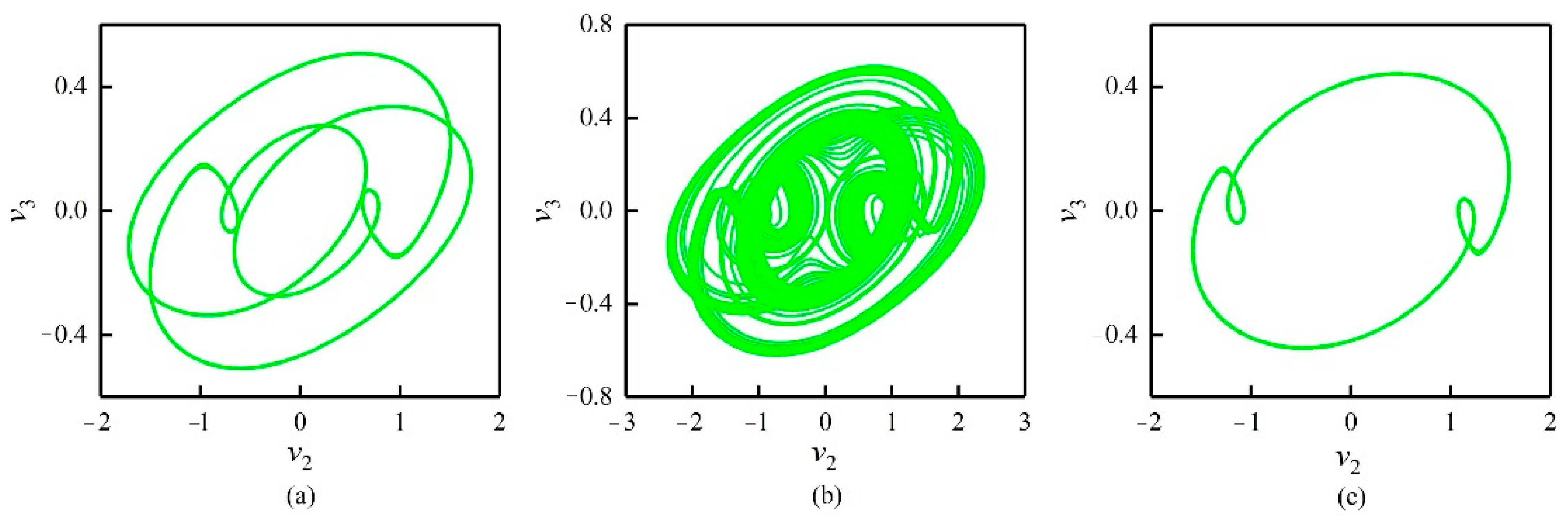
3.3.1. The Influence of the Different Orders of the FOHNN System
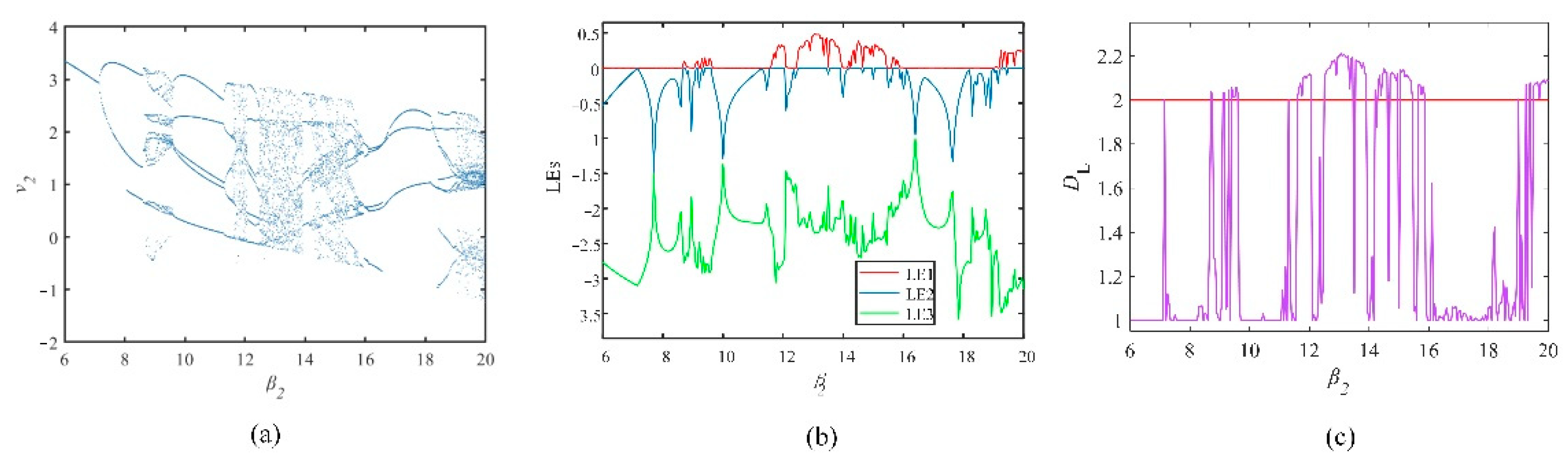
3.3.2. The Influence of the Different Synaptic Weights of the FOHNN System
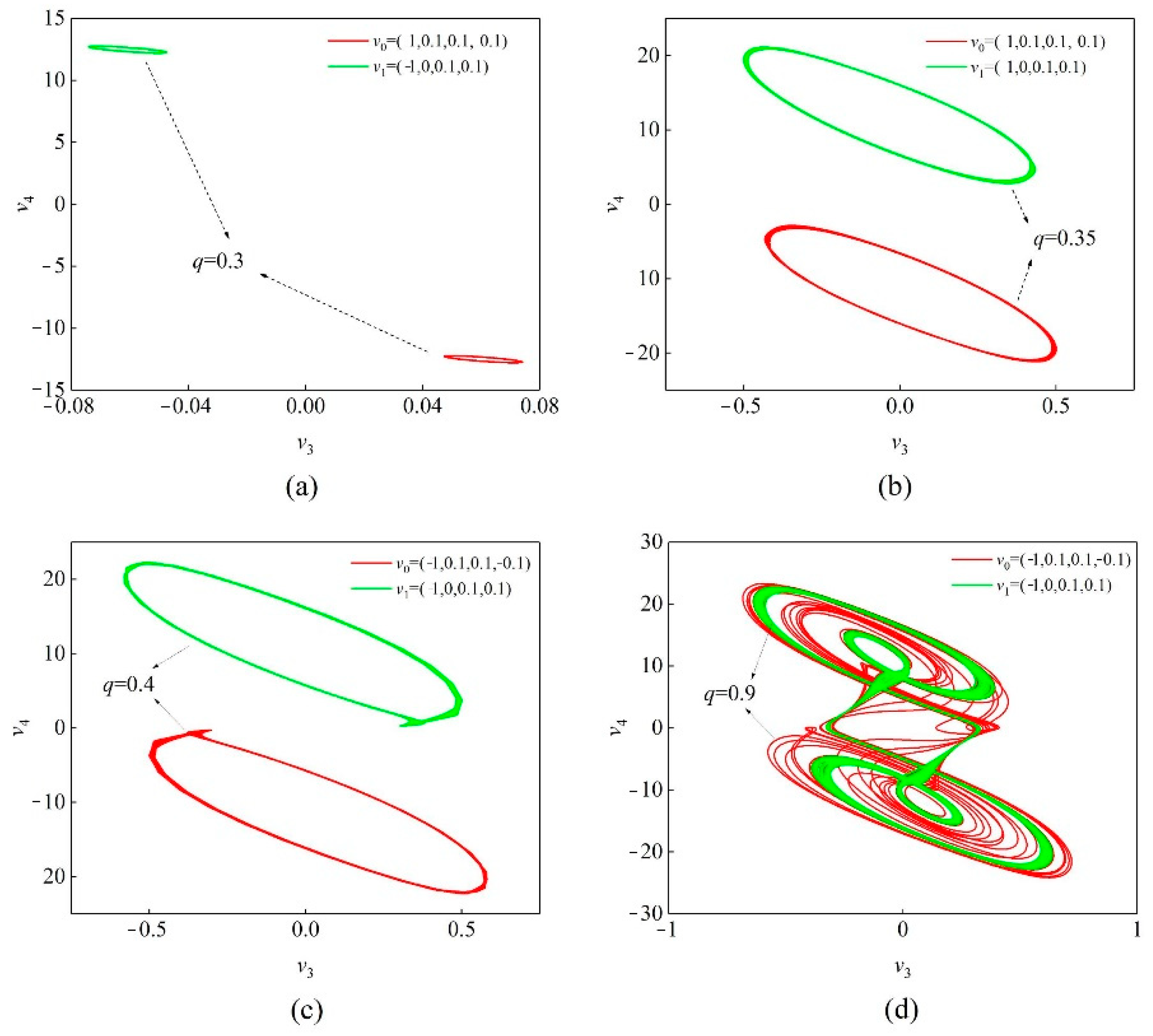
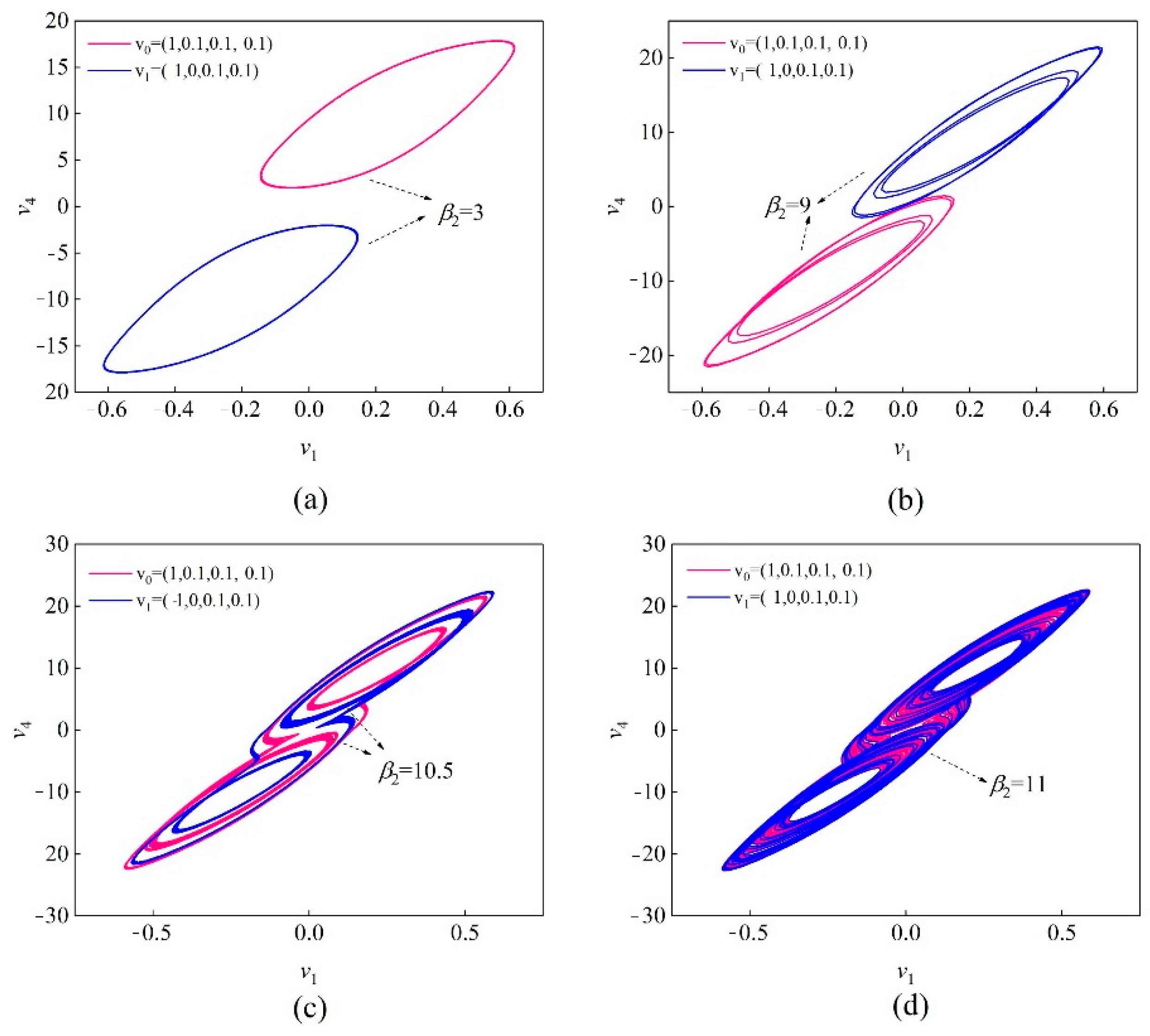
3.4. Coexistence of the Attractors with the Different Synaptic Weights
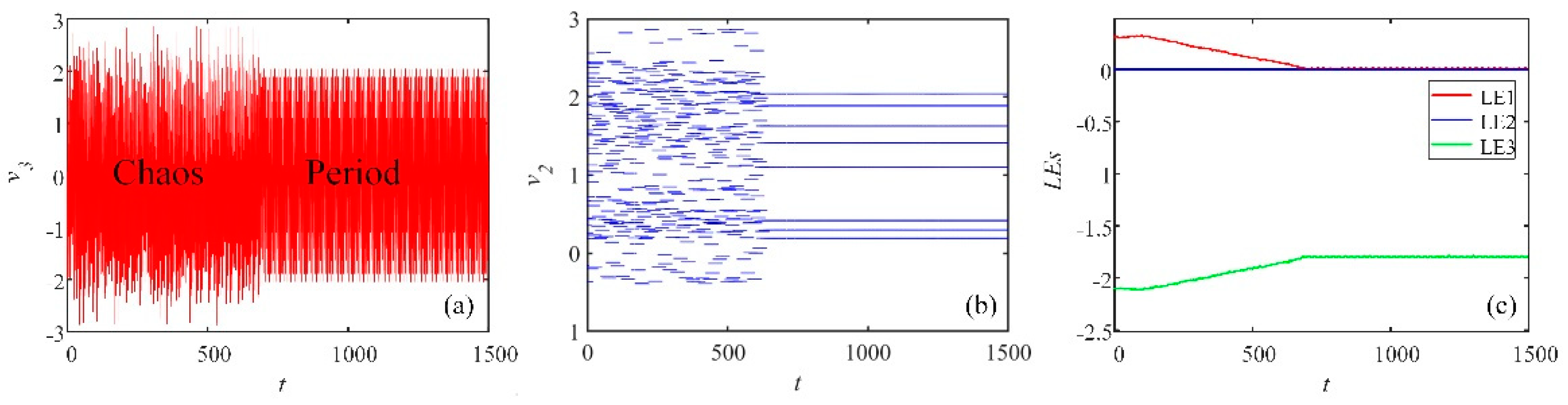
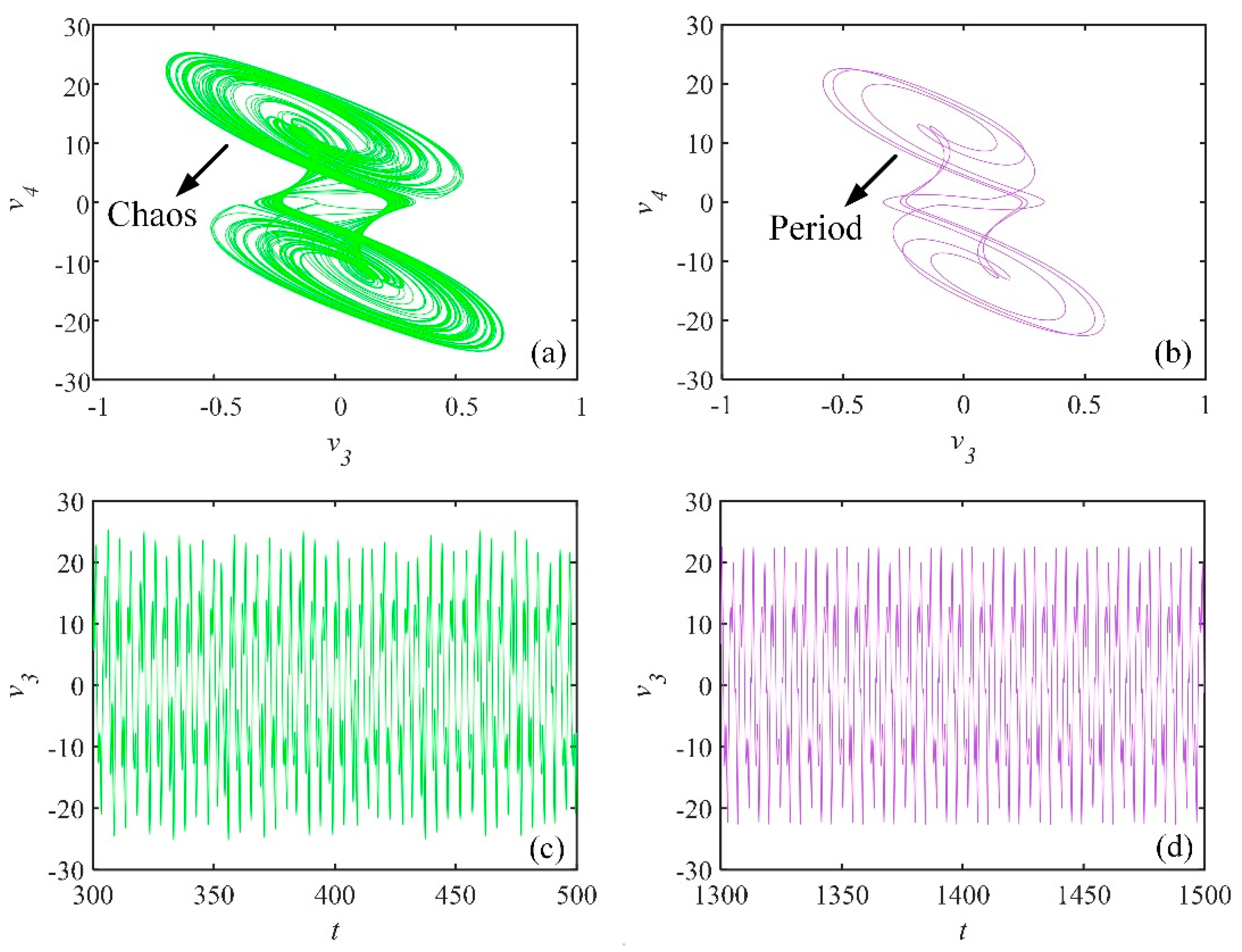
3.5. Transient Chaos in the FOHNN System
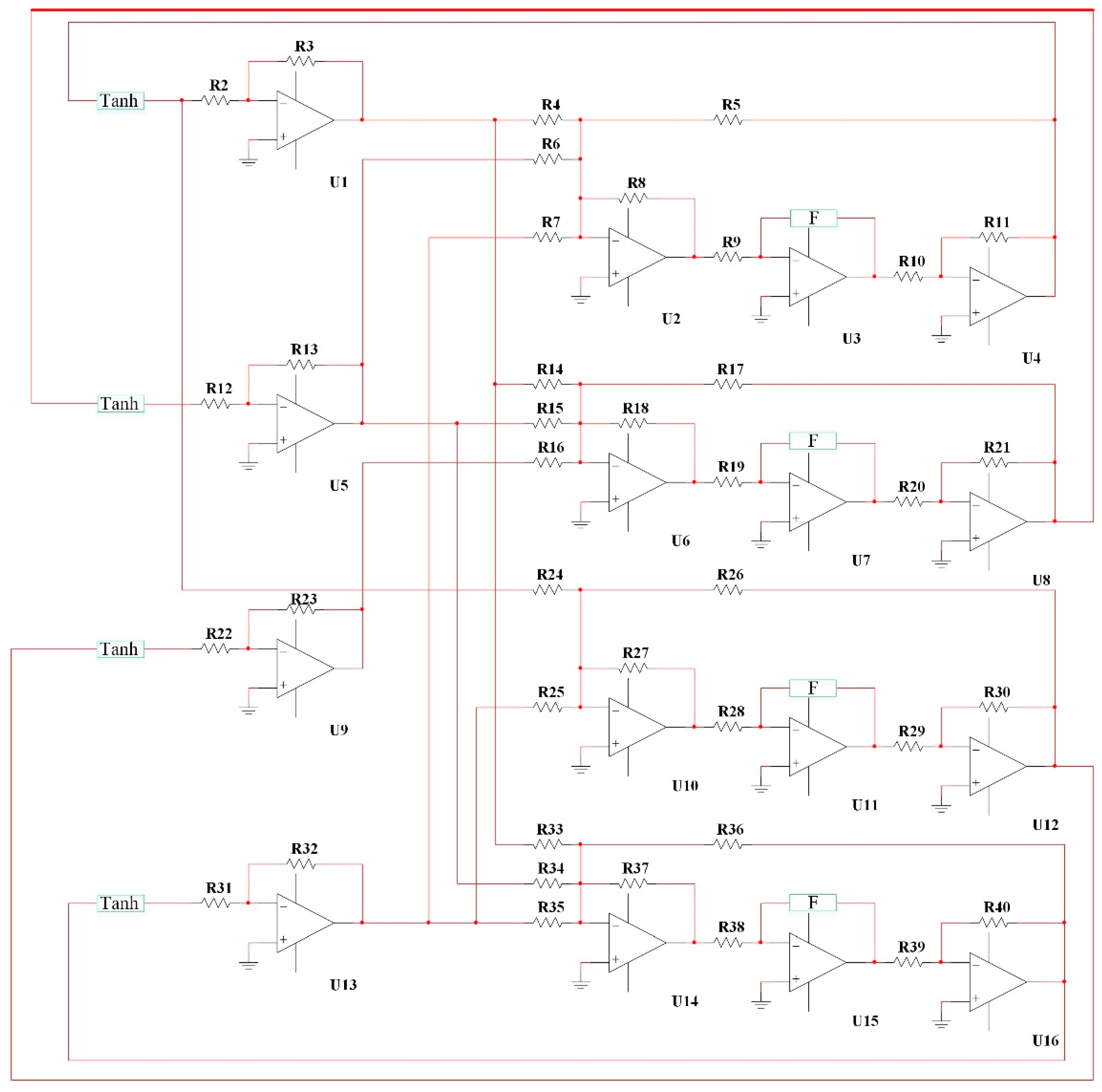
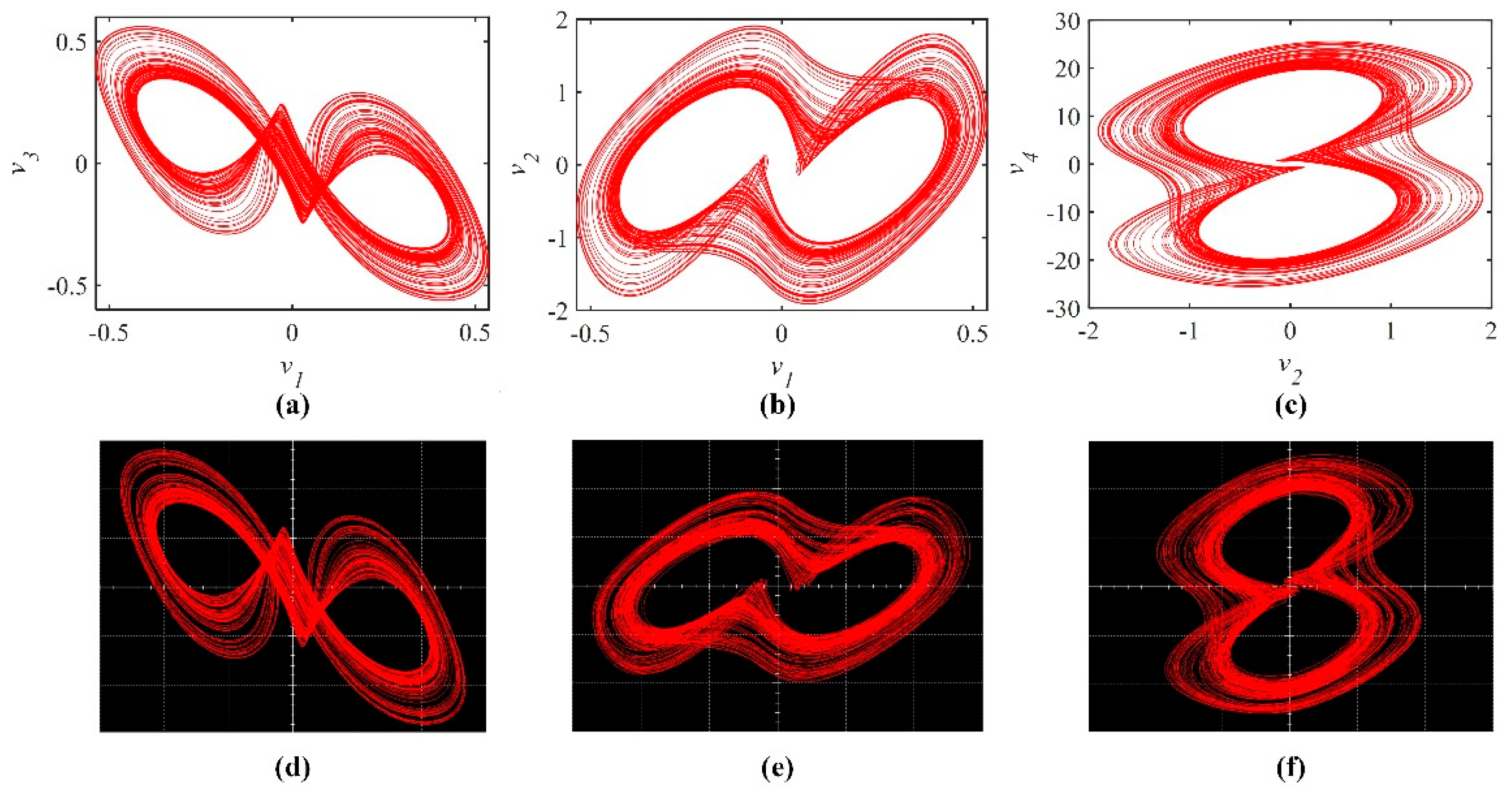
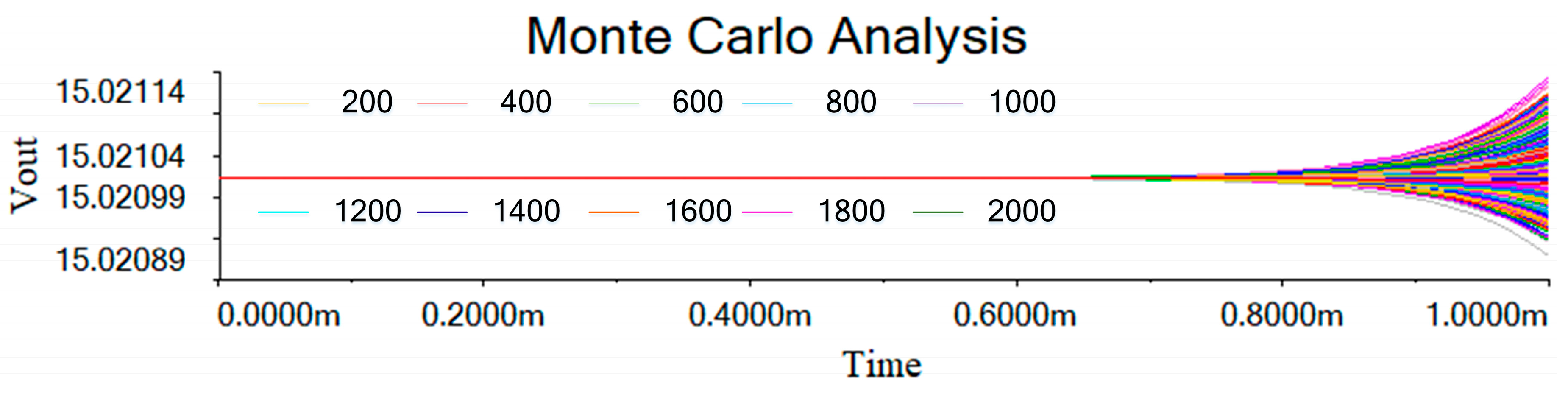
4. Circuit Design and Simulation of the FOHNN System
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Kasai, H.; Ziv, N.E.; Okazaki, H.; Yagishita, S.; Toyoizumi, T. Spine dynamics in the brain, mental disorders and artificial neural networks. Nat. Rev. Neurosci. 2021, 22, 407–422. [Google Scholar] [CrossRef] [PubMed]
- Ma, J.; Tang, J. A review for dynamics in neuron and neuronal network. Nonlinear Dyn. 2017, 89, 1569–1578. [Google Scholar] [CrossRef]
- Lin, H.; Wang, C.; Deng, Q.; Xu, C.; Deng, Z.; Zhou, C. Review on chaotic dynamics of memristive neuron and neural network. Nonlinear Dyn. 2021, 106, 959–973. [Google Scholar] [CrossRef]
- Wei, Z.; Parastesh, F.; Azarnoush, H.; Jafari, S.; Ghosh, D.; Perc, M.; Slavinec, M. Nonstationary chimeras in a neuronal network. EPL Europhys. Lett. 2018, 123, 48003. [Google Scholar] [CrossRef] [Green Version]
- Hopfield, J.J. Neural networks and physical systems with emergent collective computational abilities. Proc. Natl. Acad. Sci. USA 1982, 79, 2554–2558. [Google Scholar] [CrossRef] [Green Version]
- Njitacke, Z.T.; Isaac, S.D.; Nestor, T.; Kengne, J. Window of multistability and its control in a simple 3D Hopfield neural network: Application to biomedical image encryption. Neural Comput. Appl. 2021, 33, 6733–6752. [Google Scholar] [CrossRef]
- Yu, F.; Zhang, Z.; Shen, H.; Huang, Y.; Cai, S.; Du, S. FPGA implementation and image encryption application of a new PRNG based on a memristive Hopfield neural network with a special activation gradient. Chin. Phys. B 2022, 31, 020505. [Google Scholar] [CrossRef]
- Shen, H.; Yu, F.; Kong, X.; Mokbel, A.A.M.; Wang, C.; Cai, S. Dynamics study on the effect of memristive autapse distribution on Hopfield neural network. Chaos Interdiscip. J. Nonlinear Sci. 2022, 32, 083133. [Google Scholar] [CrossRef]
- Yang, F.; Wang, X. Dynamic characteristic of a new fractional-order chaotic system based on the Hopfield Neural Network and its digital circuit implementation. Phys. Scr. 2021, 96, 035218. [Google Scholar] [CrossRef]
- Xu, S.; Wang, X.; Ye, X. A new fractional-order chaos system of Hopfield neural network and its application in image encryption. Chaos Solitons Fractals 2022, 157, 111889. [Google Scholar] [CrossRef]
- Yang, X.-S.; Yuan, Q. Chaos and transient chaos in simple Hopfield neural networks. Neurocomputing 2005, 69, 232–241. [Google Scholar] [CrossRef]
- Araujo, N.; Duarte, A.; Pujatti, F.; Freitas-Marques, M.B.; Sebastiao, R. Kinetic models and distribution of activation energy in complex systems using Hopfield Neural Network. Thermochim. Acta 2021, 697, 178847. [Google Scholar] [CrossRef]
- Dong, T.; Gong, X.; Huang, T. Zero-Hopf Bifurcation of a memristive synaptic Hopfield neural network with time delay. Neural Netw. 2022, 149, 146–156. [Google Scholar] [CrossRef] [PubMed]
- Pu, Y.F.; Yi, Z.; Zhou, J.L. Fractional Hopfield Neural Networks: Fractional Dynamic Associative Recurrent Neural Networks. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 2319–2333. [Google Scholar] [CrossRef] [PubMed]
- Ma, T.; Mou, J.; Yan, H.; Cao, Y. A new class of Hopfield neural network with double memristive synapses and its DSP implementation. Eur. Phys. J. Plus 2022, 137, 1135. [Google Scholar] [CrossRef]
- Li, C.; Yang, Y.; Yang, X.; Zi, X.; Xiao, F. A tristable locally active memristor and its application in Hopfield neural network. Nonlinear Dyn. 2022, 108, 1697–1717. [Google Scholar] [CrossRef]
- Ding, D.; Xiao, H.; Yang, Z.; Luo, H.; Hu, Y.; Zhang, X.; Liu, Y. Coexisting multi-stability of Hopfield neural network based on coupled fractional-order locally active memristor and its application in image encryption. Nonlinear Dyn. 2022, 108, 4433–4458. [Google Scholar] [CrossRef]
- Sani, S.; Shermeh, H.E. A novel algorithm for detection of COVID-19 by analysis of chest CT images using Hopfield neural network. Expert Syst. Appl. 2022, 197, 116740. [Google Scholar] [CrossRef]
- Adachi, M.; Aihara, K. An Analysis on Instantaneous Stability of AN Associative Chaotic Neural Network. Int. J. Bifurc. Chaos 1999, 9, 2157–2163. [Google Scholar] [CrossRef]
- Aihara, K. Chaos engineering and its application to parallel distributed processing with chaotic neural networks. Proc. IEEE 2002, 90, 919–930. [Google Scholar] [CrossRef]
- Chen, L.; Aihara, K. Chaotic simulated annealing by a neural network model with transient chaos. Neural Netw. 1995, 8, 915–930. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.; Aihara, K. Global searching ability of chaotic neural networks. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 1999, 46, 974–993. [Google Scholar] [CrossRef]
- Li, Z.; Liu, L.; Dehghan, S.; Chen, Y.; Xue, D. A review and evaluation of numerical tools for fractional calculus and fractional order controls. Int. J. Control. 2017, 90, 1165–1181. [Google Scholar] [CrossRef] [Green Version]
- He, S.; Sun, K.; Banerjee, S. Dynamical properties and complexity in fractional-order diffusionless Lorenz system. Eur. Phys. J. Plus 2016, 131, 1–12. [Google Scholar] [CrossRef]
- He, S.; Sun, K.; Mei, X.; Yan, B.; Xu, S. Numerical analysis of a fractional-order chaotic system based on conformable fractional-order derivative. Eur. Phys. J. Plus 2017, 132, 1–11. [Google Scholar] [CrossRef]
- He, S.; Sun, K.; Wang, H. Complexity analysis and DSP implementation of the fractional-order Lorenz hyperchaotic system. Entropy 2015, 17, 8299–8311. [Google Scholar] [CrossRef] [Green Version]
- He, S.; Sun, K.; Wang, H.; Mei, X.; Sun, Y. Generalized synchronization of fractional-order hyperchaotic systems and its DSP implementation. Nonlinear Dyn. 2018, 92, 85–96. [Google Scholar] [CrossRef]
- Mou, J.; Sun, K.; Wang, H.; Ruan, J. Characteristic analysis of fractional-order 4D hyperchaotic memristive circuit. Math. Probl. Eng. 2017, 2017, 2313768. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Sun, K.; He, S. Characteristic analysis and DSP realization of fractional-order simplified Lorenz system based on Adomian decomposition method. Int. J. Bifurc. Chaos 2015, 25, 1550085. [Google Scholar] [CrossRef]
- Zhang, L.; Sun, K.; He, S.; Wang, H.; Xu, Y. Solution and dynamics of a fractional-order 5-D hyperchaotic system with four wings. Eur. Phys. J. Plus 2017, 132, 1–16. [Google Scholar] [CrossRef]
- Zhang, X.; Huang, W. Adaptive neural network sliding mode control for nonlinear singular fractional order systems with mismatched uncertainties. Fractal Fract. 2020, 4, 50. [Google Scholar] [CrossRef]
- Yu, F.; Yu, Q.; Chen, H.; Kong, X.; Mokbel, A.A.M.; Cai, S.; Du, S. Dynamic analysis and audio encryption application in IoT of a multi-scroll fractional-order memristive Hopfield neural network. Fractal Fract. 2022, 6, 370. [Google Scholar] [CrossRef]
- Ma, C.; Mou, J.; Yang, F.; Yan, H. A fractional-order hopfield neural network chaotic system and its circuit realization. Eur. Phys. J. Plus 2020, 135, 1–16. [Google Scholar] [CrossRef]
- Li, X.; Mou, J.; Banerjee, S.; Wang, Z.; Cao, Y. Design and DSP implementation of a fractional-order detuned laser hyperchaotic circuit with applications in image encryption. Chaos Solitons Fractals 2022, 159, 112133. [Google Scholar] [CrossRef]
- Han, X.; Mou, J.; Jahanshahi, H.; Cao, Y.; Bu, F. A new set of hyperchaotic maps based on modulation and coupling. Eur. Phys. J. Plus 2022, 137, 523. [Google Scholar] [CrossRef]
- Liu, X.; Mou, J.; Yan, H.; Bi, X. Memcapacitor-Coupled Chebyshev Hyperchaotic Map. Int. J. Bifurc. Chaos 2022, 32, 2250180. [Google Scholar] [CrossRef]
- Sha, Y.; Bo, S.; Yang, C.; Mou, J.; Jahanshahi, H. A Chaotic Image Encryption Scheme Based on Genetic Central Dogma and KMP Method. Int. J. Bifurc. Chaos 2022, 32, 2250186. [Google Scholar] [CrossRef]
- Priya, B.; Thakur, G.K.; Ali, M.S.; Stamov, G.; Stamova, I.; Sharma, P.K. On the Finite-Time Boundedness and Finite-Time Stability of Caputo-Type Fractional Order Neural Networks with Time Delay and Uncertain Terms. Fractal Fract. 2022, 6, 368. [Google Scholar] [CrossRef]
- Dubdub, I. Pyrolysis Study of Mixed Polymers for Non-Isothermal TGA: Artificial Neural Networks Application. Polymers 2022, 14, 2638. [Google Scholar] [CrossRef]
- Almeida, R.; Agarwal, R.P.; Hristova, S.; O’Regan, D. Quadratic Lyapunov Functions for Stability of the Generalized Proportional Fractional Differential Equations with Applications to Neural Networks. Axioms 2021, 10, 322. [Google Scholar] [CrossRef]
- Almatroud, A.O. Extreme multistability of a fractional-order discrete-time neural network. Fractal Fract. 2021, 5, 202. [Google Scholar] [CrossRef]
- Wei, Z.; Moroz, I.; Kuznetsov, N.V.; Zhang, W. Codimension one and two bifurcations in Cattaneo-Christov heat flux model. Discret. Contin. Dyn. Syst. B 2021, 26, 5305–5319. [Google Scholar] [CrossRef]
- Kaslik, E.; Sivasundaram, S. Nonlinear dynamics and chaos in fractional-order neural networks. Neural Netw. 2012, 32, 245–256. [Google Scholar] [CrossRef]
- Batiha, I.M.; Albadarneh, R.B.; Momani, S.; Jebril, I.H. Dynamics analysis of fractional-order Hopfield neural networks. Int. J. Biomath. 2020, 13, 2050083. [Google Scholar] [CrossRef]
- Zhang, S.; Yu, Y.; Wang, Q. Stability analysis of fractional-order Hopfield neural networks with discontinuous activation functions. Neurocomputing 2016, 171, 1075–1084. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Marzan, S.A. Nonlinear differential equations with the Caputo fractional derivative in the space of continuously differentiable functions. Differ. Equ. 2005, 41, 84–89. [Google Scholar] [CrossRef]
- Ding, D.; Qian, X.; Hu, W.; Wang, N.; Liang, D. Chaos and Hopf bifurcation control in a fractional-order memristor-based chaotic system with time delay. Eur. Phys. J. Plus 2017, 132, 1–12. [Google Scholar] [CrossRef]
- Matignon, D. Stability results for fractional differential equations with applications to control processing. Comput. Eng. Syst. Appl. 1996, 2, 963–968. [Google Scholar]

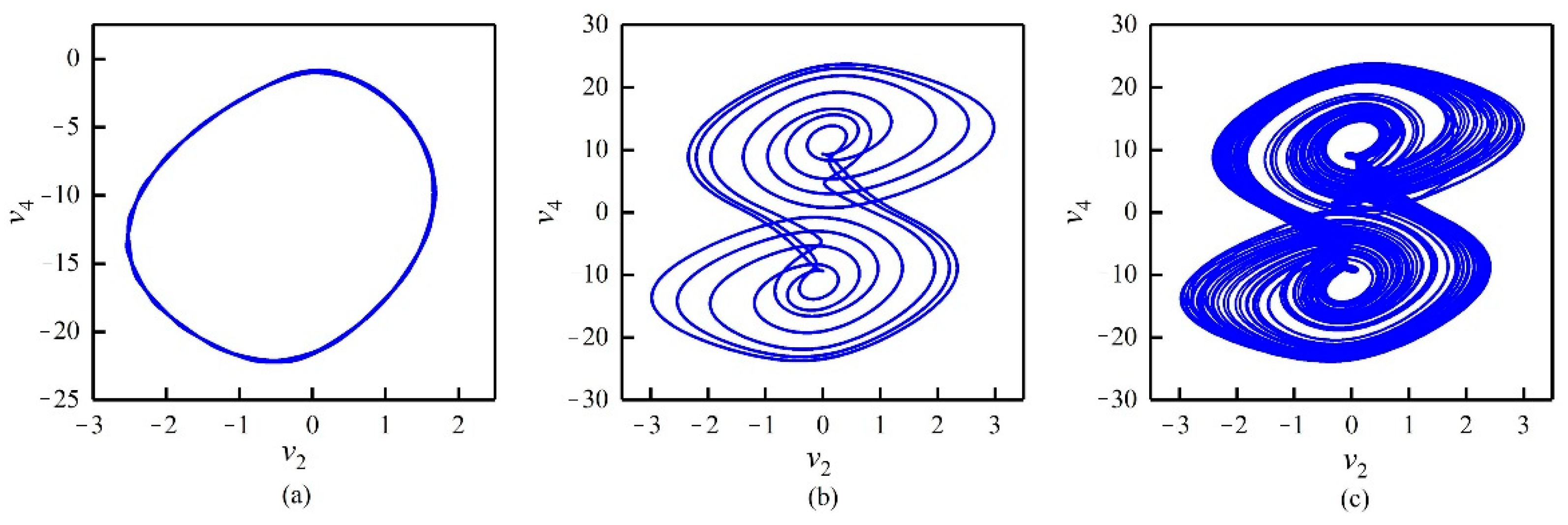


| Parameters | System Status | Parameters | System Status |
|---|---|---|---|
| q = 0.584 | Period-3 | q = 0.724 | Period-7 |
| q = 0.61 | Period-3 | q = 0.754 | Period-3 |
| q = 0.65 | Period-2 | q = 0.802 | Period-4 |
| q = 0.66 | Period-7 | q = 0.828 | Period-10 |
| Components | Values | Components | Values |
|---|---|---|---|
| R2, R3, R5, R8, R10, R11, R12, R13, R17, R18, R20, R21, R22, R23, R25, R26, R27, R29, R30, R31, R32, R35, R36, R37, R39, R40 | 10 kΩ | Rc, Rd | 1 kΩ |
| R4 | 33.333 kΩ | Rb | 0.52 kΩ |
| R6 | 20 kΩ | Rf1 | 15.3 kΩ |
| R7 | 100 kΩ | Rf2 | 1.15 MΩ |
| R14 | 4.348 kΩ | Rf3 | 692.9 MΩ |
| R15 | 28.5714 kΩ | Cf1 | 3.616 μF |
| R16 | 1.176 kΩ | Cf2 | 4.602 μF |
| R24 | 2.5 kΩ | Cf3 | 1.267 μF |
| R33 | 0.286 kΩ | U1∼16, Ua, Ub | 3288 RT |
| R34 | 0.526 kΩ | ||
| R9, R19, R28, R38 | 0.5 kΩ | ||
| Ra, Re, Rf, Rg, Rh | 10 kΩ |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, T.; Mou, J.; Li, B.; Banerjee, S.; Yan, H. Study on the Complex Dynamical Behavior of the Fractional-Order Hopfield Neural Network System and Its Implementation. Fractal Fract. 2022, 6, 637. https://doi.org/10.3390/fractalfract6110637
Ma T, Mou J, Li B, Banerjee S, Yan H. Study on the Complex Dynamical Behavior of the Fractional-Order Hopfield Neural Network System and Its Implementation. Fractal and Fractional. 2022; 6(11):637. https://doi.org/10.3390/fractalfract6110637
Chicago/Turabian StyleMa, Tao, Jun Mou, Bo Li, Santo Banerjee, and Huizhen Yan. 2022. "Study on the Complex Dynamical Behavior of the Fractional-Order Hopfield Neural Network System and Its Implementation" Fractal and Fractional 6, no. 11: 637. https://doi.org/10.3390/fractalfract6110637
APA StyleMa, T., Mou, J., Li, B., Banerjee, S., & Yan, H. (2022). Study on the Complex Dynamical Behavior of the Fractional-Order Hopfield Neural Network System and Its Implementation. Fractal and Fractional, 6(11), 637. https://doi.org/10.3390/fractalfract6110637









