Sliding Mode Control for a Class of Nonlinear Fractional Order Systems with a Fractional Fixed-Time Reaching Law
Abstract
:1. Introduction
- (1)
- The SMC method was used to control a class of fractional order systems covering a wide class of fractional chaotic systems, where a better control performance is achieved by introducing a nonlinear item to the sliding manifold.
- (2)
- A novel fixed-time reaching law with a fractional adaptive gain is proposed, which reduces the fixed-time reaching law in [6] with some specific parameters.
- (3)
2. Preliminaries
3. Main Results
3.1. System Description
3.2. Sliding Manifold Design
3.3. Fractional Fixed-Time Reaching Law
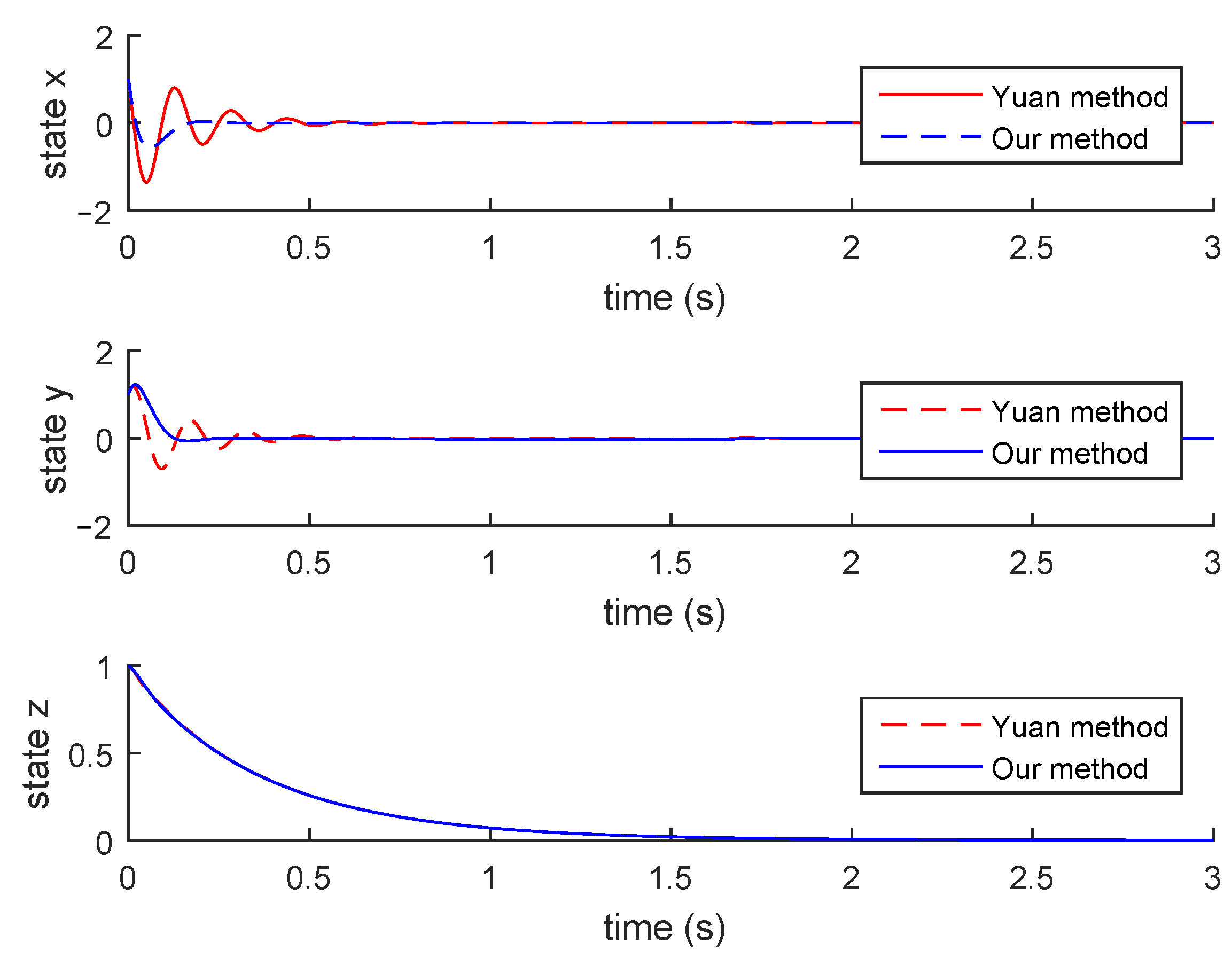
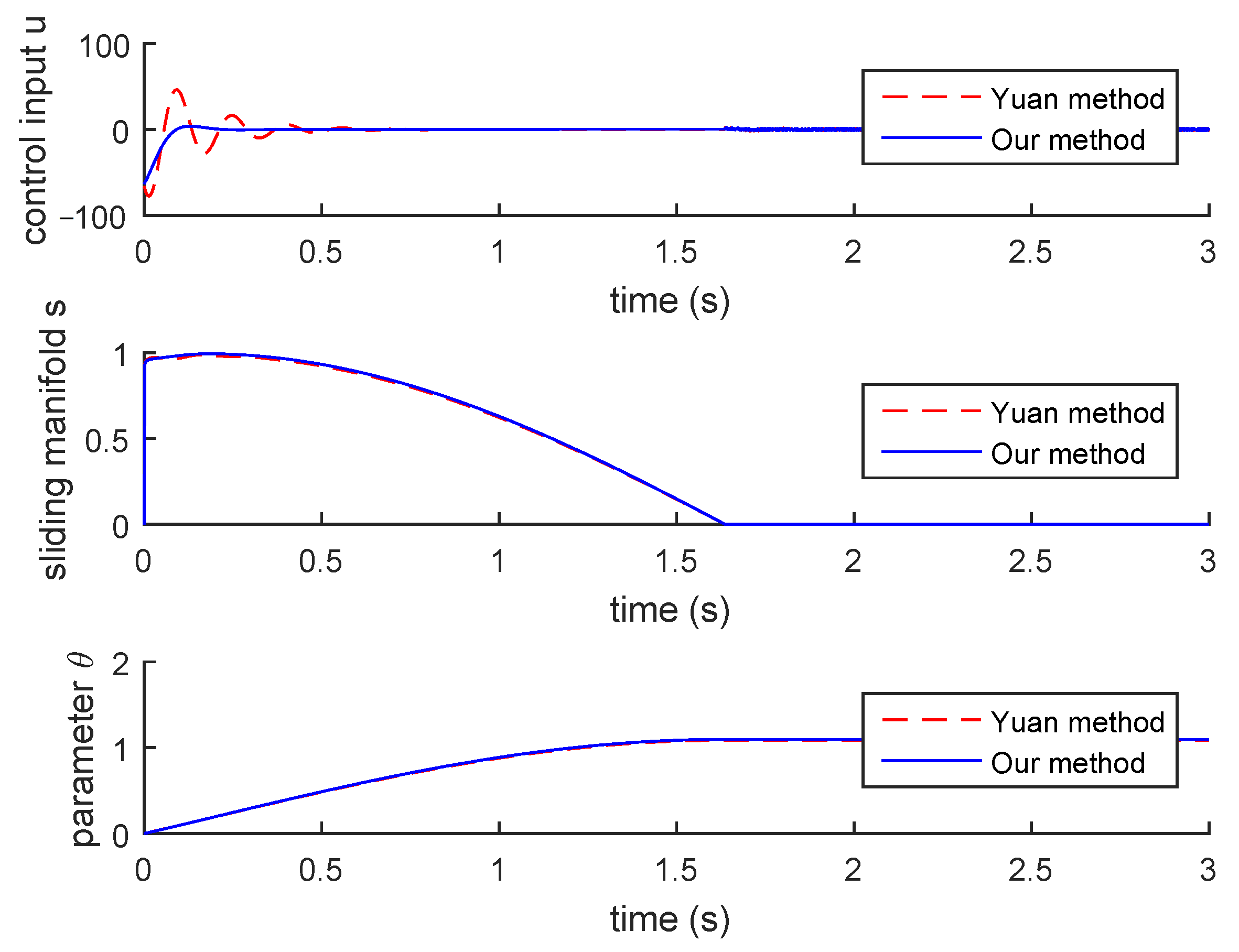
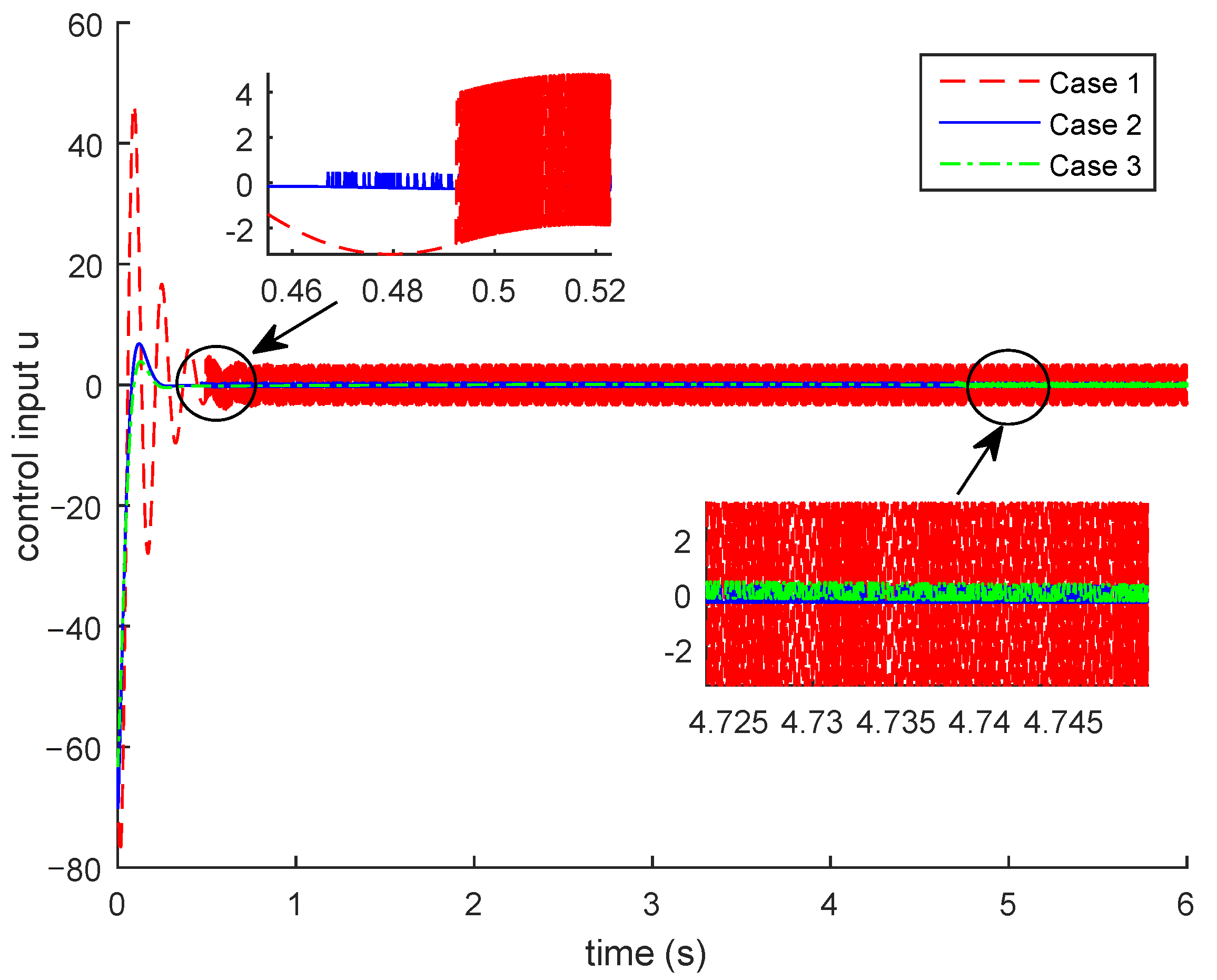
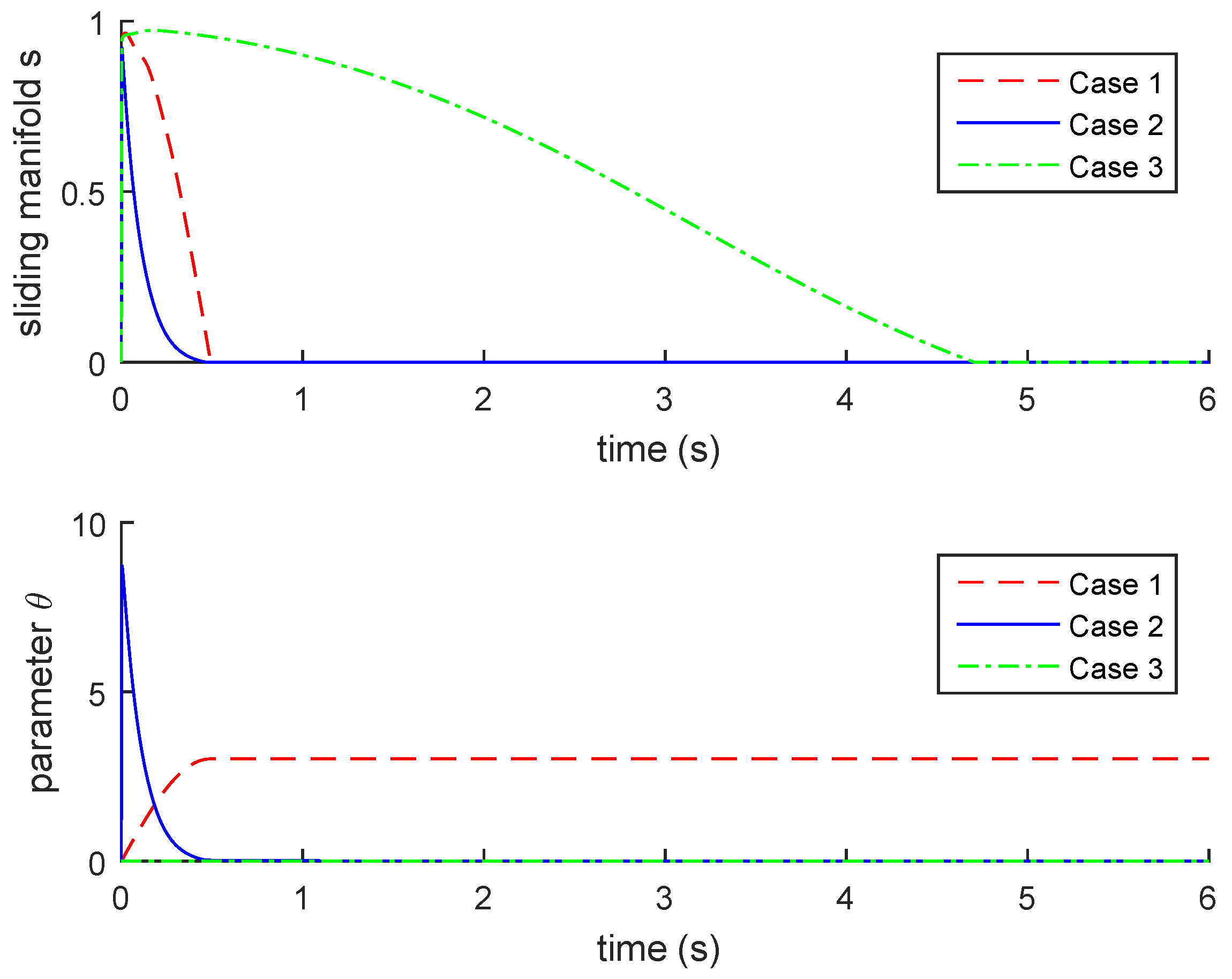
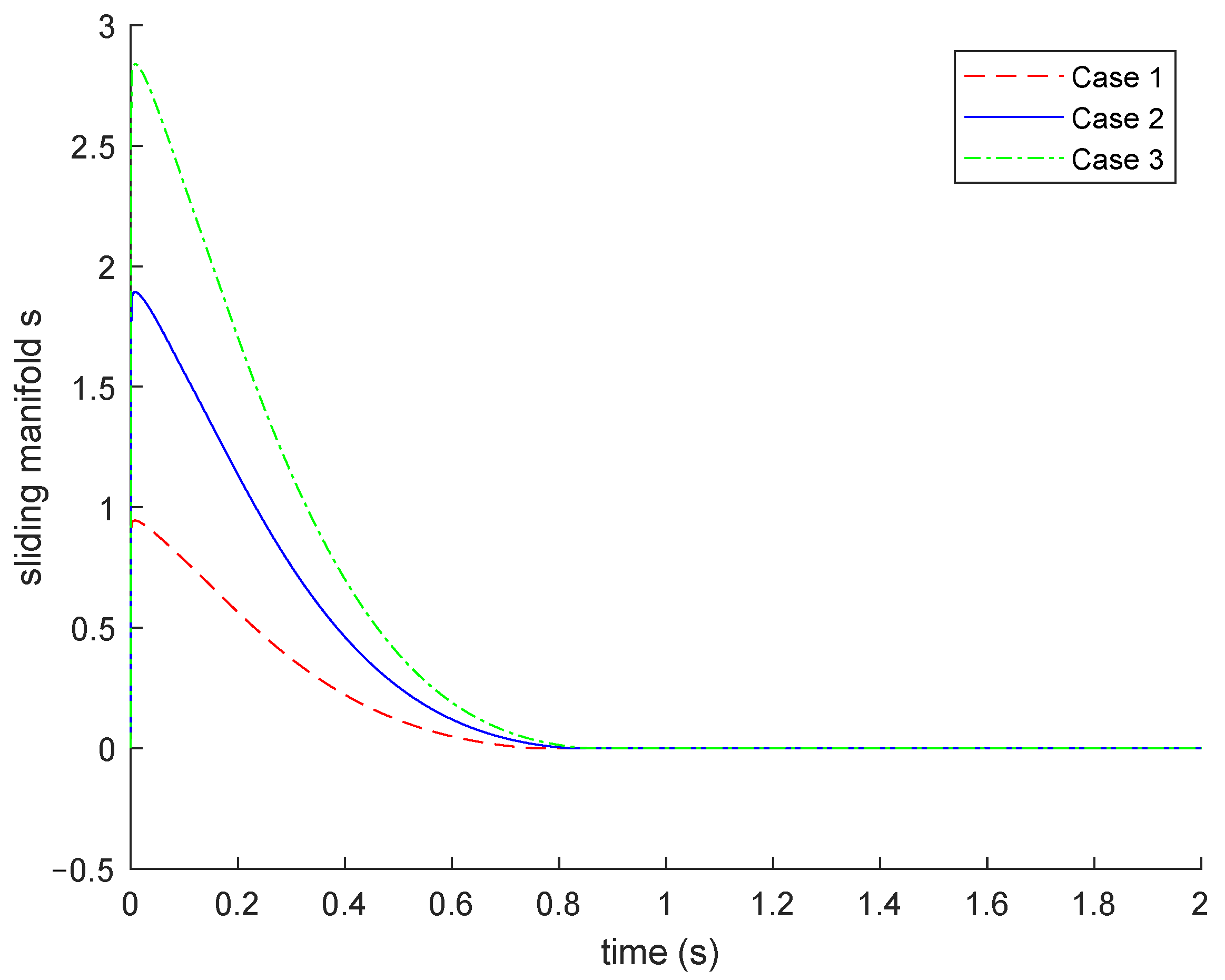
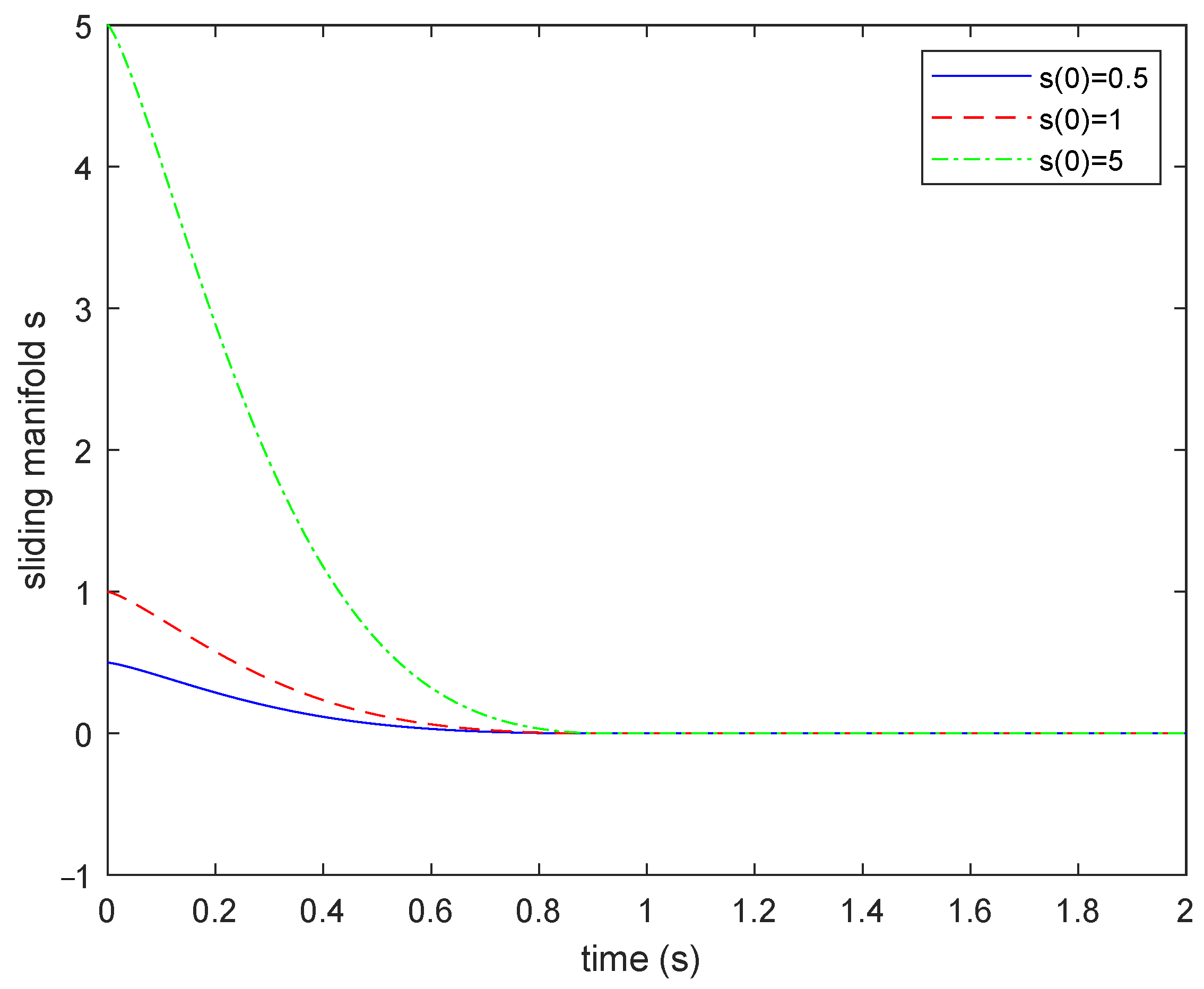
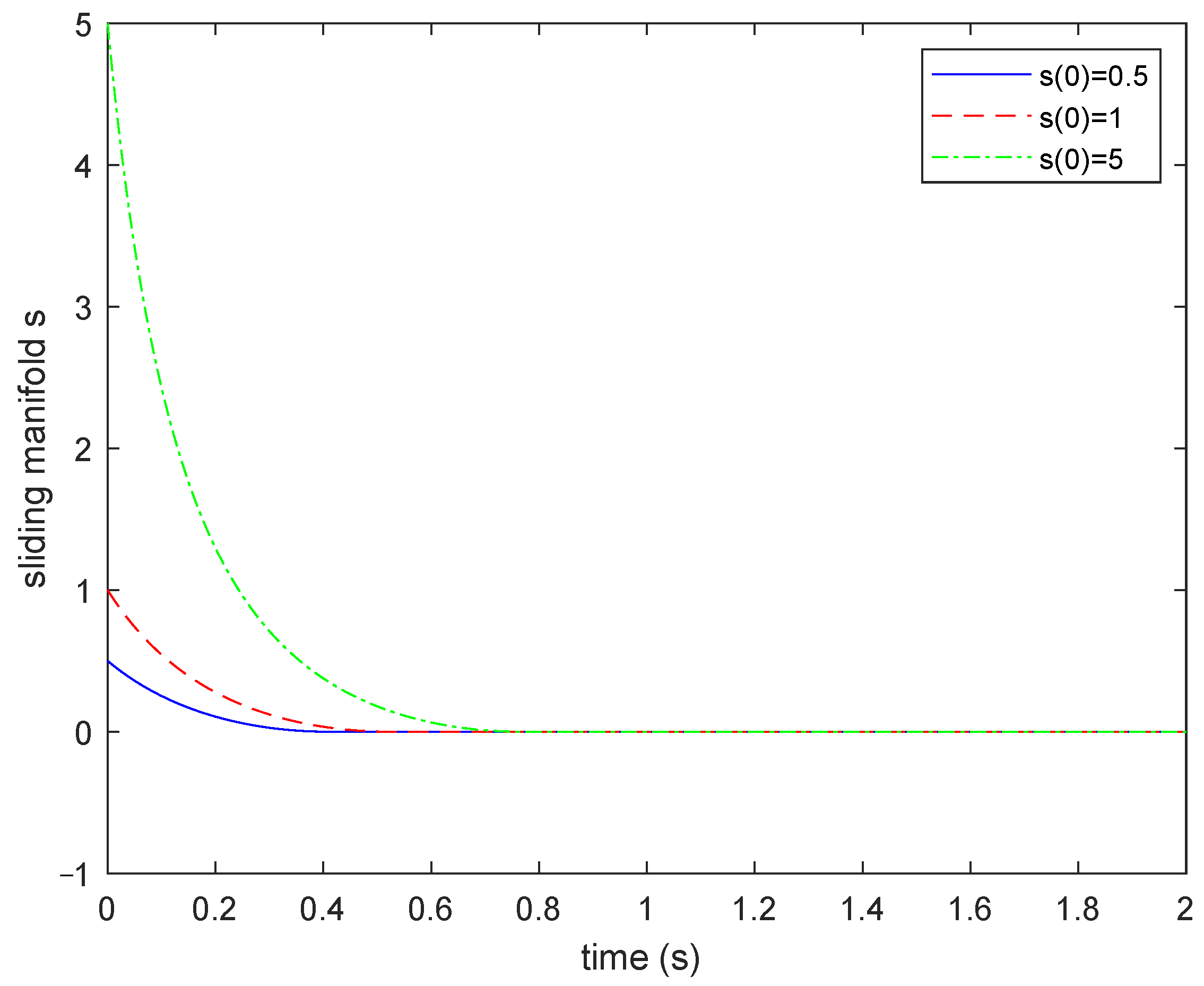
4. Illustrative Examples
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Wu, G.C.; Luo, M.; Huang, L.L.; Banerjee, S. Short memory fractional differential equations for new memristor and neural network design. Nonlinear Dyn. 2020, 100, 3611–3623. [Google Scholar] [CrossRef]
- Parisis, K.; Dimosthenis, V.; Kouris, L.; Konstantinidis, A.; Aifantis, E.C. A note on gradient/fractional one-dimensional elasticity and viscoelasticity. Fractal Fract. 2022, 6, 84–93. [Google Scholar] [CrossRef]
- Cao, X.; Abhirup, D.; Fahad, A.B.; Kumar, R.P.; Science, C.O.; University, T.B.; Biologyecology, C.; Mathematics, D.O.; University, J. Fractional-order model of the disease psoriasis: A control based mathematical approach. J. Syst. Sci. Complex. 2016, 29, 1565–1584. [Google Scholar] [CrossRef]
- Sierociuk, D.; Skovranek, T.; Macias, M.; Podlubny, I.; Petras, I.; Dzielinski, A.; Ziubinski, P. Diffusion process modeling by using fractional-order models. Appl. Math. Comput. 2015, 257, 2–11. [Google Scholar] [CrossRef] [Green Version]
- Xia, X.; Chen, Y.; Yan, L. Averaging principle for a class of time-fractal-fractional stochastic differential equations. Fractal Fract. 2022, 6, 558–568. [Google Scholar] [CrossRef]
- Chen, Y.Q.; Wei, Y.H.; Zhong, H.; Wang, Y. Sliding mode control with a second-order switching law for a class of nonlinear fractional order systems. Nonlinear Dyn. 2016, 85, 633–643. [Google Scholar] [CrossRef]
- Hou, Q.; Ding, S.; Yu, X.; Mei, K. A super-twisting-like fractional controller for SPMSM drive system. IEEE Trans. Ind. Electron. 2021, 69, 9376–9384. [Google Scholar] [CrossRef]
- Ataşlar-Ayyıldız, B.; Karahan, O.; Yılmaz, S. Control and robust stabilization at unstable equilibrium by fractional controller for magnetic levitation systems. Fractal Fract. 2021, 5, 101–127. [Google Scholar] [CrossRef]
- Sheng, Y.; Bai, W.; Xie, Y. Fractional-order PIλD sliding mode control for hypersonic vehicles with neural network disturbance compensator. Nonlinear Dyn. 2021, 103, 849–863. [Google Scholar] [CrossRef]
- Li, H.; Zhang, T.; Tie, M.; Wang, Y. Fuzzy-based adaptive higher-order sliding mode control for uncertain steer-by-wire system. J. Dyn. Syst. Meas. Control 2022, 144, 041005. [Google Scholar] [CrossRef]
- Ren, J.; Sun, J.; Li, F. Robust observer-based finite time sliding mode control for one-sided Lipschitz systems with uncertainties. J. Dyn. Syst. Meas. Control 2021, 143, 014501. [Google Scholar] [CrossRef]
- Han, S. Fractional-Order Command Filtered Backstepping Sliding Mode Control with Fractional-Order Nonlinear Disturbance Observer for Nonlinear Systems. J. Frankl. Inst. 2020, 357, 6760–6776. [Google Scholar] [CrossRef]
- Mathiyalagan, K.; Sangeetha, G. Second-order sliding mode control for nonlinear fractional-order systems. Appl. Math. Comput. 2020, 383, 125264. [Google Scholar] [CrossRef]
- Modiri, A.; Mobayen, S. Adaptive terminal sliding mode control scheme for synchronization of fractional-order uncertain chaotic systems. ISA Trans. 2020, 105, 33–50. [Google Scholar] [CrossRef]
- Kamal, S.; Sharma, R.K.; Dinh, T.N.; Ms, H.; Bandyopadhyay, B. Sliding mode control of uncertain fractional-order systems: A reaching phase free approach. Asian J. Control 2021, 23, 199–208. [Google Scholar] [CrossRef]
- Wu, X.F.; Bao, H.B.; Cao, J.D. Finite-time inter-layer projective synchronization of Caputo fractional-order two-layer networks by sliding mode control. J. Frankl. Inst. 2020, 358, 1002–1020. [Google Scholar] [CrossRef]
- Jakovljević, B.; Pisano, A.; Rapaić, M.; Usai, E. On the sliding-mode control of fractional-order nonlinear uncertain dynamics. Int. J. Robust Nonlinear Control 2015, 26, 782–798. [Google Scholar] [CrossRef]
- Martínez-Guerra, R.; Pérez-Pinacho, C.A.; Gómez-Cortés, G.C.; Cruz-Victoria, J.C. Synchronization of incommensurate fractional order system. Appl. Math. Comput. 2015, 262, 260–266. [Google Scholar] [CrossRef]
- Xiu, C.; Zhou, R.; Zhao, S.; Xu, G. Memristive hyperchaos secure communication based on sliding mode control. Nonlinear Dyn. 2021, 104, 789–805. [Google Scholar] [CrossRef]
- Song, S.; Meng, B.; Wang, Z. On sliding mode control for singular fractional-order systems with matched external disturbances. Fractal Fract. 2022, 6, 366–376. [Google Scholar] [CrossRef]
- Chen, S.; Huang, W.; Liu, Q. A new adaptive robust sliding mode control approach for nonlinear singular fractional-order systems. Fractal Fract. 2022, 6, 253–271. [Google Scholar] [CrossRef]
- Yin, C.; Zhong, S.M.; Chen, W.F. Design of sliding mode controller for a class of fractional-order chaotic systems. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 356–366. [Google Scholar] [CrossRef]
- Van Giap, N.; Vu, H.S.; Nguyen, Q.D.; Huang, S.C. Disturbance and uncertainty rejection-based on fixed-time sliding-mode control for the secure communication of chaotic systems. IEEE Access 2021, 9, 133663–133685. [Google Scholar] [CrossRef]
- Yin, C.; Cheng, Y.H.; Chen, Y.Q.; Stark, B.; Zhong, S.M. Adaptive fractional-order switching-type control method design for 3D fractional-order nonlinear systems. Nonlinear Dyn. 2015, 82, 39–52. [Google Scholar] [CrossRef]
- Yin, C.; Huang, X.G.; Chen, Y.Q.; Dadras, S.; Zhong, S.M.; Cheng, Y.H. Fractional-order exponential switching technique to enhance sliding mode control. Appl. Math. Model. 2017, 44, 705–726. [Google Scholar] [CrossRef]
- Chen, L.P.; Wu, R.C.; He, Y.G.; Chai, Y. Adaptive sliding-mode control for fractional-order uncertain linear systems with nonlinear disturbances. Nonlinear Dyn. 2015, 80, 51–58. [Google Scholar] [CrossRef]
- Labbadi, M.; Boubaker, S.; Djemai, M.; Mekni, S.K.; Bekrar, A. Fixed-time fractional-order global sliding mode control for nonholonomic mobile robot systems under external disturbances. Fractal Fract. 2022, 6, 177–195. [Google Scholar] [CrossRef]
- Brahmi, B.; Laraki, M.H.; Brahmi, A.; Saad, M.; Rahman, M.H. Improvement of sliding mode controller by using a new adaptive reaching law: Theory and experiment. ISA Trans. 2020, 97, 261–268. [Google Scholar] [CrossRef]
- Sai, H.; Xu, Z.; He, S.; Zhang, E.; Zhu, L. Adaptive nonsingular fixed-time sliding mode control for uncertain robotic manipulators under actuator saturation. ISA Trans. 2022, 123, 46–60. [Google Scholar] [CrossRef]
- Chen, Y.; Wei, Y.; Wang, Y. On 2 types of robust reaching laws. Int. J. Robust Nonlinear Control 2018, 28, 2651–2667. [Google Scholar] [CrossRef]
- Wang, A.M.; Jia, X.W.; Dong, S.H. A new exponential reaching law of sliding mode control to improve performance of permanent magnet synchronous motor. IEEE Trans. Magn. 2013, 49, 2409–2412. [Google Scholar] [CrossRef]
- Zhang, X.G.; Zhao, K.; Sun, L. A PMSM sliding mode control system based on a novel reaching law. In Proceedings of the 2011 International Conference on Electrical Machines and Systems, Beijing, China, 20–23 August 2011. [Google Scholar]
- Monje, C.A.; Chen, Y.Q.; Vinagre, B.M.; Xue, D.Y.; Feliu-Batlle, V. Fractional-Order Systems and Controls: Fundamentals and Applications; Springer: London, UK, 2010. [Google Scholar]
- Trigeassou, J.C.; Maamri, N.; Sabatier, J.; Oustaloup, A. State variables and transients of fractional order differential systems. Comput. Math. Appl. 2012, 64, 3117–3140. [Google Scholar] [CrossRef] [Green Version]
- Trigeassou, J.C.; Maamri, N.; Sabatier, J.; Oustaloup, A. A Lyapunov approach to the stability of fractional differential equations. Signal Process. 2011, 91, 437–445. [Google Scholar] [CrossRef]
- Wei, Y.H.; Tse, P.W.; Du, B.; Wang, Y. An innovative fixed-pole numerical approximation for fractional order systems. ISA Trans. 2016, 62, 94–102. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.Q.; Wei, Y.H.; Zhou, X.; Wang, Y. Stability for nonlinear fractional order systems: An indirect approach. Nonlinear Dyn. 2017, 89, 1011–1018. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Yuan, J.; Shi, B.; Ji, W.Q. Adaptive sliding mode control of a novel class of fractional chaotic systems. Adv. Math. Phys. 2013, 2013, 576709–576721. [Google Scholar] [CrossRef]
- Wei, Y.H.; Gao, Q.; Peng, C.; Wang, Y. A rational approximate method to fractional order systems. Int. J. Control Autom. Syst. 2014, 12, 1180–1186. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Wang, B.; Chen, Y.; Wang, Y. Sliding Mode Control for a Class of Nonlinear Fractional Order Systems with a Fractional Fixed-Time Reaching Law. Fractal Fract. 2022, 6, 678. https://doi.org/10.3390/fractalfract6110678
Chen Y, Wang B, Chen Y, Wang Y. Sliding Mode Control for a Class of Nonlinear Fractional Order Systems with a Fractional Fixed-Time Reaching Law. Fractal and Fractional. 2022; 6(11):678. https://doi.org/10.3390/fractalfract6110678
Chicago/Turabian StyleChen, Yuquan, Bing Wang, Yangquan Chen, and Yong Wang. 2022. "Sliding Mode Control for a Class of Nonlinear Fractional Order Systems with a Fractional Fixed-Time Reaching Law" Fractal and Fractional 6, no. 11: 678. https://doi.org/10.3390/fractalfract6110678
APA StyleChen, Y., Wang, B., Chen, Y., & Wang, Y. (2022). Sliding Mode Control for a Class of Nonlinear Fractional Order Systems with a Fractional Fixed-Time Reaching Law. Fractal and Fractional, 6(11), 678. https://doi.org/10.3390/fractalfract6110678








