Chaos Controllability in Fractional-Order Systems via Active Dual Combination–Combination Hybrid Synchronization Strategy
Abstract
1. Introduction
- The proposed DCCHS methodology considers eight non-identical, complex, FO chaotic/ hyperchaotic systems.
- It describes a robust DCCHS scheme-based controller to achieve dual combination–combination hybrid synchronization in considered systems and conducts oscillation in synchronization errors with fast convergence.
- The designing of the active controllers is carried out in a simplified manner using LSA and a master–salve configuration.
- Simulation outcomes alongside a table showing a comparison analysis demonstrate the efficacy of the introduced methodology.
2. Preliminaries
3. Problem Formulation
4. Illustrative Example
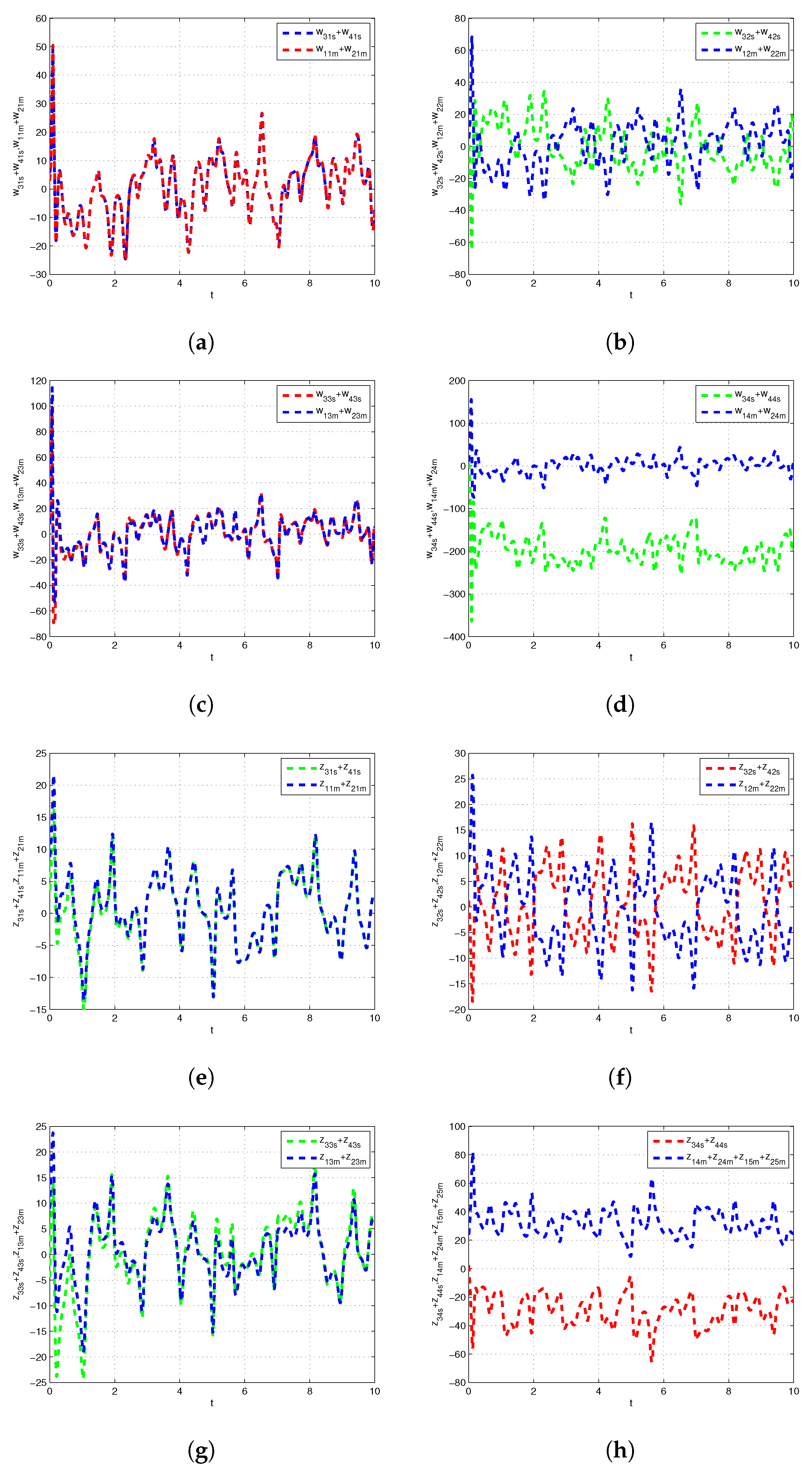
5. Numerical Simulation
A Comparative Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Khan, T.; Chaudhary, H. An investigation on hybrid projective combination difference synchronization scheme between chaotic prey-predator systems via active control method. Poincare J. Anal. Appl. 2020, 7, 211–225. [Google Scholar] [CrossRef]
- Wu, G.C.; Baleanu, D.; Lin, Z.X. Image encryption technique based on fractional chaotic time series. J. Vib. Control 2016, 22, 2092–2099. [Google Scholar] [CrossRef]
- Patle, B.; Parhi, D.; Jagadeesh, A.; Kashyap, S.K. Matrix-Binary Codes based Genetic Algorithm for path planning of mobile robot. Comput. Electr. Eng. 2018, 67, 708–728. [Google Scholar] [CrossRef]
- Das, S.; Pan, I. Fractional Order Signal Processing: Introductory Concepts and Applications; Springer Science & Business Media: London, UK, 2011. [Google Scholar]
- Tong, X.J.; Zhang, M.; Wang, Z.; Liu, Y.; Ma, J. An image encryption scheme based on a new hyperchaotic finance system. Optik 2015, 126, 2445–2452. [Google Scholar] [CrossRef]
- Khan, A.; Nigar, U.; Chaudhary, H. Secure Communication and Synchronization Dynamics in Chaotic Chua’s System via Adaptive Sliding Mode Control Technique. Int. J. Appl. Comput. Math. 2022, 8, 170. [Google Scholar] [CrossRef]
- Bouallegue, K. A new class of neural networks and its applications. Neurocomputing 2017, 249, 28–47. [Google Scholar] [CrossRef]
- Muthukumar, P.; Nasreen. Secure audio signal encryption based on triple compound-combination synchronization of fractional-order dynamical systems. Int. J. Dyn. Control 2022, 10, 2053–2071. [Google Scholar]
- Sahoo, B.; Poria, S. The chaos and control of a food chain model supplying additional food to top-predator. Chaos Solitons Fractals 2014, 58, 52–64. [Google Scholar] [CrossRef]
- Fallahi, K.; Leung, H. A chaos secure communication scheme based on multiplication modulation. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 368–383. [Google Scholar] [CrossRef]
- Wu, X.; Fu, Z.; Kurths, J. A secure communication scheme based generalized function projective synchronization of a new 5D hyperchaotic system. Phys. Scr. 2015, 90, 045210. [Google Scholar] [CrossRef]
- He, J.; Cai, J.; Lin, J. Synchronization of hyperchaotic systems with multiple unknown parameters and its application in secure communication. Optik 2016, 127, 2502–2508. [Google Scholar] [CrossRef]
- Khan, A.; Nigar, U. Combination Projective Synchronization in Fractional-Order Chaotic System with Disturbance and Uncertainty. Int. J. Appl. Comput. Math. 2020, 6, 97. [Google Scholar] [CrossRef]
- Ngouonkadi, E.M.; Fotsin, H.; Fotso, P.L. Implementing a memristive Van der Pol oscillator coupled to a linear oscillator: Synchronization and application to secure communication. Phys. Scr. 2014, 89, 035201. [Google Scholar] [CrossRef]
- Lin, J.S.; Huang, C.F.; Liao, T.L.; Yan, J.J. Design and implementation of digital secure communication based on synchronized chaotic systems. Digit. Signal Process. 2010, 20, 229–237. [Google Scholar] [CrossRef]
- Naderi, B.; Kheiri, H. Exponential synchronization of chaotic system and application in secure communication. Optik 2016, 127, 2407–2412. [Google Scholar] [CrossRef]
- Dedieu, H.; Kennedy, M.P.; Hasler, M. Chaos shift keying: Modulation and demodulation of a chaotic carrier using self-synchronizing Chua’s circuits. IEEE Trans. Circuits Syst. II Analog Digit. Signal Process. 1993, 40, 634–642. [Google Scholar] [CrossRef]
- Hou, Y.Y.; Chen, H.C.; Chang, J.F.; Yan, J.J.; Liao, T.L. Design and implementation of the Sprott chaotic secure digital communication systems. Appl. Math. Comput. 2012, 218, 11799–11805. [Google Scholar] [CrossRef]
- Wu, X.; Wang, H.; Lu, H. Modified generalized projective synchronization of a new fractional-order hyperchaotic system and its application to secure communication. Nonlinear Anal. Real World Appl. 2012, 13, 1441–1450. [Google Scholar] [CrossRef]
- Mahmoud, G.M.; Mahmoud, E.E. Complete synchronization of chaotic complex nonlinear systems with uncertain parameters. Nonlinear Dyn. 2010, 62, 875–882. [Google Scholar] [CrossRef]
- Khan, T.; Chaudhary, H. Adaptive controllability of microscopic chaos generated in chemical reactor system using anti-synchronization strategy. Numer. Algebr. Control Optim. 2021, 12, 611–620. [Google Scholar] [CrossRef]
- Khan, A.; Chaudhary, H. A Comprehensive Analysis on Controlling and Hybrid Synchronization in Identical Chaotic Systems via Active Control Method. Proc. J. Physics Conf. Ser. 2022, 2267, 012039. [Google Scholar] [CrossRef]
- Singh, A.K.; Yadav, V.K.; Das, S. Dual combination synchronization of the fractional order complex chaotic systems. J. Comput. Nonlinear Dyn. 2017, 12, 011017. [Google Scholar] [CrossRef]
- Zhang, B.; Deng, F. Double-compound synchronization of six memristor-based Lorenz systems. Nonlinear Dyn. 2014, 77, 1519–1530. [Google Scholar] [CrossRef]
- Chaudhary, H.; Khan, A.; Sajid, M. An investigation on microscopic chaos controlling of identical chemical reactor system via adaptive controlled hybrid projective synchronization. Eur. Phys. J. Spec. Top. 2021, 231, 453–463. [Google Scholar] [CrossRef]
- Chaudhary, H.; Khan, A.; Nigar, U.; Kaushik, S.; Sajid, M. An Effective Synchronization Approach to Stability Analysis for Chaotic Generalized Lotka–Volterra Biological Models Using Active and Parameter Identification Methods. Entropy 2022, 24, 529. [Google Scholar] [CrossRef]
- Khan, T.; Chaudhary, H. Controlling chaos generated in predator-prey interactions using adaptive hybrid combination synchronization. In Proceedings of the 3rd International Conference on Computing Informatics and Networks; Springer: Singapore, 2021; pp. 449–459. [Google Scholar]
- Rossler, O. An equation for hyperchaos. Phys. Lett. A 1979, 71, 155–157. [Google Scholar] [CrossRef]
- Fowler, A.; Gibbon, J.; McGuinness, M. The complex Lorenz equations. Phys. D Nonlinear Phenom. 1982, 4, 139–163. [Google Scholar] [CrossRef]
- Sun, J.; Shen, Y.; Zhang, G.; Xu, C.; Cui, G. Combination–combination synchronization among four identical or different chaotic systems. Nonlinear Dyn. 2013, 73, 1211–1222. [Google Scholar] [CrossRef]
- Yadav, V.K.; Prasad, G.; Srivastava, M.; Das, S. Combination–combination phase synchronization among non-identical fractional order complex chaotic systems via nonlinear control. Int. J. Dyn. Control 2019, 7, 330–340. [Google Scholar] [CrossRef]
- Khan, A.; Khattar, D.; Prajapati, N. Dual combination combination multi switching synchronization of eight chaotic systems. Chin. J. Phys. 2017, 55, 1209–1218. [Google Scholar] [CrossRef]
- Xiao, J.; Ma, Z.z.; Yang, Y.h. Dual synchronization of fractional-order chaotic systems via a linear controller. Sci. World J. 2013, 2013, 159194. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.; Xiang, W.; Ji, Q. Generation of fractional-order Chua’s chaotic system and it’s synchronization. In Proceedings of the 2018 Chinese Control And Decision Conference (CCDC), Shenyang, China, 9–11 June 2018; pp. 599–603. [Google Scholar]
- Yadav, V.K.; Srivastava, M.; Das, S. Dual Combination Synchronization Scheme for Nonidentical Different Dimensional Fractional Order Systems Using Scaling Matrices. In Mathematical Techniques of Fractional Order Systems; Elsevier: Amsterdam, The Netherlands, 2018; pp. 347–374. [Google Scholar]
- Khan, A.; Khattar, D.; Agrawal, N. Dual Combination Combination Anti Synchronization of Eight Fractional Order Chaotic Systems. Int. J. Appl. Comput. Math. 2022, 8, 33. [Google Scholar] [CrossRef]
- Khan, A.; Tyagi, A. Fractional order disturbance observer based adaptive sliding mode synchronization of commensurate fractional order Genesio-Tesi system. AEU-Int. J. Electron. Commun. 2017, 82, 346–357. [Google Scholar] [CrossRef]
- Mahmoud, G.M.; Mahmoud, E.E. Synchronization and control of hyperchaotic complex Lorenz system. Math. Comput. Simul. 2010, 80, 2286–2296. [Google Scholar] [CrossRef]
- Liu, X.; Hong, L.; Yang, L. Fractional-order complex T system: Bifurcations, chaos control, and synchronization. Nonlinear Dyn. 2014, 75, 589–602. [Google Scholar] [CrossRef]
- Singh, A.K.; Yadav, V.K.; Das, S. Synchronization between fractional order complex chaotic systems. Int. J. Dyn. Control 2017, 5, 756–770. [Google Scholar] [CrossRef]
- Luo, C.; Wang, X. Chaos generated from the fractional-order complex Chen system and its application to digital secure communication. Int. J. Mod. Phys. C 2013, 24, 1350025. [Google Scholar] [CrossRef]
- Chong-Xin, L.; Ling, L. Circuit implementation of a new hyperchaos in fractional-order system. Chin. Phys. B 2008, 17, 2829. [Google Scholar] [CrossRef]
- Vishal, K.; Agrawal, S.K.; Das, S. Hyperchaos control and adaptive synchronization with uncertain parameter for fractional-order Mathieu–van der Pol systems. Pramana 2016, 86, 59–75. [Google Scholar] [CrossRef]
- He, J.M.; Chen, F.Q. A new fractional order hyperchaotic Rabinovich system and its dynamical behaviors. Int. J. Non-Linear Mech. 2017, 95, 73–81. [Google Scholar] [CrossRef]
- Vaidyanathan, S.; Volos, C.K.; Pham, V. Analysis, control, synchronization and SPICE implementation of a novel 4-D hyperchaotic Rikitake dynamo system without equilibrium. J. Eng. Sci. Technol. Rev. 2015, 8, 232–244. [Google Scholar] [CrossRef]


| Types of Synchronization | Time |
|---|---|
| Dual C–C anti synchronization of eight FO chaotic systems [36] | 4.5 |
| C–C phase synchronization among FO chaotic systems [31] | 5 |
| Dual C–C multi switching synchronization [32] | 4 |
| Dual synchronization of FO chaotic systems via linear controller [33] | 30 |
| Parameter Identification and Finite-Time C–C Synchronization [34] | 3 |
| Dual C–C hybrid synchronization in FO chaotic systems [Current paper] | 2.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sajid, M.; Chaudhary, H.; Allahem, A.; Kaushik, S. Chaos Controllability in Fractional-Order Systems via Active Dual Combination–Combination Hybrid Synchronization Strategy. Fractal Fract. 2022, 6, 717. https://doi.org/10.3390/fractalfract6120717
Sajid M, Chaudhary H, Allahem A, Kaushik S. Chaos Controllability in Fractional-Order Systems via Active Dual Combination–Combination Hybrid Synchronization Strategy. Fractal and Fractional. 2022; 6(12):717. https://doi.org/10.3390/fractalfract6120717
Chicago/Turabian StyleSajid, Mohammad, Harindri Chaudhary, Ali Allahem, and Santosh Kaushik. 2022. "Chaos Controllability in Fractional-Order Systems via Active Dual Combination–Combination Hybrid Synchronization Strategy" Fractal and Fractional 6, no. 12: 717. https://doi.org/10.3390/fractalfract6120717
APA StyleSajid, M., Chaudhary, H., Allahem, A., & Kaushik, S. (2022). Chaos Controllability in Fractional-Order Systems via Active Dual Combination–Combination Hybrid Synchronization Strategy. Fractal and Fractional, 6(12), 717. https://doi.org/10.3390/fractalfract6120717







