Fractal Analysis of Particle Distribution and Scale Effect in a Soil–Rock Mixture
Abstract
:1. Introduction
2. Fractal Model
2.1. Fractal Mathematical Model
2.2. Fractal Analysis of SRM Samples
3. Predictive Theory
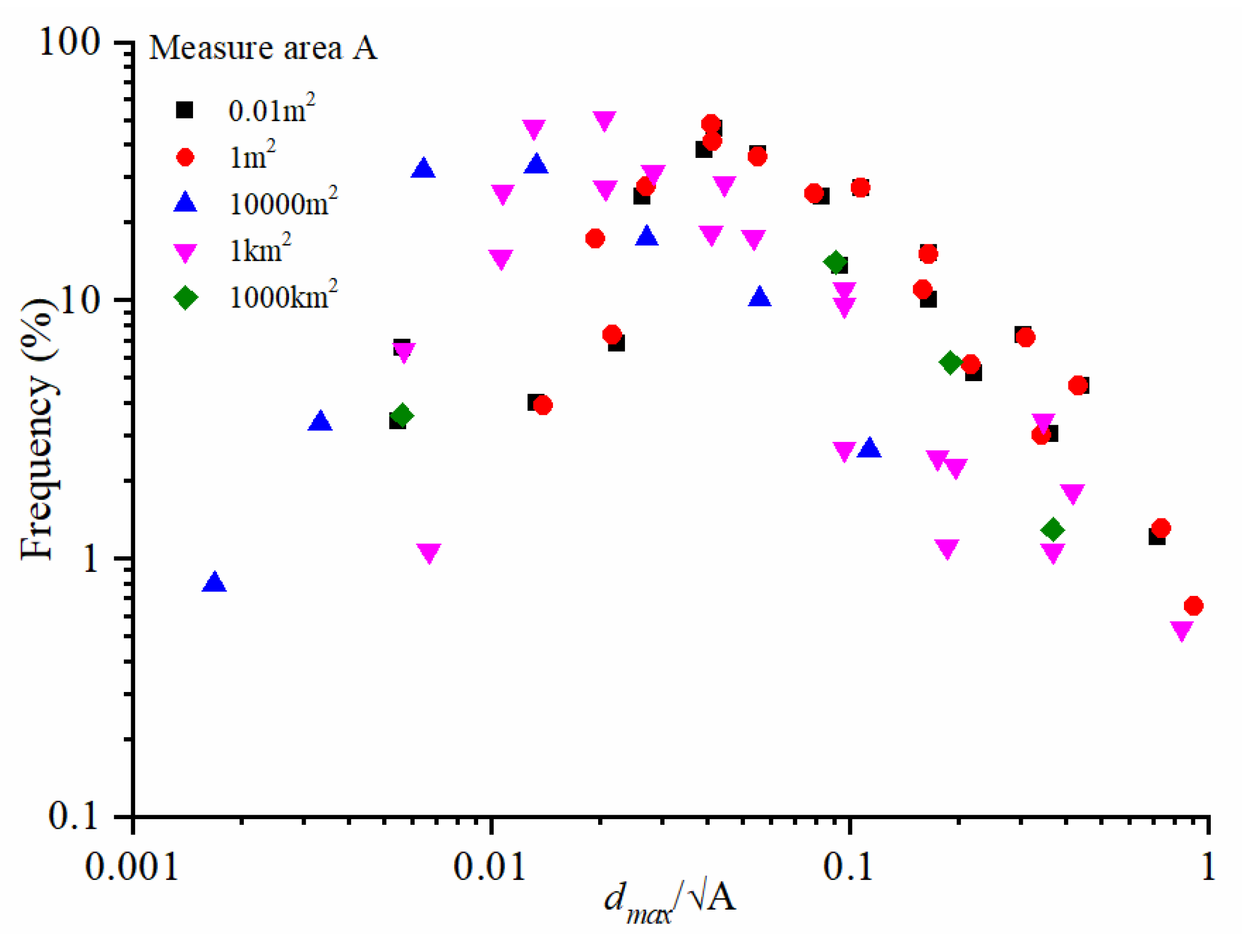
3.1. Relative Threshold between Soil and Rock Blocks
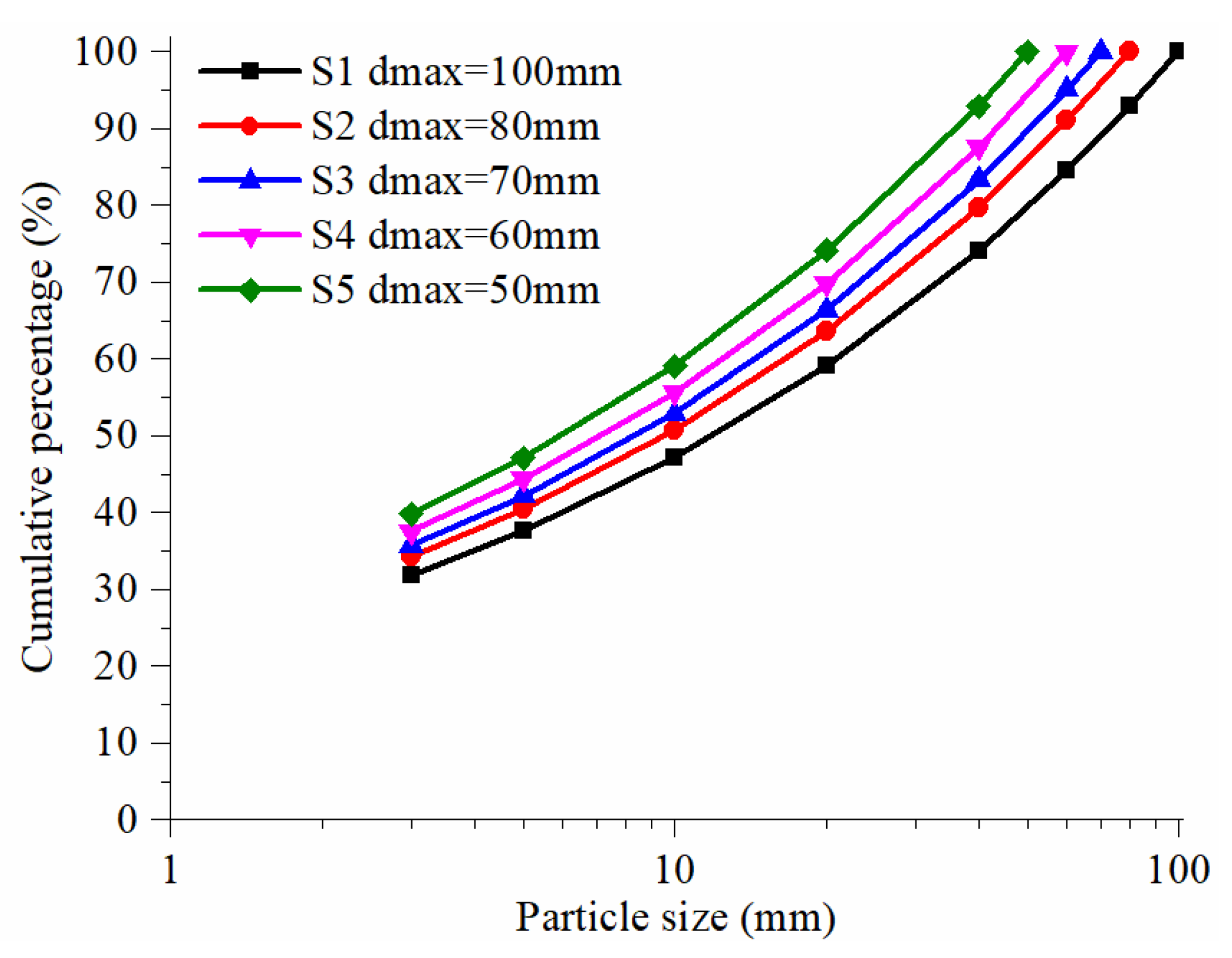
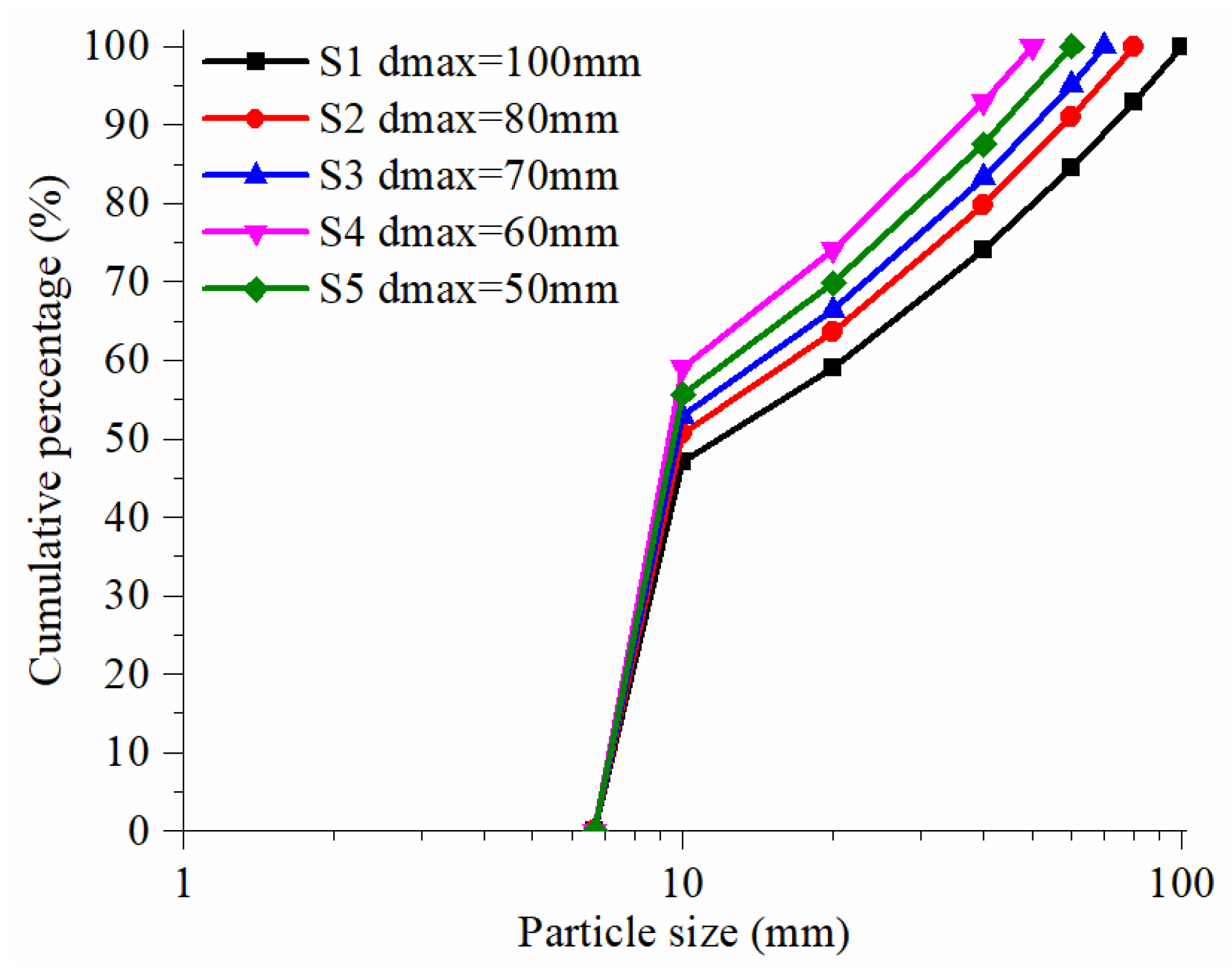
3.2. Prediction of Particle Gradation Curves at Different Scales
4. Simulation Method
4.1. Simulation of Large-Scale Direct Shear Tests of SRM
4.2. Scale Effect Analysis
4.2.1. Shear Displacement
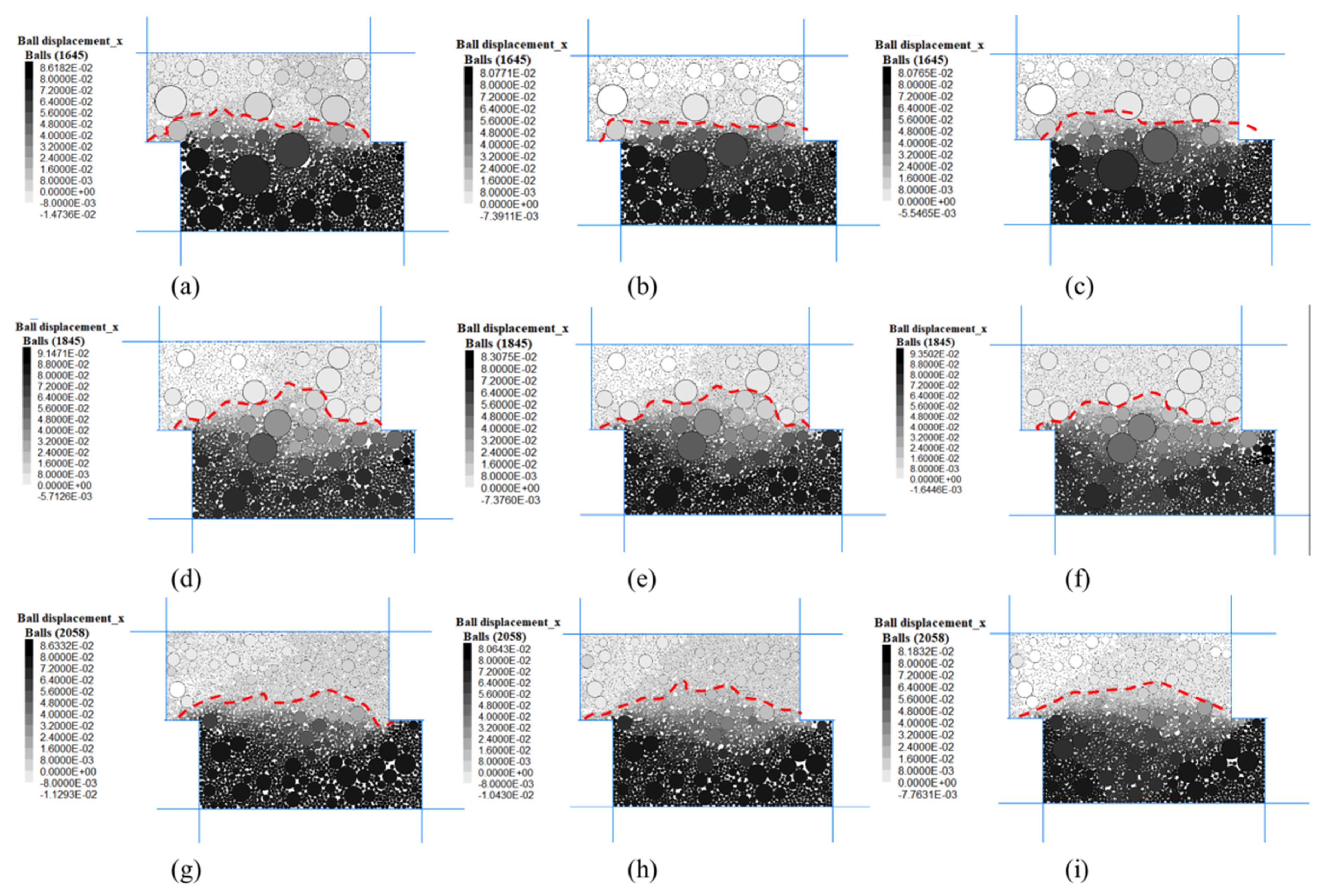
4.2.2. Shear Zone
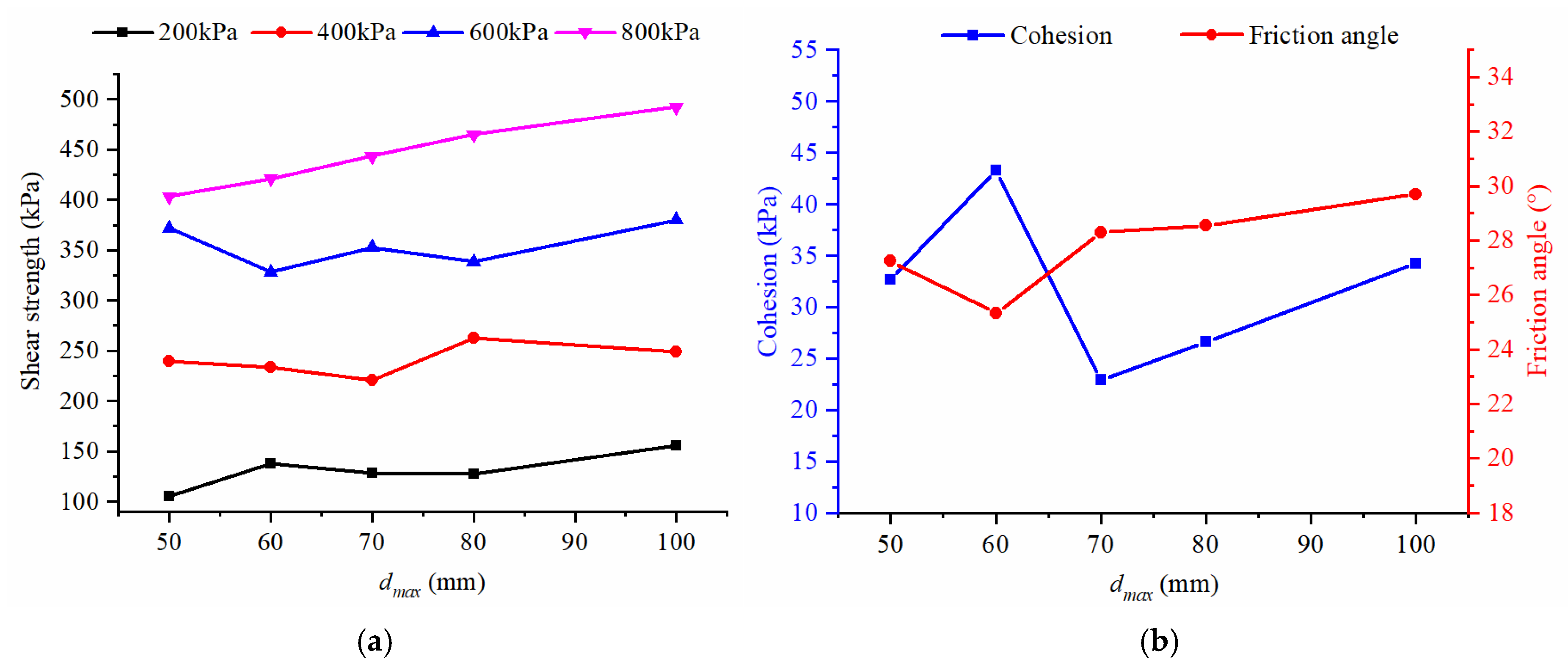
4.2.3. Shear Strength
5. Estimation of Shear Strength Parameters of SRM
6. Conclusions
- (1)
- Based on the particle gradation data of SRM, the relationship curve between particle cumulative mass percentage lg (M(r < R)/MT and particle size lg R in the double logarithmic coordinate system can be drawn, whether the SRM has a fractal structure can be judged and the corresponding fractal dimension can be obtained. The case study shows that the SRM in Zhaizi village has a fractal structure, and the fractal dimension is 2.67. In addition, there is an obvious double-fractal structure in the SRM, with a maximum particle size of 60 mm, and the threshold between soil and rock blocks of the SRM in this area was determined to be 2 mm.
- (2)
- Based on the self-similarity and fractal structure of the natural SRM, the grading curve and the particle group mass under the condition of different maximum particle diameters could be obtained. This method not only can expand the study range of particle size of SRM, but also overcome the deficiency of conventional direct shear tests, which remain limited by sample size.
- (3)
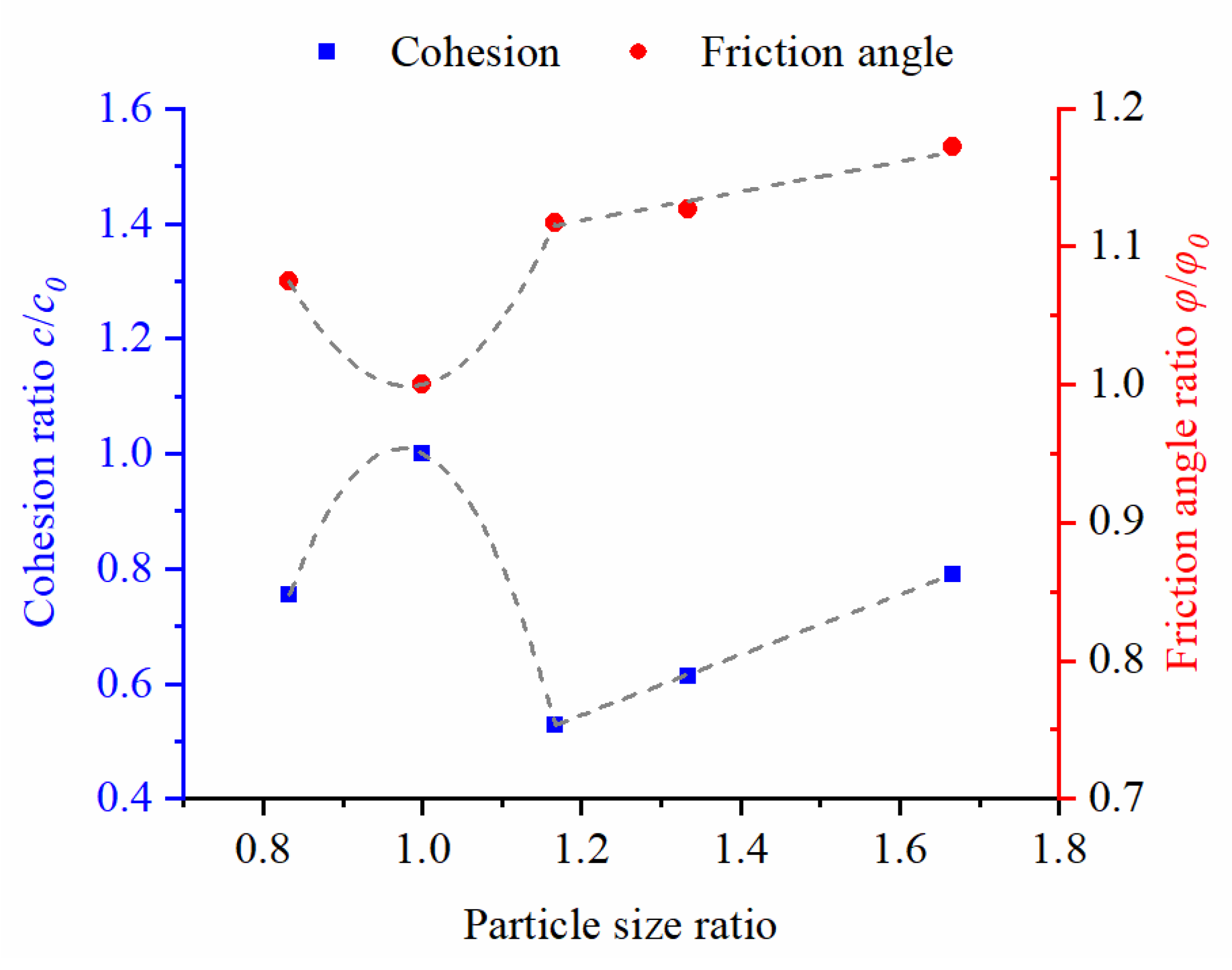
- The increase of the maximum particle size leads to a more obvious positive influence on the shear stress. The shear contraction at the beginning of shearing then becomes dilated under the low normal stress with the fluctuation in the shear zone. With the increase of the particle size ratio, the friction-angle ratio increases. Meanwhile, the cohesion ratio increases up to a particle-size ratio of 1.3 and then decreases.
- (4)
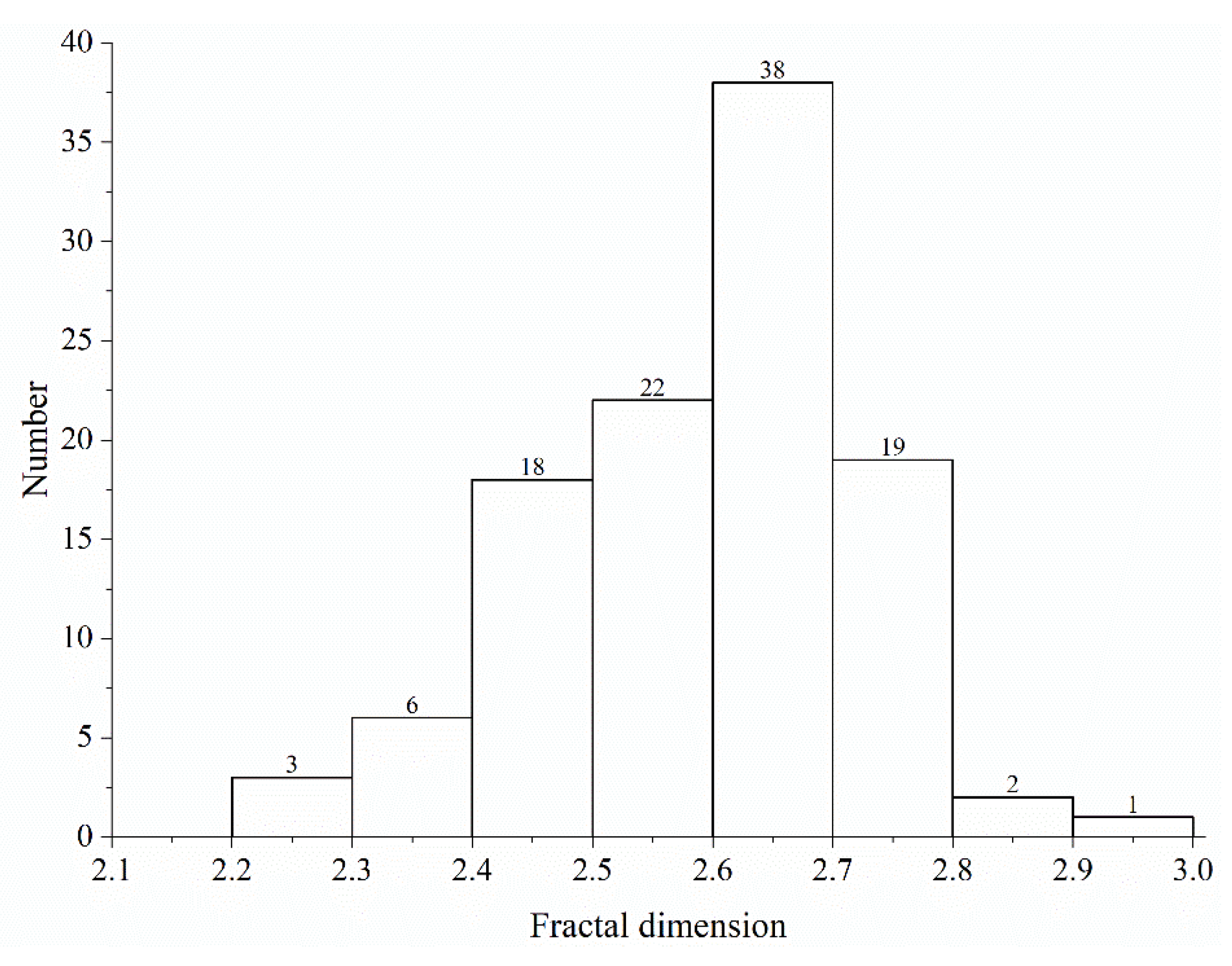
- In Southwest China, the frequency of the fractal dimension of the SRM is in the normal distribution, and the median fractal dimension is 2.62. In the range of this fractal dimension, by taking the particle diameter of 60 mm as a standard value, the piece-wise functional relationship between the strength-parameter ratio and particle-size ratio is established. When particle size is less than 70 mm, the strength parameters show a parabolic trend and the particle size increases. When the particle size is larger than 70 mm, the responses of the strength parameters keep increasing in a nearly linear trend.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Medley, E.; Goodman, E. Estimating the block volumetric proportions of melanges and similar block-in-matrix rocks (Bimrocks). In Proceedings of the 1st North American Rock Mechanics Symposium, Austin, TX, USA, 1–3 June 1994. [Google Scholar]
- Medley, E. The Engineering Characterization of Melanges and Similar Block-In-Matrix Rocks (Bimrocks). PhD Thesis, University of California, Berkeley, CA, USA, 1994. [Google Scholar]
- Lindquist, E.S.; Goodman, E. Strength and deformation properties of a physical model melange. In Proceedings of the 1st North American Rock Mechanics Symposium, Austin, TX, USA, 1–3 June 1994. [Google Scholar]
- Lindquist, E.S. The Strength and Deformation Properties of Melange. PhD Thesis, University of California, Berkeley, CA, USA, 1994. [Google Scholar]
- You, X. Stochastic Structural Model of the Earth-Rock Aggregate and Its Application; Northern Jiaotong University: Beijing, China, 2001. [Google Scholar]
- Xu, W.J.; Hu, L.; Tan, J. Some geomechanical properties of soil–rock mixtures in the Hutiao Gorge area, China. Geotechnique 2007, 57, 255–264. [Google Scholar] [CrossRef]
- Xu, W.-J.; Xu, Q.; Hu, R.-L. Study on the shear strength of soil–rock mixture by large scale direct shear test. Int. J. Rock. Mech. Min. 2011, 48, 1235–1247. [Google Scholar]
- Editorial Committee of Handbook of Engineering Geology. Handbook of Engineering Geology; China Building Industry Press: Beijing, China, 1982. [Google Scholar]
- Wang, S.; Li, Y.; Gao, X.; Xue, Q.; Zhang, P.; Wu, Z. Influence of volumetric block proportion on mechanical properties of virtual soil-rock mixtures. Eng. Geol. 2020, 278, 105850. [Google Scholar] [CrossRef]
- Zhang, Z.; Sheng, Q.; Fu, X.; Zhou, Y.; Huang, J.; Du, Y. An approach to predicting the shear strength of soil-rock mixture based on rock block proportion. Bull. Eng. Geol. Environ. 2020, 79, 2423–2437. [Google Scholar] [CrossRef]
- Marachi, N.D. Strength and Deformation Characteristics of Rockfill Materials. PhD Thesis, University of California, Berkeley, CA, USA, 1969. [Google Scholar]
- Afifipour, M.; Moarefvand, P. Mechanical behavior of bimrocks having high rock block proportion. Int. J. Rock. Mech. Min. 2014, 65, 40–48. [Google Scholar] [CrossRef]
- Kalender, A.; Sonmez, H.; Medley, E.; Tunusluoglu, C.; Kasapoglu, K.E. An approach to predicting the overall strengths of unwelded bimrocks and bimsoils. Eng. Geol. 2014, 183, 65–79. [Google Scholar] [CrossRef]
- Wang, Y.; Li, X. Experimental study on cracking damage characteristics of a soil and rock mixture by UPV testing. Bull. Eng. Geol. Environ. 2015, 74, 775–788. [Google Scholar] [CrossRef]
- Avnir, D.; Farin, D.; Pfeifer, P. Surface geometric irregularity of particulate materials: The fractal approach. J. Colloid Interface Sci. 1985, 103, 112–123. [Google Scholar] [CrossRef]
- Turcotte, D.L. Fractals and fragmentation. J. Geophys. Res. Atmos. 1986, 91, 1921. [Google Scholar] [CrossRef]
- Goldstein, G.; Benaroya, H. Fractal modelling of one-dimensional layered medium. Appl. Math. Model 1989, 13, 555–558. [Google Scholar] [CrossRef]
- Jafari, F.; Asgari, M.S.; Pishkoo, A. The fractal calculus for fractal materials. Fractal Fract. 2019, 3, 8. [Google Scholar] [CrossRef] [Green Version]
- Sun, Y.F.; Sumelka, W. Fractional viscoplastic model for soils under compression. Acta Mechanica 2019, 230, 3365–3377. [Google Scholar] [CrossRef]
- Sarkar, D.; Knig, D.; Goudarzy, M. The influence of particle characteristics on the index void ratios in granular materials. Particuology 2019, 46, 1–13. [Google Scholar] [CrossRef]
- Sun, Y.F.; Sumelka, W.; Gao, Y.F. Reformulated fractional plasticity for soil-structure interface. Mech. Res. Commun. 2020, 108, 103580. [Google Scholar] [CrossRef]
- Bohaienko, V.; Bulavatsky, V. Fractional-fractal modeling of filtration-consolidation processes in saline saturated soils. Fractal Fract. 2020, 4, 59. [Google Scholar] [CrossRef]
- Sun, Y.F.; Chen, C. Fractional order creep model for coral sand. Mech. Time Depend. Mater. 2019, 23, 465–476. [Google Scholar] [CrossRef]
- McDowell, G.R.; Bolton, M.D.; Robertson, D. The fractal crushing of granular materials. J. Mech. Phys. Solids 1996, 44, 2079–2101. [Google Scholar] [CrossRef]
- Yang, Z.Y.; Taghichian, A.; Huang, G.D. On the applicability of self-affinity concept in scale of three-dimensional rock joints. Int. J. Rock. Mech. Min. 2011, 48, 1173–1187. [Google Scholar] [CrossRef]
- Wu, L.; Zhu, S.; Wang, Y.; Wei, K.; Lu, C. A modified scale method based on fractal theory for rockfill materials. Eur. J. Environ. Civ. Eng. 2014, 18, 106–127. [Google Scholar] [CrossRef]
- Luo, M.; Glover, P.W.J.; Zhao, P.; Li, D. 3D digital rock modeling of the fractal properties of pore structures. Mar. Pet. Geol. 2020, 122, 104706. [Google Scholar] [CrossRef]
- Li, X.; Luo, M.; Liu, J. Fractal characteristics based on different statistical objects of process-based digital rock models. J. Pet. Sci. Eng. 2019, 179, 19–30. [Google Scholar] [CrossRef]
- Sun, Y.F.; Sumelka, W. State-dependent fractional plasticity model for the true triaxial behaviour of granular soil. Arch. Mech. 2019, 71, 23–47. [Google Scholar]
- Basirat, R.; Goshtasbi, K.; Ahmadi, M. Determination of the fractal dimension of the fracture network system using image processing technique. Fractal Fract. 2019, 3, 17. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.Q.; Sheng, Q.; Li, N.N.; Fu, X.D. The dynamic mechanical properties of a hard rock under true triaxial damage-controlled dynamic cyclic loading with different loading rates: A case study. Rock Mech. Rock Eng. 2022, 55, 1–22. [Google Scholar] [CrossRef]
- Sun, Y.F.; Gao, Y.F.; Chen, C. Critical-state fractional model and its numerical scheme for isotropic granular soil considering state dependence. Int. J. Geomech. 2019, 19, 4019001. [Google Scholar] [CrossRef]
- Tao, G.; Wu, Z.; Li, W.; Li, Y.; Dong, H. Simplified relation model of soil saturation permeability coefficient and air-entry value and its application. Fractal Fract. 2021, 5, 180. [Google Scholar] [CrossRef]
- Sun, Y.F.; Sumelka, W.; Gao, Y.F.; Nimbalkar, S. Phenomenological fractional stress-dilatancy model for granular soil and soil-structure interface under monotonic and cyclic loads. Acta Geotechnica 2021, 16, 3115–3132. [Google Scholar] [CrossRef]
- Zhao, Z.; Ni, X.; Cao, Y.; Shi, Y. Application of fractal theory to predict the coal permeability of multi-scale pores and fractures. Energy Rep. 2021, 7, 10–18. [Google Scholar] [CrossRef]
- Sui, L.; Yu, J.; Cang, D.; Miao, W.; Wang, H.; Zhang, J.; Yin, S.; Chang, K. The fractal description model of rock fracture networks characterization. Chaos Solitons Fractals 2019, 129, 71–76. [Google Scholar] [CrossRef]
- Xiao, Y.; Meng, M.; Daouadji, A.; Chen, Q.; Wu, Z.; Jiang, X. Effects of particle size on crushing and deformation behaviors of rockfill materials. Geosci. Front. 2020, 11, 375–388. [Google Scholar] [CrossRef]
- He, S.H.; Ding, Z.; Hu, H.-B.; Gao, M. Effect of grain size on microscopic pore structure and fractal characteristics of carbonate-based sand and silicate-based sand. Fractal Fract. 2021, 5, 152. [Google Scholar] [CrossRef]
- Xu, W.J.; Yue, Z.Q.; Hu, L. Study on the mesostructure and mesomechanical characteristics of the soil-rock mixture using digital image processing based finite element method. Int. J. Rock. Mech. Min. 2008, 45, 749–762. [Google Scholar] [CrossRef]
- Wu, L.Q.; Zhu, S.; Wei, K.M.; Lu, Y. The fractal properties of scale effect on the density of rock-fill materials. Adv. Mat. Res. 2013, 706–708, 520–525. [Google Scholar] [CrossRef]
- Pi, Z.; Zhou, Z.; Li, X.; Wang, S. Digital image processing method for characterization of fractures, fragments, and particles of soil/rock-like materials. Mathematics 2021, 9, 815. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. The fractal geometry of nature. Am. J. Phys. 1983, 51, 286–287. [Google Scholar] [CrossRef]
- Tyler, S.W.; Wheatcraft, S.W. Fractal scaling of soil particle-size distributions: Analysis and limitations. Soil Sci. Soc. Am. J. 1992, 56, 362–369. [Google Scholar] [CrossRef]
- Fu, X.; Zhang, Z.; Sheng, Q.; Zhou, Y.; Huang, J.; Wu, Z.; Liu, M. Applications of an innovative strength parameter estimation method of the soilrock mixture in evaluating the deposit slope stability under rainfall. Front. Earth Sci. 2021, 9, 868. [Google Scholar] [CrossRef]
- Zhou, W.; Wang, D.; Ma, G.; Cao, X.; Hu, C.; Wu, W. Discrete element modeling of particle breakage considering different fragment replacement modes. Powder Technol. 2020, 360, 312–323. [Google Scholar] [CrossRef]
- Zhang, Z.L.; Xu, W.J.; Xia, W.; Zhang, H.Y. Large-scale in-situ test for mechanical characterization of soil–rock mixture used in an embankment dam. Int. J. Rock. Mech. Min. 2016, 86, 317–322. [Google Scholar] [CrossRef]
- Shi, D.D.; Cao, D.; Deng, Y.B.; Xue, J.F. DEM investigations of the effects of intermediate principal stress ratio and particle breakage on the critical state behaviors of granular soils. Powder Technol. 2021, 379, 547–559. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Itasca Consulting Group. PFC2D (Particle Flow Code in 2 Dimensions) Use’s Guide: Verification Problems and Example Applications; Itasca Consulting Group: Minneapolis, MN, USA, 2008. [Google Scholar]
- Wei, H.Z.; Wang, R.; Hu, M.J.; Zhao, H.Y.; Xu, X.Y. Strength behavior of gravelly soil with different coarse-grained contents in Jiangjiagou. Rock Soil Mech. 2008, 29, 48–51. [Google Scholar]
- Hu, W. Experimental Study on Shear Strength of Soil-Rock-Mixture in Xiluodu Reservoir; Institute of Rock and Soil Mechanics, Chinese Academy of Sciences: Wuhan, China, 2014. [Google Scholar]
- Gao, W.; Hu, R.; Oyediran, I.A.; Li, Z.Q.; Zhang, X.Y. Geomechanical characterization of Zhangmu soil-rock mixture deposit. Geotech. Geol. Eng. 2014, 32, 1329–1338. [Google Scholar] [CrossRef]
- Ma, C.; Zhan, H.B.; Zhang, T.; Yao, W.M. Investigation on shear behavior of soft interlayers by ring shear tests. Eng. Geol. 2019, 254, 34–42. [Google Scholar] [CrossRef]
- Tu, G.X.; Huang, D.; Huang, Q.; Deng, H. Effect of locally accumulated crushed stone soil on the infiltration of intense rainfall: A case study on the reactivation of an old deep landslide deposit. Bull. Eng. Geol. Environ. 2019, 78, 4833–4849. [Google Scholar] [CrossRef]




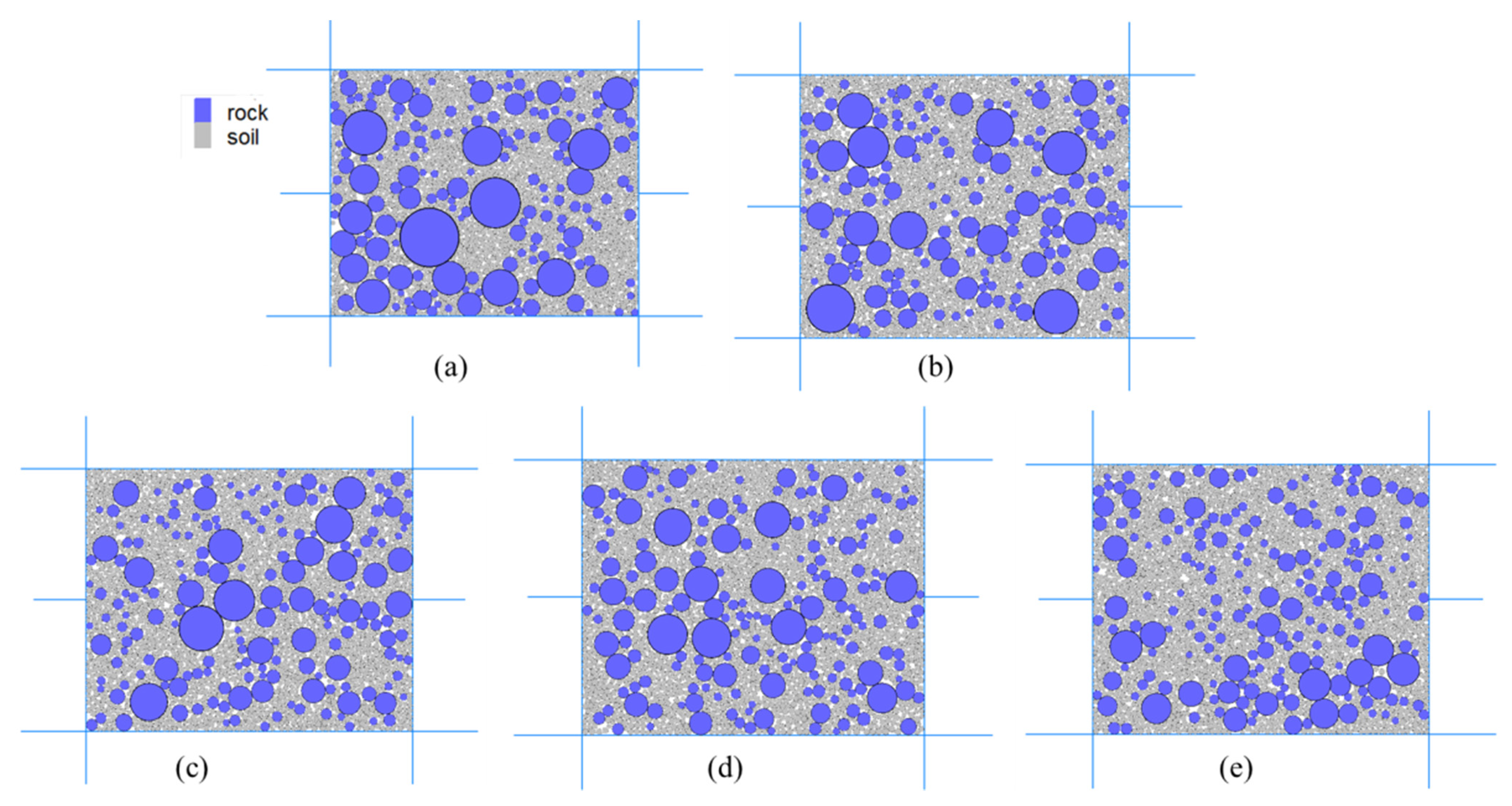

| Sample Number | Rock Proportion/% | Fine Particle/% | Maximum Particle Diameter/mm | Normal Stress/kPa |
|---|---|---|---|---|
| S1 | 52.9 | 47.1 | 100 | 200, 400, 600, 800 |
| S2 | 49.3 | 50.7 | 80 | |
| S3 | 47.1 | 52.9 | 70 | |
| S4 | 44.3 | 55.7 | 60 | |
| S5 | 40.9 | 59.1 | 50 |
| Number | Fractal Dimension | Location of the SRM | Resource |
|---|---|---|---|
| 1 | 2.67 | A deposit slope in Zhaizi village | This study |
| 2 | 2.52 | Soil–rock mixtures in the Hutiao Gorge area | Xu et al. (2007) [6] |
| 3 | 2.55 | Gravelly soil in Jiangjiagou Ravine in Yunnan | Wei et al. (2008) [50] |
| 4 | 2.62 | Fujiapingzi, Xiluodu Reservoir | Hu (2014) [51] |
| 2.64 | Ganhaizi, Xiluodu Reservoir | ||
| 2.59 | NiuGudang, Xiluodu Reservoir | ||
| 2.64 | Shuanglongba, Xiluodu Reservoir | ||
| 2.66 | Shaniwan, Xiluodu Reservoir | ||
| 5 | 2.68 | Zhangmu soil–rock mixture deposit in Southwestern China | Gao et al. (2014) [52] |
| 2.65 | |||
| 2.66 | |||
| 2.59 | |||
| 2.69 | |||
| 2.65 | |||
| 2.64 | |||
| 6 | 2.85 | Soil–rock mixture of Nuozhadu hydropower station in Yunnan | Zhang et al. (2016) [46] |
| 7 | 2.66 | An open-pit limestone mine in Esheng, Sichuan Province | Ma et al. (2019) [53] |
| 8 | 2.75 | Accumulated crushed stone soil in Deqin County, Yunnan | Tu et al. (2019) [54] |
| 2.75 | |||
| 2.74 | |||
| 2.75 | |||
| 2.45 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, X.; Ding, H.; Sheng, Q.; Zhang, Z.; Yin, D.; Chen, F. Fractal Analysis of Particle Distribution and Scale Effect in a Soil–Rock Mixture. Fractal Fract. 2022, 6, 120. https://doi.org/10.3390/fractalfract6020120
Fu X, Ding H, Sheng Q, Zhang Z, Yin D, Chen F. Fractal Analysis of Particle Distribution and Scale Effect in a Soil–Rock Mixture. Fractal and Fractional. 2022; 6(2):120. https://doi.org/10.3390/fractalfract6020120
Chicago/Turabian StyleFu, Xiaodong, Haifeng Ding, Qian Sheng, Zhenping Zhang, Dawei Yin, and Fei Chen. 2022. "Fractal Analysis of Particle Distribution and Scale Effect in a Soil–Rock Mixture" Fractal and Fractional 6, no. 2: 120. https://doi.org/10.3390/fractalfract6020120
APA StyleFu, X., Ding, H., Sheng, Q., Zhang, Z., Yin, D., & Chen, F. (2022). Fractal Analysis of Particle Distribution and Scale Effect in a Soil–Rock Mixture. Fractal and Fractional, 6(2), 120. https://doi.org/10.3390/fractalfract6020120





