Fractional Behaviours Modelling with Volterra Equations: Application to a Lithium-Ion Cell and Comparison with a Fractional Model
Abstract
:1. Introduction
2. Volterra Equations as Generalizations of Fractional Models
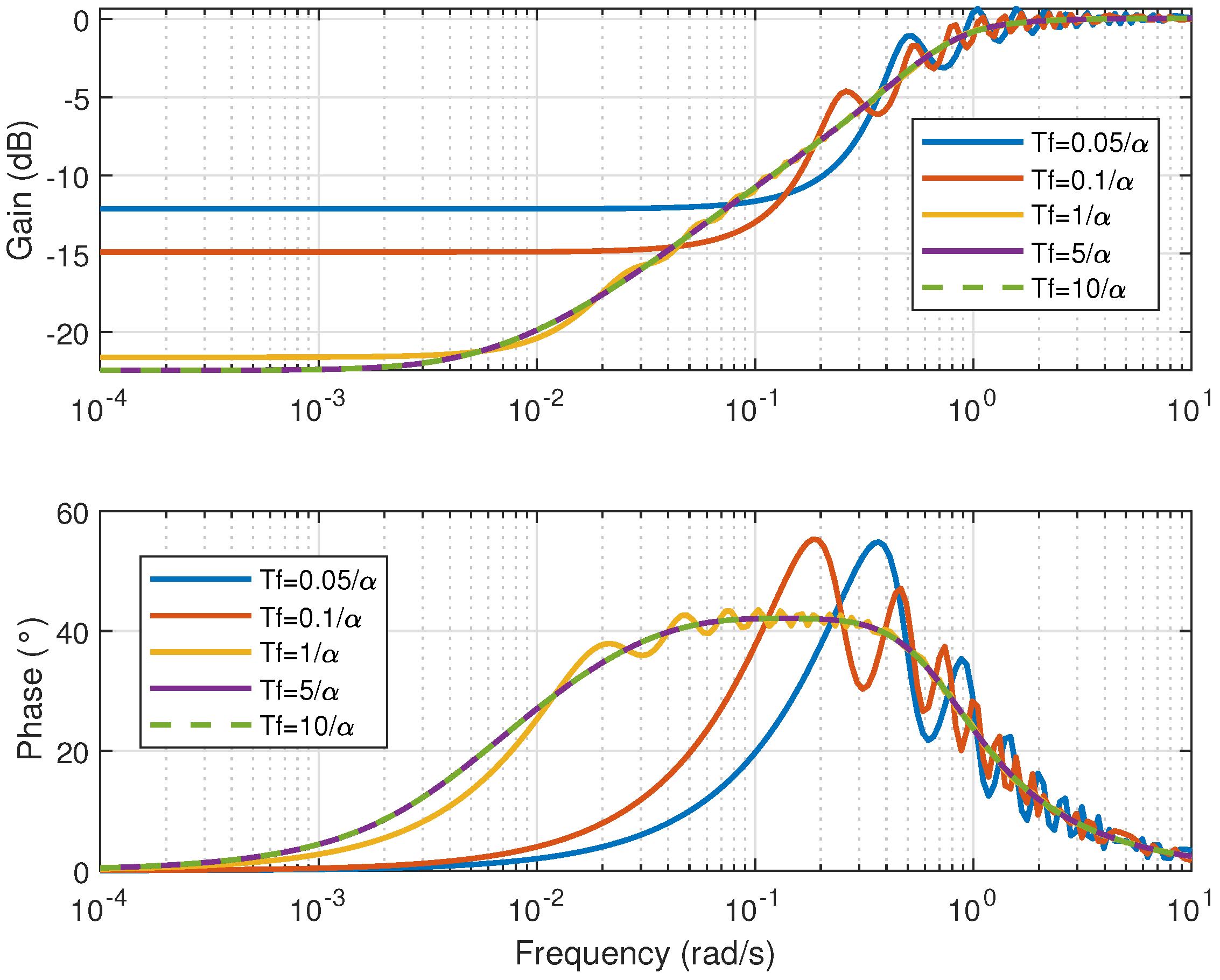
3. A Numerical Method to Determine the Kernel of the Volterra Model
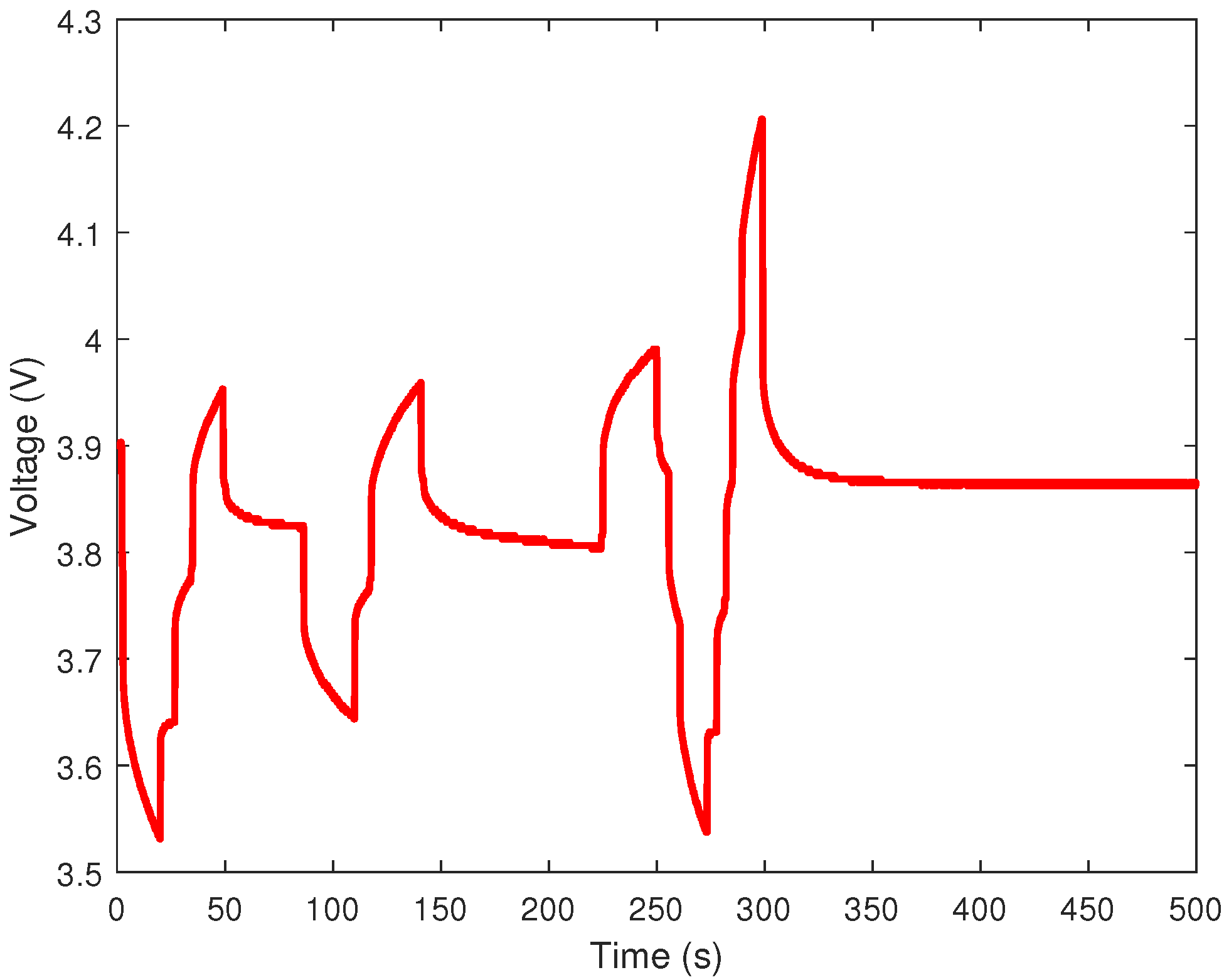
4. Application to Lithium-Ion Cell
- Electrochemical models, which accurately describe electrochemical reactions that take place in the electrodes and the electrolyte [33]—Pseudo-Two-Dimensional model and Single Particle Model belong to this category;
- Mathematical models, which are based on empirical equations or math-based stochastic models which only evaluate the charge-recovery effect and ignore all other factors. The number of equations is reduced and simplified compared to the electrochemical model [34];
- Circuit-oriented models, which are electrical-equivalent models or impedance models in which each component of the circuit is related to an electrochemical process of the battery to provide a good description of its internal behaviour [35];
- Combined models that consists of the combination of different electrical models and mathematical models in order to combine the best attributes of each model, such as the correct prediction of the battery lifetime, steady-state and transient responses, and accurate estimation of the state of charge [36].
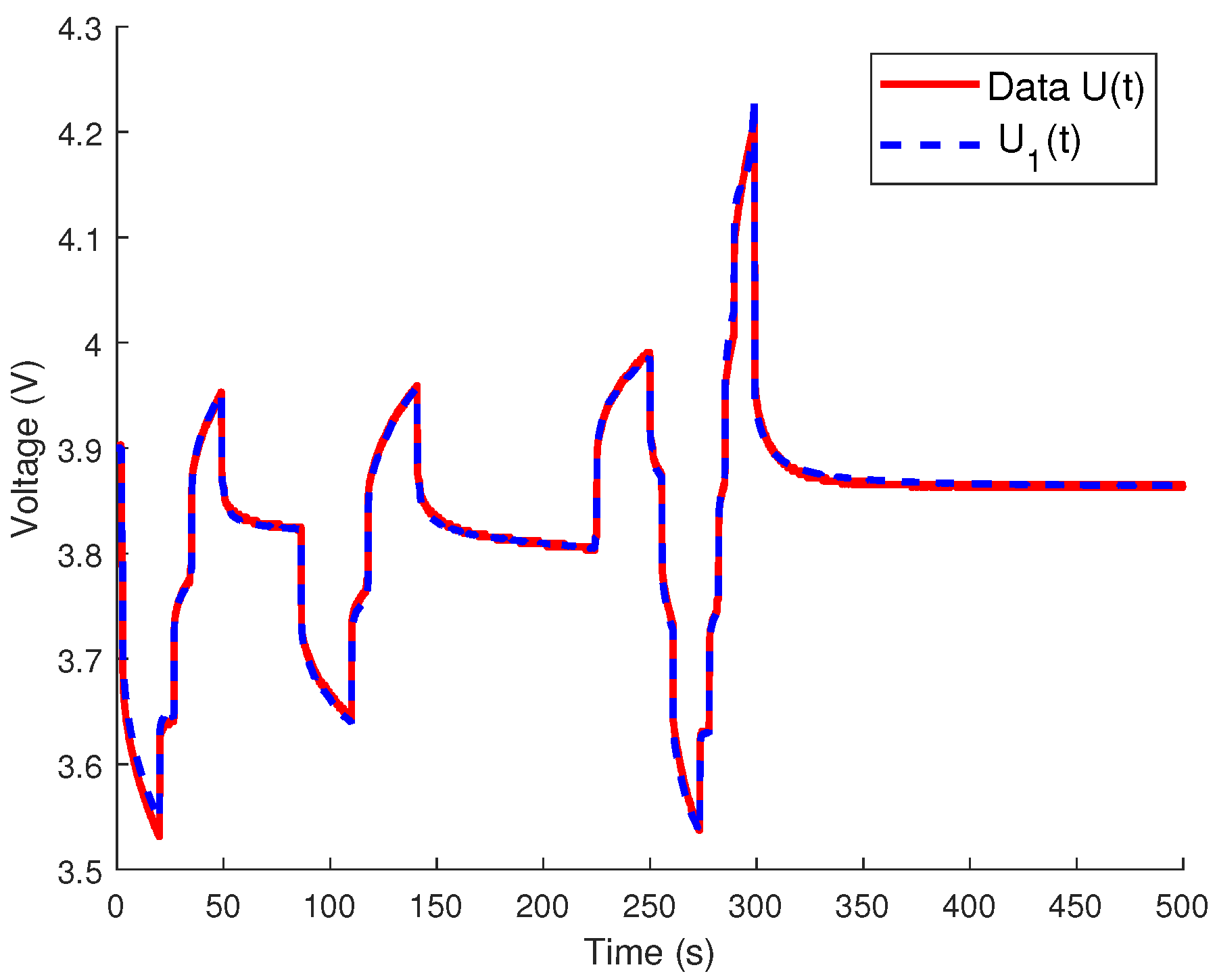
4.1. Fractional Model
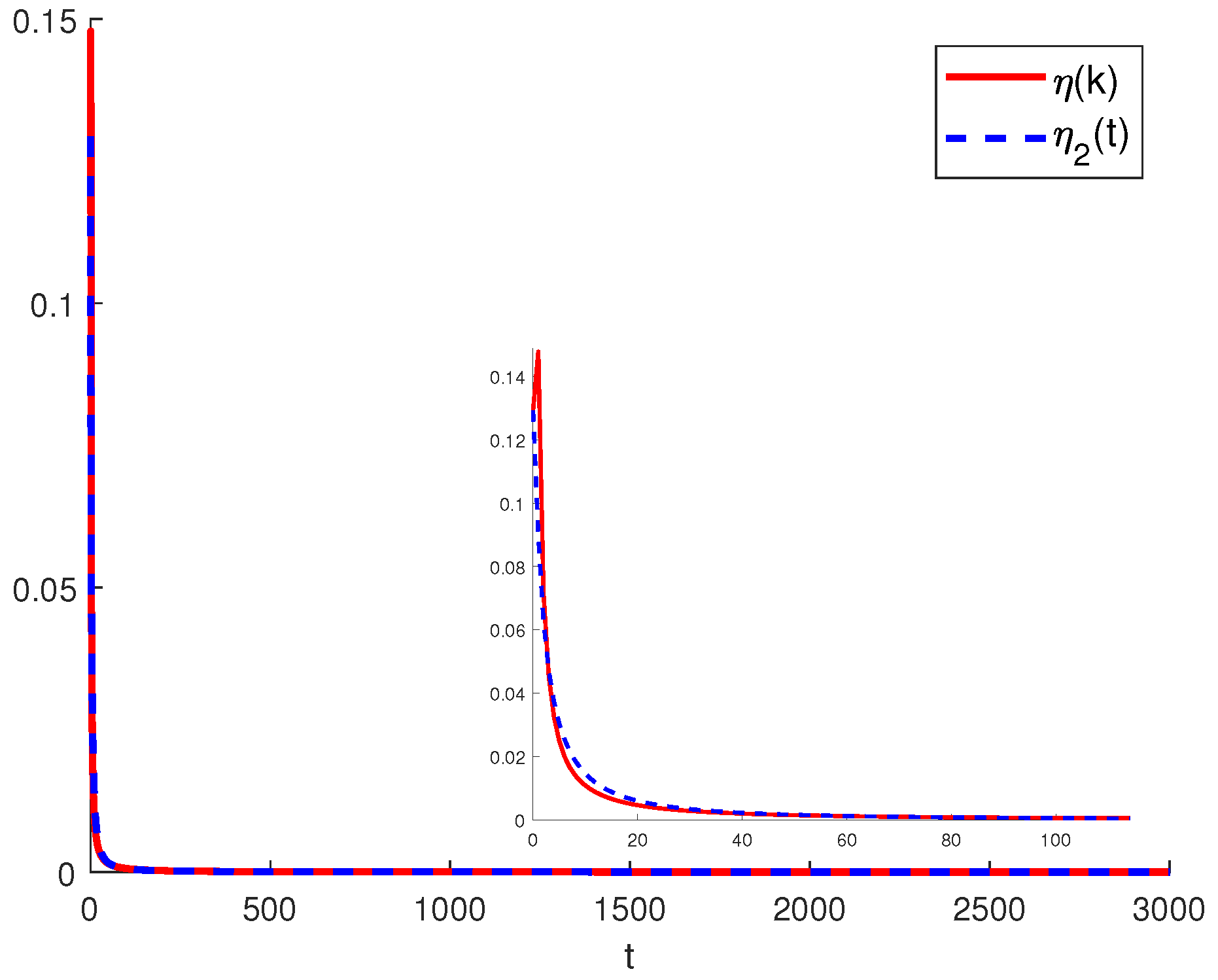
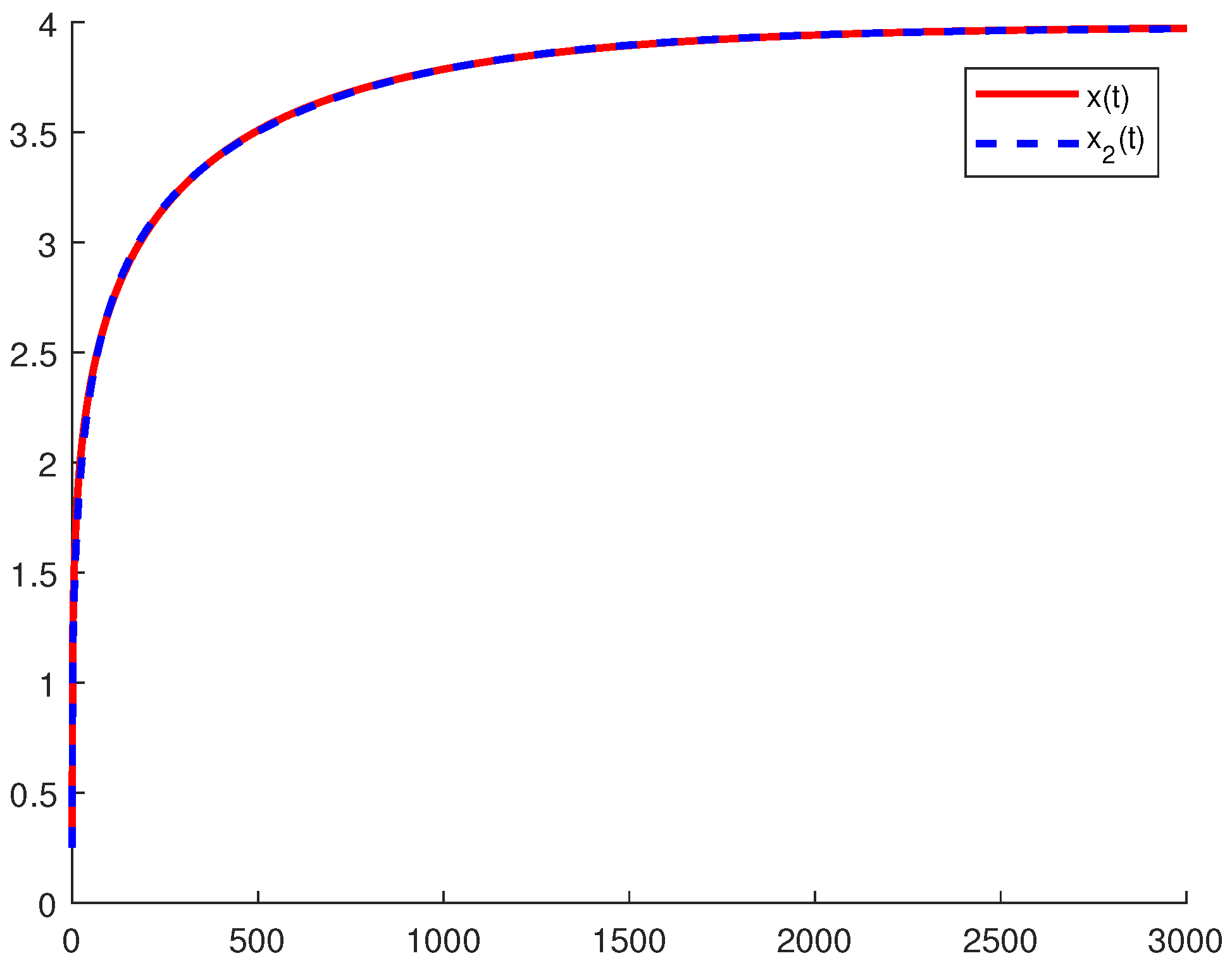
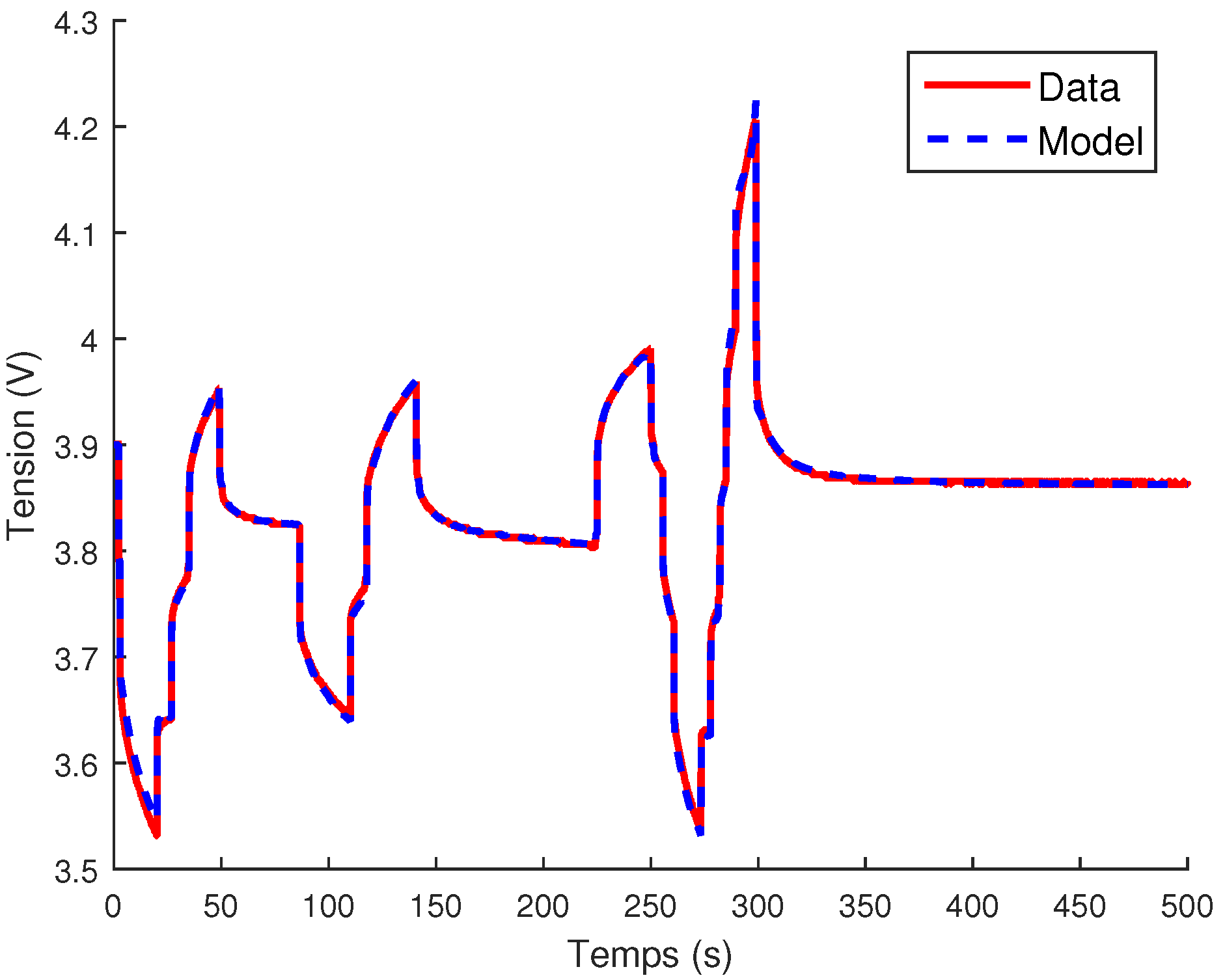
4.2. Volterra Model
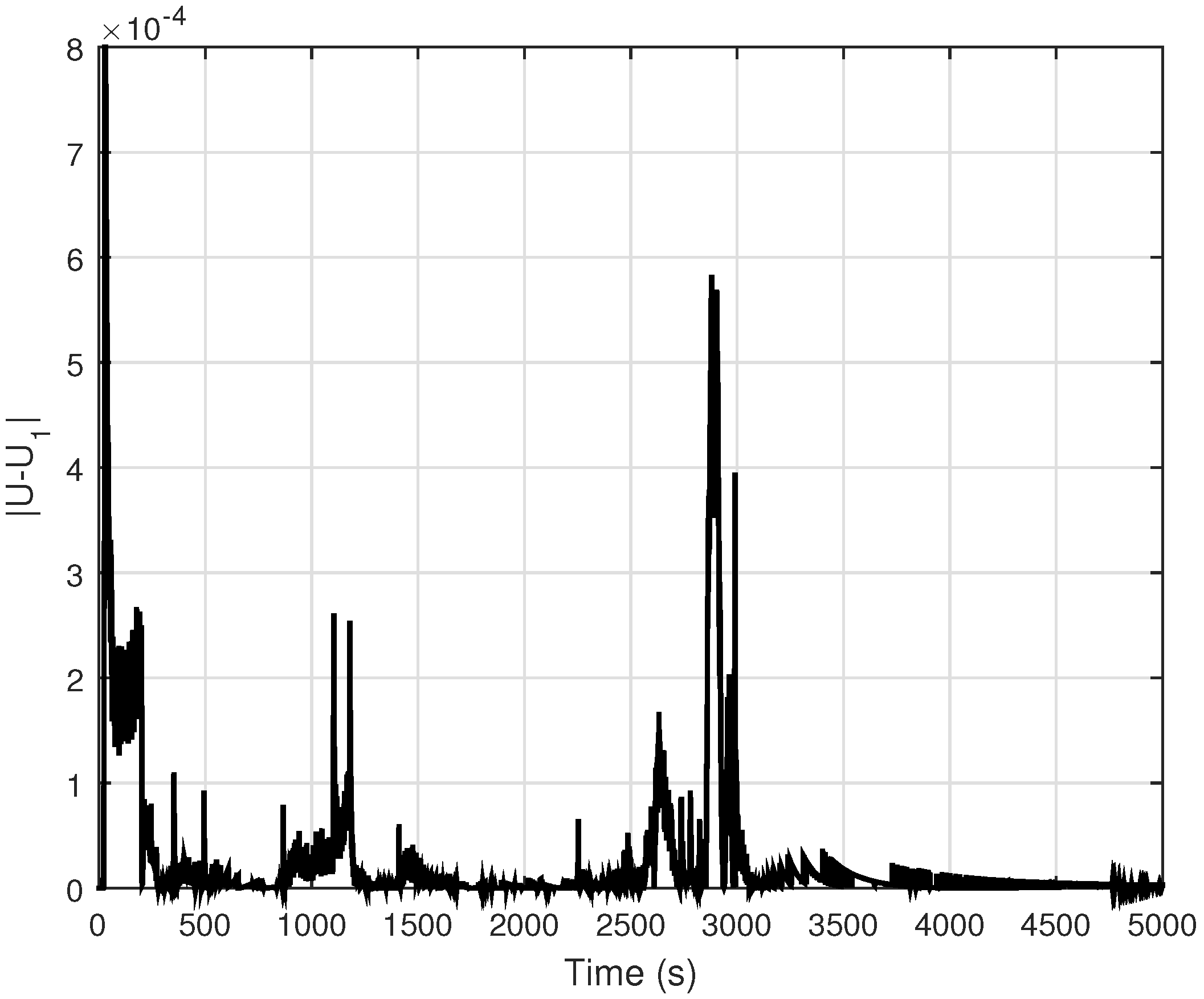
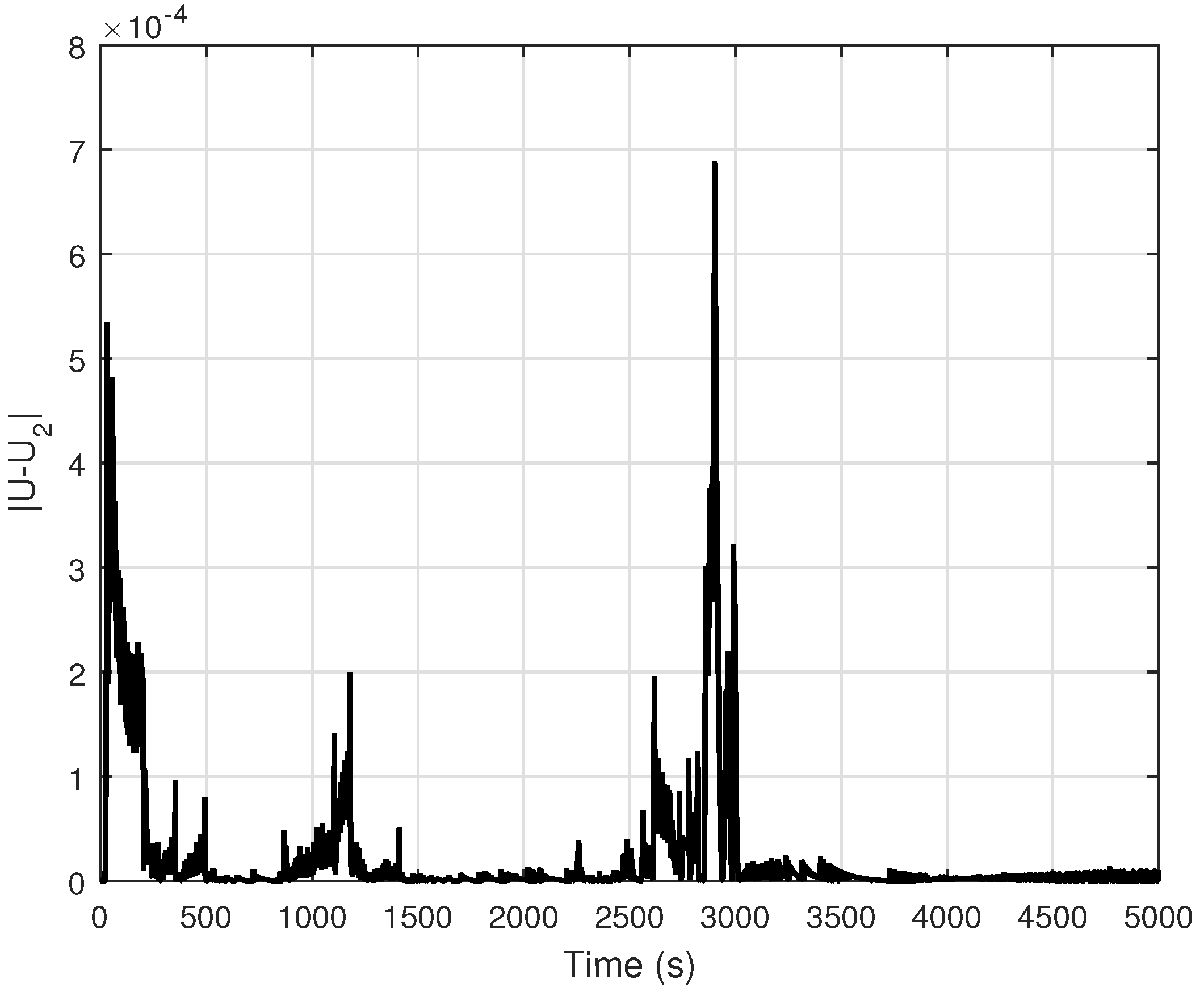
4.3. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Krapivsky, P.L.; Redner, S.; Ben-Naim, E. A Kinetic View of Statistical Physics; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Family, F.; Landau, D. Kinetics of Aggregation and Gelation; Elsevier: Amsterdam, The Netherlands, 1984. [Google Scholar]
- Rodrigues, S.; Munichandraiah, N.; Shukla, A. A review of state-of-charge indication of batteries by means of a.c. impedance measurements. J. Power Sources 2000, 87, 12–20. [Google Scholar] [CrossRef]
- Sabatier, J.; Aoun, M.; Oustaloup, A.; Grégoire, G.; Ragot, F.; Roy, P. Fractional system identification for lead acid battery state of charge estimation. Signal Process. 2006, 86, 2645–2657. [Google Scholar] [CrossRef]
- Battaglia, J.L.; Cois, O.; Puigsegur, L.; Oustaloup, A. Solving an inverse heat conduction problem using a non-integer identified model. Int. J. Heat Mass Transf. 2001, 44, 2671–2680. [Google Scholar] [CrossRef]
- Malti, R.; Sabatier, J.; Akçay, H. Thermal modeling and identification of an aluminum rod using fractional calculus. IFAC Proc. Vol. 2009, 42, 958–963. [Google Scholar] [CrossRef] [Green Version]
- Magin, R. Fractional Calculus in Bioengineering; Begell House Publishers Inc.: Danbury, CT, USA, 2006. [Google Scholar]
- Ionescu, C.; De Keyser, R.; Sabatier, J.; Oustaloup, A.; Levron, F. Low frequency constant-phase behavior in the respiratory impedance. Biomed. Signal Process. Control 2011, 6, 197–208. [Google Scholar] [CrossRef]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity; Imperial College Press: London, UK, 2010. [Google Scholar]
- Matignon, D.; D’Andréa Novel, B.; Depalle, P.; Oustaloup, A. Viscothermal Losses in Wind Instruments: A Non Integer Model. In Proceedings of the International Symposium on the Mathematical Theory of Networks and Systems (MTNS), Regensburg, Germany, 2–6 August 1993. [Google Scholar]
- Enacheanu, O. Modélisation fractale des réseaux électriques. Ph.D. Theses, Université Joseph-Fourier—Grenoble I, Grenoble, France, 2008. [Google Scholar]
- Sabatier, J.; Farges, C.; Tartaglione, V. Some Alternative Solutions to Fractional Models for Modelling Power Law Type Long Memory Behaviours. Mathematics 2020, 8, 196. [Google Scholar] [CrossRef] [Green Version]
- Dokoumetzidis, A.; Magin, R.; Macheras, P. A commentary on fractionalization of multi-compartmental models. J. Pharmacokinet. Pharmacodyn. 2010, 37, 203–207. [Google Scholar] [CrossRef] [PubMed]
- Balint, A.M.; Balint, S. Mathematical Description of the Groundwater Flow and that of the Impurity Spread, which Use Temporal Caputo or Riemann–Liouville Fractional Partial Derivatives, Is Non-Objective. Fractal Fract. 2020, 4, 36. [Google Scholar] [CrossRef]
- Sabatier, J. Fractional Order Models Are Doubly Infinite Dimensional Models and thus of Infinite Memory: Consequences on Initialization and Some Solutions. Symmetry 2021, 13, 1099. [Google Scholar] [CrossRef]
- Sabatier, J.; Farges, C. Initial value problems should not be associated to fractional model descriptions whatever the derivative definition used. AIMS Math. 2021, 6, 11318. [Google Scholar] [CrossRef]
- Volterra, V. Leçons sur les équations intégrales et les équations intégro-différentielles; Gauthier-Villars: Paris, France, 1913. [Google Scholar]
- Markova, E.; Sidler, I.; Solodusha, S. Integral Models Based on Volterra Equations with Prehistory and Their Applications in Energy. Mathematics 2021, 9, 1127. [Google Scholar] [CrossRef]
- Apartsin, A.; Sidler, I. Using the Nonclassical Volterra Equations of the First Kind to Model the Developing Systems. Autom. Remote Control 2013, 74, 899–910. [Google Scholar] [CrossRef]
- Micke, A.; Bülow, M. Application of Volterra integral equations to the modelling of the sorption kinetics of multi-component mixtures in porous media: I. Fundamentals. Gas Sep. Purif. 1990, 4, 158–164. [Google Scholar] [CrossRef]
- Szyłko-Bigus, O.; Śniady, P.; Zakęś, F. Application of Volterra integral equations in the dynamics of a multi-span Rayleigh beam subjected to a moving load. Mech. Syst. Signal Process. 2019, 121, 777–790. [Google Scholar] [CrossRef]
- Sabatier, J. Fractional State Space Description: A Particular Case of the Volterra Equations. Fractal Fract. 2020, 4, 23. [Google Scholar] [CrossRef]
- Cole, K.S.; Cole, R.H. Dispersion and Absorption in Dielectrics I. Alternating Current Characteristics. J. Chem. Phys. 1941, 9, 341–351. [Google Scholar] [CrossRef] [Green Version]
- Brewer, D.; Powers, R. Parameter identification in a Volterra equation with weakly singular kernel. J. Integral Equ. Appl. 1990, 2, 353–373. [Google Scholar] [CrossRef]
- Kannappan, K.; Kim, J.K.; Balachandran, K. Parameter Identification of an Integrodifferential Equation. Nonlinear Funct. Anal. Appl. 2015, 20, 169–185. [Google Scholar]
- Glentis, G.O.; Koukoulas, P.; Kalouptsidis, N. Efficient algorithms for Volterra system identification. IEEE Trans. Signal Process. 1999, 47, 3042–3057. [Google Scholar] [CrossRef]
- Nemeth, J.; Kollar, I.; Schoukens, J. Identification of Volterra kernels using interpolation. IEEE Trans. Instrum. Meas. 2002, 51, 770–775. [Google Scholar] [CrossRef]
- Lorenzi, A. Identification problems for integrodifferential equations. In Ill-Posed Problems in Natural Sciences, Proceedings of the International Conference, Moscow, Russia, 19–25 August 1991; De Gruyter: Berlin, Germany, 2020; pp. 342–366. [Google Scholar] [CrossRef]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives: Theory and Applications; Gordon and Breach Science Publishers: New York, NY, USA, 1993. [Google Scholar]
- Sabatier, J.; Farges, C.; Trigeassou, J.C. Fractional systems state space description: Some wrong ideas and proposed solutions. J. Vib. Control 2014, 20, 1076–1084. [Google Scholar] [CrossRef]
- Tenreiro Machado, J. A Review of Definitions for Fractional Derivatives and Integral. Math. Probl. Eng. 2014, 2014, 238459. [Google Scholar] [CrossRef] [Green Version]
- Tamilselvi, S.; Gunasundari, S.; Karuppiah, N.; Razak RK, A.; Madhusudan, S.; Nagarajan, V.M.; Sathish, T.; Shamim, M.Z.M.; Saleel, C.A.; Afzal, A. A Review on Battery Modelling Techniques. Sustainability 2021, 13, 42. [Google Scholar] [CrossRef]
- Fuller, T.F.; Doyle, M.; Newman, J. Relaxation Phenomena in Lithium-Ion-Insertion Cells. J. Electrochem. Soc. 1994, 141, 982–990. [Google Scholar] [CrossRef] [Green Version]
- Hu, T.; Zanchi, B.; Zhao, J. Simple Analytical Method for Determining Parameters of Discharging Batteries. IEEE Trans. Energy Convers. 2011, 26, 787–798. [Google Scholar] [CrossRef]
- Saxena, S.; Raman, S.R.; Saritha, B.; John, V. A novel approach for electrical circuit modeling of Li-ion battery for predicting the steady-state and dynamic I–V characteristics. Sādhanā 2016, 41, 479–487. [Google Scholar] [CrossRef] [Green Version]
- Chen, M.; Rincon-Mora, G. Accurate electrical battery model capable of predicting runtime and I-V performance. IEEE Trans. Energy Convers. 2006, 21, 504–511. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, Y.; Liao, X. State-of-art survey of fractional order modeling and estimation methods for lithium-ion batteries. Fract. Calc. Appl. Anal. 2019, 22, 1449–1479. [Google Scholar] [CrossRef]
- Sabatier, J.; Francisco, J.M.; Guillemard, F.; Lavigne, L.; Moze, M.; Merveillaut, M. Lithium-ion batteries modeling: A simple fractional differentiation based model and its associated parameters estimation method. Signal Process. 2015, 107, 290–301. [Google Scholar] [CrossRef]
- Sabatier, J. Modelling Fractional Behaviours Without Fractional Models. Front. Control Eng. 2021, 2, 716110. [Google Scholar] [CrossRef]


| K | |
|---|---|
| n | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tartaglione, V.; Farges, C.; Sabatier, J. Fractional Behaviours Modelling with Volterra Equations: Application to a Lithium-Ion Cell and Comparison with a Fractional Model. Fractal Fract. 2022, 6, 137. https://doi.org/10.3390/fractalfract6030137
Tartaglione V, Farges C, Sabatier J. Fractional Behaviours Modelling with Volterra Equations: Application to a Lithium-Ion Cell and Comparison with a Fractional Model. Fractal and Fractional. 2022; 6(3):137. https://doi.org/10.3390/fractalfract6030137
Chicago/Turabian StyleTartaglione, Vincent, Christophe Farges, and Jocelyn Sabatier. 2022. "Fractional Behaviours Modelling with Volterra Equations: Application to a Lithium-Ion Cell and Comparison with a Fractional Model" Fractal and Fractional 6, no. 3: 137. https://doi.org/10.3390/fractalfract6030137
APA StyleTartaglione, V., Farges, C., & Sabatier, J. (2022). Fractional Behaviours Modelling with Volterra Equations: Application to a Lithium-Ion Cell and Comparison with a Fractional Model. Fractal and Fractional, 6(3), 137. https://doi.org/10.3390/fractalfract6030137







