Numerical Valuation of European and American Options under Fractional Black-Scholes Model
Abstract
:1. Introduction
2. Time Fractional B-S Model
3. Discretization Scheme
3.1. The Improved L1 Scheme and Operator Splitting Method
3.2. The Radial Basis Function Finite Difference Method
4. Stability Analysis
5. Numerical Experiment
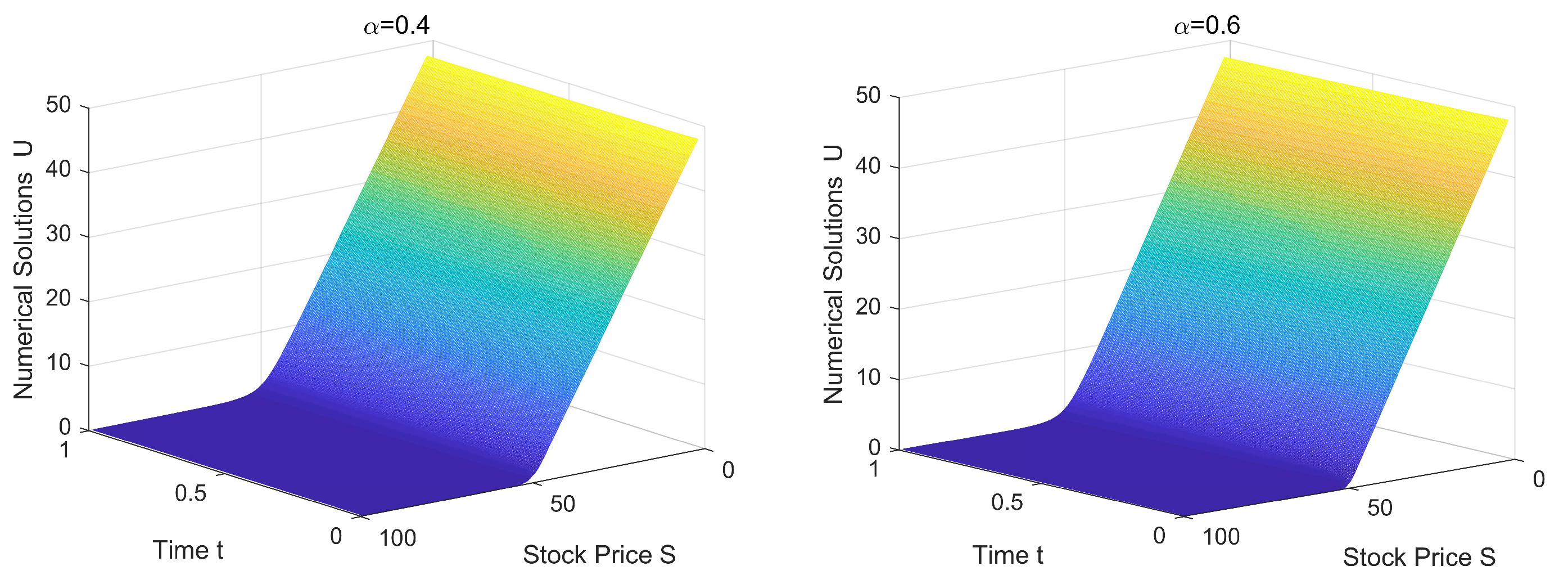
5.1. European Options
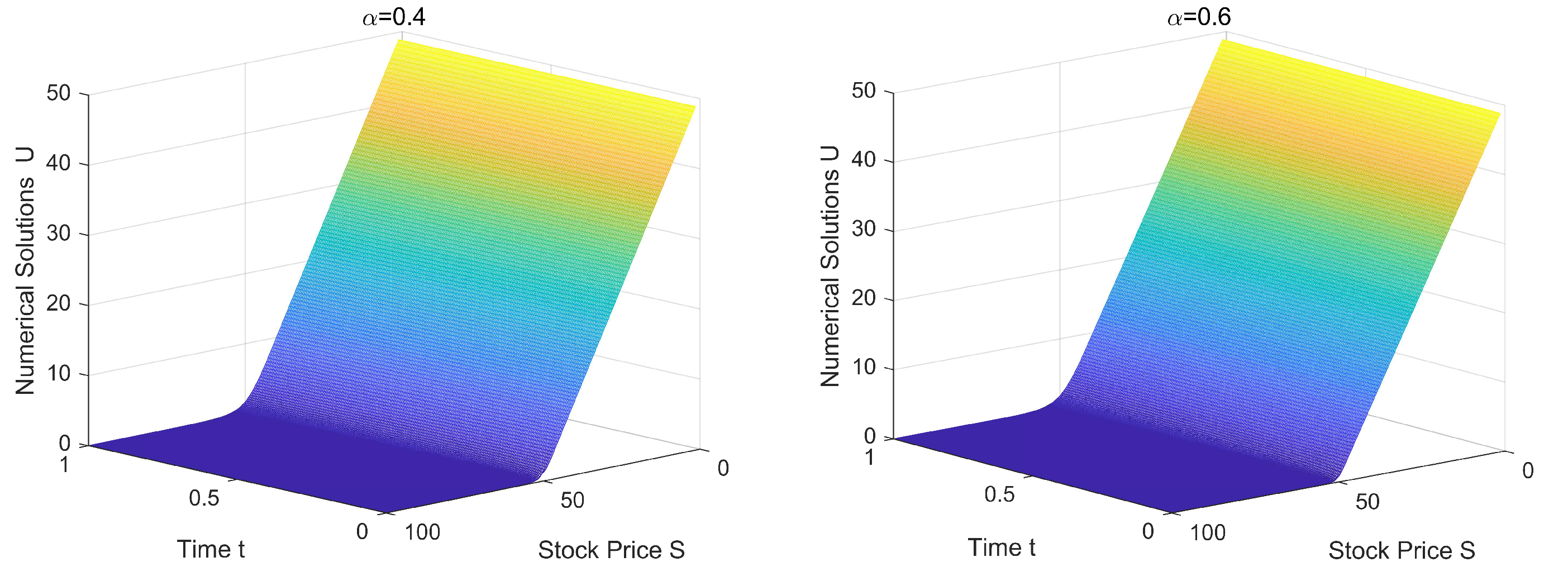
5.2. American Options
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Black, F.; Scholes, M. The pricing of options and corporate liabilities. J. Polit. Econ. 1973, 81, 637–654. [Google Scholar] [CrossRef] [Green Version]
- Merton, R.C. Option pricing when underlying stock returns are discontinuous. J. Financ. Econ. 1976, 3, 125–144. [Google Scholar] [CrossRef] [Green Version]
- Kou, S.G. A jump-diffusion model for option pricing. Manag. Sci. 2002, 48, 1086–1101. [Google Scholar] [CrossRef] [Green Version]
- Cox, J.C.; Ross, S.A. The valuation of options for alternative stochastic processes. J. Financ. Econ. 1976, 3, 145–166. [Google Scholar] [CrossRef]
- Hull, J.; White, A. The pricing of options on assets with stochastic volatilities. J. Financ. 1987, 42, 281–300. [Google Scholar] [CrossRef]
- Stein, E.M.; Stein, J.C. Stock price distributions with stochastic volatility: An analytic approach. Rev. Financ. Stud. 1991, 4, 727–752. [Google Scholar] [CrossRef]
- Heston, S.L. A closed-form solution for options with stochastic volatility with applications to bond and currency options. Rev. Financ. Stud. 1993, 6, 327–343. [Google Scholar] [CrossRef] [Green Version]
- Wyss, W. The fractional Black-Scholes equation. Fract. Calc. Appl. Anal. 2000, 3, 51–61. [Google Scholar]
- Cartea, A.; del-Castillo-Negrete, D. Fractional diffusion models of option prices in markets with jumps. Physical A 2007, 2, 749–763. [Google Scholar] [CrossRef] [Green Version]
- Jumarie, G. Stock exchange fractional dynamics defined as fractional exponential growth driven by (usual) Gaussian white noise. Application to fractional Black-Scholes equations. Insur. Math. Econ. 2008, 42, 271–287. [Google Scholar] [CrossRef]
- Liang, J.R.; Wang, J.; Zhang, W.J.; Qiu, W.Y.; Ren, F.Y. The solution to a bi-fractional Black–Scholes–Merton differential equation. Int. J. Pure Appl. Math. 2010, 58, 99–112. [Google Scholar]
- Aguilar, J.P.; Kirkby, J.L.; Korbel, J. Pricing, risk and volatility in subordinated market models. Risks 2020, 8, 124. [Google Scholar] [CrossRef]
- Tarasov, V.E. On history of mathematical economics: Application of fractional calculus. Mathematics 2019, 7, 509. [Google Scholar] [CrossRef] [Green Version]
- Carr, P.; Wu, L. The finite moment log stable process and option pricing. J. Financ. 2003, 58, 753–777. [Google Scholar] [CrossRef] [Green Version]
- Carr, P.; Geman, H.; Madan, D.; Yor, M. Stochastic volatility for Lévy processes. Math. Financ. 2003, 13, 345–382. [Google Scholar] [CrossRef] [Green Version]
- Koponen, I. Analytic approach to the problem of convergence of truncated Lévy flights towards the Gaussian stochastic process. Phys. Rev. E. 1995, 52, 1197–1199. [Google Scholar] [CrossRef]
- Boyarchenko, S.I.; Levendorskiǐ, S.Z. Non-Gaussian Merton-Black-Scholes Theory; World Scientific: Singapore, 2002. [Google Scholar]
- Jumarie, G. Derivation and solutions of some fractional Black Scholes equations in coarse-grained space and time. Application to Mertons optimal portfolio. Comput. Math. Appl. 2010, 59, 1142–1164. [Google Scholar] [CrossRef] [Green Version]
- Kleinert, H.; Korbel, J. Option pricing beyond Black-Scholes based on double-fractional diffusion. Physical A 2016, 449, 200–214. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Liu, F.; Chen, S.; Anh, V.; Chen, J. Fast numerical simulation of a new time-space fractional option pricing model governing European call option. Appl. Math. Comput. 2018, 339, 186–198. [Google Scholar] [CrossRef] [Green Version]
- Aguilar, J.P.; Korbel, J.; Pesci, N. On the quantitative properties of some market models involving fractional derivatives. Mathematics 2021, 9, 3198. [Google Scholar] [CrossRef]
- Song, L.; Wang, W. Solution of the fractional Black-Scholes option pricing model by finite difference method. Abstr. Appl. Anal. 2013, 2013, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Liu, F.; Turner, I.; Yang, Q. Numerical solution of the time fractional Black-Scholes model governing European options. Comput. Math. Appl. 2016, 71, 1772–1783. [Google Scholar] [CrossRef]
- De Staelen, R.H.; Hendy, A.S. Numerically pricing double barrier options in a time-fractional Black-Scholes model. Comput. Math. Appl. 2017, 74, 1166–1175. [Google Scholar] [CrossRef]
- Koleva, M.N.; Vulkov, L.G. Numerical solution of time-fractional Black-Scholes equation. Comput. Appl. Math. 2017, 36, 1699–1715. [Google Scholar] [CrossRef]
- Golbabai, A.; Nikan, O.; Nikazad, T. Numerical analysis of time fractional Black-Scholes European option pricing model arising in financial market. Comput. Appl. Math. 2019, 38, 173. [Google Scholar] [CrossRef]
- Chen, C.; Wang, Z.; Yang, Y. A new operator splitting method for American options under fractional Black-Scholes models. Comput. Math. Appl. 2019, 77, 2130–2144. [Google Scholar] [CrossRef]
- Farhadi, A.; Salehi, M.; Erjaee, G.H. A new version of Black–Scholes equation presented by time-fractional derivative. Iran. J. Sci. Technol. A. 2018, 42, 2159–2166. [Google Scholar] [CrossRef]
- Huang, J.; Cen, Z.; Zhao, J. An adaptive moving mesh method for a time-fractional Black-Scholes equation. Adv. Differ. Equ. 2019, 2019, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Almushaira, M.; Chen, F.; Liu, F. Efficient operator splitting and spectral methods for the time-space fractional Black-Scholes equation. Resul. Appl. Math. 2021, 10, 100149. [Google Scholar] [CrossRef]
- Haghi, M.; Mollapourasl, R.; Vanmaele, M. An RBF-FD method for pricing American options under jump-diffusion models. Comput. Math. Appl. 2018, 76, 2434–2459. [Google Scholar] [CrossRef] [Green Version]
- Bayona, V.; Moscoso, M.; Carretero, M.; Kindelan, M. RBF-FD formulas and convergence properties. J. Comput. Phys. 2010, 229, 8281–8295. [Google Scholar] [CrossRef]
- Saib, A.A.E.F.; Tangman, D.Y.; Bhuruth, M. A new radial basis functions method for pricing American options under Merton’s jump-diffusion model. Inter. J. Comput. Math. 2012, 89, 1164–1185. [Google Scholar] [CrossRef]
- Soleymani, F.; Zhu, S. RBF-FD solution for a financial partial-integro differential equation utilizing the generalized multiquadric function. Comput. Math. Appl. 2021, 82, 161–178. [Google Scholar] [CrossRef]
- Chen, W.; Xu, X.; Zhu, S. Analytically pricing double barrier options based on a time-fractional Black-Scholes equation. Comput. Math. Appl. 2015, 69, 1407–1419. [Google Scholar] [CrossRef]
- Ford, N.J.; Yan, Y. An approach to construct higher order time discretisation schemes for time fractional partial differential equations with nonsmooth data. Fract. Calc. Appl. Anal. 2017, 20, 1076–1105. [Google Scholar] [CrossRef] [Green Version]



| Method | (M,N) | S = 30 | S = 40 | S = 50 | S = 60 | S = 70 | |
|---|---|---|---|---|---|---|---|
| RBF-FD-IL1 | 0.4 | (,) | 19.44328 | 9.54620 | 1.64519 | 0.12003 | 0.01059 |
| (,) | 19.44311 | 9.54571 | 1.64504 | 0.12001 | 0.01057 | ||
| 0.6 | (,) | 19.44556 | 9.53012 | 1.69123 | 0.10952 | 0.00666 | |
| (,) | 19.44541 | 9.52962 | 1.69109 | 0.10949 | 0.00664 | ||
| FD-L1 | 0.4 | (,) | 19.44341 | 9.54595 | 1.64208 | 0.11977 | 0.01055 |
| (,) | 19.44319 | 9.54580 | 1.64408 | 0.11990 | 0.01056 | ||
| 0.6 | (,) | 19.44591 | 9.53002 | 1.68807 | 0.10918 | 0.00662 | |
| (,) | 19.44559 | 9.52978 | 1.69005 | 0.10934 | 0.00663 |
| Method | N/ | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 |
|---|---|---|---|---|---|---|---|---|---|---|
| RBF-FD-IL1 | 8.57 | 2.61 | 5.64 | 1.00 | 1.50 | 1.80 | 4.69 | 1.09 | 2.16 | |
| 2.11 | 7.13 | 1.68 | 3.23 | 5.22 | 6.75 | 1.90 | 4.76 | 1.01 | ||
| 5.46 | 2.02 | 5.13 | 1.06 | 1.84 | 2.56 | 7.67 | 2.07 | 4.71 | ||
| 1.45 | 5.79 | 1.58 | 3.52 | 6.54 | 9.76 | 3.11 | 9.01 | 2.20 | ||
| 3.88 | 1.67 | 4.90 | 1.16 | 2.32 | 3.71 | 1.26 | 3.92 | 1.03 | ||
| 1.04 | 4.83 | 1.51 | 3.85 | 8.23 | 1.41 | 5.11 | 1.71 | 4.78 | ||
| 2.82 | 1.39 | 4.68 | 1.28 | 2.92 | 5.35 | 2.07 | 7.42 | 2.23 | ||
| RBF-FD-L1 | 5.22 | 1.07 | 1.66 | 2.27 | 2.91 | 3.55 | 4.12 | 4.51 | 4.52 | |
| 2.59 | 5.30 | 8.15 | 1.12 | 1.43 | 1.75 | 2.05 | 2.26 | 2.29 | ||
| 1.29 | 2.63 | 4.04 | 5.52 | 7.07 | 8.66 | 1.02 | 1.13 | 1.16 | ||
| 6.41 | 1.31 | 2.01 | 2.74 | 3.50 | 4.30 | 5.06 | 5.68 | 5.83 | ||
| 3.20 | 6.53 | 1.00 | 1.36 | 1.74 | 2.14 | 2.52 | 2.85 | 2.94 | ||
| 1.60 | 3.26 | 4.99 | 6.79 | 8.68 | 1.06 | 1.26 | 1.43 | 1.48 | ||
| 7.99 | 1.63 | 2.49 | 3.39 | 4.33 | 5.30 | 6.28 | 7.14 | 7.46 | ||
| FD-L1 | 1.07 | 2.20 | 3.41 | 4.68 | 5.99 | 7.25 | 8.32 | 8.98 | 8.92 | |
| 5.23 | 1.07 | 1.66 | 2.27 | 2.91 | 3.55 | 4.12 | 4.51 | 4.52 | ||
| 2.59 | 5.30 | 8.15 | 1.12 | 1.43 | 1.75 | 2.05 | 2.26 | 2.29 | ||
| 1.29 | 2.63 | 4.04 | 5.52 | 7.07 | 8.66 | 1.02 | 1.13 | 1.16 | ||
| 6.41 | 1.31 | 2.01 | 2.74 | 3.51 | 4.30 | 5.07 | 5.68 | 5.83 | ||
| 3.20 | 6.53 | 1.00 | 1.36 | 1.74 | 2.14 | 2.52 | 2.85 | 2.94 | ||
| 1.60 | 3.26 | 4.99 | 6.79 | 8.68 | 1.06 | 1.26 | 1.43 | 1.48 |
| Method | N/ | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 |
|---|---|---|---|---|---|---|---|---|---|---|
| RBF-FD-IL1 | 2.02 | 1.87 | 1.75 | 1.63 | 1.52 | 1.41 | 1.31 | 1.20 | 1.10 | |
| 1.95 | 1.82 | 1.71 | 1.60 | 1.50 | 1.40 | 1.31 | 1.20 | 1.10 | ||
| 1.91 | 1.80 | 1.70 | 1.60 | 1.50 | 1.39 | 1.30 | 1.20 | 1.10 | ||
| 1.90 | 1.79 | 1.69 | 1.59 | 1.49 | 1.39 | 1.30 | 1.20 | 1.10 | ||
| 1.89 | 1.79 | 1.69 | 1.59 | 1.50 | 1.40 | 1.30 | 1.20 | 1.10 | ||
| 1.89 | 1.79 | 1.69 | 1.60 | 1.50 | 1.40 | 1.30 | 1.20 | 1.10 | ||
| RBF-FD-L1 | 1.02 | 1.02 | 1.02 | 1.03 | 1.03 | 1.02 | 1.01 | 1.00 | 0.98 | |
| 1.01 | 1.01 | 1.01 | 1.02 | 1.02 | 1.02 | 1.01 | 1.00 | 0.98 | ||
| 1.00 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.00 | 0.99 | ||
| 1.00 | 1.00 | 1.00 | 1.01 | 1.01 | 1.01 | 1.00 | 1.00 | 0.99 | ||
| 1.00 | 1.00 | 1.00 | 1.00 | 1.01 | 1.01 | 1.00 | 1.00 | 0.99 | ||
| 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.99 | ||
| FD-L1 | 1.03 | 1.04 | 1.04 | 1.04 | 1.04 | 1.03 | 1.01 | 0.99 | 0.98 | |
| 1.02 | 1.02 | 1.02 | 1.03 | 1.03 | 1.02 | 1.01 | 1.00 | 0.98 | ||
| 1.01 | 1.01 | 1.01 | 1.02 | 1.02 | 1.02 | 1.01 | 1.00 | 0.99 | ||
| 1.00 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.00 | 0.99 | ||
| 1.00 | 1.00 | 1.00 | 1.01 | 1.01 | 1.01 | 1.00 | 1.00 | 0.99 | ||
| 1.00 | 1.00 | 1.00 | 1.00 | 1.01 | 1.01 | 1.00 | 1.00 | 0.99 |
| Method | (M,N) | S = 30 | S = 40 | S = 50 | S = 60 | S = 70 | |
|---|---|---|---|---|---|---|---|
| RBF-FD-IL1-OS | 0.4 | (,) | 20.00011 | 10.00006 | 1.67939 | 0.12224 | 0.01076 |
| (,) | 20.00002 | 10.00000 | 1.67726 | 0.12200 | 0.01073 | ||
| 0.6 | (,) | 20.00011 | 10.00006 | 1.72771 | 0.11137 | 0.00675 | |
| (,) | 20.00002 | 10.00000 | 1.72583 | 0.11110 | 0.00672 | ||
| FD-L1-OS | 0.4 | (,) | 20.00000 | 10.00000 | 1.67472 | 0.12177 | 0.01071 |
| (,) | 20.00000 | 10.00000 | 1.67672 | 0.12189 | 0.01072 | ||
| 0.6 | (,) | 20.00000 | 10.00000 | 1.72316 | 0.11080 | 0.00670 | |
| (,) | 20.00000 | 10.00000 | 1.72516 | 0.11096 | 0.00671 |
| N/ | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 |
|---|---|---|---|---|---|---|---|---|---|
| 3.40 | 4.81 | 5.63 | 6.18 | 5.18 | 3.79 | 3.41 | 8.24 | 1.83 | |
| 1.45 | 2.06 | 2.44 | 2.18 | 1.69 | 1.20 | 1.38 | 3.56 | 8.52 | |
| 6.54 | 9.20 | 1.05 | 8.19 | 6.19 | 3.32 | 5.54 | 1.54 | 3.98 | |
| 3.01 | 4.20 | 3.93 | 3.31 | 2.26 | 9.81 | 2.24 | 6.69 | 1.83 | |
| 1.38 | 1.94 | 1.70 | 1.28 | 8.02 | 3.72 | 9.05 | 2.85 | 8.65 | |
| 6.50 | 8.64 | 7.10 | 4.92 | 2.82 | 1.52 | 3.52 | 1.27 | 4.07 | |
| 3.08 | 3.67 | 2.93 | 1.88 | 1.00 | 6.14 | 1.53 | 5.68 | 1.86 |
| N/ | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 |
|---|---|---|---|---|---|---|---|---|---|
| 1.23 | 1.22 | 1.21 | 1.51 | 1.61 | 1.66 | 1.30 | 1.21 | 1.10 | |
| 1.15 | 1.16 | 1.22 | 1.41 | 1.45 | 1.86 | 1.32 | 1.21 | 1.10 | |
| 1.12 | 1.13 | 1.42 | 1.31 | 1.46 | 1.76 | 1.31 | 1.20 | 1.12 | |
| 1.13 | 1.11 | 1.21 | 1.37 | 1.49 | 1.40 | 1.31 | 1.23 | 1.08 | |
| 1.08 | 1.17 | 1.26 | 1.38 | 1.51 | 1.29 | 1.36 | 1.17 | 1.09 | |
| 1.08 | 1.24 | 1.28 | 1.38 | 1.49 | 1.31 | 1.20 | 1.16 | 1.13 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, P.; Xu, Z. Numerical Valuation of European and American Options under Fractional Black-Scholes Model. Fractal Fract. 2022, 6, 143. https://doi.org/10.3390/fractalfract6030143
Yang P, Xu Z. Numerical Valuation of European and American Options under Fractional Black-Scholes Model. Fractal and Fractional. 2022; 6(3):143. https://doi.org/10.3390/fractalfract6030143
Chicago/Turabian StyleYang, Pei, and Zuoliang Xu. 2022. "Numerical Valuation of European and American Options under Fractional Black-Scholes Model" Fractal and Fractional 6, no. 3: 143. https://doi.org/10.3390/fractalfract6030143
APA StyleYang, P., & Xu, Z. (2022). Numerical Valuation of European and American Options under Fractional Black-Scholes Model. Fractal and Fractional, 6(3), 143. https://doi.org/10.3390/fractalfract6030143





