Robust Control for Variable-Order Fractional Interval Systems Subject to Actuator Saturation
Abstract
:1. Introduction
2. Problem Formulation and Preliminaries
3. Main Results
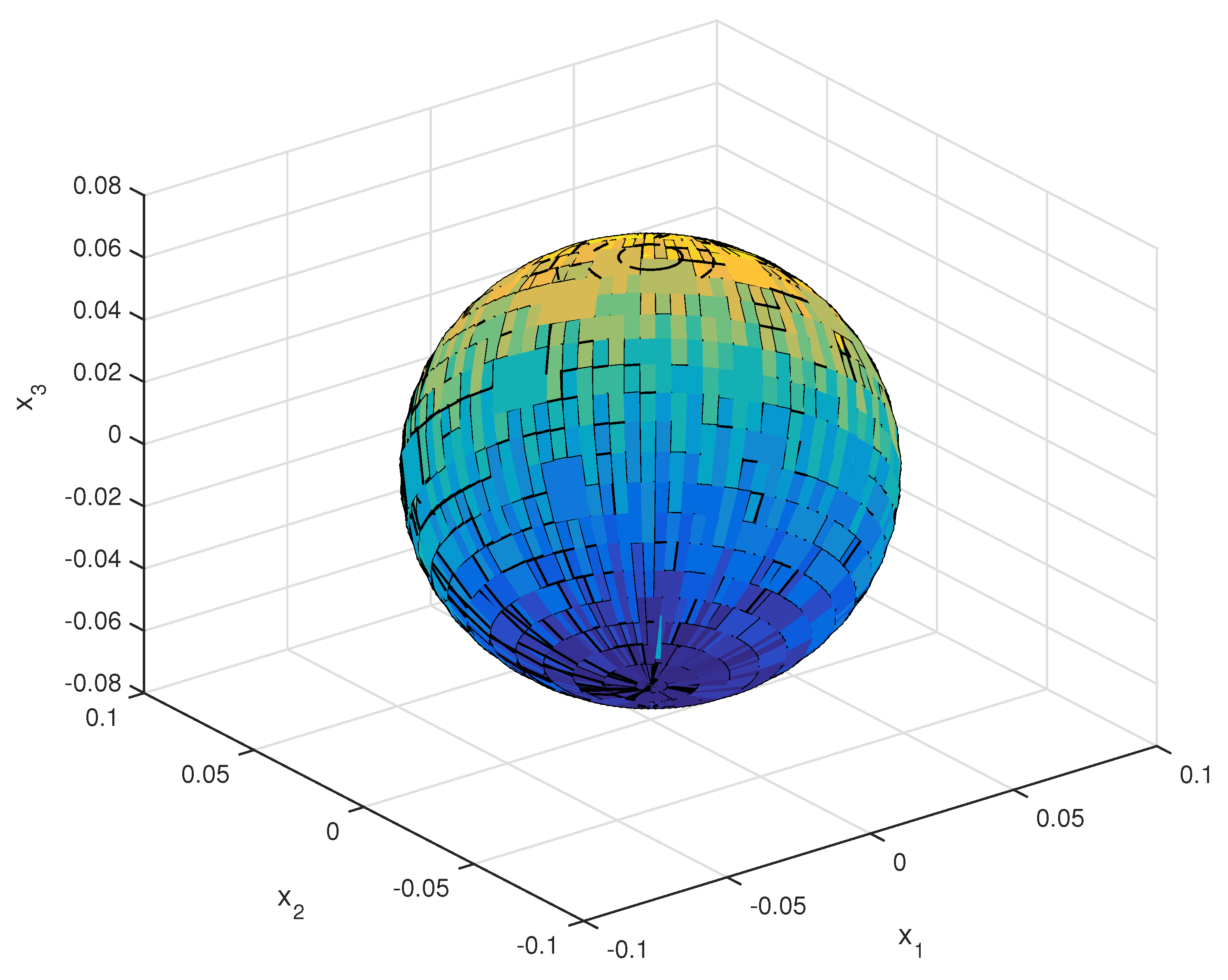
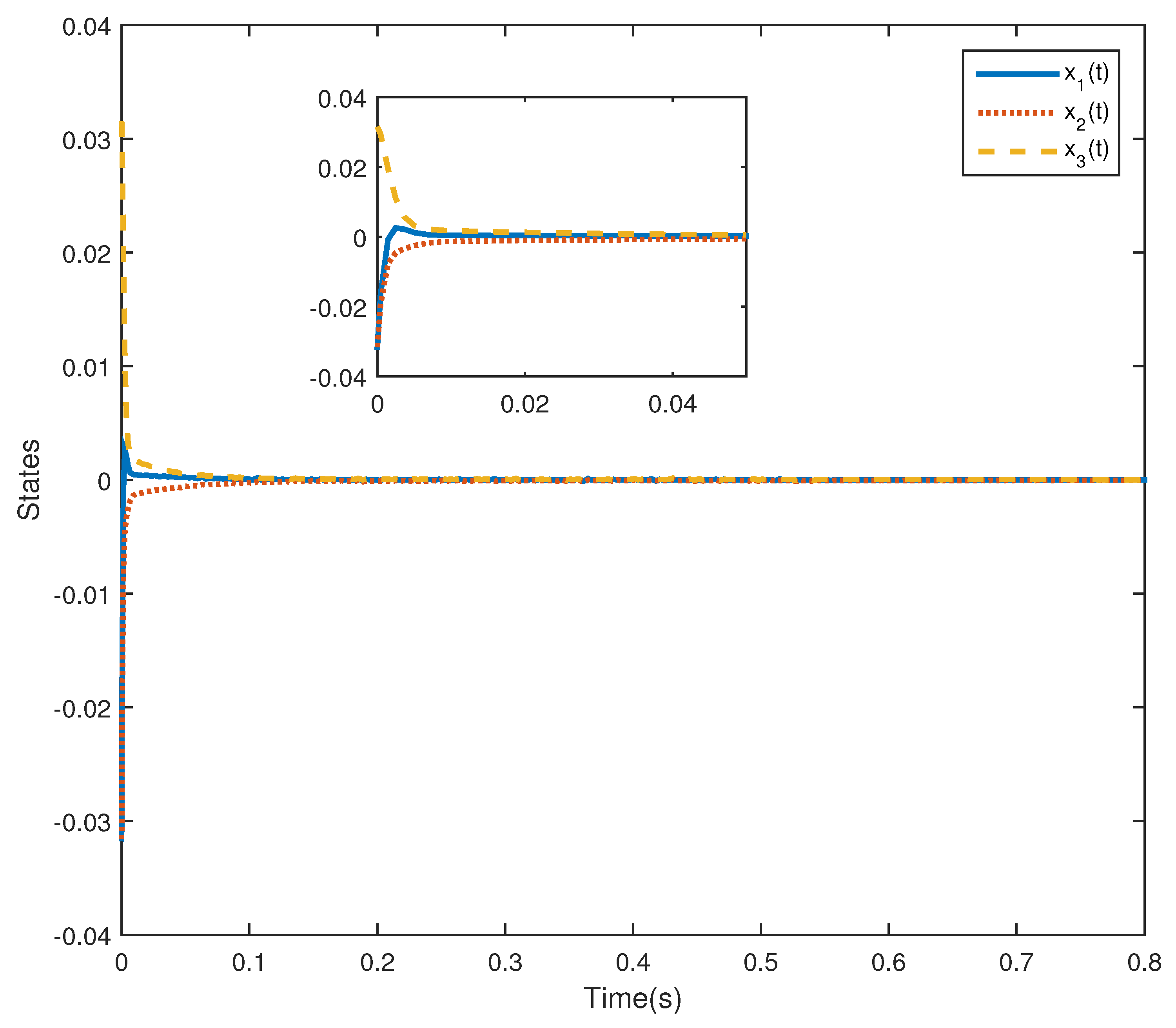
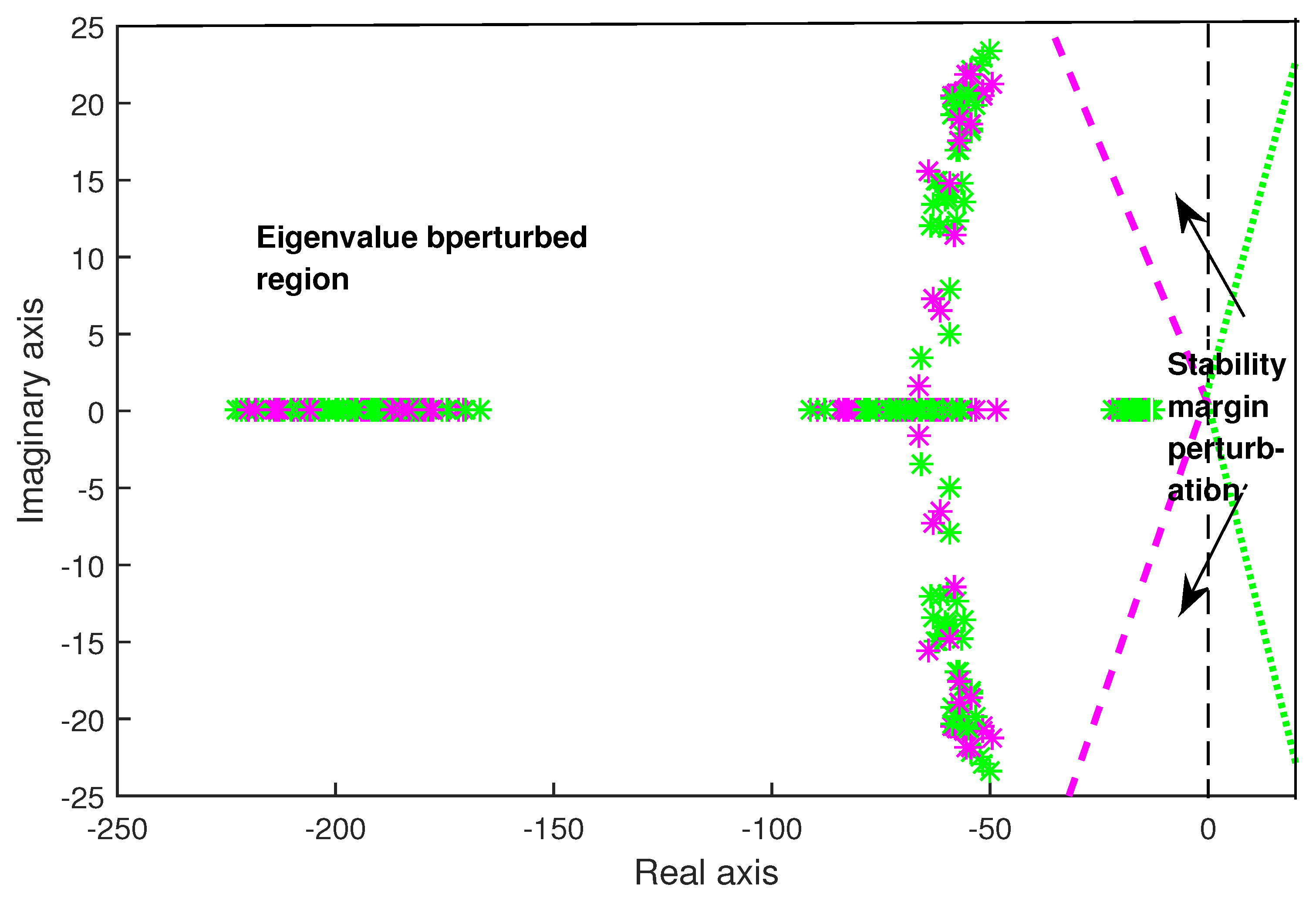
4. Numerical Examples
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mujumdar, A.; Tamhane, B.; Kurode, S. Observer-basedsliding mode control for a class of noncommensurate fractional-order systems. IEEE/ASME Trans. Mechatron. 2005, 20, 2504–2512. [Google Scholar] [CrossRef]
- Wei, Y.Q.; Liu, D.Y.; Boutat, D.; Chen, Y.M. An improved pseudo-state estimator for a class of commensurate fractional order linear systems based on fractional order modulating functions. Syst. Control Lett. 2018, 118, 29–34. [Google Scholar] [CrossRef]
- Liu, D.Y.; Zheng, G.; Boutat, D.; Liu, H.R. Non-asymptotic fractional order differentiator for a class of fractional order linear systems. Syst. Control Lett. 2017, 8, 61–71. [Google Scholar] [CrossRef] [Green Version]
- Narayanan, G.; Ali, M.S.; Alam, M.I.; Rajchakit, G.; Boonsatit, N.; Kumar, P.; Hammachukiattikul, P. Adaptive Fuzzy Feedback Controller Design for Finite-Time Mittag-Leffler Synchronization of Fractional-Order Quaternion-Valued Reaction-Diffusion Fuzzy Molecular Modeling of Delayed Neural Networks. IEEE Access 2021, 9, 130862–130883. [Google Scholar] [CrossRef]
- Syed Ali, M.; Hymavathi, M.; Kauser, S.A.; Rajchakit, G.; Hammachukiattikul, P.; Boonsatit, N. Synchronization of Fractional Order Uncertain BAM Competitive Neural Networks. Fractal Fract. 2022, 6, 14. [Google Scholar] [CrossRef]
- Poongodi, T.; Mishra, P.P.; Lim, C.P.; Saravanakumar, T.; Boonsatit, N.; Hammachukiattikul, P.; Rajchakit, G. TS Fuzzy Robust Sampled-Data Control for Nonlinear Systems with Bounded Disturbances. Computation 2021, 9, 132. [Google Scholar] [CrossRef]
- Rajchakit, G.; Chanthorn, P.; Kaewmesri, P.; Sriraman, R.; Lim, C.P. Global Mittag–Leffler Stability and Stabilization Analysis of Fractional-Order Quaternion-Valued Memristive Neural Networks. Mathematics 2020, 8, 422. [Google Scholar] [CrossRef] [Green Version]
- Humphries, U.; Rajchakit, G.; Kaewmesri, P.; Chanthorn, P.; Sriraman, R.; Samidurai, R.; Lim, C.P. Global Stability Analysis of Fractional-Order Quaternion-Valued Bidirectional Associative Memory Neural Networks. Mathematics 2020, 8, 801. [Google Scholar] [CrossRef]
- Sajad, P.; Hamed, M. Predictor-based fractional disturbance rejection control for LTI fractional order systems with input delay. Trans. Inst. Meas. Control 2020, 8, 61–71. [Google Scholar]
- Dinh, C.H.; Dao, T.H.Y. Functional interval observer design for singular fractional-order systems with disturbances. Trans. Inst. Meas. Control 2020, 8, 61–71. [Google Scholar]
- Farges, C.; Moze, M.; Sabatier, J. Pseudo-state feedback stabilization of commensurate fractional order systems. Automatica 2010, 46, 1730–1734. [Google Scholar] [CrossRef]
- Lin, C.; Chen, B.; Shi, P.; Yu, J.P. Necessary and sufficient conditions of observer-based stabilization for a class of fractional-order descriptor systems. Syst. Control Lett. 2018, 112, 31–35. [Google Scholar] [CrossRef]
- Matignon, D. Stability results on fractional differential equations with applications to control processing. Comput. Eng. Syst. Appl. 1996, 2, 963–968. [Google Scholar]
- Li, Y.; Chen, Y.Q.; Podlubny, I. Mittage-Leffler stability of fractional order nonlinear dynamic systems. Automatica 2009, 45, 1965–1969. [Google Scholar] [CrossRef]
- Wei, Y.H.; Peter, T.; Yao, Z.; Wang, Y. The output feedback control synthesis for a class of singular fractional order systems. ISA Trans. 2017, 69, 1–9. [Google Scholar] [CrossRef]
- Lenka, B.K. Fractional comparison method and asymptotic stability results for multivariable fractional order systems. Commun. Nonlinear Sci. Numer. Simulat. 2019, 69, 398–415. [Google Scholar] [CrossRef]
- Ahn, H.S.; Chen, Y.Q. Necessary and sufficient stability condition of fractional order interval linear systems. Commun. Nonlinear Sci. Numer. Simulat. 2008, 44, 2985–2988. [Google Scholar] [CrossRef]
- Sabatier, J.; Moze, M.; Farges, C. LMI stability conditions for fractional order systems. Comput. Math. Appl. 2010, 59, 1594–1609. [Google Scholar] [CrossRef]
- Zhang, J.X.; Yang, G.H. Low-complexity tracking control of strict-feedback systems with unknown control directions. IEEE Trans. Autom. Control 2019, 64, 5175–5182. [Google Scholar] [CrossRef]
- Zhang, X.F.; Chen, Y.Q. Admissibility and robust stabilization of continuous linear singular fractional order systems with the fractional order α: The 0 < α < 1 case. ISA Trans. 2018, 82, 42–50. [Google Scholar]
- Wei, Y.; Wang, J.; Liu, T.; Wang, Y. Sufficient and necessary conditions for stabilizing singular fractional order systems with partially measurable state. J. Frankl. Inst. 2019, 356, 1975–1990. [Google Scholar] [CrossRef] [Green Version]
- Marir, S.; Chadli, M.; Bouagada, D. A novel approach of admissibility for singular linear continuous-time fractional-order systems. Int. J. Control Autom. Syst 2017, 15, 959–964. [Google Scholar] [CrossRef]
- Ji, Y.D.; Qiu, J.Q. Stabilization of fractional-order singular uncertain systems. ISA Trans. 2015, 69, 53–64. [Google Scholar] [CrossRef]
- Liao, Z.; Peng, C.; Li, W.; Wang, Y. Robust stability analysis for a class of fractional order systems with uncertain parameters. J. Frankl. Inst. 2011, 348, 1101–1113. [Google Scholar] [CrossRef]
- Badri, P.; Sojoodi, M. Robust stabilisation of fractional-order interval systems via dynamic output feedback: An LMI approach. Int. J. Syst. Sci. 2019, 50, 1718–1730. [Google Scholar] [CrossRef]
- Gao, Z. Analytical method on stabilisation of fractional-order plants with interval uncertainties using fractional-order PIλDμ controllers. Int. J. Syst. Sci. 2019, 50, 935–953. [Google Scholar] [CrossRef]
- Zhang, X.F.; Zhao, Z.L. Robust stabilization for rectangular descriptor fractional order interval systems with order 0 < α < 1. Appl. Math. Comput. 2020, 366, 124766. [Google Scholar]
- Wang, L.M.; Zhang, G.S. Robust output consensus for a class of fractional-order interval multi-agent systems. Asian J. Control 2019, 69, 1679–1691. [Google Scholar] [CrossRef]
- Li, C.; Wang, J.C. Robust stability and stabilization of fractional order interval systems with coupling relationships: The 0 < α < 1 case. J. Frankl. Inst. 2012, 349, 2406–2419. [Google Scholar]
- Liang, S.; Peng, C.; Liao, Z.; Wang, Y. Robust analysis and synthesis for a class of fractional order systems with coupling uncertainties. Int. J. Control Autom. Syst 2015, 13, 494–500. [Google Scholar] [CrossRef]
- Zhang, J.X.; Yang, G.H. Robust adaptive fault-tolerant control for a class of unknown nonlinear systems. IEEE Trans. Ind. Electron. 2017, 64, 585–594. [Google Scholar] [CrossRef]
- Lu, J.G.; Chen, Y.Q. Robust stability and stabilization of fractional order interval systems with the fractional order α: The 0 < α < 1 case. IEEE Trans. Autom. Control 2010, 55, 152–158. [Google Scholar]
- Lorenzo, C.F.; Hartley, T.T. Initialization, conceptualization, and application in the (fractional) generalized calculus. Crit. Rev. Biomed. Eng. 2007, 35, 447–553. [Google Scholar] [CrossRef]
- Rossikhin, Y.A.; Shitikova, M.V. Application of fractional calculus for dynamic problems of solid mechanics: Novel trends and resent results. Appl. Mech. 2010, 63, 152–158. [Google Scholar] [CrossRef]
- Sun, H.G.; Chen, W.; Chen, Y.Q. Variable-order fractional differential operators in anomalous diffusion modeling. Phys. A Stat. Mech. Appl. 2009, 388, 4586–4592. [Google Scholar] [CrossRef]
- Yang, X.J.; Baleanu, D.; Srivastava, H. Local fractional similarity solution for the diffusion equation defined on Cantor sets. Appl. Math. Lett. 2015, 47, 54–60. [Google Scholar] [CrossRef]
- Ortigueira, M.D.; Valério, D.; Machado, J.T. Variable order fractional systems. Commun. Nonlinear Sci. Numer. Simul. 2019, 71, 231–243. [Google Scholar] [CrossRef]
- Meng, R.F.; Yin, D.S.; Zhou, C.; Wu, H. Fractional description of time-dependent mechanical property evolution in materials with Strain softening behavior. Appl. Math. Model. 2016, 40, 398–406. [Google Scholar] [CrossRef]
- Meng, R.F.; Yin, D.; Drapaca, C.S. Variable-order fractional description of compression deformation of amorphous glassy polymers. Comput. Mech. 2019, 64, 163–171. [Google Scholar] [CrossRef]
- Ramirez, L.E.; Coimbra, C.F. A variable order constitutive relation for viscoelasticity. Ann. Phys. 2007, 16, 543–552. [Google Scholar] [CrossRef]
- Jiang, J.F.; Chen, H.T.; Guirao, J.L.G.; Cao, D.Q. Existence of the solution and stability for a class of variable fractional order differential systems. Chaos Solitions Fractals 2019, 128, 269–274. [Google Scholar] [CrossRef]
- Qi, Y.W.; Xu, X.D.; Lu, S.W.; Yu, Y.Y. A waiting time based discrete event-triggered control for networked switched systems with actuator saturation. Nonlinear Anal. Hybrid Syst. 2020, 37, 100904. [Google Scholar] [CrossRef]
- Wang, Z.D.; Ho, D.W.C.; Dong, H.L.; Gao, H.J. Robust finite-horifzon control for a class of stochastic nonlinear time-xarying systems subject to sensor and actuator saturations. IEEE Trans. Autom. Control 2010, 55, 1716–1722. [Google Scholar] [CrossRef]
- Tharanidharan, V.; Sakthivel, R.; Mac, Y.K.; Ramya, L.S.; Anthoni, S.M. Finite-time decentralized non-fragile dissipative control for large-scale systems against actuator saturation. ISA Trans. 2019, 91, 90–98. [Google Scholar] [CrossRef]
- Xu, X.; Liu, L.; Feng, G. Semi-global stabilization of linear systems with distributed infinite input delays and actuator saturations. Automatica 2019, 107, 398–405. [Google Scholar] [CrossRef]
- Jin, X.Z.; Qin, J.H.; Shi, Y.; Zheng, W.X. Auxiliary fault tolerant control with actuator amplitude saturation and limited rate. IEEE Trans. Syst. Man Cybern. Syst. 2018, 48, 1816–1825. [Google Scholar] [CrossRef]
- Hu, Z.H.; Mu, X.W. Stabilization for switched stochastic systems with semi-Markovian switching signals and actuator saturation. Inf. Sci. 2019, 493, 419–431. [Google Scholar] [CrossRef]
- Chen, Y.G.; Wang, Z.D.; Fei, S.M.; Han, Q.L. Regional stabilization for discrete time-delay systems with actuator saturations via a delay-dependent polytopic approach. IEEE Trans. Autom. Control 2019, 64, 1257–1264. [Google Scholar] [CrossRef]
- Lin, Z.L.; Lv, L. Set invariance conditions for singular linear systems subject to actuator saturation. IEEE Trans. Autom. Control 2007, 52, 2351–2355. [Google Scholar] [CrossRef]
- Lv, L.; Lin, Z.L. Analysis and design of singular linear systems under actuator saturation and L2/L∞ disturbances. Syst. Control Lett. 2008, 57, 904–912. [Google Scholar] [CrossRef]
- Fang, H.J.; Lin, Z.L.; Hu, T.S. Analysis of linear systems in the prsence of actuator saturation and L2 disturbances. Automatica 2004, 40, 1229–1238. [Google Scholar] [CrossRef]
- Zhu, B.Y.; Zhang, J.J.; Zhang, Q.L.; Zhang, D.Q. Dissipative control for T-S fuzzy descriptor systems with actuator saturation and disturbances. J. Frankl. Inst. 2016, 353, 4950–4978. [Google Scholar] [CrossRef]
- Lim, Y.H.; Oh, K.K.; Ahn, H.S. Stability and stabilization of fractional order systems subject to input saturation. IEEE Trans. Autom. Control 2013, 58, 1062–1067. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, R.; Wang, Z.; Zhang, X.; Ren, J.; Gui, Q. Robust Control for Variable-Order Fractional Interval Systems Subject to Actuator Saturation. Fractal Fract. 2022, 6, 159. https://doi.org/10.3390/fractalfract6030159
Liu R, Wang Z, Zhang X, Ren J, Gui Q. Robust Control for Variable-Order Fractional Interval Systems Subject to Actuator Saturation. Fractal and Fractional. 2022; 6(3):159. https://doi.org/10.3390/fractalfract6030159
Chicago/Turabian StyleLiu, Ri, Zhe Wang, Xuefeng Zhang, Jianxu Ren, and Qinglong Gui. 2022. "Robust Control for Variable-Order Fractional Interval Systems Subject to Actuator Saturation" Fractal and Fractional 6, no. 3: 159. https://doi.org/10.3390/fractalfract6030159
APA StyleLiu, R., Wang, Z., Zhang, X., Ren, J., & Gui, Q. (2022). Robust Control for Variable-Order Fractional Interval Systems Subject to Actuator Saturation. Fractal and Fractional, 6(3), 159. https://doi.org/10.3390/fractalfract6030159






