Examining the Position of Wright’s Fallingwater in the Context of His Larger Body of Work: An Analysis Using Fractal Dimensions
Abstract
1. Introduction
2. Background to the Research
2.1. The Positioning of Fallingwater in Wright’s Architectural Styles
2.2. The Use of Fractal Analysis to Define Architectural Style
2.3. Fractal Analysis of Frank Lloyd Wright’s Buildings
3. Method and Approach
3.1. The Box-Counting Method for Architecture
3.2. Approach
- (1)
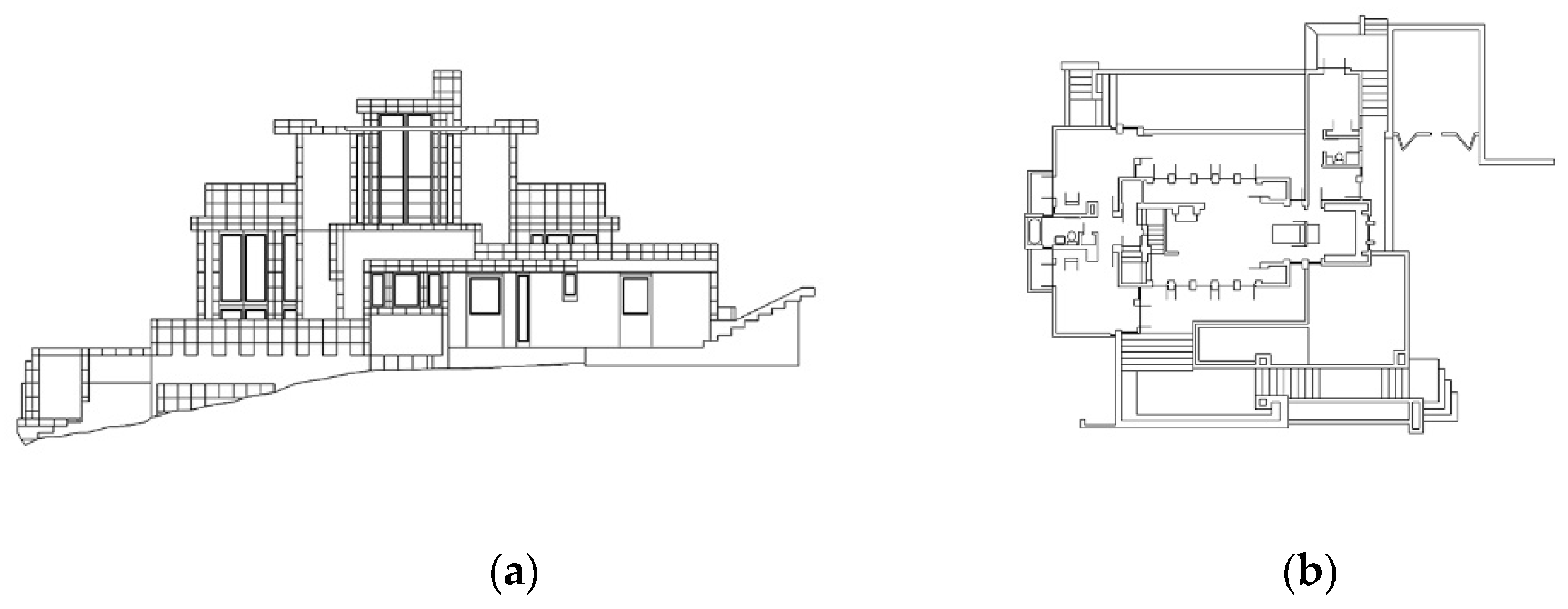
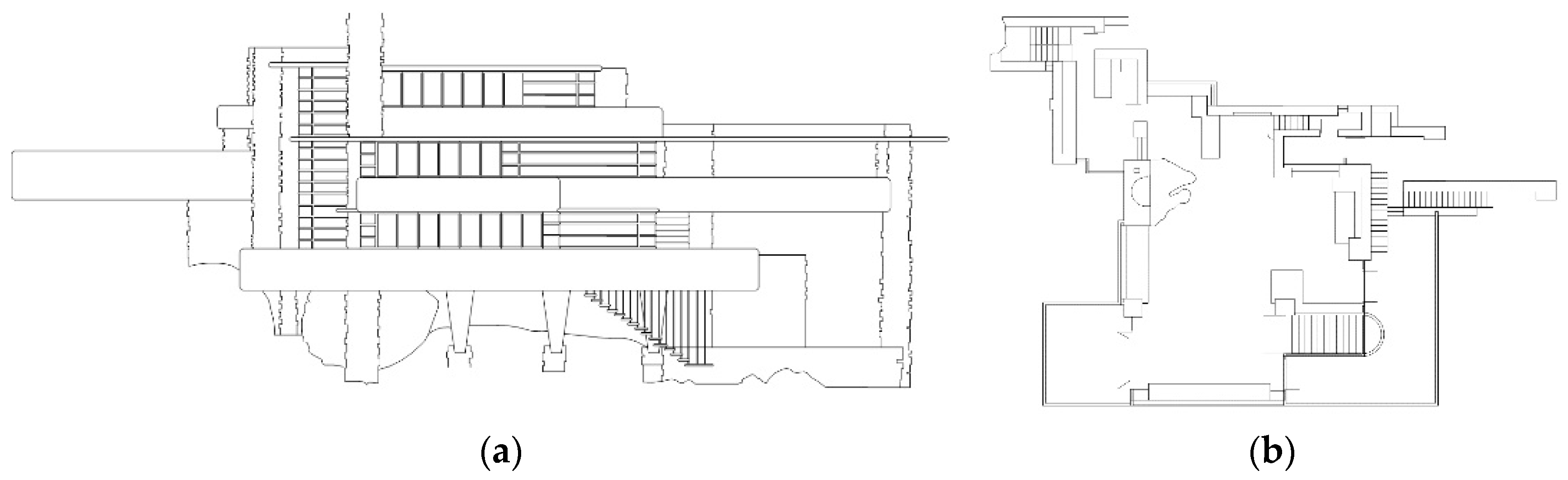
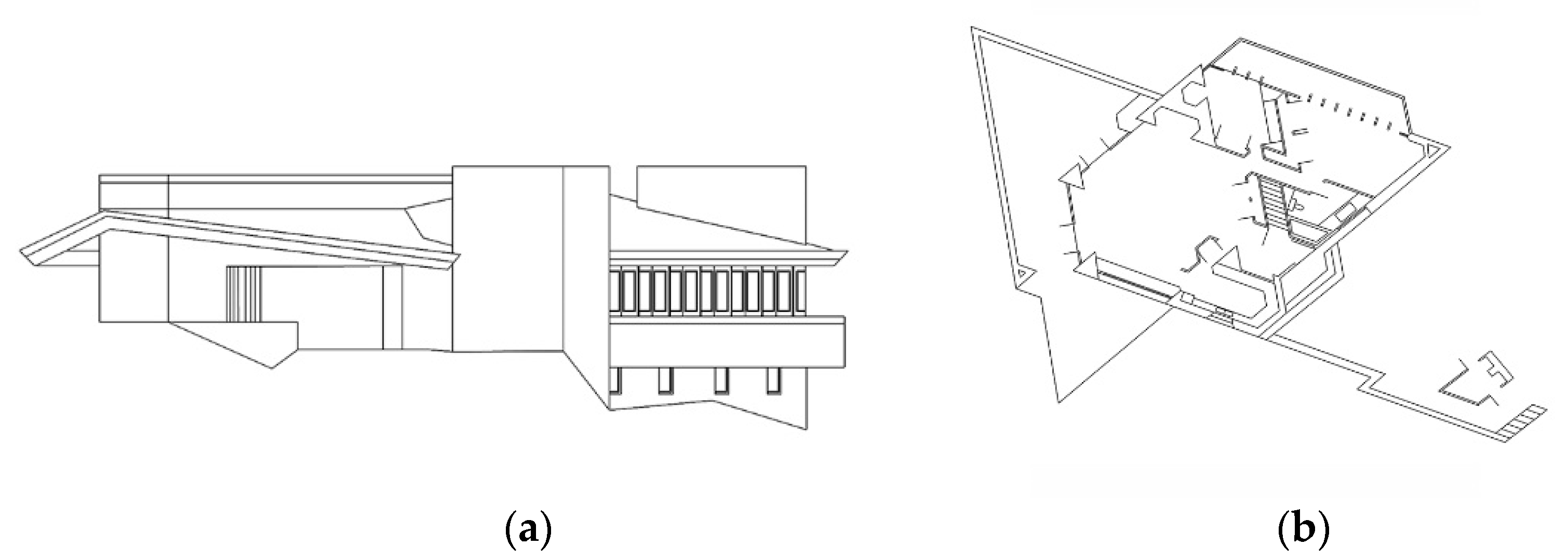
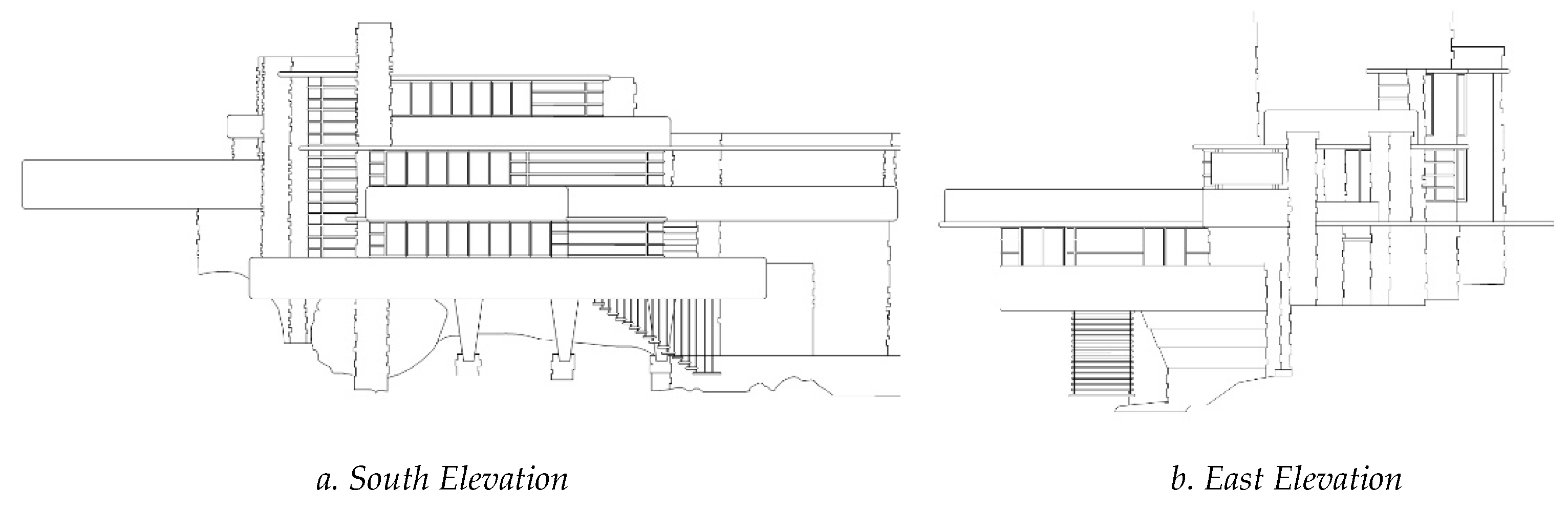
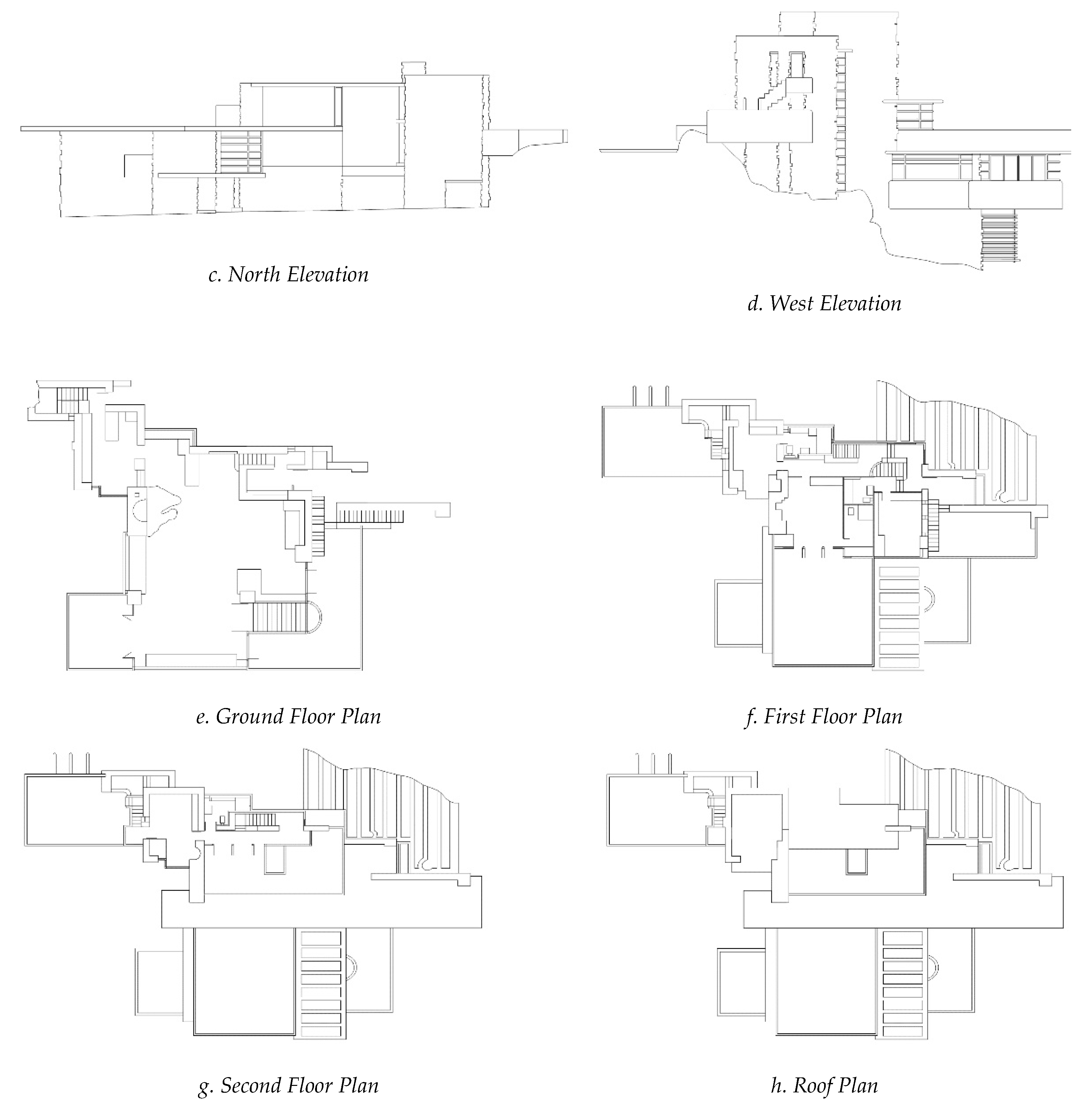
- The fractal dimensions of the elevations of Fallingwater are developed for the first time for this paper. The fractal dimensions of three floor plans and one roof plan of Fallingwater have been recently measured and published [41]. The plans were measured using the standard architectural box-counting method [18], and the elevations are also measured in the same way in this paper. In total, eight individual D results are developed from Fallingwater for comparative purposes.
- (2)
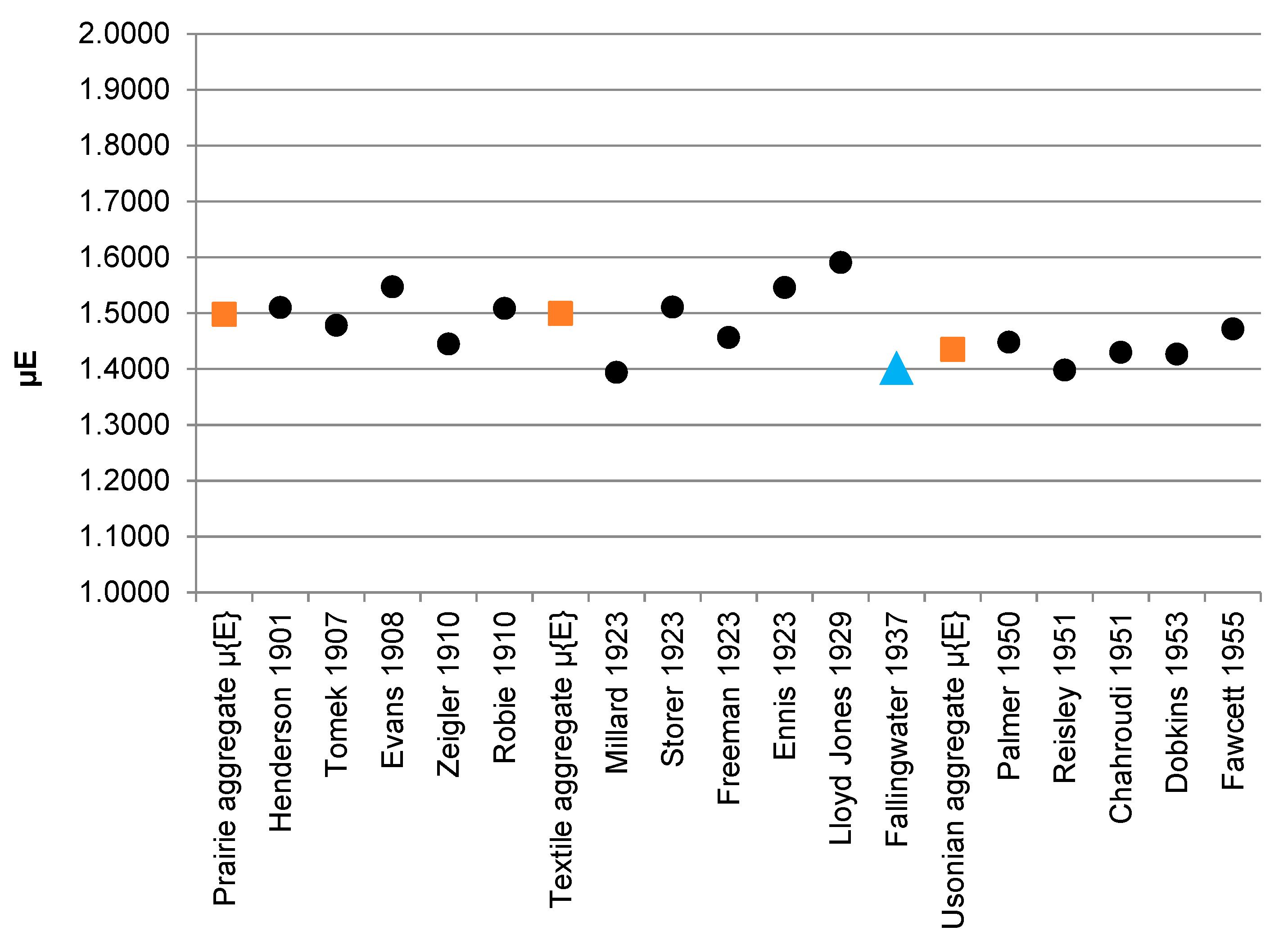
- The primary visual characteristics of Wright’s Prairie style are considered, as in past research, to be encapsulated in a set of five key works: Robie, Evans, Zeigler, Tomek and Henderson houses. For Wright’s Textile-Block style, the Ennis, Millard, Storrer, Freeman and Lloyd-Jones houses are, for all practical purposes, the complete set. For the Usonian works, the Palmer, Dobkins, Reisley, Fawcett and Chahroudi houses are considered representative of one type of Usonian planning. Fractal dimension measures for these 15 houses (58 elevations and 46 plans) were previously produced using the standard method [18].
3.3. Derived Measures and Terminology
3.4. Interpretation of the Results
4. Results
4.1. Full Set of Fractal Dimensions for Fallingwater
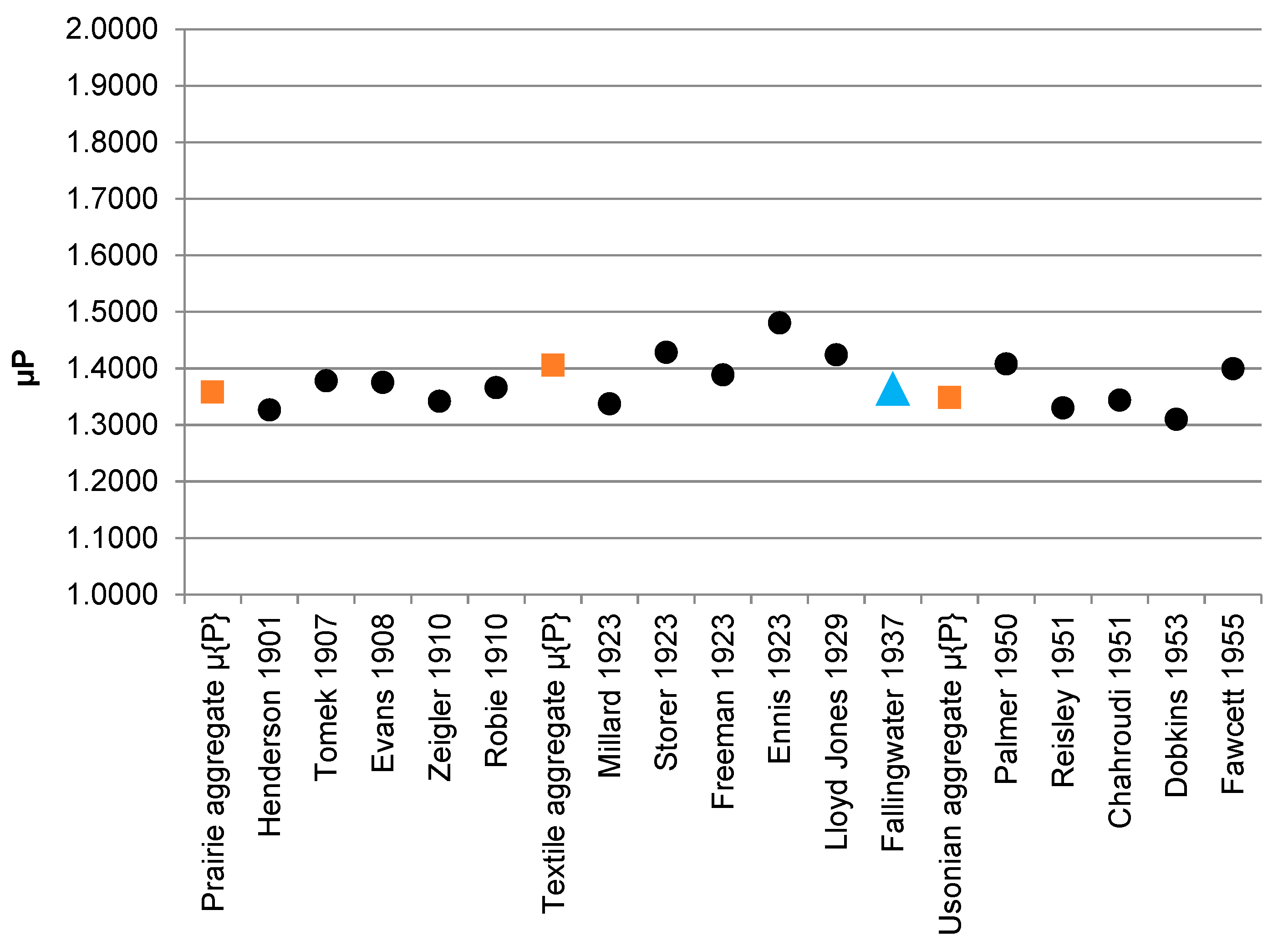
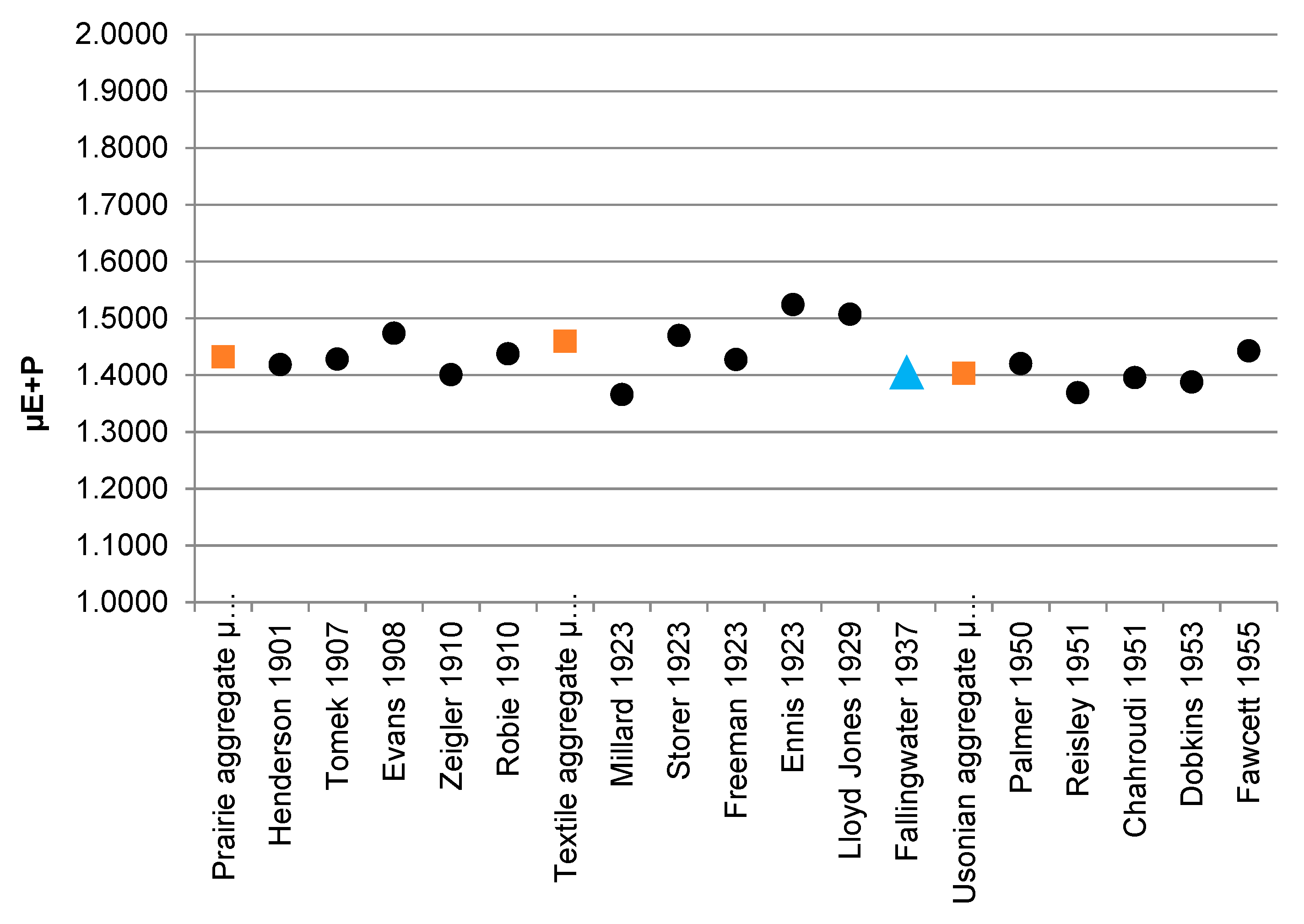
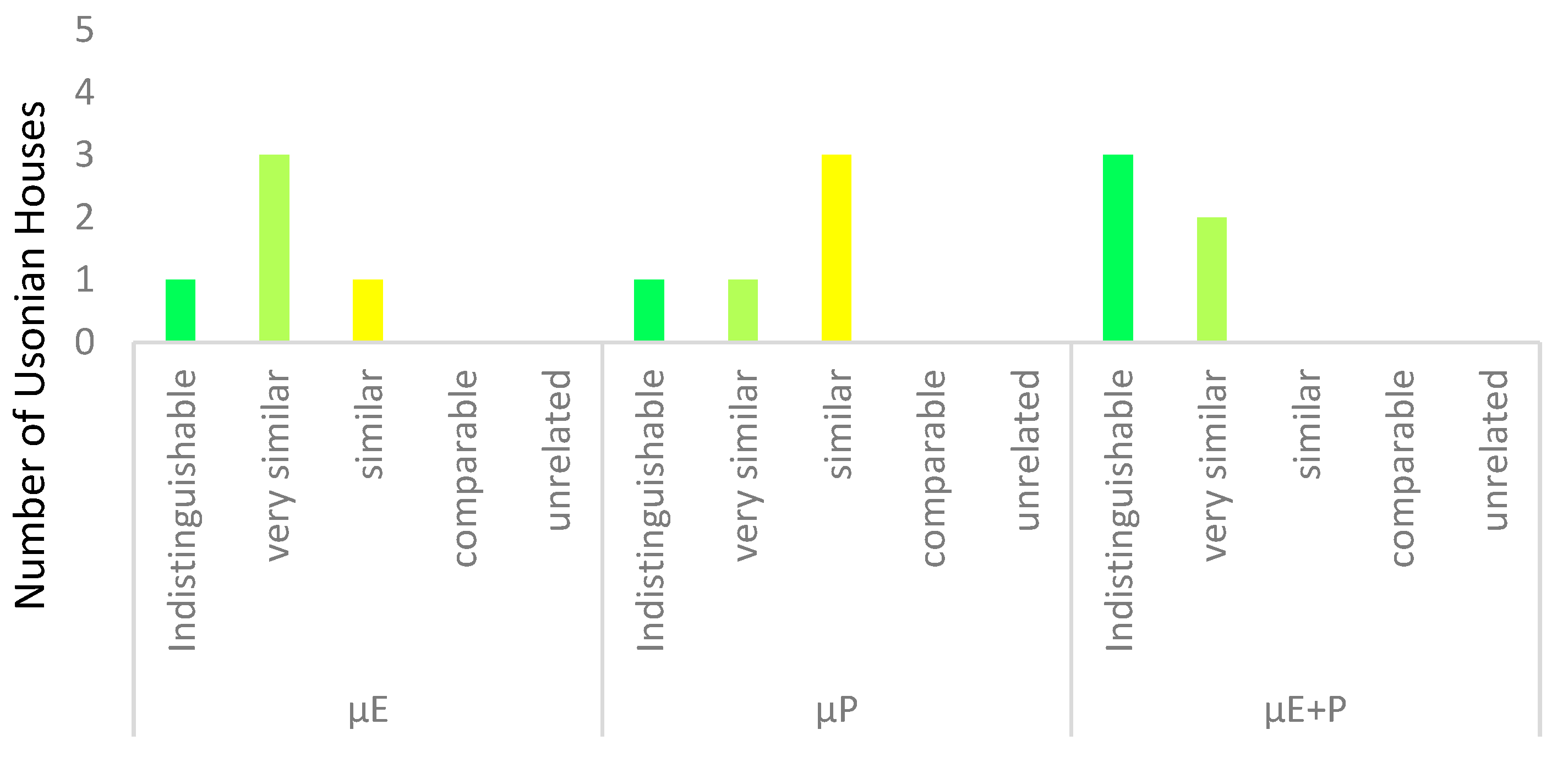
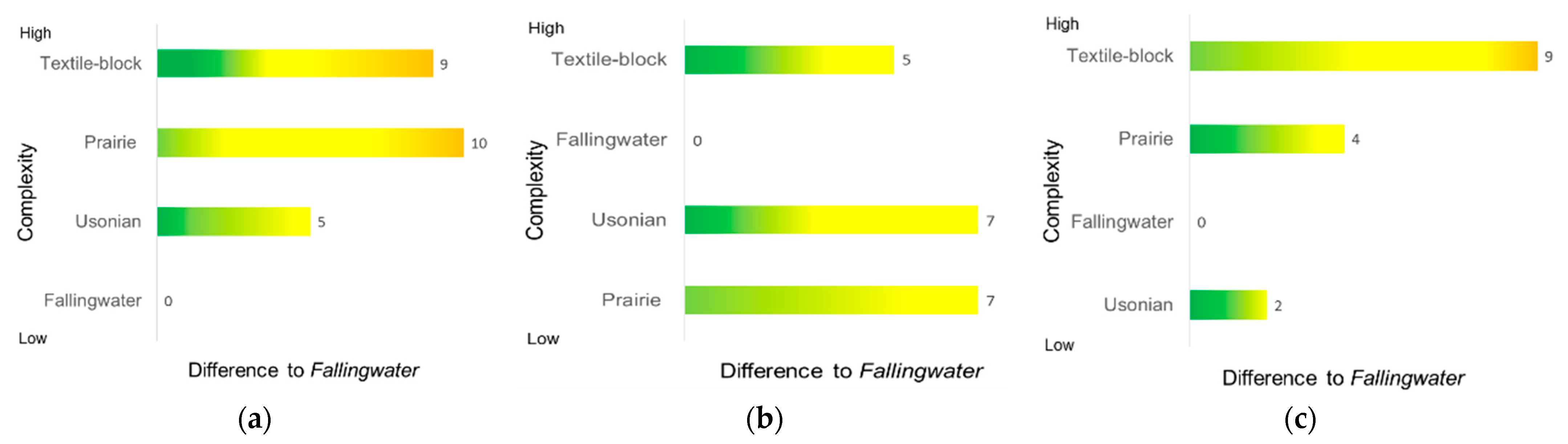
4.2. Initial Comparison Fallingwater to the Prairie, Textile-Block and Usonian Sets
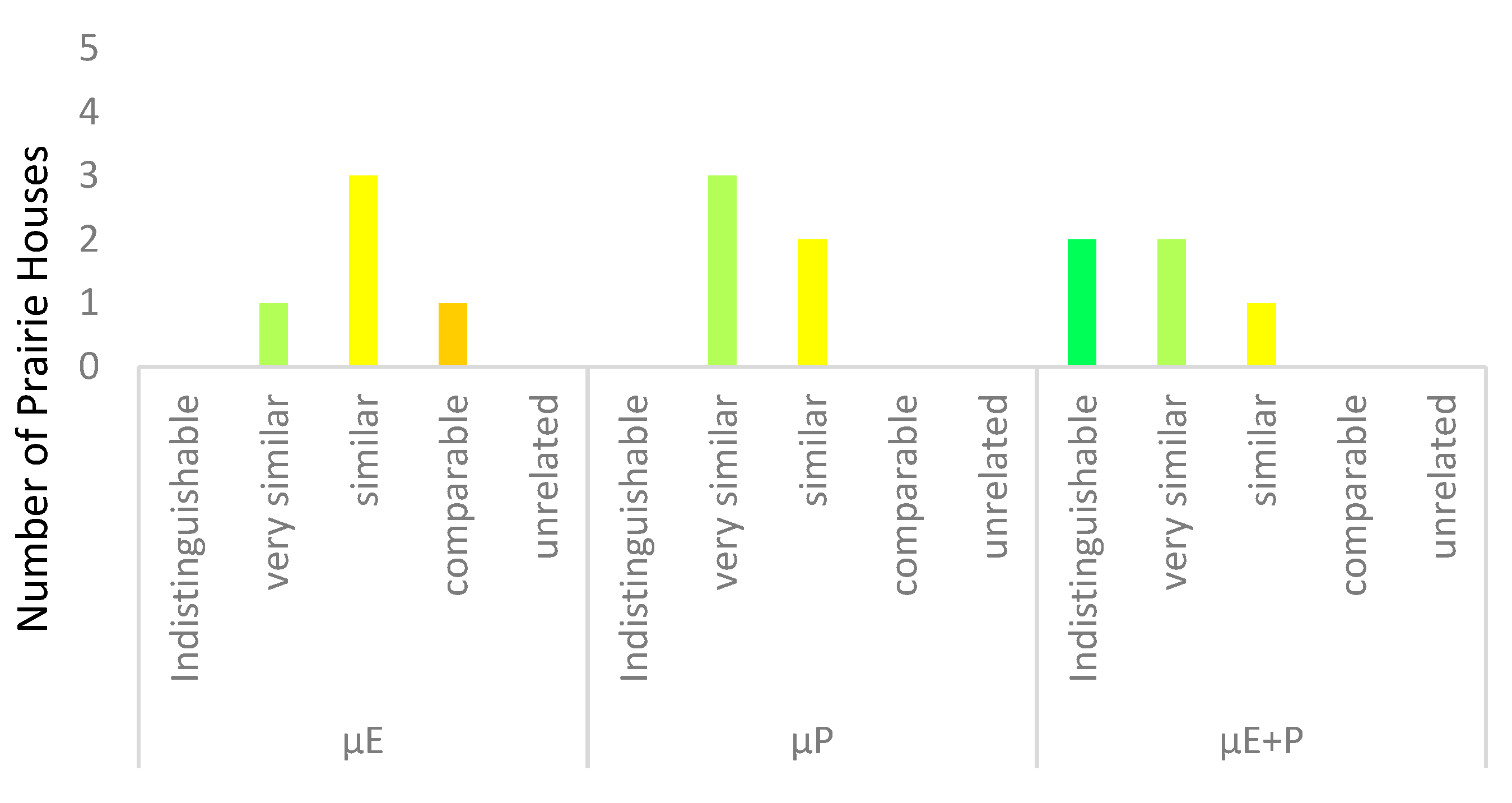
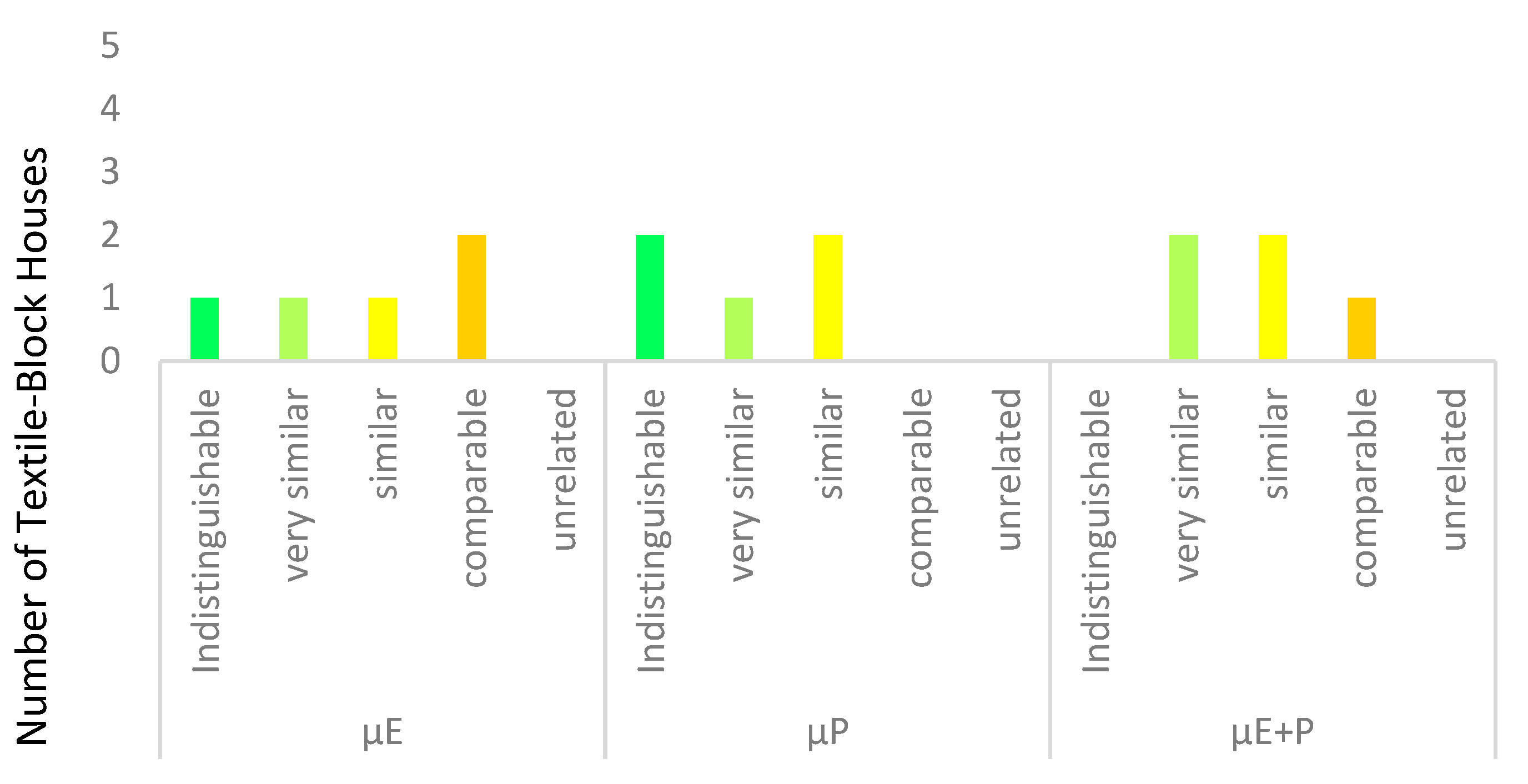
4.3. Detailed Comparison Fallingwater to the Prairie, Textile-Block and Usonian Sets
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Correction Statement
Appendix A
| Houses | Henderson | Tomek | Evans | Zeigler | Robie | Set {…} | |
|---|---|---|---|---|---|---|---|
| Elevations | DE1 | 1.5255 | 1.5103 | 1.5592 | 1.4442 | 1.5174 | |
| DE2 | 1.5177 | 1.4885 | 1.5709 | 1.4542 | 1.5708 | ||
| DE3 | 1.4910 | 1.4342 | 1.5254 | 1.4385 | 1.4785 | ||
| DE4 | 1.5072 | 1.4799 | 1.5337 | 1.4424 | 1.4677 | ||
| μE | 1.5104 | 1.4782 | 1.5473 | 1.4448 | 1.5086 | ||
| μ{E} | 1.4979 | ||||||
| M{E} | 1.4991 | ||||||
| std{E} | 0.0432 | ||||||
| Plans | DP-1 | 1.3001 | 1.4448 | ||||
| DP0 | 1.4499 | 1.3902 | 1.4307 | 1.4170 | 1.3385 | ||
| DP1 | 1.3763 | 1.3721 | 1.3817 | 1.3802 | 1.4220 | ||
| DP2 | - | - | - | - | 1.3984 | ||
| DPR | 1.1817 | 1.3077 | 1.3147 | 1.2295 | 1.3066 | ||
| μP | 1.3270 | 1.3787 | 1.3757 | 1.3422 | 1.3664 | ||
| μ{P} | 1.3579 | ||||||
| M{P} | 1.3783 | ||||||
| std{P} | 0.0734 | ||||||
| Composite | μE+P | 1.4187 | 1.4285 | 1.4738 | 1.4009 | 1.4375 | |
| Aggregate | μ{E+P} | 1.4318 |
| Houses | Millard | Storer | Freeman | Ennis | Lloyd-Jones | Set{…} | |
| Elevations | DE1 | 1.4420 | 1.5389 | 1.3603 | 1.6130 | 1.5947 | |
| DE2 | 1.4786 | 1.5543 | 1.5125 | 1.6390 | 1.5589 | ||
| DE3 | 1.3434 | 1.5111 | 1.4666 | 1.4900 | 1.6105 | ||
| DE4 | 1.3128 | 1.4395 | 1.4868 | 1.4417 | 1.5983 | ||
| μE | 1.3942 | 1.5110 | 1.4566 | 1.5459 | 1.5906 | ||
| μ{E} | 1.4996 | ||||||
| M{E} | 1.5006 | ||||||
| std{E} | 0.0925 | ||||||
| Plans | DP0 | 1.4078 | 1.4497 | 1.3964 | 1.4955 | 1.4465 | |
| DP1 | 1.3801 | 1.4330 | 1.3799 | - | 1.4228 | ||
| DP2 | 1.2826 | 1.4311 | - | - | 1.4158 | ||
| DPR | 1.2809 | 1.4024 | 1.3901 | 1.4664 | 1.4127 | ||
| μP | 1.3379 | 1.4291 | 1.3888 | 1.4810 | 1.4245 | ||
| μ{P} | 1.4055 | ||||||
| M{P} | 1.4127 | ||||||
| std{P} | 0.0557 | ||||||
| Composite | μE+P | 1.3660 | 1.4700 | 1.4275 | 1.5243 | 1.5075 | |
| Aggregate | μ{E+P} | 1.4591 |
| Houses | Palmer | Reisley | Chahroudi | Dobkins | Fawcett | Set {…} | |
|---|---|---|---|---|---|---|---|
| Elevations | DE1 | 1.4802 | 1.3865 | 1.4328 | 1.4596 | 1.3991 | |
| DE2 | 1.4461 | 1.3710 | 1.4529 | 1.3375 | 1.5575 | ||
| DE3 | 1.4642 | 1.4086 | - | 1.5359 | - | ||
| DE4 | 1.4018 | 1.4265 | 1.4045 | 1.3745 | 1.4591 | ||
| μE | 1.4481 | 1.3982 | 1.4301 | 1.4269 | 1.4719 | ||
| μ{E} | 1.4350 | ||||||
| M{E} | 1.4297 | ||||||
| std{E} | 0.0560 | ||||||
| Plans | DP-1 | - | 1.2968 | - | - | - | |
| DP0 | 1.4412 | 1.3687 | 1.3973 | 1.3810 | 1.4155 | ||
| DPR | 1.2875 | 1.3256 | 1.2908 | 1.2400 | 1.3839 | ||
| μP | 1.3644 | 1.3304 | 1.3441 | 1.3105 | 1.3997 | ||
| μ{P} | 1.3480 | ||||||
| M{P} | 1.3687 | ||||||
| std{P} | 0.0634 | ||||||
| Composite | μE+P | 1.4202 | 1.3691 | 1.3957 | 1.3881 | 1.4430 | |
| Aggregate | μ{E+P} | 1.4032 |
References
- Alofsin, A. Frank Lloyd Wright and Modernism. In Frank Lloyd Wright, Architect; Riley, T., Alofsin, A., Eds.; Museum of Modern Art (New York) and Frank Lloyd Wright Foundation: New York, NY, USA, 1994; pp. 32–57. [Google Scholar]
- Pfeiffer, B.B. Frank Lloyd Wright, 1867–1959: Building for Democracy; Taschen: Köln, Germany, 2004. [Google Scholar]
- Laseau, P.; Tice, J. Frank Lloyd Wright: Between Principle and Form; Van Nostrand Reinhold: New York, NY, USA, 1992. [Google Scholar]
- Koning, H.; Eizenberg, J. The language of the prairie: Frank Lloyd Wright’s prairie houses. Environ. Plan. B Plan. Des. 1981, 8, 295–323. [Google Scholar] [CrossRef]
- Vaughan, J.; Ostwald, M.J. The relationship between the fractal dimension of plans and elevations in the architecture of Frank Lloyd Wright: Comparing the Prairie style, Textile-block and Usonian periods. ArS Archit. Sci. 2011, 4, 21–44. [Google Scholar]
- Kaufmann, E. Fallingwater, a Frank Lloyd Wright Country House; Abbeville Press: New York, NY, USA, 1986. [Google Scholar]
- McCarter, R. Frank Lloyd Wright; Phaidon: London, UK, 1999. [Google Scholar]
- Storrer, W.A. The Frank Lloyd Wright Companion; University of Chicago Press: Chicago, IL, USA, 2006. [Google Scholar]
- Green, A.G. Organic architecture: The principles of Frank Lloyd Wright. In Frank Lloyd Wright in the Realm of Ideas; Nordland, G., Pfeiffer, B.B., Eds.; Southern Illinois University Press: Carbondale, IL, USA, 1988; pp. 133–142. [Google Scholar]
- Maddex, D. 50 Favourite Rooms by Frank Lloyd Wright; Thames & Hudson: London, UK, 1998. [Google Scholar]
- Lind, C. Frank Lloyd Wright’s Fallingwater; Pomegranate: San Francisco, CA, USA, 1996. [Google Scholar]
- Futagawa, Y.; Pfeiffer, B.B. Fallingwater; A.D.A: Tokyo, Japan, 2009. [Google Scholar]
- Hoesli, B. From the Prairie house to Fallingwater. In On and by Frank Lloyd Wright: A Primer of Architectural Principles; McCarter, R., Ed.; Phaidon: London, UK, 2005; pp. 204–215. [Google Scholar]
- Smith, K. A beat of the rhythmic clock of nature: Frank Lloyd Wright’s waterfall buildings. In Wright Studies, Volume Two: Fallingwater and Pittsburgh; Menocal, N.G., Ed.; Southern Illinois University Press: Carbondale, IL, USA, 2000; pp. 1–31. [Google Scholar]
- McCarter, R. Fallingwater; Phaidon: London, UK, 2002. [Google Scholar]
- Mandelbrot, B.B. The Fractal Geometry of Nature; W.H. Freeman: New York, NY, USA, 1977. [Google Scholar]
- Mandelbrot, B.B. The Fractal Geometry of Nature. Updated and Augmented; Freeman: San Francisco, CA, USA, 1982. [Google Scholar]
- Ostwald, M.J.; Vaughan, J. The Fractal Dimension of Architecture; Springer International Publishing: Basel, Switzerland, 2016. [Google Scholar]
- Bovill, C. Fractal Geometry in Architecture and Design; Design Science Collection; Birkhäuser: Boston, MA, USA, 1996. [Google Scholar]
- Burkle-Elizondo, G. Fractal geometry in Mesoamerica. Symmetry Cult. Sci. 2001, 12, 201–214. [Google Scholar]
- Rian, I.M.; Park, J.H.; Hyung, U.A.; Chang, D. Fractal geometry as the synthesis of Hindu cosmology in Kandariya Mahadev temple, Khajuraho. Build. Environ. 2007, 42, 4093–4107. [Google Scholar] [CrossRef]
- Lionar, M.L.; Ediz, Ö. Measuring Visual Complexity of Sedad Eldem’s SSK Complex and Its Historical Context: A Comparative Analysis Using Fractal Dimensions. Nexus Netw. J. 2020, 22, 701–715. [Google Scholar] [CrossRef]
- Vaughan, J.; Ostwald, M.J. Measuring the significance of façade transparency in Australian regionalist architecture: A computational analysis of 10 designs by Glenn Murcutt. Archit. Sci. Rev. 2014, 57, 249–259. [Google Scholar] [CrossRef]
- Ostwald, M.J.; Vaughan, J.; Tucker, C. Characteristic visual complexity: Fractal dimensions in the architecture of Frank Lloyd Wright and Le Corbusier. In Architecture and Mathematics from Antiquity to the Future; Williams, K., Ostwald, M., Eds.; Birkhäuser: Cham, The Switzerland, 2015; pp. 339–354. [Google Scholar] [CrossRef]
- Lorenz, W.E. Fractal geometry of architecture: Implementation of the box-counting method in a CAD-software. In Computation: The New Realm of Architectural Design, Proceedings of the 27th eCAADe Conference on Education and Research in Computer Aided Design in Europe, Istanbul, Turkey, 16–19 September 2009; eCAADe: Istanbul, Turkey; pp. 697–704.
- Benguigui, L.; Czamanski, D.; Marinov, M.; Portugali, Y. When and where is a city fractal? Environ. Plan. B Plan. Des. 2000, 27, 507–519. [Google Scholar] [CrossRef]
- Lorenz, W. Estimating the fractal dimension of architecture: Using two measurement methods implemented in AutoCAD by VBA. In Digital Physicality—Proceedings of the 30th eCAADe Conference, Czech Technical University in Prague, Prague, Czech Republic, 12–14 September 2012; Achten, H., Pavlicak, J., Hulin, J., Matejdan, D., Eds.; eCAADe and CVUT: Prague, Czech Republic; pp. 505–513.
- Wen, K.C.; Yu-Neng, K. An analytic study of architectural design style by fractal dimension method. In Proceedings of the 22nd ISARC, Ferrara, Italy, 11–14 September 2005; pp. 1–6. [Google Scholar]
- Vaughan, J.; Ostwald, M.J. A quantitative comparison between the formal complexity of Le Corbusier’s Pre-Modern (1905–1912) and Early Modern (1922-1928) architecture. Des. Princ. Pract. Int. J. 2009, 3, 359–372. [Google Scholar] [CrossRef]
- Samper, A.; Herrera, B. The fractal pattern of the French Gothic cathedrals. Nexus Netw. J. 2014, 16, 251–271. [Google Scholar] [CrossRef]
- Ostwald, M.J. Examining the relationship between topology and geometry: A configurational analysis of the rural houses (1984– 2005) of Glenn Murcutt. J. Space Syntax. 2011, 2, 223–246. [Google Scholar]
- Leupen, B.; Grafe, C.; Körnig, N.; Lamp, M.; de Zeeuw, P. Design and Analysis; Van Nostrand Reinhold: New York, NY, USA, 1997. [Google Scholar]
- Sala, N. Fractal models in architecture: A case of study. In Proceedings of the International Conference on Mathematics Education into the 21st Century: Mathematics for Living, The Third World Forum, Amman, Jordan, 18–23 November 2000; Rogerson, A., Ed.; The Mathematics Education into the 21st Century Project and The Third World Forum. [Google Scholar]
- Lorenz, W. Fractals and Fractal Architecture. Master’s Dissertation, Vienna University of Technology, Vienna, Austria, 2003. [Google Scholar]
- Ma, L.; Zhang, H.; Lu, M. Building’s Fractal Dimension Trend and Its Application in Visual Complexity Map. Build. Environ. 2020, 178, 106925. [Google Scholar] [CrossRef]
- Vaughan, J.; Ostwald, M.J. Using fractal analysis to compare the characteristic complexity of nature and architecture: Re-examining the evidence. Archit. Sci. Rev. 2010, 53, 323–332. [Google Scholar] [CrossRef]
- Lorenz, W. Complexity across scales in the work of Le Corbusier Using box-counting as a method for analysing facades. In Proceedings of the CAADENCE in Architecture 2016, Budapest University of Technology and Economics, Budapest, Hungary, 16–17 June 2016. [Google Scholar]
- Ostwald, M.J.; Vaughan, J. Calculating Visual Complexity in Peter Eisenman’s Architecture. In CAADRIA 2009: Between Man and Machine Integration/Intuition/Intelligence; Chang, T.-W., Champion, E., Chien, S.-F., Eds.; National Yunlin University of Science & Technology Department of Digital Media Design: Yunlin, Taiwan, 2009; pp. 75–84. [Google Scholar]
- Ohuchi, H.; Kimura, T.; Zong, S.; Kanai, S.; Kuroiwa, T. Quantitative Evaluation of Architectural Style Using Image Correlation and Fractal Dimension Analysis in Agora of Ancient Greek City Athens. AST 2020, 103, 37–45. [Google Scholar]
- Ostwald, M.J.; Vaughan, J. The mathematics of style in the architecture of Frank Lloyd Wright: A computational, fractal analysis of formal complexity in fifteen domestic designs. In Built Environment: Design Management and Applications; Geller, P.S., Ed.; NOVA Science Publishers: Hauppauge, NY, USA, 2010; pp. 63–88. [Google Scholar]
- Vaughan, J.; Ostwald, M.J. Measuring the geometry of nature and architecture: Comparing the visual properties of Frank Lloyd Wright’s Fallingwater and its natural setting. Open House Int. 2022, 47, 51–67. [Google Scholar] [CrossRef]
- Hoppen, D.W. The Seven Ages of Frank Lloyd Wright: The Creative Process; Dover Publications: New York, NY, USA, 1998. [Google Scholar]
- Hess, A.; Weintraub, A. Frank Lloyd Wright Natural Design: Organic Architecture: Lessons for Building Green from an American Original; Rizzoli International Publications: New York, NY, USA, 2012. [Google Scholar]
- Fell, D. The Gardens of Frank Lloyd Wright; Frances Lincoln: London, UK, 2009. [Google Scholar]
- Menocal, N.G. Wright Studies, Volume Two: Fallingwater and Pittsburgh; Southern Illinois University Press: Carbondale, IL, USA, 2000. [Google Scholar]


| Abbreviation | Meaning |
|---|---|
| D | Fractal Dimension |
| DE | D for a specific elevation. |
| DP | D for a specific plan. |
| μE μP μE+P. | Mean D for the elevations of a building. Mean D result for the plans of a building. Mean D result for all of the plans and elevations of a building. |
| μ{E} | Mean D for a set of elevations for multiple buildings. |
| μ{P} | Mean D for a set of plans for multiple buildings. |
| μ{E+P} | Mean D for a set of elevations and plans for multiple buildings. |
| Range (%) | Qualitative Descriptors |
|---|---|
| x < 2.0 | ‘Indistinguishable’ |
| 2.0 ≤ x < 6 | ‘Very similar’ |
| 6 ≤ x < 11 | ‘Similar’ |
| 11 ≤ x < 20 | ‘Broadly comparable’ |
| ≥21 | ‘Unrelated’ |
| Result Set | Measure | Fractal Dimension |
|---|---|---|
| Elevations | DE1 | 1.3321 |
| DE2 | 1.4628 | |
| DE3 | 1.4341 | |
| DE4 | 1.3786 | |
| μE | 1.4019 | |
| Plans | DP0 | 1.3897 |
| DP1 | 1.4439 | |
| DP2 | 1.4133 | |
| DPR | 1.3870 | |
| μP | 1.4085 | |
| Composite | μE+P | 1.4052 |
| Range | RED | 0.1307 |
| RE% | 13.07 | |
| RPD | 0.0569 | |
| RP% | 5.69 |
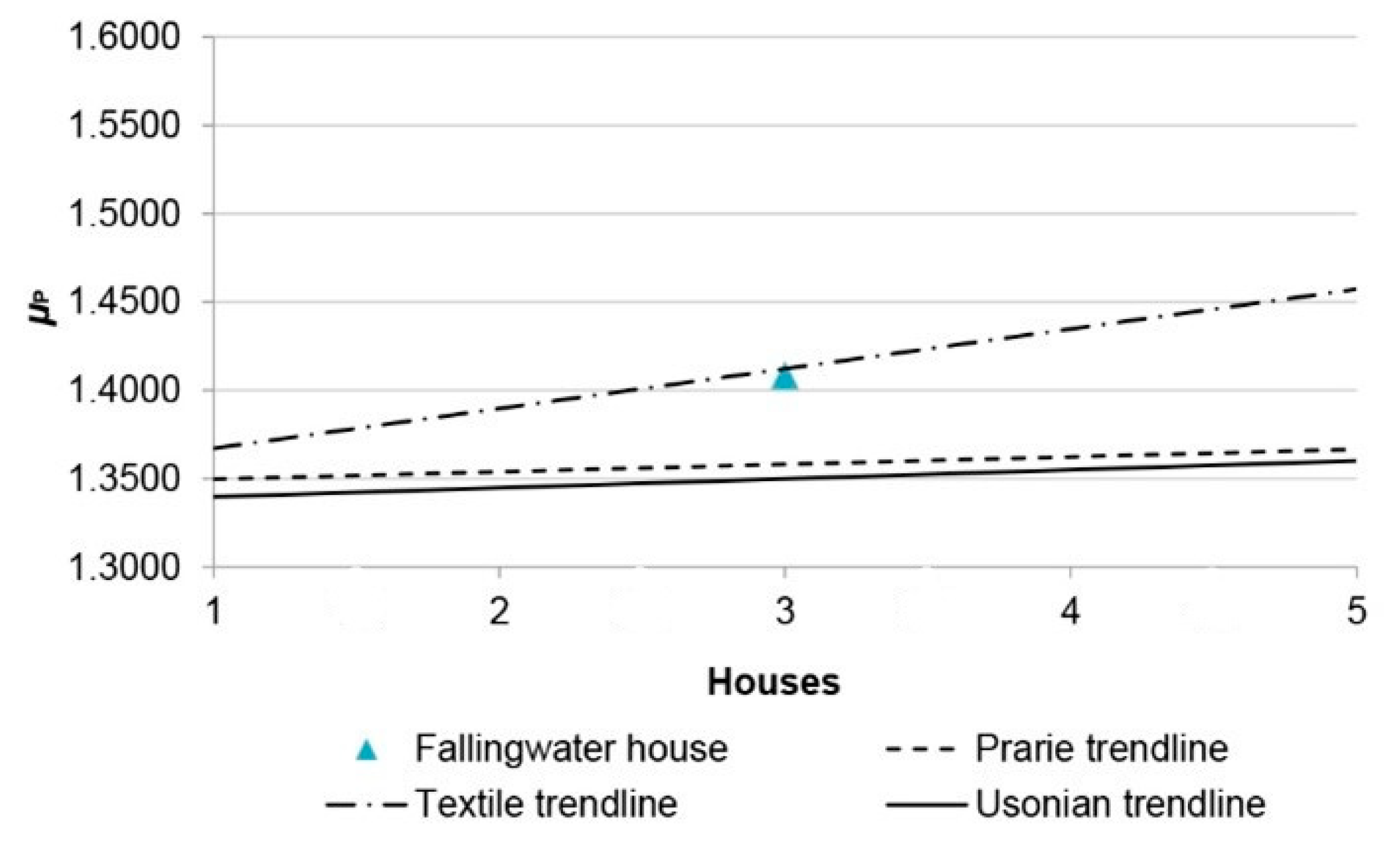
| House Set | House 1 (Earliest House) | House 2 | House 3 | House 4 | House 5 (Latest House) |
|---|---|---|---|---|---|
| Prairie μE | 1.5104 | 1.4782 | 1.5473 | 1.4448 | 1.5086 |
| Textile μE | 1.3942 | 1.5110 | 1.4566 | 1.5459 | 1.5906 |
| Usonian μE | 1.4481 | 1.3982 | 1.4301 | 1.4269 | 1.4719 |
| Fallingwater μE | 1.4019 | ||||
| House Set | House 1 (Earliest House) | House 2 | House 3 | House 4 | House 5 (Latest House) |
|---|---|---|---|---|---|
| Prairie μP | 1.3270 | 1.3787 | 1.3757 | 1.3422 | 1.3664 |
| Textile μP | 1.3379 | 1.4291 | 1.3888 | 1.4810 | 1.4245 |
| Usonian μP | 1.3644 | 1.3304 | 1.3441 | 1.3105 | 1.3997 |
| Fallingwater μP | 1.4085 | ||||
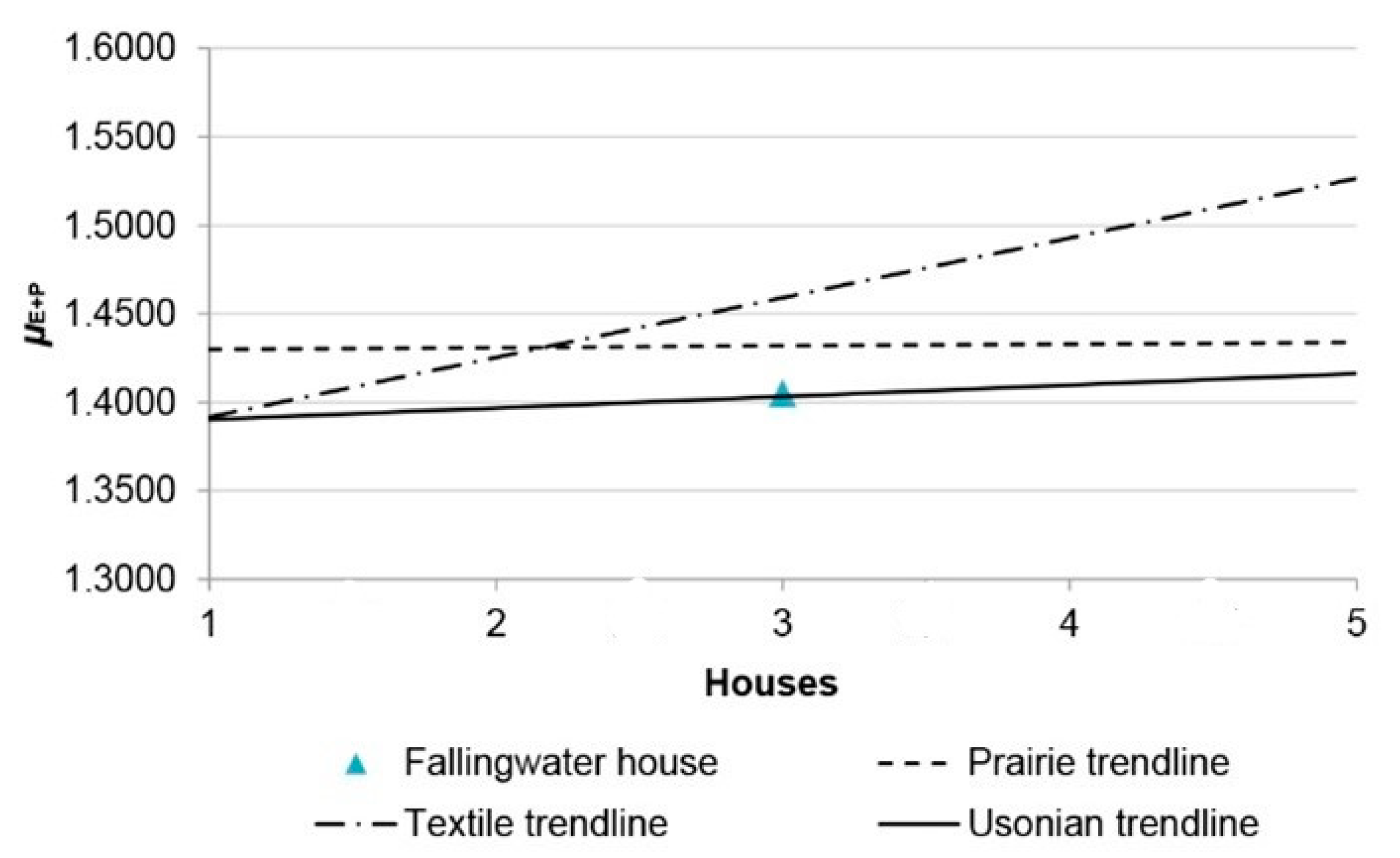
| House Set | House 1 (Earliest House) | House 2 | House 3 | House 4 | House 5 (Latest House) |
|---|---|---|---|---|---|
| Prairie μE+P | 1.4187 | 1.4285 | 1.4738 | 1.4009 | 1.4375 |
| Textile μE+P | 1.3660 | 1.4700 | 1.4275 | 1.5243 | 1.5075 |
| Usonian μE+P | 1.4202 | 1.3691 | 1.3957 | 1.3881 | 1.4430 |
| Fallingwater μE+P | 1.4052 | ||||
| Period | Houses | μE | μP | μE+P | Range Compared to Fallingwater | ||
|---|---|---|---|---|---|---|---|
| Prairie 1907–1910 | RμE% | RμP% | RμE+P% | ||||
| Henderson | 1.5104 | 1.3270 | 1.4187 | 10.8450 | 8.1500 | 1.3475 | |
| Tomek | 1.4782 | 1.3787 | 1.4285 | 7.6325 | 2.9800 | 2.3263 | |
| Evans | 1.5473 | 1.3757 | 1.4738 | 14.5400 | 3.2800 | 6.8557 | |
| Zeigler | 1.4448 | 1.3422 | 1.4009 | 4.2925 | 6.6267 | 0.4343 | |
| Robie | 1.5086 | 1.3664 | 1.4375 | 10.6700 | 4.2125 | 3.2288 | |
| Prairie-style set mean | 1.4979 | 1.3579 | 1.4318 | 9.6 | 2.9 | 2.6 | |
| Textile-Block 1923–1929 | Millard | 1.3942 | 1.3379 | 1.3660 | 0.7700 | 7.0650 | 3.9175 |
| Storer | 1.5110 | 1.4291 | 1.4700 | 10.9050 | 2.0550 | 6.4800 | |
| Freeman | 1.4566 | 1.3888 | 1.4275 | 5.4650 | 1.9700 | 2.2314 | |
| Ennis | 1.5459 | 1.4810 | 1.5243 | 14.4025 | 7.2450 | 11.9067 | |
| Lloyd-Jones | 1.5906 | 1.4245 | 1.5075 | 18.8700 | 1.5950 | 10.2325 | |
| Textile-Block-style set mean | 1.4996 | 1.4055 | 1.4591 | 9.7 | 0.3 | 5.4 | |
| 1937 | Fallingwater | 1.4019 | 1.4085 | 1.4052 | 0.0000 | 0.0000 | 0.0000 |
| Usonian 1950–1955 | Palmer | 1.4481 | 1.3644 | 1.4202 | 4.6175 | 4.4150 | 1.4967 |
| Reisley | 1.3982 | 1.3304 | 1.3691 | 0.3750 | 7.8133 | 3.6100 | |
| Chahroudi | 1.4301 | 1.3441 | 1.3957 | 2.8167 | 6.4450 | 0.9540 | |
| Dobkins | 1.4269 | 1.3105 | 1.3881 | 2.4975 | 9.8000 | 1.7117 | |
| Fawcett | 1.4719 | 1.3997 | 1.4430 | 7.0000 | 0.8800 | 3.7820 | |
| Usonian-style set mean | 1.4350 | 1.3480 | 1.4032 | 3.3 | 6.0 | 0.2 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vaughan, J.; Ostwald, M.J. Examining the Position of Wright’s Fallingwater in the Context of His Larger Body of Work: An Analysis Using Fractal Dimensions. Fractal Fract. 2022, 6, 187. https://doi.org/10.3390/fractalfract6040187
Vaughan J, Ostwald MJ. Examining the Position of Wright’s Fallingwater in the Context of His Larger Body of Work: An Analysis Using Fractal Dimensions. Fractal and Fractional. 2022; 6(4):187. https://doi.org/10.3390/fractalfract6040187
Chicago/Turabian StyleVaughan, Josephine, and Michael J. Ostwald. 2022. "Examining the Position of Wright’s Fallingwater in the Context of His Larger Body of Work: An Analysis Using Fractal Dimensions" Fractal and Fractional 6, no. 4: 187. https://doi.org/10.3390/fractalfract6040187
APA StyleVaughan, J., & Ostwald, M. J. (2022). Examining the Position of Wright’s Fallingwater in the Context of His Larger Body of Work: An Analysis Using Fractal Dimensions. Fractal and Fractional, 6(4), 187. https://doi.org/10.3390/fractalfract6040187







