Macro- and Micromechanical Assessment of the Influence of Non-Plastic Fines and Stress Anisotropy on the Dynamic Shear Modulus of Binary Mixtures
Abstract
:1. Introduction
2. Experimental Procedure and Sample Preparation
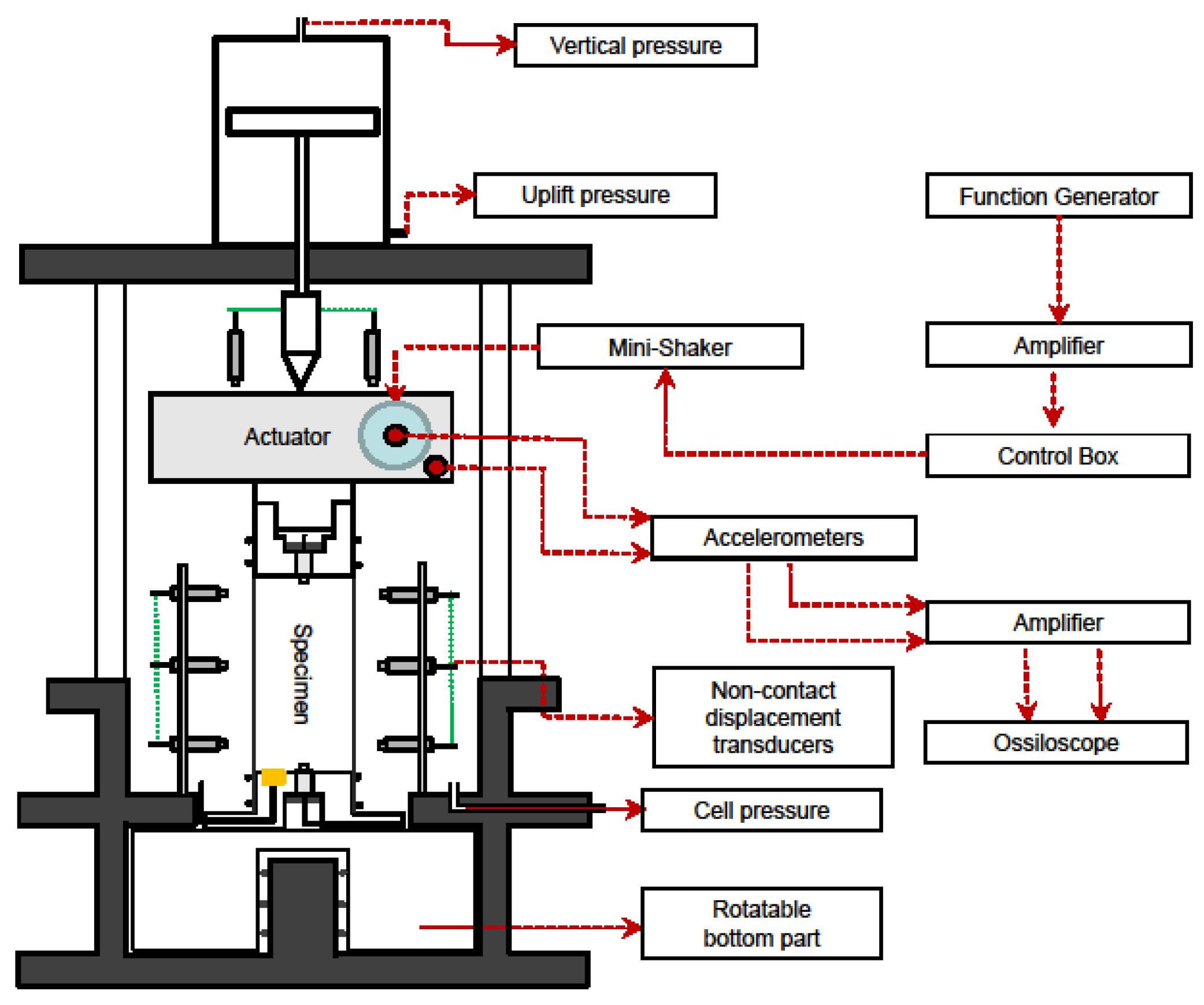
2.1. The RC Device
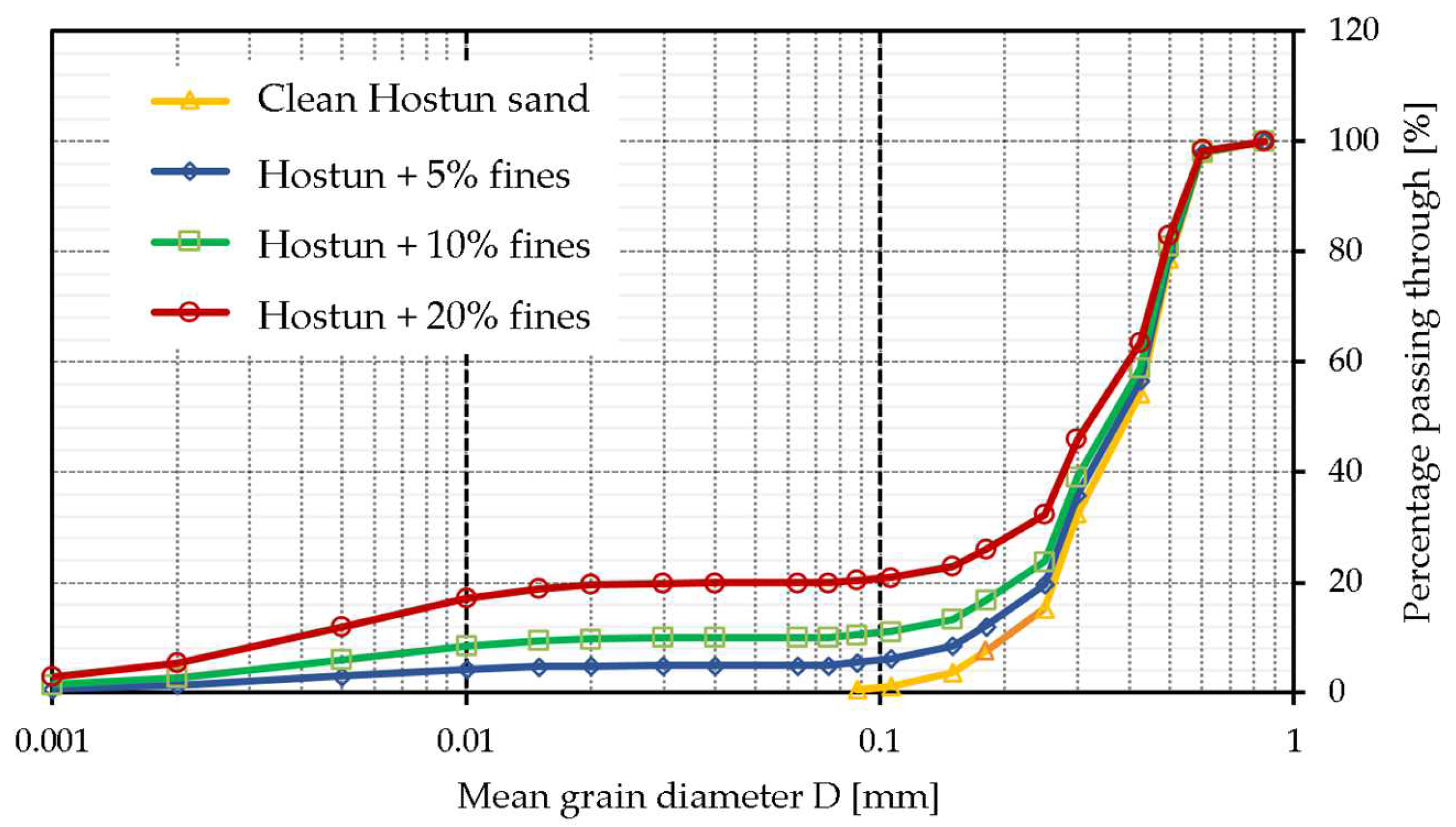
2.2. Tested Materials
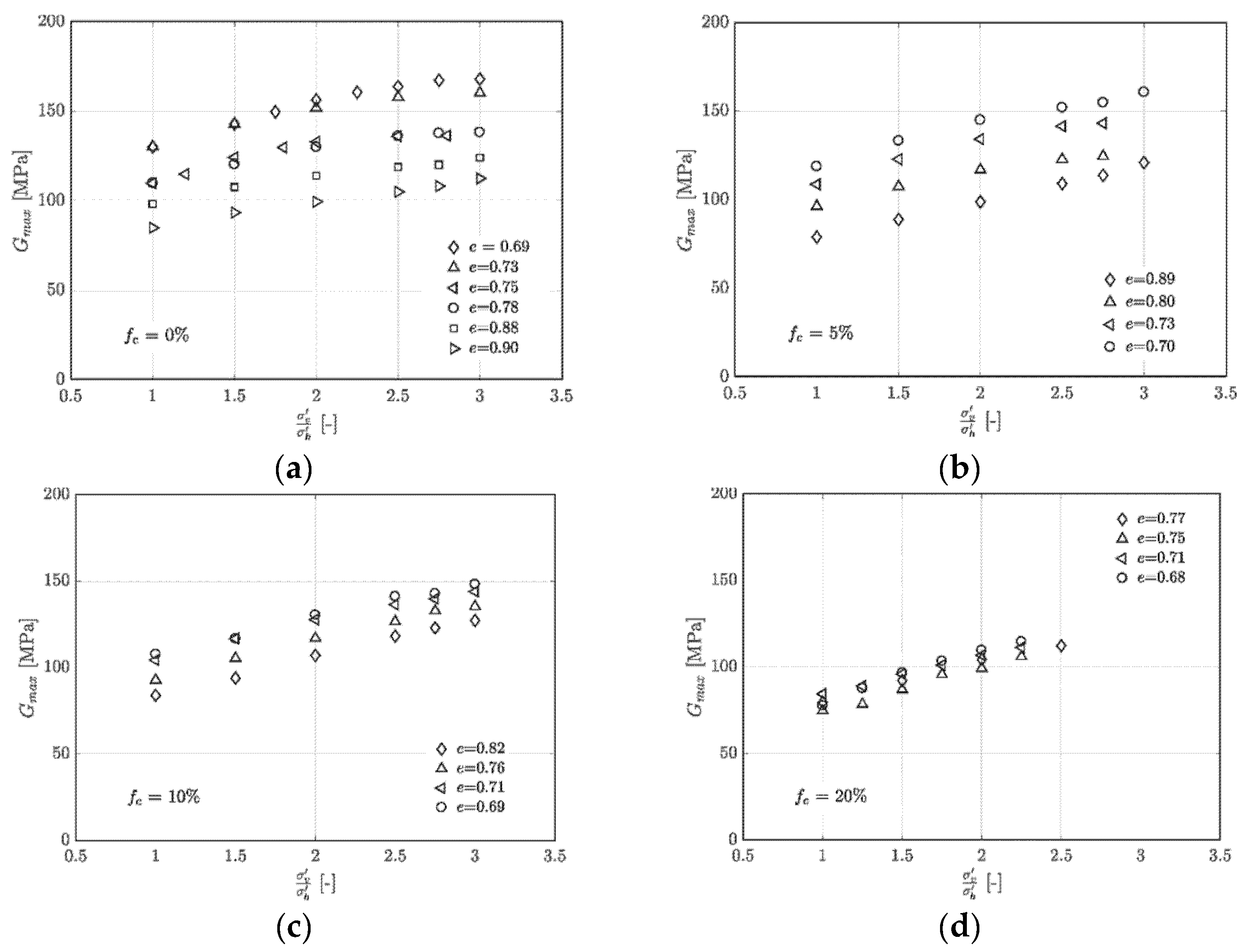
3. Experimental Results
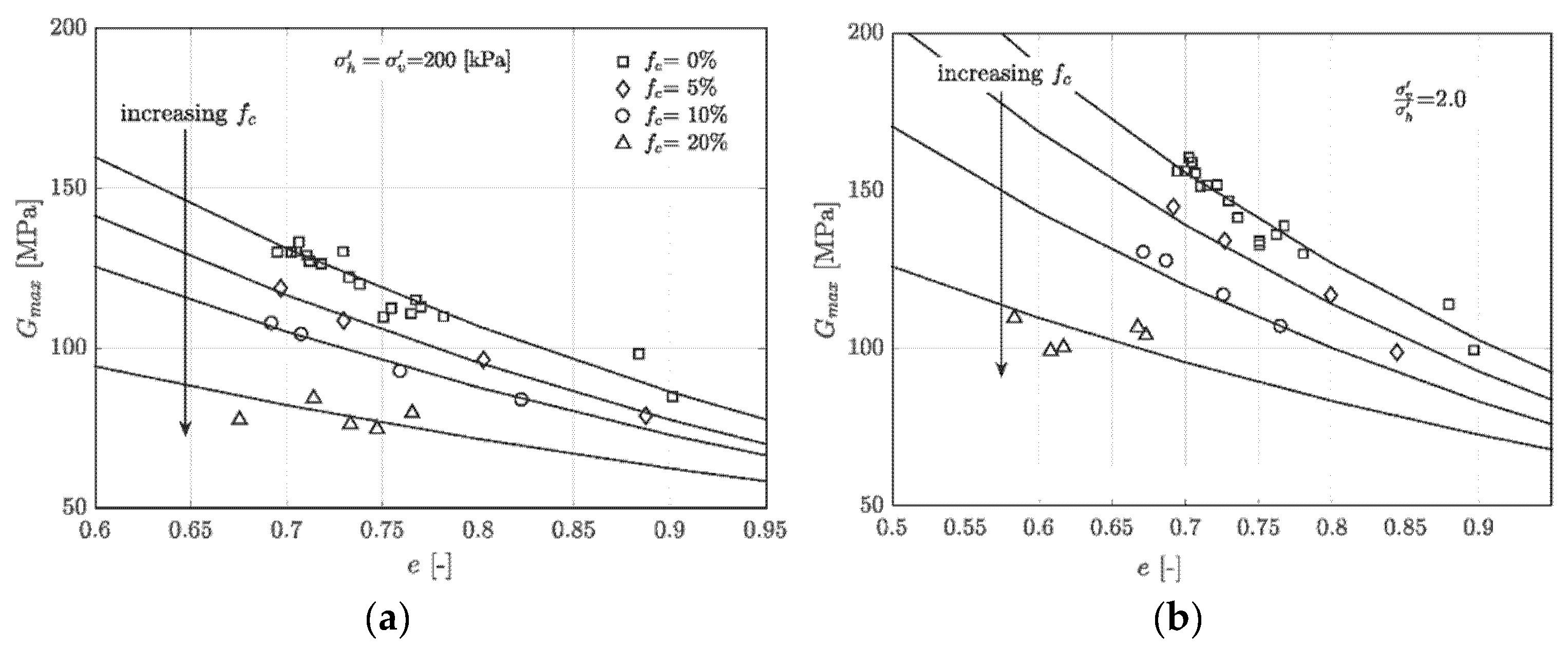
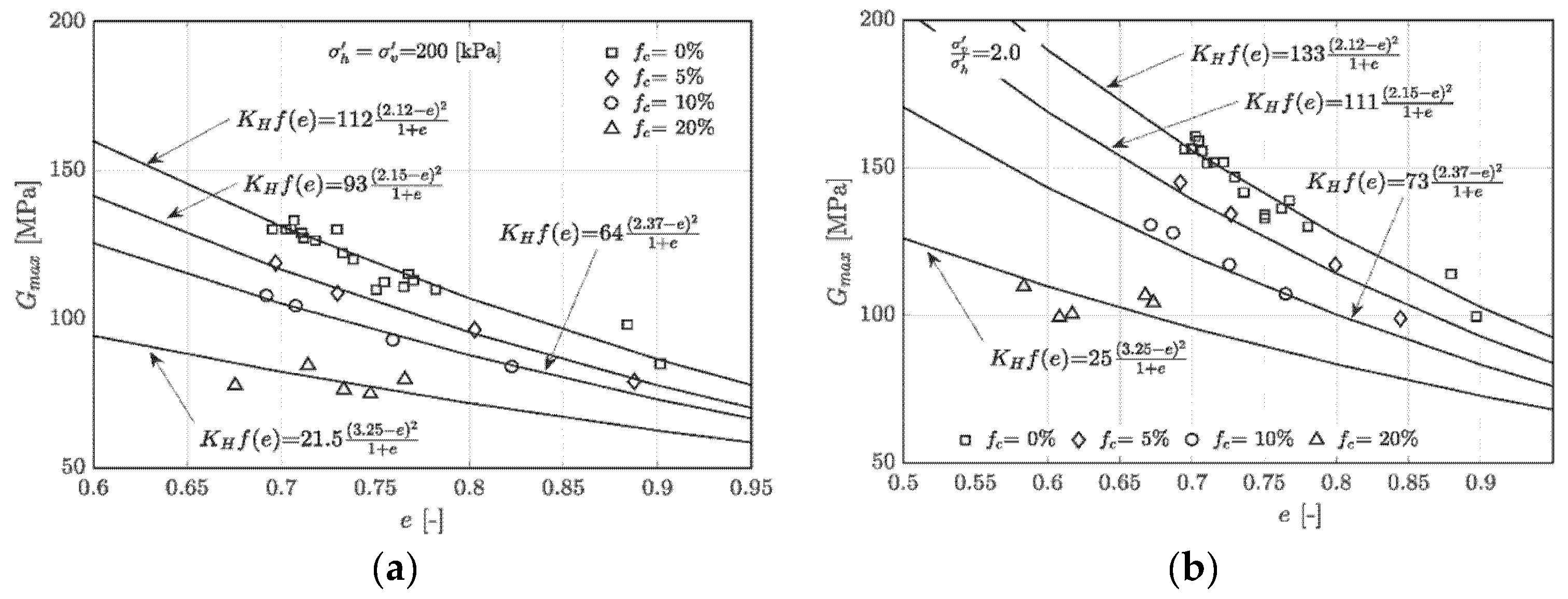
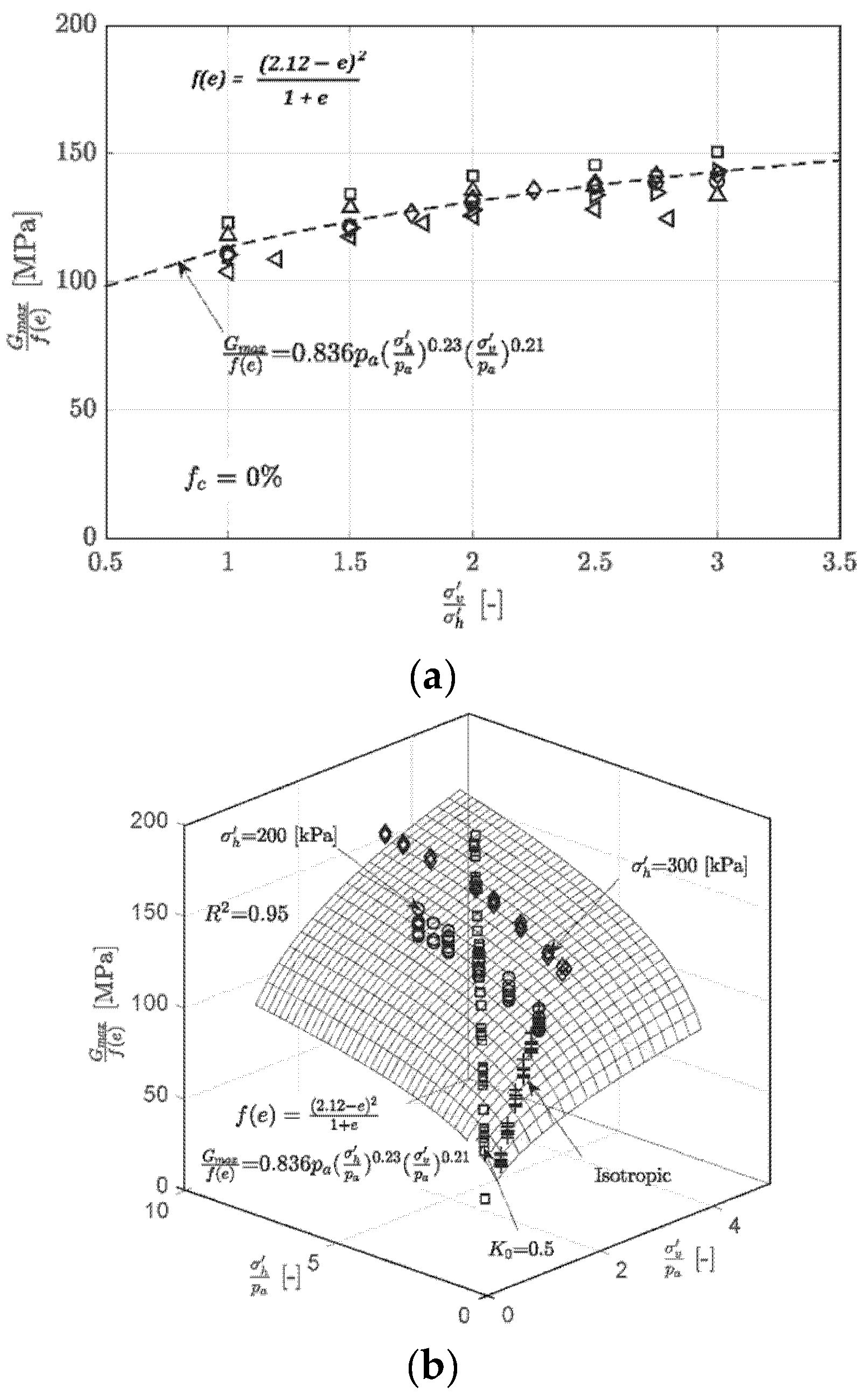
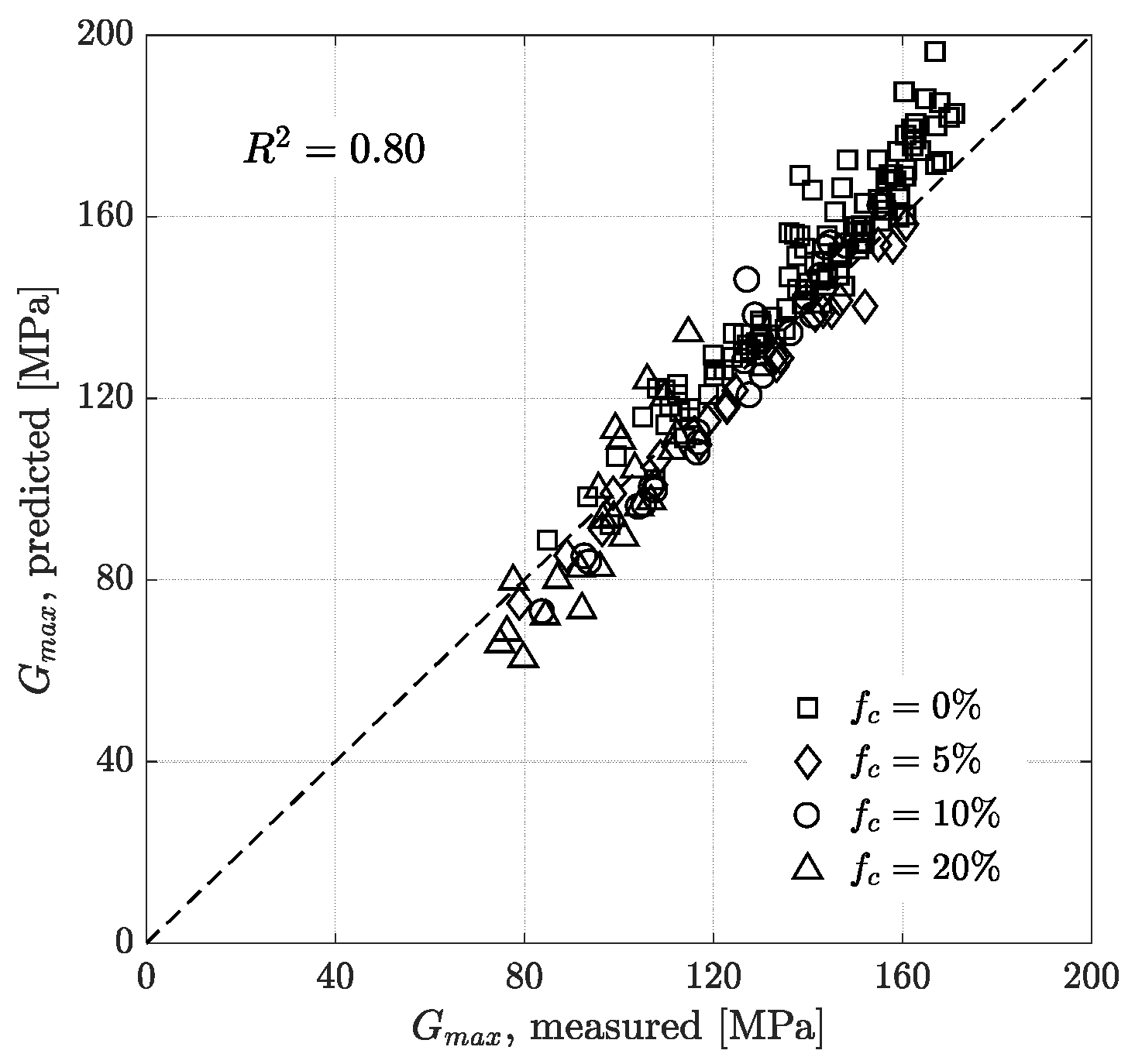
4. Analysis of Results
5. Discussion
Micromechanical Interpretation
6. Conclusions
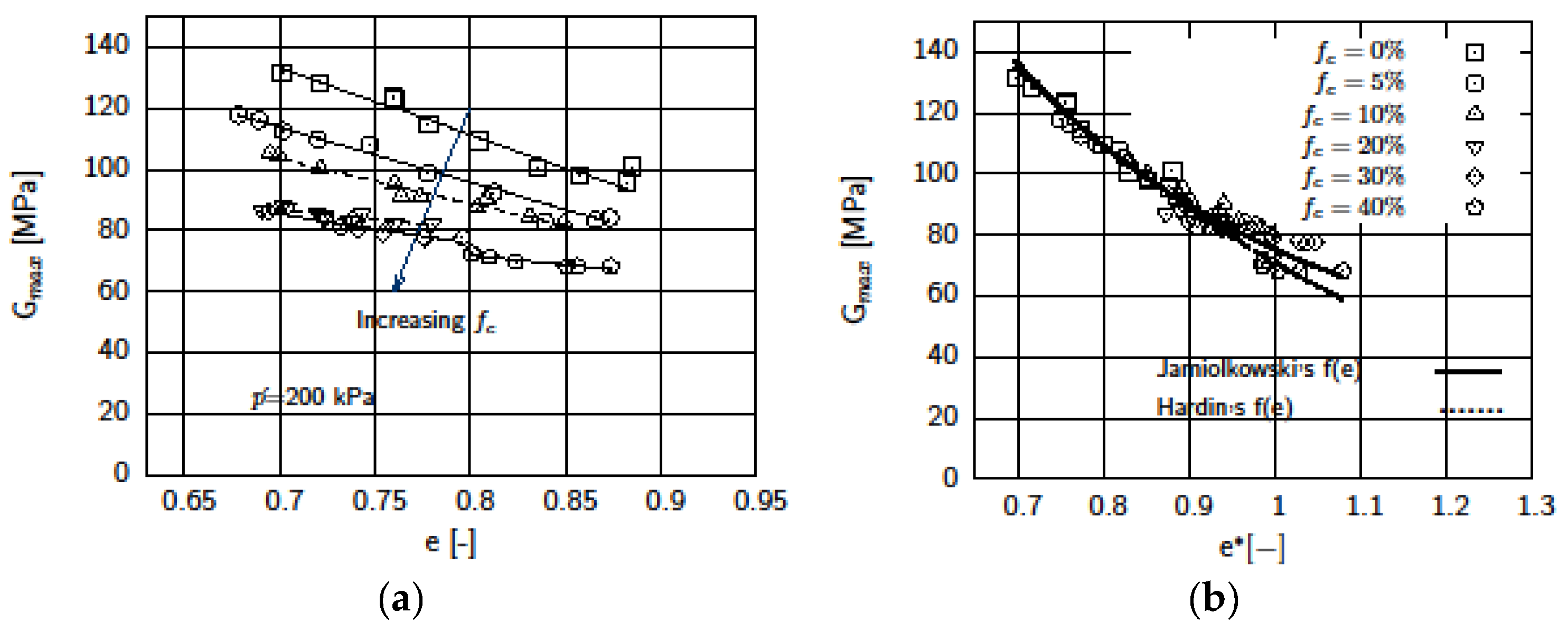
- Based on a series of resonant column tests with different initial global void ratios and confining pressures, it was found that Gmax is lower for increasing fines content as well as higher void ratios. Using a popular empirical model, the variation of Gmax with void ratio, confining pressure and stress state was captured with a good accuracy.
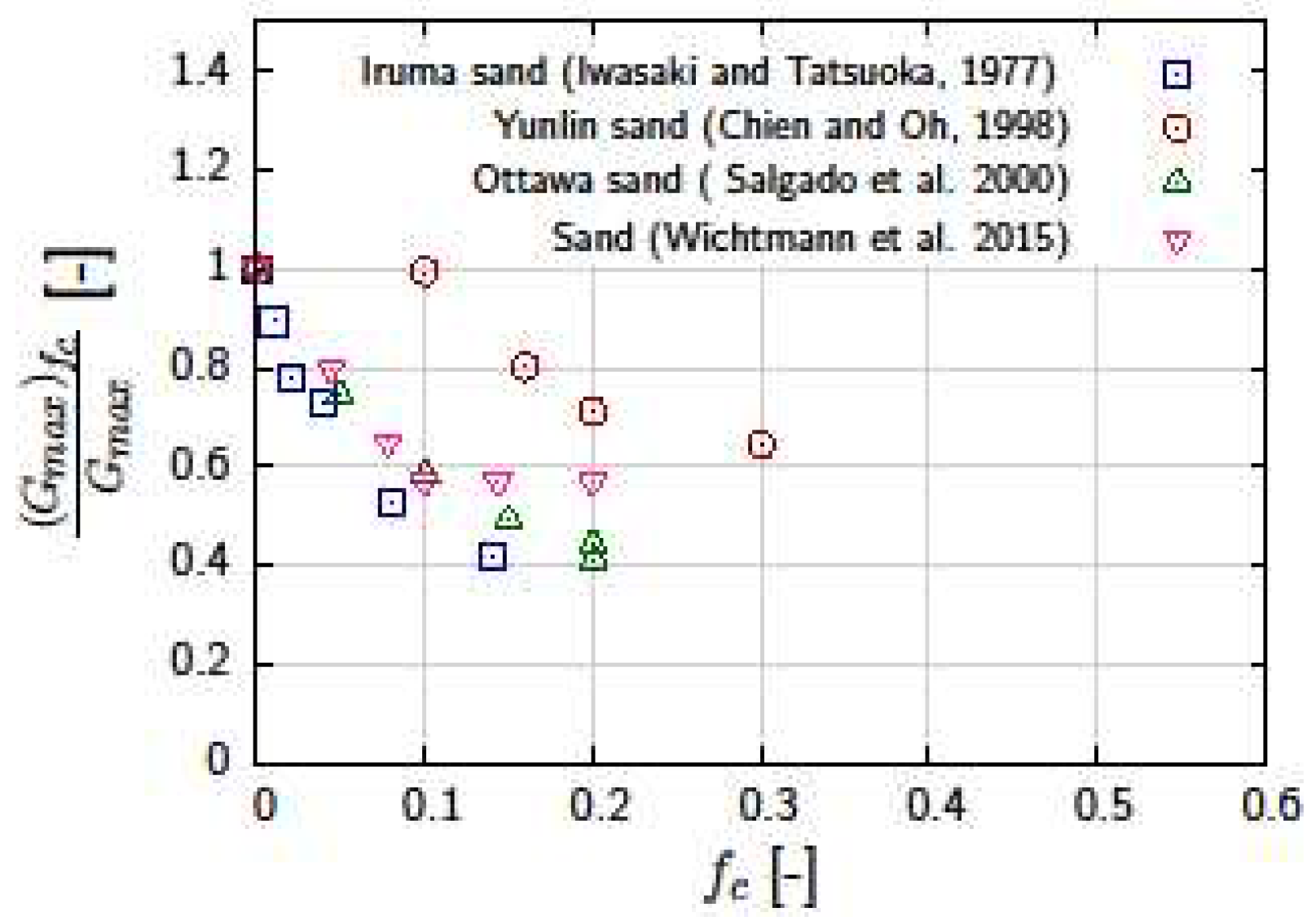
- Furthermore, to include fines content, the concept of equivalent intergranular void ratio was used where the global void ratio e was replaced by e* in the various formulations with a higher degree of accuracy, particularly for lower magnitudes of e*.
- Micro-CT scans of the binary mixtures were additionally made to enable a closer look into the microstructure, e.g., grain-to-grain contacts. From the skeletal structure, the contact forces between the individual grains were evident. In the case of anisotropic stress, a shear force acts in addition to the normal force for isotropically loaded specimens. An increase in fines results in a reduction in the friction between sand grains which leads to lower contact stiffness.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hardin, B.O.; Black, W.L. Sand stiffness under various triaxial stresses. J. Soil Mech. Found. Div. 1966, 92, 27–42. [Google Scholar] [CrossRef]
- Drnevich, V.P. Resonant-Column Testing: Problems and Solutions; Technical Report; Dynamic Geotechnical Testing: ASTM International, USA, 1978; pp. 384–398. [Google Scholar]
- Seed, B.; Wong, R.; Idriss, I.; Tokimatsu, K. Moduli and Damping Factors for Dynamic Analyses of Cohesionless Soils; Technical Report; National Science Foundation: Alexandria, VA, USA, 1984. [Google Scholar]
- Jamiolkowski, M.; Lancellotta, R.; Lo Presti, D.C.F. Remarks on the stiffness at small strains of six Italian clays. In Proceedings of the International Symposium, Sapporo, Japan, 12–14 September 1994; pp. 817–836. [Google Scholar]
- Darendeli, M.B. Development of a New Family of Normalized Modulus Reduction and Material Damping Curves. Ph.D. Thesis, University of Texas at Austin, Austin, TX, USA, 2001. [Google Scholar]
- Wichtmann, T.; Triantafyllidis, T. On the influence of the grain size distribution curve of quartz sand on the small strain shear modulus. J. Geotech. Geoenviron. Eng. 2009, 135, 1404–1418. [Google Scholar] [CrossRef]
- Thevanayagam, S. Effect of fines and confining stress on undrained shear strength of silty sands. J. Geotech. Geoenviron. Eng. 1998, 124, 479–491. [Google Scholar] [CrossRef]
- Salgado, R.; Bandini, P.; Karim, A. Shear strength and stiffness of silty sand. J. Geotech. Geoenviron. Eng. 2000, 126, 451–462. [Google Scholar] [CrossRef]
- Wichtmann, T.; Navarrete Hernández, M.A.; Triantafyllidis, T. On the influence of a non-cohesive fines content on small strain stiffness, modulus degradation and damping of quartz sand. Soil Dyn. Earthq. Eng. 2015, 69, 103–114. [Google Scholar] [CrossRef]
- Goudarzy, M.; König, D.; Schanz, T. Small strain stiffness of granular materials containing fines. Soils Found. 2016, 56, 756–764. [Google Scholar] [CrossRef]
- Goudarzy, M.; König, D.; Santamarina, J.C.; Schanz, T. Influence of anisotropic stress state on the intermediate strain behaviour of granular materials. Geotechnique 2018, 68, 221–232. [Google Scholar] [CrossRef] [Green Version]
- Iwasaki, T.; Tatsuoka, F. Effects of grain size and grading on dynamic shear moduli of sands. Soils Found. 1977, 17, 19–35. [Google Scholar] [CrossRef]
- Tao, M.; Figueroa, J.; Saada, A. Influence of non-plastic fines content on the liquefaction resistance of soils in terms of the unit energy. In Cyclic Behavior of Soils and Liquefaction Phenomena; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Chien, L.K.; Oh, Y.N. Influence of fines content and initial shear stress on dynamic properties of hydraulic reclaimed soil. Can. Geotech. J. 2002, 39, 242–253. [Google Scholar] [CrossRef] [Green Version]
- Carraro, J.A.H.; Prezzi, M.; Salgado, R. Shear strength and stiffness of sands containing plastic of non-plastic fines. J. Geotech. Geoenviron. Eng. 2009, 135, 1167–1178. [Google Scholar] [CrossRef]
- Yang, J.; Liu, X. Shear wave velocity and stiffness of sand: The role of non-plastic fines. Geotechnique 2016, 66, 500–514. [Google Scholar] [CrossRef] [Green Version]
- Goudarzy, M.; Rahman, M.M.; König, D.; Schanz, T. Influence of non-plastic fine particles on maximum shear modulus of granular materials. Soils Found. 2016, 56, 973–983. [Google Scholar] [CrossRef]
- Goudarzy, M.; König, D.; Schanz, T. Small and intermediate strain properties of sands containing fines. Soil Dyn. Earthq. Eng. 2018, 110, 110–120. [Google Scholar] [CrossRef]
- Rahman, M.M.; Cubrinovski, M.; Lo, S.R. Initial shear modulus of sandy soils and equivalent granular void ratio. Geomech. Geoengin. 2012, 7, 219–226. [Google Scholar] [CrossRef]
- Rahman, M.M.; Lo, S.C.R.; Gnanendran, C.T. On equivalent granular void ratio and steady state behavior of loose sand with fines. Can. Geotech. J. 2008, 45, 1439–1455. [Google Scholar] [CrossRef] [Green Version]
- Rahman, M.M.; Lo, S.C.R.; Gnanendran, C.T. Reply to the discussion by Wanatowski and Chu on “On equivalent granular void ratio and steady state behaviour of loose sand with fines”. Can. Geotech. J. 2008, 46, 483–486. [Google Scholar] [CrossRef] [Green Version]
- Thevanayagam, S.; Shenthan, T.; Mohan, S.; Liang, J. Undrained fragility of clean sands, silty sands, and sandy silts. J. Geotech. Geoenviron. Eng. 2002, 128, 849–859. [Google Scholar] [CrossRef]
- Zuo, L.; Baudet, B.A. Determination of the transitional fines content of sand-non plastic fines mixtures. Soils Found. 2015, 55, 213–219. [Google Scholar] [CrossRef]
- Roesler, S. Anisotropic shear modulus due to stress anisotropy. J. Geotech. Eng. Div. 1979, 105, 871–880. [Google Scholar] [CrossRef]
- Bellotti, R.; Jamiolkowski, M.; Lo Presti, D.C.; O'Neill, D.A. Anisotropy of small strain stiffness in Ticino sand. Geotechnique 1996, 46, 115–131. [Google Scholar] [CrossRef]
- Zeng, X.; Ni, B. Stress-induced anisotropic Gmax of sands and its measurement. J. Geotech. Geoenviron. Eng. 1999, 125, 741–749. [Google Scholar] [CrossRef]
- Fioravante, V. Anisotropy of small strain stiffness of Ticino and Kenya sands from seismic wave propagation measured in triaxial testing. Soils Found. 2000, 40, 129–142. [Google Scholar] [CrossRef] [Green Version]
- Sadek, T.; Lings, M.; Dihoru, L.; Wood, D.M. Wave transmission in Hostun sand: Multi-axial experiments. Riv. Ital. Geotech. 2007, 2, 69–84. [Google Scholar]
- Wang, Y.; Mok, C. Mechanisms of small strain shear modulus anisotropy in soils. J. Geotech. Geoenviron. Eng. 2008, 134, 1516–1530. [Google Scholar] [CrossRef]
- Ezaoui, A.; Di Benedetto, H. Experimental measurements of the global anisotropic elastic behaviour of dry Hostun sand during triaxial tests, and effect of sample preparation. Geotechnique 2009, 59, 621–635. [Google Scholar] [CrossRef]
- Yanagisawa, E. Influence of void ratio and stress condition on the dynamic shear modulus of granular media. Adv. Mech. Flow Granul. Mater. 1983, 2, 947–960. [Google Scholar]
- Yu, P.; Richart, F. Stress ratio effects on shear modulus of dry sands. J. Geotech. Eng. 1984, 110, 331–345. [Google Scholar] [CrossRef]
- Ishibashi, I.; Chen, Y.; Chen, M.T. Anisotropic behavior of Ottawa sand in comparison with glass spheres. Soils Found. 1991, 31, 145–155. [Google Scholar] [CrossRef] [Green Version]
- Santamarina, C.; Cascante, G. Stress anisotropy and wave propagation: A micromechanical view. Can. Geotech. J. 1996, 33, 770–782. [Google Scholar] [CrossRef]
- Payan, M.; Khoshghalb, A.; Senetakis, K.; Khalili, N. Small-strain stiffness of sand subjected to stress anisotropy. Soil Dyn. Earthq. Eng. 2016, 88, 143–151. [Google Scholar] [CrossRef]
- Wichtmann, T.; Sonntag, T.; Triantafyllidis, T. Über das Erinnerungsvermögen von Sand unter zyklischer Belastung. Bautechnik 2001, 78, 852–865. [Google Scholar] [CrossRef]
- Goudarzy, M. Micro and Macro Mechanical Assessment of Small and Intermediate Strain Properties of Granular Material. Ph.D. Thesis, Ruhr-Universität Bochum, Bochum, Germany, 2015. [Google Scholar]
- DIN 18126:1996-11; Baugrund, Untersuchung von Bodenproben—Bestimmung der Dichte Nichtbindiger Böden bei Lockerster und Dichtester Lagerung. Beuth: Berlin, Germany, 1996. (In German)
- Goudarzy, M.; König, D.; Schanz, T. Interpretation of small and intermediate strain characteristics of Hostun sand for various stress states. Soils Found. 2018, 58, 1526–1537. [Google Scholar] [CrossRef]
- Bohaienko, V.; Bulavatsky, V. Fractional-Fractal Modeling of Filtration-Consolidation Processes in Saline Saturated Soils. Fractal Fract. 2020, 4, 59. [Google Scholar] [CrossRef]
- He, S.; Ding, Z.; Hu, H.; Gao, M. Effect of Grain Size on Microscopic Pore Structure and Fractal Characteristics of Carbonate-Based Sand and Silicate-Based Sand. Fractal Fract. 2021, 5, 152. [Google Scholar] [CrossRef]
- Fu, X.; Ding, H.; Sheng, Q.; Zhang, Z.; Yin, D.; Chen, F. Fractal Analysis of Particle Distribution and Scale Effect in a Soil–Rock Mixture. Fractal Fract. 2022, 6, 120. [Google Scholar] [CrossRef]
- Xu, J.; Shen, Y.; Sun, Y. Cyclic Mobilisation of Soil–Structure Interface in the Framework of Fractional Plasticity. Fractal Fract. 2022, 6, 76. [Google Scholar] [CrossRef]
- Adeli, E.; Rosic, B.V.; Matthies, H.G.; Reinstädler, S.; Dinkler, D. Bayesian Parameter determination of a CT-Test described by a Viscoplastic-Damage model considering the Model Error. Metals 2020, 10, 1141. [Google Scholar] [CrossRef]
- Yimsiri, S.; Soga, K. Application of micromechanics model to study anisotropy of soils at small strains. Soils Found. 2002, 42, 15–26. [Google Scholar] [CrossRef] [Green Version]
- Johnson, K.L. Contact Mechanics; Cambridge University: Cambridge, UK, 1985. [Google Scholar]


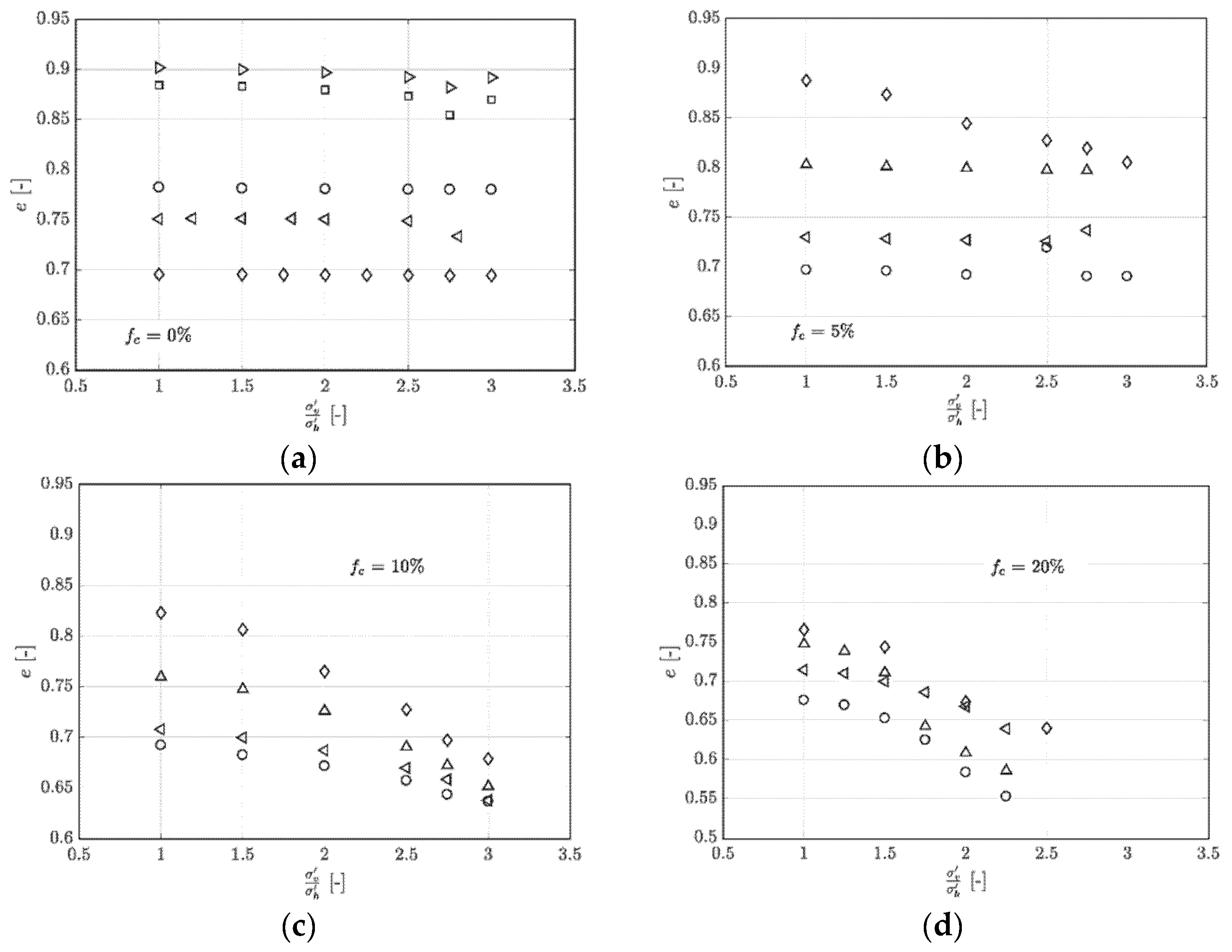



| Case | Material | Weight Ratio (%) | Sample Height (mm) | Weight (g) | Dry Density (g/cm3) | |
|---|---|---|---|---|---|---|
| Quartz | Hostun | |||||
| 1 | Quartz/Hostun | 10 | 90 | 37.5 | 1.742 | 1.207 |
| 2 | 34.5 | 1.312 | ||||
| 3 | 31.5 | 1.437 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Goudarzy, M.; Sarkar, D. Macro- and Micromechanical Assessment of the Influence of Non-Plastic Fines and Stress Anisotropy on the Dynamic Shear Modulus of Binary Mixtures. Fractal Fract. 2022, 6, 205. https://doi.org/10.3390/fractalfract6040205
Goudarzy M, Sarkar D. Macro- and Micromechanical Assessment of the Influence of Non-Plastic Fines and Stress Anisotropy on the Dynamic Shear Modulus of Binary Mixtures. Fractal and Fractional. 2022; 6(4):205. https://doi.org/10.3390/fractalfract6040205
Chicago/Turabian StyleGoudarzy, Meisam, and Debdeep Sarkar. 2022. "Macro- and Micromechanical Assessment of the Influence of Non-Plastic Fines and Stress Anisotropy on the Dynamic Shear Modulus of Binary Mixtures" Fractal and Fractional 6, no. 4: 205. https://doi.org/10.3390/fractalfract6040205
APA StyleGoudarzy, M., & Sarkar, D. (2022). Macro- and Micromechanical Assessment of the Influence of Non-Plastic Fines and Stress Anisotropy on the Dynamic Shear Modulus of Binary Mixtures. Fractal and Fractional, 6(4), 205. https://doi.org/10.3390/fractalfract6040205







