Synchronization of Incommensurate Fractional-Order Chaotic Systems Based on Linear Feedback Control
Abstract
:1. Introduction
2. System Description and Preliminaries
3. Main Results
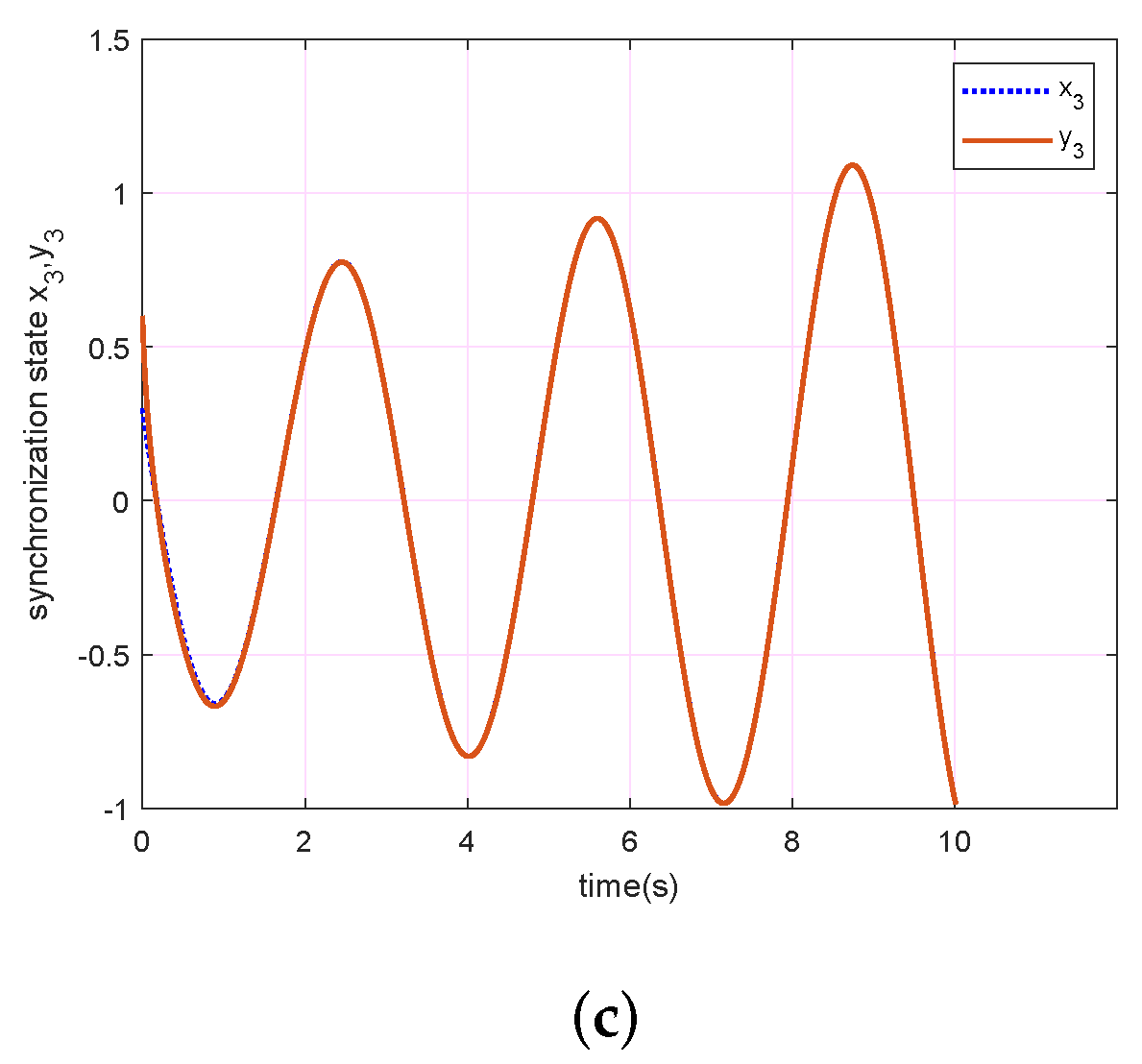
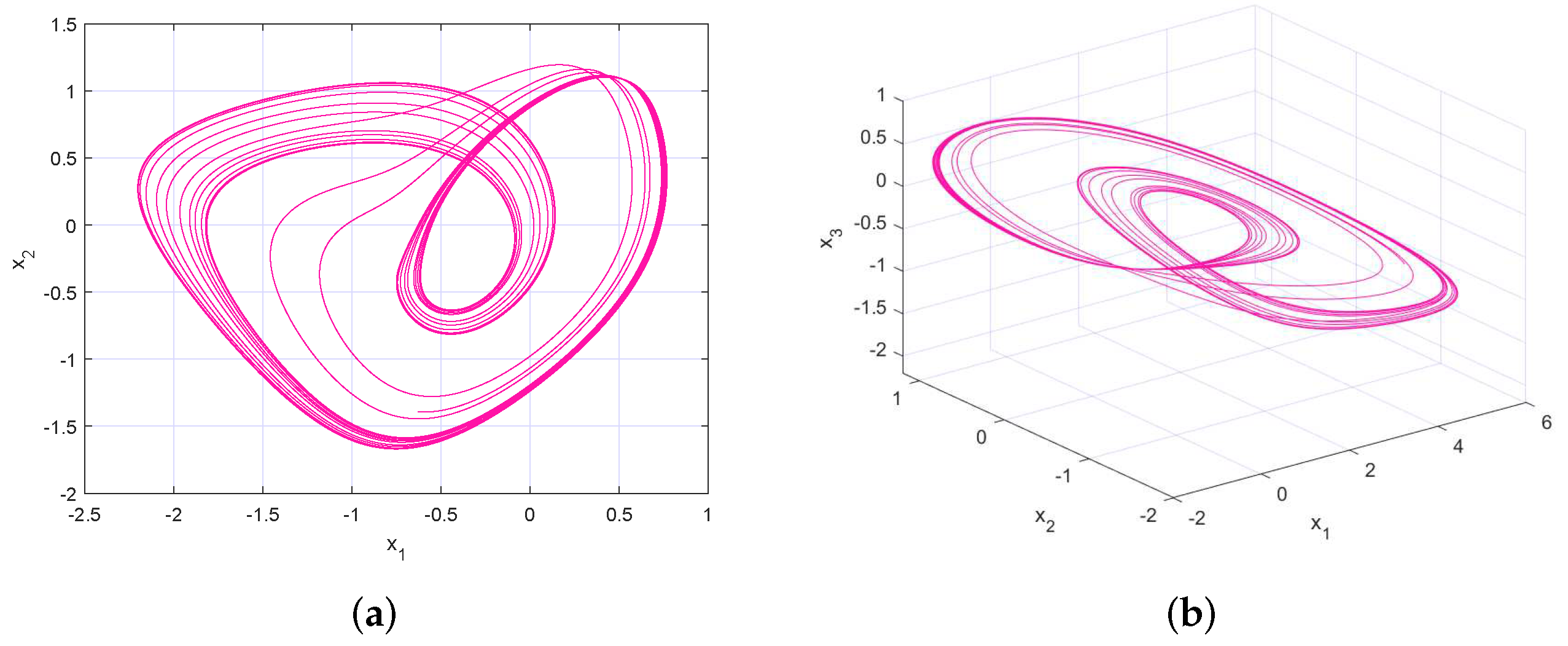
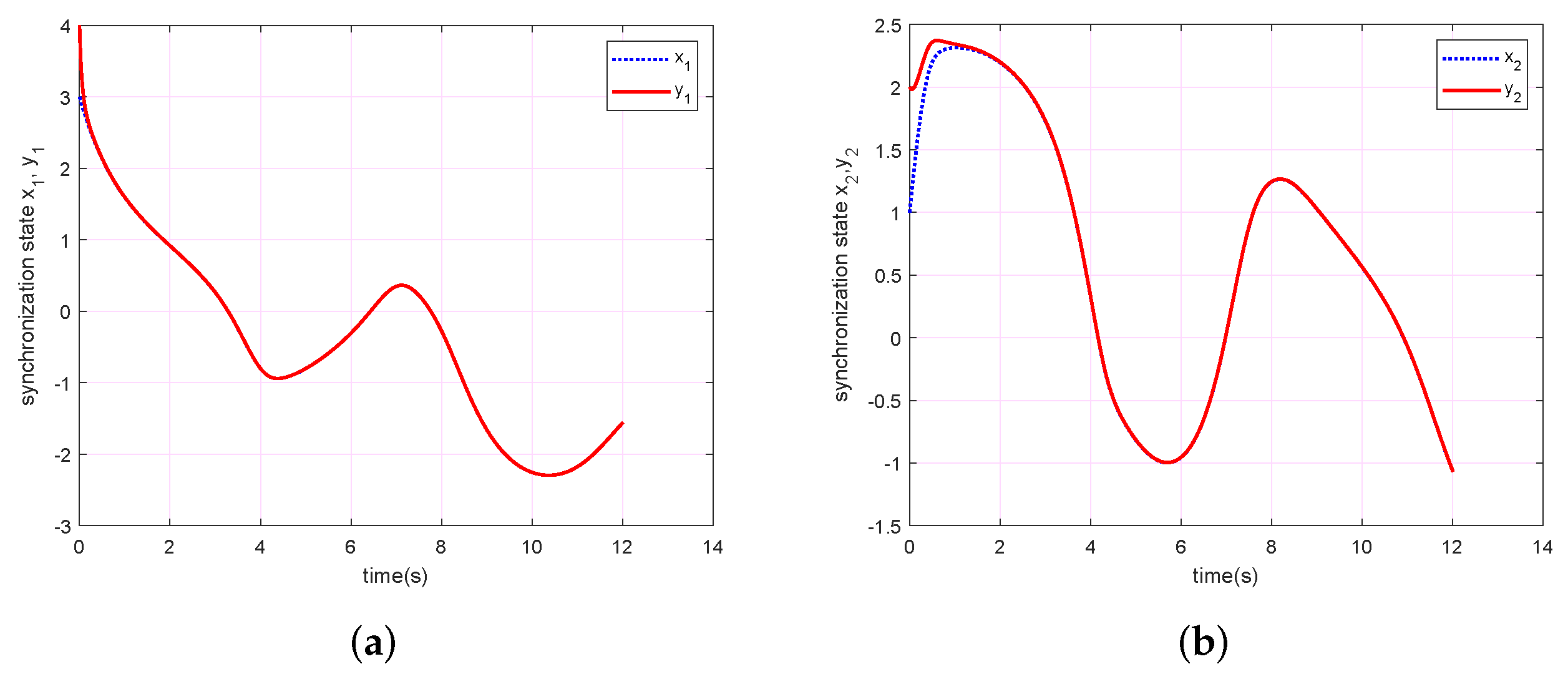
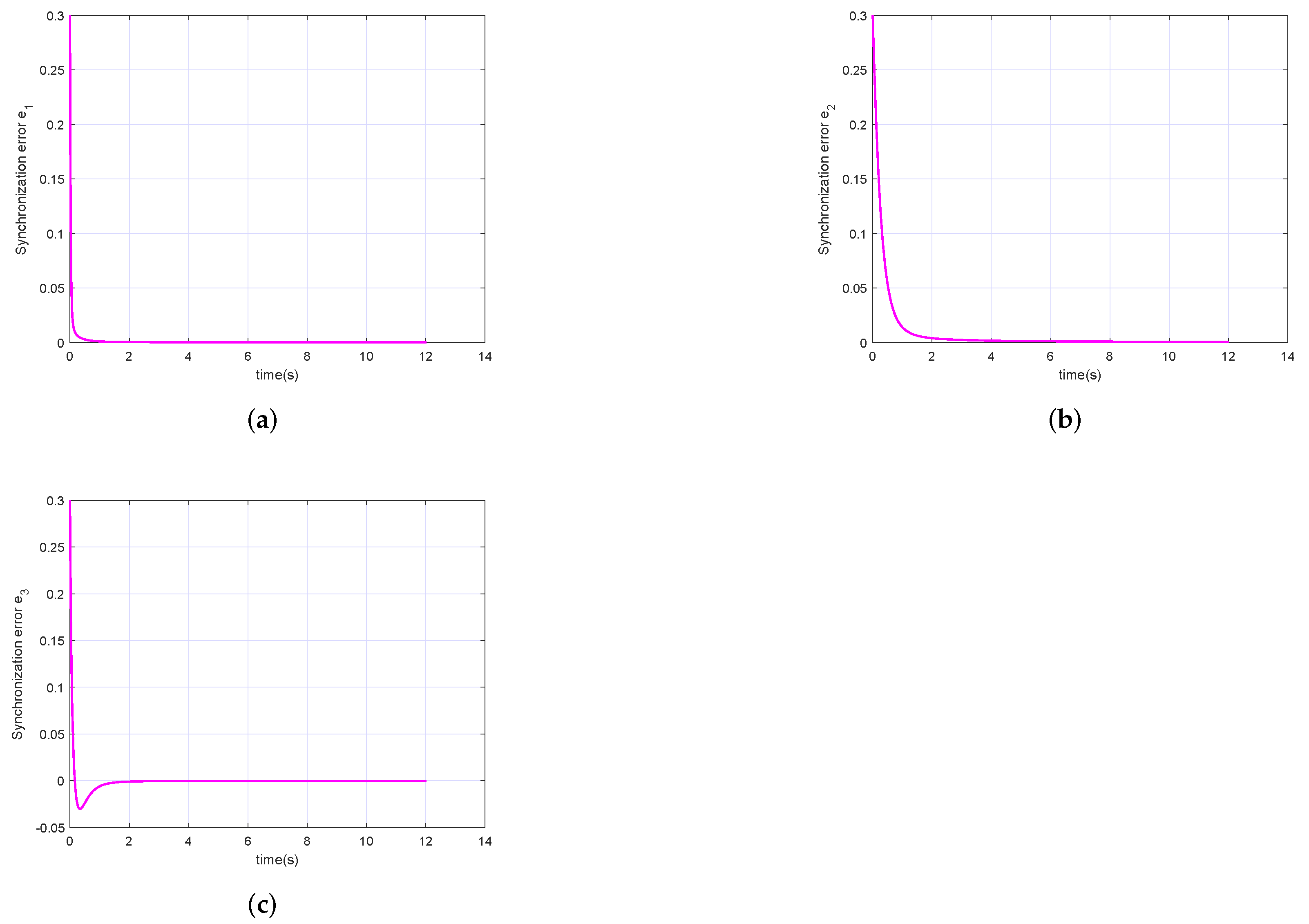
4. Applications
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xue, D. Fractional-Order Control Systems; de Gruyter: Berlin, Germany, 2017. [Google Scholar]
- Hilfer, R. Applications of Fractional Calculus in Physics; World Scientific: Singapore, 2000. [Google Scholar]
- Chen, W.; Sun, H.; Li, X. Fractional Derivative Modeling in Mechanics and Engineering; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Anastassiou, G.A. Generalized Fractional Calculus: New Advancements and Applications; Springer Nature: Berlin/Heidelberg, Germany, 2020; Volume 305. [Google Scholar]
- Petráš, I. Fractional-Order Nonlinear Systems: Modeling, Analysis and Simulation; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Tarasov, V.E.; Tarasova, V.V. Economic Dynamics with Memory: Fractional Calculus Approach; Walter de Gruyter GmbH & Co. KG: Berlin, Germany, 2021; Volume 8. [Google Scholar]
- Hartley, T.T.; Lorenzo, C.F.; Qammer, H.K. Chaos in a fractional order Chua’s system. IEEE Trans. Circ. Syst. Fundam. Theory Appl. 1995, 42, 485–490. [Google Scholar] [CrossRef]
- Deshpande, A.S.; Daftardar-Gejji, V.; Sukale, Y.V. On Hopf bifurcation in fractional dynamical systems. Chaos Solitons Fractals 2017, 98, 189–198. [Google Scholar] [CrossRef]
- Huang, C.; Li, H.; Cao, J. A novel strategy of bifurcation control for a delayed fractional predator—Prey model. Appl. Math. Comput. 2019, 347, 808–838. [Google Scholar] [CrossRef]
- Chen, L.; Yin, H.; Huang, T.; Yuan, L.; Zheng, S.; Yin, L. Chaos in fractional-order discrete neural networks with application to image encryption. Neural Netw. 2020, 125, 174–184. [Google Scholar] [CrossRef] [PubMed]
- Kamal, F.; Elsonbaty, A.; Elsaid, A. A novel fractional nonautonomous chaotic circuit model and its application to image encryption. Chaos Solitons Fractals 2021, 144, 110686. [Google Scholar] [CrossRef]
- Tavazoei, M.S.; Haeri, M. Synchronization of chaotic fractional-order systems via active sliding mode controller. Phys. Stat. Mech. Its Appl. 2008, 387, 57–70. [Google Scholar] [CrossRef]
- Akgül, A.; Rajagopal, K.; Durdu, A.; Pala, M.A.; Boyraz, Ö.F.; Yildiz, M.Z. A simple fractional-order chaotic system based on memristor and memcapacitor and its synchronization application. Chaos Solitons Fractals 2021, 152, 111306. [Google Scholar] [CrossRef]
- Bhalekar, S.; Daftardar-Gejji, V. Synchronization of different fractional order chaotic systems using active control. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 3536–3546. [Google Scholar] [CrossRef]
- Wang, F.; Zheng, Z.; Yang, Y. Quasi-synchronization of heterogenous fractional-order dynamical networks with time-varying delay via distributed impulsive control. Chaos Solitons Fractals 2021, 142, 110465. [Google Scholar] [CrossRef]
- Aadhithiyan, S.; Raja, R.; Zhu, Q.; Alzabut, J.; Niezabitowski, M.; Lim, C. Modified projective synchronization of distributive fractional order complex dynamic networks with model uncertainty via adaptive control. Chaos Solitons Fractals 2021, 147, 110853. [Google Scholar] [CrossRef]
- Zambrano-Serrano, E.; Bekiros, S.; Platas-Garza, M.A.; Posadas-Castillo, C.; Agarwal, P.; Jahanshahi, H.; Aly, A.A. On chaos and projective synchronization of a fractional difference map with no equilibria using a fuzzy-based state feedback control. Phys. Stat. Mech. Its Appl. 2021, 578, 126100. [Google Scholar] [CrossRef]
- Wu, C.J.; Zhang, Y.B.; Yang, N.N. The synchronization of a fractional order hyperchaotic system based on passive control. Chin. Phys. 2011, 20, 060505. [Google Scholar] [CrossRef]
- Chen, Y.; Tang, C.; Roohi, M. Design of a model-free adaptive sliding mode control to synchronize chaotic fractional-order systems with input saturation: An application in secure communications. J. Frankl. Inst. 2021, 358, 8109–8137. [Google Scholar] [CrossRef]
- Zhang, K.; Wang, H.; Fang, H. Feedback control and hybrid projective synchronization of a fractional-order Newton–Leipnik system. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 317–328. [Google Scholar] [CrossRef]
- Razminia, A.; Baleanu, D. Complete synchronization of commensurate fractional order chaotic systems using sliding mode control. Mechatronics 2013, 23, 873–879. [Google Scholar] [CrossRef]
- Yu, J.; Hu, C.; Jiang, H.; Fan, X. Projective synchronization for fractional neural networks. Neural Netw. 2014, 49, 87–95. [Google Scholar] [CrossRef]
- Chen, L.; Chai, Y.; Wu, R. Lag projective synchronization in fractional-order chaotic (hyperchaotic) systems. Phys. Lett. A 2011, 375, 2099–2110. [Google Scholar] [CrossRef]
- Zhang, W.; Cao, J.; Wu, R.; Alsaadi, F.E.; Alsaedi, A. Lag projective synchronization of fractional-order delayed chaotic systems. J. Frankl. Inst. 2019, 356, 1522–1534. [Google Scholar] [CrossRef]
- Matignon, D. Stability Properties for Generalized Fractional Differential Systems; ESAIM: Proceedings; EDP Sciences: Les Ulis, France, 1998; Volume 5, pp. 145–158. [Google Scholar]
- Li, Y.; Chen, Y.; Podlubny, I. Stability of fractional-order nonlinear dynamic systems: Lyapunov direct method and generalized Mittag–Leffler stability. Comput. Math. Appl. 2010, 59, 1810–1821. [Google Scholar] [CrossRef] [Green Version]
- Tavazoei, M.S.; Haeri, M. Chaotic attractors in incommensurate fractional order systems. Phys. Nonlinear Phenom. 2008, 237, 2628–2637. [Google Scholar] [CrossRef]
- Ma, C.; Mou, J.; Liu, J.; Yang, F.; Yan, H.; Zhao, X. Coexistence of multiple attractors for an incommensurate fractional-order chaotic system. Eur. Phys. J. Plus 2020, 135, 1–21. [Google Scholar] [CrossRef]
- Huang, C.; Cao, J.; Xiao, M.; Alsaedi, A.; Alsaadi, F.E. Controlling bifurcation in a delayed fractional predator–prey system with incommensurate orders. Appl. Math. Comput. 2017, 293, 293–310. [Google Scholar] [CrossRef]
- Debbouche, N.; Almatroud, A.O.; Ouannas, A.; Batiha, I.M. Chaos and coexisting attractors in glucose-insulin regulatory system with incommensurate fractional-order derivatives. Chaos Solitons Fractals 2021, 143, 110575. [Google Scholar] [CrossRef]
- Zouari, F.; Boulkroune, A.; Ibeas, A. Neural adaptive quantized output-feedback control-based synchronization of uncertain time-delay incommensurate fractional-order chaotic systems with input nonlinearities. Neurocomputing 2017, 237, 200–225. [Google Scholar] [CrossRef]
- Boulkroune, A.; Bouzeriba, A.; Bouden, T. Fuzzy generalized projective synchronization of incommensurate fractional-order chaotic systems. Neurocomputing 2016, 173, 606–614. [Google Scholar] [CrossRef]
- Martínez-Guerra, R.; Pérez-Pinacho, C.A.; Gómez-Cortés, G.C. An Observer for a Class of Incommensurate Fractional-Order Systems. In Synchronization of Integral and Fractional Order Chaotic Systems; Springer: Berlin/Heidelberg, Germany, 2015; pp. 219–236. [Google Scholar]
- Zhou, Y.; Liu, H.; Cao, J.; Li, S. Composite learning fuzzy synchronization for incommensurate fractional-order chaotic systems with time-varying delays. Int. J. Adapt. Control. Signal Process. 2019, 33, 1739–1758. [Google Scholar] [CrossRef]
- Lenka, B.K. Fractional comparison method and asymptotic stability results for multivariable fractional order systems. Commun. Nonlinear Sci. Numer. Simul. 2019, 69, 398–415. [Google Scholar] [CrossRef]
- Lu, J.G.; Zhu, Z.; Ma, Y.D. Robust stability and stabilization of multi-order fractional-order systems with interval uncertainties: An LMI approach. Int. J. Robust Nonlinear Control. 2021, 31, 4081–4099. [Google Scholar] [CrossRef]
- Liang, S.; Wu, R.; Chen, L. Adaptive pinning synchronization in fractional-order uncertain complex dynamical networks with delay. Phys. Stat. Mech. Its Appl. 2016, 444, 49–62. [Google Scholar] [CrossRef]
- Chen, L.; Qu, J.; Chai, Y.; Wu, R.; Qi, G. Synchronization of a class of fractional-order chaotic neural networks. Entropy 2013, 15, 3265–3276. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, F.; Qu, J.; Chai, Y.; Chen, L.; Lopes, A.M. Synchronization of Incommensurate Fractional-Order Chaotic Systems Based on Linear Feedback Control. Fractal Fract. 2022, 6, 221. https://doi.org/10.3390/fractalfract6040221
Qi F, Qu J, Chai Y, Chen L, Lopes AM. Synchronization of Incommensurate Fractional-Order Chaotic Systems Based on Linear Feedback Control. Fractal and Fractional. 2022; 6(4):221. https://doi.org/10.3390/fractalfract6040221
Chicago/Turabian StyleQi, Fei, Jianfeng Qu, Yi Chai, Liping Chen, and António M. Lopes. 2022. "Synchronization of Incommensurate Fractional-Order Chaotic Systems Based on Linear Feedback Control" Fractal and Fractional 6, no. 4: 221. https://doi.org/10.3390/fractalfract6040221
APA StyleQi, F., Qu, J., Chai, Y., Chen, L., & Lopes, A. M. (2022). Synchronization of Incommensurate Fractional-Order Chaotic Systems Based on Linear Feedback Control. Fractal and Fractional, 6(4), 221. https://doi.org/10.3390/fractalfract6040221







