The Tracking Control of the Variable-Order Fractional Differential Systems by Time-Varying Sliding-Mode Control Approach

Abstract

This paper is concerned with the problem of tracking control for a class of variable-order fractional uncertain system. In order to realize the global robustness of systems, two types of controllers are designed by the global sliding-mode control method. The first one is based on a full-order global sliding-mode surface with variable-order fractional type, and the control law is continuous, which is free of chattering. The other one is a novel time-varying control law, which drives the error signals to stay on the proposed reduced-order sliding-mode surface and then converges to the origin. The stability of the controllers proposed is proved by the use of the variable-order fractional type Lyapunov stability theorem and the numerical simulation is given to validate the effectiveness of the theoretical results.

1. Introduction

Fractional-order (FO) calculus has been developed rapidly over the past decades and the FO operators have been considered as an important tool to model the complex phenomena in science and engineering [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]. It is mentioned that, compared with the constant-order (CO) fractional-order operators, the variable-order (VO) fractional-order operators possess more complicated properties and are more suitable for describing some complex phenomena. It is more difficult to study the relative problems of the VO fractional differential system, see [16,17]. Recently, the theory of the variable-order fractional derivatives has been developed rapidly due to its extensive application—with many interesting results. For example, Ingman and Suzdalnitsky described a kind of variable-order fractional vibration of a one-degree-of-freedom oscillator [18]. Coimbra proposed a definition of the variable-order fractional-order operator and applied it to study the mechanics of a variable-order fractional oscillating mass that yields a VO differential equation [19]. Lorenzo [20] proposed a definition for the variable-order fractional-order operators in 1998. Then, the variable-order fractional operator was preliminarily developed in [21,22,23].

In recent decades, there exist many results on the study of the control problem for the VO fractional chaos system with uncertain and external disturbance terms [17,24,25]. From the practical view, the proposed control theory can provide the theoretical guidance for practical control problems. Thus, it is meaningful to consider the control problem for the VO fractional system with uncertain and external disturbance terms. There exist many approaches to deal with the control problem for differential systems, such as feedback control, $H_{\infty }$ control, backstepping methods, adaptive control, active disturbance rejection control and the sliding-mode control approach (SMC); for more detail, one can refer to [26,27,28,29]. Due to the advantage of robust performance, the SMC approach is considered as the most suitable method to investigate the control problem for a nonlinear chaotic system with uncertain and external terms. In recent years, in addition to the theoretical research, the sliding-mode control approach has also been successfully applied to the practical examples from an experimental perspective [30,31,32,33], which illustrates the popularity and applicability of the sliding-mode technique. Nevertheless, there exist some shortcomings of the traditional SMC method, see [34]; thus, based on the SMC method, some improved approaches have been proposed, such as the terminal sliding-mode control approach [35,36,37,38] and the global sliding-mode control (GSMC) approach [39,40,41].

It has been shown that the GSMC approach can eliminate the arrival phase from the start via the variable structure theory, which is considered to be a suitable method to deal with the control problem of chaotic systems. Moreover, the time-varying SMC or time-varying GSMC has been applied to solve the problem of control for an uncertain nonlinear system. Boukattaya, Gassara and Damak [42] investigated the tracking control problem by use of a global time-varying SMC scheme for a class of uncertain nonlinear systems in the presence of the uncertainties and external disturbances. In [43], a time-varying SMC approach was designed to deal with the tracking problem of a parametric uncertainty mechanical system. Singh and Roy [44] studied the synchronization problem of a new conservative chaotic system with hidden chaotic orbits by a second-order adaptive time-varying SMC. Based on the parameter estimation, a time-varying sliding-mode controller for the multi-motor driving servo systems was designed by Zhao, Ren and Wang [45]. Bartoszewicz and Nowacka-Leverton [46] proposed a time-varying sliding-mode controller for high-order systems. Lu, Chiu and Chen [47] conducted the investigation on a time-varying sliding-mode controller by defining a function of time and then guaranteed the convergence of the tracking error in a finite time. In [48], Eray and Tokat considered a time-varying fractional-order sliding-mode controller to realize the asymptotic stability of the system. Moreover, compared with the conventional controllers, the reaching and settling time of the proposed controller has been decreased. Hua, Chen and Guan [49] designed an FO sliding-mode based on a state-constrained controller for uncertain quadrotor UAVs. In [50], a novel numerical method is implemented for a fractional variable-order system. The control laws are designed to realize the synchronization of two identical commensurate Halvorsen systems with fractional variable-order time derivatives. Compared with the above two references, this paper has the following main differences: (i) The systems addressed in this paper are different. This paper is focused on a VO fractional nonlinear system with external disturbances and is divided into two cases. (ii) The research questions are different. This paper is concerned with the problem of the tracking control to realize the global robustness of systems. (iii) The designed controllers are different. A global sliding-mode control is proposed, which is continuous and free of chattering. In [51], the synchronization of two FO chaotic systems was studied by use of a novel time-varying SMC precisely at any arbitrary pre-specified time. By an adaptive FO terminal SMC strategy with higher convergence precision, the problem of the tracking control for the linear motor was investigated in [52]. To the best of our knowledge, there hardly exist results on the tracking control of the VO fractional differential systems.

The main contributions of the present study are listed in the following:

(i)

Through the combination of the variable-order fractional operator and the global sliding-mode control approach, a kind of novel variable-order fractional sliding-mode controller is proposed to realize the tracking control of the variable-order fractional uncertain system.

(ii)

For the two-dimensional system and the corresponding n-dimensional system, two kinds of continuous controllers are designed based on a full-order global sliding-mode surface, which is free of chattering.

The rest of this paper is organized as follows. In Section 2, the nonlinear system investigated in this paper is described. The global time-varying SMC law for a class of two-dimensional VFO system and the stability analysis are considered in Section 3. Section 4 is devoted to deal with the tracking control of n-dimensional VFO system by a global time-varying SMC, and the efficiency of the controller has been proved. The numerical simulations are conducted in Section 5.

2. Description of the System

The VO fractional Caputo integral operators is defined as follows

$$I_t^{q\left(t\right)}f\left(t\right)=\frac{1}{\Gamma \left(q\right(t\left)\right)}{\int }_0^t{(t-s)}^{q\left(t\right)-1}f\left(s\right)ds, 0<q\left(t\right)<1,$$

(1)

respectively, the VO fractional derivative is

$${}^C{D}_t^{q\left(t\right)}f\left(t\right)=\frac{1}{\Gamma (1-q(t\left)\right)}{\int }_0^t{(t-s)}^{-q\left(t\right)}{f}^{\prime }\left(s\right)ds, 0<q\left(t\right)<1,$$

(2)

where $\Gamma (·)$ is the Gamma function, $t\in [0,T]$. The VO fractional nonlinear system considered in this paper is

$${}_0^C{D}_t^{q\left(t\right)}X\left(t\right)=g(X,t)u\left(t\right)+F(X,t)+d\left(t\right),$$

(3)

where $0<q_1\le q\left(t\right)\le q_2<1$, $X\left(t\right)=[x_1,x_2,\dots ,x_n]\in {\mathbb{R}}^n$ are the vector variables of the system, $g(X,t)$ is a reversible matrix. $F(X,t)\in {\mathbb{R}}^n$ and $d\left(t\right)\in {\mathbb{R}}^n$ represent the nonlinear functions and the external disturbances, respectively. $u\left(t\right)\in {\mathbb{R}}^n$ denotes the control input signal.

Suppose the reference signals $x_{id}, i=q,2,\dots ,n$ are continuously differential functions, let ${\tau }_i\left(t\right), i=1,2,\dots ,n$ be the tracking error signal, which are given in the following:

$${\tau }_i\left(t\right)=x_i\left(t\right)-x_{id}\left(t\right).$$

(4)

Thus, the system (3) can be transformed into the following error state space form:

$${}^C{D}_t^{q\left(t\right)}{\tau }_i\left(t\right)=g(X,t)u\left(t\right)+F(X,t)+d\left(t\right)-{}^C{D}_t^{q\left(t\right)}\left[x_{id}\left(t\right)\right],$$

(5)

where ${}^C{D}_t^{q\left(t\right)}\left[x_{id}\left(t\right)\right]=x_{(i+1)d}\left(t\right), i=1,2,\dots ,n-1$.

Hypothesis 1.

Suppose that there exists a positive constant $0<\delta <\infty$ such that $\left|d\right(t\left)\right|\le \delta$.

3. The Global Time-Varying Sliding-Mode Control of Two-Dimensional of the VO Fractional System

This section is devoted to the design of a global sliding-mode control law for the following two-dimensional VO fractional system, which is a special case of system (3). It guarantees the tracking property.

$$\left\{\begin{array}{c}{}_0^C{D}_t^{q\left(t\right)}{x}_1\left(t\right)=x_2,\hfill \\ {}_0^C{D}_t^{q\left(t\right)}{x}_2\left(t\right)=g(X,t)u_1\left(t\right)+F(X,t)+d\left(t\right),\hfill \end{array}\right.$$

(6)

where $0<q_1\le q\left(t\right)\le q_2<1$, the states vector is $X\left(t\right)={[x_1\left(t\right),x_2\left(t\right)]}^T$. According to (5), we have

$$\left\{\begin{array}{c}{}_0^C{D}_t^{q\left(t\right)}{\tau }_1\left(t\right)={\tau }_2,\hfill \\ {}_0^C{D}_t^{q\left(t\right)}{\tau }_2\left(t\right)=g(X,t)u_1\left(t\right)+F(X,t)+d\left(t\right)-{}_0^C{D}_t^{q\left(t\right)}{x}_{2d}.\hfill \end{array}\right.$$

(7)

A global sliding-mode surface is given as follows

$$\overline{S}\left(t\right)={\tau }_2\left(t\right)+m_1{\tau }_1\left(t\right)-p\left(0\right)e^{-at},$$

(8)

where $p\left(t\right)={\tau }_2\left(t\right)+m_1{\tau }_1\left(t\right)$, $m_1>0$ is a constant. Let $\overline{S}\left(t\right)=0$, then ${}_0^C{D}_t^{q\left(t\right)}\overline{S}\left(t\right)=0$, one can obtain the corresponding sliding-mode dynamics

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{}_0^C{D}_t^{q\left(t\right)}{\tau }_1\left(t\right)+m_1{\tau }_1\left(t\right)=p\left(0\right)e^{-at},\hfill \\ {}_0^C{D}_t^{q\left(t\right)}{\tau }_2\left(t\right)+m_1{\tau }_2\left(t\right)=p{\left(0\right)}_0^C{D}_t^{q\left(t\right)}\left[e^{-at}\right].\hfill \end{array}\right.\end{array}$$

(9)

Let the Lyapunov function be

$$\begin{array}{c}\hfill V_1\left(t\right)=\frac{1}{2}{\tau }_1^2\left(t\right)+\frac{1}{2}{\tau }_2^2\left(t\right).\end{array}$$

(10)

Based on the reference [28], it yields that by taking the VO fractional operator with order $q\left(t\right)$ with respect to time on both sides of (10)

$$\begin{array}{cc}\hfill {}_0^C{D}_t^{q\left(t\right)}{V}_1\left(t\right)& \le {\tau }_1{\left(t\right)}_0^C{D}_t^{q\left(t\right)}{\tau }_1\left(t\right)+{\tau }_2{\left(t\right)}_0^C{D}_t^{q\left(t\right)}{\tau }_2\left(t\right)\hfill \\ \hfill & ={\tau }_1\left(t\right)(-m_1{\tau }_1\left(t\right)+p\left(0\right)e^{-at})+{\tau }_2\left(t\right)(-m_1{\tau }_2\left(t\right)+p{\left(0\right)}_0^C{D}_t^{q\left(t\right)}\left[e^{-at}\right])\hfill \\ \hfill & =-m_1{\tau }_1^2\left(t\right)-m_1{\tau }_2^2\left(t\right)+{\tau }_1\left(t\right)p\left(0\right)e^{-at}+{\tau }_2\left(t\right)p{\left(0\right)}_0^C{D}_t^{q\left(t\right)}\left[e^{-at}\right].\hfill \end{array}$$

Combined with ${}_0^C{D}_t^{q\left(t\right)}\left(e^{-at}\right)\le \frac{\Gamma (1-q_1)}{\Gamma (1-q_2)}{}_0^C{D}_t^{q_1}\left(e^{-at}\right)$, it implies that

$$\underset{t\to \infty }{lim}{}_0^C{D}_t^{q\left(t\right)}\left(e^{-{\overline{p}}_{i}t}\right)=\underset{t\to \infty }{lim}{}_0^C{D}_t^{q_1}\left(e^{-at}\right)=0.$$

Thus, when $t\to \infty$, one can obtain that

$$\begin{array}{c}\hfill {}_0^C{D}_t^{q\left(t\right)}{V}_1\left(t\right)\le -m_1{\tau }_1^2\left(t\right)-m_1{\tau }_2^2\left(t\right),\end{array}$$

which indicates that the sliding-mode error dynamics (9) are asymptotically stable, and the error states converge to the origin.

The following is to design a VO fractional control law to realize the convergence of the states

$$\begin{array}{cc}\hfill u_1\left(t\right)& =-g{(X,t)}^{-1}[F(X,t)-{}_0^C{D}_t^{q\left(t\right)}{x}_{2d}\left(t\right)+m_1{\tau }_2+k\overline{S}\left(t\right)+Msgn\left(\overline{S}\right)+\mu {\left|\overline{S}\left(t\right)\right|}^{\gamma }sgn\left(\overline{S}\left(t\right)\right)\hfill \\ \hfill & -{}_0^C{D}_t^{q\left(t\right)}\left(p\left(0\right)e^{-at}\right)]\hfill \end{array}$$

(11)

where $k>0, M>0$ and $\mu >0$.

It is emphasized that the proposed scheme described by (11) is a novel global time-varying sliding-mode control law, and it possesses a strong robustness against the uncertain and disturbance terms.

Choose the Lyapunov function $V_2\left(t\right)=\frac{1}{2}{\overline{S}}^2\left(t\right)$, then, one can obtain that

$$\begin{array}{ccc}\hfill {}_0^C{D}_t^{q\left(t\right)}{V}_2\left(t\right)& \le & \overline{S}\left(t\right){}_0^C{D}_t^{q\left(t\right)}\overline{S}\left(t\right)\hfill \\ \hfill & =& \overline{S}\left(t\right){}_0^C{D}_t^{q\left(t\right)}[{\tau }_2\left(t\right)+m_1{\tau }_1\left(t\right)-p\left(0\right)e^{-at}]\hfill \\ \hfill & =& \overline{S}\left(t\right)[{}_0^C{D}_t^{q\left(t\right)}{\tau }_2\left(t\right)+m_1{\tau }_2\left(t\right)-p\left(0\right){}_0^C{D}_t^{q\left(t\right)}\left(e^{-at}\right)]\hfill \\ & =& \overline{S}\left(t\right)[g(X,t)u_1\left(t\right)+F(X,t)+d\left(t\right)-{}_0^C{D}_t^{q\left(t\right)}{x}_{2d}+m_1{\tau }_2\left(t\right)-{}_0^C{D}_t^{q\left(t\right)}\left(p\left(0\right)e^{-at}\right)]\hfill \\ \hfill & \le & \overline{S}\left(t\right)[-k\overline{S}\left(t\right)-Msgn\left(\overline{S}\left(t\right)\right)-\mu |\overline{S}\left(t\right){|}^{\gamma }sgn\left(\overline{S}\left(t\right)\right)+\delta ]\hfill \\ \hfill & \le & -k|\overline{S}{\left(t\right)|}^2-(M-\delta )|\overline{S}\left(t\right)|-\mu |\overline{S}{\left(t\right)|}^{1+\gamma }.\hfill \\ \hfill \end{array}$$

(12)

If the constant satisfies $M>\delta$, based on (13), Hypothesis 1 and the VO fractional type Lyapunov stability theorem, we can determine that the trajectories of the closed-loop system are first driven to the sliding surface $\overline{S}\left(t\right)$, then converged to the origin. As indicated above, the main results of this section can be obtained.

Theorem 1.

If $M>\delta$, where M and δ are derived in (11) and (13), respectively, and Hypothesis 1 holds, when the system (6) is applied the sliding-mode surface (8) and the control (11), the tracking errors ${\tau }_1\left(t\right)$ and ${\tau }_2\left(t\right)$ converge to zero asymptotically.

4. The Global Time-Varying Sliding-Mode Control of n-Dimensional of the VO Fractional System

In this section, we apply the global time-varying sliding-mode control approach to investigate the control problem for the VO fractional system (3) in the n-dimensional situation.

4.1. The First VO Fractional Sliding-Mode Control Law

We write the n-dimensional nonlinear VO fractional system (3) in the following form

$$\left\{\begin{array}{c}{}_0^C{D}_t^{q\left(t\right)}{x}_1\left(t\right)=g_1(x,t)u_1\left(t\right)+F_1(t,x)+d_1\left(t\right),\hfill \\ {}_0^C{D}_t^{q\left(t\right)}{x}_2\left(t\right)=g_2(x,t)u_2\left(t\right)+F_2(t,x)+d_2\left(t\right),\hfill \\ \dots \hfill \\ {}_0^C{D}_t^{q\left(t\right)}{x}_n\left(t\right)=g_n(x,t)u_n\left(t\right)+F_n(t,x)+d_n\left(t\right),\hfill \end{array}\right.$$

(13)

where $x_i\in R^n$ are the system states, $u_i\in R^n, i=1,2\dots ,n$ are the control input. $g_i(x,t)$, $i=1,2,\dots ,n$ are invertible for all $x,t$. $F_i(t,x), i=1,2,\dots ,n$ and $d_i\left(t\right), i=1,2,\dots ,n$ are nonlinear functions, which represent the uncertain and disturbance terms.

Hypothesis 2.

There exists a positive constant $0<{\delta }_i<\infty$, which satisfies $|d_i\left(t\right)|\le {\delta }_i$ for $i=1,2,\dots ,n$.

According to the tracking error signals, system (13) can be transformed into the following form

$$\left\{\begin{array}{c}{}^C{D}_t^{q\left(t\right)}{\tau }_1\left(t\right)=g_1(x,t)u_1\left(t\right)+F_1(t,x)+d_1\left(t\right)-{}^C{D}_t^{q\left(t\right)}\left[x_{1d}\left(t\right)\right],\hfill \\ {}^C{D}_t^{q\left(t\right)}{\tau }_2\left(t\right)=g_2(x,t)u_2\left(t\right)+F_2(t,x)+d_2\left(t\right)-{}^C{D}_t^{q\left(t\right)}\left[x_{2d}\left(t\right)\right],\hfill \\ \dots \hfill \\ {}^C{D}_t^{q\left(t\right)}{\tau }_n\left(t\right)=g_n(x,t)u_n\left(t\right)+F_n(t,x)+d_n\left(t\right)-{}^C{D}_t^{q\left(t\right)}\left[x_{nd}\left(t\right)\right].\hfill \end{array}\right.$$

(14)

Combined with the definition of VO fractional operator, a full-order sliding-mode surface is presented as

$${\overline{S}}_i\left(t\right)={}^C{D}_t^{q\left(t\right)}{\tau }_i\left(t\right)+{\overline{m}}_i{\tau }_i\left(t\right)-F_0\left(t\right), i=1,2,\dots ,n,$$

(15)

where ${\overline{m}}_i>0, i=1,2,\dots ,n$, and the function $F_0\left(t\right)$ satisfies

• $F_0\left(0\right)={}_0^C{D}_t^{q\left(t\right)}{\tau }_i{\left(t\right)|}_{t=0}+{\overline{m}}_i{\tau }_i\left(0\right)$,
• $F_0\left(t\right)\to 0$ as $t\to \infty$,
• $F_0\left(t\right)$ has a continuous derivative.

When ${\overline{S}}_i\left(t\right)=0$, we can obtain

$$\begin{array}{c}\hfill {}_0^C{D}_t^{q\left(t\right)}{\tau }_i\left(t\right)=-{\overline{m}}_i{\tau }_i\left(t\right)+F_0\left(t\right).\end{array}$$

(16)

Let

$$V_3\left(t\right)=\frac{1}{2}\sum _{i=1}^n{\tau }_i^2\left(t\right),$$

(17)

obviously, the function $V_3\left(t\right)$ is a Lyapunov function. By operating the variable-order fractional ${}_0^C{D}_t^{q\left(t\right)}$ on both sides of Equation (17), we can obtain

$$\begin{array}{cc}\hfill {}_0^C{D}_t^{q\left(t\right)}{V}_3\left(t\right)& \le \sum _{i=1}^n{\tau }_i\left(t\right){}_0^C{D}_t^{q\left(t\right)}{\tau }_i\left(t\right)\hfill \\ \hfill & =\sum _{i=1}^n{\tau }_i\left(t\right)(-{\overline{m}}_i{\tau }_i\left(t\right)+F_0\left(t\right))\hfill \\ \hfill & =-\sum _{i=1}^n{\overline{m}}_i{\tau }_i^2\left(t\right)+\sum _{i=1}^n{\tau }_i\left(t\right)F_0\left(t\right).\hfill \end{array}$$

Let $t\to \infty$, we obtain that

$$\begin{array}{c}\hfill {}_0^C{D}_t^{q\left(t\right)}{V}_3\left(t\right)\le -\sum _{i=1}^n{\overline{m}}_i{\tau }_i^2\left(t\right)\le -2\overline{m}{V}_3\left(t\right).\end{array}$$

where $\overline{m}=min\{{\overline{m}}_1,{\overline{m}}_2,\cdots ,{\overline{m}}_n\}$. Thus, based on the VO fractional Lyapunov stability theorem, the tracking error of the dynamical system (16) is driven to the origin asymptotically.

Theorem 2.

If the system (14) is applied the sliding-mode surface (15) and the following time-varying control law

$$\left\{\begin{array}{c}{u}_i\left(t\right)=u_{eq}^i+u_{sw}^i\hfill \\ u_{eq}^i=-g_i{(x,t)}^{-1}[F_i(t,x)+d_i\left(t\right)-{}_0^C{D}_t^{q\left(t\right)}\left[x_{id}\left(t\right)\right]+m_i{\tau }_i\left(t\right)-F_0\left(t\right)],\hfill \\ {}_0^C{D}_t^{q\left(t\right)}\left[g_i(x,t)u_{sw}^i\right]=-k_{i}sgn\left({\overline{S}}_i\left(t\right)\right){\left|{\overline{S}}_i\left(t\right)\right|}^{{\eta }_i}-m_i{\overline{S}}_i\left(t\right), i=1,2,\dots ,n.\hfill \end{array}\right.$$

(18)

Then, the tracking errors ${\tau }_i\left(t\right), i=1,2,\dots ,n$ converge to zero asymptotically.

Proof. 

Choose the Lyapunov function:

$$V_4\left(t\right)=\frac{1}{2}\sum _{i=1}^n{\overline{S}}_i^2\left(t\right).$$

(19)

By applying the VO fractional operator ${}_0^C{D}_t^{q\left(t\right)}$ on both sides of (19), we can obtain

$$\begin{array}{cc}\hfill {}_0^C{D}_t^{q\left(t\right)}{V}_4\left(t\right)& \le \sum _{i=1}^n{\overline{S}}_i\left(t\right){}_0^C{D}_t^{q\left(t\right)}{\overline{S}}_i\left(t\right)\hfill \\ \hfill & =\sum _{i=1}^n{\overline{S}}_i\left(t\right){}_0^C{D}_t^{q\left(t\right)}[{}_0^C{D}_t^{q\left(t\right)}{\tau }_i\left(t\right)+m_i{\tau }_i\left(t\right)-F_0\left(t\right)]\hfill \\ \hfill & =\sum _{i=1}^n{\overline{S}}_i\left(t\right){}_0^C{D}_t^{q\left(t\right)}[g_i(x,t)u_i\left(t\right)+F_i(t,x)+d_i\left(t\right)-{}_0^C{D}_t^{q\left(t\right)}\left[x_{id}\left(t\right)\right]+m_i{\tau }_i\left(t\right)-F_0\left(t\right)]\hfill \\ \hfill & =\sum _{i=1}^n{\overline{S}}_i\left(t\right)[-k_{i}sgn\left({\overline{S}}_i\left(t\right)\right)|{\overline{S}}_i\left(t\right){|}^{{\eta }_i}-m_i{\overline{S}}_i\left(t\right)]\hfill \\ \hfill & =\sum _{i=1}^n[-k_i|{\overline{S}}_i\left(t\right){|}^{1+{\eta }_i}-m_i{\overline{S}}_i^2\left(t\right)].\hfill \end{array}$$

(20)

Similar to the previous analysis, the error states of the system converge to zero as $t\to \infty$. □

The scheme proposed in Theorem 2 possesses the advantages of the global time-varying sliding-mode control law and the VO fractional operator; it also generates the continuous signals, which are free of chattering.

4.2. The Second VO Fractional Sliding-Mode Control Scheme

Consider the following sliding-mode surface:

$$\begin{array}{c}\hfill {}_0^C{D}_t^{q\left(t\right)}{\tilde{S}}_i\left(t\right)={}_0^C{D}_t^{q\left(t\right)}{\tau }_i\left(t\right)+m_i{\tau }_i\left(t\right)-p_i\left(0\right)e^{-a_{i}t}, i=1,2,\dots ,n,\end{array}$$

(21)

where $m_i>0,p_i>0$, and $a_i>0$. When ${\tilde{S}}_i\left(t\right)=0$, we obtain ${}_0^C{D}_t^{q\left(t\right)}{\tilde{S}}_i\left(t\right)=0$. Then

$$\begin{array}{c}\hfill {}_0^C{D}_t^{q\left(t\right)}{\tau }_i\left(t\right)=-m_i{\tau }_i\left(t\right)+p_i\left(0\right)e^{-a_{i}t}.\end{array}$$

(22)

Set

$$\begin{array}{c}\hfill V_5\left(t\right)=\sum _{i=1}^n\frac{1}{2}{\tau }_i^2\left(t\right),\end{array}$$

(23)

we can obtain

$$\begin{array}{cc}\hfill {}_0^C{D}_t^{q\left(t\right)}{V}_5\left(t\right)& \le \sum _{i=1}^n{\tau }_i\left(t\right){}_0^C{D}_t^{q\left(t\right)}{\tau }_i\left(t\right)\hfill \\ \hfill & =\sum _{i=1}^n{\tau }_i\left(t\right)[-m_i{\tau }_i\left(t\right)+p_i\left(0\right)e^{-a_{i}t}]\hfill \\ \hfill & =\sum _{i=1}^n[-m_i|{\tau }_i\left(t\right){|}^2+{\tau }_i\left(t\right)p_i\left(0\right)e^{-a_{i}t}].\hfill \end{array}$$

Let $t\to \infty$, we have

$$\begin{array}{cc}\hfill {}_0^C{D}_t^{q\left(t\right)}{V}_5\left(t\right)& \le -\sum _{i=1}^n{m}_i{\left|{\tau }_i\left(t\right)\right|}^2.\hfill \end{array}$$

which implies that the error dynamics (22) are asymptotically stable. Then, the error states converge to the origin.

The control law is designed as

$$\begin{array}{cc}\hfill u_i& =-g_i{(x,t)}^{-1}[F_i(x,t)-{}_0^C{D}_t^{q\left(t\right)}{x}_{id}\left(t\right)+m_i{\tau }_i\left(t\right)+k_i{\tilde{S}}_i\left(t\right)+M_{i}sgn({\tilde{S}}_i)\hfill \\ \hfill & +{\mu }_i|{\tilde{S}}_i{\left(t\right)|}^{{\gamma }_i}sgn({\tilde{S}}_i\left(t\right))-{}_0^C{D}_t^{q\left(t\right)}\left(p_i\left(0\right)e^{-a_{i}t}\right)],\hfill \end{array}$$

(24)

where $i=1,2,\dots ,n$. Let

$$V_6({\tilde{S}}_i)=\sum _{i=1}^n\frac{1}{2}{\tilde{S}}_i^2,$$

we can obtain

$$\begin{array}{ccc}\hfill {}_0^C{D}_t^{q\left(t\right)}{V}_6\left(t\right)& \le & \sum _{i=1}^n{\tilde{S}}_i{}_0^C{D}_t^{q\left(t\right)}{\tilde{S}}_i\hfill \\ \hfill & =& \sum _{i=1}^n{\tilde{S}}_i[{}_0^C{D}_t^{q\left(t\right)}{\tau }_i\left(t\right)+m_i{\tau }_i\left(t\right)-p_i\left(0\right)e^{-a_{i}t}]\hfill \\ \hfill & \le & \sum _{i=1}^n{\tilde{S}}_i[-k_i{\tilde{S}}_i\left(t\right)-{\mu }_i|{\tilde{S}}_i\left(t\right){|}^{{\gamma }_i}-M_{i}sgn({\tilde{S}}_i)+{\delta }_i]\hfill \\ \hfill & \le & \sum _{i=1}^n[-k_i|{\tilde{S}}_i{\left(t\right)|}^2-{\mu }_i|{\tilde{S}}_i{\left(t\right)|}^{1+{\gamma }_i}-(M_i-{\delta }_i)|{\tilde{S}}_i\left(t\right)\left|\right],\hfill \end{array}$$

(25)

if $M_i>{\delta }_i$ for $i=1,2,\dots ,n,$ by (26), we have ${}_0^C{D}_t^{q\left(t\right)}{V}_6\left(t\right)<0$, which gives the following assertion according to Hypothesis 2.

Theorem 3.

If $M_i>{\delta }_i, i=1,2,\dots ,n$, where $M_i,{\delta }_i, i=1,2,\dots ,n$ are given in (26), and the Hypothesis 2 holds. Then, the error states ${\tau }_i\left(t\right),i=1,2,\dots ,n$ of system (14) converge asymptotically to zero by applying sliding-mode surface (21) and the proposed control law (24).

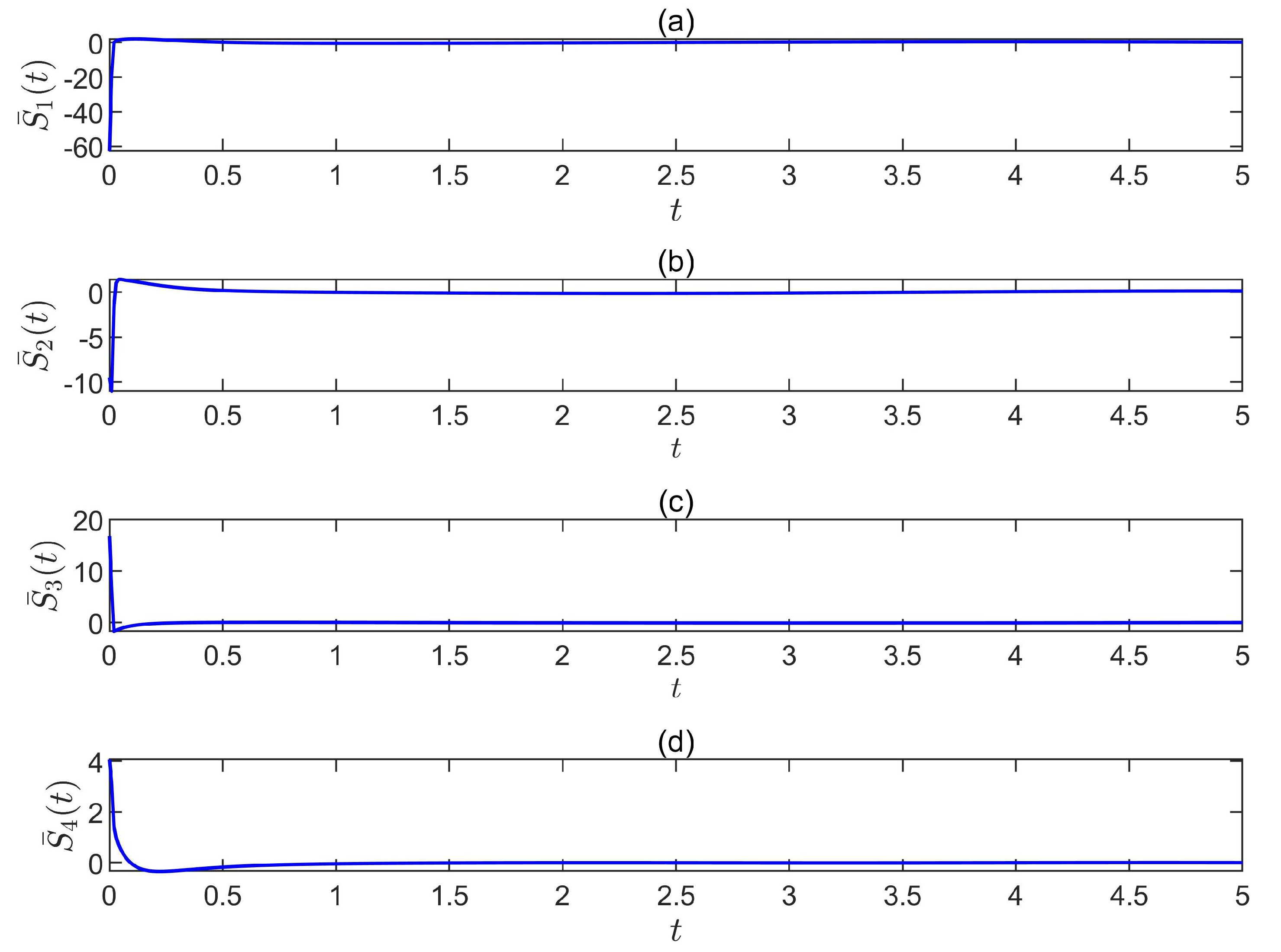
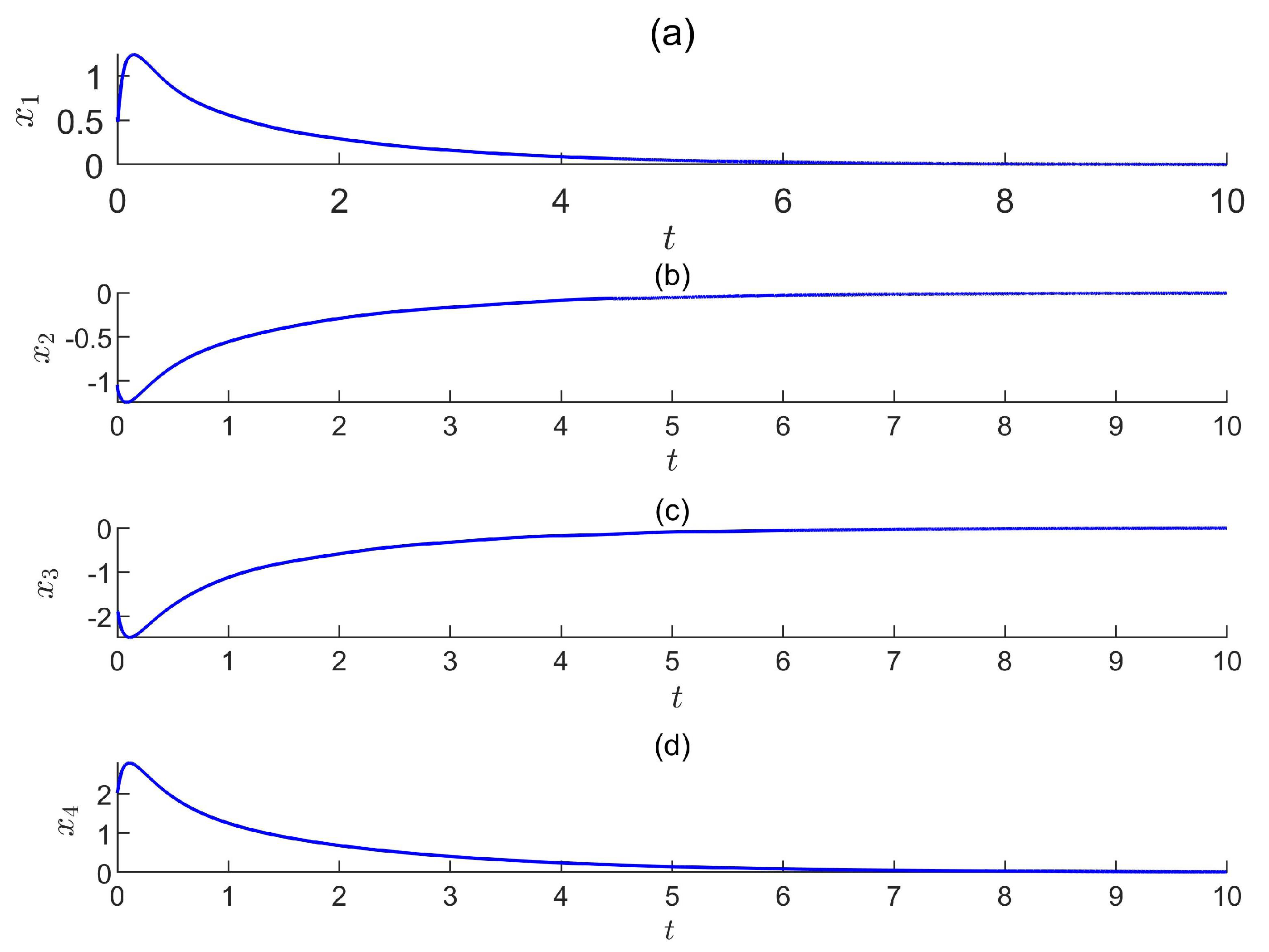
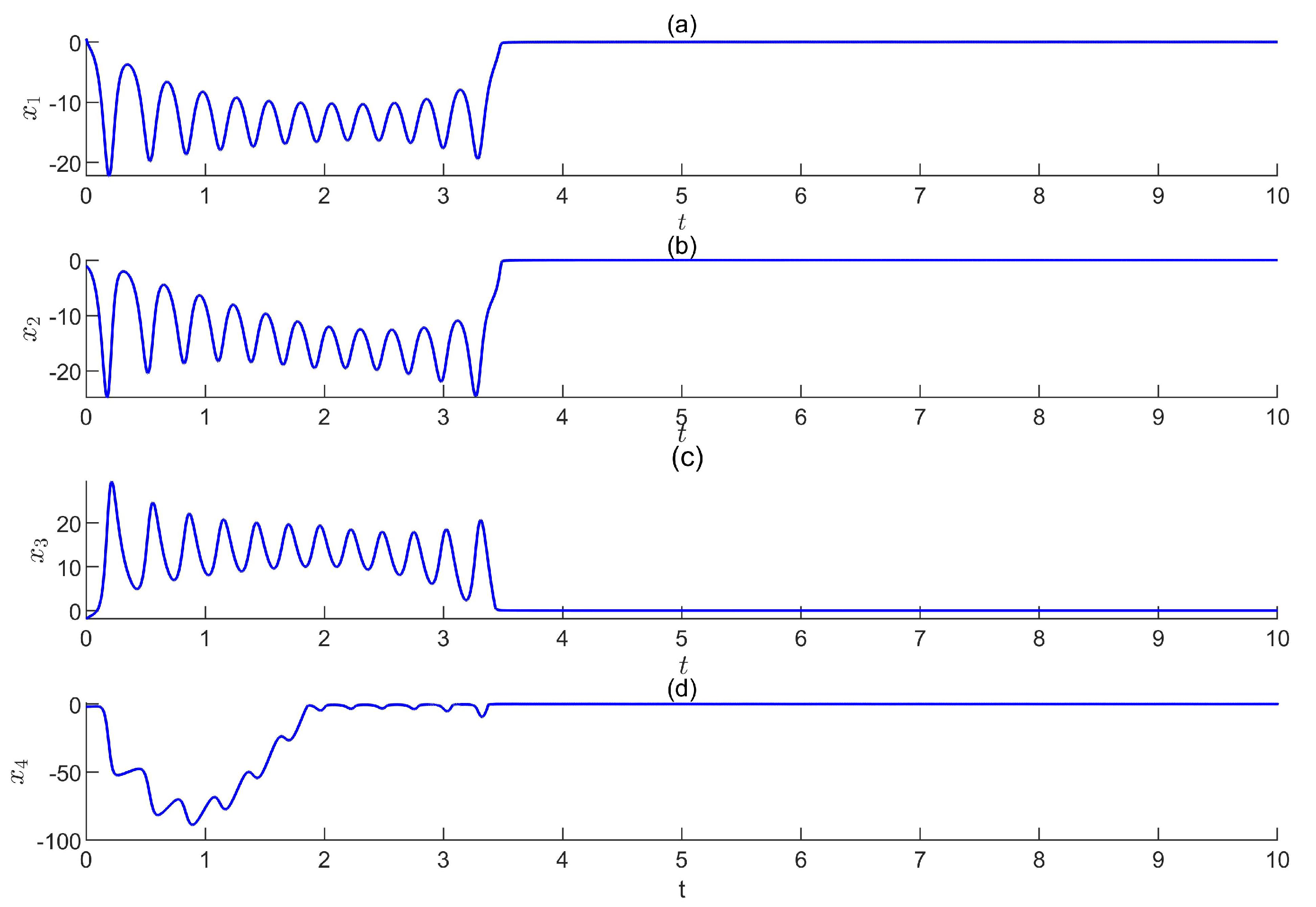
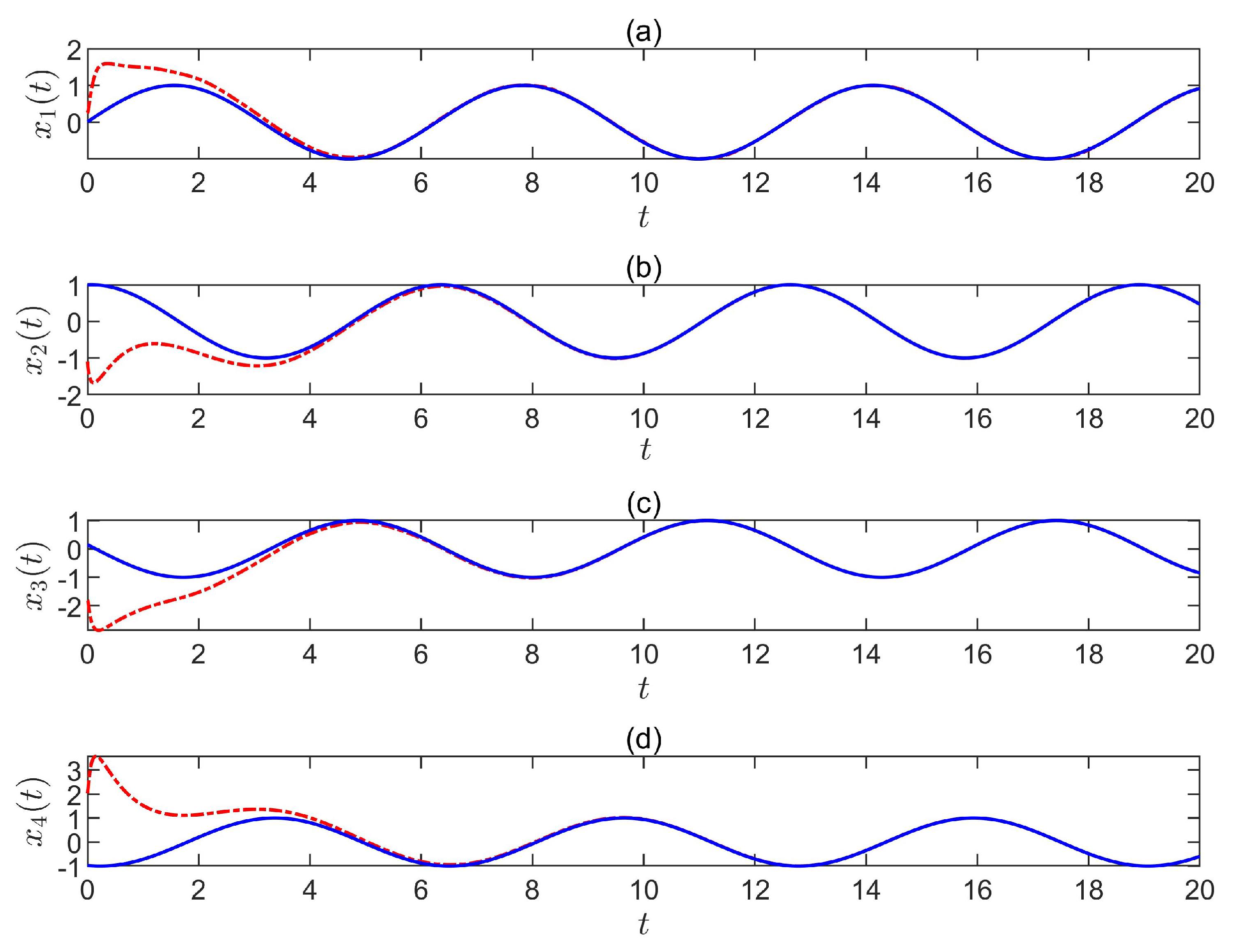
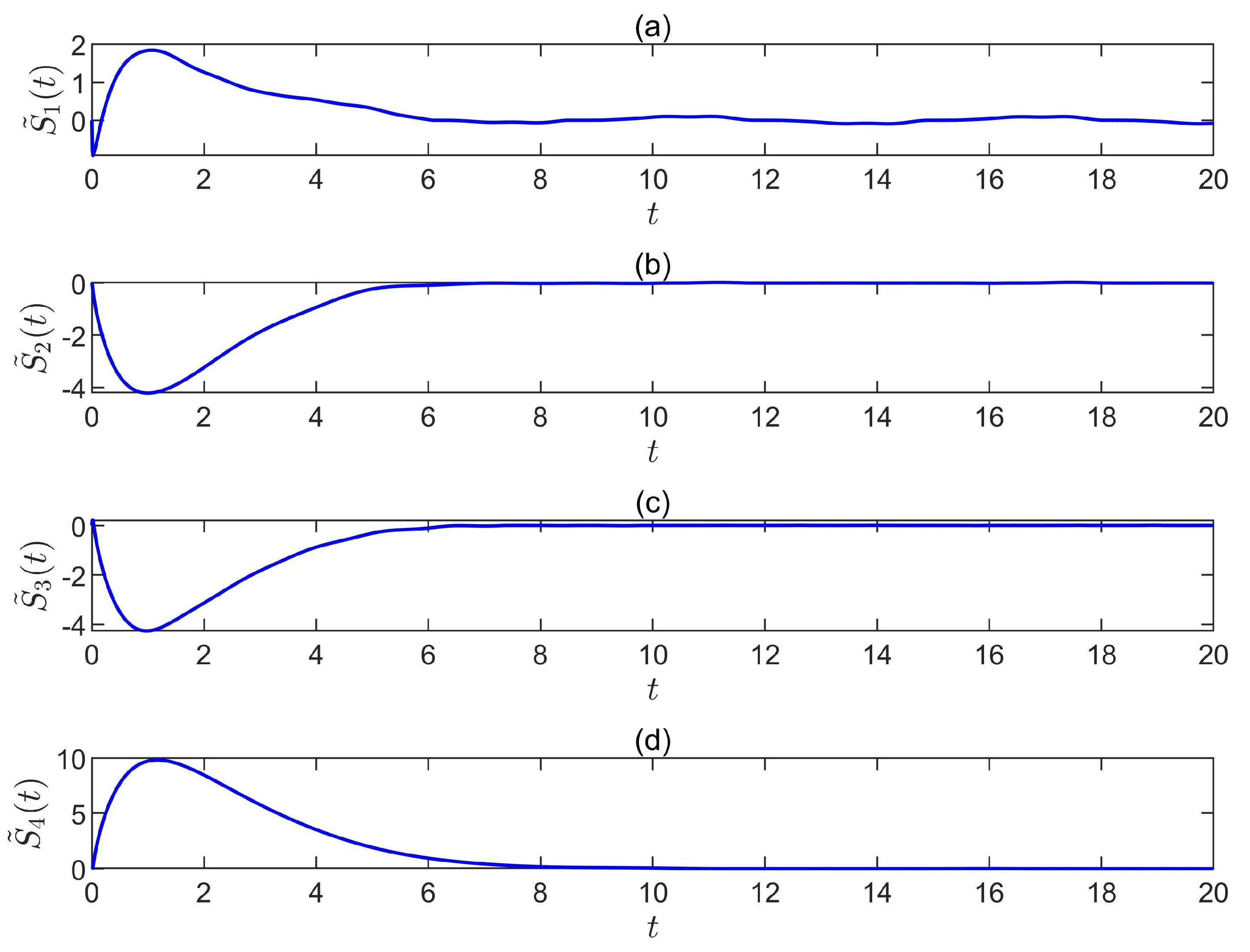
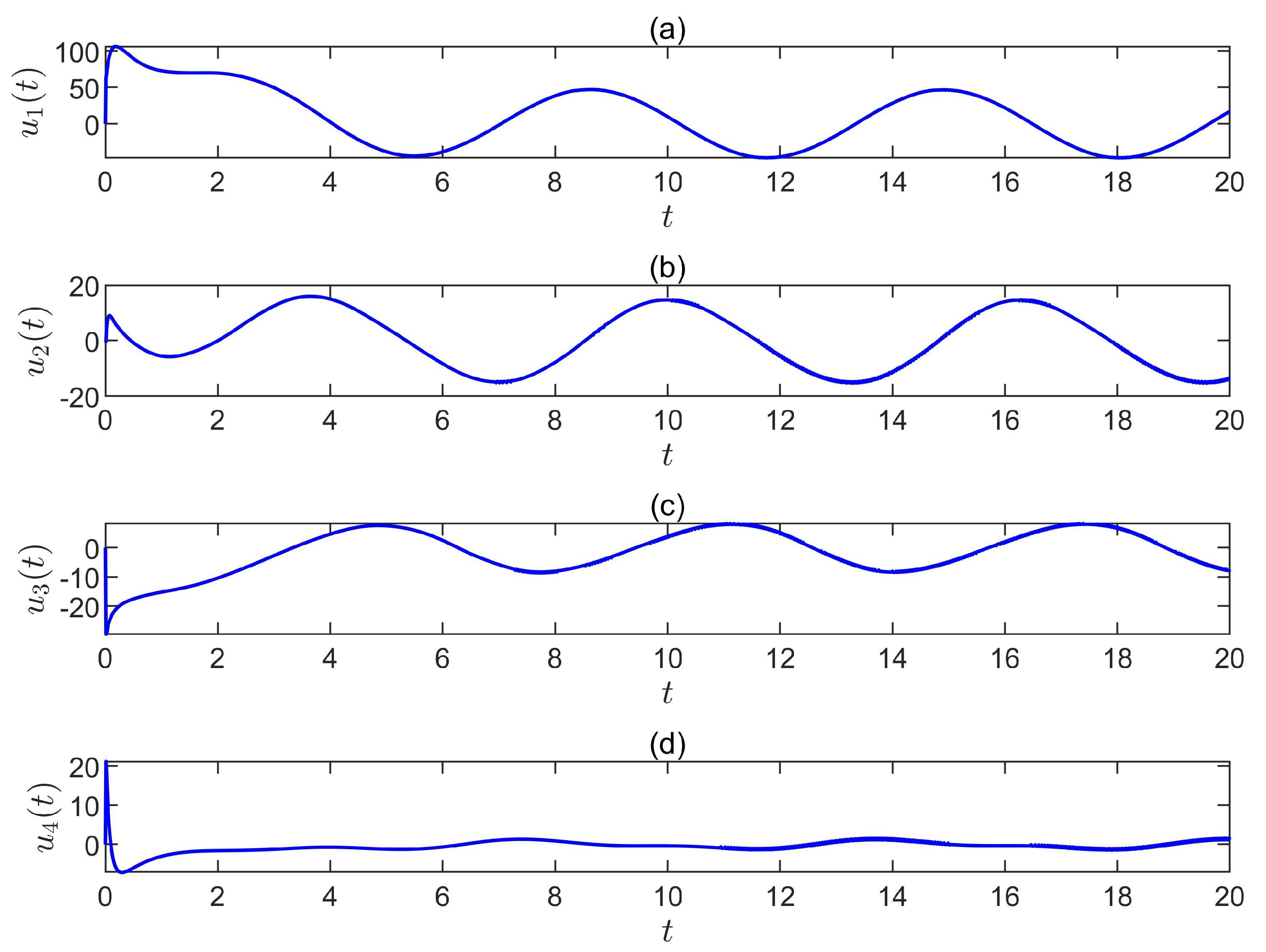
5. Simulation Results

This section is used to accomplish some numerical simulations to validate the efficiency of the control scheme proposed.

Consider the following Caputo-type VO fractional hyper-chaotic Chen system with uncertain and external disturbance terms

$$\left\{\begin{array}{c}{}_0^C{D}_t^{q\left(t\right)}{x}_1=35(x_2-x_1)+x_4+\Delta F_1(X,t),\hfill \\ {}_0^C{D}_t^{q\left(t\right)}{x}_2=7x_1+12x_2-x_1{x}_3+\Delta F_2(X,t),\hfill \\ {}_0^C{D}_t^{q\left(t\right)}{x}_3=x_1{x}_2-8x_3+\Delta F_3(X,t),\hfill \\ {}_0^C{D}_t^{q\left(t\right)}{x}_4=x_2{x}_3+0.3x_4+\Delta F_4(X,t),\hfill \end{array}\right.$$

(26)

where the function q(t) is continuous with 0 < q(t) < 1, and

$$\left\{\begin{array}{c}\Delta F_1(X,t)=0.1cos\left(6t\right)x_1-0.1sin\left(t\right),\hfill \\ \Delta F_2(X,t)=-0.1cos\left(2t\right)x_2+0.1sin\left(3t\right),\hfill \\ \Delta F_3(X,t)=0.1sin\left(3t\right)x_3+0.1cos\left(5t\right),\hfill \\ \Delta F_4(X,t)=-0.1cos\left(t\right)x_4-0.1cos\left(t\right).\hfill \end{array}\right.$$

(27)

Given the reference signals $x_{iR}\left(t\right), i=1,2,3$ as

$$\left\{\begin{array}{c}{x}_{1R}=sint, x_{2R}=sin(t+q\left(t\right)\pi /2),\hfill \\ x_{3R}=sin(t+q\left(t\right)\pi ), x_{4R}=sin(t+3q\left(t\right)\pi /2),\hfill \end{array}\right.$$

(28)

then, the tracking error terms ${\tau }_i\left(t\right)$ are defined as

$$\left\{\begin{array}{c}{\tau }_1\left(t\right)=x_1\left(t\right)-x_{1R}\left(t\right),\hfill \\ {\tau }_2\left(t\right)=x_2\left(t\right)-x_{2R}\left(t\right),\hfill \\ {\tau }_3\left(t\right)=x_3\left(t\right)-x_{3R}\left(t\right),\hfill \\ {\tau }_4\left(t\right)=x_4\left(t\right)-x_{4R}\left(t\right).\hfill \end{array}\right.$$

(29)

5.1. The First-Type Sliding-Mode Control Scheme

By (15), the representation of the global sliding-mode surface of system (26) is employed as

$$\left\{\begin{array}{c}{\overline{S}}_1\left(t\right)={\tau }_1\left(t\right)+{\overline{m}}_1{\tau }_1\left(t\right)-p_1\left(0\right)e^{-a_{1}t},\hfill \\ {\overline{S}}_2\left(t\right)={}_0^C{D}_t^{q\left(t\right)}{\tau }_2\left(t\right)+{\overline{m}}_2{\tau }_2\left(t\right)-p_2\left(0\right)e^{-a_{2}t},\hfill \\ {\overline{S}}_3\left(t\right)={}_0^C{D}_t^{q\left(t\right)}{\tau }_3\left(t\right)+{\overline{m}}_3{\tau }_3\left(t\right)-p_3\left(0\right)e^{-a_{3}t},\hfill \\ {\overline{S}}_4\left(t\right)={}_0^C{D}_t^{q\left(t\right)}{\tau }_4\left(t\right)+{\overline{m}}_4{\tau }_4\left(t\right)-p_4\left(0\right)e^{-a_{4}t},\hfill \end{array}\right.$$

(30)

where $p_i\left(t\right)={}_0^C{D}_t^{q\left(t\right)}{\tau }_i\left(t\right)+{\overline{m}}_i{\tau }_i\left(t\right), i=1,2,3,4.$

By using (18), the following VO fractional control law is given with the initial conditions $u_1\left(0\right)=0, u_2\left(0\right)=0, u_3\left(0\right)=0, u_4\left(0\right)=0$,

$$\left\{\begin{array}{c}{u}_1\left(t\right)=u_{eq}^1+u_{sw}^1\hfill \\ u_{eq}^1=-[35(x_2-x_1)+x_4+0.1cos\left(6t\right)x_1-0.1sin\left(t\right)-{}_0^C{D}_t^{q\left(t\right)}\left[x_{1R}\left(t\right)\right]+{\overline{m}}_1{\tau }_1\left(t\right)\hfill \\ -p_1\left(0\right)e^{-a_{1}t}],{}_0^C{D}_t^{q\left(t\right)}\left[u_{sw}^1\right]=-k_{1}sgn\left({\overline{S}}_1\left(t\right)\right){\left|{\overline{S}}_1\left(t\right)\right|}^{{\eta }_1}-m_1{\overline{S}}_1\left(t\right);\hfill \\ u_2\left(t\right)=u_{eq}^2+u_{sw}^2\hfill \\ u_{eq}^2=-7x_1-12x_2+x_1{x}_3+0.1cos\left(2t\right)x_2-0.1sin\left(3t\right)+{}_0^C{D}_t^{q\left(t\right)}\left[x_{2R}\left(t\right)\right]-{\overline{m}}_2{\tau }_2\left(t\right)\hfill \\ +p_2\left(0\right)e^{-a_{2}t},{}_0^C{D}_t^{q\left(t\right)}\left[u_{sw}^2\right]=-k_{2}sgn\left({\overline{S}}_2\left(t\right)\right){\left|{\overline{S}}_2\left(t\right)\right|}^{{\eta }_2}-m_2{\overline{S}}_2\left(t\right);\hfill \\ u_3\left(t\right)=u_{eq}^3+u_{sw}^3\hfill \\ u_{eq}^3=-[x_1{x}_2-8x_3+0.1sin\left(3t\right)x_3+0.1cos\left(5t\right)-{}_0^C{D}_t^{q\left(t\right)}\left[x_{3R}\left(t\right)\right]+{\overline{m}}_3{\tau }_3\left(t\right)\hfill \\ -p_3\left(0\right)e^{-a_{3}t}],{}_0^C{D}_t^{q\left(t\right)}\left[u_{sw}^3\right]=-k_{3}sgn\left({\overline{S}}_3\left(t\right)\right){\left|{\overline{S}}_3\left(t\right)\right|}^{{\eta }_3}-m_3{\overline{S}}_3\left(t\right);\hfill \\ u_4\left(t\right)=u_{eq}^4+u_{sw}^4\hfill \\ u_{eq}^4=-[x_2{x}_3+0.3x_4-0.1cos\left(t\right)x_4-0.1cos\left(t\right)-{}_0^C{D}_t^{q\left(t\right)}\left[x_{4R}\left(t\right)\right]+{\overline{m}}_4{\tau }_4\left(t\right)\hfill \\ -p_4\left(0\right)e^{-a_{4}t}],{}_0^C{D}_t^{q\left(t\right)}\left[u_{sw}^4\right]=-k_{4}sgn\left({\overline{S}}_4\left(t\right)\right){\left|{\overline{S}}_4\left(t\right)\right|}^{{\eta }_4}-m_4{\overline{S}}_4\left(t\right);\hfill \end{array}\right.$$

(31)

let ${\overline{m}}_1=10, {\overline{m}}_2=10, {\overline{m}}_3=9, {\overline{m}}_4=9, m_1=2, m_2=3, m_3=3, m_4=2, k_1=2, k_2=3$, $k_3$ = 4, $k_4=2, {\eta }_1=0.5, {\eta }_2=0.5, {\eta }_3=0.5, {\eta }_4=0.5$, and $a_1=6, a_2=6, a_3=6, a_4=5$. The initial conditions of the system (26) is $x_1\left(0\right)=1, x_2\left(0\right)=-1, x_3\left(0\right)=-2, x_4\left(0\right)=2$ and the VO parameter is $q\left(t\right)=0.96+0.02t/T, t\in [0,T]$.

The time history of the state trajectories of the controlled VO fractional hyper-chaotic Chen system is depicted in Figure 1, it is seen that the error signals between the states of the system and the reference signals converge to zero. Moreover, Figure 2 and Figure 3 illustrate the time trajectories of the VO fractional sliding-mode surface (30) and the controller (31), respectively. It is obvious that the sliding-mode surface approaches to zero from the start and the reaching stage is removed. Additionally, in this practical application, the control input is free of chattering and the time histories of the controller achieve the stability in a finite time. Thus, it implies from the simulation results that the theoretical result of the proposed control scheme is feasible and the good performance of the tracking control is realized.

The following is intended to compare the performance of the proposed the first-type control strategy in this paper with the controller proposed in [53]. For system (26), with $x_{1R}=x_{2R}=x_{3R}=x_{4R}=0$, we validate the control performance of the two control strategies in Figure 4 and Figure 5 with the same initial value and the fractional-order parameter with the value of $q=q\left(t\right)=0.92$. Figure 4 depicts the state trajectories of the controlled fractional-order uncertain Chen system (26) under the control law (31). Figure 5 depicts the state trajectories of the controlled fractional-order uncertain Chen system (26) under the control law proposed in [53]. One can see that, from the two figures, although the system states converges asymptotically to zero under the controllers, it takes a much better performance compared with Figure 5. Moreover, with the change of parameters, the controller is extremely unstable. The controlled states under the proposed technique in this paper are more smooth and stable with the change of the parameters. In addition, the control input proposed in this paper can be applied to the variable-order fractional systems.

5.2. The Second-Type Sliding-Mode Control Law

This part is devoted to verifying the feasibility of the second type of proposed controller of the VO fractional hyper-chaotic Chen system.

By (21), the full-order sliding-mode surface is given as

$$\left\{\begin{array}{c}{}_0^C{D}_t^{q\left(t\right)}{\tilde{S}}_1\left(t\right)={}_0^C{D}_t^{q\left(t\right)}{\tau }_1\left(t\right)+m_1{\tau }_1\left(t\right)-r_1\left(0\right)e^{-a_{1}t},\hfill \\ {}_0^C{D}_t^{q\left(t\right)}{\tilde{S}}_2\left(t\right)={}_0^C{D}_t^{q\left(t\right)}{\tau }_2\left(t\right)+m_2{\tau }_2\left(t\right)-r_2\left(0\right)e^{-a_{2}t},\hfill \\ {}_0^C{D}_t^{q\left(t\right)}{\tilde{S}}_3\left(t\right)={}_0^C{D}_t^{q\left(t\right)}{\tau }_3\left(t\right)+m_3{\tau }_3\left(t\right)-r_3\left(0\right)e^{-a_{3}t},\hfill \\ {}_0^C{D}_t^{q\left(t\right)}{\tilde{S}}_4\left(t\right)={}_0^C{D}_t^{q\left(t\right)}{\tau }_4\left(t\right)+m_4{\tau }_4\left(t\right)-r_4\left(0\right)e^{-a_{4}t},\hfill \end{array}\right.$$

(32)

where $r_i\left(t\right)={}_0^C{D}_t^{q\left(t\right)}{\tau }_i\left(t\right)+m_i{\tau }_i\left(t\right), i=1,2,3,4$. According to the Equation (24), the control input scheme is designed as

$$\left\{\begin{array}{c}{u}_1=-[35(x_2-x_1)+x_4]+{}_0^C{D}_t^{q\left(t\right)}{x}_{1R}-m_1{\tau }_1\left(t\right)-k_1{\tilde{S}}_1\left(t\right)-M_{1}sgn({\tilde{S}}_1)\hfill \\ -{\mu }_1{\left|{\tilde{S}}_1\right|}^{r_1}sgn({\tilde{S}}_1),\hfill \\ u_2=-[7x_1+12x_2-x_1{x}_3]+{}_0^C{D}_t^{q\left(t\right)}{x}_{2R}-m_2{\tau }_2\left(t\right)-k_2{\tilde{S}}_2\left(t\right)-M_{2}sgn({\tilde{S}}_2)\hfill \\ -{\mu }_2{\left|{\tilde{S}}_2\right|}^{r_2}sgn({\tilde{S}}_2),\hfill \\ u_3=-[x_1{x}_2-8x_3]+{}_0^C{D}_t^{q\left(t\right)}{x}_{3R}-m_3{\tau }_3\left(t\right)-k_3{\tilde{S}}_3\left(t\right)-M_{3}sgn({\tilde{S}}_3)\hfill \\ -{\mu }_3{\left|{\tilde{S}}_3\right|}^{r_3}sgn({\tilde{S}}_3),\hfill \\ u_4=-[x_2{x}_3+0.3x_4]+{}_0^C{D}_t^{q\left(t\right)}{x}_{4R}-m_4{\tau }_4\left(t\right)-k_4{\tilde{S}}_4\left(t\right)-M_{4}sgn({\tilde{S}}_4)\hfill \\ -{\mu }_4{\left|{\tilde{S}}_4\right|}^{r_4}sgn({\tilde{S}}_4).\hfill \end{array}\right.$$

(33)

Let $m_1=10, m_2=10, m_3=9, m_4=9, M_1=0.15, M_2=0.15, M_3=0.15$, $M_4$ = 0.15, $k_1=1, k_2=1, k_3=1, k_4=1, {\mu }_1=1, {\mu }_2=1, {\mu }_3=1, {\mu }_4=1, a_1=0.6, a_2=0.6$, $a_3$ = 0.6, $a_4=0.5$ and $r_1=0.5, r_2=0.5, r_3=0.5, r_4=0.5$, $q\left(t\right)=0.96+0.02t/T, t\in [0,T]$ and the simulation time is activated at time $t=20$; the desired effect of the state trajectories is depicted in Figure 6. As expected, it is verified that the asymptotic properties of the error signals can be realized. Furthermore, the time trajectories of the proposed sliding-mode surface (32) and the controller (33) are described in Figure 7 and Figure 8. The desired results can be observed for the selected system parameters; these simulation results show that the asymptotic tracking performances can be achieved under the proposed sliding-mode controller in the presence of unknown actuator uncertainties.

Remark 1.

The value of the parameters of the above two simulations is estimated according to the aim of control. On the basis of the parameter values of the corresponding integer-order system, the final value for these parameters such as the one in this paper is obtained by adjusting step by step through the computer simulation until the desired control results appeared.

6. Conclusions

In this present study, the problem of colorred tracking control is dealt with for a class of VO fractional uncertain systems. Firstly, a global varying-time sliding-mode control is proposed to drive the reference signal to track the states of the two dimensional system. Then, for the corresponding n-dimensional system, based on the global sliding-mode surfaces proposed above, a kind of time-varying control schemes have been derived to ensure the robustness from the beginning time and guarantee the convergence of tracking error signals to the origin. Furthermore, the controllers designed in this paper are smooth signals, which avoid the undesirable chattering or singularity, which are verified by the numerical simulation.

For future research, we will further study the design of different controllers by adopting different control methods, and how to apply this controller to the practical problems of engineering.