Application of Asymmetric Notched Semi-Circular Bending Specimen to Evaluate Mixed-Mode I-II Fracture Behaviors of Sandstone
Abstract
:1. Introduction
2. Test Procedures
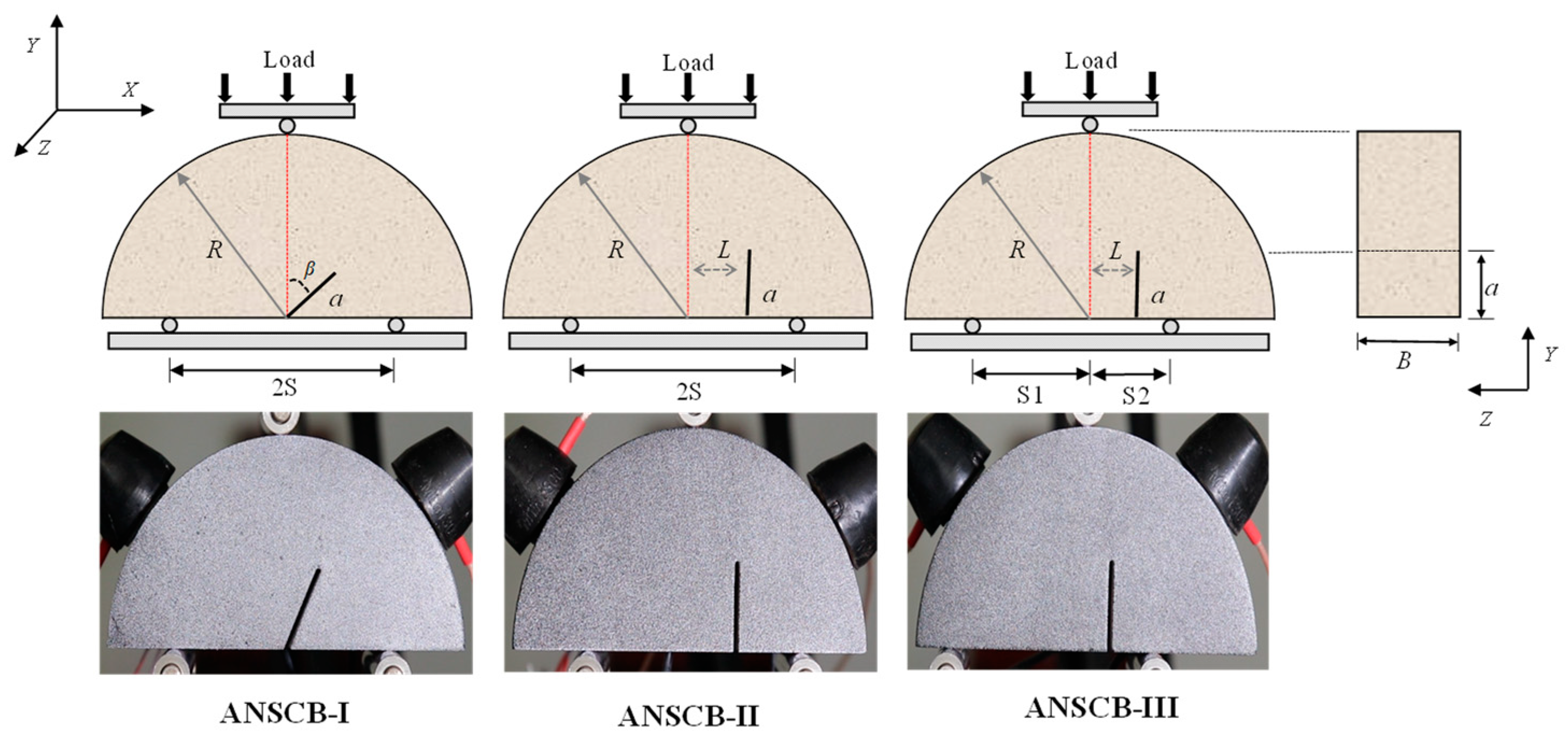
2.1. Materials and Specimen Preparation
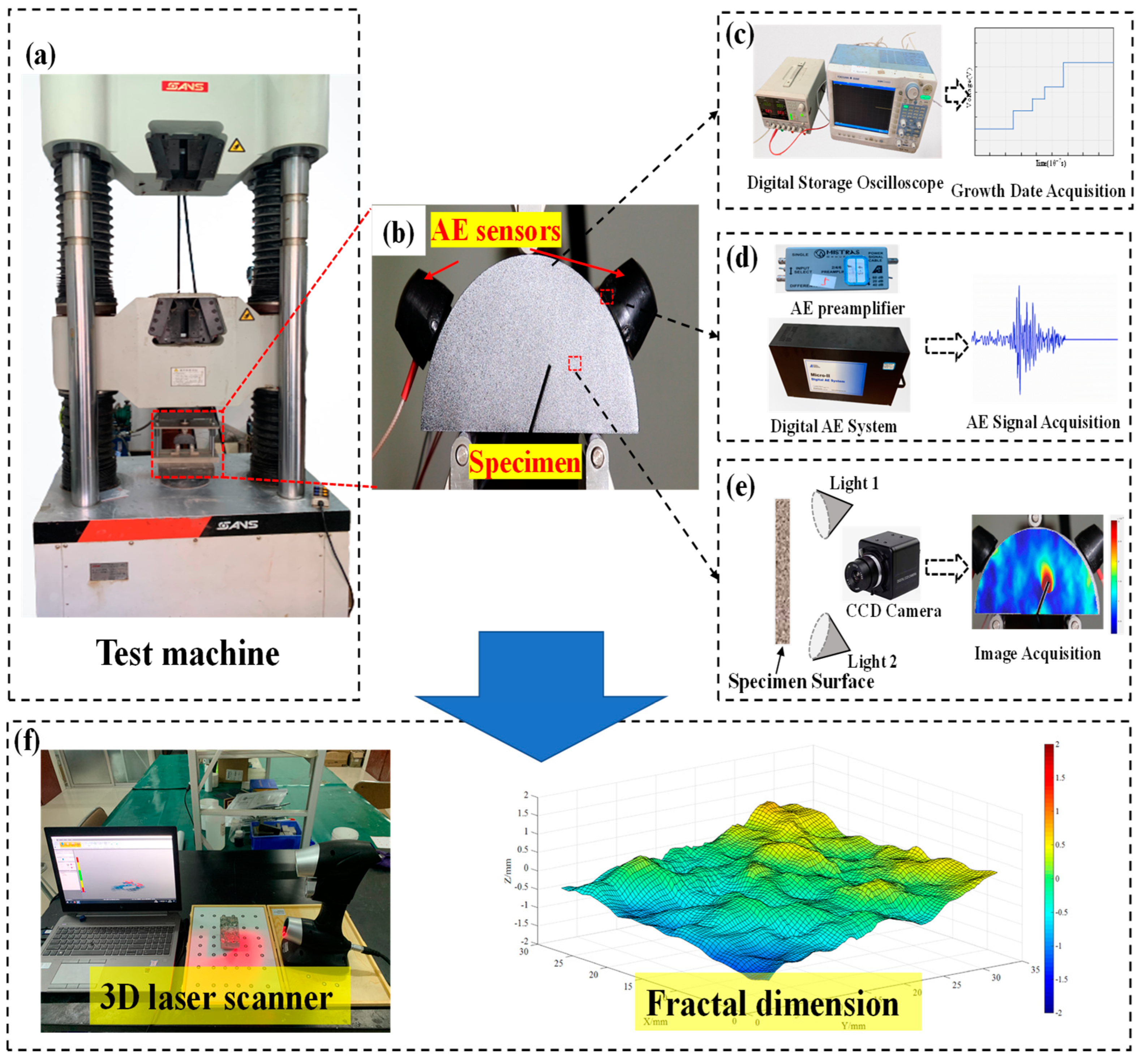
2.2. Test Apparatus
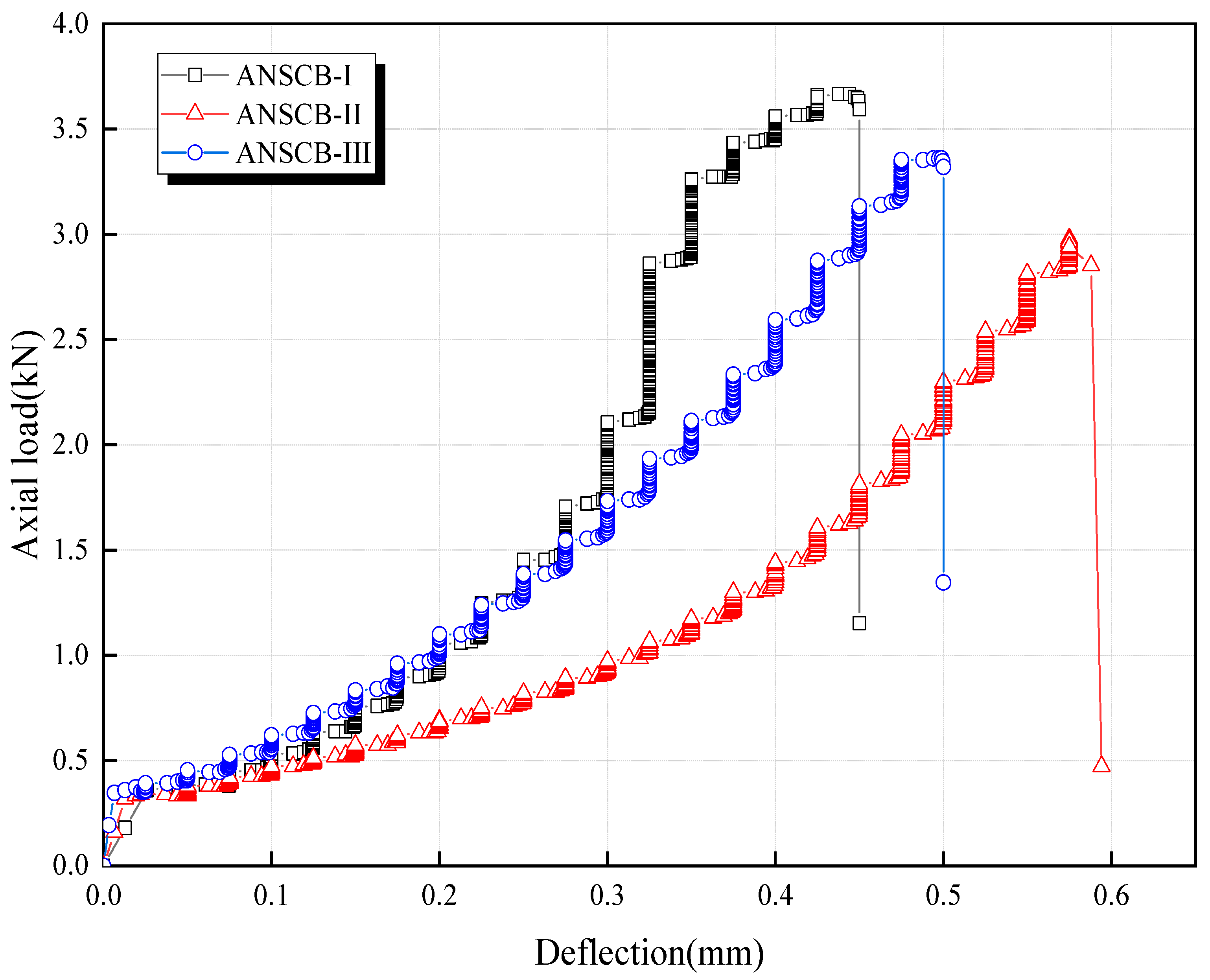
3. Results and Discussion
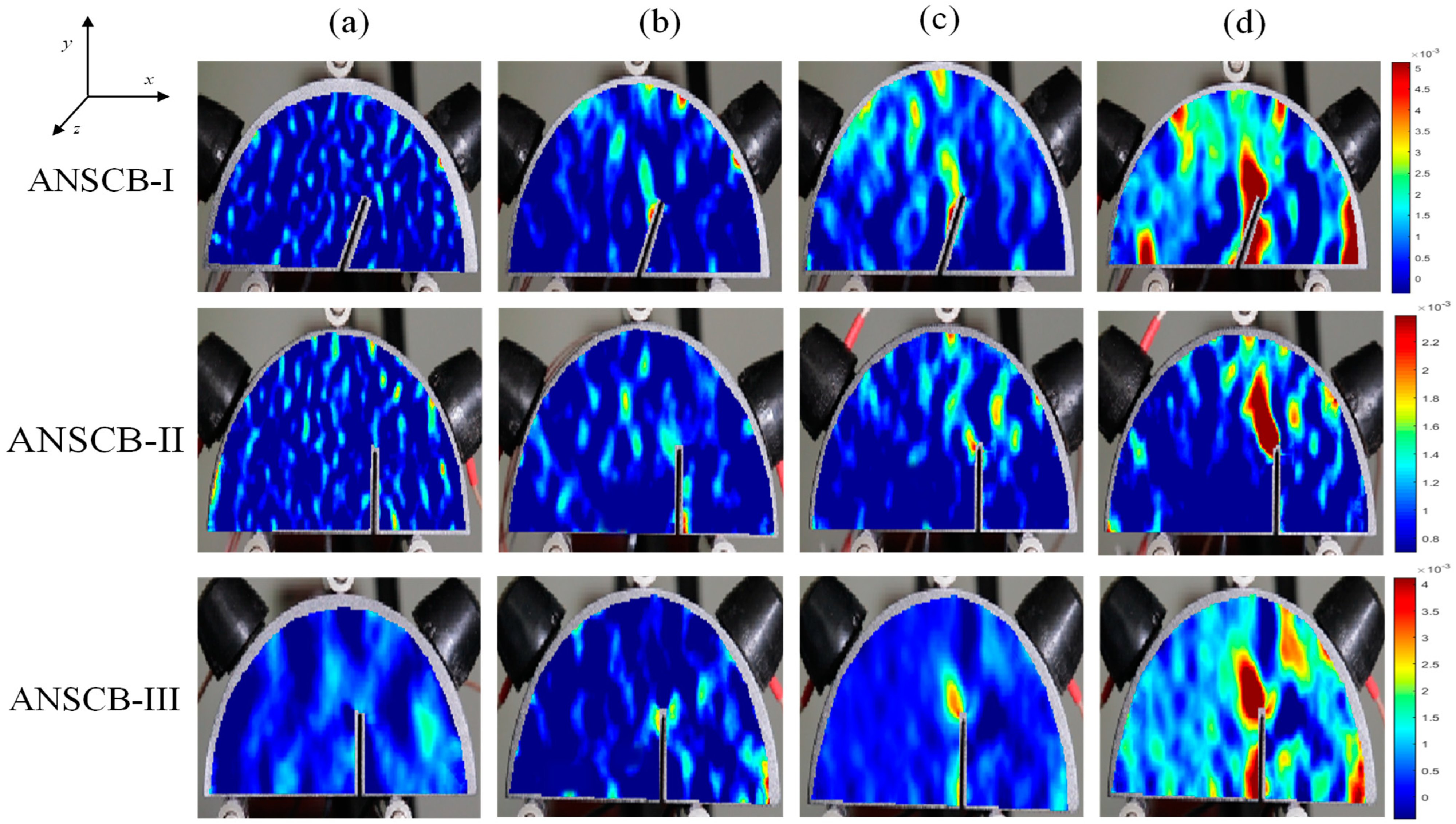
3.1. AE Response to Fracture Behavior
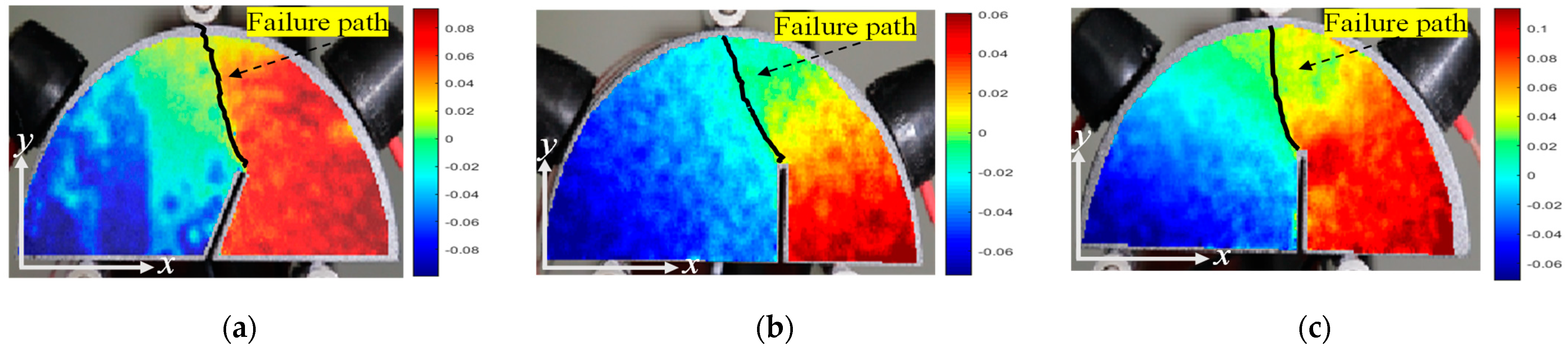
3.2. Multiscale Analysis of Fracturing Process
3.3. Microcrack Classification and Propagation
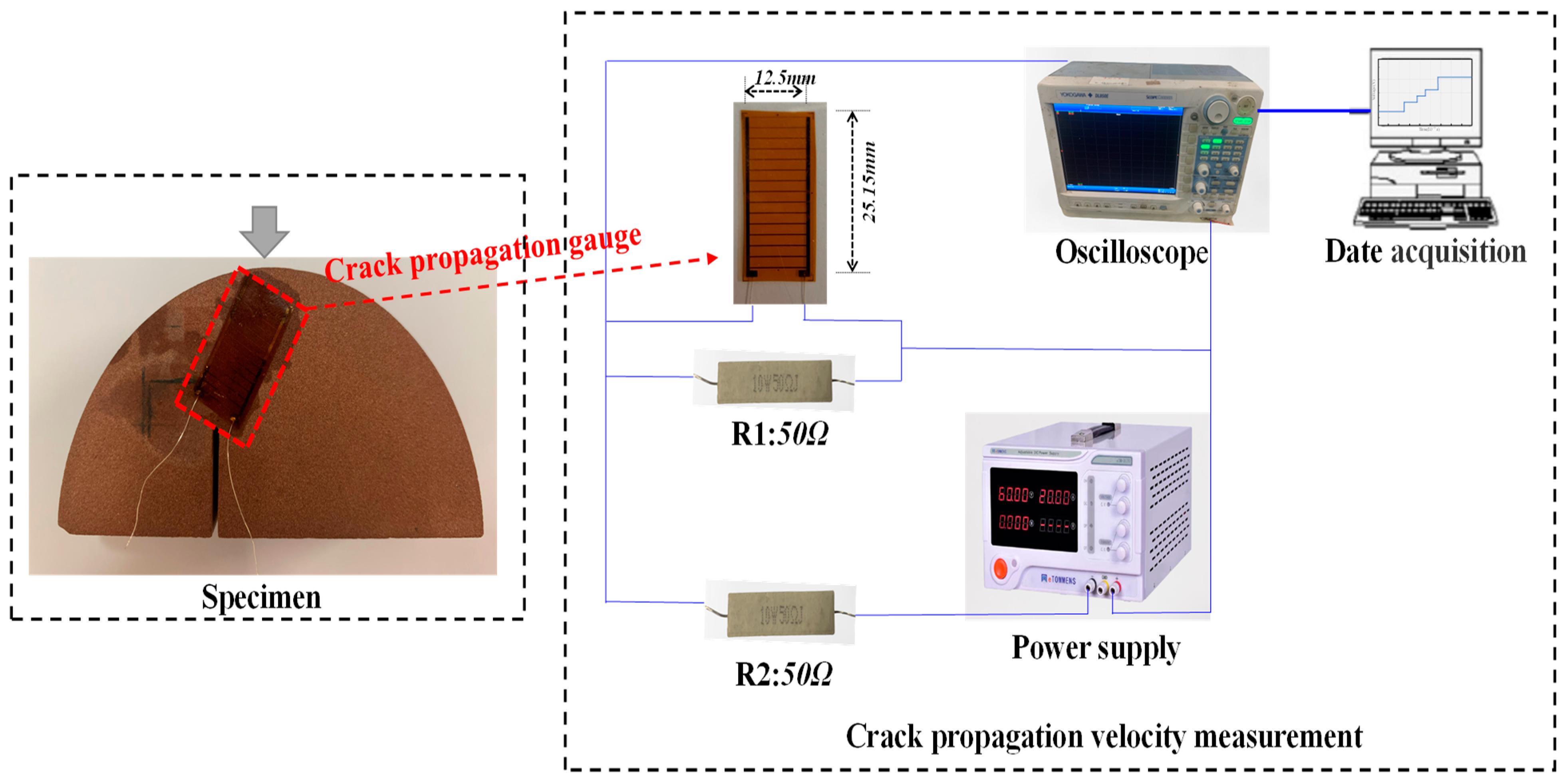
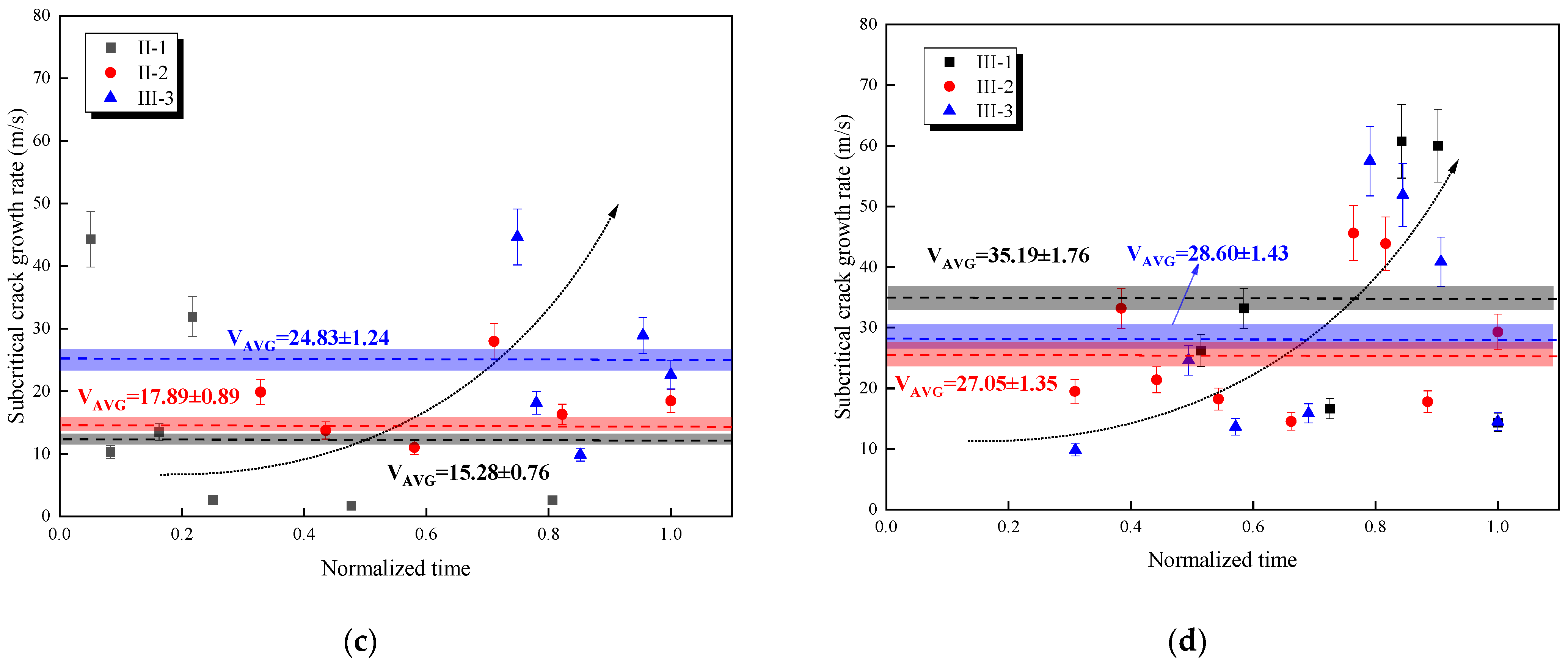
3.4. Subcritical Crack Growth Rate
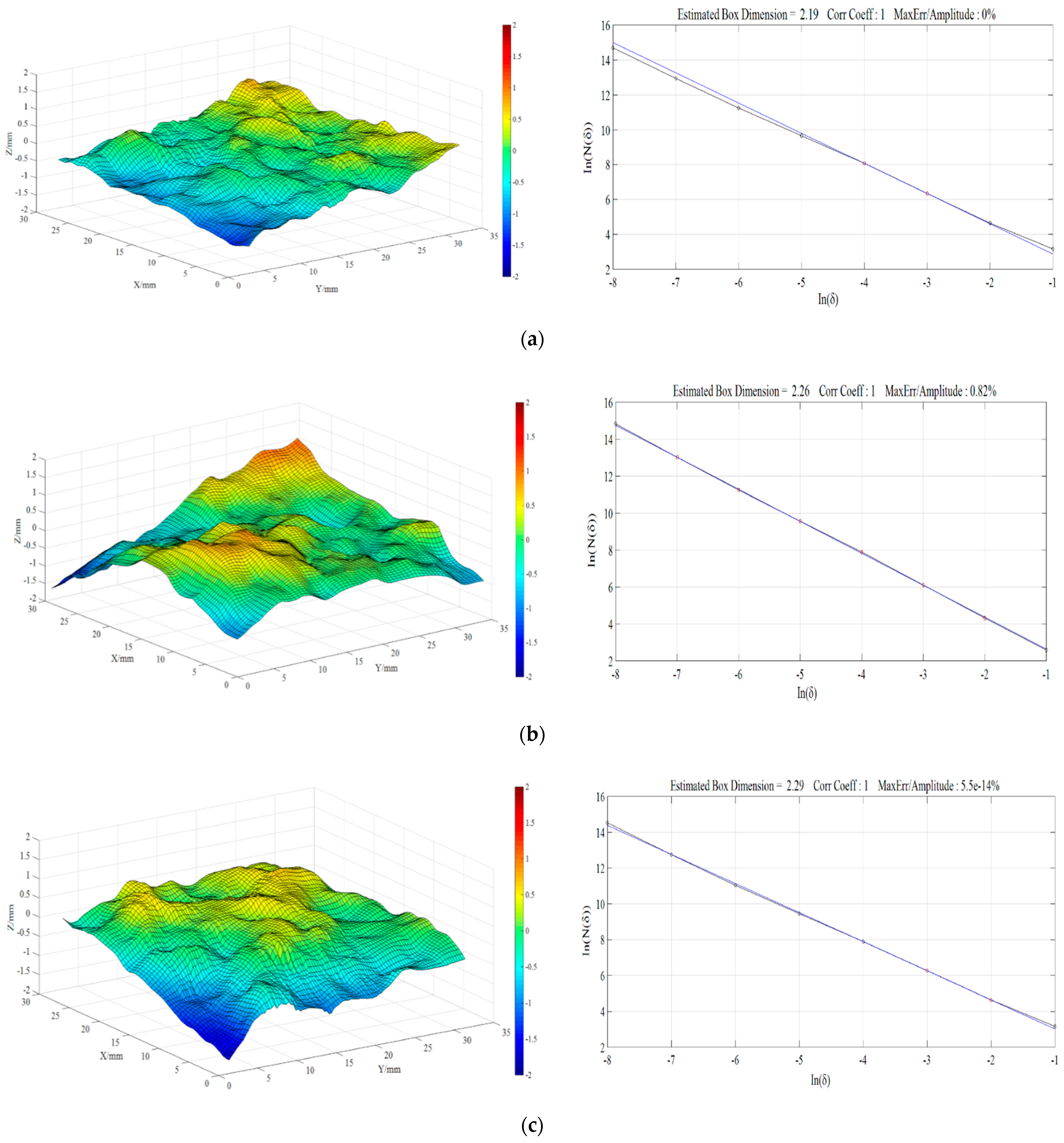
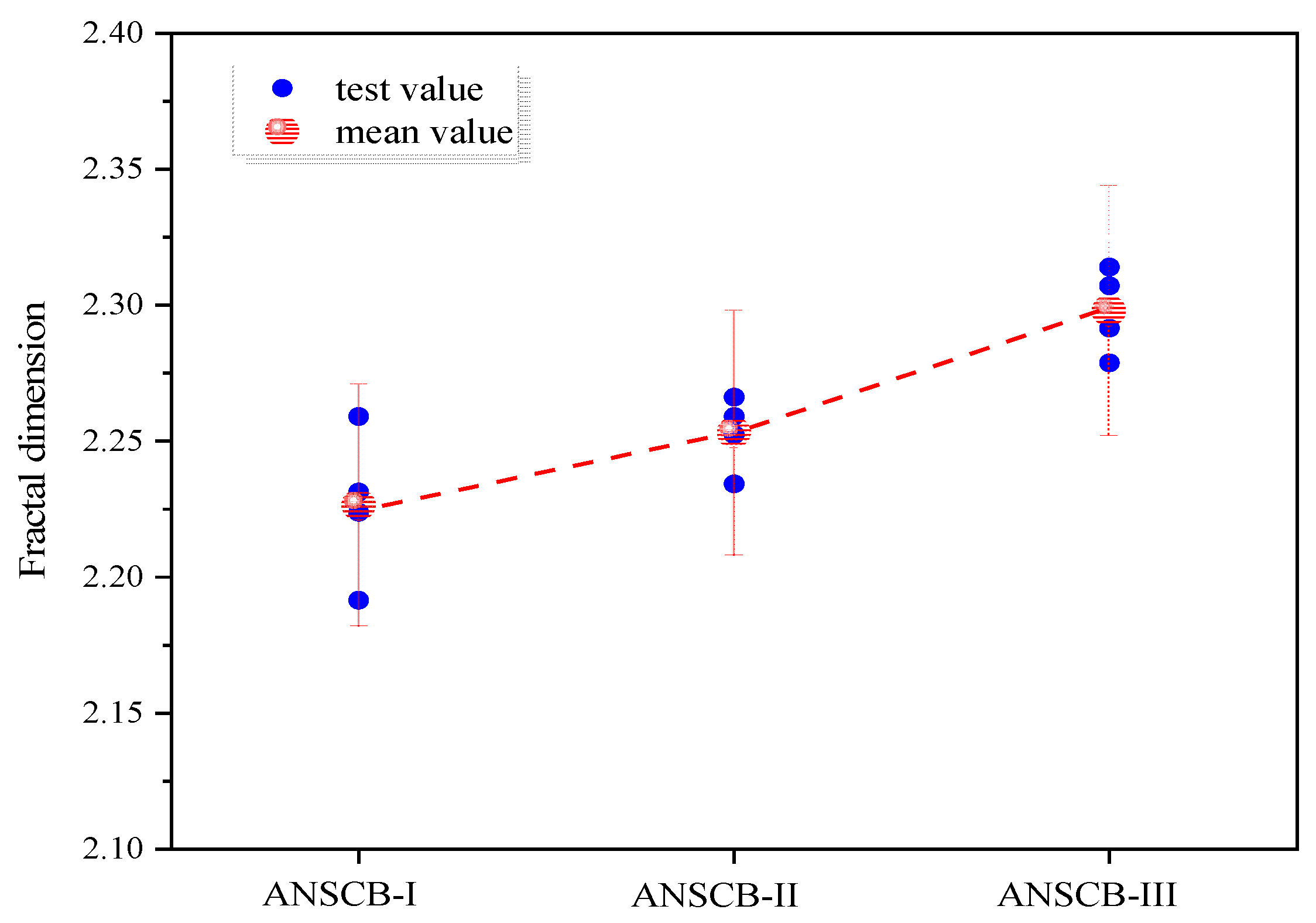
3.5. Fractal Dimension of the Fracture Surface
4. Conclusions
- (1)
- The fracture process of mixed I-II ANSCB specimens mainly includes three stages: a compaction and initiation stage, steady-state stage, and an unsteady-state crack propagation stage. An obviously brittle failure was observed, and if applied loading approaches the peak value, the main crack is rapidly transfixed, and the bearing capacity decreases sharply.
- (2)
- Based on the digital image correlation method, it can be determined that the whole fracture process consists of a nonlinear elastic stage, fracture process zone, crack initiation stage, and crack propagation stage. The crack initiation is mainly caused by the tension-shear strain concentration at the pre-existing crack tip. In addition, insight from a microscale, the crack propagation path is always along the grain boundary where the resultant stress is weakest.
- (3)
- According to the monitoring of the acoustic emission, it can be found that micro-tensile cracks are mainly responsible for the asymmetric three-point bending fracture, and the number of tensile cracks is more than that of shear cracks.
- (4)
- The subcritical crack growth rate is positively correlated to the ultimate load. The subcritical crack growth rate is gradually accelerated at the subcritical crack growth stage, and it is related to the subcritical crack growth resistance.
- (5)
- Asymmetric loading can affect the propagation path of the crack and the morphology of the final fracture surface, and a higher fractal dimension value indicates a coarser fracture surface.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhao, Y.L.; Liu, Q.; Zhang, C.S.; Liao, J.; Lin, H.; Wang, Y.X. Coupled seepage-damage effect in fractured rock masses: Model development and a case study. Int. J. Rock Mech. Min. Sci. 2021, 144, 104822. [Google Scholar] [CrossRef]
- Wu, J.Y.; Jing, H.W.; Gao, Y.; Meng, Q.B.; Yin, Q.; Du, Y. Effects of carbon nanotube dosage and aggregate size distribution on mechanical property and microstructure of cemented rockfill. Cem. Concr. Compos. 2022, 127, 104408. [Google Scholar] [CrossRef]
- Lin, Q.B.; Cao, P.; Wen, G.P.; Meng, J.J.; Cao, R.H.; Zhao, Z.Y. Crack coalescence in rock-like specimens with two dissimilar layers and pre-existing double parallel joints under uniaxial compression. Int. J. Rock Mech. Min. Sci. 2021, 139, 104621. [Google Scholar] [CrossRef]
- Erarslan, N. Analysing mixed mode (I-II) fracturing of concrete discs including chevron and straight-through notch cracks. Int. J. Solids Struct. 2019, 167, 79–92. [Google Scholar] [CrossRef]
- Wang, J.; Li, J.T.; Shi, Z.M. Deformation damage and acoustic emission characteristics of red sandstone under fatigue–creep interaction. Theor. Appl. Fract. Mech. 2022, 117, 103192. [Google Scholar] [CrossRef]
- Zhou, X.P.; Fu, Y.H.; Wang, Y.; Zhou, J.N. Experimental study on the fracture and fatigue behaviors of flawed sandstone under coupled freeze–thaw and cyclic loads. Theor. Appl. Fract. Mech. 2022, 119, 103299. [Google Scholar] [CrossRef]
- Zhang, L.Y.; Mao, X.B.; Li, M.; Li, B.; Liu, R.X.; Lu, A.H. Brittle–Ductile Transition of Mudstone in Coal Measure Rock Strata under High Temperature. Int. J. Geomech. 2020, 20, 04019149. [Google Scholar] [CrossRef]
- Qiu, P.T.; Zhang, L.Y.; Li, Y.; Li, B.; Zhu, J.; Ma, C.; Bi, X.X.; Yu, Y. Permeability evolution model of coarse porous concrete under sulphuric acid corrosion. Constr. Build. Mater. 2022, 326, 126475. [Google Scholar] [CrossRef]
- Wong, L.N.Y.; Guo, T.Y. Microcracking behavior of two semi-circular bend specimens in mode I fracture toughness test of granite. Eng. Fract. Mech. 2019, 221, 106565. [Google Scholar] [CrossRef]
- Rao, Q.H.; Sun, Z.Q.; Stephansson, O.; Li, C.L.; Stillborg, B. Shear fracture (Mode II) of brittle rock. Int. J. Rock Mech. Min. Sci. 2003, 40, 355–375. [Google Scholar] [CrossRef]
- Sun, D.L.; Rao, Q.H.; Wang, S.Y.; Shen, Q.Q.; Yi, W. Shear fracture (Mode II) toughness measurement of anisotropic rock. Theor. Appl. Fract. Mech. 2021, 115, 103043. [Google Scholar] [CrossRef]
- Cao, R.H.; Wang, C.S.; Yao, R.B.; Hu, T.; Lei, D.X.; Lin, H. Effects of cyclic freeze-thaw treatments on the fracture characteristics of sandstone under different fracture modes: Laboratory testing. Theor. Appl. Fract. Mech. 2020, 109, 102738. [Google Scholar] [CrossRef]
- Cao, R.H.; Wang, C.S.; Hu, T.; Yao, R.B.; Li, T.B.; Lin, Q.B. Experimental investigation of plane shear fracture characteristics of sandstone after cyclic freeze–thaw treatments. Theor. Appl. Fract. Mech. 2022, 118, 103214. [Google Scholar] [CrossRef]
- Yin, T.B.; Wu, Y.; Li, Q.; Wang, C.; Wu, B.Q. Determination of double-K fracture toughness parameters of thermally treated granite using notched semi-circular bending specimen. Eng. Fract. Mech. 2020, 226, 106865. [Google Scholar] [CrossRef]
- Yin, T.B.; Wu, Y.; Wang, C.; Zhuang, D.D.; Wu, B.Q. Mixed-mode I plus II tensile fracture analysis of thermally treated granite using straight-through notch Brazilian disc specimens. Eng. Fract. Mech. 2020, 234, 107111. [Google Scholar] [CrossRef]
- Qin, X.F.; Su, H.J.; Feng, Y.J.; Zhao, H.H.; Pham, T.N. Fracture and deformation behaviors of saturated and dried single-edge notched beam sandstones under three-point bending based on DIC. Theor. Appl. Fract. Mech. 2022, 117, 103204. [Google Scholar] [CrossRef]
- Zhou, X.P.; Wang, L.F.; Shou, Y.D. Understanding the fracture mechanism of ring Brazilian disc specimens by the phase field method. Int. J. Fract. 2020, 226, 17–43. [Google Scholar] [CrossRef]
- Wang, W.; Zhao, Y.X.; Teng, T.; Zhang, C.; Jiao, Z.H. Influence of Bedding Planes on Mode I and Mixed-Mode (I-II) Dynamic Fracture Toughness of Coal: Analysis of Experiments. Rock Mech. Rock Eng. 2021, 54, 173–189. [Google Scholar] [CrossRef]
- Guo, T.Y.; Wong, L.N.Y. Cracking mechanisms of a medium-grained granite under mixed-mode I-II loading illuminated by acoustic emission. Int. J. Rock Mech. Min. Sci. 2021, 145, 104852. [Google Scholar] [CrossRef]
- Zhou, X.P.; Zhang, J.Z.; Qian, Q.H.; Niu, Y. Experimental investigation of progressive cracking processes in granite under uniaxial loading using digital imaging and AE techniques. J. Struct. Geol. 2019, 126, 129–145. [Google Scholar] [CrossRef]
- Zhou, X.P.; Lian, Y.J.; Wong, L.N.Y.; Berto, F. Understanding the fracture behavior of brittle and ductile multi-flawed rocks by uniaxial loading by digital image correlation. Eng. Fract. Mech. 2018, 199, 438–460. [Google Scholar] [CrossRef]
- Chen, J.C.; Li, J.T.; Ma, G. Experimental investigation on Mode I crack growth and damage mechanism of sandstone subjected to cyclic loading. Eng. Fract. Mech. 2022, 267, 108429. [Google Scholar] [CrossRef]
- Ma, G.; Xie, Y.J.; Long, G.C.; Tang, Z.; Zhou, X.; Zeng, X.H.; Li, J.T. Mesoscale investigation on concrete creep behaviors based on discrete element method. Constr. Build. Mater. 2022, 342, 127957. [Google Scholar] [CrossRef]
- Zhou, X.P.; Zhang, J.Z. Damage progression and acoustic emission in brittle failure of granite and sandstone. Int. J. Rock Mech. Min. Sci. 2021, 143, 104789. [Google Scholar] [CrossRef]
- Cui, Z.; Sheng, Q.; Zhang, G.M.; Zhang, M.C. An Experimental Investigation of the Influence of Loading Rate on Rock Tensile Strength and Split Fracture Surface Morphology. Rock Mech. Rock Eng. 2021, 54, 1969–1983. [Google Scholar] [CrossRef]
- Zhuang, D.D.; Yin, T.B.; Li, Q.; Wu, Y.; Chen, Y.J.; Yang, Z. Fractal fracture toughness measurements of heat-treated granite using hydraulic fracturing under different injection flow rates. Theor. Appl. Fract. Mech. 2022, 119, 103340. [Google Scholar] [CrossRef]
- Ayatollahi, M.R.; Aliha, M.R.M.; Saghafi, H. An improved semi-circular bend specimen for investigating mixed mode brittle fracture. Eng. Fract. Mech. 2011, 78, 110–123. [Google Scholar] [CrossRef]
- Liu, R.F.; Zhu, Z.M.; Li, Y.X.; Liu, B.; Wan, D.Y.; Li, M. Study of rock dynamic fracture toughness and crack propagation parameters of four brittle materials under blasting. Eng. Fract. Mech. 2020, 225, 106460. [Google Scholar] [CrossRef]
- Ju, M.H.; Li, J.C.; Yao, Q.L.; Li, X.F.; Zhao, J. Rate effect on crack propagation measurement results with crack propagation gauge, digital image correlation, and visual methods. Eng. Fract. Mech. 2019, 219, 106537. [Google Scholar] [CrossRef]
- Zhou, H.W.; Xie, H.P. Direct Estimation of the Fractal Dimensions of a Fracture Surface of Rock. Surf. Rev. Lett. 2003, 10, 751–762. [Google Scholar] [CrossRef]
- Ai, T.; Zhang, R.; Zhou, H.W.; Pei, J.L. Box-counting methods to directly estimate the fractal dimension of a rock surface. Appl. Surf. Sci. 2014, 314, 610–621. [Google Scholar] [CrossRef]
- Wang, X.R.; Wang, E.Y.; Liu, X.F.; Zhou, X. Failure mechanism of fractured rock and associated acoustic behaviors under different loading rates. Eng. Fract. Mech. 2021, 247, 107674. [Google Scholar] [CrossRef]
- Ghamgosar, M.; Bahaaddini, M.; Erarslan, N.; Williams, D.J. A new experimental approach to quantify microfractures in the Fracture Process Zone (FPZ) under various loading conditions. Eng. Geol. 2021, 283, 106024. [Google Scholar] [CrossRef]
- Zuo, J.P.; Wang, X.S.; Mao, D.Q. SEM in-situ study on the effect of offset-notch on basalt cracking behavior under three-point bending load. Eng. Fract. Mech. 2014, 131, 504–513. [Google Scholar] [CrossRef]
- Erarslan, N.; Alehossein, H.; Williams, D.J. Tensile Fracture Strength of Brisbane Tuff by Static and Cyclic Loading Tests. Rock Mech. Rock Eng. 2014, 47, 1135–1151. [Google Scholar] [CrossRef]
- Niu, Y.; Zhou, X.P.; Berto, F. Evaluation of fracture mode classification in flawed red sandstone under uniaxial compression. Theor. Appl. Fract. Mech. 2020, 107, 102528. [Google Scholar] [CrossRef]
- Ohno, K.; Uji, K.; Ueno, A.; Ohtsu, M. Fracture process zone in notched concrete beam under three-point bending by acoustic emission. Constr. Build. Mater. 2014, 67, 139–145. [Google Scholar] [CrossRef]
- De Smedt, M.; Vrijdaghs, R.; Van Steen, C.; Verstrynge, E.; Vandewalle, L. Damage analysis in steel fibre reinforced concrete under monotonic and cyclic bending by means of acoustic emission monitoring. Cem. Concr. Compos. 2020, 114, 103765. [Google Scholar] [CrossRef]
- Du, K.; Li, X.F.; Tao, M.; Wang, S.F. Experimental study on acoustic emission (AE) characteristics and crack classification during rock fracture in several basic lab tests. Int. J. Rock Mech. Min. Sci. 2020, 133, 104411. [Google Scholar] [CrossRef]
- Li, D.Y.; Ma, J.J.; Wan, Q.R.; Zhu, Q.Q.; Han, Z.Y. Effect of thermal treatment on the fracture toughness and subcritical crack growth of granite in double-torsion test. Eng. Fract. Mech. 2021, 253, 425. [Google Scholar] [CrossRef]
- Xie, Q.; Li, S.X.; Liu, X.L.; Gong, F.; Li, X.B. Effect of loading rate on fracture behaviors of shale under mode I loading. J. Cent. South Univ. 2020, 27, 3118–3132. [Google Scholar] [CrossRef]
- Ma, G.; Li, J.T.; Wang, H.W. Related Rule Study of Subcritical Crack Growth and Threshold Values in Transversely Isotropic Slates. Geofluids 2020, 2020, 8843381. [Google Scholar] [CrossRef]
- Fineberg, J.; Gross, S.P.; Marder, M.; Swinney, H.L. Instability in the propagation of fast cracks. Phys. Rev. B Condens. Matter 1992, 45, 5146–5154. [Google Scholar] [CrossRef] [PubMed]
- Ying, P.; Zhu, Z.M.; Wang, F.; Wang, M.; Niu, C.Y.; Zhou, L. The characteristics of dynamic fracture toughness and energy release rate of rock under impact. Measurement 2019, 147, 106884. [Google Scholar] [CrossRef]
- Meng, T.; Yue, Y.; Ma, J.W.; Jiao, B.; Niu, H.J.; Wen, L.; Xue, Y.B. Use of DC voltage fluctuation method to investigate real-time Mode I and Mode II subcritical crack growth behavior in gypsum rock. Eng. Fract. Mech. 2020, 234, 107104. [Google Scholar] [CrossRef]
- Zhou, Z.L.; Cai, X.; Ma, D.; Cao, W.; Chen, L.; Zhou, J. Effects of water content on fracture and mechanical behavior of sandstone with a low clay mineral content. Eng. Fract. Mech. 2018, 193, 47–65. [Google Scholar] [CrossRef]
- Xie, H.P.; Sun, H.Q.; Ju, Y.; Feng, Z.G. Study on generation of rock fracture surfaces by using fractal interpolation. Int. J. Solids Struct. 2001, 38, 57–65. [Google Scholar] [CrossRef]





| Density | Porosity | Elasticity Modulus | Poisson Ratio | UCS | TS |
|---|---|---|---|---|---|
| 2.436 g·cm−3 | 2.488% | 43.702 GPa | 0.233 | 70.841 MPa | 5.921 MPa |
| Specimen Model | R/mm | B/mm | a/mm | S1/mm | S2/mm | Differences |
|---|---|---|---|---|---|---|
| ANSCB-I | 50 | 35 | 20 | 30 | 30 | |
| ANSCB-II | 50 | 35 | 20 | 30 | 30 | L = 13.6 mm |
| ANSCB-III | 50 | 35 | 20 | 40 | 20 | L = 7 mm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, G.; Li, J.; Zhou, X.; Zhang, L.; Qiu, P.; Yu, Y. Application of Asymmetric Notched Semi-Circular Bending Specimen to Evaluate Mixed-Mode I-II Fracture Behaviors of Sandstone. Fractal Fract. 2022, 6, 336. https://doi.org/10.3390/fractalfract6060336
Ma G, Li J, Zhou X, Zhang L, Qiu P, Yu Y. Application of Asymmetric Notched Semi-Circular Bending Specimen to Evaluate Mixed-Mode I-II Fracture Behaviors of Sandstone. Fractal and Fractional. 2022; 6(6):336. https://doi.org/10.3390/fractalfract6060336
Chicago/Turabian StyleMa, Gang, Jiangteng Li, Xiang Zhou, Lianying Zhang, Peitao Qiu, and Yang Yu. 2022. "Application of Asymmetric Notched Semi-Circular Bending Specimen to Evaluate Mixed-Mode I-II Fracture Behaviors of Sandstone" Fractal and Fractional 6, no. 6: 336. https://doi.org/10.3390/fractalfract6060336






