Coupled Seepage Mechanics Model of Coal Containing Methane Based on Pore Structure Fractal Features
Abstract
:1. Introduction
| Authors | Models | Notes | Limitations |
|---|---|---|---|
| Seidle [18] | kf is cleat permeability, 10−3 μm2 pp is pore pressure, 0.6895 × 10−2 MPa. | The relationship equation between coal seam permeability, stress, and burial depth. | Does not explain the local permeability changes in coal seam caused by stress. |
| Li et al. [19] | . ka is absolute permeability, 10−3 μm2; , 1/ks = Cm, Cm is the coal matrix shrinkage factor, MPa−1; εs is the volumetric strain from coal rock adsorption/desorption; εTp is the volumetric strain from thermal cracking of the coal rock; εe is the volumetric strain caused by thermal expansion. | Correction of the strain caused by the permeability of coal and rock under the action of temperature. | No consideration of the effect of pore deformation on permeability. |
| Palmer and Mansoori [16] | φ is coalbed porosity, fraction. | Under stable low pressure, permeability can rebound when matrix shrinkage is strong enough. | No consideration of pressure changes. |
| Shi and Durucan [17] | The S&D model is perfected based on the P&M model. The rebound pressure predicted by this model is greater than that of the P&M model. | The same as the P&M model, the pressure changes are not considered. |
2. Experiments and Theory
2.1. Samples
2.2. Triaxial Stress–Strain-Permeability Test
2.3. Pore Structure Test
2.4. Pore Fractal Theory
3. Results and Discussion
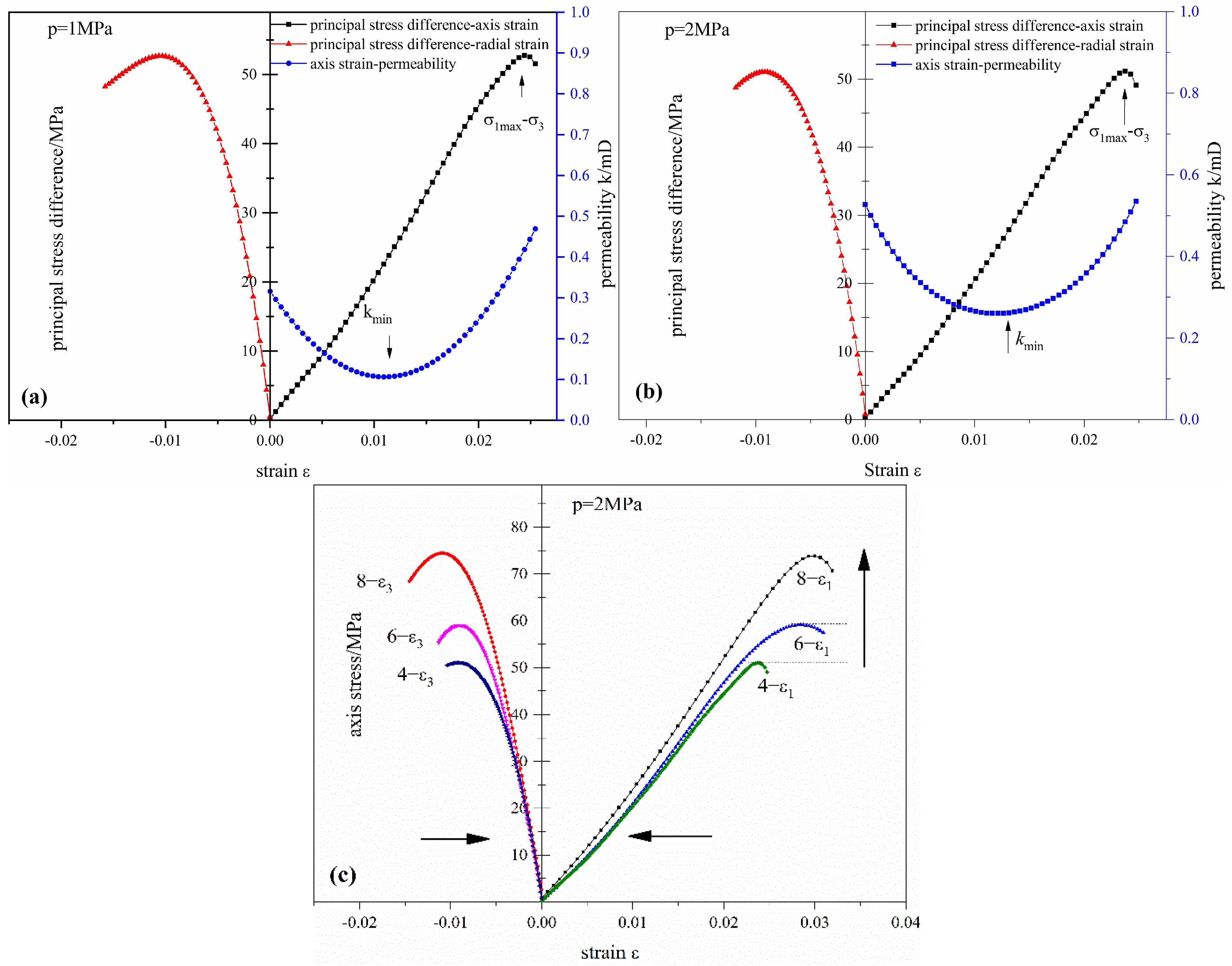
3.1. Coal Deformation Seepage Characteristics
3.2. Pore Structure Characteristics and Fractal Dimension
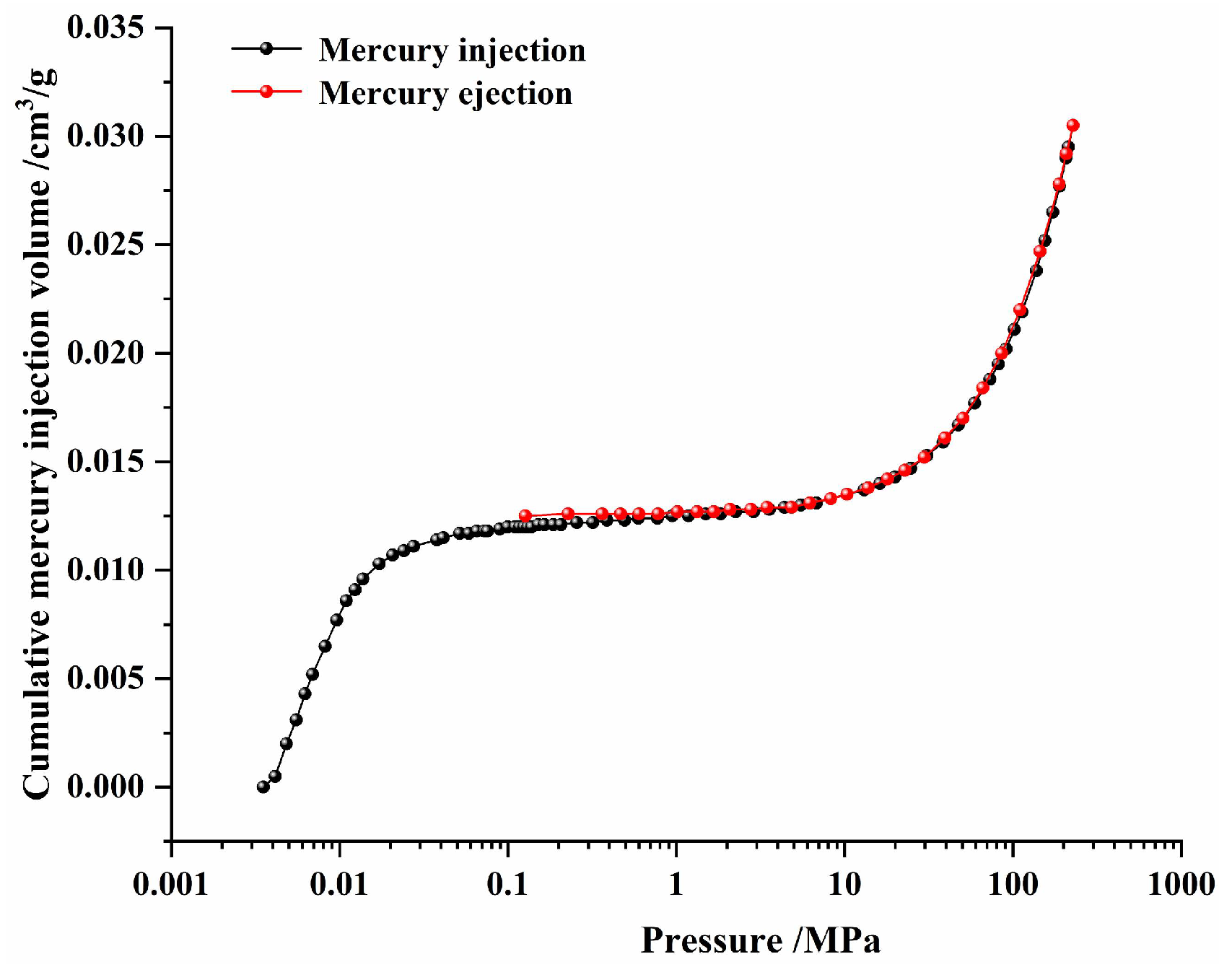
3.2.1. Pore Structure Characteristics—Mercury Intrusion Method
3.2.2. Pore Structure Fractal Characteristics—N2 Adsorption
3.2.3. Comprehensive Fractal Dimension
3.3. Model Establishment and Derivation
- (1)
- The adsorption and desorption are completed instantaneously, the occurrence state conforms to the Gibbs interface model, the adsorption process conforms to the Langmuir equation, the temperature is constant, and the moisture of the coal body is the same;
- (2)
- The gas-bearing coal body is assumed to be an isotropic homogeneous medium with the same isotropic adsorption and surface tension;
- (3)
- Under the ideal confinement state, the expansion stress generated during the gas absorption of the coal rock is completely transformed into elastic expansion energy;
- (4)
- The surface of the coal body is smooth and completely in contact with the constraint boundary.
3.4. Model Applicability
4. Conclusions
- (1)
- The model considers the effect of coal body adsorption deformation on effective stress (skeleton shrinkage caused by pore pressure and adsorption expansion caused by adsorbed gas). The analysis reveals that the effective stress coefficient varies with pore pressure, that is, with the increase in pore pressure, the effective stress coefficient of the coal skeleton increases. The entire stress–strain-percolation curve of gas-bearing coal bodies can be divided into three stages: pore compression unstable flow, linear elastic stable flow, and plastic deformation seepage acceleration. The permeability of coal samples is intrinsically related to deformation; changes in external stress and pore pressure are the dominant factors causing changes in coal permeability, and changes in coal permeability reflect the appearance of the solid and are an external manifestation of deformation.
- (2)
- The general expression of the fractal stress–strain-permeability model based on coal heterogeneity is theoretically deduced based on the integrated consideration of gas adsorption deformation and matrix shrinkage deformation. When the fractal dimension of coal pores is Df = 2, the model can be transformed into the Langmuir model, . The Langmuir model can be regarded as a special case of the fractal stress–strain-permeability model, so the established fractal model has more general theoretical significance.
- (3)
- The fractal Langmuir model is validated, and the goodness-of-fit was greater than 0.95. Nevertheless, the error between the theoretical solution of the model and the measured value is small, which is in good agreement with the experimental data. It shows that the prediction model is more accurate than the traditional Euclidean geometric method in calculating permeability and can accurately reflect the coupled response of coal mechanical deformation and permeability under different gas pressure, which can better characterize the variation law of gas-bearing coal permeability during the gas extraction process.
Author Contributions
Funding
Conflicts of Interest
References
- Sun, W.; Feng, Y.; Jiang, C.; Chu, W. Fractal characterization and methane adsorption features of coal particles taken from shallow and deep coalmine layers. Fuel 2015, 155, 7–13. [Google Scholar] [CrossRef]
- Liu, X.; He, X. Effect of pore characteristics on coalbed methane adsorption in middle-high rank coals. Adsorpt. J. Int. Adsorpt. Soc. 2017, 23, 3–12. [Google Scholar] [CrossRef]
- Wang, K.; Zhao, W. Research Progress on the Control Mechanism of Coal Pore Space Geometric Characteristics on the Shape of Gas Desorption Curves. Bull. Natl. Nat. Sci. Found. China 2021, 35, 917–923. [Google Scholar]
- Liu, Y.; Zhu, Y.; Li, W.; Zhang, C.; Wang, Y. Ultra micropores in macromolecular structure of subbituminous coal vitrinite. Fuel 2017, 210, 298–306. [Google Scholar] [CrossRef]
- Wei, Q.; Li, X.; Zhang, J.; Hu, B.; Zhu, W.; Liang, W.; Sun, K. Full-size pore structure characterization of deep-buried coals and its impact on methane adsorption capacity: A case study of the Shihezi Formation coals from the Panji Deep Area in Huainan Coalfield, Southern North China. J. Pet. Sci. Eng. 2019, 173, 975–989. [Google Scholar] [CrossRef]
- Wang, D.; Zhang, H.; Wei, J.; Wu, Y.; Zhang, H.; Yao, B.; Fu, J.; Zhao, L. Dynamic evolution characteristics of fractures in gas-bearing coal under the influence of gas pressure using industrial CT scanning technology. J. China Coal Soc. 2021, 46, 3550–3564. [Google Scholar]
- Cai, Y.; Liu, D.; Yao, Y.; Li, J.; Liu, J. Fractal Characteristics of Coal Pores Based on Classic Geometry and Thermodynamics Models. Acta Geol. Sin. 2011, 85, 1150–1162. [Google Scholar] [CrossRef]
- Ha, A.; Ak, A.; Fura, A.; Az, B.; Si, A.; Ml, C. Coal cleat network evolution through liquid nitrogen freeze-thaw cycling. Fuel 2022, 314, 123069. [Google Scholar]
- Wang, G.; Ju, Y.; Yan, Z.; Li, Q. Pore structure characteristics of coal-bearing shale using fluid invasion methods: A case study in the Huainan-Huaibei Coalfield in China. Mar. Pet. Geol. 2015, 62, 1–13. [Google Scholar] [CrossRef]
- Giesche, H. Mercury Porosimetry: A General (Practical) Overview. Part. Part. Syst. Charact. 2006, 23, 9–19. [Google Scholar] [CrossRef]
- Fu, X.; Zhou, R.; Zhang, W.; Qin, Y.; Wei, C. Study on fractal and natural classification of coal pore based on coalbed methane migration. Chin. Sci. Bull. 2005, z1, 51–55. [Google Scholar]
- Mahnke, M.; Mögel, H.J. Fractal analysis of physical adsorption on material surfaces. Colloids Surf. A Physicochem. Eng. Asp. 2003, 216, 215–228. [Google Scholar] [CrossRef]
- Zhao, J.; Tang, D.; Qin, Y.; Xu, H. Fractal characterization of pore structure for coal macrolithotypes in the Hancheng area, southeastern Ordos Basin, China. J. Pet. Sci. Eng. 2019, 178, 666–677. [Google Scholar] [CrossRef]
- Jin, Y.; Quan, W.; Qin, J.; Liu, X.; Zheng, J.; Song, H. Quantitative characterization of complex assembly in fractalpore-throat porous media. J. China Coal Soc. 2020, 45, 1845–1854. [Google Scholar]
- Jin, Y.; Wang, Q.; Dong, J.; Liu, S.; Zheng, J.; Li, Y. Characterization of the complexity assembly of fractal bed-packing porous media. Chin. J. Rock Mech. Eng. 2022, 41, 1160–1171. [Google Scholar]
- Palmer, I.; Mansoori, J. How Permeability Depends on Stress and Pore Pressure in Coalbeds: A New Model. Spe Reserv. Eval. Eng. 1996, 1, 539–544. [Google Scholar] [CrossRef]
- Shi, J.Q.; Durucan, S. Drawdown Induced Changes in Permeability of Coalbeds: A New Interpretation of the Reservoir Response to Primary Recovery. Transp. Porous Media 2004, 56, 1–16. [Google Scholar] [CrossRef]
- Seidle, J.P.; Jeansonne, M.W.; Erickson, D.J. Application of Matchstick Geometry to Stress Dependent Permeability in Coals. In Proceedings of the SPE Rocky Mountain Regional Meeting, Casper, WY, USA, 18–21 May 1992; p. 433. [Google Scholar]
- Li, B.; Gao, Z.; Yang, K.; Li, J.; Ren, C.; Xu, J.; Cao, J. Study on coal adsorption-permeability model under the coupling of temperature and pore pressure. Chin. J. Rock Mech. Eng. 2020, 39, 668–681. [Google Scholar]
- Joubert, J.I.; Grein, C.T.; Bienstock, D. Effect of moisture on the methane capacity of american coals. Fuel 1974, 53, 186–191. [Google Scholar] [CrossRef]
- Li, A.; Ding, W.; He, J.; Dai, P.; Shuai, Y.; Fei, X. Investigation of pore structure and fractal characteristics of organic-rich shale reservoirs: A case study of Lower Cambrian Qiongzhusi formation in Malong block of eastern Yunnan Province, South China. Mar. Pet. Geol. 2016, 70, 46–57. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, G.; Cao, Y.; Lin, J.; Jin, Y.; Xian, B.; Lv, R.; Zhang, Z. Experimental Investigation of CS2 Extraction to Enhance the Permeability of Coal. Transp. Porous Media 2021, 136, 899–922. [Google Scholar] [CrossRef]
- Yao, Y.; Liu, D.; Tang, D.; Tang, S.; Huang, W.; Liu, Z.; Yao, C. Fractal characterization of seepage-pores of coals from China: An investigation on permeability of coals. Comput. Geosci. 2009, 35, 1159–1166. [Google Scholar] [CrossRef]
- Fu, H.; Tang, D.; Xu, T.; Xu, H.; Shu, T.; Li, S.; Yin, Z.Y.; Chen, B.; Zhang, C.; Wang, L. Characteristics of pore structure and fractal dimension of low-rank coal: A case study of Lower Jurassic Xishanyao coal in the southern Junggar Basin, NW China. Fuel 2017, 193, 254–264. [Google Scholar] [CrossRef]
- Chen, X.; Zhao, S.; Si, Z.; Qi, L.; Kang, N. Fractal characteristics of pore structure of coal with different metamorphicdegrees and its effect on gas adsorption characteristics. Coal Sci. Technol. 2020, 48, 118–124. [Google Scholar]
- Chen, Y.; Zou, C.; Maria, M.; Zhu, R.; Bai, B.; Yang, Z. Porosity and fractal characteristics of shale across a maturation gradient. Nat. Gas Geosci. 2015, 26, 1646–1656. [Google Scholar]
- Hu, J.; Tang, S.; Zhang, S. Investigation of pore structure and fractal characteristics of the Lower Silurian Longmaxi shales in western Hunan and Hubei Provinces in China. J. Nat. Gas Sci. Eng. 2016, 28, 522–535. [Google Scholar] [CrossRef]
- Zhang, S.; Tang, S.; Tang, D.; Huang, W.; Pan, Z. Determining fractal dimensions of coal pores by FHH model: Problems and effects. J. Nat. Gas Sci. Eng. 2014, 21, 929–939. [Google Scholar] [CrossRef]
- Liu, G. Mechanism and Model of Coal Adsorption Gas in High Temperature and Pressure and Three-Phase Medium. Ph.D. Thesis, Henan Polytechnic University, Jiaozuo, China, 2011. [Google Scholar]
- Wang, Z.; Cheng, Y.; Qi, Y.; Wang, R.; Wang, L.; Jiang, J. Experimental study of pore structure and fractal characteristics of pulverized intact coal and tectonic coal by low temperature nitrogen adsorption. Powder Technol. 2019, 350, 15–25. [Google Scholar] [CrossRef]
- Jaroniec, M. Evaluation of the Fractal Dimension from a Single Adsorption Isotherm. Langmuir 1995, 11, 2316–2317. [Google Scholar] [CrossRef]
- Fang, Y.; Cao, Y.; Jin, M.; Yang, J.; Qian, Z. Effect of Anthracite in Coal Blend on Micro-Crystal and Pore Structure of Coke. Iron Steel 2006, 41, 16. [Google Scholar]
- Ye, Z.; Hou, E.; Duan, Z.; Wen, Q.; Huang, M.; He, D. Fractal characteristics of pores and microfractures of coals with different structure and their effect on permeability. Coal Geol. Explor. 2019, 47, 70–78. [Google Scholar]
- Wang, Z.; Cheng, Y.; Zhang, K.; Hao, C.; Wang, L.; Li, W.; Hu, B. Characteristics of microscopic pore structure and fractal dimension of bituminous coal by cyclic gas adsorption/desorption: An experimental study. Fuel 2018, 232, 495–505. [Google Scholar]
- Pan, Z.; Connell, L.D. A theoretical model for gas adsorption-induced coal swelling. Int. J. Coal Geol. 2007, 69, 243–252. [Google Scholar] [CrossRef]
- Ttinger, I.L. Swelling stress in the gas-coal system as an energy source in the development of gas bursts. Sov. Min. Sci. 1979, 15, 494–501. [Google Scholar] [CrossRef]
- Xu, J.; Peng, S.; Yin, G.; Tao, Y.; Yang, H.; Wang, W. Development and Application of Triaxial Servo-controlled Seepage Equipment for Thermo-fluid-solid Coupling of Coal Containing Methane. Chin. J. Rock Mech. Eng. 2010, 29, 907–914. [Google Scholar]
- Zhao, Y.; Zhang, L.; Wang, W.; Tang, J.; Lin, H.; Wan, W. Transient pulse test and morphological analysis of single rock fractures. Int. J. Rock Mech. Min. Sci. 2017, 91, 139–154. [Google Scholar] [CrossRef]
- Zhao, J.; Xu, H.; Tang, D.; Mathews, J.P.; Li, S.; Tao, S. Coal seam porosity and fracture heterogeneity of macrolithotypes in the Hancheng Block, eastern margin, Ordos Basin, China. Int. J. Coal Geol. 2016, 159, 18–29. [Google Scholar] [CrossRef]
- Lv, R.; Peng, S.; Liu, G.; Li, B.; Pan, J.; Lin, X. High-pressure methane adsorption-induced coal swelling on equilibrium moisture coal samples. Energy Sources Part A Recovery Util. Environ. Eff. 2016, 38, 2119–2127. [Google Scholar]
- Lv, R.; Li, B.; Song, Z.; Liu, G. Experimental Investigation on Permeability and Mechanical Deformation of Coal Containing Gas under Load. Adv. Civ. Eng. 2018, 2018, 7341523. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Liu, Q.; Zhang, C.; Liao, J.; Lin, H.; Wang, Y. Coupled seepage-damage effect in fractured rock masses: Model development and a case study. Int. J. Rock Mech. Min. Sci. 2021, 144, 104822. [Google Scholar]
- Zhao, Y.; Wang, Y.; Wang, W.; Tang, L.; Liu, Q.; Cheng, G. Modeling of rheological fracture behavior of rock cracks subjected to hydraulic pressure and far field stresses. Theor. Appl. Fract. Mech. 2019, 101, 59–66. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, C.; Wang, Y.; Lin, H. Shear-related roughness classification and strength model of natural rock joint based on fuzzy comprehensive evaluation. Int. J. Rock Mech. Min. Sci. 2021, 137, 104550. [Google Scholar] [CrossRef]
- Liu, J.; Zhao, Y.; Tan, T.; Zhang, L.; Zhu, S.; Xu, F. Evolution and modeling of mine water inflow and hazard characteristics in southern coalfields of China: A case of Meitanba mine. Int. J. Min. Sci. Technol. 2022, 32, 513–524. [Google Scholar] [CrossRef]
- Liu, Q.; Zhao, Y.; Tang, L.; Liao, J.; Wang, X.; Tan, T.; Chang, L.; Luo, S.; Wang, M. Mechanical characteristics of single cracked limestone in compression-shear fracture under hydro-mechanical coupling. Theor. Appl. Fract. Mech. 2022, 119, 103371. [Google Scholar] [CrossRef]
- Wei, M.; Liu, J.; Feng, X.; Wang, C.; Fang, K.; Zhou, F.; Zhang, S.; Xia, T. Quantitative study on coal permeability evolution with consideration of shear dilation. J. Nat. Gas Sci. Eng. 2016, 36, 1199–1207. [Google Scholar] [CrossRef]
- Zhou, J.; Xian, X.; Jiang, Y.; Li, X.; Jiang, D. Permeability model considering effective stress and shrinkage effect of coal matrix. J. Southwest Pet. Univ. Sci. Technol. Ed. 2009, 31, 4–8. [Google Scholar]




| Coal Sample Number | Place of Origin | Ro,max/% | Microcomponents/% | |||
|---|---|---|---|---|---|---|
| Vitrinite | Exinite | Inertinite | Mineral | |||
| 1 | Jiaozuo Guhanshan Mine | 3.49 | 92 | Microscale | 6 | 2 |
| Coal Sample Number | Industrial Analysis | Porosity φ/% | |||
|---|---|---|---|---|---|
| Mad/% | Ad/% | Vdaf/% | FCad/% | ||
| 1 | 1.26 | 6.31 | 7.71 | 84.72 | 4.61 |
| Type | Test No. | σc Location | σ3/MPa | p/MPa | Permeability/10−3 μm2 | Compressive Strength/MPa | Poisson’s Ratio/μ | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| ε1% | ε3% | εv% | Initial Value | Minimum | σc Location | ||||||
| Raw coal | 1 | 2.385 | −0.893 | 0.599 | 4 | 1 | 0.513 | 0.239 | 0.430 | 55.22 | 0.85 |
| 2 | 2.669 | −0.913 | 0.843 | 6 | 0.042 | 0.108 | 0.232 | 65.23 | 0.84 | ||
| 3 | 3.052 | −0.968 | 1.116 | 8 | 0.028 | 0.023 | 0.112 | 83.35 | 0.91 | ||
| 4 | 2.518 | −1.121 | 0.276 | 4 | 2 | 0.265 | 0.106 | 1.600 | 46.77 | 0.93 | |
| 5 | 2.717 | −1.130 | 0.457 | 6 | 0.161 | 0.095 | 0.457 | 57.89 | 0.82 | ||
| 6 | 2.935 | −1.213 | 0.509 | 8 | 0.096 | 0.033 | 0.046 | 69.32 | 0.87 | ||
| Sample Number | Pore Volume/(mL/g) | Pore Volume Ratio/% | |||||||
|---|---|---|---|---|---|---|---|---|---|
| V1 | V2 | V3 | V4 | Vt | V1/Vt | V2/Vt | V3/Vt | V4/Vt | |
| 1 | 0.0007 | 0.001 | 0.0084 | 0.0086 | 0.0187 | 3.74 | 5.35 | 44.92 | 45.99 |
| Sample Number | Pore Specific Surface Area/(m2/g) | Pore Specific Surface Area Ratio/% | |||||||
|---|---|---|---|---|---|---|---|---|---|
| S1 | S2 | S3 | S4 | St | S1/St | S2/St | S3/St | S4/St | |
| 1 | 0.001 | 0.017 | 1.628 | 4.631 | 6.277 | 0.02 | 0.27 | 25.94 | 73.78 |
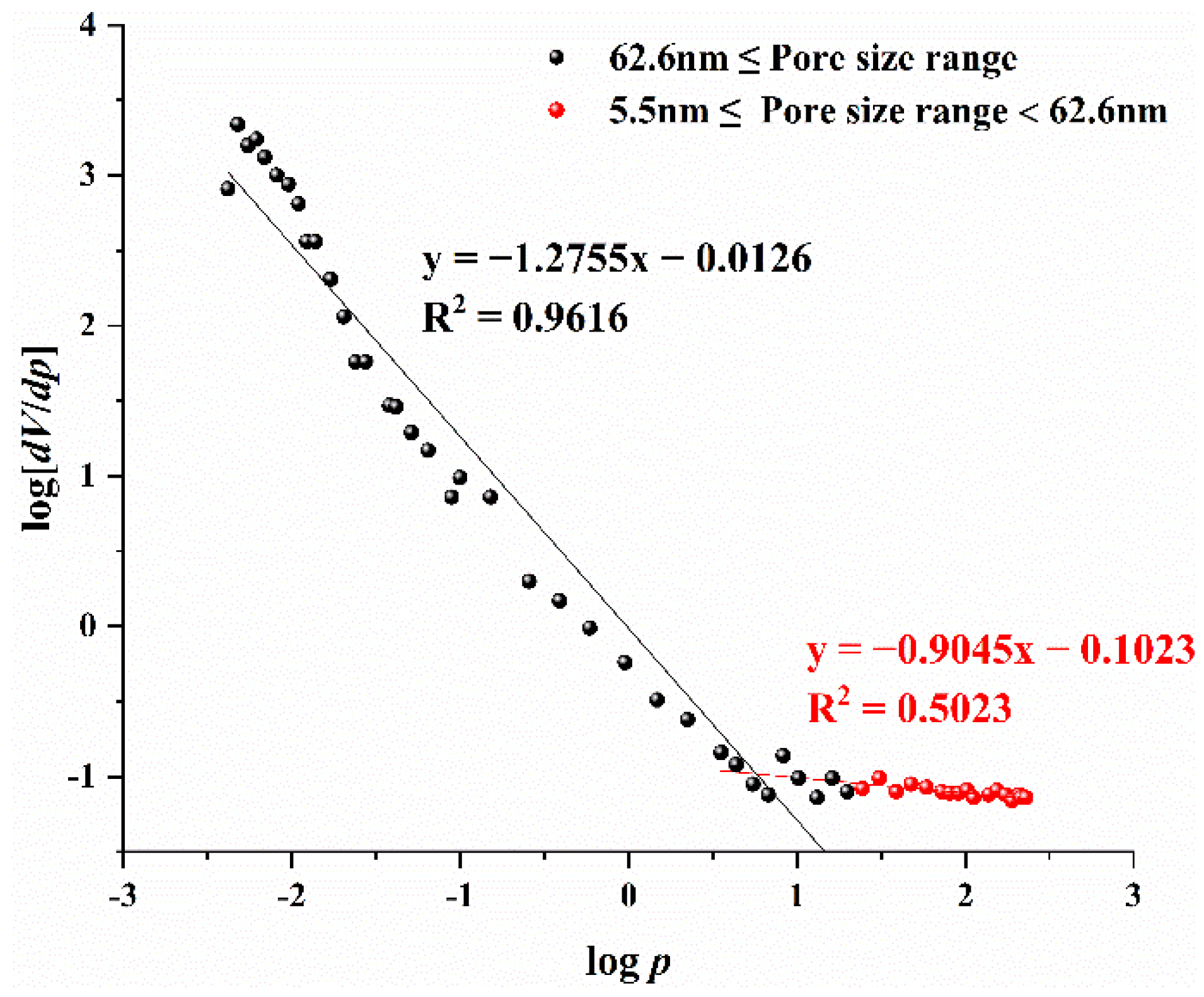
| Coal Sample Number | Pore Size Range/nm | Slope K | D1 | Correlation Coefficient r |
|---|---|---|---|---|
| 1 | 62.6 ≤ r ≤ 357057.1 | −1.2755 | 2.7245 | 0.9616 |
| Coal Type | Sample Number | Ro,max/% | Pore Volume/(mL/g) | Pore Volume Ratio/% | |||||
|---|---|---|---|---|---|---|---|---|---|
| V2 | V3 | V4 | Vt | V2/Vt | V3/Vt | V4/Vt | |||
| Anthracite | 1 | 3.49 | 0.001212 | 0.002502 | 0.003773 | 0.007487 | 16.19 | 33.42 | 50.39 |
| Coal Type | Sample Number | Ro,max/% | Pore Volume/(mL/g) | Pore Volume Ratio/% | |||||
|---|---|---|---|---|---|---|---|---|---|
| S2 | S3 | S4 | St | S2/St | S3/St | S4/St | |||
| Anthracite | 1 | 3.49 | 0.032 | 0.411 | 5.169 | 5.612 | 0.57 | 7.32 | 92.11 |
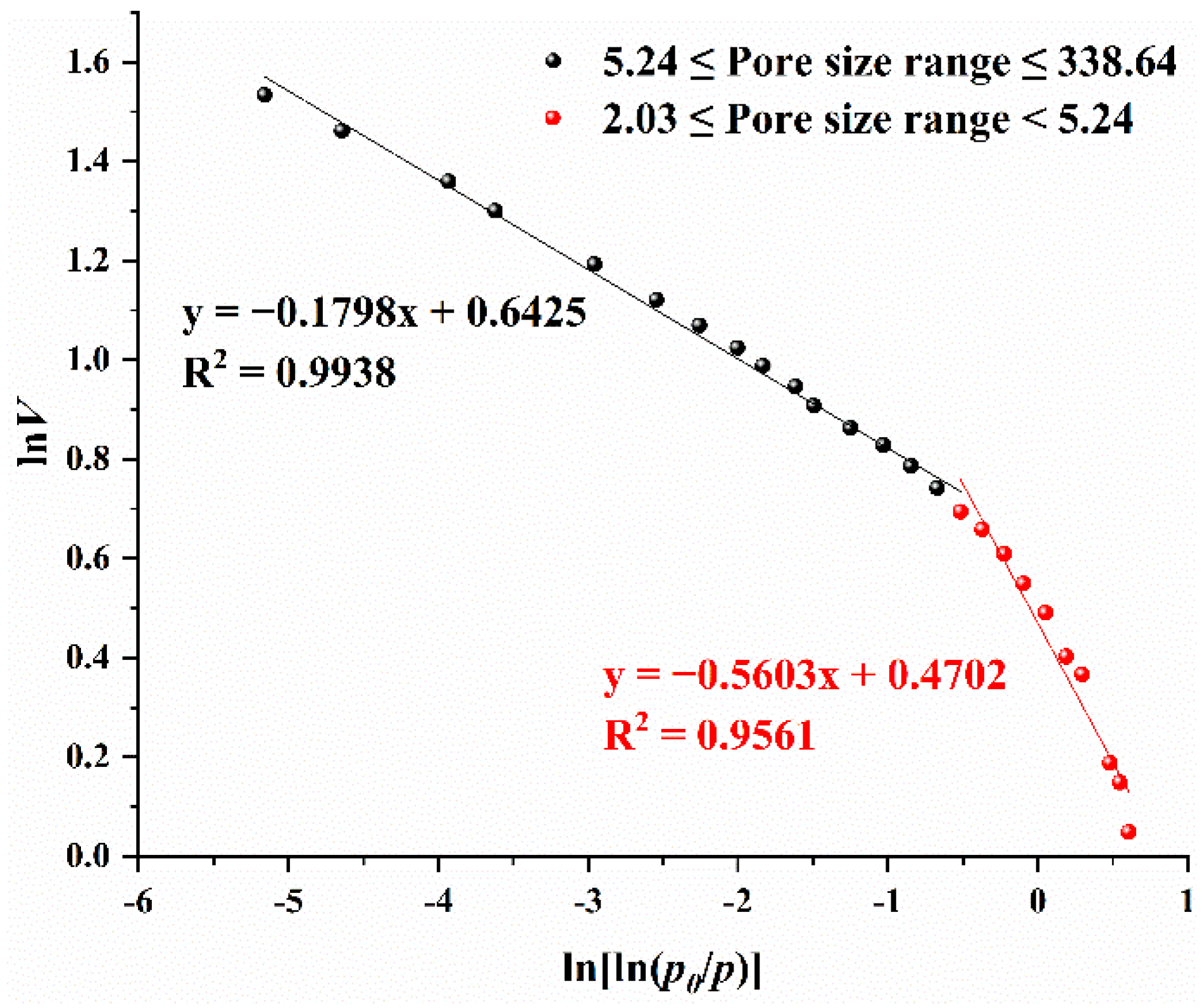
| Coal Sample Number | Pore Size Range/nm | Slope K | D2 | Correlation Coefficient r |
|---|---|---|---|---|
| 1 | 5.24 ≤ d ≤ 338.64 | −0.1798 | 2.8202 | 0.9938 |
| 2.03 ≤ d ≤ 5.24 | −0.5603 | 2.4397 | 0.9561 |
| Coal Sample Number | Pore Size Range/nm | Di | Specific Surface Area/(m2/g) | Specific Surface Area Ratio/% | Dz |
|---|---|---|---|---|---|
| 1 | d > 100 | 2.7245 | 0.0185 | 0.33 | 2.6615 |
| 5.24 ≤ d ≤ 100 | 2.8202 | 4.717 | 84.51 | ||
| 2 < d < 5.24 | 2.4397 | 0.846 | 15.16 |
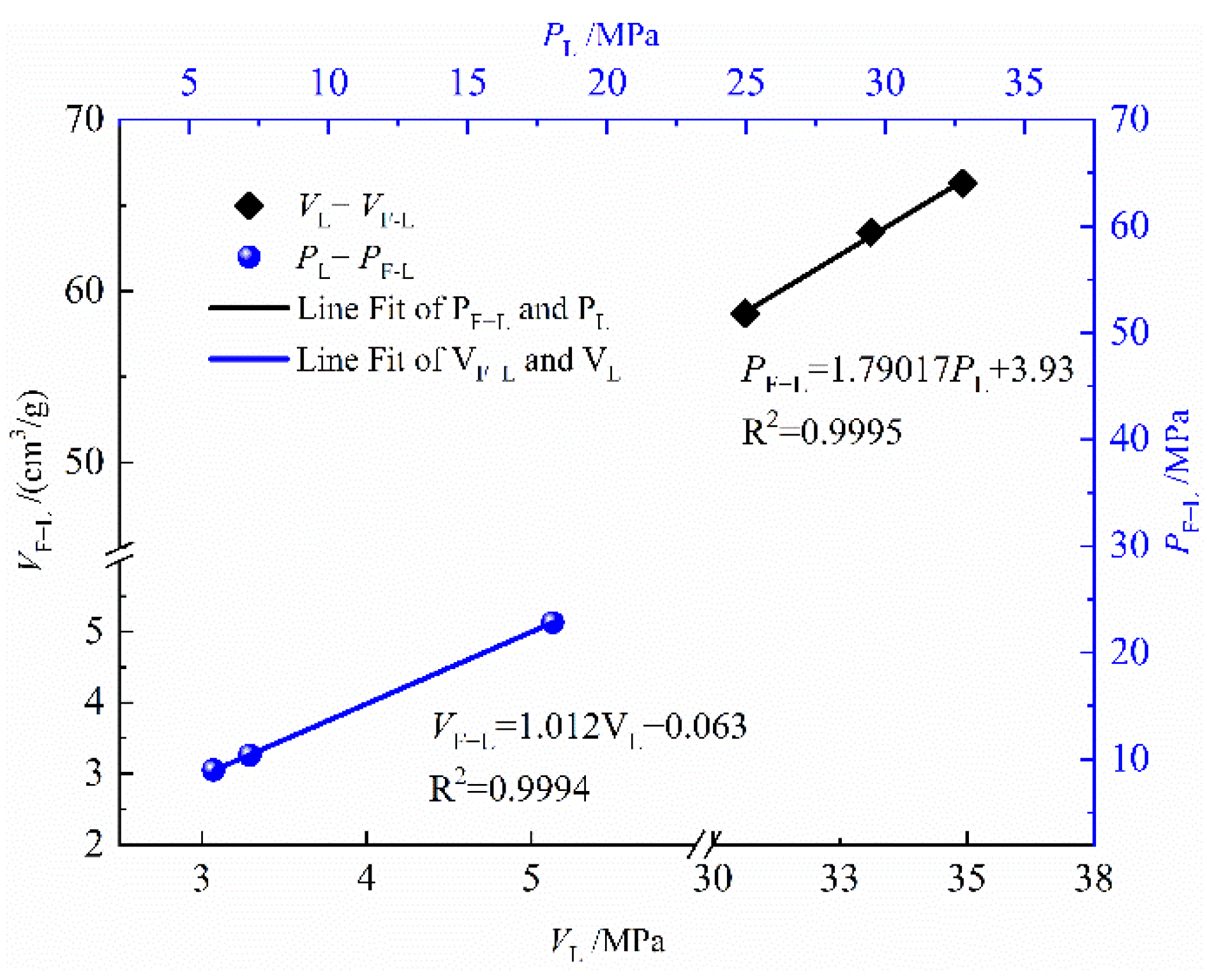
| No. | Temperature/°C | Adsorption Volume/(cm3/g) | Adsorption Pressure/MPa | ||
|---|---|---|---|---|---|
| VL | VF-L | PL | PF-L | ||
| 1 | 30 | 33.28 | 63.42 | 5.02 | 5.02 |
| 40 | 34.91 | 66.59 | 3.27 | 3.28 | |
| 50 | 30.75 | 58.55 | 3.07 | 3.05 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, R.; Zhu, Y.; Ma, X.; Ni, X.; Ren, J. Coupled Seepage Mechanics Model of Coal Containing Methane Based on Pore Structure Fractal Features. Fractal Fract. 2022, 6, 391. https://doi.org/10.3390/fractalfract6070391
Lv R, Zhu Y, Ma X, Ni X, Ren J. Coupled Seepage Mechanics Model of Coal Containing Methane Based on Pore Structure Fractal Features. Fractal and Fractional. 2022; 6(7):391. https://doi.org/10.3390/fractalfract6070391
Chicago/Turabian StyleLv, Runsheng, Yuchen Zhu, Xinyu Ma, Xiaoming Ni, and Jiangang Ren. 2022. "Coupled Seepage Mechanics Model of Coal Containing Methane Based on Pore Structure Fractal Features" Fractal and Fractional 6, no. 7: 391. https://doi.org/10.3390/fractalfract6070391
APA StyleLv, R., Zhu, Y., Ma, X., Ni, X., & Ren, J. (2022). Coupled Seepage Mechanics Model of Coal Containing Methane Based on Pore Structure Fractal Features. Fractal and Fractional, 6(7), 391. https://doi.org/10.3390/fractalfract6070391






