Computational Analysis of Local Fractional LWR Model Occurring in a Fractal Vehicular Traffic Flow
Abstract
:1. Introduction
2. Preliminaries
2.1. Local Fractional Calculus
2.2. LFNT
3. LFNHAM: Basic Approach
4. LFNDM: Fundamental Approach
5. Application of LFNHAM for LFLWR Model
6. Application of LFNDM for LFLWR Model
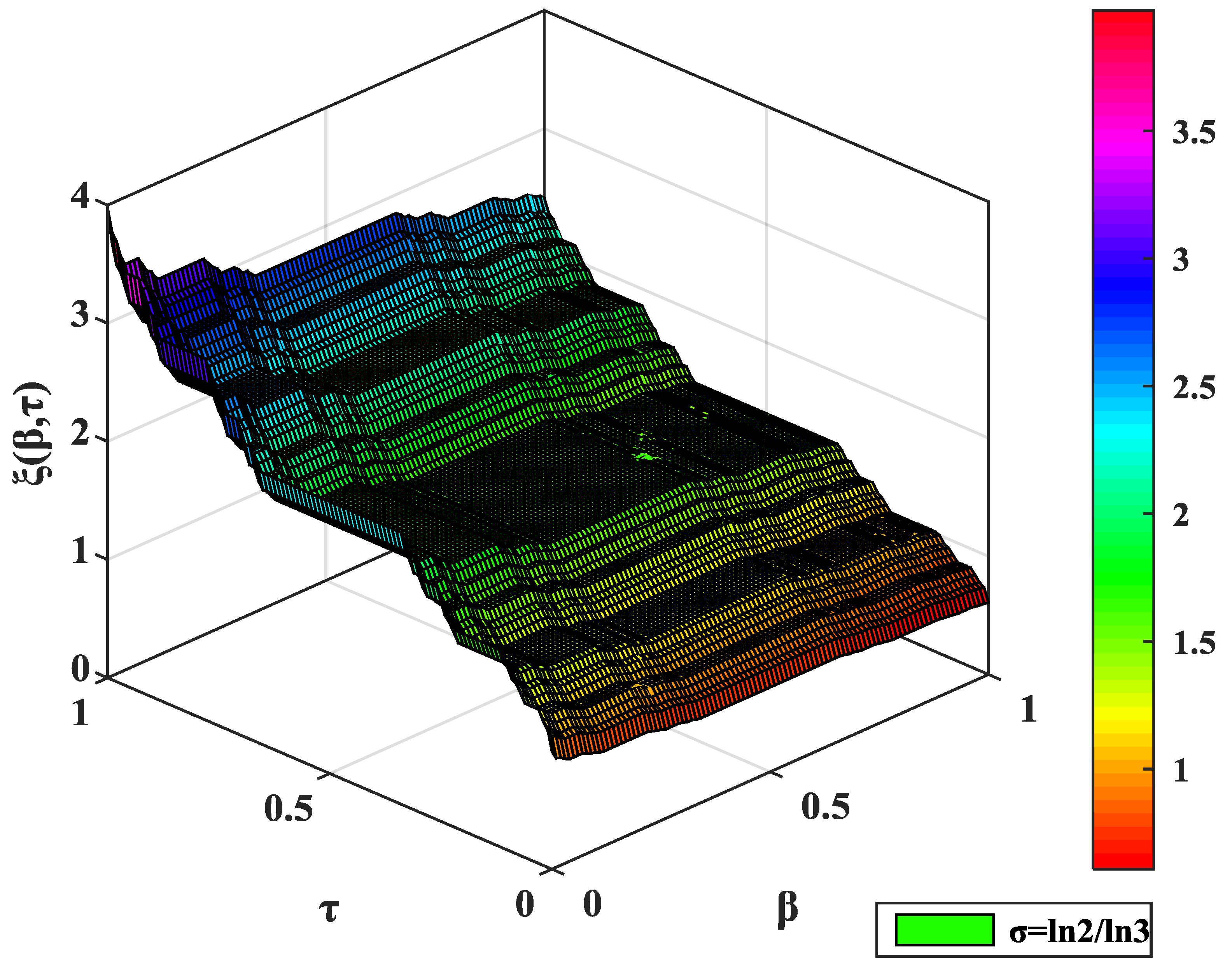
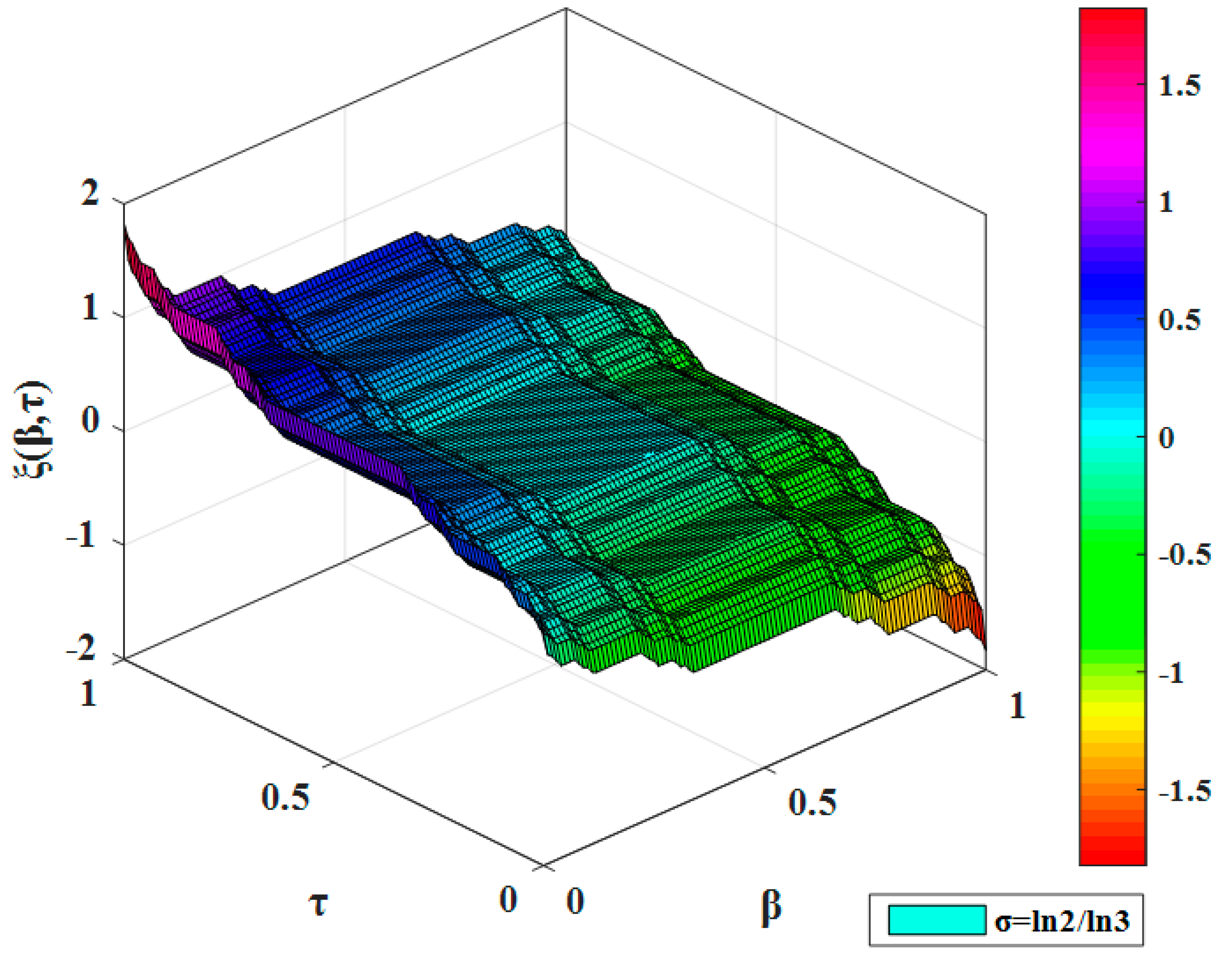
7. Computer Simulation
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Peeta, S.; Ziliaskopoulos, A.K. Foundations of dynamic traffic assignment: The past, the present and the future. Netw. Spat. Econ. 2001, 1, 233–265. [Google Scholar] [CrossRef]
- Daganzo, C.F. A continuum theory of traffic dynamics for freeways with special lanes. Transp. Res. B Methodol. 1997, 31, 83–102. [Google Scholar] [CrossRef]
- Lighthill, M.J.; Whitham, G.B. On kinematic waves-II. A theory of traffic flow on long crowded roads. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1955, 229, 317–345. [Google Scholar]
- Richards, P.I. Shock waves on the highway. Oper. Res. 1956, 4, 42–51. [Google Scholar] [CrossRef]
- Zhang, H.M. New perspectives on continuum traffic flow models. Netw. Spat. Econ. 2001, 1, 9–33. [Google Scholar] [CrossRef]
- Li, T. L1 stability of conservation laws for a traffic flow model. Electron. J. Differ. Equ. 2001, 2001, 1–18. [Google Scholar]
- Gasser, I. On non-entropy solutions of scalar conservation laws for traffic flow. J. Appl. Math. Mech. 2003, 83, 137–143. [Google Scholar] [CrossRef]
- Aw, A.; Klar, A.; Materne, T.; Rascle, M. Derivation of continuum traffic flow models from microscopic follow-the-leader models. SIAM J. Appl. Math. 2002, 63, 259–278. [Google Scholar] [CrossRef]
- Bellomo, N.; Coscia, V. First order models and closure of the mass conservation equation in the mathematical theory of vehicular traffic flow. Comptes Rendus Mec. 2005, 333, 843–851. [Google Scholar] [CrossRef]
- Bellomo, N.; Delitala, M.; Coscia, V. On the mathematical theory of vehicular traffic flow—I: Fluid dynamic and kinetic modeling. Math. Models Methods Appl. Sci. 2002, 12, 1801–1843. [Google Scholar] [CrossRef]
- Ansorge, R. What does the entropy condition mean in traffic flow theory. Transp. Res. Part B 1990, 24, 133–143. [Google Scholar] [CrossRef]
- Towers, J.D. A splitting algorithm for LWR traffic models with flux discontinuities in the unknown. J. Comput. Phys. 2020, 421, 109722. [Google Scholar] [CrossRef]
- Bürger, R.; Chalons, C.; Ordoñez, R.; Villada, L.M. A multiclass Lighthill-Whitham-Richards traffic model with a discontinuous velocity function. Netw. Heterog. Media 2021, 16, 187–219. [Google Scholar] [CrossRef]
- Babakhani, A.; Gejji, V.D. On calculus of local fractional derivatives. J. Math. Anal. Appl. 2002, 270, 66–79. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.J. Local Fractional Functional Analysis and Its Applications; Asian Academic: Hong Kong, China, 2011. [Google Scholar]
- Yang, X.J. Advanced Local Fractional Calculus and Its Applications; World Science: New York, NY, USA, 2012. [Google Scholar]
- Yang, X.J.; Srivastava, H.M.; Cattani, C. Local fractional homotopy perturbation method for solving fractional partial differential equations arising in mathematical physics. Rom. Rep. Phys. 2015, 67, 752–761. [Google Scholar]
- Zhang, Y.; Cattani, C.; Yang, X.J. Local fractional homotopy perturbation method for solving non-homogeneous heat conduction equations in fractal domains. Entropy 2015, 17, 6753–6764. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.J.; Machado, J.A.T.; Hristov, J. Nonlinear dynamics for local fractional Burger’s equations arising in fractal flow. Nonlinear Dyn. 2016, 84, 3–7. [Google Scholar] [CrossRef] [Green Version]
- Ziane, D.; Baleanu, D.; Belghaba, K.; Cherif, M. Local fractional Sumudu decomposition method for linear partial differential equations with local fractional derivative. J. King Saud Univ. Sci. 2019, 31, 83–88. [Google Scholar] [CrossRef]
- Baleanu, D.; Jassim, H.K. A modification fractional homotopy perturbation method for solving Helmholtz and coupled Helmholtz equations on cantor sets. Fractal Fract. 2019, 3, 30. [Google Scholar] [CrossRef] [Green Version]
- Baleanu, D.; Jassim, H.K.; Al-Qurashi, M. Solving Helmholtz equation with local fractional derivative operators. Fractal Fract. 2019, 3, 43. [Google Scholar] [CrossRef] [Green Version]
- Singh, J.; Kumar, D.; Baleanu, D.; Rathore, S. On the local fractional wave equation in fractal strings. Math. Meth. Appl. Sci. 2019, 42, 1588–1595. [Google Scholar] [CrossRef]
- Liu, J.G.; Yang, X.J.; Feng, Y.Y.; Cui, P. A new perspective to study the third-order modified KDV equation on fractal set. Fractals 2020, 28, 2050110. [Google Scholar] [CrossRef]
- Li, X.X.; Tian, D.; He, C.H. A fractal modification of the surface coverage model for an electrochemical arsenic sensor. Electrochim. Acta 2019, 296, 491–493. [Google Scholar] [CrossRef]
- Dubey, V.P.; Singh, J.; Alshehri, A.M.; Dubey, S.; Kumar, D. A comparative analysis of two computational schemes for solving local fractional Laplace equations. Math. Meth. Appl. Sci. 2021, 44, 13540–13559. [Google Scholar] [CrossRef]
- Dubey, V.P.; Singh, J.; Alshehri, A.M.; Dubey, S.; Kumar, D. A hybrid computational method for local fractional dissipative and damped wave equations in fractal media. Waves Random Complex Media 2022, 1–23. [Google Scholar] [CrossRef]
- Dubey, V.P.; Singh, J.; Alshehri, A.M.; Dubey, S.; Kumar, D. An efficient analytical scheme with convergence analysis for computational study of local fractional Schrödinger equations. Math. Comput. Simul. 2022, 196, 296–318. [Google Scholar] [CrossRef]
- Dubey, V.P.; Singh, J.; Alshehri, A.M.; Dubey, S.; Kumar, D. Analysis of local fractional coupled Helmholtz and coupled Burgers’ equations in fractal media. AIMS Math. 2022, 7, 8080–8111. [Google Scholar] [CrossRef]
- Dubey, S.; Dubey, V.P.; Singh, J.; Alshehri, A.M.; Kumar, D. Computational study of a local fractional Tricomi equation occurring in fractal transonic flow. J. Comput. Nonlinear Dynam. 2022, 17, 081006. [Google Scholar] [CrossRef]
- Gao, W.; Baskonus, H.M. Deeper investigation of modified epidemiological computer virus propagation model containing the Caputo operator. Chaos Solitons Fractals 2022, 158, 112050. [Google Scholar] [CrossRef]
- Veeresha, P.; Ilhan, E.; Prakash, D.G.; Baskonus, H.M.; Gao, W. A new numerical investigation of fractional order susceptible-infected-recovered epidemic model of childhood disease. Alex. Eng. J. 2022, 61, 1747–1756. [Google Scholar] [CrossRef]
- Ciancio, A.; Yel, G.; Kumar, A.; Baskonus, H.M.; Ilhan, E. On the complex mixed dark-bright wave distributions to some conformable nonlinear integrable models. Fractals 2022, 30, 2240018. [Google Scholar] [CrossRef]
- Chen, Q.; Baskonus, H.M.; Gao, W.; Ilhan, E. Soliton theory and modulation instability analysis: The Ivancevic option pricing model in economy. Alex. Eng. J. 2022, 61, 7843–7851. [Google Scholar] [CrossRef]
- Sabir, Z.; Wahab, H.A.; Javeed, S.; Baskonus, H.M. An efficient stochastic numerical computing framework for the nonlinear higher order singular models. Fractal Fract. 2021, 5, 176. [Google Scholar] [CrossRef]
- Wang, L.F.; Yang, X.J.; Baleanu, D.; Cattani, C.; Zhao, Y. Fractal dynamical model of vehicular traffic flow within the local fractional conservation laws. Abstr. Appl. Anal. 2014, 2014, 1–5. [Google Scholar] [CrossRef]
- Yang, X.J.; Baleanu, D.; Machado, J.A.T. Systems of Navier-Stokes equations on Cantor sets. Math. Probl. Eng. 2013, 2013, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Hao, Y.J.; Srivastava, H.M.; Jafari, H.; Yang, X.J. Helmholtz and diffusion equations associated with local fractional derivative operators involving the Cantorian and Cantor-type cylindrical coordinates. Adv. Math. Phys. 2013, 2013, 1–5. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Baleanu, D.; Cattani, C.; Cheng, D.F.; Yang, X.J. Maxwell’s equations on Cantor sets: A local fractional approach. Adv. High Energy Phys. 2013, 2013, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Yang, A.M.; Cattani, C.; Zhang, C.; Xie, G.N.; Yang, X.J. Local fractional Fourier series solutions for non-homogeneous heat equations arising in fractal heat flow with local fractional derivative. Adv. Mech. Eng. 2014, 2014, 1–5. [Google Scholar]
- Guo, Y.M.; Zhao, Y.; Zhou, Y.M.; Xiao, Z.B.; Yang, X.J. On the local fractional LWR model in fractal traffic flows in the entropy condition. Math. Meth. Appl. Sci. 2017, 40, 6127–6132. [Google Scholar] [CrossRef]
- Li, Y.; Wang, L.F.; Zeng, S.D.; Zhao, Y. Local fractional Laplace variational iteration method for fractal vehicular traffic flow. Adv. Theor. Math. Phys. 2014, 2014, 649318. [Google Scholar] [CrossRef]
- Singh, N.; Kumar, K.; Goswami, P.; Jafari, H. Analytical method to solve the local fractional vehicular traffic flow model. Math. Meth. Appl. Sci. 2022, 45, 3983–4001. [Google Scholar] [CrossRef]
- Jassim, H.K. On approximate methods for fractal vehicular traffic flow. TWMS J. App. Eng. Math. 2017, 7, 58–65. [Google Scholar]
- Kumar, D.; Tchier, F.; Singh, J.; Baleanu, D. An efficient computational technique for fractal vehicular traffic flow. Entropy 2018, 20, 259. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhao, D.; Singh, J.; Kumar, D.; Rathore, S.; Yang, X.J. An efficient computational technique for local fractional heat conduction equations in fractal media. J. Nonlinear Sci. Appl. 2017, 10, 1478–1486. [Google Scholar] [CrossRef] [Green Version]
- Singh, J.; Kumar, D.; Nieto, J.J. A reliable algorithm for local fractional Tricomi equation arising in fractal transonic flow. Entropy 2016, 18, 206. [Google Scholar] [CrossRef] [Green Version]
- Kumar, D.; Singh, J.; Baleanu, D. A hybrid computational approach for Klein-Gordon equations on Cantor sets. Nonlinear Dyn. 2017, 87, 511–517. [Google Scholar] [CrossRef]
- Jafari, H.; Jassim, H.K.; Moshokoa, S.P.; Ariyan, V.M.; Tchier, F. Reduced differential transform method for partial differential equations within local fractional derivative operators. Adv. Mech. Eng. 2016, 8, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Keskin, Y.; Oturanc, G. Reduced differential transform method for partial differential equations. Int. J. Nonlinear Sci. Numer. Simul. 2009, 10, 741–750. [Google Scholar] [CrossRef]
- Ziane, D.; Bokhari, A.; Belgacem, R. Local fractional homotopy analysis method for solving coupled nonlinear systems of Burger’s equations. Int. J. Open Probl. Comput. Math. 2019, 12, 47–57. [Google Scholar]
- Maitama, S.; Zhao, W. Local fractional homotopy analysis method for solving nondifferentiable problems on Cantor sets. Adv. Differ. Equ. 2019, 2019, 1–22. [Google Scholar] [CrossRef] [Green Version]
- Baleanu, D.; Machado, J.A.T.; Cattani, C.; Baleanu, M.C.; Yang, X.J. Local fractional variational iteration and decomposition methods for wave equation on cantor sets within local fractional operators. Abstr. Appl. Anal. 2014, 2014, 1–6. [Google Scholar] [CrossRef]
- Yang, X.J.; Baleanu, D.; Zhong, W.P. Approximate solutions for diffusion equations on cantor space-time. Proc. Rom. Aca. Ser. A 2013, 14, 127–133. [Google Scholar]
- Yang, X.J.; Baleanu, D.; Lazarevic, M.P.; Cajic, M.S. Fractal boundary value problems for integral and differential equations fractional operators. Therm. Sci. 2015, 19, 959–966. [Google Scholar] [CrossRef]
- Maitama, S. Local fractional natural homotopy perturbation method for solving partial differential equations with local fractional derivative. Prog. Fract. Differ. Appl. 2018, 4, 219–228. [Google Scholar] [CrossRef]
- Jafari, H.; Jassim, H.K.; Al Qurashi, M.; Baleanu, D. On the existence and uniqueness of solutions for local fractional differential equations. Entropy 2016, 18, 420. [Google Scholar] [CrossRef] [Green Version]
- Khan, Z.H.; Khan, W.A. N-transform properties and applications. NUST J. Eng. Sci. 2008, 1, 127–133. [Google Scholar]
- Belgacem, F.B.M.; Silambarasan, R. Theory of the natural transform. Math. Eng. Sci. Aerosp. (MESA) J. 2012, 3, 99–124. [Google Scholar]
- Belgacem, F.B.M.; Silambarasan, R. Advances in the Natural Transform. AIP Conf. Proc. 2012, 1493, 106–110. [Google Scholar]
- Silambarasan, R.; Belgacem, F.B.M. Application of the Natural Transform to Maxwell’s Equations. In Proceedings of the Progress in Electromagnetics Research Symposium, Suzhou, China, 12–16 September 2011; pp. 899–902. [Google Scholar]
- Odibat, Z.; Bataineh, S.A. An adaptation of homotopy analysis method for reliable treatment of strongly nonlinear problems: Construction of homotopy polynomials. Math. Meth. Appl. Sci. 2014, 38, 991–1000. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dubey, V.P.; Kumar, D.; Alshehri, H.M.; Dubey, S.; Singh, J. Computational Analysis of Local Fractional LWR Model Occurring in a Fractal Vehicular Traffic Flow. Fractal Fract. 2022, 6, 426. https://doi.org/10.3390/fractalfract6080426
Dubey VP, Kumar D, Alshehri HM, Dubey S, Singh J. Computational Analysis of Local Fractional LWR Model Occurring in a Fractal Vehicular Traffic Flow. Fractal and Fractional. 2022; 6(8):426. https://doi.org/10.3390/fractalfract6080426
Chicago/Turabian StyleDubey, Ved Prakash, Devendra Kumar, Hashim M. Alshehri, Sarvesh Dubey, and Jagdev Singh. 2022. "Computational Analysis of Local Fractional LWR Model Occurring in a Fractal Vehicular Traffic Flow" Fractal and Fractional 6, no. 8: 426. https://doi.org/10.3390/fractalfract6080426
APA StyleDubey, V. P., Kumar, D., Alshehri, H. M., Dubey, S., & Singh, J. (2022). Computational Analysis of Local Fractional LWR Model Occurring in a Fractal Vehicular Traffic Flow. Fractal and Fractional, 6(8), 426. https://doi.org/10.3390/fractalfract6080426








