Nonlinear Control and Circuit Implementation in Coupled Nonidentical Fractional-Order Chaotic Systems
Abstract
:1. Introduction
2. Fractional-Order Rucklidge Systems and Its Circuit Realization
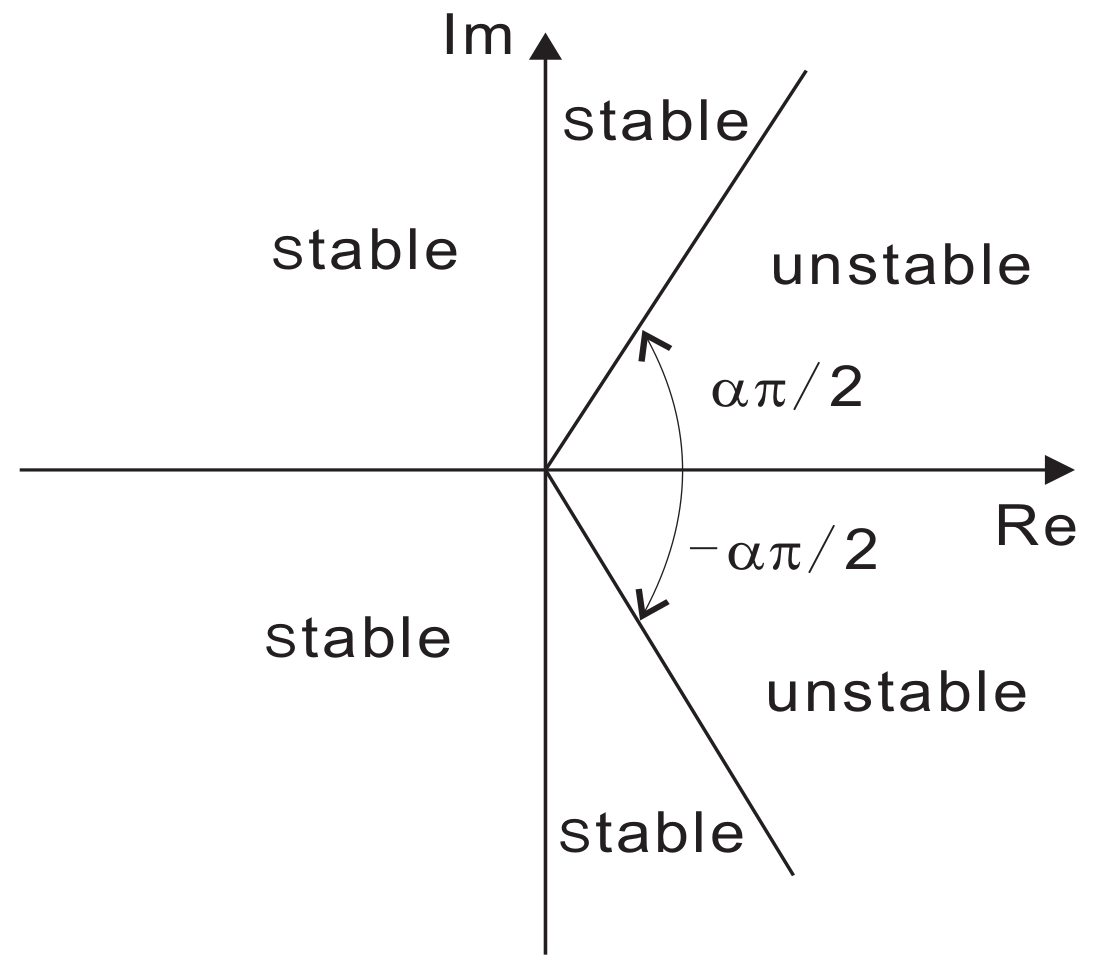
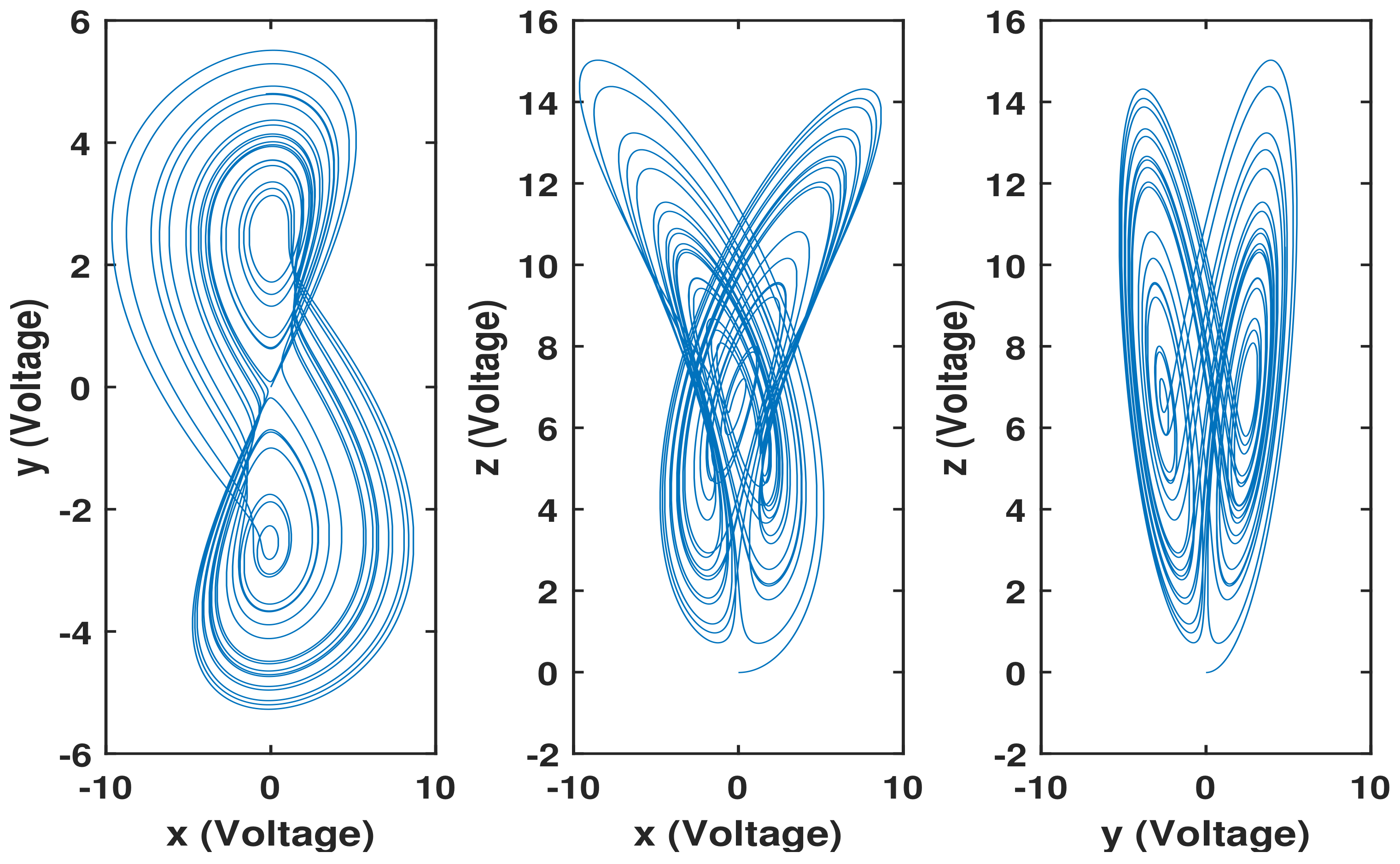
2.1. Fractional-Order Rucklidge Systems
2.2. Circuit Realization of Commensurate Fractional-Order Rucklidge Systems
3. Anti-Synchronization of Coupled Nonidentical Fractional-Order Rucklidge Systems
3.1. Open-Loop and Closed-Loop Design
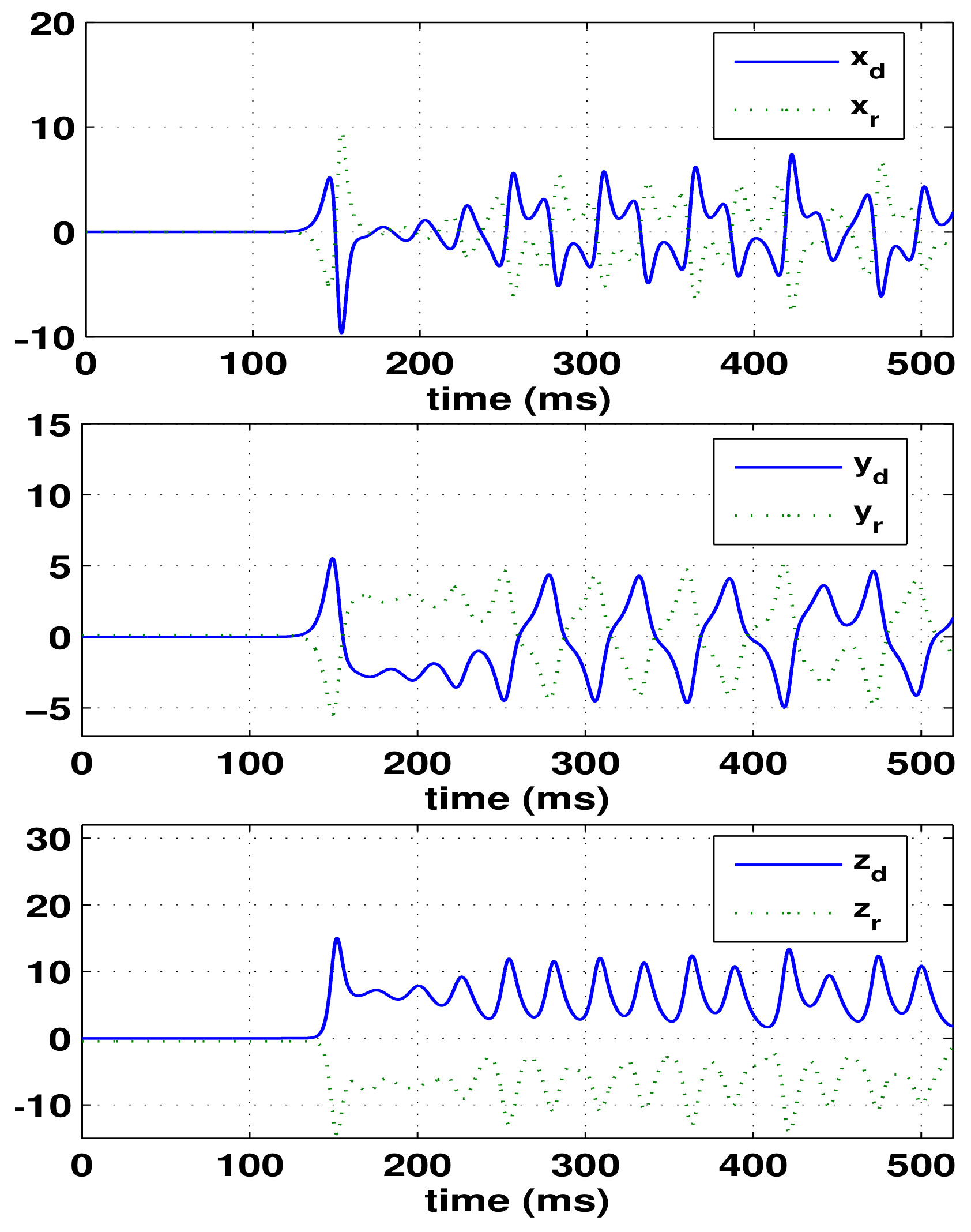
3.2. OPCL Nonlinear Control for Fractional-Order Rucklidge System
3.3. Circuit Implementation
3.4. Time-Domain Numerical Methods
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jahanshahi, H.; Yousefpour, A.; Munoz Pacheco, J.M.; Kacar, S.; Pham, V.-T.; Alsaadi, F.E. A new fractional-order hyperchaotic memristor oscillator: Dynamic analysis, robust adaptive synchronization, and its application to voice encryption. Appl. Math. Comput. 2020, 383, 125310. [Google Scholar] [CrossRef]
- Sayed, W.S.; Radwan, A.G. Generalized switched synchronization and dependent image encryption using dynamically rotating fractional-order chaotic systems. AEU-Int. J. Electron. Commun. 2020, 123, 153268. [Google Scholar] [CrossRef]
- Khan, A.; Jahanzaib, L.S.; Trikha, P. Secure communication: Using parallel synchronization technique on novel fractional order chaotic system. IFAC-Papers OnLine 2020, 53, 307–312. [Google Scholar] [CrossRef]
- Qi, F.; Qu, J.; Chai, Y.; Chen, L.; Lopes, A.M. Synchronization of incommensurate fractional-order chaotic systems based on linear feedback control. Fractal Fract. 2022, 6, 221. [Google Scholar] [CrossRef]
- Adedayo, O.A. OPCL coupling of mixed integer-fractional order oscillators: Tree and chain implementation. Phys. Scr. 2021, 96, 125270. [Google Scholar]
- Martínez-Fuentes, O.; Montesinos-García, J.J.; Gómez-Aguilar, J.F. Generalized synchronization of commensurate fractional-order chaotic systems: Applications in secure information transmission. Digit. Signal Process. 2022, 126, 103494. [Google Scholar] [CrossRef]
- Tlelo-Cuautle, E.; Dalia Pano-Azucena, A.; Guillén-Fernández, O.; Silva-Juárez, A. Synchronization and Applications of Fractional-Order Chaotic Systems. In Analog/Digital Implementation of Fractional Order Chaotic Circuits and Applications; Springer: Cham, Switzerland, 2020; pp. 175–201. [Google Scholar]
- Vaidyanathan, S.; Volos, C.K.; Tacha, O.I.; Kyprianidis, I.; Stouboulos, I.; Pham, V.T. Analysis, control and circuit simulation of a novel 3-D finance chaotic system. In Advances and Applications in Chaotic Systems; Springer: Cham, Switzerland, 2016; pp. 495–512. [Google Scholar]
- Borah, M.; Roy, B.K. Design of fractional-order hyperchaotic systems with maximum number of positive lyapunov exponents and their antisynchronisation using adaptive control. Int. J. Control 2016, 91, 2615–2630. [Google Scholar] [CrossRef]
- El-Sayed, A.; Nour, H.; Elsaid, A.; Matouk, A.; Elsonbaty, A. Dynamical behaviors, circuit realization, chaos control, and synchronization of a new fractional order hyperchaotic system. Appl. Math. Model. 2016, 40, 3516–3534. [Google Scholar] [CrossRef]
- Grosu, I.; Banerjee, R.; Roy, P.K.; Dana, S.K. Design of coupling for synchronization of chaotic oscillators. Phys. Rev. E 2009, 80, 016212. [Google Scholar] [CrossRef]
- Padmanaban, E.; Hens, C.; Dana, S.K. Engineering synchronization of chaotic oscillators using controller based coupling design. Chaos 2011, 21, 013110. [Google Scholar] [CrossRef]
- Roy, P.K.; Hens, C.; Grosu, I.; Dana, S.K. Engineering generalized synchronization in chaotic oscillators. Chaos 2011, 21, 013106. [Google Scholar] [CrossRef]
- Bhowmick, S.K.; Ghosh, D. Targeting engineering synchronization in chaotic systems. Int. J. Mod. Phys. C 2016, 27, 1650006. [Google Scholar] [CrossRef]
- Liu, H.; Zhu, Z.; Yu, H.; Zhu, Q. Modified projective synchronization between different fractional-order systems based on open-plus-closed-loop control and its application in image encryption. Math. Probl. Eng. 2014, 2014, 567898. [Google Scholar] [CrossRef]
- Wang, J.W.; Zeng, L.; Ma, Q.H. Inverse synchronization of coupled fractional-order systems through open-plus-closed-loop control. Pramana-J. Phys. 2011, 76, 385–396. [Google Scholar] [CrossRef]
- Wang, J.W.; Zhang, Y.B. Synchronization in coupled nonidentical incommensurate fractional-order systems. Phys. Lett. A 2009, 374, 202–207. [Google Scholar] [CrossRef]
- Banerjee, R.; Padmanaban, E.; Dana, S.K. Control of partial synchronization in chaotic oscillators. Pramana-J. Phys. 2015, 84, 203–215. [Google Scholar] [CrossRef]
- Bhowmick, S.K.; Bera, B.K.; Ghosh, D. Generalized counter-rotating oscillators: Mixed synchronization. Commun. Nonlinear Sci. Numer. Simul. 2015, 22, 692–701. [Google Scholar] [CrossRef]
- Chen, X.; Cao, J.; Qiu, J.; Yang, C. Transmission synchronization control of multiple non-identical coupled chaotic systems. IEEE Trans. Neural Netw. Learn. Syst. 2016, 26, 1115–1120. [Google Scholar]
- Sene, N.; G’omez-Aguilar, J.F. Analytical solutions of electrical circuits considering certain generalized fractional derivatives. Eur. Phys. J. Plus 2019, 134, 260. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications, 1st ed.; Academic Press: Cambridge, MA, USA, 1999; p. 62. [Google Scholar]
- Matignon, D. Stability results for fractional differential equations with applications to control processing. In Proceedings of the Computational Engineering in Systems and Application Multi-Conference, IMACS, Lille, France, 9–12 July 1996; pp. 963–968. [Google Scholar]
- Bahatdin, D. Stability analysis of an incommensurate fractional-order SIR model. Math. Model. Numer. Simul. Appl. 2021, 1, 44–55. [Google Scholar]
- Zhang, Y.B.; Zhou, T.S. Three schemes to synchronize chaotic fractional-order Rucklidge systems. Int. J. Mod. Phys. B 2007, 21, 2033–2044. [Google Scholar] [CrossRef]
- Zhang, R.X.; Yang, S.P. Chaos in fractional-order generalized Lorenz system and its synchronization circuit simulation. Chin. Phys. B 2009, 18, 03295. [Google Scholar]
- Hammouch, Z.; Yavuz, M.; Özdemir, N. Numerical solutions and synchronization of a variable-order fractional chaotic system. Math. Model. Numer. Simul. Appl. 2021, 1, 11–23. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.J.; Freed, A.D. Detailed error analysis for a fractional Adams method. Numer. Algorithms 2004, 36, 31–52. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Lin, P.; Sun, W. Nonlinear Control and Circuit Implementation in Coupled Nonidentical Fractional-Order Chaotic Systems. Fractal Fract. 2022, 6, 428. https://doi.org/10.3390/fractalfract6080428
Zhang Y, Lin P, Sun W. Nonlinear Control and Circuit Implementation in Coupled Nonidentical Fractional-Order Chaotic Systems. Fractal and Fractional. 2022; 6(8):428. https://doi.org/10.3390/fractalfract6080428
Chicago/Turabian StyleZhang, Yanbin, Ping Lin, and Weigang Sun. 2022. "Nonlinear Control and Circuit Implementation in Coupled Nonidentical Fractional-Order Chaotic Systems" Fractal and Fractional 6, no. 8: 428. https://doi.org/10.3390/fractalfract6080428
APA StyleZhang, Y., Lin, P., & Sun, W. (2022). Nonlinear Control and Circuit Implementation in Coupled Nonidentical Fractional-Order Chaotic Systems. Fractal and Fractional, 6(8), 428. https://doi.org/10.3390/fractalfract6080428






