On the Numerical Approximation of Mobile-Immobile Advection-Dispersion Model of Fractional Order Arising from Solute Transport in Porous Media
Abstract
:1. Introduction
2. Proposed Method
2.1. Local RBF Method
2.2. Selecting Optimal Shape Parameter
- Step i:
- set
- Step ii:
- select
- Step iii:
- Step iv:
- Step v:
- Step vi:
- Step vii:
2.3. Numerical Inverse Laplace Transform
2.4. Accuracy and Convergence of the Method
3. Stability
4. Numerical Experiments
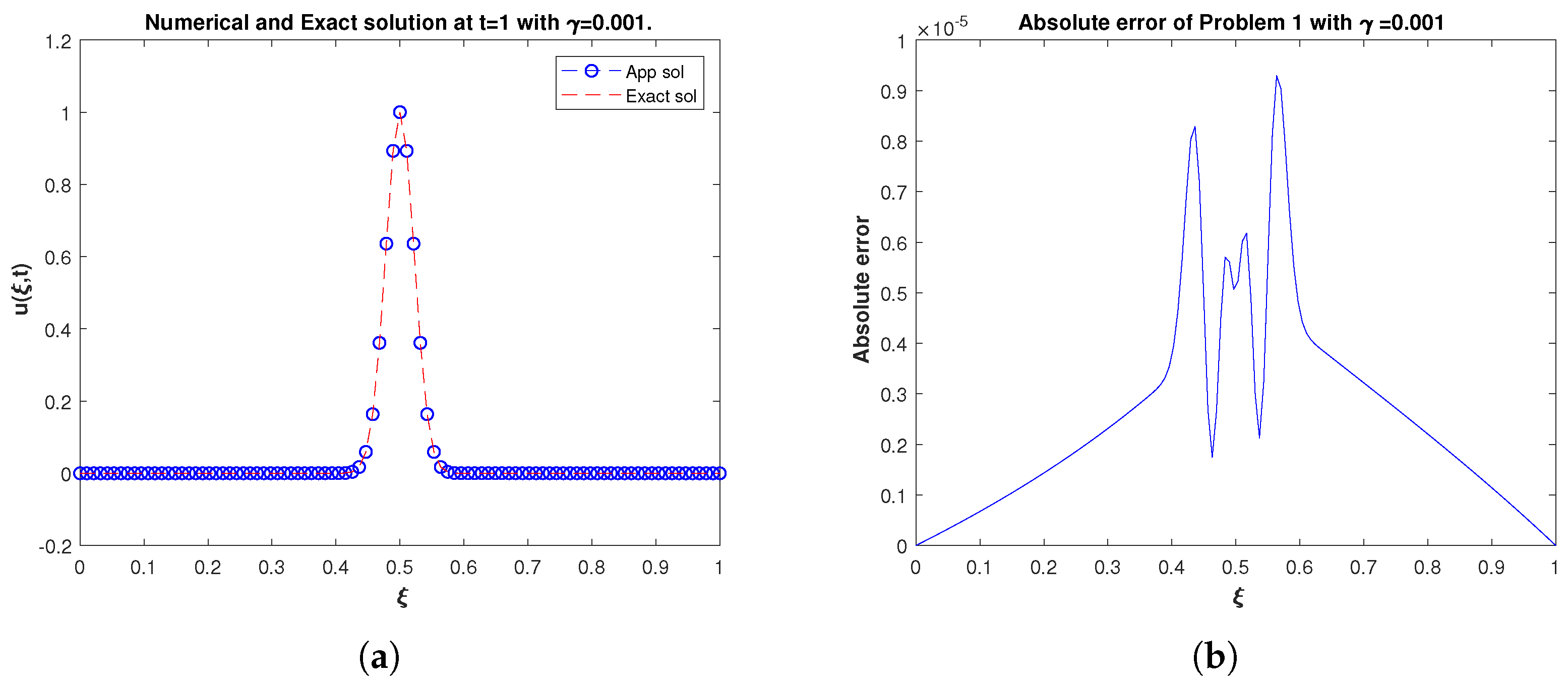
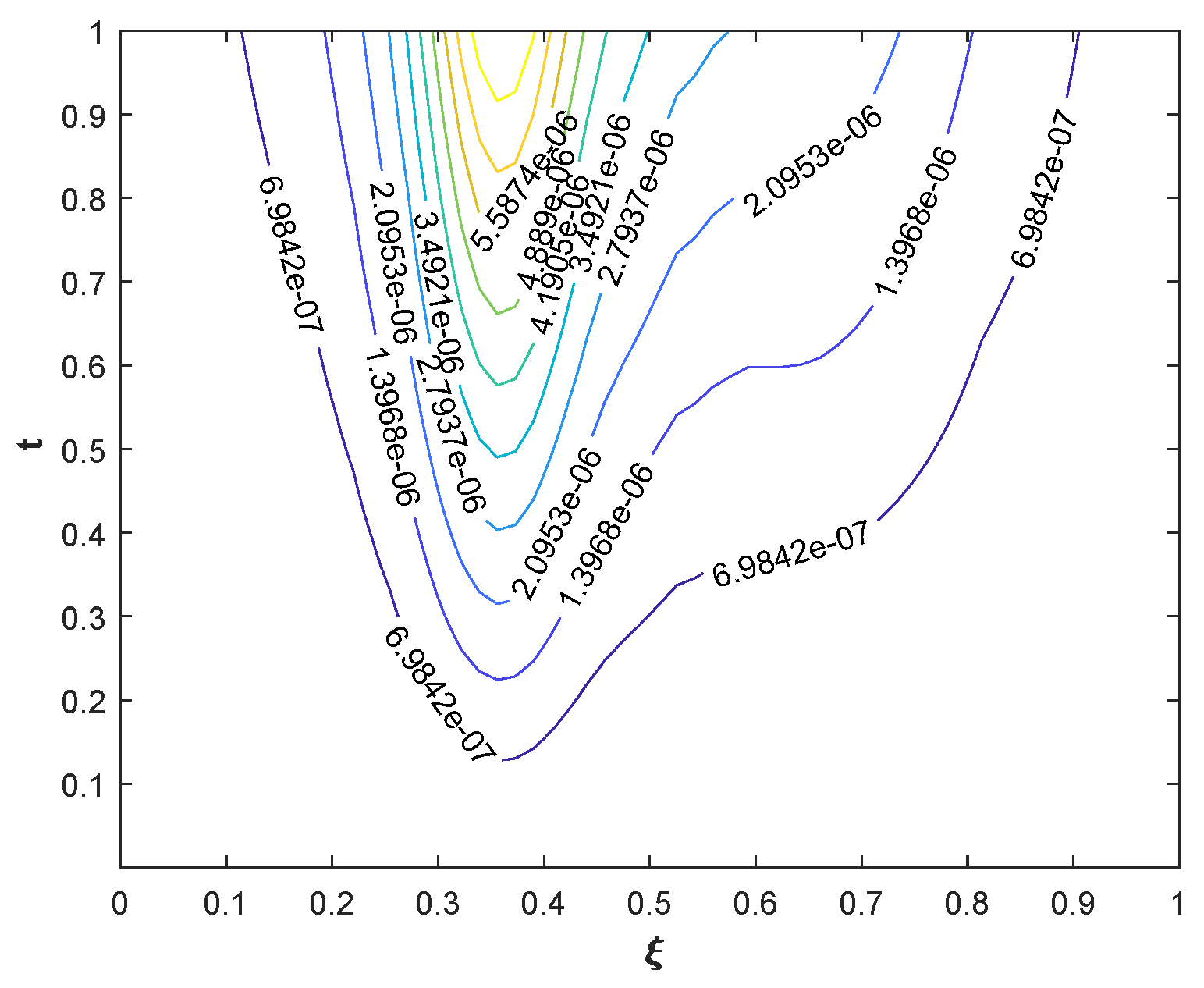
4.1. Problem 1
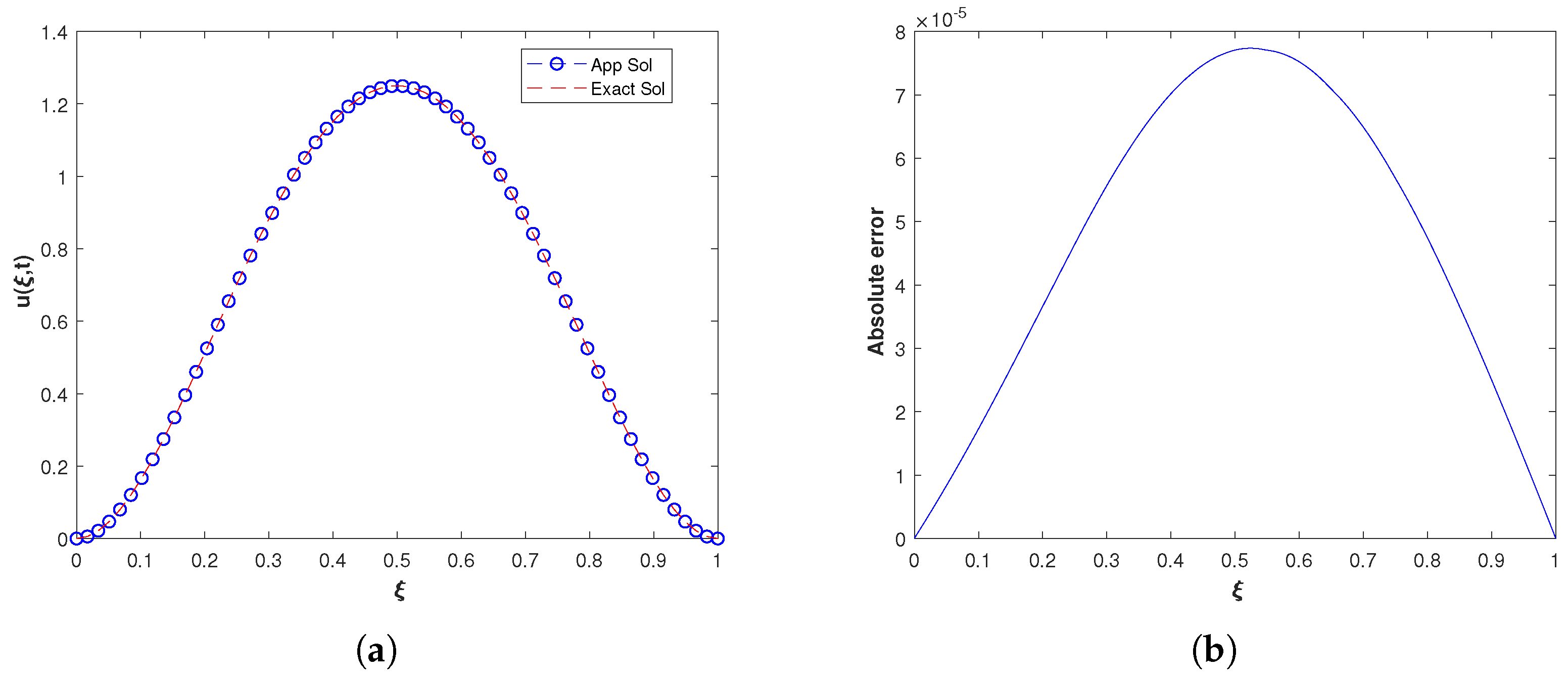
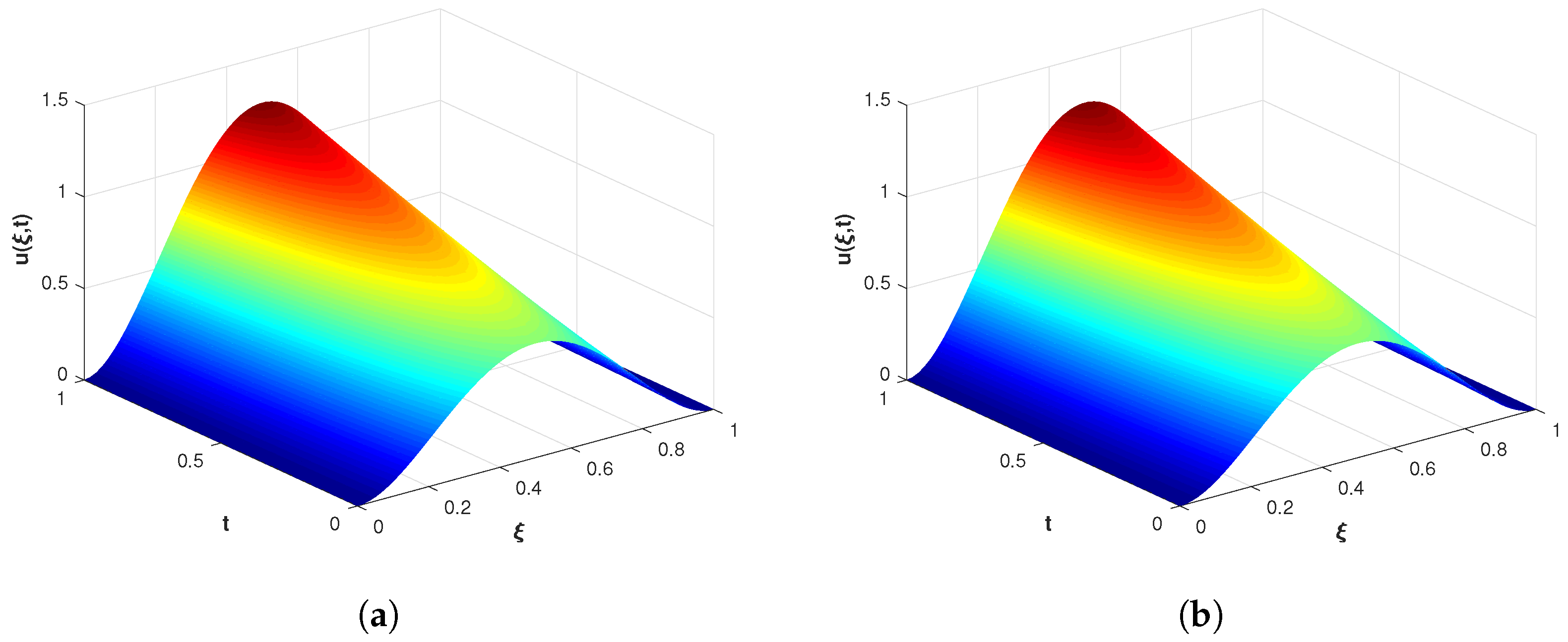
4.2. Problem 2
4.3. Problem 3
4.4. Problem 4
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Coats, K.H.; Smith, B.D. Dead-end pore volume and dispersion in porous media. Soc. Pet. Eng. J. 1964, 4, 73–84. [Google Scholar] [CrossRef]
- Chen, Z.; Qian, J.; Zhan, H.; Chen, L.; Luo, S. Mobile-immobile model of solute transport through porous and fractured media. IAHS-AISH Publ. 2011, 341, 154–158. [Google Scholar]
- Bauget, F.; Fourar, M. Non-Fickian dispersion in a single fracture. J. Contam. Hydrol. 2008, 100, 137–148. [Google Scholar] [CrossRef] [PubMed]
- Berkowitz, B. Characterizing flow and transport in fractured geological media: A review. Adv. Water. Resour. 2002, 25, 861–884. [Google Scholar] [CrossRef]
- Benson, D.A.; Schumer, R.; Meerschaert, M.M.; Wheatcraft, S.W. Fractional dispersion, Lévy motion, and the MADE tracer tests. Transp. Porous. Media. 2001, 42, 211–240. [Google Scholar] [CrossRef]
- Golbabai, A.; Nikan, O.; Nikazad, T. Numerical investigation of the time fractional mobile-immobile advection-dispersion model arising from solute transport in porous media. Int. J. Appl. Comput. Math. 2019, 5, 1–22. [Google Scholar] [CrossRef]
- Podlubny, I. An introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications. Math. Sci. Eng 1999, 198, 340. [Google Scholar]
- Diethelm, K.; Ford, N.J. Analysis of fractional differential equations. J. Math. Anal. Appl. 2002, 265, 229–248. [Google Scholar] [CrossRef]
- Mainardi, F.; Carpinteri, A. Fractals and Fractional Calculus in Continuum Mechanics; Springer: Berlin/Heidelberg, Germany, 1997. [Google Scholar]
- Tarasov, V.E. Fractional Dynamics: Applications of Fractional Calculus to Dynamics of Particles, Fields and Media; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Kamran Ali, A.; Gómez-Aguilar, J.F. A transform based local RBF method for 2D linear PDE with Caputo-Fabrizio derivative. Comptes Rendus. Math. 2020, 358, 831–842. [Google Scholar] [CrossRef]
- Kamran; Shah, Z.; Kumam, P.; Alreshidi, N.A. A meshless method based on the Laplace transform for the 2D multi-term time fractional partial integro-differential equation. Mathematics 2020, 8, 1972. [Google Scholar] [CrossRef]
- Schumer, R.; Benson, D.A.; Meerschaert, M.M.; Baeumer, B. Fractal mobile/immobile solute transport. Water Resour. Res. 2003, 39, 10. [Google Scholar] [CrossRef]
- Liu, Q.; Liu, F.; Turner, I.; Anh, V.; Gu, Y. A RBF meshless approach for modeling a fractal mobile/immobile transport model. Appl. Math. Comput. 2014, 226, 336–347. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, F.; Phanikumar, M.S.; Meerschaert, M.M. A novel numerical method for the time variable fractional order mobile-immobile advection-dispersion model. Comput. Math. Appl. 2013, 66, 693–701. [Google Scholar] [CrossRef]
- Liu, F.; Zhuang, P.; Burrage, K. Numerical methods and analysis for a class of fractional advection-dispersion models. Comput. Math. Appl. 2012, 64, 2990–3007. [Google Scholar] [CrossRef]
- Ma, H.; Yang, Y. Jacobi spectral collocation method for the time variable-order fractional mobile-immobile advection-dispersion solute transport model. East Asian J. Appl. Math. 2016, 6, 337–352. [Google Scholar] [CrossRef]
- Jaiswal, S.; Chopra, M.; Das, S. Numerical solution of a space fractional order solute transport system. J. Porous Media. 2018, 21, 145–160. [Google Scholar] [CrossRef]
- Nong, L.; Chen, A. Numerical schemes for the time-fractional mobile/immobile transport equation based on convolution quadrature. J. Appl. Math. Comput. 2022, 68, 199–215. [Google Scholar] [CrossRef]
- Bendjaballah-Lalaoui, N.; Merzougui, A.; Rennane, S. Modeling Solute Transport in Saturated Soil Column: Coupling Physical Nonequilibrium Model and Nonlinear Freundlich Isotherm. J. Porous Media 2021, 24, 19–35. [Google Scholar]
- Sharma, P.K.; Shukla, S.K.; Choudhary, R.; Swami, D. Modeling for solute transport in mobile-immobile soil column experiment. ISH J. Hydraul. Eng. 2016, 22, 204–211. [Google Scholar] [CrossRef]
- Gao, G.; Feng, S.; Zhan, H.; Huang, G.; Mao, X. Evaluation of anomalous solute transport in a large heterogeneous soil column with mobile-immobile model. J. Hydrol. Eng. 2009, 14, 966–974. [Google Scholar] [CrossRef]
- Nikan, O.; Machado, J.T.; Golbabai, A.; Nikazad, T. Numerical approach for modeling fractal mobile/immobile transport model in porous and fractured media. Int. Commun. Heat Mass Transf. 2020, 111, 104443. [Google Scholar] [CrossRef]
- Salomoni, V.A.L.; De Marchi, N. Numerical Solutions of Space-Fractional Advection-Diffusion-Reaction Equations. Fractal. Fract. 2022, 6, 21. [Google Scholar] [CrossRef]
- Belytschko, T.; Lu, Y.Y.; Gu, L. Element-free Galerkin methods. Int. J. Numer. Methods. Eng. 1994, 37, 229–256. [Google Scholar] [CrossRef]
- Fu, Z.; Chen, W.; Zhang, C. Boundary particle method for Cauchy inhomogeneous potential problems. Inverse Probl. Sci. Eng. 2012, 20, 189–207. [Google Scholar] [CrossRef]
- Babuska, I.; Melenk, J. The partition of unity method. Int. J. Numer. Meth. Engrg. 1997, 40, 727–758. [Google Scholar] [CrossRef]
- Sarra, S.A.; Kansa, E.J. Multiquadric radial basis function approximation methods for the numerical solution of partial differential equations. Adv. Comput. Mech. 2009, 2, 220. [Google Scholar]
- Kansa, E.J. Multiquadrics scattered data approximation scheme with applications to computational fluid-dynamics-I, surface approximations and partial derivative estimates. Comput. Math. Appl. 1990, 19, 127–145. [Google Scholar] [CrossRef]
- Sarra, S.A. A local radial basis function method for advection-diffusion-reaction equations on complexly shaped domains. Appl. Math. Comput. 2012, 218, 9853–9865. [Google Scholar] [CrossRef]
- Fasshauer, G.E.; Zhang, J.G. On choosing “optimal” shape parameters for RBF approximation. Numer. Algorithms 2007, 45, 345–368. [Google Scholar] [CrossRef]
- Koupaei, J.A.; Firouznia, M.; Hosseini, S.M.M. Finding a good shape parameter of RBF to solve PDEs based on the particle swarm optimization algorithm. Alex. Eng. J. 2018, 57, 3641–3652. [Google Scholar] [CrossRef]
- Uddin, M. On the selection of a good value of shape parameter in solving time-dependent partial differential equations using RBF approximation method. Appl. Math. Model. 2014, 38, 135–144. [Google Scholar] [CrossRef]
- Šarler, B.; Vertnik, R. Meshfree explicit local radial basis function collocation method for diffusion problems. Comput. Math. Appl. 2006, 51, 1269–1282. [Google Scholar] [CrossRef]
- Yao, G.; Duo, J.; Chen, C.S.; Shen, L.H. Implicit local radial basis function interpolations based on function values. Appl. Math. Comput. 2015, 265, 91–102. [Google Scholar] [CrossRef]
- Divo, E.; Kassab, A.J. An efficient localized RBF meshless method for fluid flow and conjugate heat transfer. ASME J. Heat. Trans. 2007, 129, 124–136. [Google Scholar] [CrossRef]
- Vertnik, R.; Šarler, B. Meshless local radial basis function collocation method for convective-diffusive solid-liquid phase change problems. Int. J. Numer. Methods. Heat Fluid Flow 2006, 16, 617–640. [Google Scholar] [CrossRef]
- Yao, G.; Islam, S.; Šarler, B. Assessment of global and local meshless methods based on collocation with radial basis functions for parabolic partial differential equations in three dimensions. Eng. Anal. Bound. Elem. 2012, 36, 1640–1648. [Google Scholar] [CrossRef]
- Kamran; Ahmadian, A.; Salahshour, S.; Salimi, M. A robust numerical approximation of advection diffusion equations with nonsingular kernel derivative. Phys. Scr. 2021, 96, 124015. [Google Scholar] [CrossRef]
- Davies, A.J.; Crann, D.; Kane, S.J.; Lai, C.H. A hybrid Laplace transform/finite difference boundary element method for diffusion problems. Comput. Model. Eng. Sci. 2007, 18, 79–86. [Google Scholar]
- Fu, Z.J.; Chen, W.; Yang, H.T. Boundary particle method for Laplace transformed time fractional diffusion equations. J. Comput. Phys. 2013, 235, 52–66. [Google Scholar] [CrossRef]
- Rizzo, F.J.; Shippey, D.J. A method of solution of certain problems of transient heat conduction. AIAA J. 1970, 8, 2004–2009. [Google Scholar] [CrossRef]
- Thomée, V. A high order parallel method for time discretization of parabolic type equations based on Laplace transformation and quadrature. Int. J. Numer. Anal. Model. 2005, 2, 85–96. [Google Scholar]
- McLean, W.; Thomée, V. Numerical solution via Laplace transforms of a fractional order evolution equation. J. Integral Equ. Appl. 2010, 22, 57–94. [Google Scholar] [CrossRef]
- López-Fernández, M.; Palencia, C.; Schädle, A. A spectral order method for inverting sectorial Laplace transforms. SIAM J. Numer. Anal. 2006, 44, 1332–1350. [Google Scholar] [CrossRef]
- Kamran; Uddin, M.; Ali, A. On the approximation of time-fractional telegraph equations using localized kernel-based method. Adv. Differ. Equ. 2018, 2018, 305. [Google Scholar] [CrossRef]
- Schaback, R. Error estimates and condition numbers for radial basis function interpolation. Adv. Comput. Math. 1995, 3, 251–264. [Google Scholar] [CrossRef]
- Trefethen, L.N.; Bau, D. Numerical Linear Algebra; SIAM: Philadelphia, PA, USA, 1997. [Google Scholar]
- Weideman, J.A.C. Optimizing Talbot’s contours for the inversion of the Laplace transform. SIAM J. Numer. Anal. 2006, 44, 2342–2362. [Google Scholar] [CrossRef]
- Talbot, A. The accurate numerical inversion of Laplace transforms. IMA J. Appl. Math. 1979, 23, 97–120. [Google Scholar] [CrossRef]
- Martensen, E. Zur numerischen auswertung uneigentlicher integrale. Z. Angew. Math. Mech 1968, 48, T83–T85. [Google Scholar]
- Dingfelder, B.; Weideman, J.A.C. An improved Talbot method for numerical Laplace transform inversion. Numer. Algorithms 2015, 68, 167–183. [Google Scholar] [CrossRef]




| N | n | M | ||||||
|---|---|---|---|---|---|---|---|---|
| 20 | 5 | 24 | 0.5 | 1.53 | 5.46 | 0.089142 | 5.55 | 0.089602 |
| 30 | 0.8 | 1.05 | 5.98 | 0.194214 | 5.93 | 0.110046 | ||
| 50 | 1.3 | 1.43 | 1.41 | 0.133385 | 1.40 | 0.141561 | ||
| 60 | 1.6 | 1.20 | 2.84 | 0.118387 | 5.13 | 0.105559 | ||
| 70 | 1.9 | 1.06 | 1.66 | 0.122090 | 1.46 | 0.109360 | ||
| 80 | 2.1 | 1.41 | 6.72 | 0.110556 | 9.10 | 0.108059 | ||
| 100 | 2.7 | 1.15 | 9.11 | 0.132338 | 9.11 | 0.131337 | ||
| 75 | 5 | 26 | 2.0 | 1.23 | 2.94 | 0.108321 | 2.92 | 0.108939 |
| 7 | 4.5 | 1.08 | 2.99 | 0.111992 | 2.96 | 0.108220 | ||
| 8 | 5.5 | 1.05 | 5.11 | 0.112198 | 5.05 | 0.107458 | ||
| 9 | 6.2 | 1.21 | 7.79 | 0.117348 | 7.70 | 0.123790 | ||
| 10 | 6.9 | 1.06 | 8.26 | 0.113088 | 8.16 | 0.120238 | ||
| 12 | 7.8 | 1.09 | 7.12 | 0.141167 | 7.06 | 0.386028 | ||
| [6] | 4.07 | 4.56 | ||||||
| N | n | M | ||||
|---|---|---|---|---|---|---|
| 20 | 5 | 26 | 1.26 | 0.179173 | 1.26 | 0.104272 |
| 40 | 4.37 | 0.125094 | 4.44 | 0.133066 | ||
| 60 | 1.34 | 0.150076 | 1.34 | 0.132823 | ||
| 70 | 1.28 | 0.210703 | 1.31 | 0.121223 | ||
| 80 | 1.48 | 0.126827 | 1.51 | 0.158628 | ||
| 100 | 3.28 | 0.171984 | 3.29 | 0.141549 | ||
| 75 | 5 | 28 | 1.18 | 0.252266 | 1.20 | 0.130174 |
| 7 | 6.86 | 0.191000 | 6.99 | 0.129424 | ||
| 8 | 6.31 | 0.116571 | 6.42 | 0.142768 | ||
| 12 | 3.35 | 0.132618 | 3.37 | 0.148221 | ||
| 16 | 4.03 | 0.146538 | 4.04 | 0.147644 | ||
| [6] | 3.36 | 2.96 | ||||
| Exact Solution | Method of [15] | Our Method | |||
|---|---|---|---|---|---|
| Approximate Solution | Approximate Solution | ||||
| 0.1620 | 0.1618 | 1.56 | 0.1620 | 4.35 | |
| 0.5120 | 0.5105 | 1.40 | 0.5119 | 1.33 | |
| 0.8820 | 0.8790 | 2.97 | 0.8818 | 1.14 | |
| 1.1520 | 1.1477 | 4.29 | 1.1517 | 2.66 | |
| 1.2500 | 1.2450 | 4.97 | 1.2497 | 2.89 | |
| 1.1520 | 1.1471 | 4.80 | 1.1517 | 2.97 | |
| 0.8820 | 0.8781 | 3.81 | 0.8818 | 2.39 | |
| 0.5120 | 0.5097 | 2.27 | 0.5118 | 1.67 | |
| 0.1620 | 0.1612 | 7.20 | 0.1619 | 8.13 | |
| M | n | N | ||||
|---|---|---|---|---|---|---|
| 26 | 30 | 20 | 1.99 | 1.97 | 1.96 | 1.95 |
| 22 | 1.30 | 1.29 | 1.29 | 1.28 | ||
| 24 | 9.67 | 9.65 | 9.63 | 9.63 | ||
| 26 | 7.97 | 7.96 | 7.95 | 7.95 | ||
| 28 | 6.81 | 6.79 | 6.77 | 6.76 | ||
| 28 | 26 | 25 | 4.61 | 4.56 | 4.50 | 4.48 |
| 27 | 4.48 | 4.42 | 4.37 | 4.35 | ||
| 28 | 2.87 | 2.83 | 2.80 | 2.78 | ||
| 29 | 8.38 | 8.37 | 8.35 | 8.35 | ||
| 30 | 8.32 | 8.31 | 8.30 | 8.30 |
| M | n | N | ||||
|---|---|---|---|---|---|---|
| 24 | 30 | 16 | 6.83 | 6.80 | 6.78 | 6.77 |
| 18 | 7.84 | 7.82 | 7.79 | 7.78 | ||
| 20 | 8.30 | 8.28 | 8.27 | 8.26 | ||
| 22 | 7.82 | 7.80 | 7.78 | 7.77 | ||
| 24 | 7.88 | 7.85 | 7.81 | 7.79 | ||
| 26 | 9.95 | 9.87 | 9.79 | 9.76 | ||
| 26 | 25 | 26 | 2.86 | 2.82 | 2.79 | 2.77 |
| 26 | 2.63 | 2.61 | 2.58 | 2.57 | ||
| 27 | 1.51 | 1.50 | 1.49 | 1.49 | ||
| 28 | 1.03 | 1.02 | 1.02 | 1.01 | ||
| 29 | 9.04 | 8.99 | 8.93 | 8.90 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kamran; Khan, S.; Alhazmi, S.E.; Alotaibi, F.M.; Ferrara, M.; Ahmadian, A. On the Numerical Approximation of Mobile-Immobile Advection-Dispersion Model of Fractional Order Arising from Solute Transport in Porous Media. Fractal Fract. 2022, 6, 445. https://doi.org/10.3390/fractalfract6080445
Kamran, Khan S, Alhazmi SE, Alotaibi FM, Ferrara M, Ahmadian A. On the Numerical Approximation of Mobile-Immobile Advection-Dispersion Model of Fractional Order Arising from Solute Transport in Porous Media. Fractal and Fractional. 2022; 6(8):445. https://doi.org/10.3390/fractalfract6080445
Chicago/Turabian StyleKamran, Shahzad Khan, Sharifah E. Alhazmi, Fahad M. Alotaibi, Massimiliano Ferrara, and Ali Ahmadian. 2022. "On the Numerical Approximation of Mobile-Immobile Advection-Dispersion Model of Fractional Order Arising from Solute Transport in Porous Media" Fractal and Fractional 6, no. 8: 445. https://doi.org/10.3390/fractalfract6080445
APA StyleKamran, Khan, S., Alhazmi, S. E., Alotaibi, F. M., Ferrara, M., & Ahmadian, A. (2022). On the Numerical Approximation of Mobile-Immobile Advection-Dispersion Model of Fractional Order Arising from Solute Transport in Porous Media. Fractal and Fractional, 6(8), 445. https://doi.org/10.3390/fractalfract6080445







