Integer and Fractional-Order Sliding Mode Control Schemes in Wind Energy Conversion Systems: Comprehensive Review, Comparison, and Technical Insight
Abstract
:1. Introduction
2. Motivation of This Study
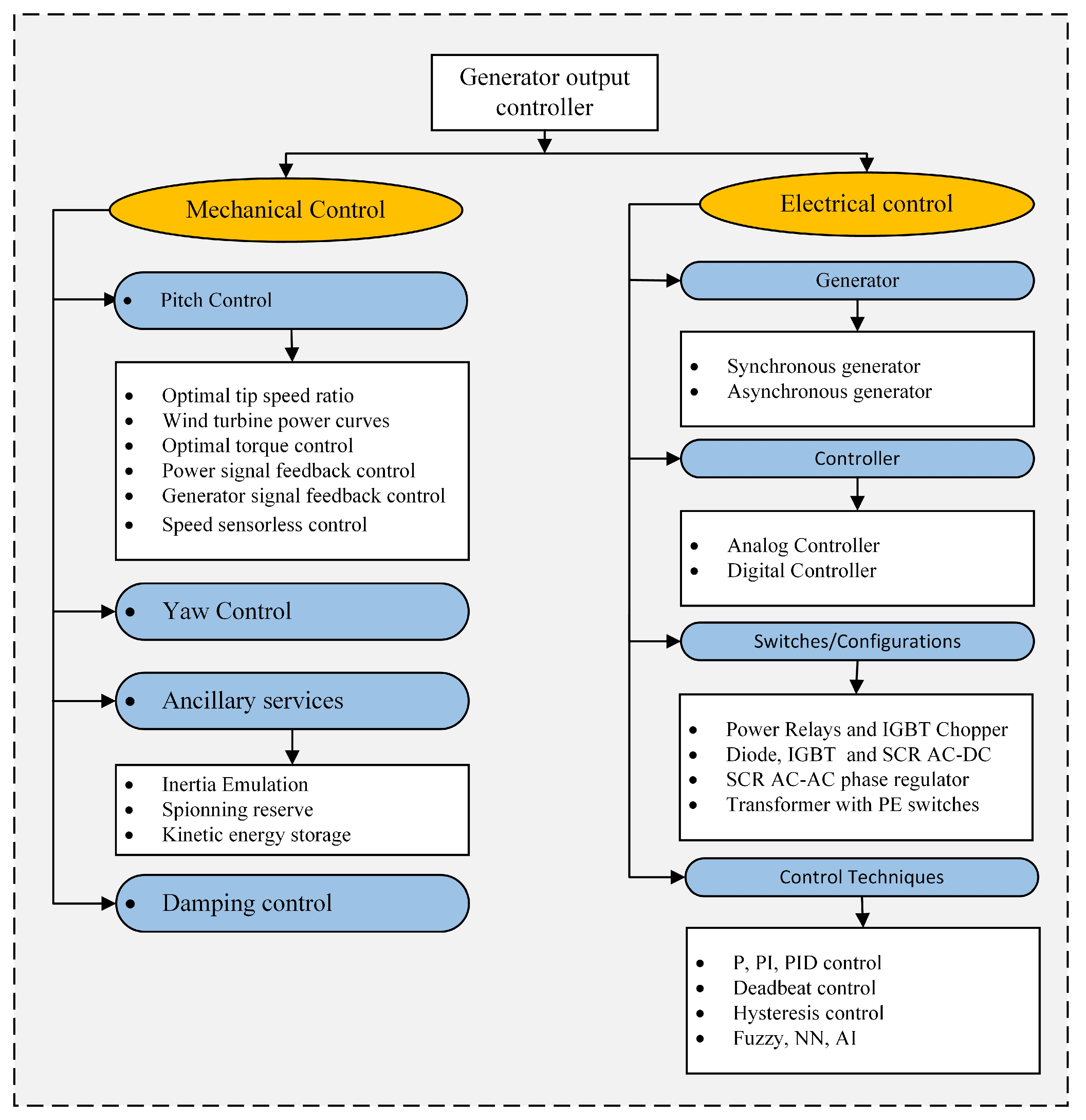
3. Modeling of WECS and Generators for Closed Loop Control
3.1. Wind Turbine Model
3.2. Doubly Fed Induction Generator Model
3.3. Grid Model
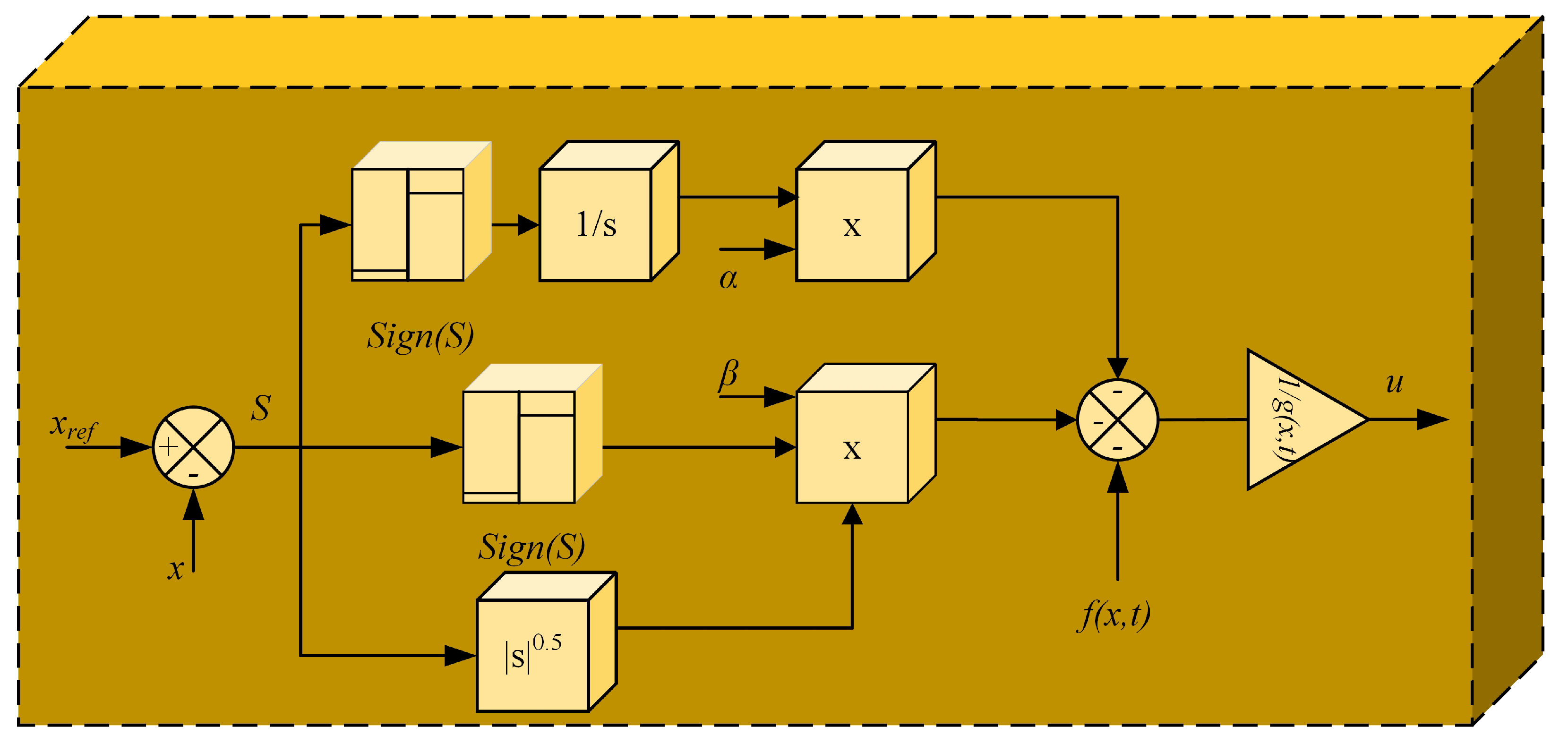
4. Sliding Mode Control Theory
Errors Definition for SMC and Its Variants
5. Sliding Mode Control for DFIG Based WECS
5.1. First-Order Sliding Mode Control Schemes
5.2. Supertwisitng Sliding Mode Control
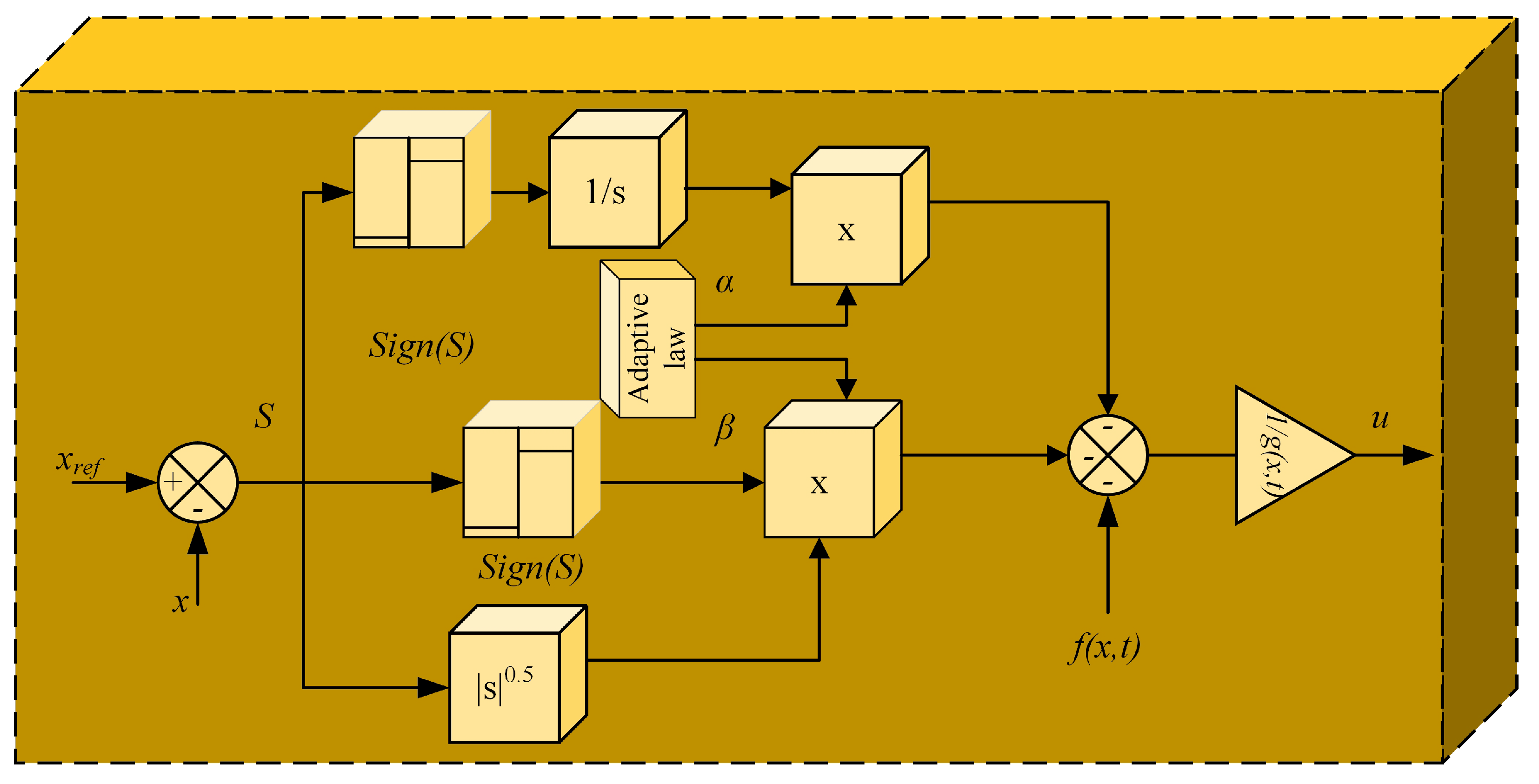
5.3. Adaptive High-Order Sliding Mode Control
5.4. Integral Type Sliding Mode Control
5.5. Terminal Sliding Mode Control
5.6. Fuzzy logic Sliding Mode Control
6. Passivity and AI Based Sliding Mode Control
7. Fractional-Order Sliding Mode Control Schemes
| Technique | Ref. | Year | Errors | Surfaces | Generator, Control, and Converter-Type Hardware | Remarks |
|---|---|---|---|---|---|---|
| Passivity-based SMC | [215] | 2021 | where , = stationary value of x | = = the is the energy function obtained using energy-based model of DFIG. | Brushless DFIG RSC control No | An energy or passivity-based SMC is presented in this paper. Energy-based model of brushless DFIG is also presented, and practical implementation issues are also depicted in the article. |
| [216] | 2018 | where | = | Multipole SG Yes | A passivity-based SMC is presented in this paper. Extensive analysis was conducted in this paper to evaluate the passivity-based SMC performance. | |
| AI-based SMC | [184] | 2014 | IG RSC control No | Feed forward ANN is used to estimate the sigmoid function in the discontinuous control part of SMC. | ||
| [217] | 2018 | where are the states estimated using high-order neural network trained by extended Kalman filter | DFIG RSC control No | A neural network of high order is used and trained online using extended Kalman filter. The estimated states are then used to proposed a SMC scheme. |
7.1. Fractional-Order Sliding Mode Control Design
7.2. Fractional-Order Terminal Sliding Mode Control Schemes
7.3. Fractional-Order Super Twisting Sliding Mode Control Schemes
7.4. Fractional-Order Fuzzy Sliding Mode Control
8. Comparative Analysis of Integer and Fractional-Order SMC Schemes
8.1. Mathematical Comparison
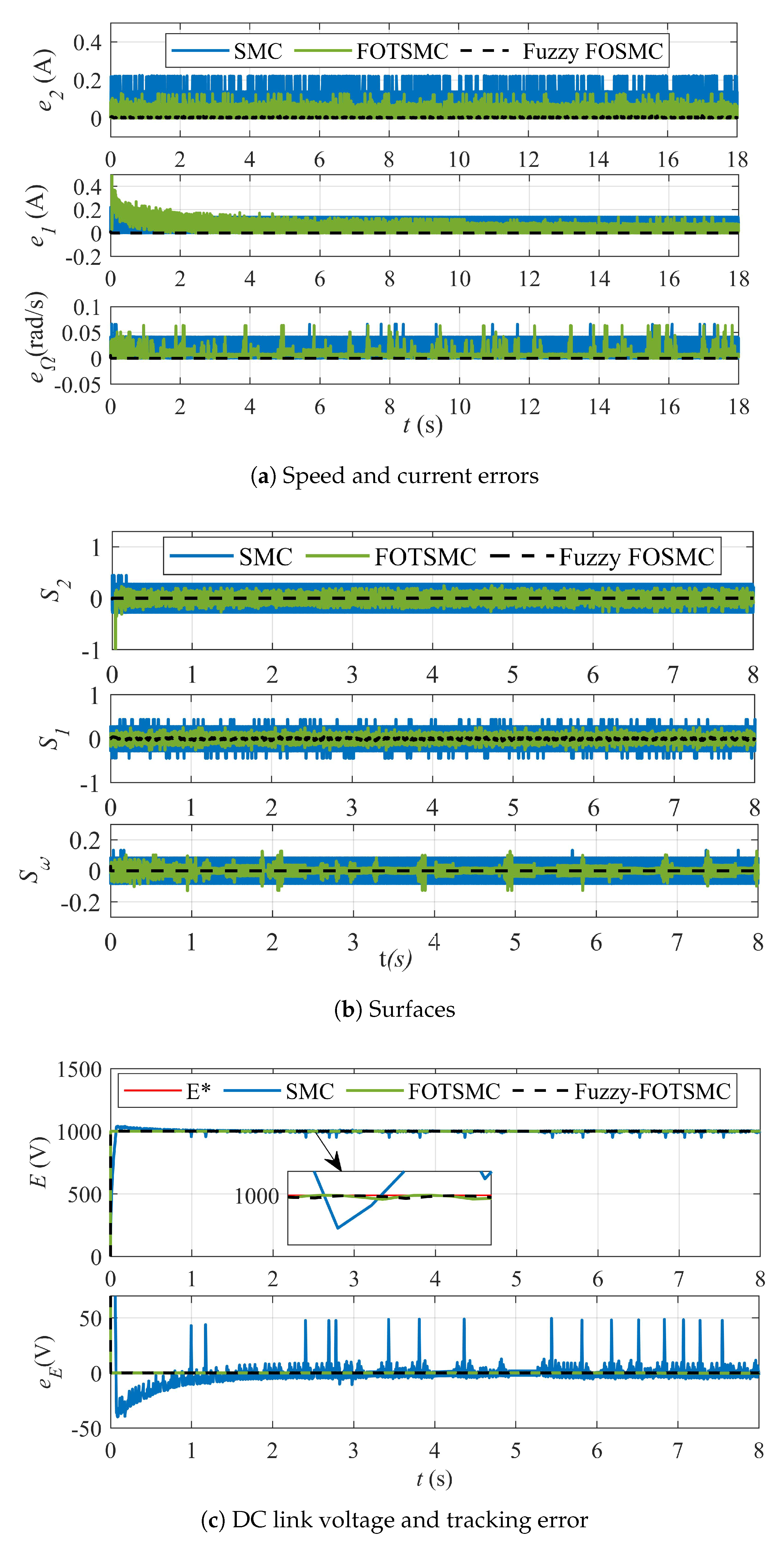
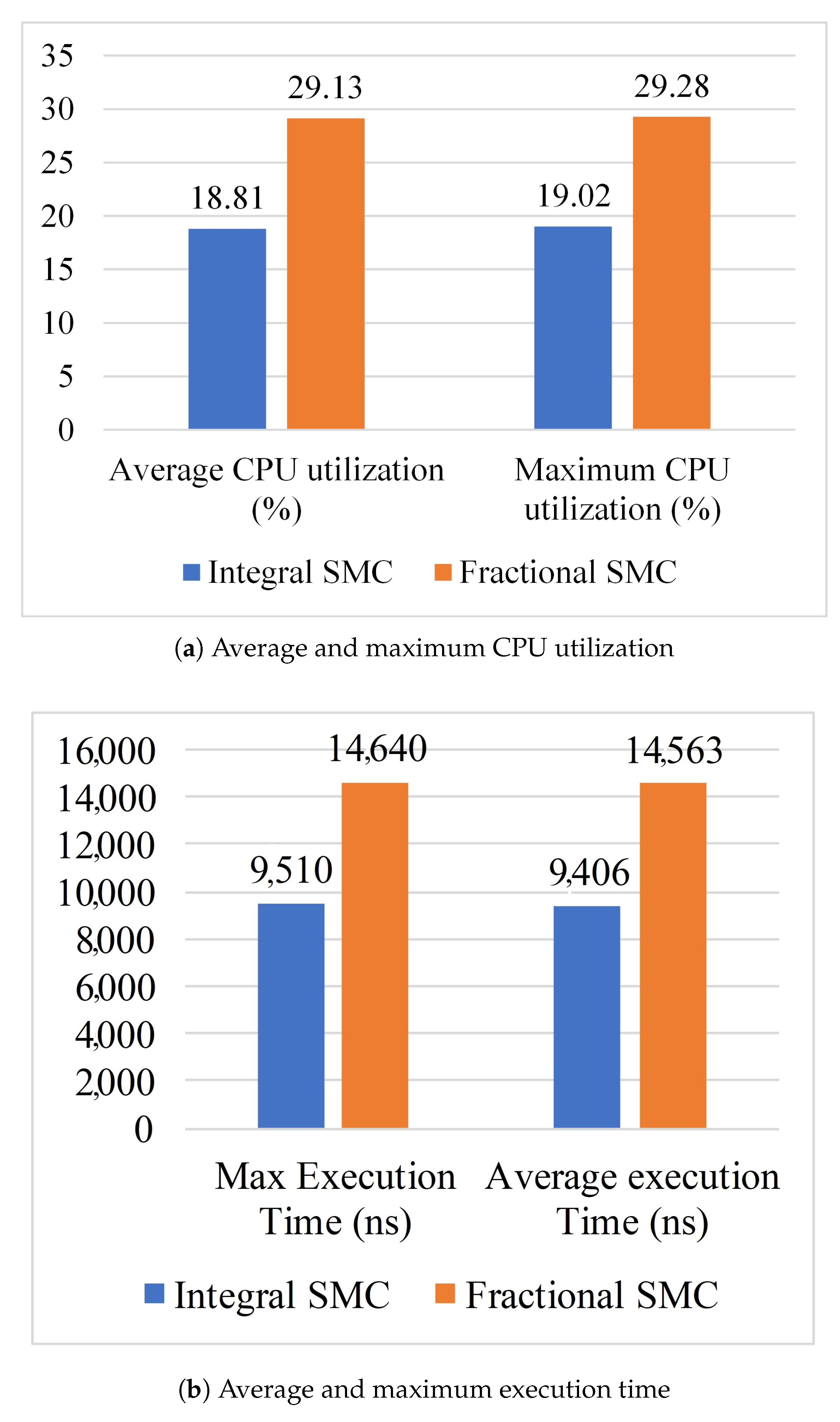
8.2. Case Study: Implementation and Numerical Comparison
9. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- IEA. World Energy Balances; OECD Publishing: Paris, France, 2018; Available online: https://www.oecd-ilibrary.org/energy/world-energy-balances-2018_world_energy_bal-2018-en (accessed on 15 January 2022).
- Sami, I.; Ullah, S.; Ullah, N.; Ro, J.-S.J. Sensorless fractional order composite sliding mode control design for wind generation system. Isa Trans. 2021, 111, 275–289. [Google Scholar] [CrossRef] [PubMed]
- Nazir, M.S.; Ali, N.; Bilal, M.; Iqbal, H.M.J. Potential environmental impacts of wind energy development: A global perspective. Curr. Opin. Environ. Sci. Health 2020, 13, 85–90. [Google Scholar] [CrossRef]
- Sonderegger, R.C.; Henderson, D.; Bubb, S.; Steury, J.J. Distributed asset insight. IEEE Power Energy Mag. 2004, 2, 32–39. [Google Scholar] [CrossRef]
- Puttgen, H.B.; Macgregor, P.R.; Lambert, F.C.J. Distributed generation: Semantic hype or the dawn of a new era? IEEE Power Energy Mag. 2003, 1, 22–29. [Google Scholar] [CrossRef]
- Rahman, S.J. Green power: What is it and where can we find it? IEEE Power Energy Mag. 2003, 1, 30–37. [Google Scholar] [CrossRef]
- Martin, G.J. Renewable energy gets the “green” light in Chicago. IEEE Power Energy Mag. 2003, 1, 34–39. [Google Scholar] [CrossRef]
- Kumar, D.; Chatterjee, K.J. A review of conventional and advanced MPPT algorithms for wind energy systems. Renew. Sustain. Energy Rev. 2016, 55, 957–970. [Google Scholar] [CrossRef]
- Fernando, D.B.; Hernán, d.B.; Ricardo, J.M. Wind Turbine Control Systems: Principles, Modelling and Gain Scheduling Design; advances in industrial control; Springer: London, UK, 2006. [Google Scholar]
- Xu, F.; Zhang, J.; Cheng, M. Analysis of double objectives control for wind power generation system with frequency separation. In Proceedings of the 2011 4th International Conference on Electric Utility Deregulation and Restructuring and Power Technologies (DRPT), Weihai, China, 6–9 July 2011; pp. 1366–1371. [Google Scholar]
- Abad, G.; Lopez, J.; Rodriguez, M.; Marroyo, L.; Iwanski, G. Doubly Fed Induction Machine: Modeling and Control for Wind Energy Generation; John Wiley & Sons: New York, NY, USA, 2011. [Google Scholar]
- Baroudi, J.A.; Dinavahi, V.; Knight, A.M. A review of power converter topologies for wind generators. Renew. Energy 2007, 32, 2369–2385. [Google Scholar] [CrossRef]
- Iglesias, R.L.; Arantegui, R.L.; Alonso, M.A.J. Power electronics evolution in wind turbines—A market-based analysis. Renew. Sustain. Energy Rev. 2011, 15, 4982–4993. [Google Scholar] [CrossRef]
- Chakraborty, A. Advancements in power electronics and drives in interface with growing renewable energy resources. Renew. Sustain. Energy Rev. 2011, 15, 1816–1827. [Google Scholar] [CrossRef]
- Boldea, I. Wound Rotor Induction Generators (Wrigs). Variable Speed Generators. Politehnica University of Timisoara; CRC Press: Boca Raton, FL, USA, 2015; pp. 1–36. [Google Scholar]
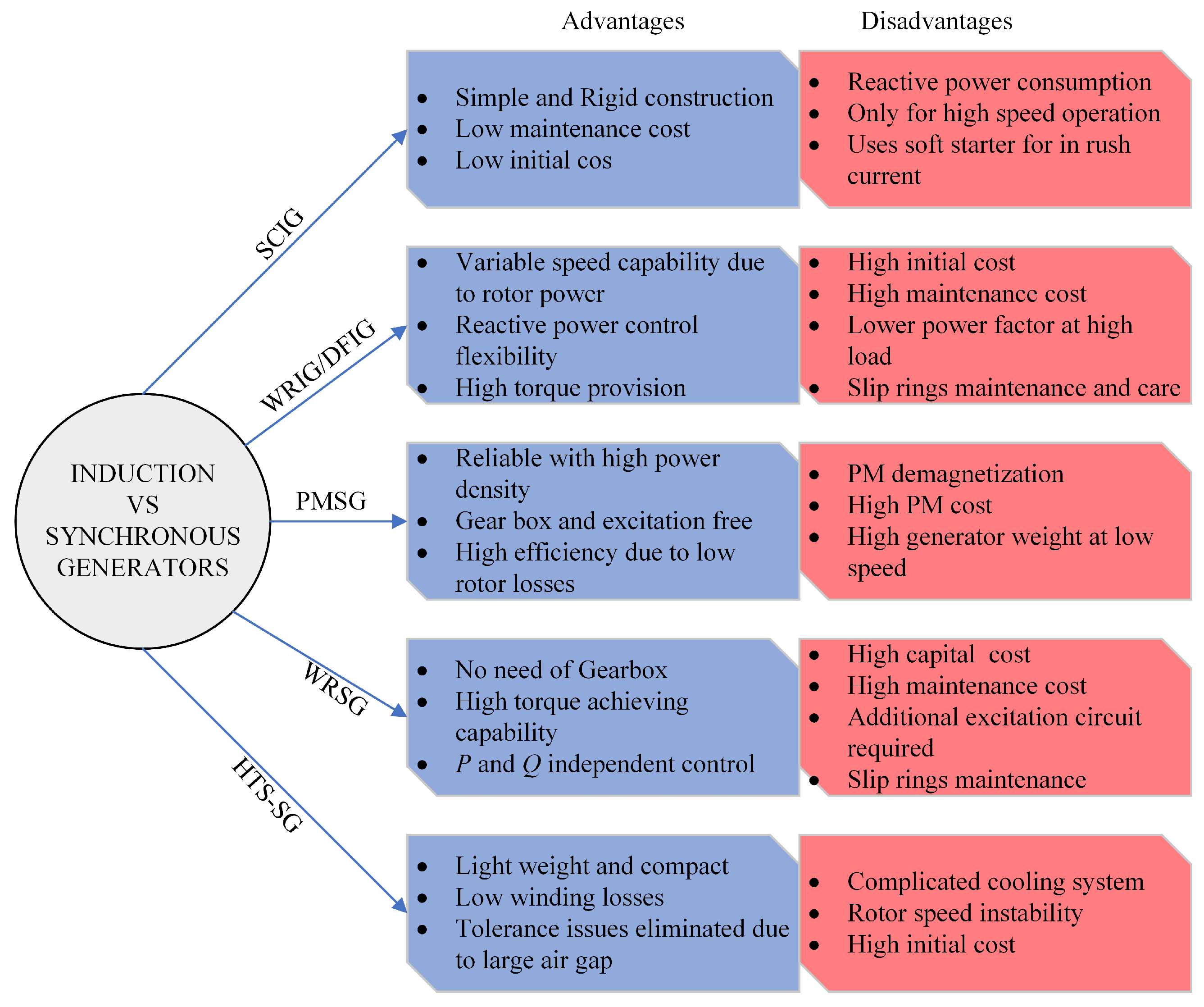
- Li, H.; Chen, Z.J. Overview of different wind generator systems and their comparisons. IET Renew. Power Gener. 2008, 2, 123–138. [Google Scholar] [CrossRef]
- Bellarmine, G.T.; Urquhart, J. Wind energy for the 1990s and beyond. Energy Convers. Manag. 1996, 37, 1741–1752. [Google Scholar] [CrossRef]
- Sule, A.H.; Mokhtar, A.S.B.; Jamian, J.J.B. Optimal PI Pitch Control of SCIG Wind Turbine Using Grey Wolf Optimizer for Dynamic Stability. Nov. Perspect. Eng. Res. 2022, 7, 45–68. [Google Scholar]
- Zribi, M.; Alrifai, M.; Rayan, M.J. Sliding mode control of a variable-speed wind energy conversion system using a squirrel cage induction generator. Energies 2017, 10, 604. [Google Scholar] [CrossRef]
- Naik, K.; Gupta, C. Fuzzy logic based pitch angle controller/or SCIG based wind energy system. In Proceedings of the 2017 Recent Developments in Control, Automation & Power Engineering (RDCAPE), Noida, India, 26–27 October 2017; pp. 60–65. [Google Scholar]
- Parida, A.; Chatterjee, D.J. Integrated DFIG–SCIG-based wind energy conversion system equipped with improved power generation capability. IET Gener. Transm. Distrib. 2017, 11, 3791–3800. [Google Scholar] [CrossRef]
- Torrey, D.A. Variable-reluctance generators in wind-energy systems. In Proceedings of the IEEE Power Electronics Specialist Conference-PESC’93, Seattle, WA, USA, 20–24 June 1993; pp. 561–567. [Google Scholar]
- Arifin, A.; Al-Bahadly, I. Switched reluctance generator for variable speed wind energy applications. Smart Grid Renew. Energy 2011, 2, 27. [Google Scholar] [CrossRef]
- Xia, Y.; Ahmed, K.H.; Williams, B.W.J. A new maximum power point tracking technique for permanent magnet synchronous generator based wind energy conversion system. IEEE Trans. Power Electron. 2011, 26, 3609–3620. [Google Scholar] [CrossRef]
- Rolan, A.; Luna, A.; Vazquez, G.; Aguilar, D.; Azevedo, G. Modeling of a variable speed wind turbine with a permanent magnet synchronous generator. In Proceedings of the 2009 IEEE International Symposium on Industrial Electronics, Seoul, Korea, 5–8 July 2009; pp. 734–739. [Google Scholar]
- Levy, D.J. Stand alone induction generators. Electr. Power Syst. Res. 1997, 41, 191–201. [Google Scholar] [CrossRef]
- Blaabjerg, F.; Ma, K. Future on power electronics for wind turbine systems. IEEE J. Emerg. Sel. Top. Power Electron. 2013, 1, 139–152. [Google Scholar] [CrossRef]
- Hatziadoniu, C.; Nikolov, E.; Pourboghrat, F.J. Power conditioner control and protection for distributed generators and storage. IEEE Trans. Power Syst. 2003, 18, 83–90. [Google Scholar] [CrossRef]
- Santelo, T.N.; de Oliveira, C.M.R.; Maciel, C.D.; de A Monteiro, J.R.B. Wind Turbine Failures Review and Trends. J. Control. Autom. Electr. Syst. 2022, 33, 505–521. [Google Scholar] [CrossRef]
- Hansen, A.D.; Iov, F.; Blaabjerg, F.; Hansen, L.H.J. Review of contemporary wind turbine concepts and their market penetration. Wind. Eng. 2004, 28, 247–263. [Google Scholar] [CrossRef]
- Chinchilla, M.; Arnaltes, S.; Burgos, J.C. Control of permanent-magnet generators applied to variable-speed wind-energy systems connected to the grid. IEEE Trans. Energy Convers. 2006, 21, 130–135. [Google Scholar] [CrossRef]
- Yamamura, N.; Ishida, M.; Hori, T. A simple wind power generating system with permanent magnet type synchronous generator. In Proceedings of the IEEE 1999 International Conference on Power Electronics and Drive Systems. PEDS’99 (Cat. No. 99TH8475), Hong Kong, China, 27–29 July 1999; Volume 2, pp. 849–854. [Google Scholar]
- Muller, S.; Deicke, M.; Doncker, R.W.J.D. Doubly fed induction generator systems for wind turbines. IEEE Ind. Appl. Mag. 2002, 8, 26–33. [Google Scholar] [CrossRef]
- Santos-Martin, D.; Rodriguez-Amenedo, J.L.; Arnaltes, S.J. Providing ride-through capability to a doubly fed induction generator under unbalanced voltage dips. IEEE Trans. Power Electron. 2009, 24, 1747–1757. [Google Scholar] [CrossRef]
- Blaabjerg, F.; Chen, Z.; Kjaer, S.B. Power electronics as efficient interface in dispersed power generation systems. IEEE Trans. Power Electron. 2004, 19, 1184–1194. [Google Scholar] [CrossRef]
- Sami, I.; Ullah, N.; Muyeen, S.; Techato, K.; Chowdhury, M.S.; Ro, J.-S.J. Control methods for standalone and grid connected micro-hydro power plants with synthetic inertia frequency support: A comprehensive review. IEEE Access 2020, 8, 176313–176329. [Google Scholar] [CrossRef]
- Islam, M.R.; Guo, Y.; Zhu, J.J. A review of offshore wind turbine nacelle: Technical challenges, and research and developmental trends. Renew. Sustain. Energy Rev. 2014, 33, 161–176. [Google Scholar] [CrossRef]
- Zhu, Z.; Hu, J.J. Electrical machines and power-electronic systems for high-power wind energy generation applications: Part II–power electronics and control systems. Compel- Int. J. Comput. Math. Electr. Electron. Eng. 2013, 32. [Google Scholar] [CrossRef]
- Melício, R.; Mendes, V.; Catalão, J.P.d.S.J. Fractional-order control and simulation of wind energy systems with PMSG/full-power converter topology. Energy Convers. Manag. 2010, 51, 1250–1258. [Google Scholar] [CrossRef]
- Slootweg, J.; Haan, S.D.; Polinder, H.; Kling, W.J. General model for representing variable speed wind turbines in power system dynamics simulations. IEEE Trans. Power Syst. 2010, 18, 144–151. [Google Scholar] [CrossRef]
- Chen, Z.; Spooner, E. Grid power quality with variable speed wind turbines. IEEE Trans. Energy Convers. 2001, 16, 148–154. [Google Scholar] [CrossRef]
- Yazdani, A.; Iravani, R.J. A neutral-point clamped converter system for direct-drive variable-speed wind power unit. IEEE Trans. Energy Convers. 2006, 21, 596–607. [Google Scholar] [CrossRef]
- Carrasco, J.M.; Franquelo, L.G.; Bialasiewicz, J.T.; Galván, E.; PortilloGuisado, R.C.; Prats, M.M.; Moreno-Alfonso, N. Power-electronic systems for the grid integration of renewable energy sources: A survey. IEEE Trans. Ind. Electron. 2006, 53, 1002–1016. [Google Scholar] [CrossRef]
- Chen, Z.; Guerrero, J.M.; Blaabjerg, F. A review of the state of the art of power electronics for wind turbines. IEEE Trans. Power Electron. 2009, 24, 1859–1875. [Google Scholar] [CrossRef]
- Amei, K.; Takayasu, Y.; Ohji, T.; Sakui, M. A maximum power control of wind generator system using a permanent magnet synchronous generator and a boost chopper circuit. In Proceedings of the Power Conversion Conference-Osaka 2002 (Cat. No. 02TH8579), Osaka, Japan, 2–5 April 2002; Volume 3, pp. 1447–1452. [Google Scholar]
- Datta, R.; Ranganathan, V. Variable-speed wind power generation using doubly fed wound rotor induction machine-a comparison with alternative schemes. IEEE Trans. Energy Convers. 2002, 17, 414–421. [Google Scholar] [CrossRef]
- Suzuki, T.; Okitsu, H.; Kawahito, T. Characteristics of a small wind-power system with DC generator. IEE Proc. -Electr. Power Appl. 1982, 129, 217–220. [Google Scholar] [CrossRef]
- Yang, G.; Li, H. Design and analysis of a newly brushless DC wind generator. In Proceedings of the 2008 World Automation Congress, Waikoloa, HI, USA, 28 September–2 October 2008; pp. 1–5. [Google Scholar]
- Buehring, I.; Freris, L. Control policies for wind-energy conversion systems. IET J. 1981, 128, 253–261. [Google Scholar] [CrossRef]
- Abdullah, M.A.; Yatim, A.; Tan, C.W.; Saidur, R.J. A review of maximum power point tracking algorithms for wind energy systems. Renew. Sustain. Energy Rev. 2012, 16, 3220–3227. [Google Scholar] [CrossRef]
- Kooning, J.D.D.; Gevaert, L.; de Vyver, J.V.; Vandoorn, T.L.; Vandevelde, L. Online estimation of the power coefficient versus tip-speed ratio curve of wind turbines. In Proceedings of the IECON 2013-39th Annual Conference of the IEEE Industrial Electronics Society, Vienna, Austria, 10–13 November 2013; pp. 1792–1797. [Google Scholar]
- Knight, A.M.; Peters, G.E.J. Simple wind energy controller for an expanded operating range. IEEE Trans. Energy Convers. 2005, 20, 459–466. [Google Scholar] [CrossRef]
- Nasiri, M.; Milimonfared, J.; Fathi, S.J. Modeling, analysis and comparison of TSR and OTC methods for MPPT and power smoothing in permanent magnet synchronous generator-based wind turbines. Energy Convers. Manag. 2014, 86, 892–900. [Google Scholar] [CrossRef]
- Yaramasu, V.; Wu, B. Basics of Wind Energy Conversion Systems (Wecs); Wiley-IEEE Press: New York, NY, USA, 2017. [Google Scholar]
- Tan, K.; Islam, S.J. Optimum control strategies in energy conversion of PMSG wind turbine system without mechanical sensors. IEEE Trans. Energy Convers. 2004, 19, 392–399. [Google Scholar] [CrossRef]
- Ganjefar, S.; Ghassemi, A.A.; Ahmadi, M.M.J. Improving efficiency of two-type maximum power point tracking methods of tip-speed ratio and optimum torque in wind turbine system using a quantum neural network. Energy Convers. Manag. 2014, 67, 444–453. [Google Scholar] [CrossRef]
- Agarwal, V.; Aggarwal, R.K.; Patidar, P.; Patki, C.J. A novel scheme for rapid tracking of maximum power point in wind energy generation systems. IEEE Trans. Energy Convers. 2009, 25, 228–236. [Google Scholar] [CrossRef]
- Yan, R.; Saha, T.K.J. A new tool to estimate maximum wind power penetration level: In perspective of frequency response adequacy. Appl. Energy 2015, 154, 209–220. [Google Scholar]
- Wei, C.; Zhang, Z.; Qiao, W.; Qu, L.J. Reinforcement-learning-based intelligent maximum power point tracking control for wind energy conversion systems. IEEE Trans. Ind. Electron. 2015, 62, 6360–6370. [Google Scholar] [CrossRef]
- Simoes, M.G.; Bose, B.K.; Spiegel, R.J.J. Fuzzy logic based intelligent control of a variable speed cage machine wind generation system. IEEE Trans. Power Electron. 1997, 12, 87–95. [Google Scholar] [CrossRef]
- Hilloowala, R.M.; Sharaf, A.M. A rule-based fuzzy logic controller for a PWM inverter in a stand alone wind energy conversion scheme. In Proceedings of the Conference Record of the 1993 IEEE Industry Applications Conference Twenty-Eighth IAS Annual Meeting, Toronto, ON, Canada, 2–8 October 1993; pp. 2066–2073. [Google Scholar]
- Chen, Z.; Gomez, S.A.; McCormick, M. A fuzzy logic controlled power electronic system for variable speed wind energy conversion systems. In Proceedings of the 8th International Conference on Power Electronics and Variable Speed Drives, London, UK, 18–19 September 2000. [Google Scholar]
- Mohamed, A.Z.; Eskander, M.N.; Ghali, F.A.J. Fuzzy logic control based maximum power tracking of a wind energy system. Renew. Energy 2001, 23, 235–245. [Google Scholar] [CrossRef]
- Kumar, G.B. Optimal power point tracking of solar and wind energy in a hybrid wind solar energy system. Int. J. Energy Environ. Eng. 2022, 13, 77–103. [Google Scholar] [CrossRef]
- Morimoto, S.; Nakayama, H.; Sanada, M.; Takeda, Y.J. Sensorless output maximization control for variable-speed wind generation system using IPMSG. IEEE Trans. Ind. Appl. 2005, 41, 60–67. [Google Scholar] [CrossRef]
- Hui, J.; Bakhshai, A.; Jain, P.K. An adaptive approximation method for maximum power point tracking (MPPT) in wind energy systems. In Proceedings of the 2011 IEEE Energy Conversion Congress and Exposition, Phoenix, AZ, USA, 17–22 September 2011; pp. 2664–2669. [Google Scholar]
- Yessef, M.; Bossoufi, B.; Taoussi, M.; Lagrioui, A.; Chojaa, H. Overview of control strategies for wind turbines: ANNC, FLC, SMC, BSC, and PI controllers. Wind Energy 2022. [Google Scholar] [CrossRef]
- Noussi, K.; Abouloifa, A.; Katir, H.; Lachkar, I.; Aouadi, C.; Aourir, M.; Otmani, F.E. Integral Backstepping Control Based on High Gain Observer for DFIG-Based Wind Energy Conversion System. IFAC-PapersOnLine 2022, 55, 653–658. [Google Scholar] [CrossRef]
- Civelek, Z.; Lüy, M.; Çam, E.; Mamur, H. A new fuzzy logic proportional controller approach applied to individual pitch angle for wind turbine load mitigation. Renew. Energy 2017, 111, 708–717. [Google Scholar] [CrossRef]
- Medjber, A.; Guessoum, A.; Belmili, H.; Mellit, A.J. New neural network and fuzzy logic controllers to monitor maximum power for wind energy conversion system. Energy 2016, 106, 137–146. [Google Scholar] [CrossRef]
- Lin, W.-M.; Hong, C.-M.; Cheng, F.-S.J. Fuzzy neural network output maximization control for sensorless wind energy conversion system. Energy 2010, 35, 592–601. [Google Scholar] [CrossRef]
- Pichan, M.; Rastegar, H.; Monfared, M.J. Two fuzzy-based direct power control strategies for doubly-fed induction generators in wind energy conversion systems. Energy 2013, 51, 154–162. [Google Scholar] [CrossRef]
- Yang, B.; Jiang, L.; Wang, L.; Yao, W.; Wu, Q.J. Nonlinear maximum power point tracking control and modal analysis of DFIG based wind turbine. Int. J. Electr. Power Energy Syst. 2016, 74, 429–436. [Google Scholar] [CrossRef]
- Liu, X.; Kong, X.J. Nonlinear model predictive control for DFIG-based wind power generation. IEEE Trans. Autom. Sci. Eng. 2013, 11, 1046–1055. [Google Scholar] [CrossRef]
- Gani, A.; Mohammadi, K.; Shamshirband, S.; Altameem, T.A.; Petković, D.J. A combined method to estimate wind speed distribution based on integrating the support vector machine with firefly algorithm. Environ. Prog. Sustain. Energy 2016, 35, 867–875. [Google Scholar] [CrossRef]
- Chen, P.; Han, D.; Li, K.-C. Robust Adaptive Control of Maximum Power Point Tracking for Wind Power System. IEEE Access 2020, 8, 214538–214550. [Google Scholar] [CrossRef]
- Cao, Z.; Niu, Y.; Karimi, H.R.J.I.S. Sliding mode control of automotive electronic valve system under weighted try-once-discard protocol. Inf. Sci. 2020, 515, 324–340. [Google Scholar] [CrossRef]
- Surinkaew, T.; Ngamroo, I.J. Robust power oscillation damper design for DFIG-based wind turbine based on specified structure mixed H2/H∞ control. Renew. Energy 2014, 66, 15–24. [Google Scholar] [CrossRef]
- Das, S.; Subudhi, B.J. A robust active and reactive power control scheme with multiloop disturbance rejection for a wind energy conversion system. IEEE Trans. Sustain. Energy 2018, 10, 1664–1671. [Google Scholar] [CrossRef]
- Ghanbarpour, K.; Bayat, F.; Jalilvand, A.J. Dependable power extraction in wind turbines using model predictive fault tolerant control. Int. J. Electr. PowerEnergy Syst. 2020, 118, 105802. [Google Scholar] [CrossRef]
- Kühne, P.; Pöschke, F.; Schulte, H.J. Fault estimation and fault-tolerant control of the FAST NREL 5-MW reference wind turbine using a proportional multi-integral observer. Int. J. Adapt. Control. Process. 2018, 32, 568–585. [Google Scholar] [CrossRef]
- Aguilar, M.E.B.; Coury, D.V.; Reginatto, R.; Monaro, R.M.J. Multi-objective PSO applied to PI control of DFIG wind turbine under electrical fault conditions. Electr. Power Syst. Res. 2020, 180, 106081. [Google Scholar] [CrossRef]
- Shaker, M.S.; Patton, R.J.J. Active sensor fault tolerant output feedback tracking control for wind turbine systems via T–S model. Eng. Appl. Artif. Intell. 2014, 34, 1–12. [Google Scholar] [CrossRef]
- Kamal, E.; Aitouche, A.; Oueidat, M.J. Fuzzy fault-tolerant control of wind-diesel hybrid systems subject to sensor faults. IEEE Trans. Sustain. Energy 2013, 4, 857–866. [Google Scholar] [CrossRef]
- Alqahtani, A.H.; Utkin, V.I. Self-optimization of photovoltaic system power generation based on sliding mode control. In Proceedings of the IECON 2012-38th Annual Conference on IEEE Industrial Electronics Society, Montreal, QC, Canada, 25–28 October 2012; pp. 3468–3474. [Google Scholar]
- Levron, Y.; Shmilovitz, D.J. Maximum power point tracking employing sliding mode control. IEEE Trans. Circuits Syst. Regul. Pap. 2013, 60, 724–732. [Google Scholar] [CrossRef]
- Costa, J.P.D.; Pinheiro, H.; Degner, T.; Arnold, G. Robust controller for DFIGs of grid-connected wind turbines. IEEE Trans. Ind. Electron. 2010, 58, 4023–4038. [Google Scholar] [CrossRef]
- Pande, V.; Mate, U.; Kurode, S.J. Discrete sliding mode control strategy for direct real and reactive power regulation of wind driven DFIG. Electr. Power Syst. Res. 2013, 100, 73–81. [Google Scholar] [CrossRef]
- Majout, B.; Bossoufi, B.; Bouderbala, M.; Masud, M.; Al-Amri, J.F.; Taoussi, M.; El Mahfoud, M.; Motahhir, S.; Karim, M. Improvement of PMSG-Based Wind Energy Conversion System Using Developed Sliding Mode Control. Energies 2022, 15, 1625. [Google Scholar] [CrossRef]
- Ardjoun, S.A.E.M.; Abid, M. Fuzzy sliding mode control applied to a doubly fed induction generator for wind turbines. Turk. J. Electr. Eng. Comput. Sci. 2015, 23, 1673–1686. [Google Scholar] [CrossRef]
- Djoudi, A.; Chekireb, H.; Bacha, S.J. Low-cost sliding mode control of WECS based on DFIG with stability analysis. Turk. J. Electr. Eng. Comput. Sci. 2015, 23, 1698–1714. [Google Scholar] [CrossRef]
- Utkin, V.; Lee, H. Chattering problem in sliding mode control systems. In Proceedings of the VSS’06: International Workshop on Variable Structure Systems, Alghero, Italy, 5–7 June 2006; pp. 346–350. [Google Scholar]
- Kassem, A.M.; Hasaneen, K.M.; Yousef, A.M.J. Dynamic modeling and robust power control of DFIG driven by wind turbine at infinite grid. Int. J. Electr. Power Energy Syst. 2013, 44, 375–382. [Google Scholar] [CrossRef]
- Laghrouche, S.; Plestan, F.; Glumineau, A.J. Higher order sliding mode control based on integral sliding mode. Automatica 2007, 43, 531–537. [Google Scholar] [CrossRef]
- Zholtayev, D.; Rubagotti, M.; Do, T.D. Adaptive super-twisting sliding mode control for maximum power point tracking of PMSG-based wind energy conversion systems. Renew. Energy 2022, 183, 877–889. [Google Scholar] [CrossRef]
- Mazouz, F.; Belkacem, S.; Boukhalfa, G. Second Order Sliding Mode Control Based DPC of DFIG Using SVM. In Proceedings of the International Conference on Artificial Intelligence in Renewable Energetic Systems, Tipasa, Algeriapp, 24–26 November 2021; Springer: Cham, Siwtzerland, 2021; pp. 743–750. [Google Scholar]
- Dekali, Z.; Baghli, L.; Boumediene, A. Improved Super Twisting Based High Order Direct Power Sliding Mode Control of a Connected DFIG Variable Speed Wind Turbine. Period. Polytech. Electr. Eng. Comput. Sci. 2021. [Google Scholar] [CrossRef]
- Abdeddaim, S.; Betka, A. Optimal tracking and robust power control of the DFIG wind turbine. Int. J. Electr. Power Energy Syst. 2013, 49, 234–242. [Google Scholar] [CrossRef]
- Du, C.; Han, Y.; Li, S. A Barrier Function-Based Variable-Gain SOSM Power Control Scheme for DFIG Wind Turbine. In Proceedings of the 2021 Chinese Intelligent Automation Conference, Zhanjiang, China, 5–7 November 2021; Springer: Singapore, 2022; pp. 116–123. [Google Scholar]
- Hwang, S.; Park, J.B.; Joo, Y.H.J. Disturbance observer-based integral fuzzy sliding-mode control and its application to wind turbine system. IET Control. Theory Appl. 2019, 13, 1891–1900. [Google Scholar] [CrossRef]
- Song, Z.; Shi, T.; Xia, C.; Chen, W.J. A novel adaptive control scheme for dynamic performance improvement of DFIG-Based wind turbines. Energy 2012, 38, 104–117. [Google Scholar] [CrossRef]
- Ebrahimkhani, S.J. Robust fractional order sliding mode control of doubly-fed induction generator (DFIG)-based wind turbines. ISA Trans. 2016, 63, 343–354. [Google Scholar] [CrossRef] [PubMed]
- Xiong, L.; Li, P.; Ma, M.; Wang, Z.; Wang, J.J. Output power quality enhancement of PMSG with fractional order sliding mode control. Int. J. Electr. Power Energy Syst. 2020, 115, 105402. [Google Scholar] [CrossRef]
- Ullah, N.; Ali, M.A.; Ibeas, A.; Herrera, J.J. Adaptive fractional order terminal sliding mode control of a doubly fed induction generator-based wind energy system. IEEE Access 2017, 5, 21368–21381. [Google Scholar] [CrossRef]
- Sami, I.; Ullah, S.; Ali, Z.; Ullah, N.; Ro, J.-S.J. A Super Twisting Fractional Order Terminal Sliding Mode Control for DFIG-Based Wind Energy Conversion System. Energies 2020, 13, 2158. [Google Scholar] [CrossRef]
- Ullah, N.; Sami, I.; Chowdhury, M.S.; Techato, K.; Alkhammash, H.J. Artificial Intelligence Integrated Fractional Order Control of Doubly Fed Induction Generator Based Wind Energy System. IEEE Access 2020, 9, 5734–5748. [Google Scholar] [CrossRef]
- Tamaarat, A.; Benakcha, A.J. Performance of PI controller for control of active and reactive power in DFIG operating in a grid-connected variable speed wind energy conversion system. Front. Energy 2014, 8, 371–378. [Google Scholar] [CrossRef]
- Bossoufi, B.; Karim, M.; Lagrioui, A.; Taoussi, M.; Derouich, A.J. Observer backstepping control of DFIG-Generators for wind turbines variable-speed: FPGA-based implementation. Renew. Energy 2015, 81, 903–917. [Google Scholar] [CrossRef]
- Taraft, S.; Rekioua, D.; Aouzellag, D.; Bacha, S.J. A proposed strategy for power optimization of a wind energy conversion system connected to the grid. Energy Convers. Manag. 2015, 101, 489–502. [Google Scholar] [CrossRef]
- Hu, J.; Nian, H.; Hu, B.; He, Y.; Zhu, Z.J. Direct active and reactive power regulation of DFIG using sliding-mode control approach. IEEE Trans. Energy Convers. 2010, 25, 1028–1039. [Google Scholar] [CrossRef]
- Fallaha, C.J.; Saad, M.; Kanaan, H.Y.; Al-Haddad, K.J. Sliding-mode robot control with exponential reaching law. IEEE Trans. Ind. Electron. 2010, 58, 600–610. [Google Scholar] [CrossRef]
- Wang, J.; Bo, D.; Ma, X.; Zhang, Y.; Li, Z.; Miao, Q.J. Adaptive back-stepping control for a permanent magnet synchronous generator wind energy conversion system. Int. J. Hydrogen Energy 2019, 44, 3240–3249. [Google Scholar] [CrossRef]
- Shihabudheen, K.; Raju, S.K.; Pillai, G.N.J. Control for grid-connected DFIG-based wind energy system using adaptive neuro-fuzzy technique. Int. Trans. Electr. Energy Syst. 2018, 28, e2526. [Google Scholar] [CrossRef]
- Mérida, J.; Aguilar, L.T.; Dávila, J.J. Analysis and synthesis of sliding mode control for large scale variable speed wind turbine for power optimization. Renew. Energy 2014, 71, 715–728. [Google Scholar] [CrossRef]
- Xiong, L.; Li, P.; Wu, F.; Ma, M.; Khan, M.W.; Wang, J.J. A coordinated high-order sliding mode control of DFIG wind turbine for power optimization and grid synchronization. Int. J. Electr. Power Energy Syst. 2019, 105, 679–689. [Google Scholar] [CrossRef]
- Beltran, B.; Benbouzid, M.E.H.; Ahmed-Ali, T.J. Second-order sliding mode control of a doubly fed induction generator driven wind turbine. IEEE Trans. Energy Convers. 2012, 27, 261–269. [Google Scholar] [CrossRef]
- Beltran, B.; Ahmed-Ali, T.; Benbouzid, M.E.H.J. High-order sliding-mode control of variable-speed wind turbines. IEEE Trans. Ind. Electron. 2008, 56, 3314–3321. [Google Scholar] [CrossRef]
- Zhang, C.; Gutierrez, S.; Plestan, F.; de León-Morales, J.J. Adaptive super-twisting control of floating wind turbines with collective blade pitch control. IFAC-PapersOnLine 2019, 52, 117–122. [Google Scholar] [CrossRef]
- Chen, H.; Li, Q.; Tang, S.; Nadia, A.A.; Han, J.; Wang, T.; Benbouzid, M. Adaptive super-twisting control of doubly salient permanent magnet generator for tidal stream turbine. Int. J. Electr. Power Energy Syst. 2021, 128, 106772. [Google Scholar] [CrossRef]
- Milosavljevic, D. General conditions for existence of a quasi-sliding mode on the switching hyperplane in discrete variable structure systems. Autom. Remote Control 1985, 46, 307–314. [Google Scholar]
- Bartoszewicz, A. Discrete-time quasi-sliding-mode control strategies. IEEE Trans. Ind. Electron. 1998, 45, 633–637. [Google Scholar] [CrossRef]
- Ngadungon, R.B.N.; Sam, Y.B.M. Discrete time sliding mode control using multirate output feedback to reduce chattering. In Proceedings of the 2010 IEEE Student Conference on Research and Development (SCOReD), Kuala Lumpur, Malaysia, 13–14 December 2010; pp. 236–239. [Google Scholar]
- Beltran, B.; Ahmed-Ali, T.; Benbouzid, M.E.H. Sliding mode power control of variable-speed wind energy conversion systems. IEEE Trans. Energy Convers. 2008, 23, 551–558. [Google Scholar] [CrossRef]
- Mozayan, S.M.; Saad, M.; Vahedi, H.; Fortin-Blanchette, H.; Soltani, M.J. Sliding mode control of PMSG wind turbine based on enhanced exponential reaching law. IEEE Trans. Ind. Electron. 2016, 63, 6148–6159. [Google Scholar] [CrossRef]
- Hung, J.Y.; Gao, W.; Hung, J.C. Variable structure control: A survey. IEEE Trans. Ind. Electron. 1993, 40, 2–22. [Google Scholar] [CrossRef]
- Kelkoul, B.; Boumediene, A.J. Stability analysis and study between classical sliding mode control (SMC) and super twisting algorithm (STA) for doubly fed induction generator (DFIG) under wind turbine. Energy Convers. Manag. 2020, 214, 118871. [Google Scholar] [CrossRef]
- Fridman, L.; Moreno, J.A.; Bandyopadhyay, B.; Kamal, S.; Chalanga, A. Continuous nested algorithms: The fifth generation of sliding mode controllers. In Recent Advances in Sliding Modes: From Control to Intelligent Mechatronics; Springer: Cham, Switzerland, 2015; pp. 5–35. [Google Scholar]
- Bekakra, Y.; Attous, D.B. Sliding mode controls of active and reactive power of a DFIG with MPPT for variable speed wind energy conversion. Aust. J. Basic Appl. Sci. 2011, 5, 2274–2286. [Google Scholar]
- Machmoum, M.; Poitiers, F. Sliding mode control of a variable speed wind energy conversion system with DFIG. In Proceedings of the International Conference and Exhibition on Ecologic Vehicles and Renewable Energies, Monte-Carlo, Monaco, 8–10 May 2019; pp. 26–29. [Google Scholar]
- Liu, X.; Han, Y.; Wang, C.J. Second-order sliding mode control for power optimisation of DFIG-based variable speed wind turbine. IET Renew. Power Gener. 2016, 11, 408–418. [Google Scholar] [CrossRef]
- Beltran, B.; Benbouzid, M.; Ahmed-Ali, T. High-order sliding mode control of a DFIG-based wind turbine for power maximization and grid fault tolerance. In Proceedings of the 2009 IEEE International Electric Machines and Drives Conference, Miami, FL, USA, 3–6 May 2009; pp. 183–189. [Google Scholar]
- Levant, A.J. Higher-order sliding modes, differentiation and output-feedback control. Int. J. Control 2003, 76, 924–941. [Google Scholar] [CrossRef]
- Benelghali, S.; Benbouzid, M.; Charpentier, J.; Ahmed-Ali, T.; Munteanu, I. Experimental validation of a marine current turbine simulator: Application to a PMSG-based system second-order sliding mode control. IEEE Trans. Ind. Electron. 2011, 58, 118–126. [Google Scholar] [CrossRef]
- Elghali, S.E.B.; Benbouzid, M.E.H.; Ahmed-Ali, T.; Charpentier, J.F.J. High-order sliding mode control of a marine current turbine driven doubly-fed induction generator. IEEE J. Ocean. Eng. 2010, 35, 402–411. [Google Scholar] [CrossRef]
- Benbouzid, M.; Beltran, B.; Amirat, Y.; Yao, G.; Han, J.; Mangel, H. Second-order sliding mode control for DFIG-based wind turbines fault ride-through capability enhancement. ISA Trans. 2014, 53, 827–833. [Google Scholar] [CrossRef] [PubMed]
- Dursun, E.H.; Kulaksiz, A.A.J. Second-order sliding mode voltage-regulator for improving MPPT efficiency of PMSG-based WECS. Int. J. Electr. Power Energy Syst. 2020, 121, 106149. [Google Scholar] [CrossRef]
- Wang, J.; Bo, D.; Miao, Q.; Li, Z.; Wu, X.; Lv, D.J. Maximum power point tracking control for a doubly fed induction generator wind energy conversion system based on multivariable adaptive super-twisting approach. Int. J. Electr. Power Energy Syst. 2021, 124, 106347. [Google Scholar] [CrossRef]
- Valenciaga, F.; Puleston, P.J. High-order sliding control for a wind energy conversion system based on a permanent magnet synchronous generator. IEEE Trans. Energy Convers. 2008, 23, 860–867. [Google Scholar] [CrossRef]
- Evangelista, C.; Puleston, P.; Valenciaga, F.; Fridman, L.M.J. Lyapunov-designed super-twisting sliding mode control for wind energy conversion optimization. IEEE Trans. Ind. Electron. 2012, 60, 538–545. [Google Scholar] [CrossRef]
- Evangelista, C.; Valenciaga, F.; Puleston, P.J. Active and reactive power control for wind turbine based on a MIMO 2-sliding mode algorithm with variable gains. IEEE Trans. Energy Convers. 2013, 28, 682–689. [Google Scholar] [CrossRef]
- Merabet, A.; Ahmed, K.T.; Ibrahim, H.; Beguenane, R.J. Implementation of sliding mode control system for generator and grid sides control of wind energy conversion system. IEEE Trans. Sustain. Energy 2016, 7, 1327–1335. [Google Scholar] [CrossRef]
- Morshed, M.J.; Fekih, A.J. A new fault ride-through control for DFIG-based wind energy systems. Electr. Power Syst. Res. 2017, 146, 258–269. [Google Scholar] [CrossRef]
- Evangelista, C.A.; Pisano, A.; Puleston, P.; Usai, E.J. Receding horizon adaptive second-order sliding mode control for doubly-fed induction generator based wind turbine. IEEE Trans. Control. Syst. Technol. 2016, 25, 73–84. [Google Scholar] [CrossRef]
- Benamor, A.; Benchouia, M.; Srairi, K.; Benbouzid, M. A novel rooted tree optimization apply in the high order sliding mode control using super-twisting algorithm based on DTC scheme for DFIG. Int. J. Electr. Power Energy Syst. 2019, 108, 293–302. [Google Scholar] [CrossRef]
- Berrada, Y.; Boumhidi, I. New structure of sliding mode control for variable speed wind turbine. IFAC J. Syst. Control 2020, 14, 100113. [Google Scholar] [CrossRef]
- Karabacak, M.J. A new perturb and observe based higher order sliding mode MPPT control of wind turbines eliminating the rotor inertial effect. Renew. Energy 2019, 133, 807–827. [Google Scholar] [CrossRef]
- Xiong, L.; Li, P.; Wang, J.J. High-order sliding mode control of DFIG under unbalanced grid voltage conditions. Int. J. Electr. Power Energy Syst. 2020, 117, 105608. [Google Scholar] [CrossRef]
- Shtessel, Y.; Taleb, M.; Plestan, F.J. A novel adaptive-gain supertwisting sliding mode controller: Methodology and application. Automatica 2012, 48, 759–769. [Google Scholar] [CrossRef]
- Utkin, V.; Shi, J. Integral sliding mode in systems operating under uncertainty conditions. In Proceedings of the 35th IEEE Conference on Decision and Control, Kobe, Japan, 13 December 1996; Volume 4, pp. 4591–4596. [Google Scholar]
- Suleimenov, K.; Sarsembayev, B.; Phuc, B.D.H.; Do, T.D.J. Disturbance observer-based integral sliding mode control for wind energy conversion systems. Wind. Energy 2020, 23, 1026–1047. [Google Scholar] [CrossRef]
- Saravanakumar, R.; Jena, D.J. Validation of an integral sliding mode control for optimal control of a three blade variable speed variable pitch wind turbine. Int. J. Electr. Power Energy Syst. 2015, 69, 421–429. [Google Scholar] [CrossRef]
- Li, S.; Wang, H.; Tian, Y.; Aitouch, A.; Klein, J.J. Direct power control of DFIG wind turbine systems based on an intelligent proportional-integral sliding mode control. ISA Trans. 2016, 64, 431–439. [Google Scholar] [CrossRef]
- Chen, S.Z.; Cheung, N.C.; Wong, K.C.; Wu, J. Integral sliding-mode direct torque control of doubly-fed induction generators under unbalanced grid voltage. IEEE Trans. Energy Convers. 2009, 25, 356–368. [Google Scholar] [CrossRef]
- Martinez, M.I.; Susperregui, A.; Tapia, G.; Camblong, H.J. Sliding-Mode Control for a DFIG-based Wind Turbine under Unbalanced Voltage. Ifac Proc. Vol. 2011, 44, 538–543. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Z.; Xiong, L.; Wang, J.; Jiang, X.; Bai, G.; Liu, S. DFIG wind turbine sliding mode control with exponential reaching law under variable wind speed. Int. J. Electr. Power Energy Syst. 2018, 96, 253–260. [Google Scholar] [CrossRef]
- Errouissi, R.; Al-Durra, A.J. A novel PI-type sliding surface for PMSG-based wind turbine with improved transient performance. IEEE Trans. Energy Convers. 2017, 33, 834–844. [Google Scholar] [CrossRef]
- Sarsembayev, B.; Suleimenov, K.; Mirzagalikova, B.; Do, T.D.J. SDRE-based integral sliding mode control for wind energy conversion systems. IEEE Access 2020, 8, 51100–51113. [Google Scholar] [CrossRef]
- Nayeh, R.F.; Moradi, H.; Vossoughi, G.J. Multivariable robust control of a horizontal wind turbine under various operating modes and uncertainties: A comparison on sliding mode and H∞ control. Int. J. Electr. Power Energy Syst. 2020, 115, 105474. [Google Scholar] [CrossRef]
- Yin, X.; Jiang, Z.; Pan, L.J. Recurrent neural network based adaptive integral sliding mode power maximization control for wind power systems. Renew. Energy 2020, 145, 1149–1157. [Google Scholar] [CrossRef]
- Dali, A.; Abdelmalek, S.; Bakdi, A.; Bettayeb, M. A new robust control scheme: Application for MPP tracking of a PMSG-based variable-speed wind turbine. Renew. Energy 2021, 172, 1021–1034. [Google Scholar] [CrossRef]
- Xiong, L.; Li, J.; Li, P.; Huang, S.; Wang, Z.; Wang, J.J. Event triggered prescribed time convergence sliding mode control of DFIG with disturbance rejection capability. Int. J. Electr. Power Energy Syst. 2021, 131, 106970. [Google Scholar] [CrossRef]
- Yu, X.; Kaynak, O.J. Sliding-mode control with soft computing: A survey. IEEE Trans. Ind. Electron. 2009, 56, 3275–3285. [Google Scholar]
- Utkin, V.; Poznyak, A.; Orlov, Y.; Polyakov, A.J. Conventional and high order sliding mode control. J. Frankl. Inst. 2020, 357, 10244–10261. [Google Scholar] [CrossRef]
- Yu, X.; Feng, Y.; Man, Z.J. Terminal Sliding Mode Control-An Overview. IEEE Open J. Ind. Electron. Soc. 2020, 2, 36–52. [Google Scholar] [CrossRef]
- Zak, M.J. Terminal attractors for addressable memory in neural networks. Phys. Lett. A 1988, 133, 18–22. [Google Scholar] [CrossRef]
- Venkataraman, S.; Gulati, S. Control of nonlinear systems using terminal sliding modes. J. Dyn. Sys. Meas. Control. 1993, 115, 554–560. [Google Scholar] [CrossRef]
- Yu, X.; Man, Z.J. Model reference adaptive control systems with terminal sliding modes. Int. J. Control 1996, 64, 1165–1176. [Google Scholar] [CrossRef]
- Zhihong, M.; Paplinski, A.P.; Wu, H.R.J. A robust MIMO terminal sliding mode control scheme for rigid robotic manipulators. IEEE Trans. Autom. Control 1994, 39, 2464–2469. [Google Scholar] [CrossRef]
- Zhihong, M.; Yu, X.H.J. Terminal sliding mode control of MIMO linear systems. IEEE Trans. Circuits Syst. Fundam. Theory Appl. 1997, 44, 1065–1070. [Google Scholar] [CrossRef]
- Feng, Y.; Yu, X.; Man, Z.J. Non-singular terminal sliding mode control of rigid manipulators. Automatica 2002, 38, 2159–2167. [Google Scholar] [CrossRef]
- Yu, X.; Zhihong, M.J. Fast terminal sliding-mode control design for nonlinear dynamical systems. IEEE Trans. Circuits Syst. Fundam. Theory Appl. 2002, 49, 261–264. [Google Scholar]
- Yu, S.; Yu, X.; Shirinzadeh, B.; Man, Z.J. Continuous finite-time control for robotic manipulators with terminal sliding mode. Automatica 2005, 41, 1957–1964. [Google Scholar] [CrossRef]
- Patnaik, R.; Dash, P.J. Fast adaptive finite-time terminal sliding mode power control for the rotor side converter of the DFIG based wind energy conversion system. Sustain. Energy, Grids Netw. 2015, 1, 63–84. [Google Scholar] [CrossRef]
- Patnaik, R.; Dash, P.; Mahapatra, K.J. Adaptive terminal sliding mode power control of DFIG based wind energy conversion system for stability enhancement. Int. Trans. Electr. Energy Syst. 2016, 26, 750–782. [Google Scholar] [CrossRef]
- Yazıcı, İ.; Yaylacı, E.K.J. Discrete-time integral terminal sliding mode based maximum power point controller for the PMSG-based wind energy system. Iet Power Electron. 2019, 12, 3688–3696. [Google Scholar] [CrossRef]
- Zheng, X.; Feng, Y.; Han, F.; Yu, X.J. Integral-type terminal sliding-mode control for grid-side converter in wind energy conversion systems. IEEE Trans. Ind. Electron. 2018, 66, 3702–3711. [Google Scholar] [CrossRef]
- Morshed, M.J.; Fekih, A.J. Design of a chattering-free integral terminal sliding mode approach for DFIG-based wind energy systems. Optim. Control. Appl. Methods 2020, 41, 1718–1734. [Google Scholar] [CrossRef]
- Balamurugan, S.; Venkatesh, P.; Varatharajan, M. Fuzzy sliding-mode control with low pass filter to reduce chattering effect: An experimental validation on Quanser SRIP. Sādhanā 2017, 42, 1693–1703. [Google Scholar] [CrossRef]
- Xu, N.; Chen, Y.; Xue, A.; Zong, G.; Zhao, X.J. Event-trigger-based adaptive fuzzy hierarchical sliding mode control of uncertain under-actuated switched nonlinear systems. ISA Trans. 2019, 124, 301–310. [Google Scholar] [CrossRef]
- Yin, X.-x.; Lin, Y.-g.; Li, W.; Gu, Y.-j.; Lei, P.-f.; Liu, H.-w.J. Sliding mode voltage control strategy for capturing maximum wind energy based on fuzzy logic control. Int. J. Electr. Power Energy Syst. 2015, 70, 45–51. [Google Scholar] [CrossRef]
- Yin, X.-X.; Lin, Y.-G.; Li, W.; Liu, H.-W.; Gu, Y.-J.J. Fuzzy-logic sliding-mode control strategy for extracting maximum wind power. IEEE Trans. Energy Convers. 2015, 30, 1267–1278. [Google Scholar] [CrossRef]
- Do, T.D.J. Disturbance observer-based fuzzy SMC of WECSs without wind speed measurement. IEEE Access 2016, 5, 147–155. [Google Scholar] [CrossRef]
- Bounar, N.; Labdai, S.; Boulkroune, A. PSO–GSA based fuzzy sliding mode controller for DFIG-based wind turbine. ISA Trans. 2019, 85, 177–188. [Google Scholar] [CrossRef]
- Hong, C.-M.; Huang, C.-H.; Cheng, F.-S.J. Sliding mode control for variable-speed wind turbine generation systems using artificial neural network. Energy Procedia 2014, 61, 1626–1629. [Google Scholar] [CrossRef]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley: Hoboken, NJ, USA, 1993. [Google Scholar]
- Srivastava, H.J. Fractional Differential Equations. I Podlubny. Appl. Mech. Rev. 2000, 53, B51. [Google Scholar]
- Matignon, D. Stability properties for generalized fractional differential systems. In ESAIM: Proceedings; EDP Sciences: Paris, France, 1998; Volume 5, pp. 145–158. [Google Scholar]
- Zhang, Q.; Zhuang, X.; Liu, Y.; Wang, C.; Guo, H.J. A novel control strategy for mode seamless switching of PV converter in DC microgrid based on double integral sliding mode control. ISA Trans. 2020, 100, 469–480. [Google Scholar] [CrossRef] [PubMed]
- Incremona, G.P.; Rubagotti, M.; Ferrara, A.J. Sliding mode control of constrained nonlinear systems. IEEE Trans. Autom. Control. 2016, 62, 2965–2972. [Google Scholar] [CrossRef]
- Liu, C.; Sun, W.; Zhang, J.J. Adaptive sliding mode control for 4–wheel SBW system with Ackerman geometry. ISA Trans. 2020, 96, 103–115. [Google Scholar] [CrossRef]
- Chen, L.; Wang, H.; Huang, Y.; Ping, Z.; Yu, M.; Zheng, X.; Hu, Y. Robust hierarchical sliding mode control of a two-wheeled self-balancing vehicle using perturbation estimation. Mech. Syst. Process. 2020, 139, 106584. [Google Scholar] [CrossRef]
- Kang, S.; Yan, H.; Dong, L.; Li, C.J. Finite-time adaptive sliding mode force control for electro-hydraulic load simulator based on improved GMS friction model. Mech. Syst. Process. 2018, 102, 117–138. [Google Scholar] [CrossRef]
- Pradhan, S.; Singh, B.; Panigrahi, B.K.; Murshid, S.J. A composite sliding mode controller for wind power extraction in remotely located solar PV–wind hybrid system. IEEE Trans. Ind. Electron. 2018, 66, 5321–5331. [Google Scholar] [CrossRef]
- Yashar, M.; Bevan, G.; Kucukdemiral, I.B.; Fekih, A. Sliding mode control of wind energy conversion systems: Trends and applications. Renew. Sustain. Energy Rev. 2022, 167, 112734. [Google Scholar]
- Wang, H.; Shi, L.; Man, Z.; Zheng, J.; Li, S.; Yu, M.; Cao, Z. Continuous fast nonsingular terminal sliding mode control of automotive electronic throttle systems using finite-time exact observer. IEEE Trans. Ind. Electron. 2018, 65, 7160–7172. [Google Scholar] [CrossRef]
- Yao, X.; Park, J.H.; Dong, H.; Guo, L.; Lin, X.J. Robust adaptive nonsingular terminal sliding mode control for automatic train operation. IEEE Trans. Syst. ManCybern. Syst. 2018, 49, 2406–2415. [Google Scholar] [CrossRef]
- Farid, Y.; Majd, V.J.; Ehsani-Seresht, A.J. Fractional-order active fault-tolerant force-position controller design for the legged robots using saturated actuator with unknown bias and gain degradation. Mech. Syst. Process. 2018, 104, 465–486. [Google Scholar] [CrossRef]
- Mousavi, Y.; Alfi, A.J. A memetic algorithm applied to trajectory control by tuning of fractional order proportional-integral-derivative controllers. Appl. Soft Comput. 2015, 36, 599–617. [Google Scholar] [CrossRef]
- Wei, Y.-Q.; Liu, D.-Y.; Boutat, D.J. Innovative fractional derivative estimation of the pseudo-state for a class of fractional order linear systems. Automatica 2019, 99, 157–166. [Google Scholar] [CrossRef]
- Mousavi, Y.; Alfi, A.J. Fractional calculus-based firefly algorithm applied to parameter estimation of chaotic systems. Chaos Solitons Fractals 2018, 114, 202–215. [Google Scholar] [CrossRef]
- Sun, G.; Ma, Z.; Yu, J.J. Discrete-time fractional order terminal sliding mode tracking control for linear motor. IEEE Trans. Ind. Electron. 2017, 65, 3386–3394. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, J.; Yan, F.; Zhu, K.; Chen, B.J. Adaptive super-twisting fractional-order nonsingular terminal sliding mode control of cable-driven manipulators. ISA Trans. 2019, 86, 163–180. [Google Scholar] [CrossRef] [PubMed]
- Sun, G.; Ma, Z.J. Practical tracking control of linear motor with adaptive fractional order terminal sliding mode control. IEEE/ASME Trans. Mechatronics 2017, 22, 2643–2653. [Google Scholar] [CrossRef]
- Yashar, M.; Zarei, A.; Jahromi, Z.S. Robust adaptive fractional-order nonsingular terminal sliding mode stabilization of three-axis gimbal platforms. ISA Trans. 2022, 123, 98–109. [Google Scholar]
- Delghavi, M.B.; Shoja-Majidabad, S.; Yazdani, A. Fractional-order sliding-mode control of islanded distributed energy resource systems. IEEE Trans. Sustain. Energy 2016, 7, 1482–1491. [Google Scholar] [CrossRef]
- Aghababa, M.P. A Lyapunov-based control scheme for robust stabilization of fractional chaotic systems. Nonlinear Dyn. 2014, 78, 2129–2140. [Google Scholar] [CrossRef]
- Li, C.; Deng, W.J. Remarks on fractional derivatives. Appl. Math. Comput. 2007, 187, 777–784. [Google Scholar] [CrossRef]
- Zhang, F.; Li, C.J. Stability analysis of fractional differential systems with order lying in (1, 2). Adv. Differ. Equ. 2011, 2011, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Gao, Z.; Liao, X.J. Improved Oustaloup approximation of fractional-order operators using adaptive chaotic particle swarm optimization. J. Syst. Eng. Electron. 2012, 23, 145–153. [Google Scholar] [CrossRef]
- Burton, T.; Sharpe, D.; Jenkins, N.; Bossanyi, E. Wind Energy Handbook; Wiley Online Library: Hoboken, NJ, USA, 2001. [Google Scholar]
- Kiruthiga, B.J. Implementation of first order sliding mode control of active and reactive power for DFIG based wind turbine. Int. J. Inf. Futur. Res. 2015, 2, 2487–2497. [Google Scholar]
- Lima, F.; Watanabe, E.H.; Rodriguez, P.; Luna, A. A simplified model for wind turbine based on doubly fed induction generator. In Proceedings of the 2011 International Conference on Electrical Machines and Systems, Beijing, China, 20–23 August 2011; pp. 1–6. [Google Scholar]
- Mechter, A.; Kemih, K.; Ghanes, M.J. Sliding mode control of a wind turbine with exponential reaching law. Acta Polytech. Hung. 2015, 12, 167–183. [Google Scholar]
- Patton, R.J.; Frank, P.M.; Clark, R.N. Issues of Fault Diagnosis for Dynamic Systems; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Huerta, H.; Loukianov, A.J. E nergy based sliding mode control of Brushless Double-fed Induction Generator. Int. J. Electr. Power Energy Syst. 2021, 130, 107002. [Google Scholar] [CrossRef]
- Yang, B.; Yu, T.; Shu, H.; Zhang, Y.; Chen, J.; Sang, Y.; Jiang, L. Passivity-based sliding-mode control design for optimal power extraction of a PMSG based variable speed wind turbine. Renew. Energy 2018, 119, 577–589. [Google Scholar] [CrossRef]
- Djilali, L.; Caballero-Barragán, H.; Osuna-Ibarra, L.; Sanchez, E.N.; Loukianov, A.J. Neural Sliding Mode Control of a DFIG Based Wind Turbine with Measurement Delay. IFAC-PapersOnLine 2018, 51, 456–461. [Google Scholar] [CrossRef]
- Xiong, L.; Wang, J.; Mi, X.; Khan, M.W.J. Fractional order sliding mode based direct power control of grid-connected DFIG. IEEE Trans. Power Syst. 2017, 33, 3087–3096. [Google Scholar] [CrossRef]
- Dong, H.; Su, M.; Liu, K.; Zou, W.J. Mitigation Strategy of Subsynchronous Oscillation Based on Fractional-Order Sliding Mode Control for VSC-MTDC Systems With DFIG-Based Wind Farm Access. IEEE Access 2020, 8, 209242–209250. [Google Scholar] [CrossRef]
- Zhang, B.; Pi, Y.; Luo, Y.J. Fractional order sliding-mode control based on parameters auto-tuning for velocity control of permanent magnet synchronous motor. ISA Trans. 2012, 51, 649–656. [Google Scholar] [CrossRef]
- Amin, U.S.; Ullah, M.; Sajjad, M.; Cheikh, F.A.; Hijji, M.; Hijji, A.; Muhammad, K. EADN: An Efficient Deep Learning Model for Anomaly Detection in Videos. Mathematics 2022, 10, 1555. [Google Scholar] [CrossRef]



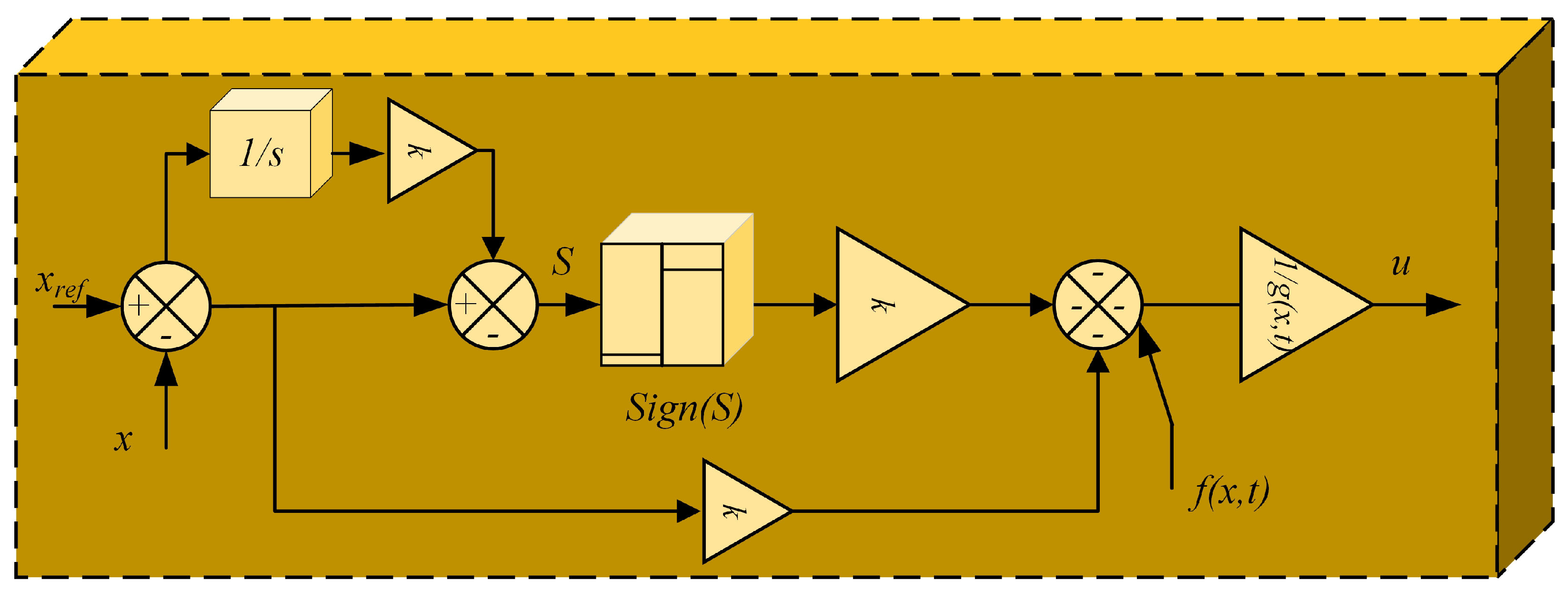

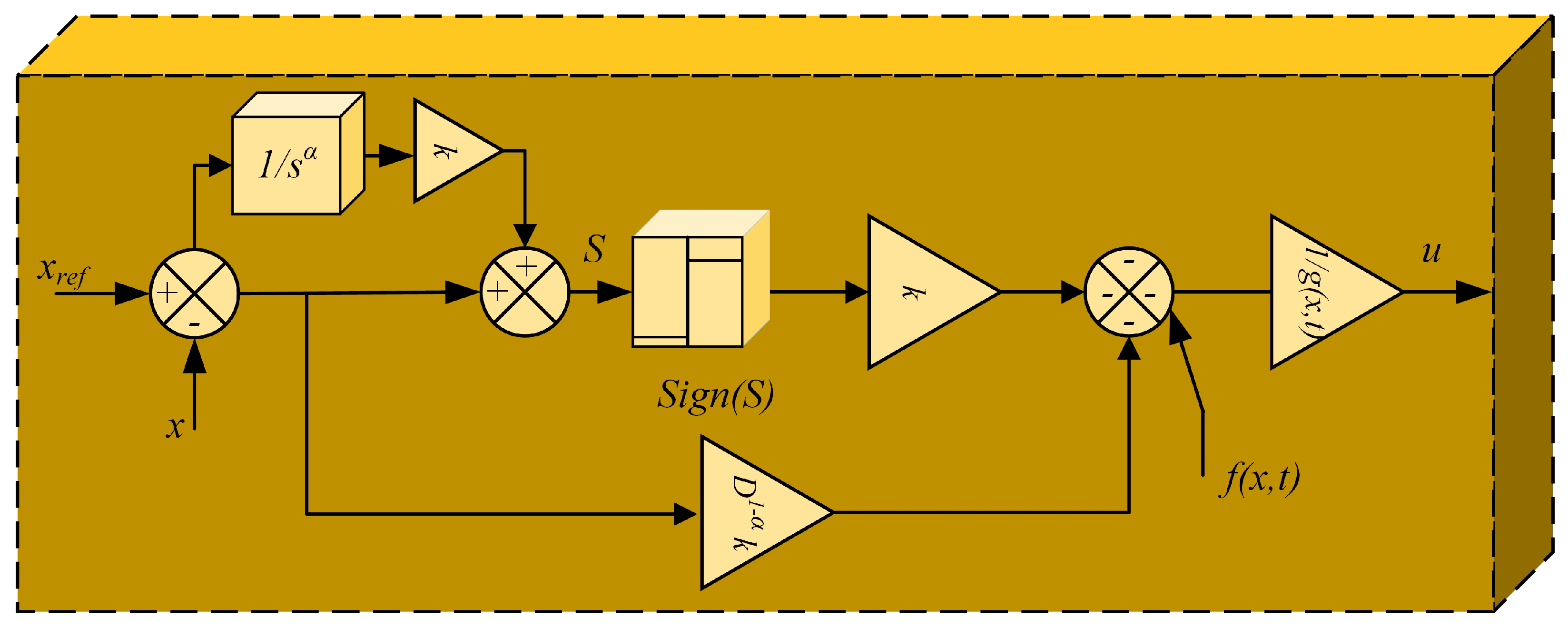
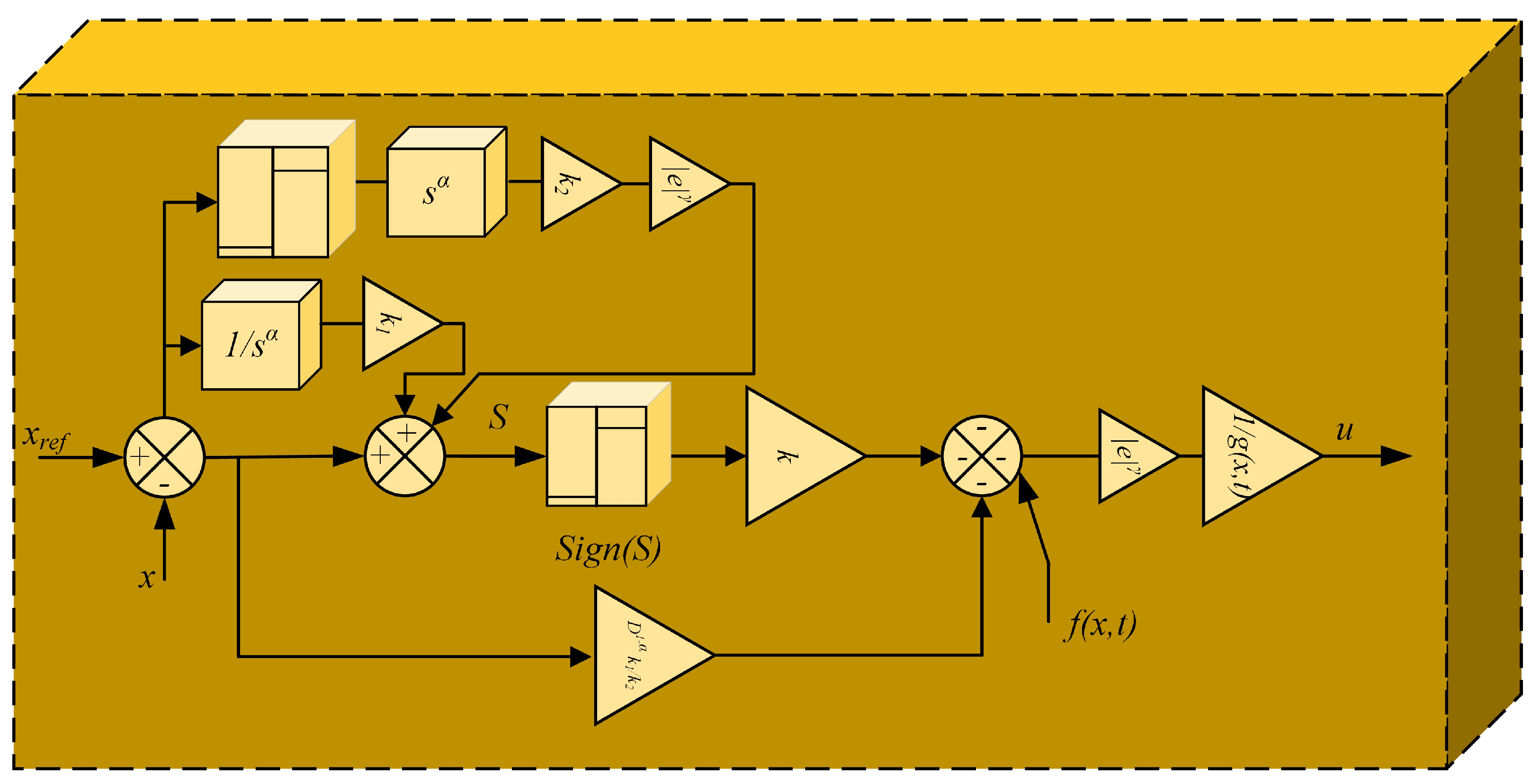
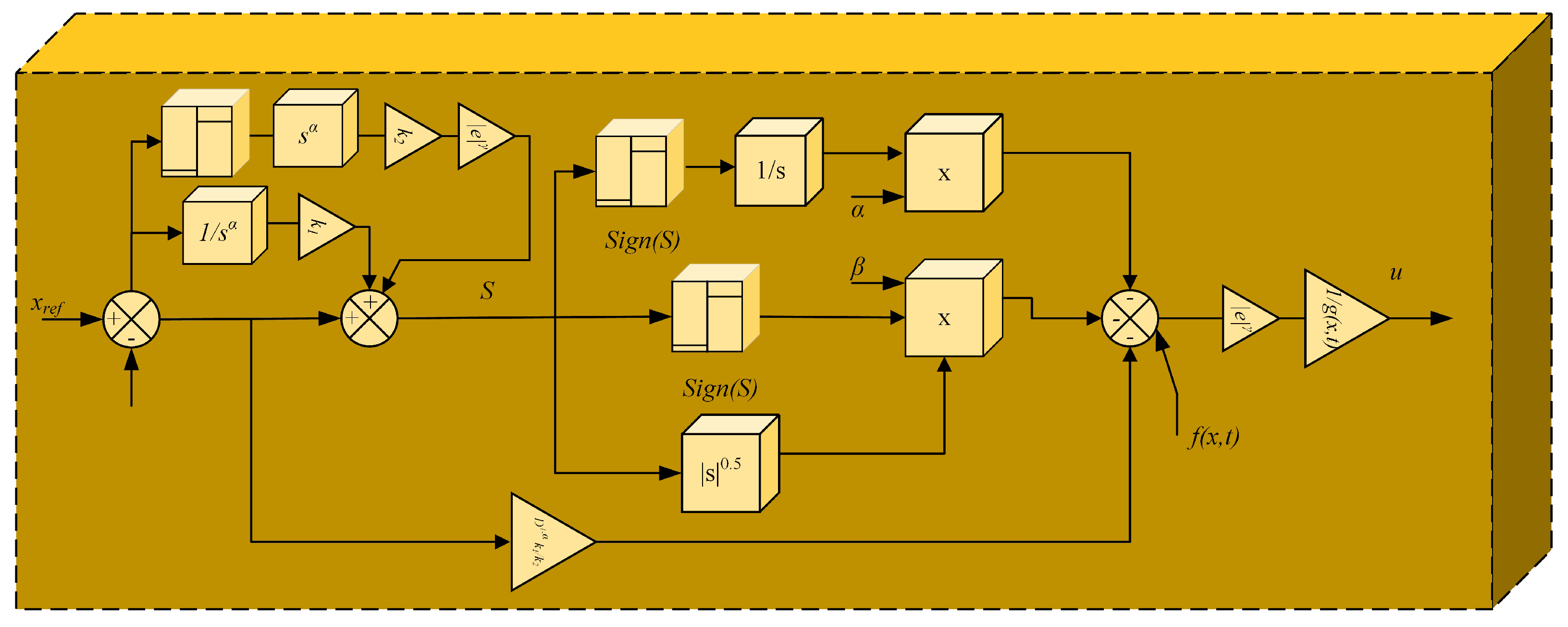
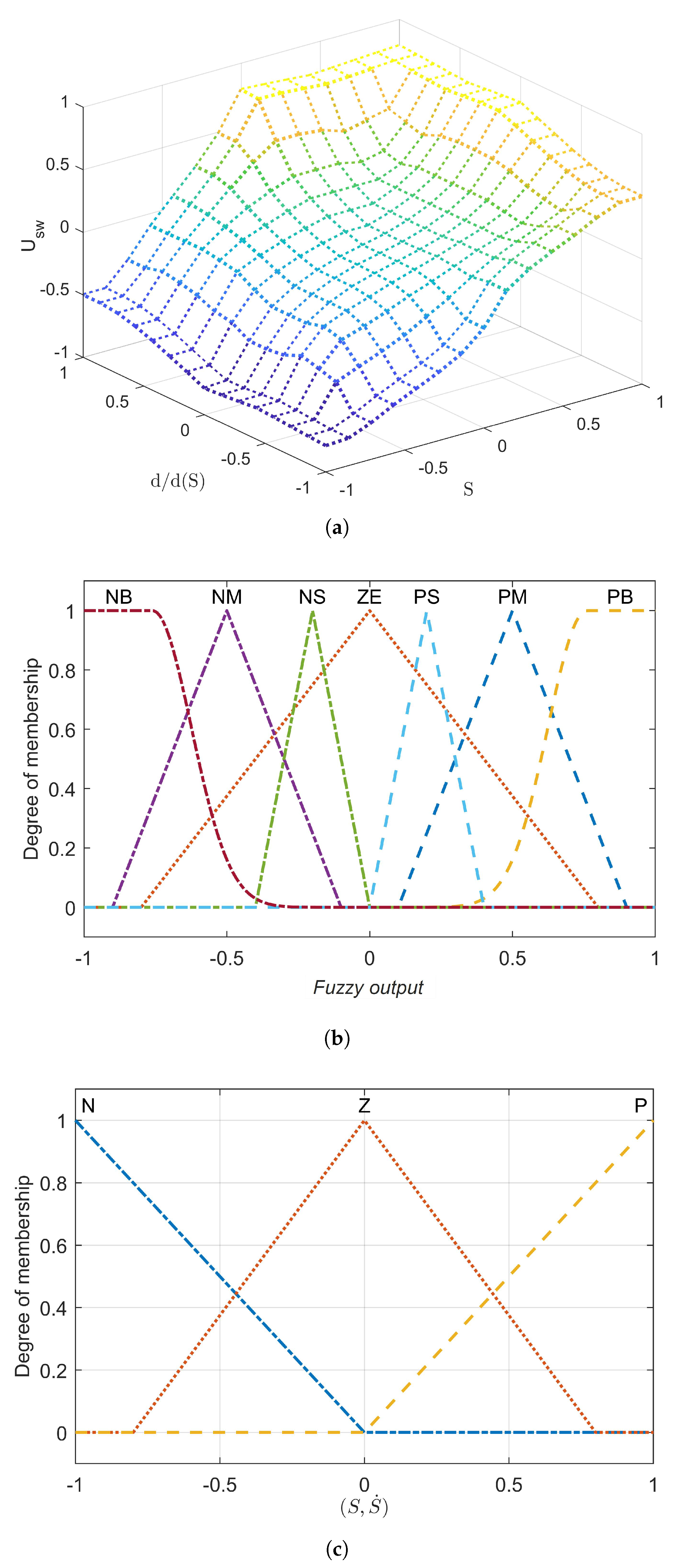
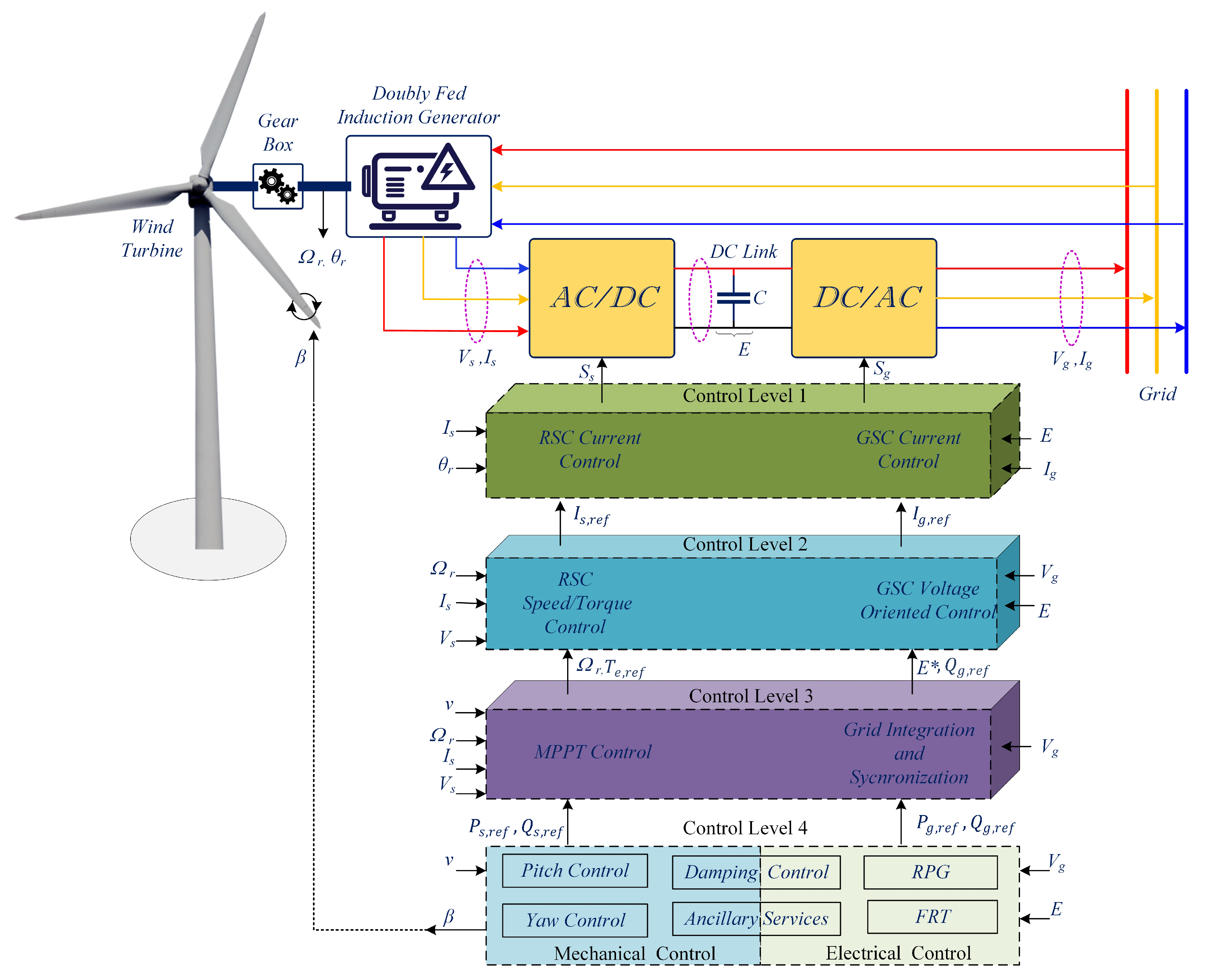
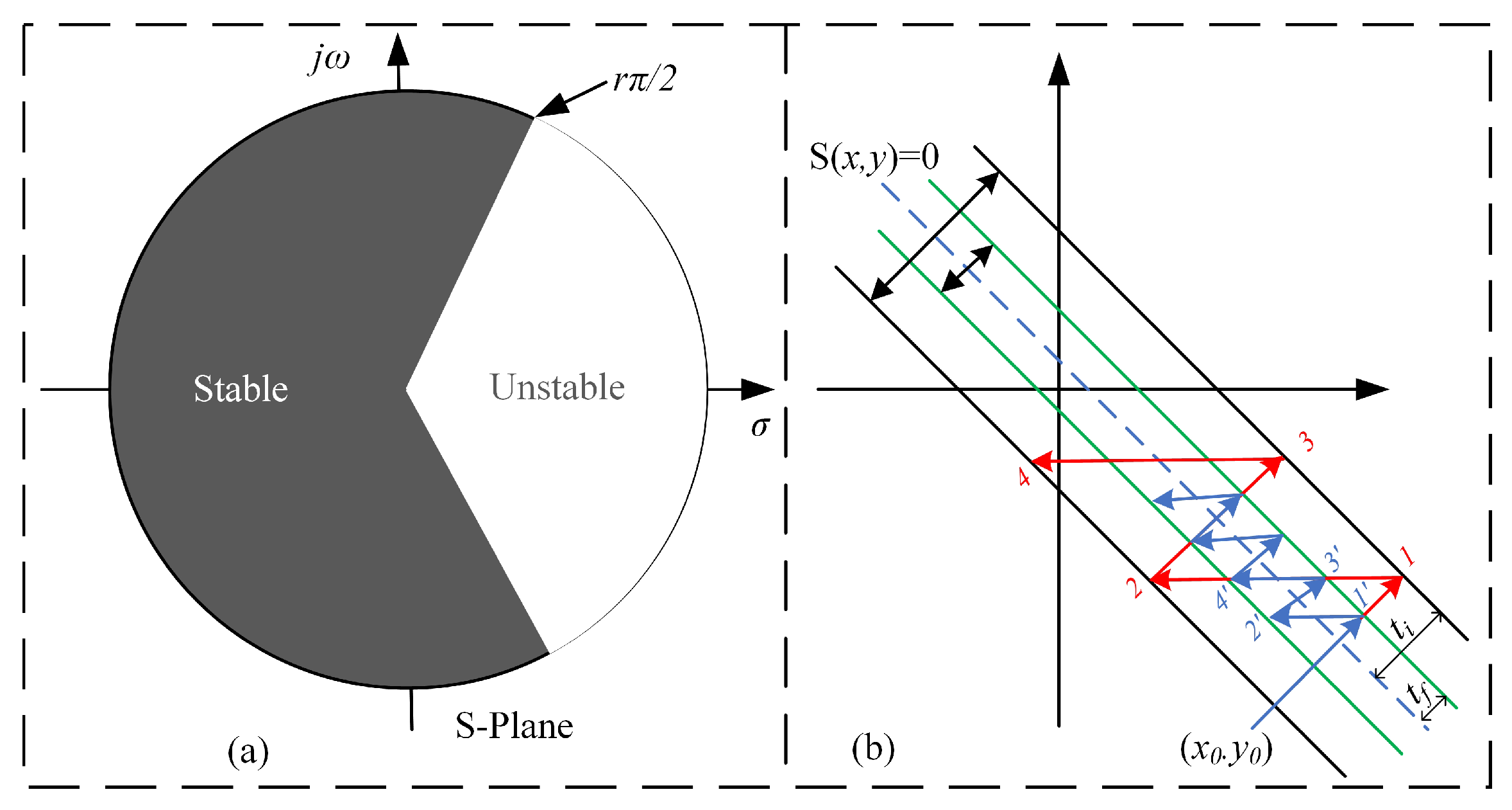

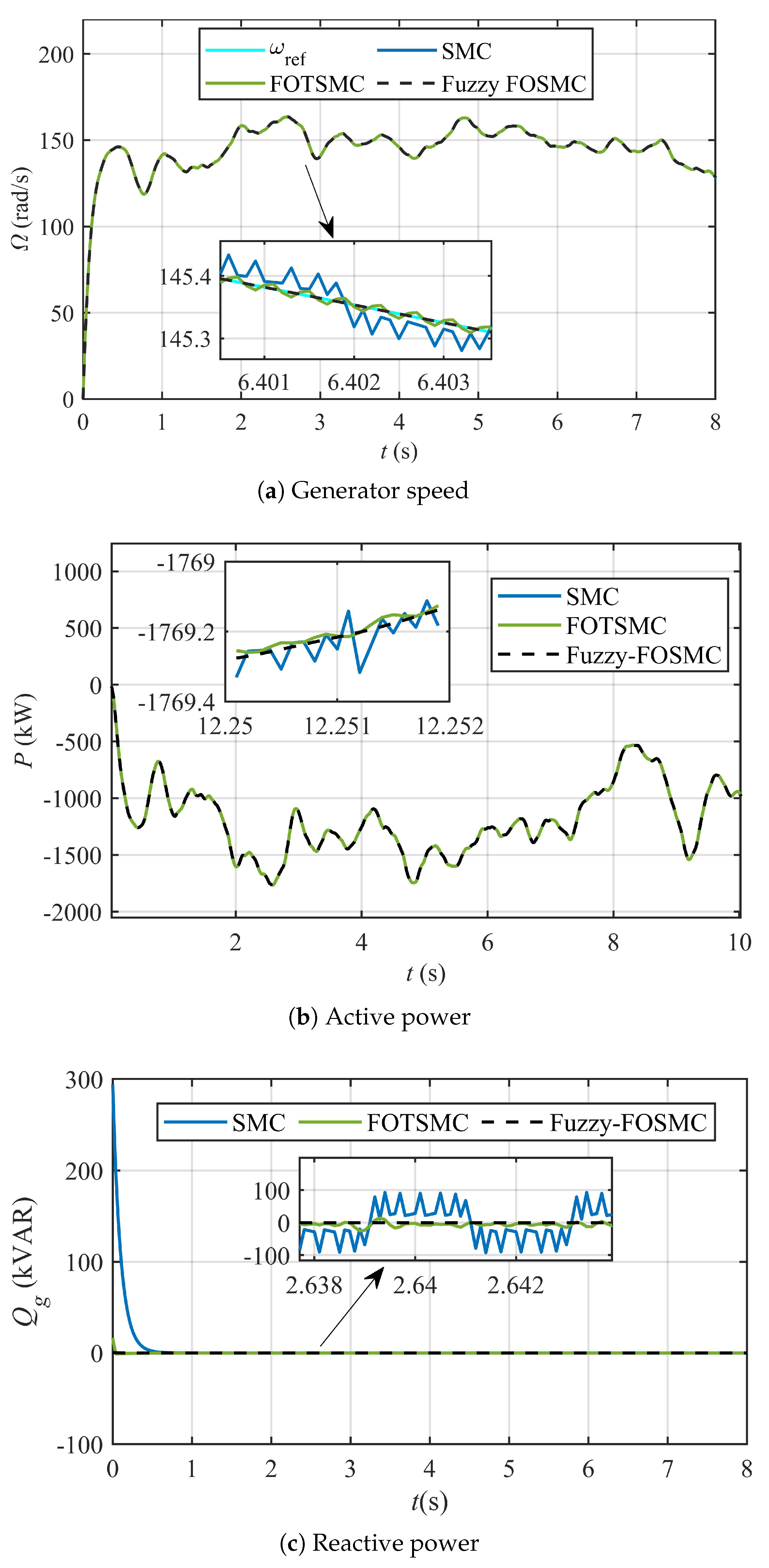
| Ref. | Technique Employed | SC | PU | ED | UBD | CE | R | DS | FTC |
|---|---|---|---|---|---|---|---|---|---|
| [107] | PI | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| [108] | Backstepping | ✓ | ✓ | ✗ | ✗ | ✓ | ✓ | ✗ | ✗ |
| [109] | SMC | ✓ | ✗ | ✗ | ✗ | ✗ | ✓ | ✓ | ✗ |
| [110] | SMC | ✓ | ✓ | ✓ | ✗ | ✓ | ✓ | ✓ | ✗ |
| [111] | SMC with ERL | ✓ | ✓ | ✓ | ✗ | ✓ | ✓ | ✓ | ✗ |
| [112] | Adaptive backstepping | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✗ |
| [101] | ADR control using ESO | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✗ |
| [113] | Adaptive neuro-fuzzy | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✗ |
| [114] | SMC | ✓ | ✓ | ✓ | ✗ | ✓ | ✓ | ✓ | ✓ |
| [115] | Coordinated HOSMC | ✓ | ✓ | ✓ | ✗ | ✓ | ✓ | ✓ | ✗ |
| [116] | HOSMC | ✓ | ✓ | ✓ | ✗ | ✓ | ✓ | ✓ | ✓ |
| [117] | HOSMC | ✓ | ✓ | ✓ | ✗ | ✓ | ✓ | ✓ | ✓ |
| [118] | Adaptive STSMC | ✗ | ✓ | ✓ | ✗ | ✓ | ✓ | ✓ | ✓ |
| Technique | Ref. | Year | Errors | Surfaces | Generator, Control, and Converter-Type Hardware | Remarks |
|---|---|---|---|---|---|---|
| First-order SMC | [123] | 2008 | Standalone No | – | ||
| [88] | 2013 | DFIG BTB converter RSC control No | An SMC in discrete domain is presented to control the DFIG plant using power control. Harmonic spectra are also presented in the paper. | |||
| [124] | 2016 | PMSG Diode rectifier Boost converter NPC inverter at GSC Yes | The conventional reaching law is replaced by a new enhanced reaching law to reduce the chattering. A gain K is used to trade off between chattering and reaching. The is error between boost converter current and reference, whereas is taken as error between reference and actual grid current. | |||
| [126] | 2020 | RSC side control No | Stability analysis of SMC and STSMC are presented and performance is evaluated. |
| Technique | Ref. | Year | Errors | Surfaces | Generator, Control, and Converter-Type Hardware | Remarks |
|---|---|---|---|---|---|---|
| High-order SMC | [138] | 2008 | PMSG Rectifier and inverter No | Rectifier is controlled using STSMC with two different surfaces for two operation modes, which are optimum power conversion and power regulation. | ||
| [116] | 2012 | DFIG BTB converters Yes | STSMC-based high-order control scheme is proposed. The simulation is carried out in FAST wind turbine simulator. A chattering-free and robust behavior with less mechanical stress is experienced. | |||
| [139] | 2012 | DFIG No | A Lyapunov-based modified STSMC is presented with variable gains. The results are validated using extensive simulations. | |||
| [140] | 2013 | DFIG BTB converters RSC control No | STSMC with variable gains is presented in this paper and convergence analysis is provided for DFIG-based WECS. | |||
| [135] | 2014 | DFIG BTB converter No | An STSMC-based second-order SMC is presented using FAST code | |||
| [141] | 2016 | | | PMSG IGBT 8837 BTB Yes | ||
| [142] | 2017 | | | DFIG BTB converters RSC and GSC control No | A fault ride through technique using fuzzy integral terminal STSMC is presented in this paper. | |
| [143] | – | DFIG BTB converters No | A second-order SMC is proposed and made adaptive using time-varying receding horizon. The conservative bounds are calculated and then adaptation strategy is proposed. | |||
| [144] | 2019 |
DFIG RSC control No | An STSMC is proposed where the gains of the STSMC are optimally selected using new rooted tree optimization. | |||
| [145] | 2020 | RSC outer loop control No | A new structure of SMC based on switching sector is presented to minimize the chattering phenomenon. | |||
| [146] | 2019 | RSC control Yes | A new inertial perturb-and-observe MPPT technique is presented. A third-order STSMC is proposed for speed tracking. | |||
| [136] | 2020 | | PMSG Rectifier + Boost converter + Inverter No | An SOSMC is presented for the boost converter in PMSG -based WECS to control the DC link voltage. | ||
| [147] | 2020 | DFIG RSC control Yes | Am HOSMC is presented with enhancing power quality using six power compensation techniques. | |||
| [126] | 2020 | RSC side control NO | Stability analysis of SMC and STSMC is presented, and performance is evaluated. | |||
| [137] | 2021 | |
| DFIG RSC control No | Adaptive STSMC is proposed for DFIG-based WECS. The adaptive gains are given as follows: , where |
| Technique | Ref. | Year | Errors | Surfaces | Generator, Control, and Converter-Type Hardware | Remarks |
|---|---|---|---|---|---|---|
| Integral SMC | [153] | 2009 | DFIG BTB converters RSC control Yes | Integral SMC is proposed to remove the pulsations on torque and power at frequency twice the grid frequency. Concept of positive and negative SRF is used. | ||
| [110] | 2010 | | | DFIG BTB converters RSC control No | DPC of DFIG-based WECS is presented and compared with conventional vector control and look-up-table-based DPC. | |
| [154] | 2011 | DFIG BTB converters RSC control No | Concept of positive and negative SRF is used to remove the pulsations on torque and reactive power using ISMC. | |||
| [155] | surface derivative is: | RSC control No | RSC control is presented with a new exponential reaching law introduced in the derivative of surface, where the surface is taken as integral type surface. | |||
| [156] | 2018 | PMSG BTB converters Yes | An integral SMC with integral and novel proportional integral-based surfaces is proposed. | |||
| [157] | 2020 | where | PMSG | Integral SMC is designed using state dependent Ricatti equation (SDRE) with the nonlinear control law based on Ricatti and Lyapunov equation. | ||
| [158] | 2020 | DFIG RSC control No | Comparative analysis of SMC and control is presented. SMC provided good transient performance whereas provided less tracking error. | |||
| [159] | 2020 | PMSG RSC control No | The uncertain wind turbine dynamics are controlled and estimated using recurrent neural network. Adaptive ISMC is proposed to track optimum rotation speed. | |||
| [160] | 2021 | | with | PMSG Rectifier + Buck converter + Inverter Yes | An SMC technique with new MPPT algorithm is proposed to control the DC link voltage. | |
| [161] | 2021 | PMSG RSC control Yes | An event-triggered integral SMC is presented with extended state observer. The event triggering is used to minimize the communication between execution units and controller. |
| Technique | Ref. | Year | Errors | Surfaces | Generator, Control, and Converter-Type Hardware | Remarks |
|---|---|---|---|---|---|---|
| Terminal SMC | [173] | 2015 | where , and | DFIG BTB converters RSC/GSC control No | An adaptive fast TSMC is presented in this paper. The GSC is controlled using PI control scheme to mitigate the chattering and remove the control input saturation. | |
| [174] | 2018 | DFIG BTB converters RSC No | The transient response of DFIG-WECS is improved using adaptive TSMC. The analysis is conducted for both sub-synchronous and synchronous modes of operation. | |||
| [176] | 2018 | PMSG Yes | An integral type of terminal SMC is proposed in the paper for the power conversion between grid and GSC. Time-varying gains are adopted for the reduction in control energy waste. | |||
| [175] | 2019 | PMSG Rectifier + Boost converter Yes | This paper proposed a discrete time terminal SMC for PMSG WECS. The author achieved 94% efficiency at 9 m/s wind speed. | |||
| [177] | 2020 | DFIG BTB converters RSC/GSC control No | A chattering-free ITSMC is proposed where the fuzzy control theory is used to tune the gains. |
| Technique | Ref. | Year | Errors | Surfaces | Generator, Control, and Converter-Type Hardware | Remarks |
|---|---|---|---|---|---|---|
| Fuzzy Logic SMC | [180] | 2015 | PMSG Diode rectifier +Boost converter Yes | The authors proposed fuzzy-logic-based ISMC to track the derived voltage. FL is used to calculate the . An integral-based SMC is adopted using the FL output. | ||
| [181] | 2015 | PMSG Diode rectifier + Boost converter Yes | The authors proposed fuzzy-logic-based SMC to reduce the harmonics in GSC current. FL is used to calculate the . A double-integral-based SMC is adopted using the FL output. | |||
| [182] | 2016 | where | PMSG RSC control No | A fuzzy-based SMC is presented with disturbance observer. The discontinuous part is estimated using fuzzy control theory. | ||
| [183] | 2019 | DFIG BTB converters RSC control No | The authors proposed fuzzy-logic-based SMC to reduce the chattering by replacing the sign function with FL control theory. PSO-GSA optimization is used to adjust the membership functions. |
| Technique | Ref. | Year | Errors | Surfaces | Generator, Control, and Converter-Type Hardware | Remarks |
|---|---|---|---|---|---|---|
| Fractional SMC | [102] | 2016 | DFIG RSC control No | An FOSMC is proposed to mitigate the inherent chattering in SMC without the knowledge of uncertainties boundaries. | ||
| [218] | 2017 | DFIG BTB converter RSC DPC Yes | An FOSMC with an enhanced exponential reaching law is proposed. The FOSMC is used to mitigate the inherent chattering in SMC. | |||
| [219] | 2020 | DFIG RSC control connected to voltage-source-converter -based multi-terminal DC system No | A feedback linearization-based system is used to control the DFIG using FOSMC. The considered wind system is connected to a multi-terminal DC system. | |||
| [103] | 2020 | PMSG BTB converters RSC and GSC Yes | FOSMC-based control is presented. A sign function is replace by saturation function. |
| Technique | Ref. | Year | Errors | Surfaces | Generator, Control, and Converter-Type Hardware | Remarks |
|---|---|---|---|---|---|---|
| Fractional-order terminal SMC | [104] | 2017 | DFIG BTB converters Yes | An artificial intelligence and fractional-order system are integrated to improve the system efficiency. The discontinuous terms of controllers are proposed using FL theory. The experiments are validated using PIL-based workbench. | ||
| [106] | 2020 | DFIG BTB converters Yes | ||||
| Fractional-order super twisting | [105] | 2017 | DFIG BTB converters Yes | A fractional-order terminal control is combined with the attributes of super twisting control. The chattering in fractional-order terminal SMC is improved by using super twisting algorithm | ||
| Fractional-order composite SMC | [2] | 2020 | DFIG BTB converters Yes | A sensorless FOTSMC is presented in this paper. The speed is estimated using Gaussian process regression. The sign function is replaced by fuzzy control theory to reduce chattering. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sami, I.; Ullah, S.; Khan, L.; Al-Durra, A.; Ro, J.-S. Integer and Fractional-Order Sliding Mode Control Schemes in Wind Energy Conversion Systems: Comprehensive Review, Comparison, and Technical Insight. Fractal Fract. 2022, 6, 447. https://doi.org/10.3390/fractalfract6080447
Sami I, Ullah S, Khan L, Al-Durra A, Ro J-S. Integer and Fractional-Order Sliding Mode Control Schemes in Wind Energy Conversion Systems: Comprehensive Review, Comparison, and Technical Insight. Fractal and Fractional. 2022; 6(8):447. https://doi.org/10.3390/fractalfract6080447
Chicago/Turabian StyleSami, Irfan, Shafaat Ullah, Laiq Khan, Ahmed Al-Durra, and Jong-Suk Ro. 2022. "Integer and Fractional-Order Sliding Mode Control Schemes in Wind Energy Conversion Systems: Comprehensive Review, Comparison, and Technical Insight" Fractal and Fractional 6, no. 8: 447. https://doi.org/10.3390/fractalfract6080447
APA StyleSami, I., Ullah, S., Khan, L., Al-Durra, A., & Ro, J.-S. (2022). Integer and Fractional-Order Sliding Mode Control Schemes in Wind Energy Conversion Systems: Comprehensive Review, Comparison, and Technical Insight. Fractal and Fractional, 6(8), 447. https://doi.org/10.3390/fractalfract6080447










