A Fractal Entropy-Based Effective Particle Model Used to Deduce Hydraulic Conductivity of Granular Soils
Abstract
:1. Introduction
2. Effective Particle Diameter Based on Fractal Entropy
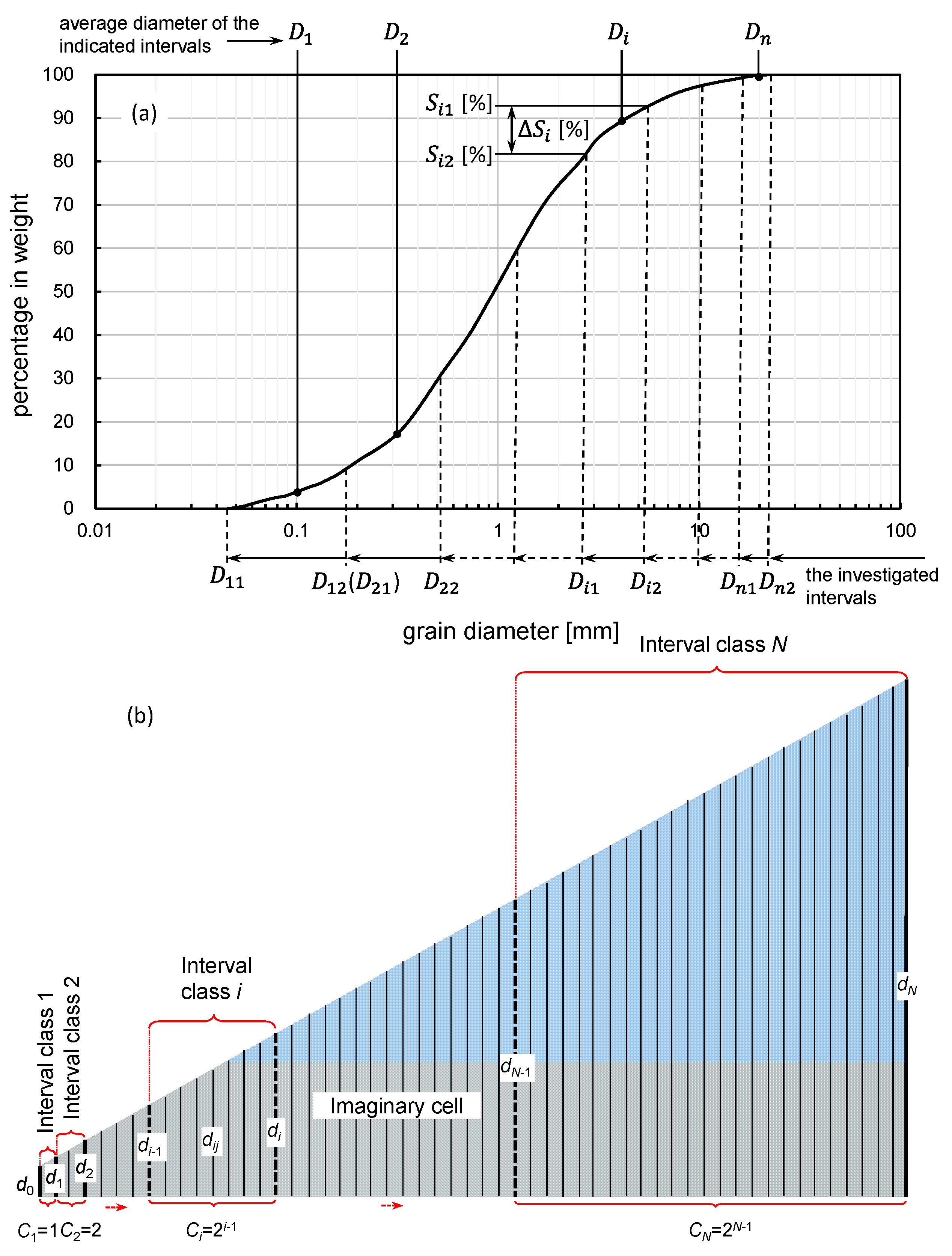
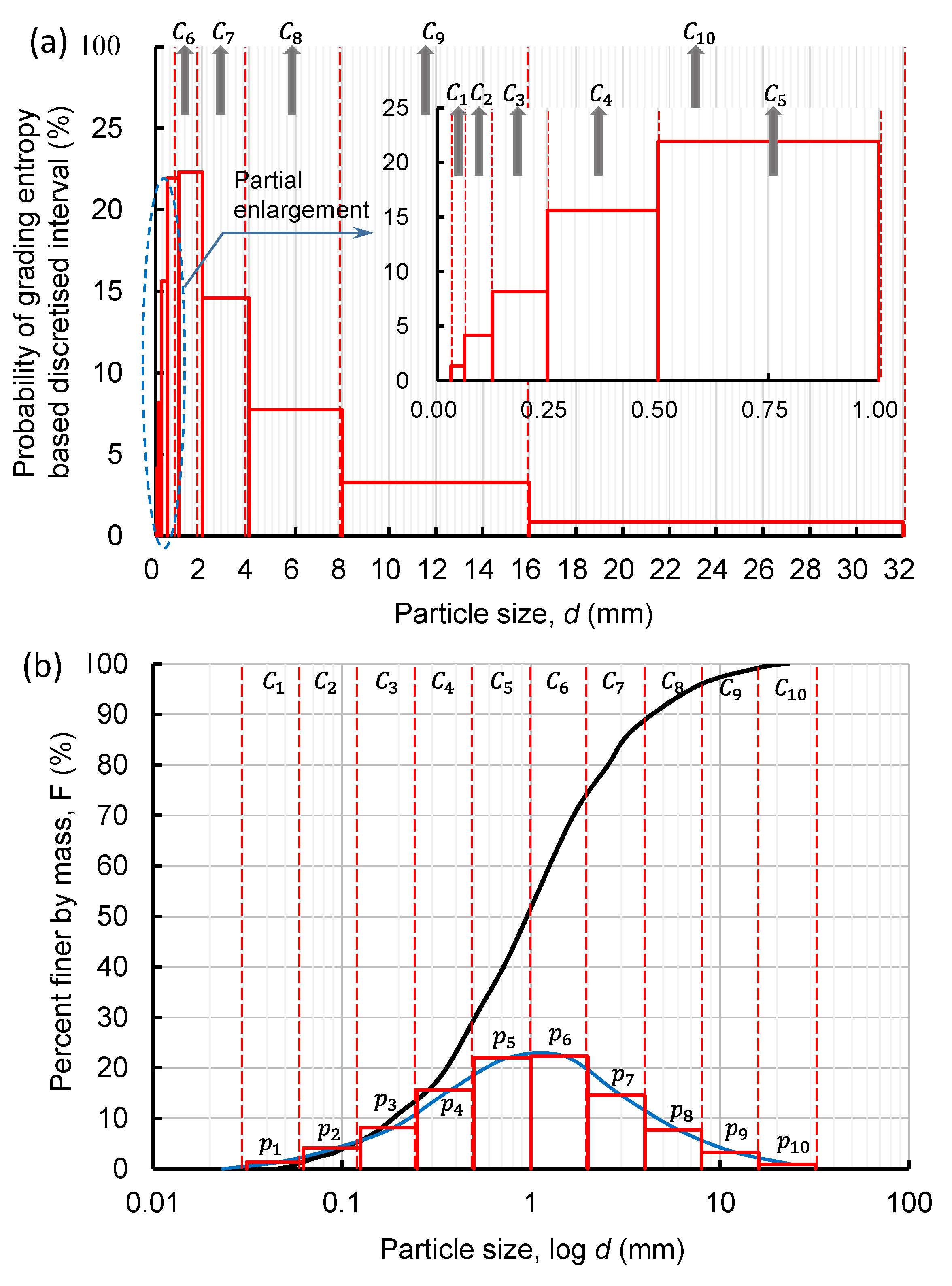
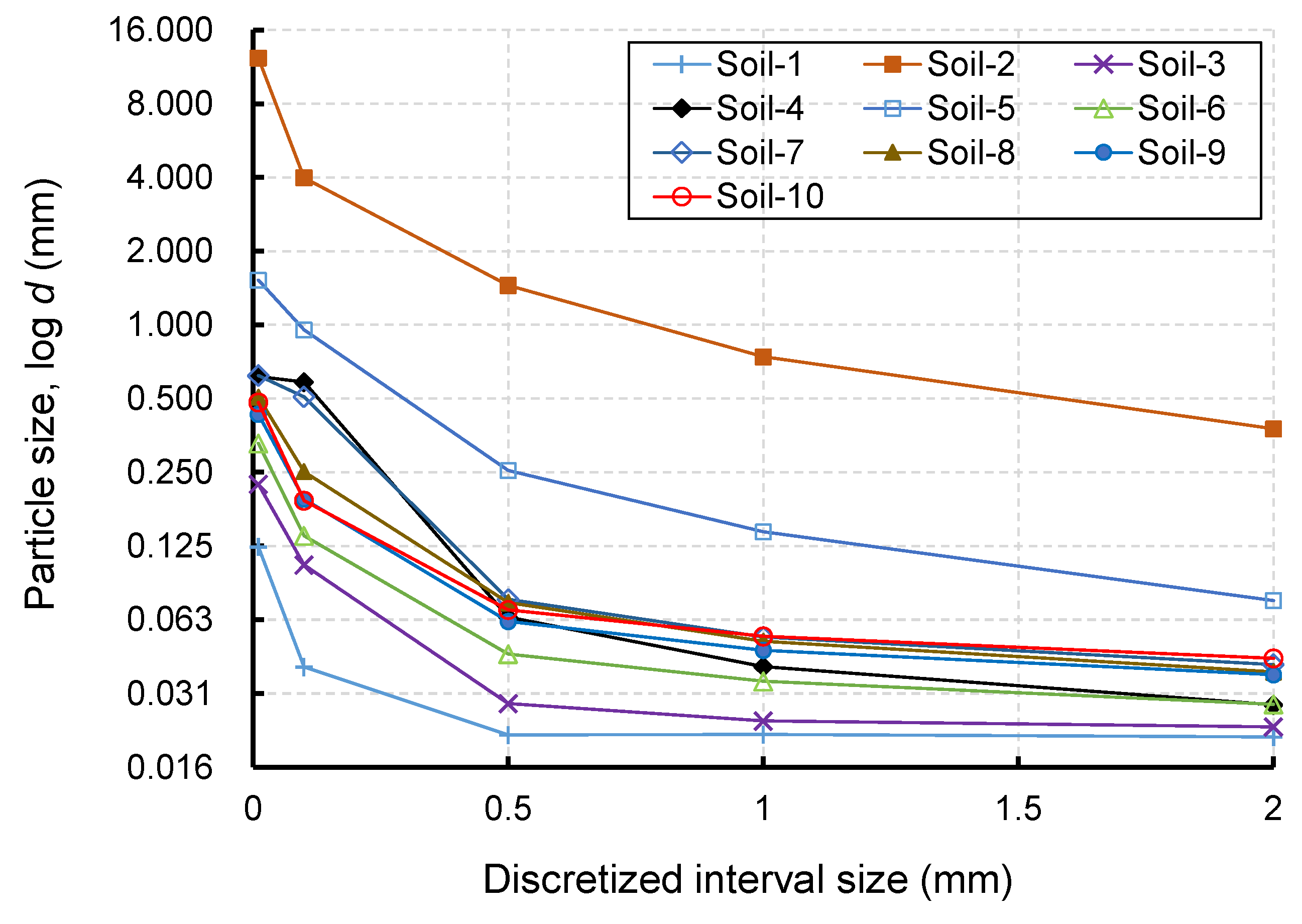
2.1. Interval Class Discretization Based on Grading Entropy
2.2. Effective Particle Diameter Based on Grading Entropy
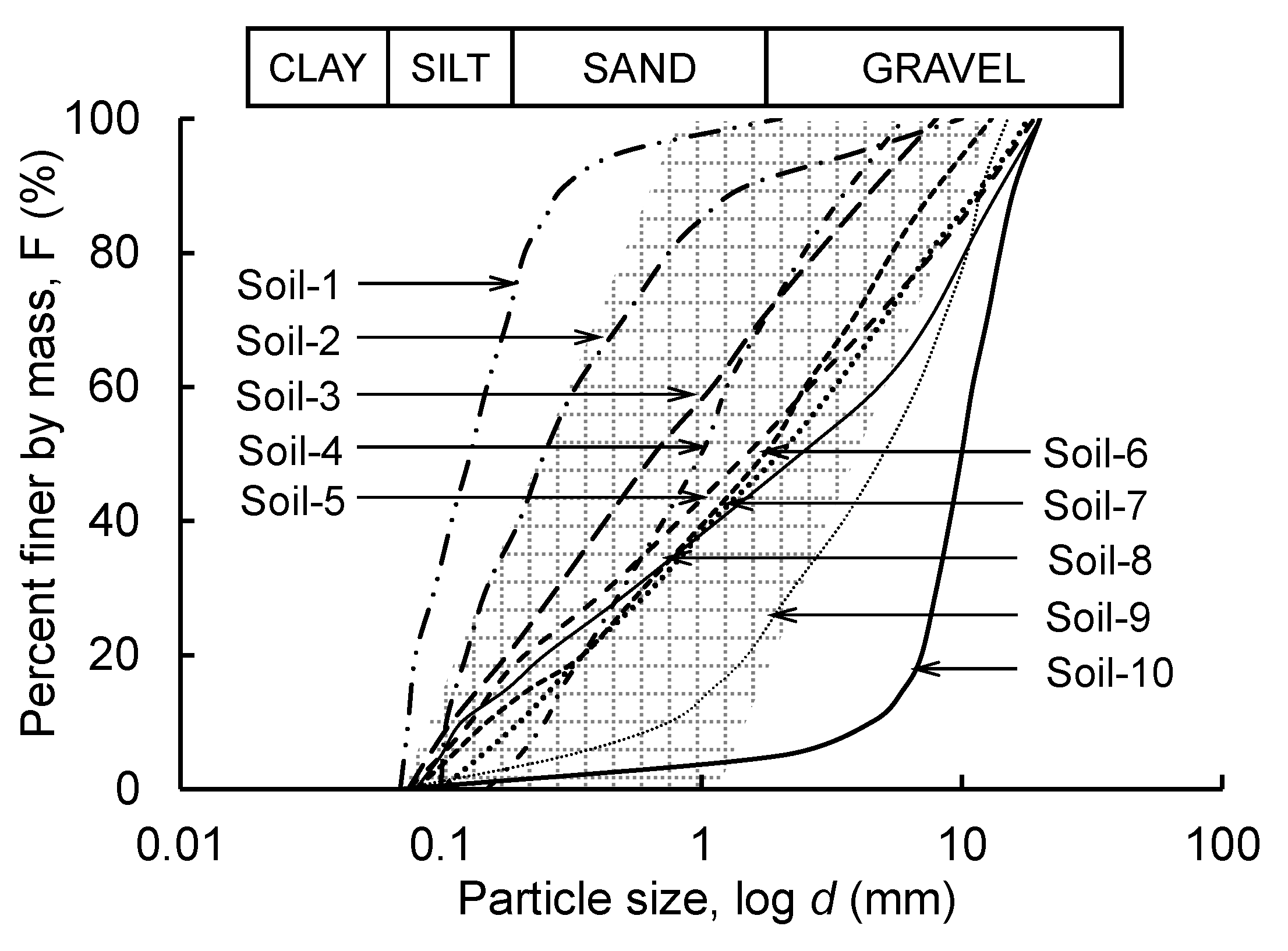
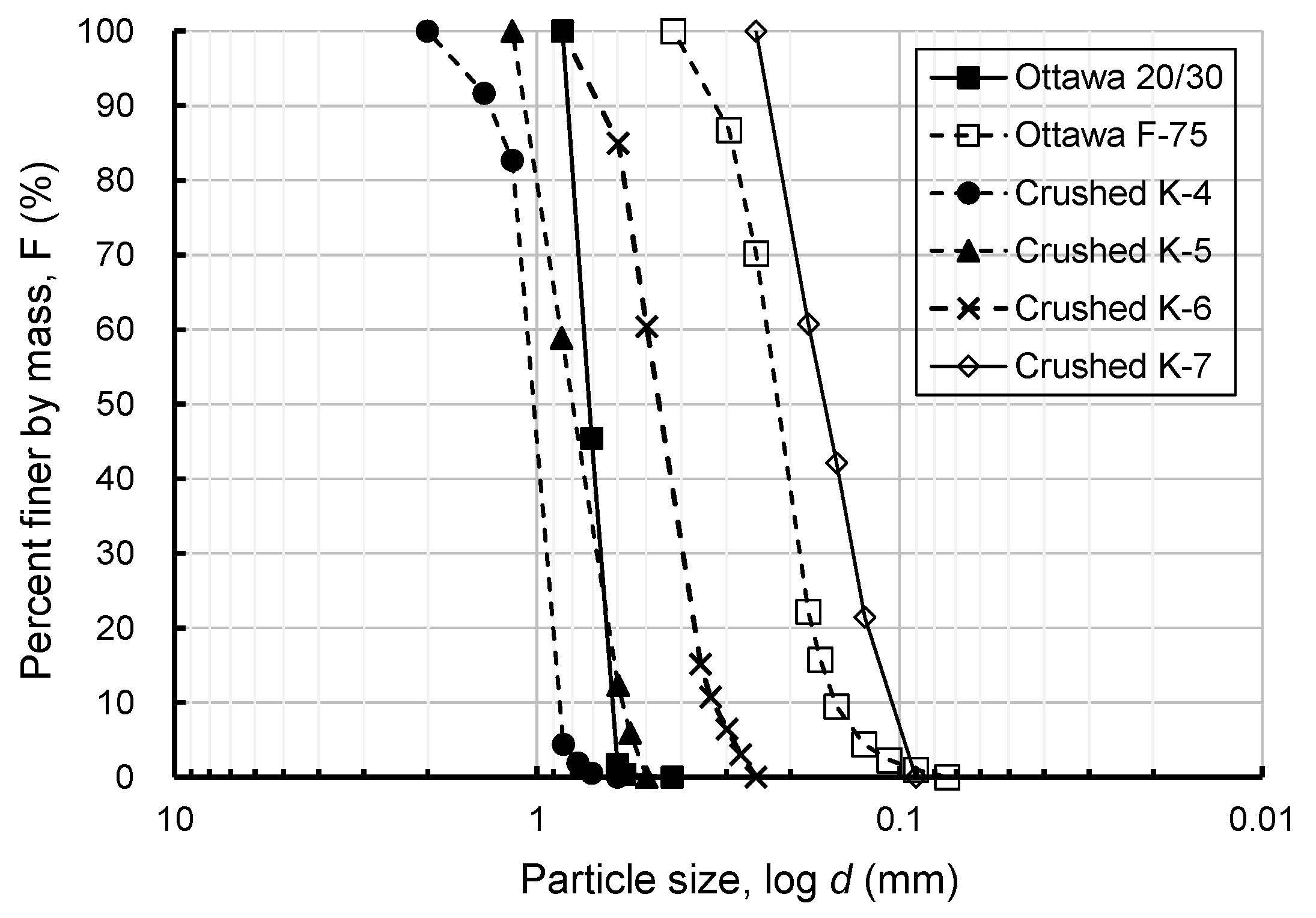
3. Effective Particle Diameters for Different Soils
3.1. Widely Graded Soils
3.2. Gap-Graded Soils
4. Implication of Proposed Model into K-C Formula
4.1. Modified K-C Formula Based on Grading Entropy Effective Diameter
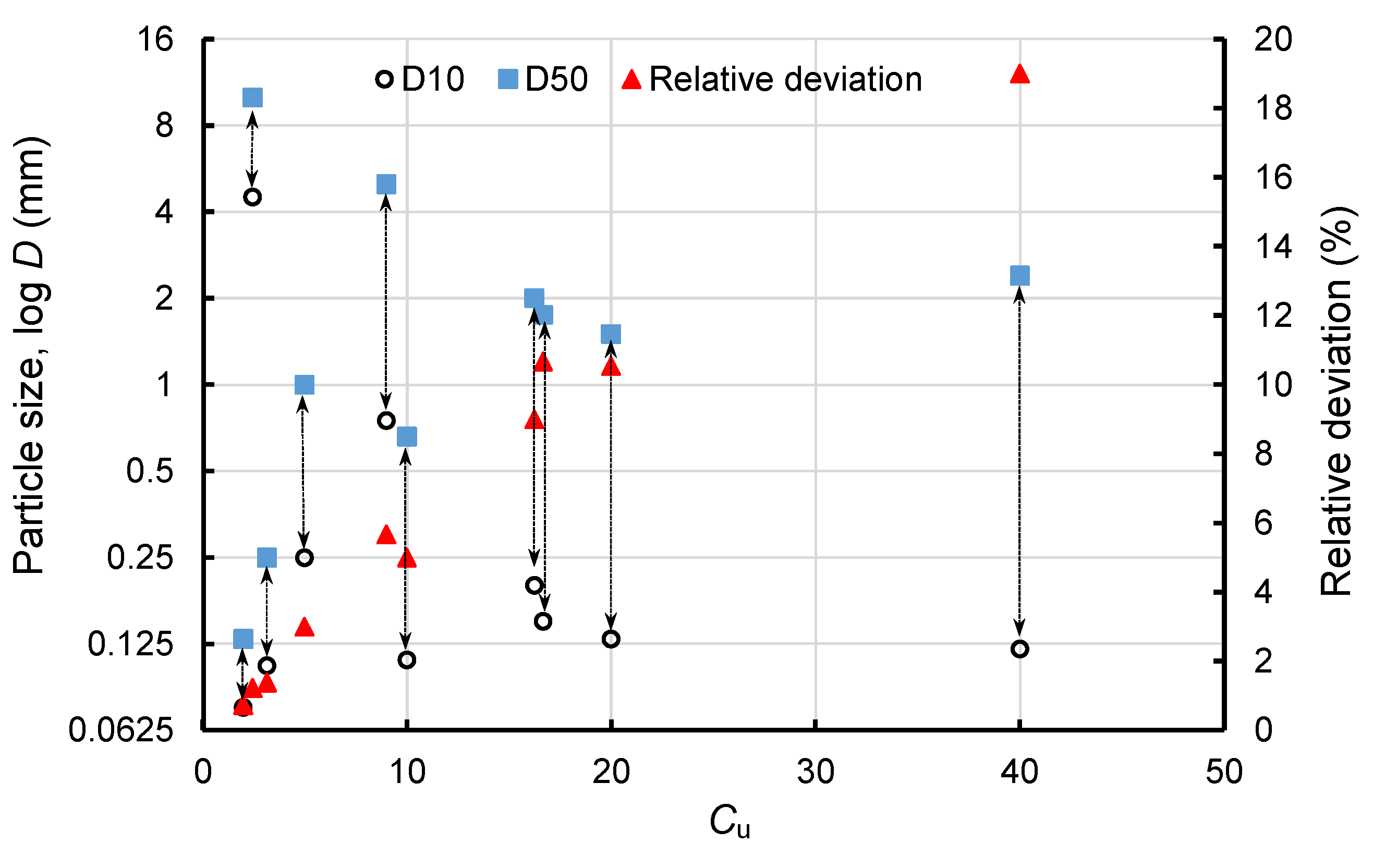
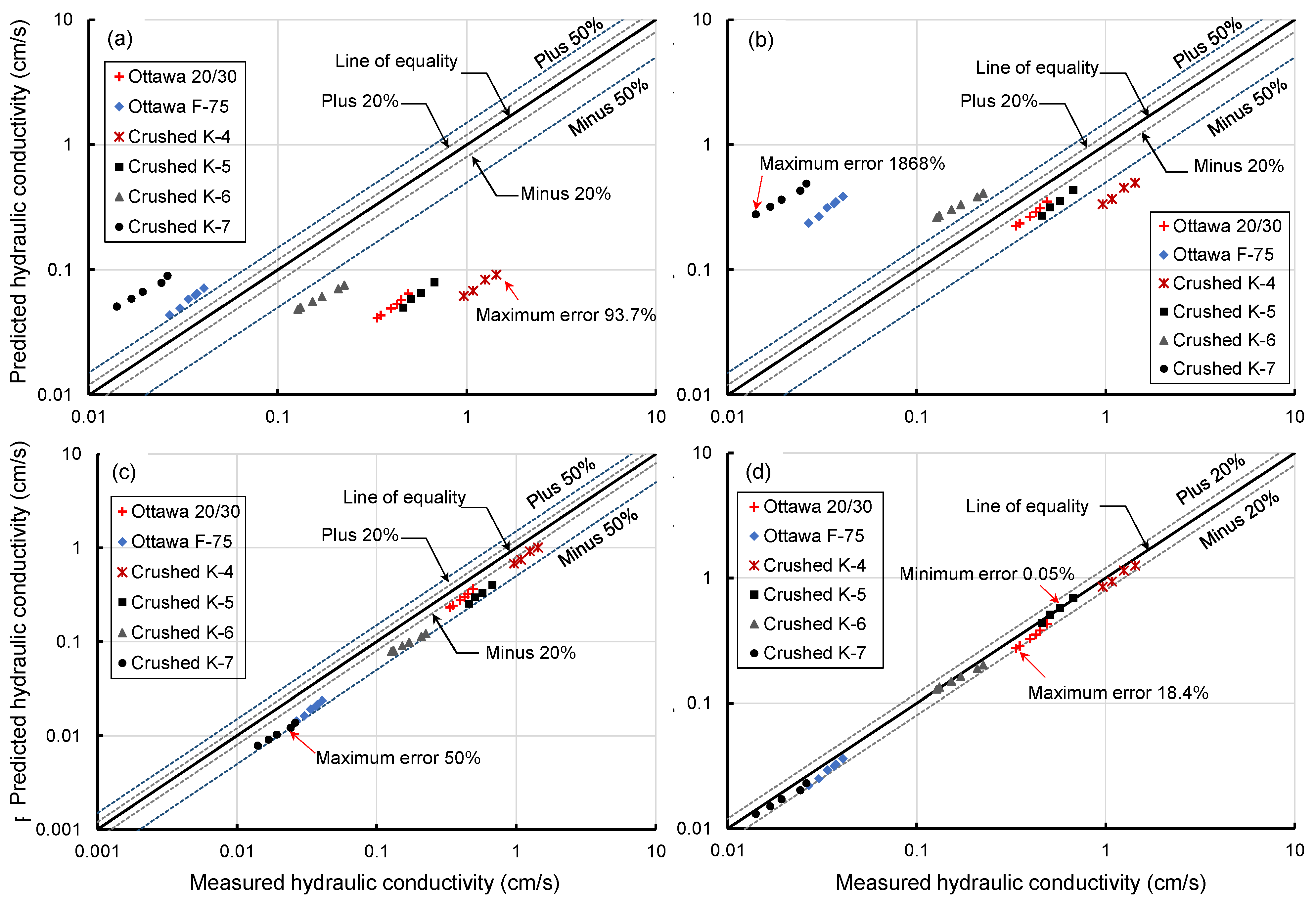
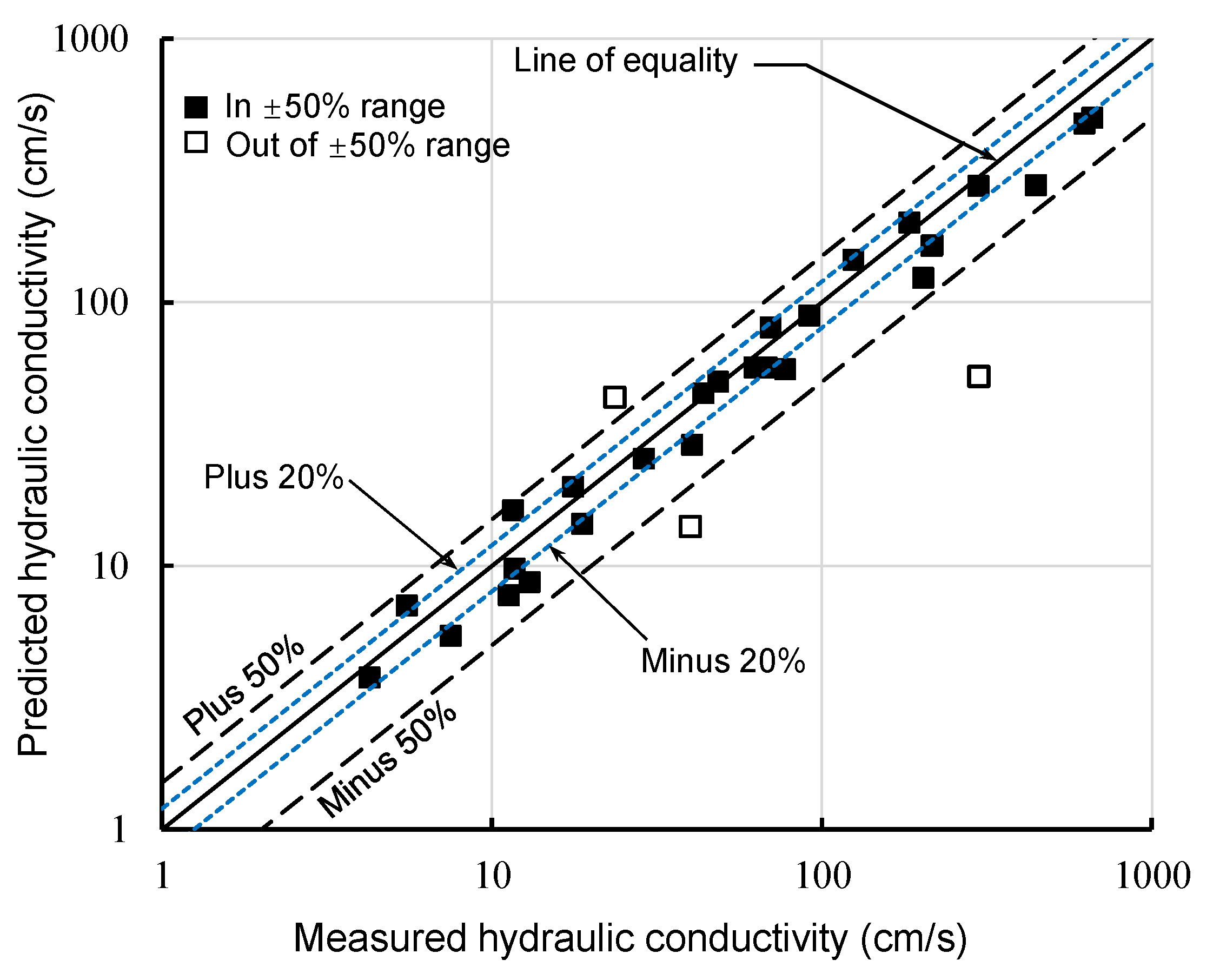
4.2. Determination of Saturated Hydraulic Conductivity and Comparisons
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
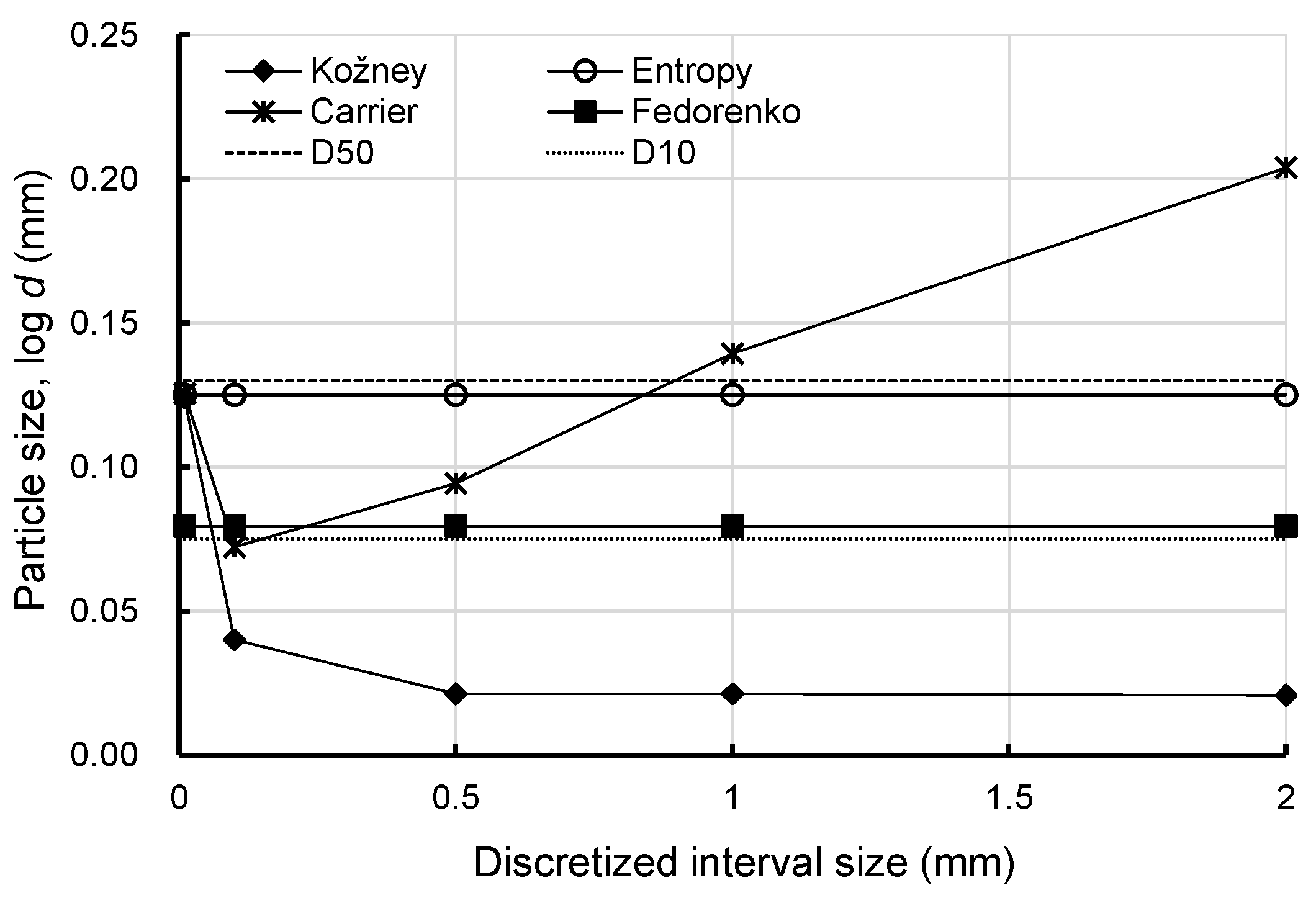
Appendix A. Review of Existing Methods of Effective Diameter Computations
References
- Chapuis, R.P. Predicting the saturated hydraulic conductivity of sand and gravel using effective diameter and void ratio. Can. Geotech. J. 2004, 41, 787–795. [Google Scholar] [CrossRef]
- Dyka, I.; Srokosz, P.E.; Bujko, M. Influence of grain size distribution on dynamic shear modulus of sands. Open Eng. 2017, 7, 317–329. [Google Scholar] [CrossRef]
- Kenney, T.; Lau, D. Internal stability of granular filters. Can. Geotech. J. 1985, 22, 215–225. [Google Scholar] [CrossRef]
- Tong, C.-X.; Burton, G.J.; Zhang, S.; Sheng, D. A simple particle-size distribution model for granular materials. Can. Geotech. J. 2018, 55, 246–257. [Google Scholar] [CrossRef]
- Tsuda, A.; Henry, F.S.; Butler, J.P. Particle transport and deposition: Basic physics of particle kinetics. Compr. Physiol. 2013, 3, 1437–1471. [Google Scholar] [PubMed]
- Seelheim, F. Methoden zur bestimmung der durchlassigkeit des bodens. Z. Anal. Chem. 1880, 19, 387–402. [Google Scholar] [CrossRef]
- Hazen, A. Some Physical Properties of Sands and Gravels, with Special Reference to Their Use in Filtration; 24th Annual Report; Massachusetts State Board of Health: Boston, MA, USA, 1892; pp. 539–555. [Google Scholar]
- Carrier, W.D. Goodbye, Hazen; Hello, Kozeny-Carman. J. Geotech. Geoenviron. Eng. 2003, 129, 1054–1056. [Google Scholar] [CrossRef]
- Chen, H.; Lv, X.; Qiao, Y. Fitting four-modal sedimentary grain-size distribution with gradient descent method. In Proceedings of the 2011 International Conference on Remote Sensing, Environment and Transportation Engineering, Nanjing, China, 24–26 June 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 5987–5990. [Google Scholar]
- Wichtmann, T.; Triantafyllidis, T. Influence of the Grain-Size Distribution Curve of Quartz Sand on the Small Strain Shear Modulus Gmax. J. Geotech. Geoenviron. Eng. 2009, 135, 1404–1418. [Google Scholar] [CrossRef]
- Burenkova, V. Assessment of suffusion in non-cohesive and graded soils. In Proceedings of the 1st International Conference “Geo-Filters”, Filters in geotechnical and hydraulic engineering, Karlsruhe, Germany, 20–22 October 1992; pp. 357–360. [Google Scholar]
- Chapuis, R.P. Similarity of internal stability criteria for granular soils. Can. Geotech. J. 1992, 29, 711–713. [Google Scholar] [CrossRef]
- Kezdi, A. Soil Physics: Selected Topics; Elsevier Science: Amsterdam, The Netherlands, 1979. [Google Scholar]
- Lőrincz, J. Relationship between grading entropy and dry bulk density of granular soils. Period. Polytech. Civ. Eng. 1990, 34, 255–263. [Google Scholar]
- Indraratna, B.; Israr, J.; Rujikiatkamjorn, C. Geometrical method for evaluating the internal instability of granular filters based on constriction size distribution. J. Geotech. Geoenviron. Eng. 2015, 141, 4015045. [Google Scholar] [CrossRef] [Green Version]
- Israr, J.; Zhang, G. Geometrical assessment of internal instability potential of granular soils based on grading entropy. Acta Geotech. 2021, 16, 1961–1970. [Google Scholar] [CrossRef]
- Lőrincz, J.; Imre, E.; Fityus, S.; Trang, P.Q.; Tarnai, T.; Talata, I.; Singh, V.P. The grading entropy-based criteria for structural stability of granular materials and filters. Entropy 2015, 17, 2781–2811. [Google Scholar] [CrossRef]
- Hateren, J.A.; Prins, M.A.; van Balen, R.T. On the genetically meaningful decomposition of grain-size distributions: A comparison of different end-member modelling algorithms. Sediment. Geol. 2018, 375, 49–71. [Google Scholar] [CrossRef]
- Varga, G.; Újvári, G.; Kovács, J. Interpretation of sedimentary (sub) populations extracted from grain size distributions of Central European loess-paleosol series. Quat. Int. 2019, 502, 60–70. [Google Scholar] [CrossRef]
- Chapuis, R.P.; Saucier, A. Assessing internal erosion with the modal decomposition method for grain size distribution curves. Acta Geotech. 2020, 15, 1595–1605. [Google Scholar] [CrossRef]
- Fredlund, M.D.; Fredlund, D.; Wilson, G.W. An equation to represent grain-size distribution. Can. Geotech. J. 2000, 37, 817–827. [Google Scholar] [CrossRef]
- Foster, M.; Fell, R. Assessing embankment dam filters that do not satisfy design criteria. J. Geotech. Geoenviron. Eng. 2001, 127, 398–407. [Google Scholar] [CrossRef]
- Indraratna, B.; Raut, A.K.; Khabbaz, H. Constriction-based retention criterion for granular filter design. J. Geotech. Geoenviron. Eng. 2007, 133, 266–276. [Google Scholar] [CrossRef]
- Khor, C.H.; Woo, H.K. Investigation of crushed rock filters for dam embankment. J. Geotech. Eng. 1989, 115, 399–412. [Google Scholar] [CrossRef]
- Lafleur, J. Filter testing of broadly graded cohesionless tills. Can. Geotech. J. 1984, 21, 634–643. [Google Scholar] [CrossRef]
- Sherard, J.; Dunnigan, L. Critical filters for impervious soils. J. Geotech. Eng. 1989, 115, 927–947. [Google Scholar] [CrossRef]
- Terzaghi, K. Der grundgruch an stauwerken und seine verhutung (The failure of dams by piping and Its prevention). Die Wasserkraft 1922, 17, 445–449. [Google Scholar]
- Trani, L.D.O.; Indraratna, B. The use of particle size distribution by surface area method in predicting the saturated hydraulic conductivity of graded granular soils. Géotechnique 2010, 60, 957–962. [Google Scholar] [CrossRef]
- Beyer, W. On the determination of hydraulic conductivity of gravels and sands from grain-size distribution. Wasserwirtsch. Wassertech. 1964, 14, 165–169. [Google Scholar]
- Harleman, D.R.F.; Melhorn, P.F.; Rumer, R.R. Dispersion-permeability correlation in porous media. J. Hydraul. Div. 1963, 89, 67–85. [Google Scholar] [CrossRef]
- Terzaghi, C. Principles of soil mechanics: III—Determination of permeability of clay. Eng. News Rec. 1925, 95, 832–836. [Google Scholar]
- Kozeny, J. Ueber kapillare Leitung des Wassers im Boden. Sitzungsber Akad. Wiss. 1927, 136, 271–306. [Google Scholar]
- Vukovic, M.; Soro, A. Determination of Hydraulic Conductivity of Porous Media from Grain-Size Composition; Water Resources Publications: Littleton, CO, USA, 1992. [Google Scholar]
- Koenders, M.A.; Williams, A.F. Flow equations of particle fluid mixtures. Acta Mech. 1992, 92, 91–116. [Google Scholar] [CrossRef]
- Waters, T.J. A study of water infiltration through ASPHALT road surface materials. In Proceedings of the International Symposium on Subdrainage in Roadway Pavements and Subgrades, Granada, Spain, 11–13 November 1998; pp. 311–317. [Google Scholar]
- Vardanega, P.J.; Waters, T.J. Analysis of Asphalt Concrete Permeability Data Using Representative Pore Size. J. Mater. Civ. Eng. 2011, 23, 169–176. [Google Scholar] [CrossRef]
- Bear, J. Dynamics of Fluids in Porous Media; Dover Publications, Inc.: New York, NY, USA, 1972. [Google Scholar]
- Koltermann, C.E.; Gorelick, S.M. Fractional packing model for hydraulic conductivity derived from sediment mixtures. Water Resour. Res. 1995, 31, 3283–3297. [Google Scholar] [CrossRef]
- Kovács, G. Seepage Hydraulics; Akadénmiai Kiadó: Budapest, Hungary, 1981. [Google Scholar]
- Kozeny, J. Das Wasser im Boden. Grundwasserbewegung. In Hydraulik; Springer: Vienna, Austria, 1953; pp. 380–445. [Google Scholar]
- Vienken, T.; Dietrich, P. Field evaluation of methods for determining hydraulic conductivity from grain size data. J. Hydrol. 2011, 400, 58–71. [Google Scholar] [CrossRef]
- Lőrincz, J.; Imre, E.; Gálos, M.; Trang, Q.P.; Rajkai, K.; Fityus, S.; Telekes, G. Grading entropy variation due to Soil crushing. Int. J. Geomech. 2005, 5, 311–319. [Google Scholar] [CrossRef]
- Zunker, F. Fertilization and soil science. J. Plant Nutr. A 1932, 25. [Google Scholar]
- Israr, J. Internal Instability of Granular Filters under Cyclic Loading. Ph.D Thesis, University of Wollongong, Wollongong, Australia, 2016. [Google Scholar]
- Andrianatrehina, L.; Souli, H.; Fry, J.-J.; Phan, Q.; Fleureau, J.-M. Internal stability of granular materials in triaxial tests. In Proceedings of the 6th International Conference on Scour and Erosion, France, Paris, 27–31 August 2012. ISSMGE. [Google Scholar]
- Li, M. Seepage Induced Instability in Widely Graded Soils. Ph.D. Thesis, University of British Columbia, Vancouver, BC, Canada, 2008. [Google Scholar]
- Das, B.M. Advanced Soil Mechanics; Tayor & Francis Group: New York, NY, USA, 2008. [Google Scholar]
- Chapuis, R.P.; Aubertin, M. On the use of the Kozeny—Carman equation to predict the hydraulic conductivity of soils. Can. Geotech. J. 2003, 40, 616–627. [Google Scholar] [CrossRef]
- Choo, H.; Kim, J.; Lee, W.; Lee, C. Relationship between hydraulic conductivity and formation factor of coarse-grained soils as a function of particle size. J. Appl. Geophys. 2016, 127, 91–101. [Google Scholar] [CrossRef]
- Feng, S.; Vardanega, P.J.; Ibraim, E.; Widyatmoko, I.; Ojum, C.; O’Kelly, B.C.; Nogal, M. Permeability assessment of some granular mixtures. Géotechnique 2019, 70, 845–847. [Google Scholar] [CrossRef]
- Saleh, A.; Puspita, K.; Sanjaya, A. Implementation of equal width interval discretization on smarter method for selecting computer laboratory assistant. In Proceedings of the 2018 6th International Conference on Cyber and IT Service Management (CITSM), Parapat, Indonesia, 7–9 August 2018; pp. 1–4. [Google Scholar]
- Hacibeyoglu, M.; Ibrahim, M.H. EF_Unique: An improved version of unsupervised equal frequency discretization method. Arab. J. Sci. Eng. 2018, 43, 7695–7704. [Google Scholar] [CrossRef]
- McDougall, J.R.; Imre, E.; Barreto, D.; Kelly, D. Volumetric consequences of particle loss by grading entropy. Géotechnique 2013, 63, 262–266. [Google Scholar] [CrossRef]
- Imre, E.; Lőrincz, J.; Szendefy, J.; Trang, P.Q.; Nagy, L.; Singh, V.P.; Fityus, S. Case studies and benchmark examples for the use of grading entropy in geotechnics. Entropy 2012, 14, 1079–1102. [Google Scholar] [CrossRef]
- Singh, V.P. Entropy Theory in Hydraulic Engineering: An Introduction; ASCE Press: Reston, VA, USA; ProQuest Ebook Central: Ann Arbor, MI, USA, 2014. [Google Scholar]
- Henry, D.; Dymnicki, A.B.; Mohatt, N.; Allen, J.; Kelly, J.G. Clustering methods with qualitative data: A mixed-methods approach for prevention research with small samples. Prev. Sci. 2015, 16, 1007–1016. [Google Scholar] [CrossRef]
- Full, W.E.; Ehrlich, R.; Kennedy, S.K. Optimal definition of class intervals for frequency tables. Part. Sci. Technol. 1983, 1, 281–293. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, G.; Wang, H.; Israr, J.; Ma, W.; Yang, Y.; Ren, K. A Fractal Entropy-Based Effective Particle Model Used to Deduce Hydraulic Conductivity of Granular Soils. Fractal Fract. 2022, 6, 474. https://doi.org/10.3390/fractalfract6090474
Zhang G, Wang H, Israr J, Ma W, Yang Y, Ren K. A Fractal Entropy-Based Effective Particle Model Used to Deduce Hydraulic Conductivity of Granular Soils. Fractal and Fractional. 2022; 6(9):474. https://doi.org/10.3390/fractalfract6090474
Chicago/Turabian StyleZhang, Gang, Hongyu Wang, Jahanzaib Israr, Wenguo Ma, Youzhen Yang, and Keliang Ren. 2022. "A Fractal Entropy-Based Effective Particle Model Used to Deduce Hydraulic Conductivity of Granular Soils" Fractal and Fractional 6, no. 9: 474. https://doi.org/10.3390/fractalfract6090474
APA StyleZhang, G., Wang, H., Israr, J., Ma, W., Yang, Y., & Ren, K. (2022). A Fractal Entropy-Based Effective Particle Model Used to Deduce Hydraulic Conductivity of Granular Soils. Fractal and Fractional, 6(9), 474. https://doi.org/10.3390/fractalfract6090474





