Adaptive Intelligent High-Order Sliding Mode Fractional Order Control for Harmonic Suppression
Abstract
:1. Introduction
2. Mathematical Model of APF
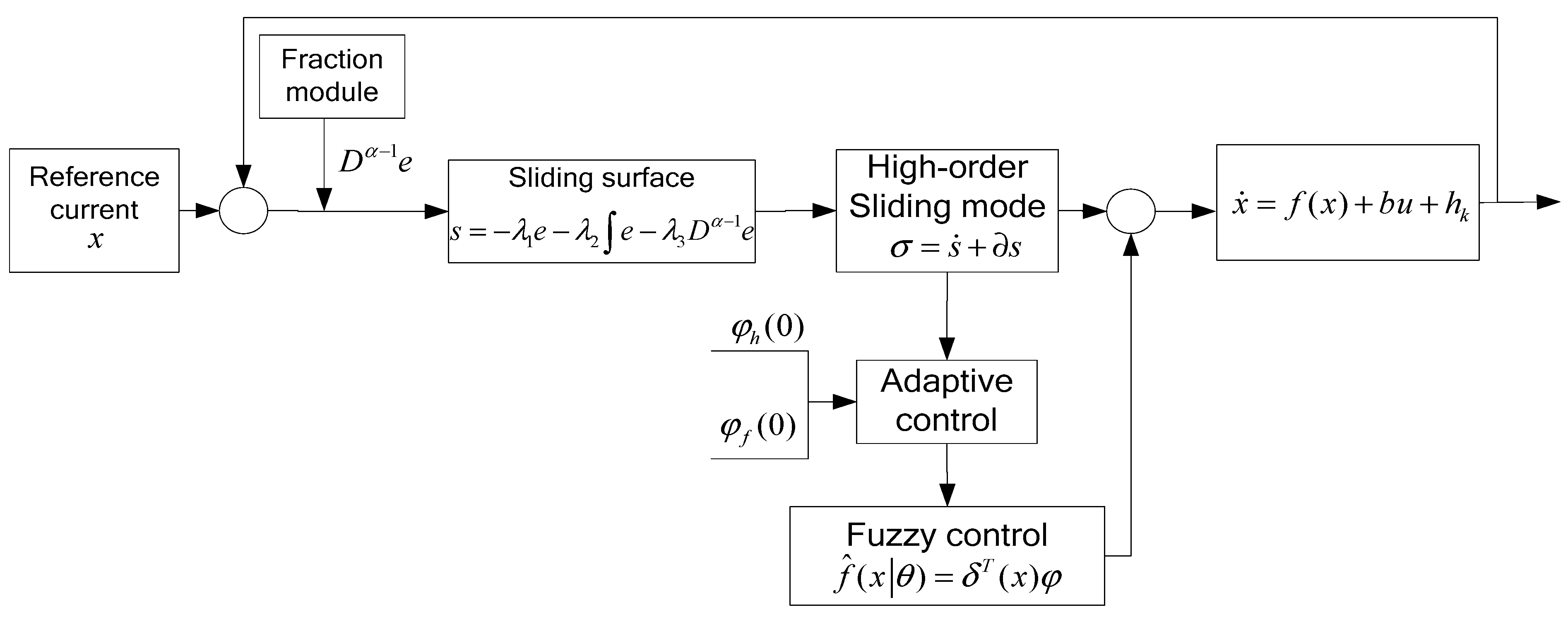
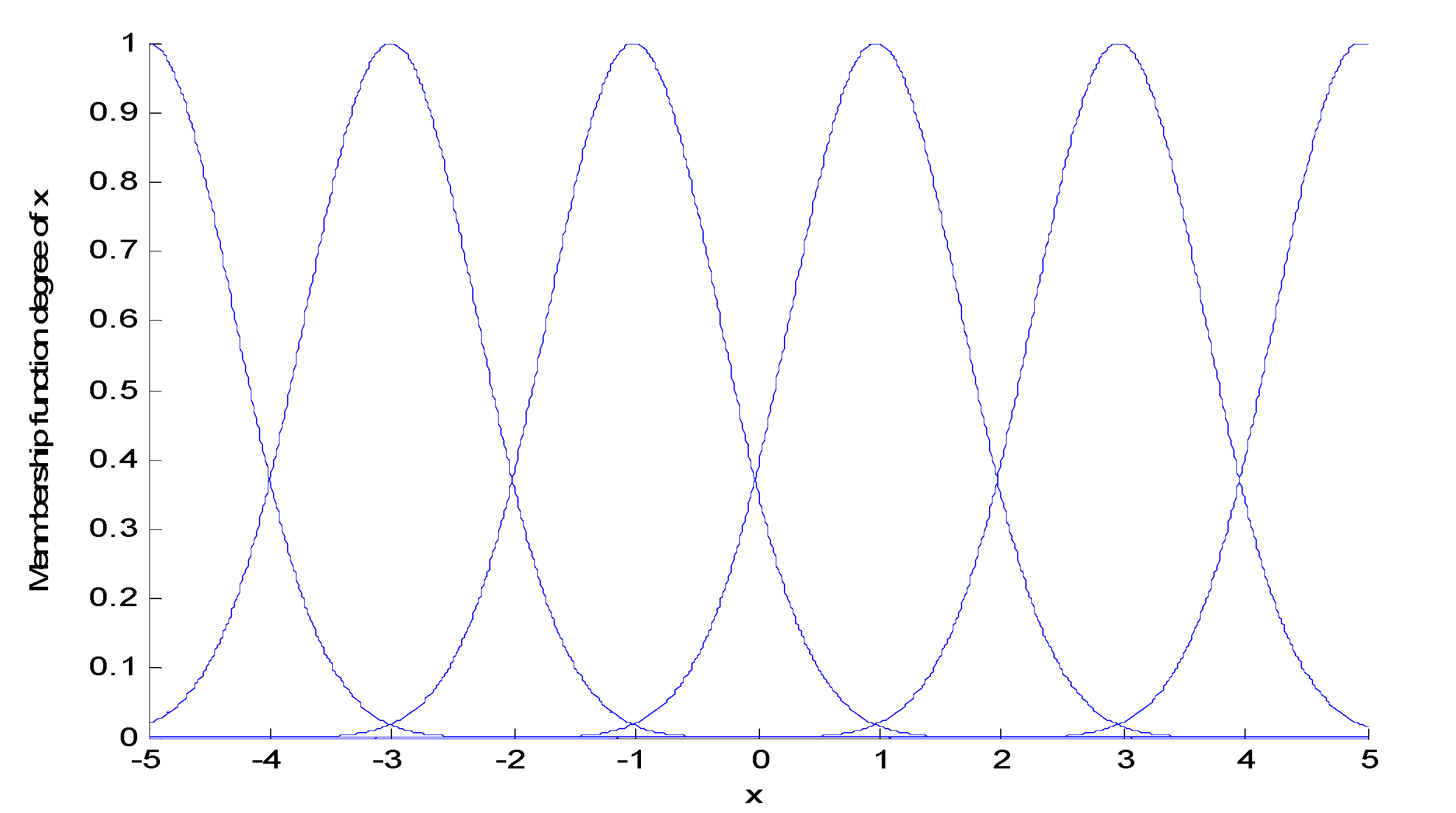
3. Design of Adaptive Fractional Second-Order Sliding Mode Fuzzy Control
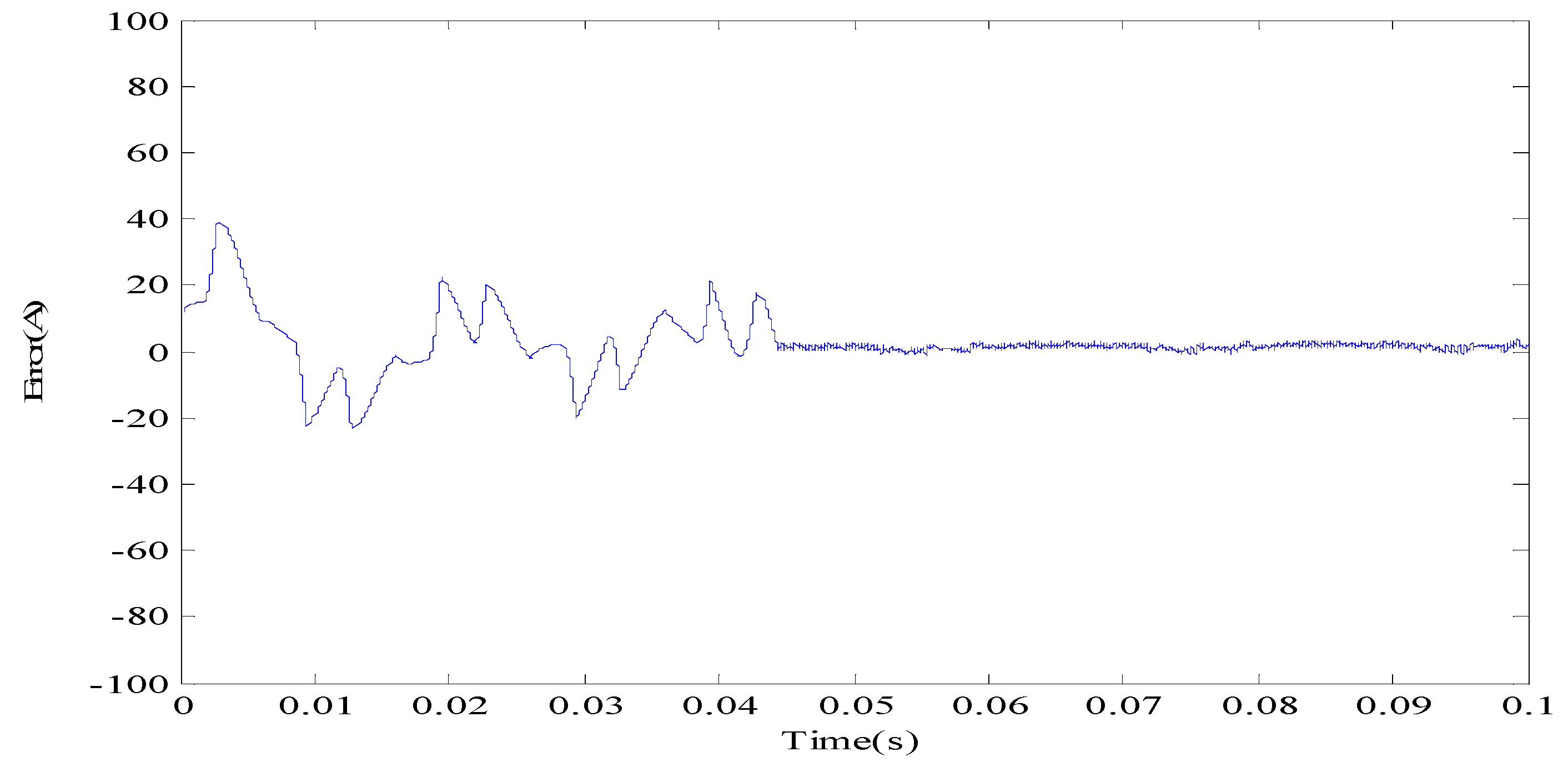
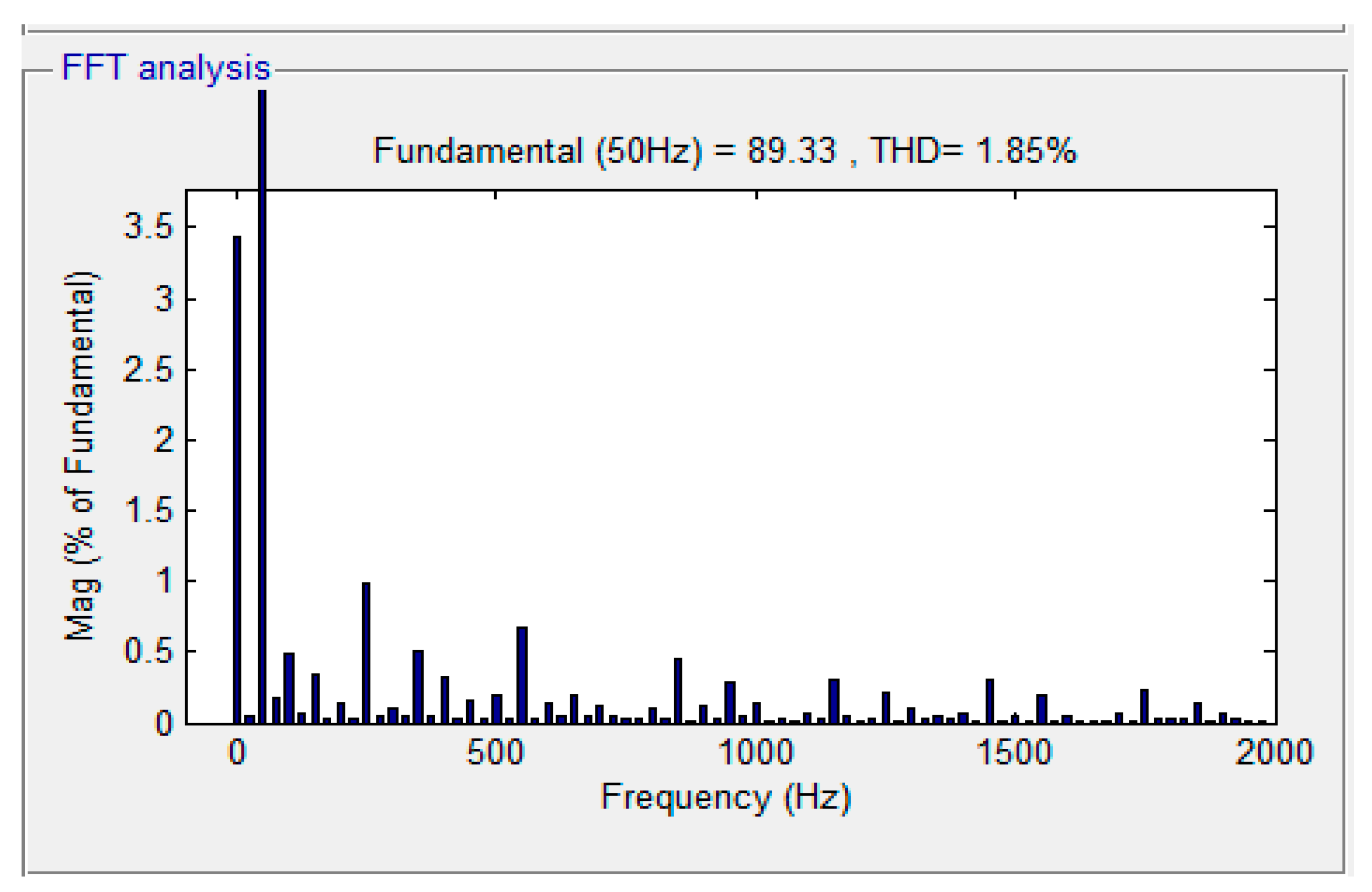
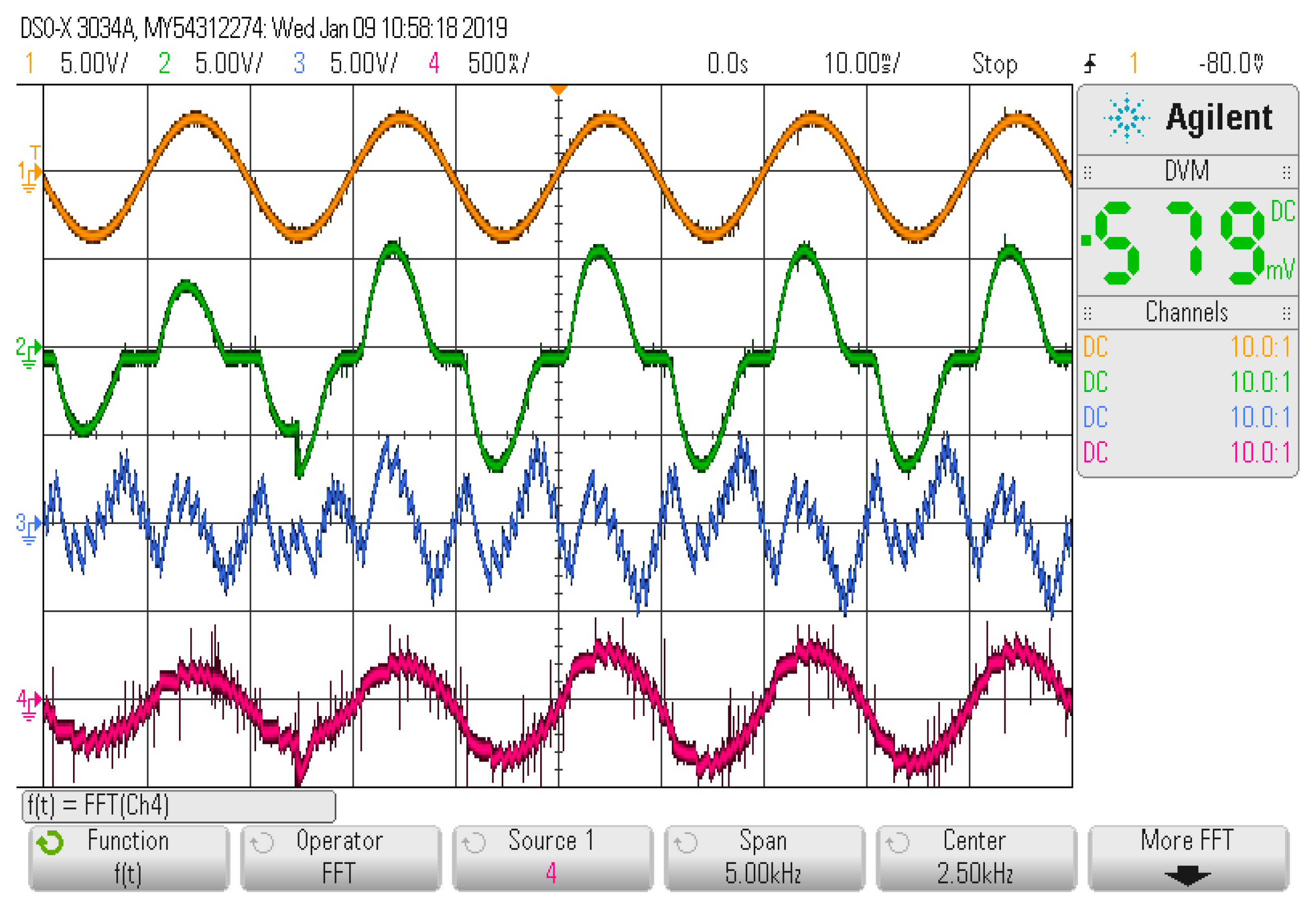
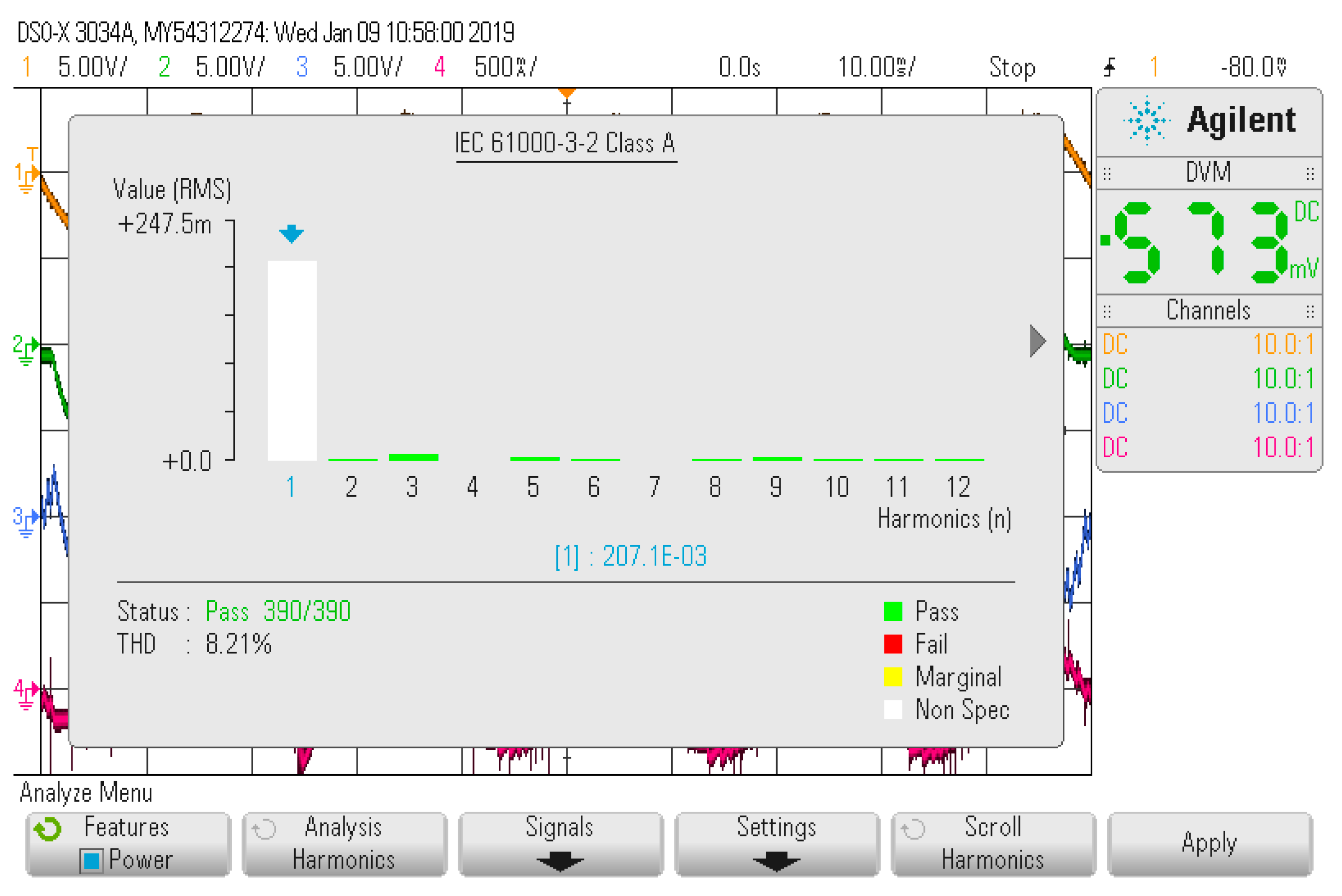
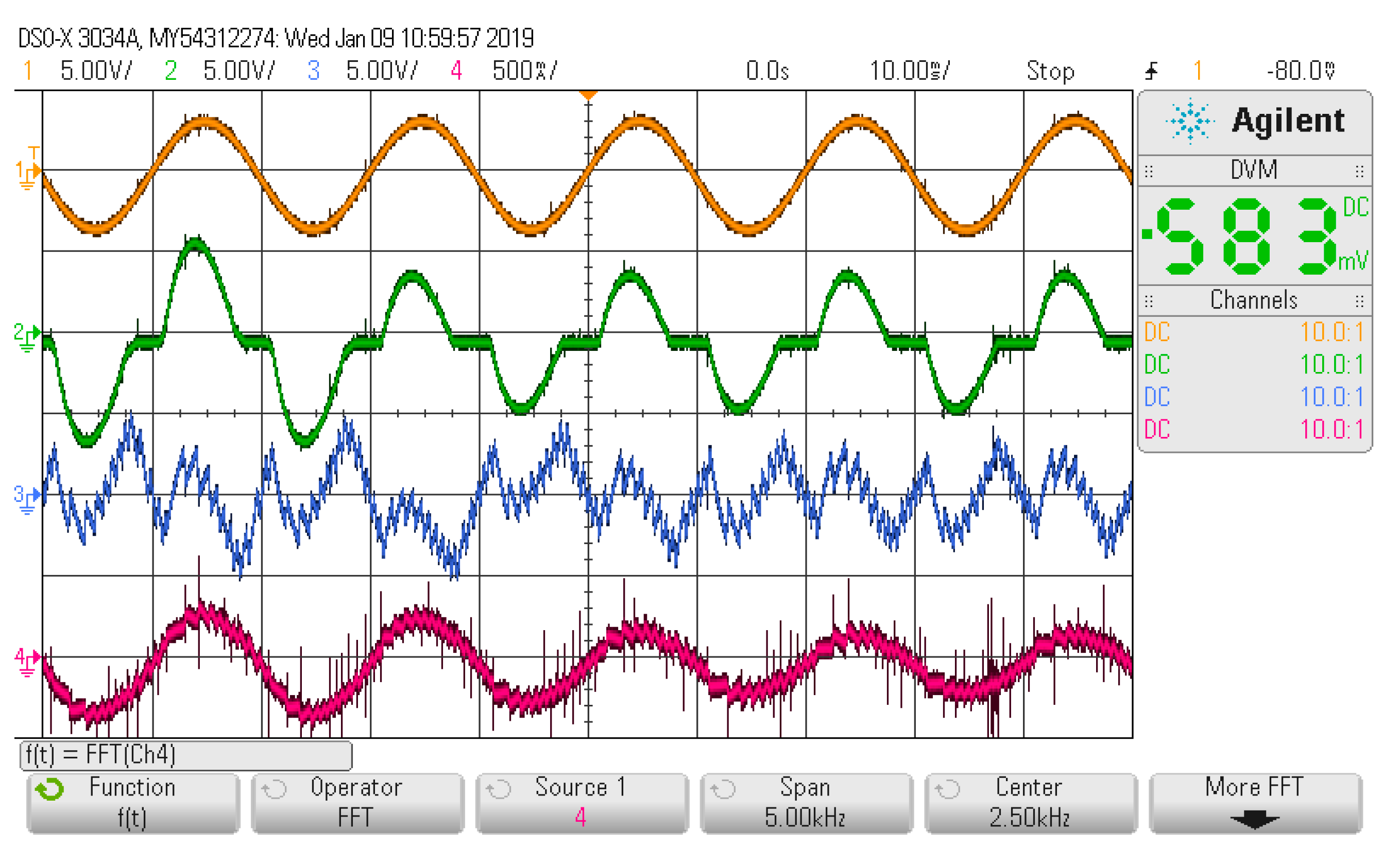
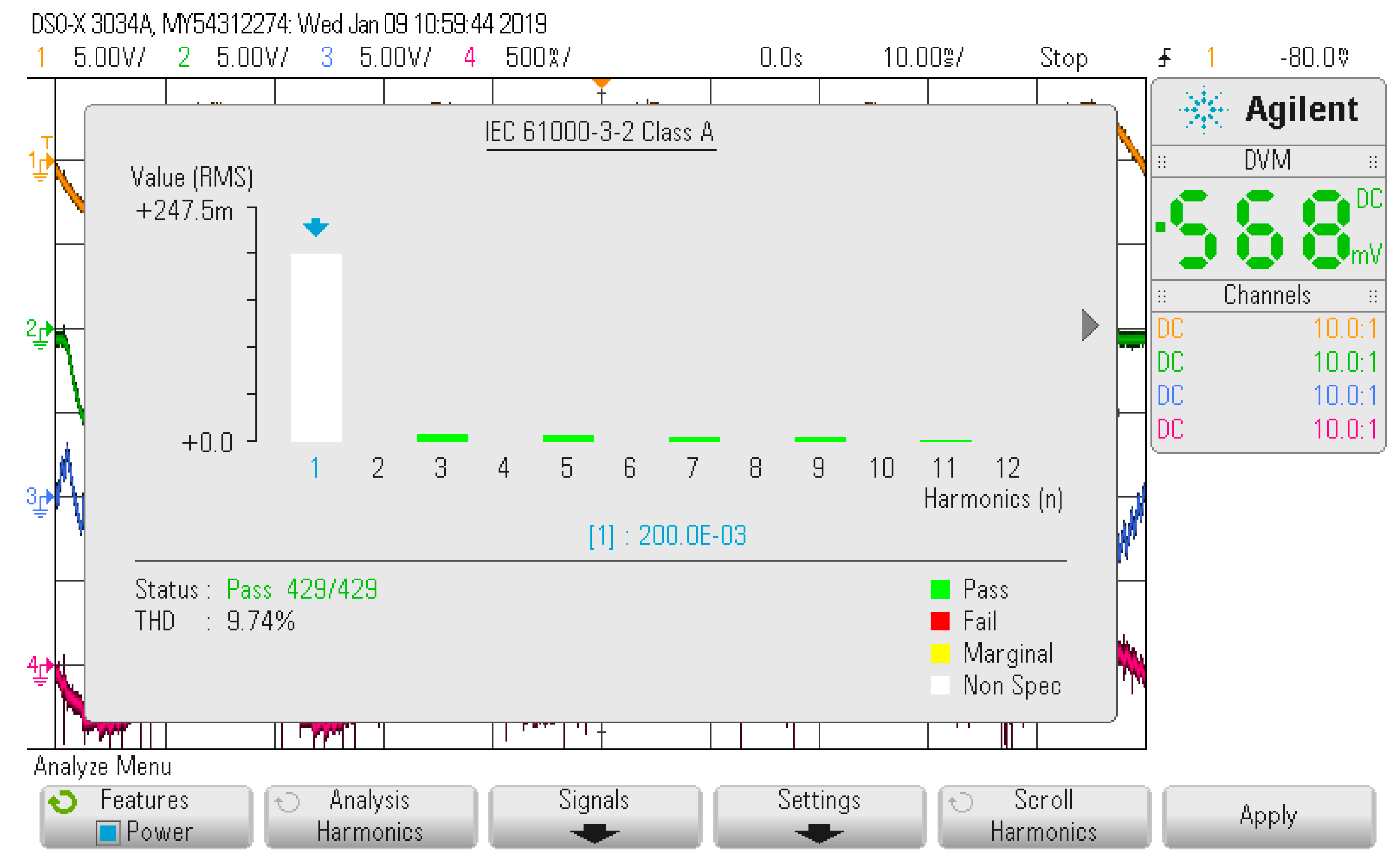
4. Experiment Verification
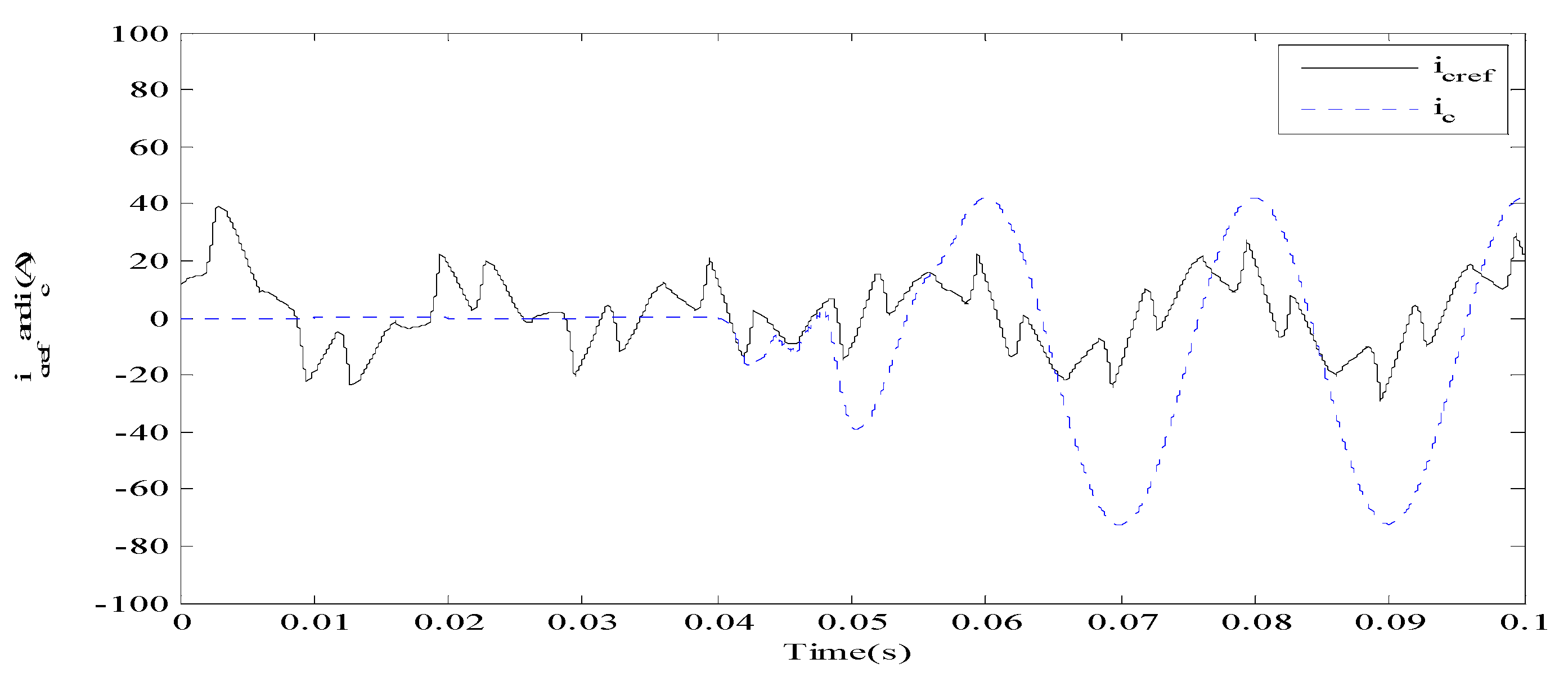
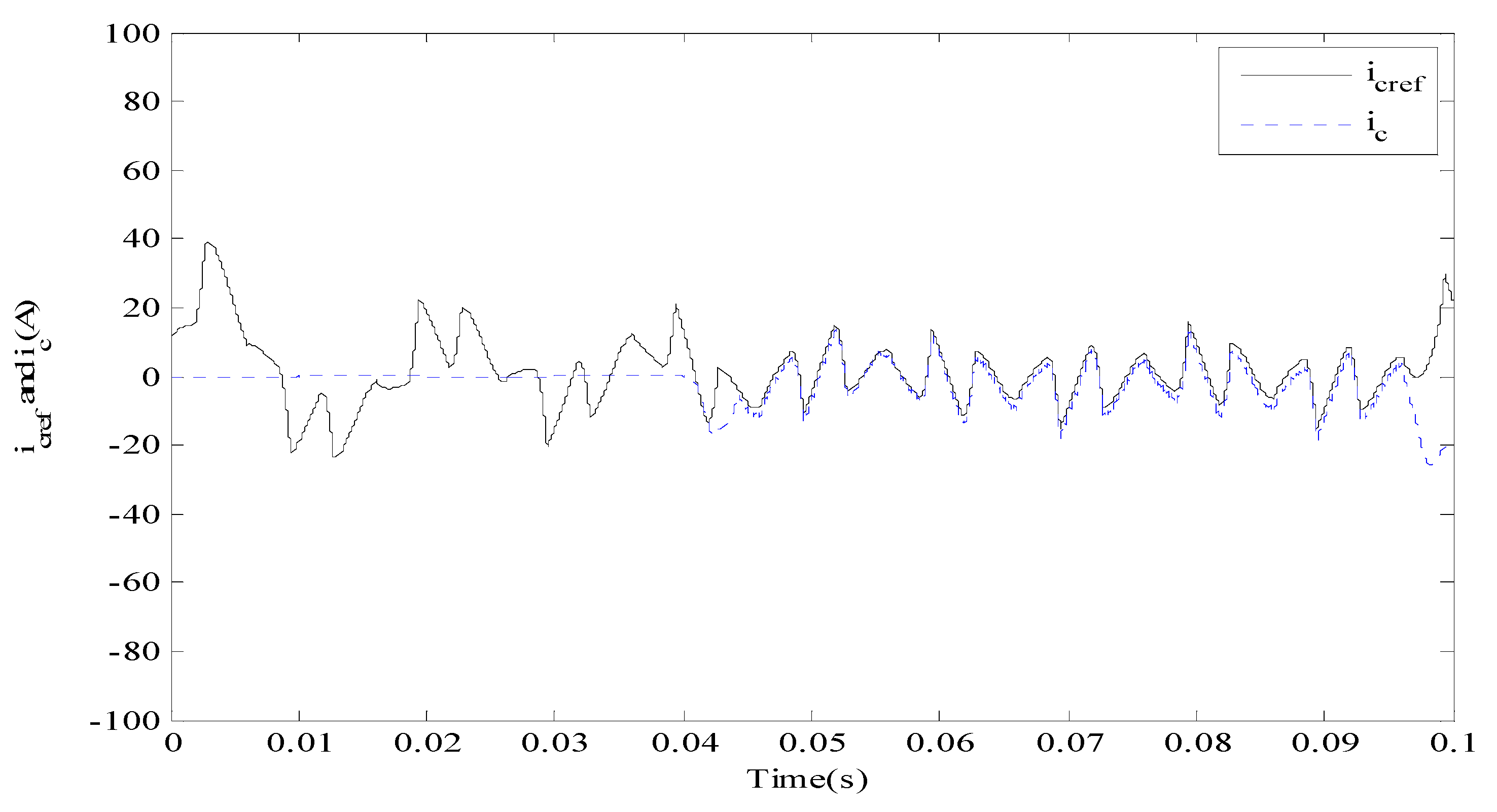
4.1. Simulation Study
4.2. Experiment Set-Up
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Thao, N.; Uchida, K.; Kofuji, K.; Jintsugawa, T.; Nakazawa, C. An Automatic-Tuning Scheme Based on Fuzzy Logic for Active Power Filter in Wind Farms. IEEE Trans. Control Syst. Technol. 2019, 27, 1694–1702. [Google Scholar] [CrossRef]
- Fei, J.; Wang, Z.; Pan, Q. Self-Constructing Fuzzy Neural Fractional-Order Sliding Mode Control for Active Power Filter. IEEE Trans. Neural Netw. Learn. Syst. 2022, 1–12. [Google Scholar] [CrossRef]
- Ray, A.; Bhattacharya, A. Improved Tracking of Shunt Active Power Filter by Sliding Mode Control. Int. J. Electr. Power Energy Syst. 2016, 78, 916–925. [Google Scholar]
- Pradhan, R.; Subudhi, B. Double Integral Sliding Mode MPPT Control of a Photovoltaic System. IEEE Trans. Control Syst. Technol. 2016, 24, 285–292. [Google Scholar] [CrossRef]
- Baek, J.; Jin, M.; Han, S. A New Adaptive Sliding-Mode Control Scheme for Application to Robot Manipulators. IEEE Trans. Ind. Electron. 2016, 63, 3628–3637. [Google Scholar] [CrossRef]
- Hamad, M.; Gadoue, S.; Williams, B.W. Harmonic Compensation of a Six-Pulse Current Source Controlled Converter using Neural Network-Based Shunt Active Power Filter. IET Power Electron. 2012, 5, 747–754. [Google Scholar] [CrossRef]
- Wai, R.; Lin, Y.; Liu, Y. Design of Adaptive Fuzzy-Neural-Network Control for a Single-Stage Boost Inverter. IEEE Trans. Power Electron. 2015, 30, 7282–7298. [Google Scholar] [CrossRef]
- Fei, J.; Liu, L. Real-Time Nonlinear Model Predictive Control of Active Power Filter Using Self-Feedback Recurrent Fuzzy Neural Network Estimator. IEEE Trans. Ind. Electron. 2022, 69, 8366–8376. [Google Scholar] [CrossRef]
- Khanesar, M.; Oniz, Y.; Kaynak, O.; Gao, H. Direct Model Reference Adaptive Fuzzy Control of Networked SISO Nonlinear Systems. IEEE/ASME Trans. Mechatron. 2016, 21, 205–213. [Google Scholar]
- Sahraei, B.; Shabaninia, F.; Nemati, A.; Stan, S. A Novel Robust Decentralized Adaptive Fuzzy Control for Swarm Formation of Multiagent Systems. IEEE Trans. Ind. Electron. 2012, 59, 3124–3134. [Google Scholar] [CrossRef]
- Lopes, A.; Machado, J. Fractional-Order Sensing and Control: Embedding the Nonlinear Dynamics of Robot Manipulators into the Multidimensional Scaling Method. Sensors 2021, 21, 7736. [Google Scholar] [CrossRef] [PubMed]
- Chen, T.; Cheng, J. On the Algorithmic Stability of Optimal Control with Derivative Operators. Circuits Syst. Signal Process. 2020, 39, 5863–5881. [Google Scholar] [CrossRef]
- David, S.; Fischera, C.; Machado, J. Fractional electronic circuit simulation of a nonlinear macroeconomic model. AEU-Int. J. Electron. Commun. 2018, 84, 210–220. [Google Scholar] [CrossRef]
- Muthukumar, P.; Balasubramaniam, P.; Ratnavelu, K. Sliding mode control design for synchronization of fractional order chaotic systems and its application to a new cryptosystem. Int. J. Dyn. Control 2017, 5, 115–123. [Google Scholar] [CrossRef]
- Han, Z.; Li, S.; Li, H. Composite learning sliding mode synchronization of chaotic fractional-order neural network. J. Adv. Res. 2020, 25, 87–96. [Google Scholar] [CrossRef] [PubMed]
- Fei, J.; Wang, Z.; Fang, Y. Self-Evolving Chebyshev Fuzzy Neural Fractional-Order Sliding Mode Control for Active Power Filter. IEEE Trans. Ind. Inform. 2022. [Google Scholar] [CrossRef]
- Chen, S.; Chiang, H.; Liu, T.; Chang, C. Precision Motion Control of Permanent Magnet Linear Synchronous Motors Using Adaptive Fuzzy Fractional-Order Sliding-Mode Control. IEEE/ASME Trans. Mechatron. 2019, 24, 741–752. [Google Scholar] [CrossRef]
- Fei, J.; Wang, Z.; Liang, X.; Feng, Z.; Xue, Y. Adaptive Fractional Sliding Mode Control of Micro Gyroscope System Using Double Loop Recurrent Fuzzy Neural Network Structure. IEEE Trans. Fuzzy Syst. 2022, 30, 1712–1721. [Google Scholar] [CrossRef]
- Wang, Z.; Fei, J. Fractional-Order Terminal Sliding Mode Control Using Self-Evolving Recurrent Chebyshev Fuzzy Neural Network for MEMS Gyroscope. IEEE Trans. Fuzzy Syst. 2022, 30, 2747–2758. [Google Scholar] [CrossRef]
- Wang, Y.; Gu, L.; Xu, Y.; Cao, X. Practical Tracking Control of Robot Manipulators With Continuous Fractional-Order Nonsingular Terminal Sliding Mode. IEEE Trans. Ind. Electron. 2016, 63, 6194–6204. [Google Scholar] [CrossRef]
- Ferrara, A.; Incremona, G.P. Design of an Integral Suboptimal Second-Order Sliding Mode Controller for the Robust Motion Control of Robot Manipulators. IEEE Trans. Control Syst. Technol. 2015, 23, 2316–2325. [Google Scholar] [CrossRef]
- Ling, R.; Shu, Z.; Hu, Q.; Song, Y. Second-Order Sliding-Mode Controlled Three-Level Buck DC-DC Converters. IEEE Trans. Ind. Electron. 2018, 65, 898–906. [Google Scholar] [CrossRef]
- Fei, J.; Li, S. Adaptive Fractional High Order Sliding Mode Fuzzy Control of Active Power Filter. In Proceedings of the 2018 Joint 10th International Conference on Soft Computing and Intelligent Systems and 19th International Symposium on Advanced Intelligent Systems, Toyama, Japan, 5–8 December 2018; pp. 576–580. [Google Scholar]
- Evangelista, C.; Pisano, A.; Puleston, P.; Usai, E. Receding Horizon Adaptive Second-Order Sliding Mode Control for Doubly-Fed Induction Generator Based Wind Turbine. IEEE Trans. Control Syst. Technol. 2017, 25, 73–84. [Google Scholar] [CrossRef]
- Martinez, M.; Susperregui, A.; Zubia, I.; Tapia, G. Design and Tuning of Fixed-Switching-Frequency Second-Order Sliding-Mode Controller for Doubly Fed Induction Generator Power Control. IET Electr. Power Appl. 2012, 6, 696–706. [Google Scholar]








| Parameters | Values |
|---|---|
| Supply voltage | Us = 24 V; f = 50 Hz |
| Steady load | R1 = 5 Ω, R2 = 15 Ω, C = 1 × 10−3 F |
| Dynamic load | R1 = 15 Ω, R2 = 15 Ω, C = 1 × 10−3 F |
| APF main circuit parameters | Rc = 0.1 Ω, Lc = 10 mH, = 50 V |
| Sample time | Ts = 5 × 10−5 s |
| Mean Square Error | Adaptive Fuzzy Sliding Mode Control | Integer Order SOSMC Fuzzy Control | Fractional Order SOSMC Fuzzy Control | |
|---|---|---|---|---|
| 1.9023 | 1.6058 | 1.1919 | ||
| THD | Adaptive Fuzzy Sliding Mode Control | Integer Order SOSMC Fuzzy Control | Fractional Order SOSMC Fuzzy Control | |
|---|---|---|---|---|
| Time (s) | ||||
| 0 s | 24.71 | 24.71 | 24.71 | |
| 0.06 s | 2.56 | 2.14 | 1.82 | |
| 0.16 s | 2.29 | 1.98 | 1.90 | |
| 0.26 s | 1.99 | 1.93 | 1.85 | |
Publisher"s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, Y.; Li, S.; Fei, J. Adaptive Intelligent High-Order Sliding Mode Fractional Order Control for Harmonic Suppression. Fractal Fract. 2022, 6, 482. https://doi.org/10.3390/fractalfract6090482
Fang Y, Li S, Fei J. Adaptive Intelligent High-Order Sliding Mode Fractional Order Control for Harmonic Suppression. Fractal and Fractional. 2022; 6(9):482. https://doi.org/10.3390/fractalfract6090482
Chicago/Turabian StyleFang, Yunmei, Siyang Li, and Juntao Fei. 2022. "Adaptive Intelligent High-Order Sliding Mode Fractional Order Control for Harmonic Suppression" Fractal and Fractional 6, no. 9: 482. https://doi.org/10.3390/fractalfract6090482
APA StyleFang, Y., Li, S., & Fei, J. (2022). Adaptive Intelligent High-Order Sliding Mode Fractional Order Control for Harmonic Suppression. Fractal and Fractional, 6(9), 482. https://doi.org/10.3390/fractalfract6090482







