Hermite Fitted Block Integrator for Solving Second-Order Anisotropic Elliptic Type PDEs
Abstract
1. Introduction
2. Methodology
Mathematical Formulation of the HFBI
3. Basic Properties of the HFBI
3.1. Order and Error Terms of the HFBI
3.2. Zero-Stability of the HFBI
3.3. Consistency
3.4. Convergence
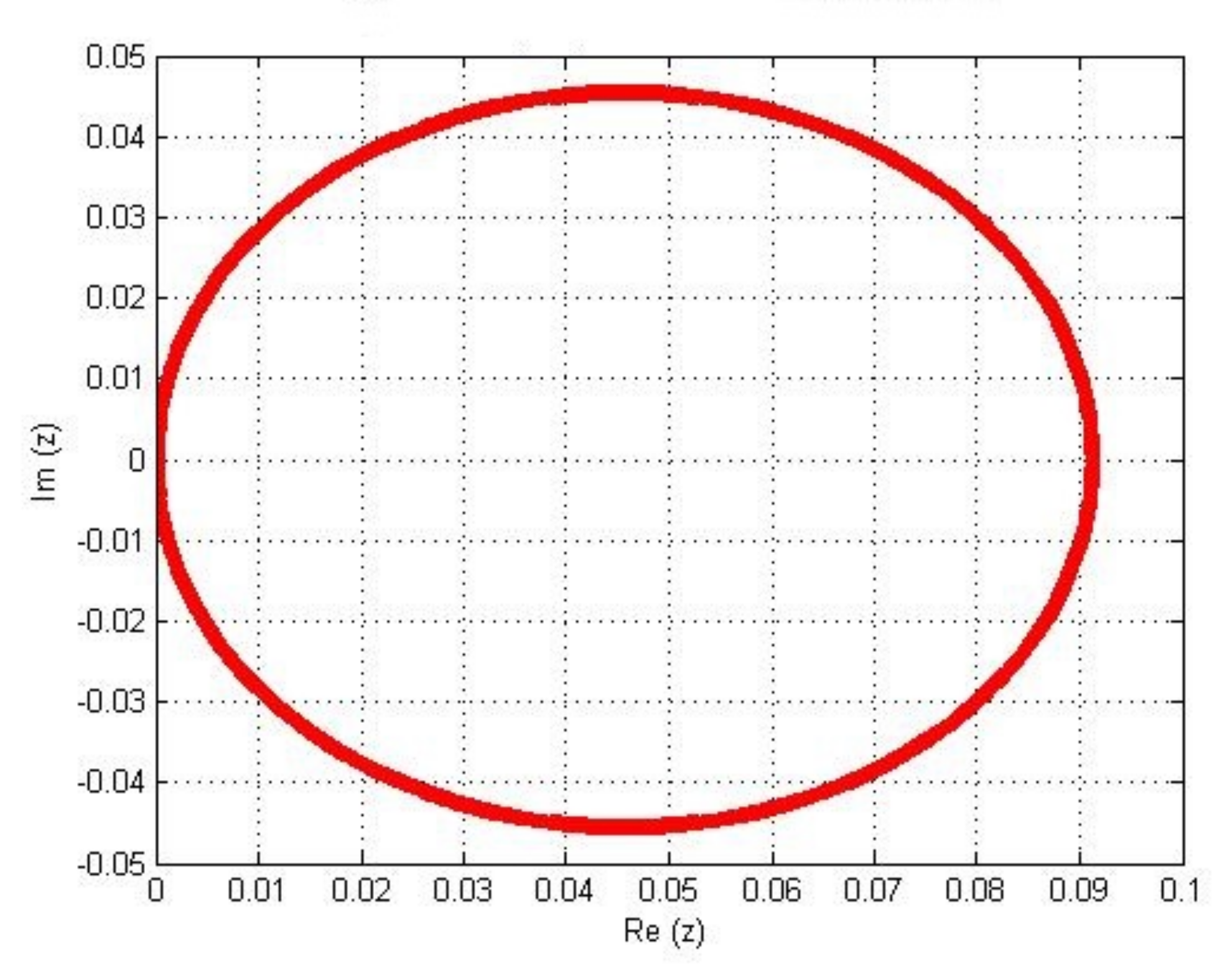
3.5. Region of Absolute Stability of HFBI
4. Computational Approach
5. Numerical Examples
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Ahmed, B.S.; Monaquel, S.J. Fourth Order Accurate Scheme with Multigrid Method for Solving Anisotropic Elliptic Partial Differential Equations. Adv. Differ. Equ. Control Process. 2010, 5, 103–110. [Google Scholar]
- Juraev, D.A.; Gasimov, Y.S. On the regularization Cauchy problem for matrix factorizations of the Helmholtz equation in a multidimensional bounded domain. Azerbaijan J. Math. 2022, 12, 142–161. [Google Scholar]
- Musaev, H.K. The Cauchy problem for degenerate parabolic convolution equation. TWMS J. Pure Appl. Math. 2021, 12, 278–288. [Google Scholar]
- Pankov, P.S.; Zheentaeva, Z.K.; Shirinov, T. Asymptotic reduction of solution space dimension for dynamical systems. TWMS J. Pure Appl. Math. 2021, 12, 243–253. [Google Scholar]
- Adiguzel, R.S.; Aksoy, U.; Karapinar, E.; Erhan, I.M. On the solutions of fractional differential equations via Geraghty type hybrid contractions. Appl. Comput. Math. 2021, 20, 313–333. [Google Scholar]
- Ozyapici, A.; Karanfiller, T. New integral operator for solution of differential equations. TWMS J. Pure Appl. Math. 2020, 11, 131–143. [Google Scholar]
- Quinlan, J.E. Variable Compact Multi-Point Upscaling Schemes for Anisotropic Diffusion Problems in Three-Dimensions. Ph.D. Thesis, University of Southern Mississippi, Hattiesburg, MS, USA, 2020. Available online: https://aquila.usm.edu/dissertations/1800 (accessed on 30 June 2022).
- Bourantas, G.C.; Burganos, V.N. An implicit meshless scheme for the solution of transient non-linear poisson-type equations. Eng. Anal. Bound. Elem. 2013, 37, 1117–1126. [Google Scholar] [CrossRef]
- Aziz, I.; Islam, S. An efficient Modified Haar Wavelet Collocation Method for Numerical Solution of Two-dimensional Elliptic PDEs. Differ. Equ. Dyn. Syst. 2015, 4, 39–50. [Google Scholar] [CrossRef]
- Faydaoglu, S.; Ozis, T. Periodic solutions for certain non-smooth oscillators with high nonlinearities. Appl. Comput. Math. 2021, 20, 366–380. [Google Scholar]
- Zargari, E.A.; Jimack, P.K.; Walkley, M.A. An investigation of the film thickness calculation for elastohydrodynamic lubrication problems. Int. J. Numer. Methods Fluids 2007, 1–6. Available online: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.67.2470&rep=rep1&type=pdf (accessed on 30 June 2022).
- Datta, S. Quantum Transport: Atom to Transistor; Cambridge University Press: London, UK, 2015. [Google Scholar]
- Iskenderov, N.S.; Allahverdiyeva, S.I. An inverse boundary value problem for the boussinesq-love equation with nonlocal integral condition. TWMS J. Pure Appl. Math. 2020, 11, 226–237. [Google Scholar]
- Qalandarov, A.A.; Khaldjigitov, A.A. Mathematical and numerical modeling of the coupled dynamic thermoelastic problems for isotropic bodies. TWMS J. Pure Appl. Math. 2020, 11, 119–126. [Google Scholar]
- Ashyralyev, A.; Agirseven, D.; Agarwal, R.P. Stability estimates for delay parabolic differential and difference equations. Appl. Comput. Math. 2020, 19, 175–204. [Google Scholar]
- Duan, J.; Rach, R. A new modification of the Adomian decomposition method for solving boundary value problems for higher order nonlinear differential equations. Appl. Math. Comput. 2011, 218, 4090–4118. [Google Scholar] [CrossRef]
- Tatari, M.; Dehghan, M. The use of the Adomian decomposition method for solving multipoint boundary value problems. Phys. Scr. 2006, 73, 672–676. [Google Scholar] [CrossRef]
- Saparova1, B.; Mamytova1, R.; Kurbanbaeva, N.; Ahmedov, A.A. A Haar Wavelet Series Solution of Heat Equation with Involution. J. Adv. Res. Fluid Mech. Therm. Sci. 2021, 86, 50–55. [Google Scholar] [CrossRef]
- Ramos, H.; Abdulganiy, R.; Olowe, R.; Jator, S. A family of functionally-fitted third derivative block falkner methods for solving second-order initial-value problems with oscillating solutions. Mathematics 2021, 9, 713. [Google Scholar] [CrossRef]
- Shokri, A.; Saadat, H.; Khodadadi, A. A new high order closed Newton-Cotes trigonometrically-fitted formulae for the numerical solution of the Schrodinger equation. Iranian J. Math. Sci. Inform. 2018, 13, 111–129. [Google Scholar]
- Yousif, M.A.; Mahmood, B.A. Approximate solutions for solving the Klein-Gordon and sine-Gordon equations. J. Assoc. Arab. Univ. Basic Appl. Sci. 2017, 22, 83–90. [Google Scholar] [CrossRef]
- Martinsson, P. A direct solver for variable coefficient elliptic PDEs discretized via a composite spectral collocation method. J. Comput. Phys. 2013, 242, 460–479. [Google Scholar] [CrossRef]
- Abolarin, O.E.; Kuboye, J.O.; Adeyefa, E.O.; Ogunware, B.G. New efficient numerical model for solving second, third and fourth order ordinary differential equations directly. Gazi J. Sci. 2020, 33, 821–833. [Google Scholar] [CrossRef]
- Ukpebor, L.A.; Omole, E.O. Three-step Optimized Block Backward Differentiation Formulae (TOBBDF) for Solving Stiff Ordinary Differential Equations. Afr. J. Math. Comput. Sci. Res. 2020, 13, 51–57. [Google Scholar] [CrossRef][Green Version]
- Modebei, M.I.; Adeniyi, R.B. A Six-step block unification integrator for numerical solution of fourth order boundary value problems. Gen. Lett. Math. 2018, 5, 71–83. [Google Scholar] [CrossRef]
- Aigbiremhon, A.A.; Familua, A.B.; Omole, E.O. A three-step interpolation technique with perturbation term for direct solution of third-order ordinary differential equations. FUDMA J. Sci. 2021, 5, 365–376. [Google Scholar] [CrossRef]
- Sunday, J.; Shokri, A.; Marian, D. Variable Step Hybrid Block Method for the Approximation of Kepler Problem. Fractal Fract. 2022, 6, 343. [Google Scholar] [CrossRef]
- Sun, H.; Zhang, J. A high order finite difference discretization strategy based on extrapolation for convection diffusion equations. Numer. Methods Partial. Differ. Equ. 2004, 20, 18–32. [Google Scholar] [CrossRef]
- Marian, D.; Semi-Hyers-Ulam-Rassias, D. Stability of the Convection Partial Differential Equation via Laplace Transform. Mathematics 2021, 9, 2980. [Google Scholar] [CrossRef]
- Raslan, K.R.; Ali, K.K.; Al-Bayatti, H.M.Y. Construct extended cubic B-splines in n-dimensional for solving n-Dimentional partial differential equations. Appl. Math. Inf. Sci. 2021, 15, 599–611. [Google Scholar]
- Kamran, M.; Abbas, M.; Majeed, A.; Emadifar, H.; Nazir, T. Numerical Simulation of Time Fractional BBM-Burger Equation Using Cubic B-Spline Functions. Hindawi J. Funct. Spaces 2022, 2022, 2119416. [Google Scholar] [CrossRef]
- Rashidinia, J.; Mohammadi, R. Sextic spline solution of variable coefficient fourth-order parabolic equations. Int. J. Comput. Math. 2010, 87, 3443–3454. [Google Scholar] [CrossRef]
- Lambert, J.D. Computational Methods in Ordinary Differential Equations; John Wiley & Sons Inc.: Hoboken, NJ, USA, 1973. [Google Scholar]
- Henrici, P. Discrete Variable Method in Ordinary Differential Equations; John Wiley and Sons: New York, NY, USA, 1962. [Google Scholar]
- Salzer, H.E.; Zucker, R.; Capuano, R. Table of the zeros and weight factors of the first twenty Hermite polynomials. J. Res. Nat. Bur. Stand. 1952, 48, 111–116. [Google Scholar] [CrossRef]
- Fatunla, S.O. Numerical Methods for Initial Value Problems in Ordinary Differential Equations; Academic Press Inc.: Cambridge, MA, USA; Harcourt Brace Jovanovich Publishers: New York, NY, USA, 1988. [Google Scholar]
- Omole, E.O.; Jeremiah, O.A.; Adoghe, L.O. A Class of Continuous Implicit Seventh-eight method for solving y′ = f(x,y) using power series as basic function. Int. J. Chem. Math. Phys. (IJCMP) 2020, 4, 39–50. [Google Scholar] [CrossRef]
- Ramos, H.; Vigo-Aguiar, J. An almost L-stable BDF-type method for the numerical solution of stiff ODEs arising from the method of lines. Int. J. Numer. Methods Partial. Differ. Equ. 2006, 23, 1110–1121. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, J. Sixth order compact scheme combined with multigrid method and extrapolation technique for 2D poisson equation. J. Comput. Phys. 2009, 228, 137–146. [Google Scholar] [CrossRef]
- Ashry, H.; Abd-Elhameed, W.M.; Moatimid, G.M.; Youssri, Y.H. Spectral Treatment of One and Two Dimensional Second-Order BVPs via Certain Modified Shifted Chebyshev Polynomials. Int. J. Appl. Comput. Math. 2021, 7, 248. [Google Scholar] [CrossRef]



| Equation | Formulae | Error Constant | Order p |
|---|---|---|---|
| 13 | 8 | ||
| 14 | 8 | ||
| 15 | 8 | ||
| 16 | 8 | ||
| 17 | 8 | ||
| 18 | 8 | ||
| 19 | 8 | ||
| 20 | 8 | ||
| 21 | 8 | ||
| 22 | 8 | ||
| 23 | 8 | ||
| 24 | 8 | ||
| 25 | 8 | ||
| 26 | 8 |
| N | Exact-Solution | Computed-Solution | AE in HFBI |
|---|---|---|---|
| 2 | |||
| 4 | |||
| 8 | |||
| 16 | |||
| 32 | |||
| 64 | |||
| 128 |
| x | Exact-Solution | Computed-Solution | AE in HFBI |
|---|---|---|---|
| 0.1 | |||
| 0.2 | |||
| 0.3 | |||
| 0.4 | |||
| 0.5 | |||
| 0.6 | |||
| 0.7 | |||
| 0.8 | |||
| 0.9 |
| x | AE in HFBI | AE in [30] |
|---|---|---|
| 0.2 | ||
| 0.4 | ||
| 0.6 | ||
| 0.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adeyefa, E.O.; Omole, E.O.; Shokri, A.; Yao, S.-W. Hermite Fitted Block Integrator for Solving Second-Order Anisotropic Elliptic Type PDEs. Fractal Fract. 2022, 6, 497. https://doi.org/10.3390/fractalfract6090497
Adeyefa EO, Omole EO, Shokri A, Yao S-W. Hermite Fitted Block Integrator for Solving Second-Order Anisotropic Elliptic Type PDEs. Fractal and Fractional. 2022; 6(9):497. https://doi.org/10.3390/fractalfract6090497
Chicago/Turabian StyleAdeyefa, Emmanuel Oluseye, Ezekiel Olaoluwa Omole, Ali Shokri, and Shao-Wen Yao. 2022. "Hermite Fitted Block Integrator for Solving Second-Order Anisotropic Elliptic Type PDEs" Fractal and Fractional 6, no. 9: 497. https://doi.org/10.3390/fractalfract6090497
APA StyleAdeyefa, E. O., Omole, E. O., Shokri, A., & Yao, S.-W. (2022). Hermite Fitted Block Integrator for Solving Second-Order Anisotropic Elliptic Type PDEs. Fractal and Fractional, 6(9), 497. https://doi.org/10.3390/fractalfract6090497









