Fractal Dimension Characteristics of the Soil Cracking Process When Saline-Alkali Soil Is Mixed with Hippophae Roots
Abstract
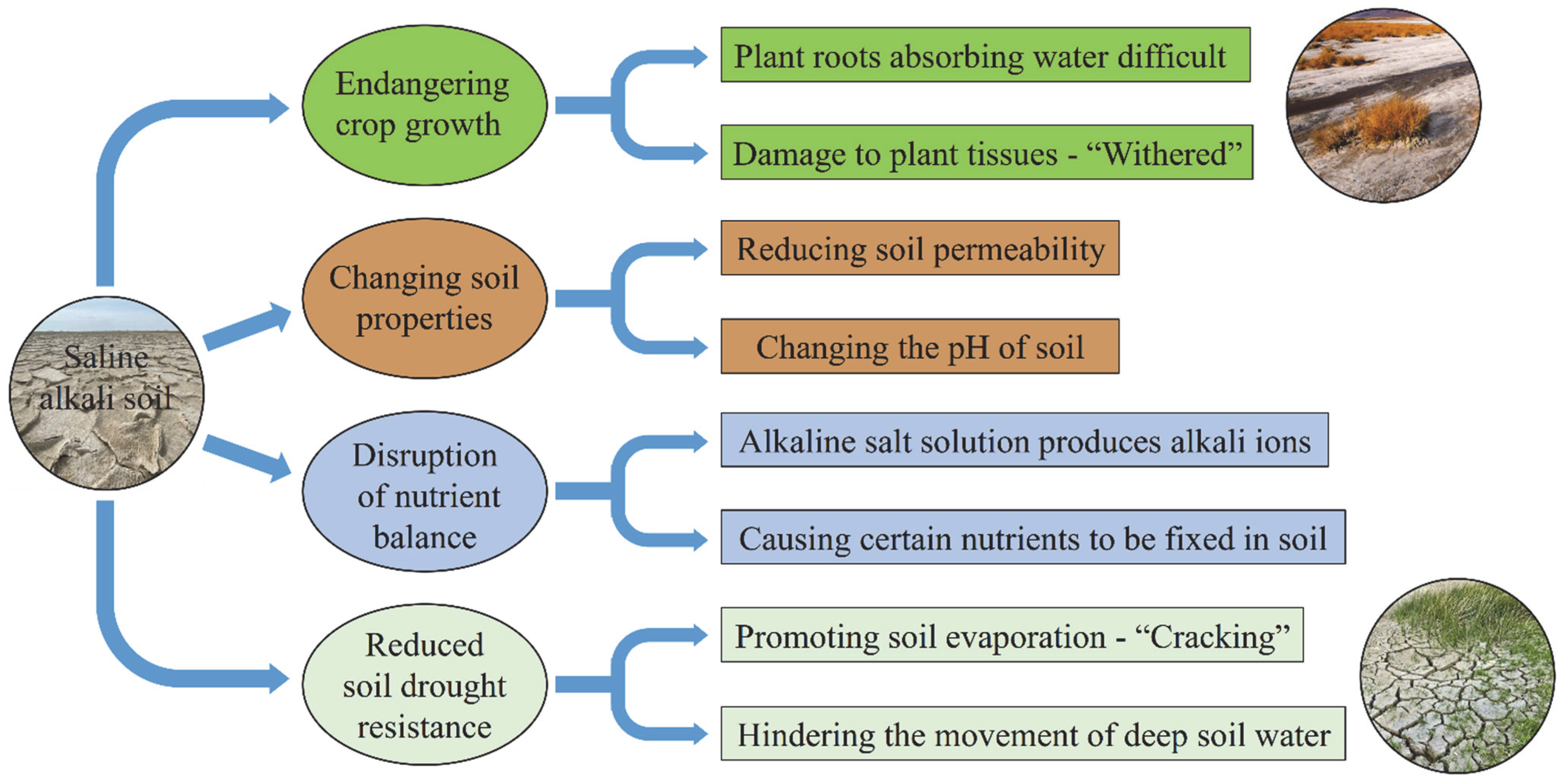
:1. Introduction
2. Materials and Methods
2.1. Test Materials
2.2. Image and Data Processing
3. Results
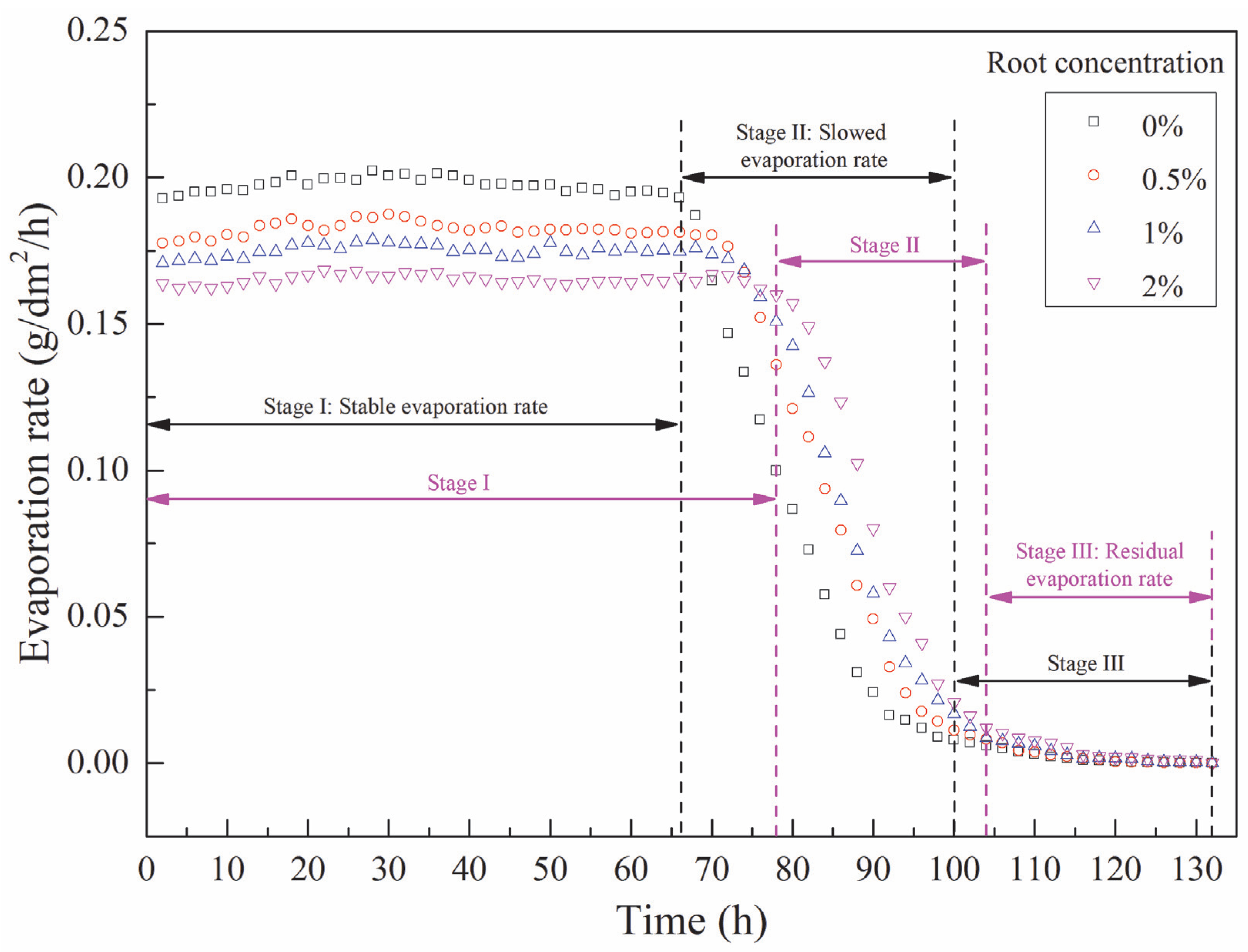
3.1. Change in Water Content and Evaporation Rate
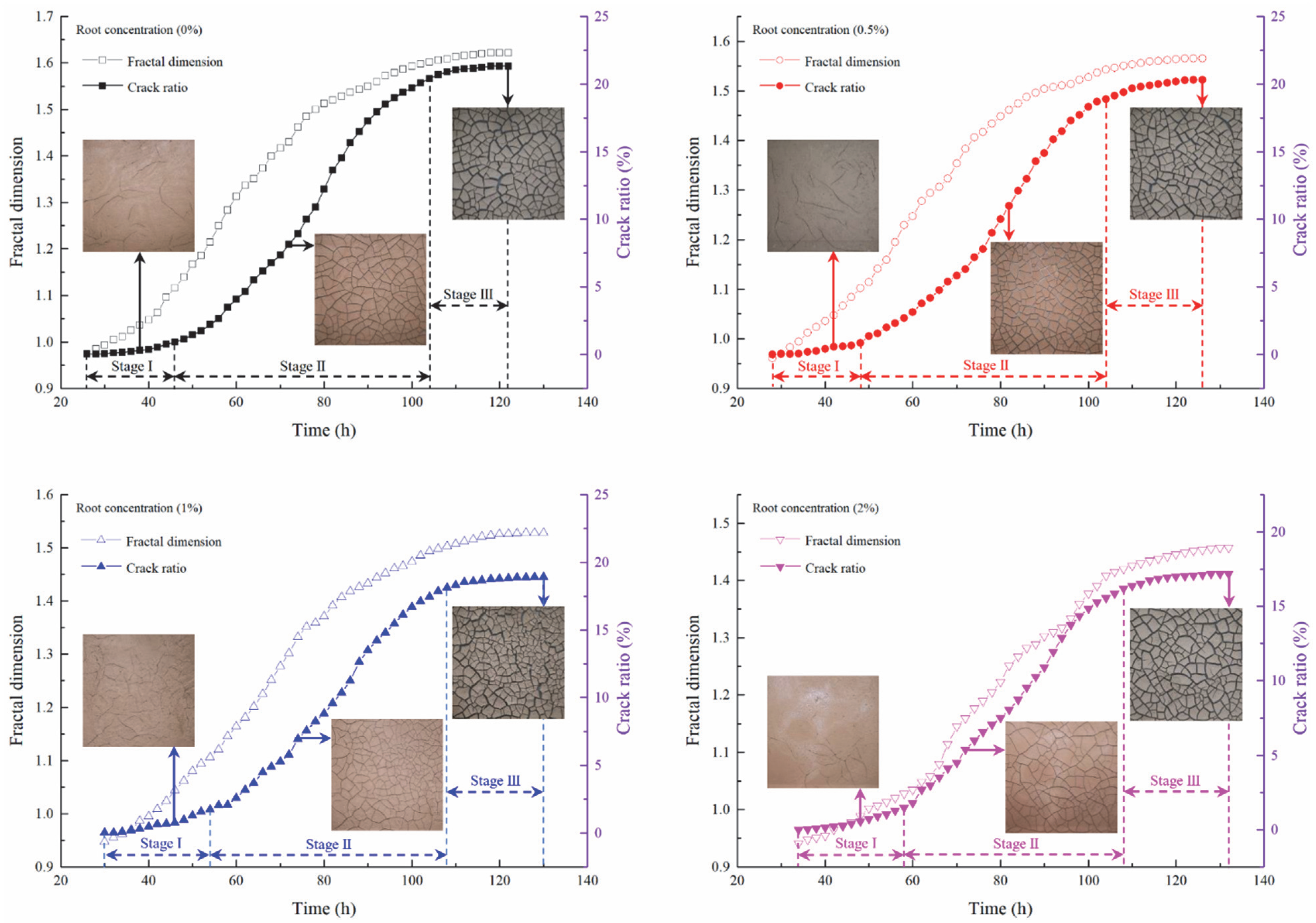
3.2. Changes in Crack Ratio and Fractal Dimension
4. Discussion
4.1. Application of Fractal Theory
4.2. Analysis of Fractal Dimension
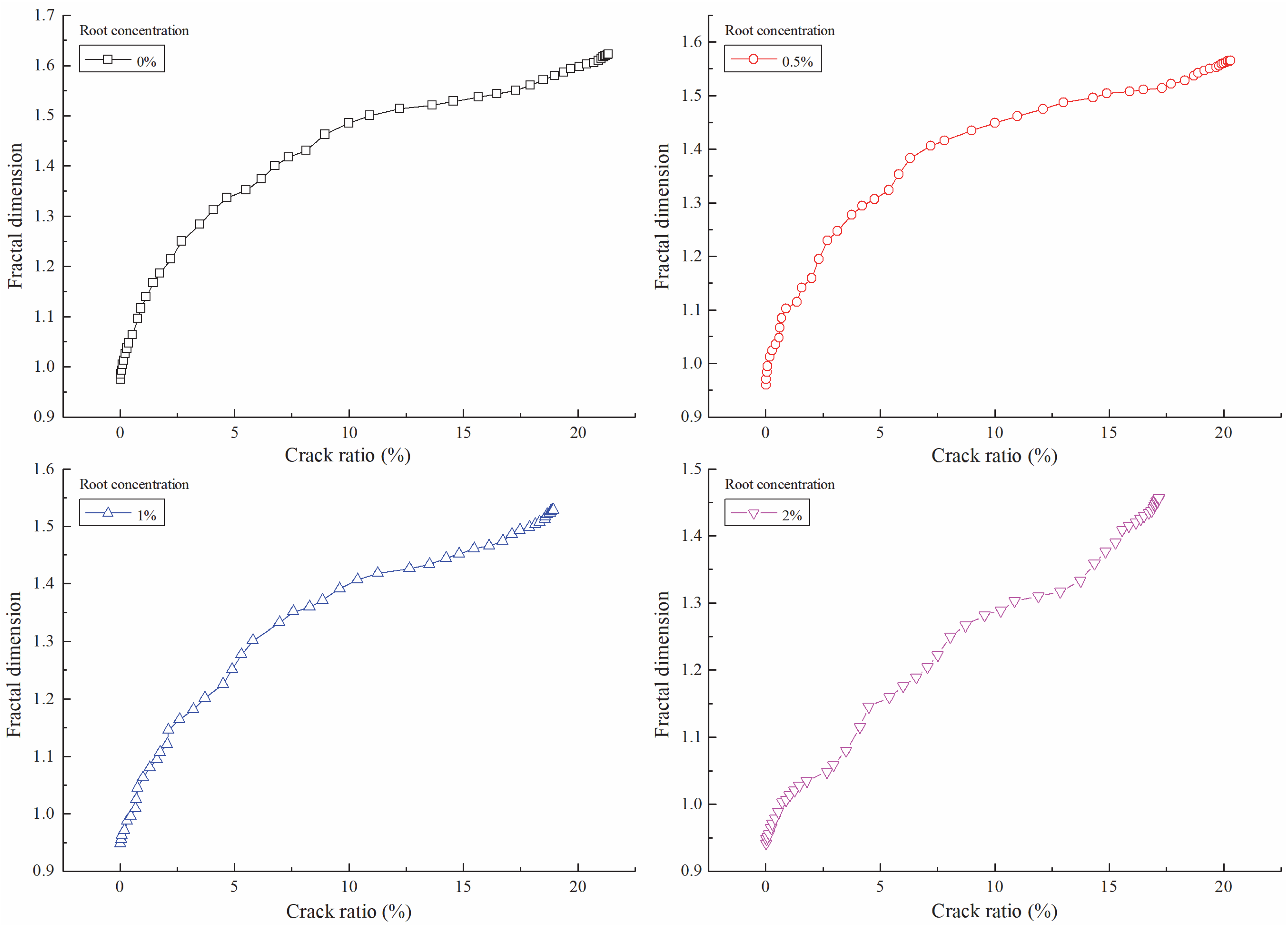
4.2.1. Relationship between Crack Ratio and Fractal Dimension
4.2.2. Relationship between Water Content and Fractal Dimension
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gholizadeh, A.; Kopačková, V. Detecting vegetation stress as a soil contamination proxy: A review of optical proximal and remote sensing techniques. Int. J. Environ. Sci. Technol. 2019, 16, 2511–2524. [Google Scholar] [CrossRef]
- Abou Samra, R.M.; Ali, R.R. The development of an overlay model to predict soil salinity risks by using remote sensing and GIS techniques: A case study in soils around Idku Lake, Egypt. Environ. Monit. Assess. 2018, 190, 706. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Hou, Z.; Wu, L.; Liang, Y.; Wei, C. Evaluating salinity distribution in soil irrigated with saline water in arid regions of northwest China. Agric. Water Manag. 2010, 97, 2001–2008. [Google Scholar] [CrossRef]
- Wichelns, D.; Qadir, M. Achieving sustainable irrigation requires effective management of salts, soil salinity, and shallow groundwater. Agric. Water Manag. 2015, 157, 31–38. [Google Scholar] [CrossRef]
- Xing, X.G.; Kang, D.G.; Ma, X.Y. Differences in loam water retention and shrinkage behavior: Effects of various types and concentrations of salt ions. Soil Till. Res. 2017, 167, 61–72. [Google Scholar] [CrossRef]
- Brown, C.E.; Pezeshki, S.R.; Delaune, R.D. The effects of salinity and soil drying on nutrient uptake and growth of Spartina alterniflora in a simulated tidal system. Environ. Exp. Bot. 2006, 58, 140–148. [Google Scholar] [CrossRef]
- Dodd, K.; Guppy, C.N.; Lockwood, P.V.; Rochester, I.J. The effect of sodicity on cotton: Does soil chemistry or soil physical condition have the greater role? Crop Pasture Sci. 2013, 64, 806–815. [Google Scholar] [CrossRef]
- Qadir, M.; Oster, J.D. Crop and irrigation management strategies for saline-sodic soils and waters aimed at environmentally sustainable agriculture. Sci. Total Environ. 2004, 323, 1–19. [Google Scholar] [CrossRef]
- Crescimanno, G.; Santis, A.D. Bypass flow, salinization and sodication in a cracking clay soil. Geoderma 2004, 121, 307–321. [Google Scholar] [CrossRef]
- Crescimanno, G.; Garofalo, P. Management of irrigation with saline water in cracking clay soils. Soil Sci. Soc. Am. J. 2006, 70, 1774–1787. [Google Scholar] [CrossRef]
- Mahmoud, M.; Janssen, M.; Haboub, N.; Nassour, A.; Lennartz, B. The impact of olive mill wastewater application on flow and transport properties in soils. Soil Till. Res. 2010, 107, 36–41. [Google Scholar] [CrossRef]
- Decarlo, K.F.; Shokri, N. Salinity effects on cracking morphology and dynamics in 3-D desiccating clays. Water Resour. Res. 2014, 50, 3052–3072. [Google Scholar] [CrossRef]
- Levy, J.; Fountain, A.; Lyons, W.B.; Welch, K. Experimental formation of pore fluids in McMurdo Dry Valleys soils. Antarct. Sci. 2015, 27, 163–171. [Google Scholar] [CrossRef]
- Ren, J.H.; Li, X.J.; Zhao, K.; Fu, B.L.; Jiang, T. Study of an on-line measurement method for the salt parameters of soda-saline soils based on the texture features of cracks. Geoderma 2016, 263, 60–69. [Google Scholar] [CrossRef]
- Ren, J.H.; Zhao, K.; Wu, X.W.; Zheng, X.M.; Li, X.J. Comparative Analysis of the Spectral Response to Soil Salinity of Saline-Sodic Soils under Different Surface Conditions. Int. J. Env. Res. Public Health 2018, 15, 2721. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Chen, Y.; Ye, W.; Cui, Y.; Deng, Y.; Chen, B. Effect of salt concentration on desiccation cracking behavior of GMZ bentonite. Environ. Earth Sci. 2017, 76, 531. [Google Scholar] [CrossRef]
- Zhang, T.W.; Deng, Y.F.; Cui, Y.J.; Lan, H.X.; Zhang, F.Y.; Zhang, H.Y. Porewater salinity effect on flocculation and desiccation cracking behaviour of kaolin and bentonite considering working condition. Eng. Geol. 2019, 251, 11–23. [Google Scholar] [CrossRef]
- Tran, D.; Ralaizafisoloarivony, N.; Charlier, R.; Mercatoris, B.; Léonard, A.; Toye, D.; Degré, A. Studying the effect of desiccation cracking on the evaporation process of a Luvisol—From a small-scale experimental and numerical approach. Soil Till. Res. 2019, 193, 142–152. [Google Scholar] [CrossRef]
- Zhang, Y.; Ye, W.; Chen, B.; Chen, Y.; Ye, B. Desiccation of NaCl-contaminated soil of earthen heritages in the Site of Yar City, northwest China. Appl. Clay Sci. 2016, 124–125, 1–10. [Google Scholar] [CrossRef]
- Dos Santos, J.; de Andrade, E.; Guerreiro, M.; Medeiros, P.; de Queiroz Palácio, H.; de Araújo Neto, J. Effect of dry spells and soil cracking on runoff generation in a semiarid micro watershed under land use change. J. Hydrol. 2016, 541, 1057–1066. [Google Scholar] [CrossRef]
- Kurtzman, D.; Baram, S.; Dahan, O. Soil-aquifer phenomena affecting groundwater under vertisols: A review. Hydrol. Earth Syst. Sci. 2016, 20, 1–12. [Google Scholar] [CrossRef]
- Rayhani, M.; Yanful, E.; Fakher, A. Desiccation-induced cracking and its effect on the hydraulic conductivity of clayey soils from Iran. Can. Geotech. J. 2007, 44, 276–283. [Google Scholar] [CrossRef]
- Abd El-Halim, A. Image processing technique to assess the use of sugarcane pith to mitigate clayey soil cracks: Laboratory experiment. Soil Till. Res. 2017, 169, 138–145. [Google Scholar] [CrossRef]
- Baer, J.; Kent, T.; Anderson, S. Image analysis and fractal geometry to characterize soil desiccation cracks. Geoderma 2009, 154, 153–163. [Google Scholar] [CrossRef]
- Sun, D.; Wang, L.; Li, L. Stability of Unsaturated Soil Slopes with Cracks under Steady-Infiltration Conditions. Int. J. Geomech. 2019, 19, 04019044. [Google Scholar] [CrossRef]
- Zhang, J.; Zhu, D.; Zhang, S. Shallow slope stability evolution during rainwater infiltration considering soil cracking state. Comput. Geotech. 2020, 117, 103285. [Google Scholar] [CrossRef]
- Mostafazadeh-Fard, B.; Jafari, F.; Mousavi, S.; Yazdani, M. Effects of irrigation water management on yield and water use efficiency of rice in cracked paddy soils. Aust. J. Crop Sci. 2010, 4, 136–141. [Google Scholar]
- Bayat, H.; Neyshaburi, M.; Mohammadi, K.; Nariman-Zadeh, N.; Irannejad, M.; Gregory, A. Combination of artificial neural networks and fractal theory to predict soil water retention curve. Comput. Electron. Agric. 2013, 92, 92–103. [Google Scholar] [CrossRef]
- Mohammadi, M.; Shabanpour, M.; Mohammadi, M.H.; Davatgar, N. Characterizing Spatial Variability of Soil Textural Fractions and Fractal Parameters Derived from Particle Size Distributions. Pedosphere 2019, 29, 224–234. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhong, X.; Lin, J.; Zhao, D.; Jiang, F.; Wang, M.; Ge, H.; Huang, Y. Effects of fractal dimension and water content on the shear strength of red soil in the hilly granitic region of southern China. Geomorphology 2020, 351, 106956. [Google Scholar] [CrossRef]
- Xu, Q.; Xiong, K.; Chi, Y. Effects of Intercropping on Fractal Dimension and Physicochemical Properties of Soil in Karst Areas. Forests 2021, 12, 1422. [Google Scholar] [CrossRef]
- Lu, S.; Tang, H.; Zhang, Y.; Gong, W.; Wang, L. Effects of the particle-size distribution on the micro and macro behavior of soils: Fractal dimension as an indicator of the spatial variability of a slip zone in a landslide. Bull. Eng. Geol. Environ. 2018, 77, 665–677. [Google Scholar]
- Preston, S.; Griffiths, B.; Young, I. An investigation into sources of soil crack heterogeneity using fractal geometry. Eur. J. Soil Sci. 1997, 48, 31–37. [Google Scholar] [CrossRef]
- Collins, T.J. ImageJ for microscopy. Biotechniques 2007, 43, S25–S30. [Google Scholar] [CrossRef]
- Yang, R.; He, S.; Yi, J.Z.; Hu, Q.H. Nano-scale pore structure and fractal dimension of organic-rich Wufeng-Longmaxi shale from Jiaoshiba area, Sichuan Basin: Investigations using FE-SEM, gas adsorption and helium pycnometry. Mar. Petrol Geol. 2016, 70, 27–45. [Google Scholar] [CrossRef]
- Xu, L.F.; Zhang, J.C.; Ding, J.H.; Liu, T.; Shi, G.; Li, X.Q.; Dang, W.; Cheng, Y.S.; Guo, R.B. Pore Structure and Fractal Characteristics of Different Shale Lithofacies in the Dalong Formation in the Western Area of the Lower Yangtze Platform. Minerals 2020, 10, 72. [Google Scholar] [CrossRef]
- Alruwaily, Y.; Ahmad, B.; Ntouyas, S.K.; Alzaidi, A.S.M. Existence results for coupled nonlinear sequential fractional differential equations with coupled Riemann-Stieltjes integro-multipoint boundary conditions. Fractal Fract. 2022, 6, 123. [Google Scholar] [CrossRef]
- Owolabi, K.M.; Atangana, A.; Akgul, A. Modelling and analysis of fractal-fractional partial differential equations: Application to reaction-diffusion model. Alex Eng. J. 2020, 59, 2477–2490. [Google Scholar] [CrossRef]
- Evagelopoulos, V.; Zoras, S.; Triantafyllou, A.G.; Albanis, T.A. PM10-PM2. 5 time series and fractal analysis. Global Nest J. 2006, 8, 234–240. [Google Scholar]
- Yang, B.B.; Liu, Y. Application of fractals to evaluate fractures of rock due to mining. Fractal Fract. 2022, 6, 96. [Google Scholar] [CrossRef]
- Asadi, H.H.; Kianpouryan, S.; Lu, Y.J.; McCuaig, T.C. Exploratory data analysis and C-A fractal model applied in mapping multi-element soil anomalies for drilling: A case study from the Sari Gunay epithermal gold deposit, NW Iran. J. Geochem. Explor. 2014, 145, 233–241. [Google Scholar] [CrossRef]
- Li, C.J.; Ma, T.H.; Shi, J.F. Application of a fractal method relating concentrations and distances for separation of geochemical anomalies from background. J. Geochem. Explor. 2003, 77, 167–175. [Google Scholar] [CrossRef]
- Ergün, S.; Saraçoglu, A.; Guneri, P.; Ozpınar, B. Application of fractal analysis in hyperparathyroidism. Dentomaxillofac. Rad. 2009, 38, 281–289. [Google Scholar] [CrossRef] [PubMed]
- Gao, G.L.; Ding, G.D.; Zhao, Y.Y.; Wu, B.; Zhang, Y.Q.; Qin, S.G.; Bao, Y.F.; Yu, M.H.; Liu, Y.D. Fractal approach to estimating changes in soil properties following the establishment of Caragana korshinskii shelterbelts in Ningxia, NW China. Ecol. Indic. 2014, 43, 236–243. [Google Scholar] [CrossRef]
- Li, Z.F.; Wang, Z.M. Experimental study on the relation between the fractal characteristics and solute transport parameters of sandy soil. J. Soil Sediment 2020, 20, 3181–3191. [Google Scholar] [CrossRef]
- Cumbrera, R.; Tarquis, A.M.; Gascó, G.; Millán, H. Fractal scaling of apparent soil moisture estimated from vertical planes of Vertisol pit images. J. Hydrol. 2012, 452, 205–212. [Google Scholar] [CrossRef]
- Chen, Y.; Yeh, H.; Gui, M.; Wei, C.; He, C. Estimation of surface soil moisture content using fractals. Environ. Monit. Assess. 2021, 193, 91. [Google Scholar] [CrossRef]



| Soil Properties | Values |
|---|---|
| Specific gravity (g/cm3) | 2.56 |
| Particle composition | |
| Clay (<0.002 mm) | 56.5 |
| Silt (0.002–0.075 mm) | 33.7 |
| Sand (>0.075 mm) | 9.8 |
| Liquid limit (%) | 37.2 |
| Plasticity limit (%) | 18.3 |
| Plasticity Index | 17.9 |
| Main chemical composition | |
| K+ (mg/g) | 0.14 |
| Na+ (mg/g) | 6.56 |
| Ca2+ (mg/g) | 1.25 |
| Cl− (mg/g) | 2.77 |
| CO32− (mg/g) | 1.16 |
| SO42− (mg/g) | 1.37 |
| Salinity (mg/g) | 26.5 |
| pH | 8.52 |
| Group | Box Size | DB | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 3 | 4 | 6 | 8 | 12 | 16 | 32 | 64 | ||
| Count 1 (S) | 9362 | 5699 | 4129 | 2666 | 1971 | 1376 | 1031 | 563 | 310 | 0.9749 |
| Count 2 (S) | 5872 | 3474 | 2464 | 1574 | 1176 | 818 | 613 | 352 | 204 | 0.9602 |
| Count 3 (S) | 17,144 | 10,508 | 7628 | 5005 | 3787 | 2668 | 2023 | 1118 | 614 | 0.9478 |
| Count 4 (S) | 6561 | 4094 | 3032 | 2018 | 1544 | 1053 | 811 | 436 | 246 | 0.9414 |
| Count 1 (E) | 497,154 | 234,234 | 138,561 | 67,700 | 41,457 | 21303 | 13,557 | 4868 | 1803 | 1.6217 |
| Count 2 (E) | 431,982 | 208,839 | 126,111 | 63,351 | 39,540 | 20,855 | 13,445 | 4956 | 1903 | 1.5656 |
| Count 3 (E) | 400,536 | 195,593 | 119,005 | 60,865 | 38,546 | 20,835 | 13,614 | 5206 | 1958 | 1.5282 |
| Count 4 (E) | 264,178 | 131,407 | 81,099 | 42,434 | 27,478 | 15,325 | 10,248 | 4095 | 1657 | 1.4568 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, L.; Zhang, S.; Xu, Y. Fractal Dimension Characteristics of the Soil Cracking Process When Saline-Alkali Soil Is Mixed with Hippophae Roots. Fractal Fract. 2022, 6, 504. https://doi.org/10.3390/fractalfract6090504
Jin L, Zhang S, Xu Y. Fractal Dimension Characteristics of the Soil Cracking Process When Saline-Alkali Soil Is Mixed with Hippophae Roots. Fractal and Fractional. 2022; 6(9):504. https://doi.org/10.3390/fractalfract6090504
Chicago/Turabian StyleJin, Lichuang, Shuai Zhang, and Yingjie Xu. 2022. "Fractal Dimension Characteristics of the Soil Cracking Process When Saline-Alkali Soil Is Mixed with Hippophae Roots" Fractal and Fractional 6, no. 9: 504. https://doi.org/10.3390/fractalfract6090504
APA StyleJin, L., Zhang, S., & Xu, Y. (2022). Fractal Dimension Characteristics of the Soil Cracking Process When Saline-Alkali Soil Is Mixed with Hippophae Roots. Fractal and Fractional, 6(9), 504. https://doi.org/10.3390/fractalfract6090504






