A Fast High-Order Predictor–Corrector Method on Graded Meshes for Solving Fractional Differential Equations

Abstract

In this paper, we focus on the computation of Caputo-type fractional differential equations. A high-order predictor–corrector method is derived by applying the quadratic interpolation polynomial approximation for the integral function. In order to deal with the weak singularity of the solution near the initial time of the fractional differential equations caused by the fractional derivative, graded meshes were used for time discretization. The error analysis of the predictor–corrector method is carefully investigated under suitable conditions on the data. Moreover, an efficient sum-of-exponentials (SOE) approximation to the kernel function was designed to reduce the computational cost. Lastly, several numerical examples are presented to support our theoretical analysis.

1. Introduction

Growing interest has focused on the study of fractional differential equations (FDEs) over the last few decades; see [1,2] and the references therein. Obtaining the exact solutions for FDEs can be very challenging, especially for general right-hand-side functions. Thus, there is a need to develop numerical methods for FDEs, for which extensive work has been conducted. One idea is to directly approximate the fractional derivative operators, e.g., [3,4,5]. Another idea is first to transform the FDEs into the integral forms and then use the numerical schemes to solve the integral equation; see, e.g., [6,7,8,9,10,11,12,13,14,15]. There are also some other numerical methods for FDEs, such as the variational iteration [16], Adomian decomposition [17], finite-element [18], and spectral [19] methods.

Adams methods are one of the most studied implicit–explicit linear multistep method groups. They play a major rule in the numerical processing of various differential equations. Therefore, great interest has been devoted to generalizing Adams methods to FDEs, especially the Adams-type predictor–corrector method. For example, Diethelm et al. [7,8,9,10] suggested the numerical approximation of FDEs using the Adams-type predictor–corrector method on uniform meshes. Deng [20] apprehended the short memory principle of fractional calculus and further applied the Adams-type predictor–corrector method for the numerical solution of FDEs on uniform meshes. Nguyen and Jang [21] studied a new Adams-type predictor–corrector method on uniform meshes by introducing a new prediction stage which is the same accuracy order as that of the correction stage for solving FDEs. Zhou et al. [22] considered the fast second-order Adams-type predictor–corrector method on graded meshes to solve a nonlinear time-fractional Benjamin–Bona–Mahony–Burgers equation.

Solutions to FDEs typically exhibit weak singularity at the initial time. In order to handle such problems, several techniques were developed, such as using nonuniform grids to keep errors small near the singularity [5,12,13,23,24,25], or employing correction terms to recover theoretical accuracy [6,15,26,27], or choosing a simple change in variable to derive a new and equivalent time-rescaled FDE [28,29].

In this paper, our goals are to construct high-order numerical methods and deal with the singularity of the solution of FDEs. Motivated by the above research, we follow the predictor–corrector method proposed in [21] and apply graded meshes to solve the following FDEs

$${}^C{D}_0^{\alpha }y\left(t\right)=f(t,y\left(t\right))\mathrm{for}\alpha \in (0,1),t\in (0,T];y\left(0\right)=y_0,$$

(1)

where $y_0$ is a real number; ${}^C{D}_0^{\alpha }$ denotes the fractional derivative in the Caputo sense, which is defined for all functions w that are absolutely continuous on $t>0$ by (e.g., [1])

$${}^C{D}_0^{\alpha }w\left(t\right):=\frac{1}{\mathsf{\Gamma }(1-\alpha )}{\int }_{s=0}^t{(t-s)}^{-\alpha }{w}^{\prime }\left(s\right)ds\mathrm{for}\alpha \in (0,1).$$

(2)

To ensure that the existence and uniqueness of the solution of Problem (1) (e.g., [8], Theorems 2.1, 2.2), we assumed that the continuous function f fulfilled the Lipschitz condition with respect to its second argument on a suitable set G, i.e., for any $y,\widehat{y}\in G$,

$$|f(t,y)-f(t,\widehat{y})|\le L|y-\widehat{y}|\mathrm{for}t\in [0,T],$$

(3)

where $L>0$ is the Lipschitz constant independent of $t,y$ and $\widehat{y}$. Equation (1) can be rewritten as the following Volterra integral equation (e.g., [8])

$$y\left(t\right)=y_0+\frac{1}{\mathsf{\Gamma }\left(\alpha \right)}{\int }_{s=0}^t{(t-s)}^{\alpha -1}{f}_y\left(s\right)ds\mathrm{with}{f}_y\left(t\right)=f(t,y\left(t\right)).$$

(4)

The following regularity assumptions on the solution are also used for our proposed method:

$$y\in C[0,T]\cap C^3(0,T]\mathrm{with}\left|y^{\left(k\right)}\left(t\right)\right|\le C(1+t^{\alpha -k})\mathrm{for}k=0,1,2,3,t\in (0,T].$$

(5)

Moreover, we can learn from ([30], Section 2) or ([10], Theorem 2.1) that the analytical solution of (1) can be written as the summation of the singular and the regular parts; see the following lemma where for each $s\in \mathbb{R}$, $\lceil s\rceil :=min\left\{n\in \mathbb{N}:n\ge s\right\}$.

Lemma 1

([10], Theorem 2.1).

(a) 

Suppose that $f\in C^2\left(G\right)$. Then, there exist some constants $c_1,c_2,\dots ,c_{\widehat{v}}\in \mathbb{R}$ and a function $\psi \in C^1[0,T]$ such that

$$y\left(t\right)=\psi \left(t\right)+\sum _{v=1}^{\widehat{v}}{c}_v{t}^{v\alpha }\mathit{with}\widehat{v}:=\lceil 1/\alpha \rceil -1.$$

(b) 

Suppose that $f\in C^3\left(G\right)$. Then, there exist some constants $c_1,c_2,\dots ,c_{\widehat{v}}\in \mathbb{R}$, $d_1,d_2,\dots ,d_{\tilde{v}}\in \mathbb{R}$ and a function $\psi \in C^2[0,T]$, such that

$$y\left(t\right)=\psi \left(t\right)+\sum _{v=1}^{\widehat{v}}{c}_v{t}^{v\alpha }+\sum _{v=1}^{\tilde{v}}{d}_v{t}^{1+v\alpha }\mathit{with}\widehat{v}:=\lceil 2/\alpha \rceil -1,\tilde{v}:=\lceil 1/\alpha \rceil -1.$$

From the above lemma, when $f\in C^m\left(G\right),m\ge 2$, there are some constants $c_1,c_2,\dots ,c_{\widehat{v}}\in \mathbb{R}$, such that

$$y\left(t\right)=c_1{t}^{\alpha }+c_2{t}^{2\alpha }+\cdots +c_{\widehat{v}}{t}^{\widehat{v}\alpha }+\mathrm{smoother}\mathrm{terms}.$$

Then

$${}^C{D}_0^{\alpha }y\left(t\right)=d_1+d_2{t}^{\alpha }+\cdots +d_{\widehat{v}}{t}^{(\widehat{v}-1)\alpha }+\mathrm{smoother}\mathrm{terms},$$

where $d_1,d_2,\dots ,d_{\widehat{v}}\in \mathbb{R}$ are some constants. Therefore, assumptions (5) are reasonable, and we can also obtain for $z:={}^C{D}_0^{\alpha }y$ that

$$z\in C[0,T]\cap C^3(0,T],\left|z^{\left(k\right)}\left(t\right)\right|\le C(1+t^{\alpha -k})\mathrm{for}k=0,1,2,3,t\in (0,T].$$

(6)

The computational work and storage of the predictor–corrector method still remain very high due to the nonlocality of the fractional derivatives. Therefore, fast methods to reduce computational cost and storage were also investigated. For example, on the basis of an efficient sum-of-exponentials (SOE) approximation for the kernel function $t^{-\beta -1}$, Jiang et al. [31] introduced a fast evaluation of the Caputo fractional derivative on the interval $[\mathsf{\Delta }t,T]$ with a uniform absolute error $ϵ$, where $\beta \in (0,1)$ and $\mathsf{\Delta }t$ is the time step size. One can also refer to [32,33,34,35]. In the present paper, we also use this SOE technique to construct the corresponding fast predictor–corrector method for (1).

The rest of this paper is organized as follows. In Section 2, we formulate the high-order predictor–corrector method for (1). In Section 3, we discuss the error estimates of the predictor–corrector method. In Section 4, we propose a fast algorithm for the presented predictor–corrector method. Several numerical examples are given in Section 5 to illustrate the computational flexibility and verify our error estimates of the used methods. A brief conclusion is given in Section 6.

Notation: In this paper, notation C is used to denote a generic positive constant that is always independent of mesh size, but may take different values at different occurrences.

2. High-Order Predictor–Corrector Method

In order to handle the weak singularity of the solution of (1), we consider the graded meshes

$$t_n=T{(n/N)}^r\mathrm{for}n=0,1,\dots ,N,{\tau }_n=t_n-t_{n-1}\mathrm{for}n=1,2,\dots ,N,$$

where constant mesh grading $r\ge 1$ is chosen by the user. One can obtain that

$$t_n\le C{N}^{-r}{n}^r\mathrm{and}{\tau }_n=T{N}^{-r}[n^r-{(n-1)}^r]\le C{N}^{-r}{n}^{r-1}\mathrm{for}n=1,2,\dots ,N.$$

(7)

The discretized version of (4) at $t=t_{n+1}$ is given as

$$y\left(t_{n+1}\right)=y_0+\frac{1}{\mathsf{\Gamma }\left(\alpha \right)}\sum _{j=0}^n{\int }_{s=t_j}^{t_{j+1}}{(t_{n+1}-s)}^{\alpha -1}{f}_y\left(s\right)ds.$$

(8)

To construct the high-order predictor–corrector method for (1), on each small interval $[t_j,t_{j+1}]$, we denote the linear interpolation polynomial and quadratic interpolation polynomial of a function $w\left(t\right)$ as ${\mathsf{\Pi }}_{1,j}w\left(t\right)$ and ${\mathsf{\Pi }}_{2,j}w\left(t\right)$, respectively, i.e.,

$$\begin{array}{cc}\hfill {\mathsf{\Pi }}_{1,j}w\left(t\right)& =\frac{t-t_{j+1}}{t_j-t_{j+1}}w\left(t_j\right)+\frac{t-t_j}{t_{j+1}-t_j}w\left(t_{j+1}\right)\hfill \\ \hfill & :=L_{j,0}\left(t\right)w\left(t_j\right)+L_{j,1}\left(t\right)w\left(t_{j+1}\right)\mathrm{for}j=0,1,\dots ,N-1,\hfill \end{array}$$

(9)

and

$$\begin{array}{cc}\hfill {\mathsf{\Pi }}_{2,j}w\left(t\right)& =\frac{(t-t_j)(t-t_{j+1})}{(t_{j-1}-t_j)(t_{j-1}-t_{j+1})}w\left(t_{j-1}\right)+\frac{(t-t_{j-1})(t-t_{j+1})}{(t_j-t_{j-1})(t_j-t_{j+1})}w\left(t_j\right)\hfill \\ \hfill & +\frac{(t-t_{j-1})(t-t_j)}{(t_{j+1}-t_{j-1})(t_{j+1}-t_j)}w\left(t_{j+1}\right)\hfill \\ \hfill & :=Q_{j,-1}\left(t\right)w\left(t_{j-1}\right)+Q_{j,0}\left(t\right)w\left(t_j\right)+Q_{j,1}\left(t\right)w\left(t_{j+1}\right)\mathrm{for}j=1,2,\dots ,N-1.\hfill \end{array}$$

(10)

Set

$$\begin{array}{cc}\hfill a_{j,\theta }^{n+1}& :={\int }_{s=t_j}^{t_{j+1}}{(t_{n+1}-s)}^{\alpha -1}{L}_{j,\theta }\left(s\right)ds\mathrm{with}\theta =0\mathrm{or}1,j=0,1,\dots ,n,\hfill \end{array}$$

(11a)

$$\begin{array}{cc}\hfill b_{j,\theta }^{n+1}& :={\int }_{s=t_j}^{t_{j+1}}{(t_{n+1}-s)}^{\alpha -1}{Q}_{j,\theta }\left(s\right)ds\mathrm{with}\theta =-1,0\mathrm{or}1,j=1,2,\dots ,n,\hfill \end{array}$$

(11b)

$$\begin{array}{cc}\hfill c_{j,\theta }^{n+1}& :={\int }_{s=t_j}^{t_{j+1}}{(t_{n+1}-s)}^{\alpha -1}{Q}_{j-1,\theta }\left(s\right)ds\mathrm{with}\theta =-1,0\mathrm{or}1,j=2,3,\dots ,n.\hfill \end{array}$$

(11c)

For the calculation of the predictor formula of (8), we do not use the unknown value $y\left(t_{n+1}\right)$ when computing ${\int }_{s=t_n}^{t_{n+1}}{(t_{n+1}-s)}^{\alpha -1}{f}_y\left(s\right)ds$. Three cases are divided for n as follows:

• When $n=0$, we use $f_y\left(t_0\right)$ to approximate $f_y\left(t\right)$ on interval $[t_0,t_1]$.
• When $n=1$, we use ${\mathsf{\Pi }}_{1,0}{f}_y\left(t\right)$ to approximate $f_y\left(t\right)$ on intervals $[t_0,t_1]$ and $[t_1,t_2]$.
• When $n\ge 2$, we use ${\mathsf{\Pi }}_{1,0}{f}_y\left(t\right)$ to approximate $f_y\left(t\right)$ on first small interval $[t_0,t_1]$, ${\mathsf{\Pi }}_{2,j}{f}_y\left(t\right)$ to approximate $f_y\left(t\right)$ on each interval $[t_j,t_{j+1}](j=1,2,\dots ,n-1)$ and ${\mathsf{\Pi }}_{2,n-1}{f}_y\left(t\right)$ to approximate $f_y\left(t\right)$ on the last small interval $[t_n,t_{n+1}]$.

Then, it follows from (8) that

$$\begin{array}{cc}\hfill y\left(t_{n+1}\right)& \approx y_0+\frac{1}{\mathsf{\Gamma }\left(\alpha \right)}{\int }_{s=t_0}^{t_1}{(t_{n+1}-s)}^{\alpha -1}{\mathsf{\Pi }}_{1,0}{f}_y\left(s\right)ds\hfill \\ \hfill & +\frac{1}{\mathsf{\Gamma }\left(\alpha \right)}\sum _{j=1}^{n-1}{\int }_{s=t_j}^{t_{j+1}}{(t_{n+1}-s)}^{\alpha -1}{\mathsf{\Pi }}_{2,j}{f}_y\left(s\right)ds\hfill \\ \hfill & +\frac{1}{\mathsf{\Gamma }\left(\alpha \right)}{\int }_{s=t_n}^{t_{n+1}}{(t_{n+1}-s)}^{\alpha -1}{\mathsf{\Pi }}_{2,n-1}{f}_y\left(s\right)ds\hfill \\ \hfill & =y_0+\frac{1}{\mathsf{\Gamma }\left(\alpha \right)}\left(\sum _{j=0}^n{d}_j^{n+1}{f}_y\left(t_j\right)+c_{n,-1}^{n+1}{f}_y\left(t_{n-2}\right)+c_{n,0}^{n+1}{f}_y\left(t_{n-1}\right)+c_{n,1}^{n+1}{f}_y\left(t_n\right)\right),\hfill \end{array}$$

(12)

where ${\mathsf{\Pi }}_{2,-1}w\left(t\right):=-{\mathsf{\Pi }}_{1,0}w\left(t\right)+w\left(t_0\right)$, ${\mathsf{\Pi }}_{2,0}w\left(t\right):={\mathsf{\Pi }}_{1,0}w\left(t\right)$ for a function $w\left(t\right)$, and

$$\begin{array}{cc}\hfill & d_0^1=0,c_{0,-1}^1=c_{0,0}^1=0,c_{0,1}^1={\int }_{s=t_0}^{t_1}{(t_1-s)}^{\alpha -1}ds(\mathrm{for}n=0);\hfill \\ \hfill & d_0^2=a_{0,0}^2,d_1^2=a_{0,1}^2,c_{1,-1}^2=0,\hfill \end{array}$$

(13a)

$$\begin{array}{cc}\hfill & c_{1,\theta }^2={\int }_{s=t_1}^{t_2}{(t_2-s)}^{\alpha -1}{L}_{0,\theta }\left(s\right)ds\mathrm{with}\theta =0\mathrm{or}1(\mathrm{for}n=1);\hfill \end{array}$$

(13b)

$$\begin{array}{cc}\hfill & d_0^3=a_{0,0}^3+b_{1,-1}^3,d_1^3=a_{0,1}^3+b_{1,0}^3,d_2^3=b_{1,1}^3(\mathrm{for}n=2);\hfill \end{array}$$

(13c)

and, for $n\ge 3$,

$$d_j^{n+1}=\left\{\begin{array}{cc}{a}_{0,0}^{n+1}+b_{1,-1}^{n+1},\hfill & \mathrm{for}j=0,\hfill \\ a_{0,1}^{n+1}+b_{1,0}^{n+1}+b_{2,-1}^{n+1},\hfill & \mathrm{for}j=1,\hfill \\ b_{j-1,1}^{n+1}+b_{j,0}^{n+1}+b_{j+1,-1}^{n+1},\hfill & \mathrm{for}2\le j\le n-2,\hfill \\ b_{n-2,1}^{n+1}+b_{n-1,0}^{n+1},\hfill & \mathrm{for}j=n-1,\hfill \\ b_{n-1,1}^{n+1},\hfill & \mathrm{for}j=n.\hfill \end{array}\right.$$

(14)

For the corrector formula of (8), we use ${\mathsf{\Pi }}_{1,0}{f}_y\left(t\right)$ to approximate $f_y\left(t\right)$ on the first small interval $[t_0,t_1]$, and ${\mathsf{\Pi }}_{2,j}{f}_y\left(t\right)$ to approximate $f_y\left(t\right)$ on intervals $[t_j,t_{j+1}](j=1,2,\dots ,n)$. Hence, we can obtain from (8) that

$$\begin{array}{cc}\hfill y\left(t_{n+1}\right)& \approx y_0+\frac{1}{\mathsf{\Gamma }\left(\alpha \right)}{\int }_{s=t_0}^{t_1}{(t_{n+1}-s)}^{\alpha -1}{\mathsf{\Pi }}_{1,0}{f}_y\left(s\right)ds\hfill \\ \hfill & +\frac{1}{\mathsf{\Gamma }\left(\alpha \right)}\sum _{j=1}^n{\int }_{s=t_j}^{t_{j+1}}{(t_{n+1}-s)}^{\alpha -1}{\mathsf{\Pi }}_{2,j}{f}_y\left(s\right)ds\hfill \\ \hfill & =y_0+\frac{1}{\mathsf{\Gamma }\left(\alpha \right)}\left(\sum _{j=0}^n{d}_j^{n+1}{f}_y\left(t_j\right)+b_{n,-1}^{n+1}{f}_y\left(t_{n-1}\right)+b_{n,0}^{n+1}{f}_y\left(t_n\right)+b_{n,1}^{n+1}{f}_y\left(t_{n+1}\right)\right),\hfill \end{array}$$

(15)

where

$$b_{0,-1}^1=0,b_{0,0}^1=a_{0,0}^1,b_{0,1}^1=a_{0,1}^1(\mathrm{for}n=0).$$

(16)

We denote the preliminary approximation of $y\left(t_{n+1}\right)$ from (12) as $y_{n+1}^P$ (used in (15)) and the final approximation of $y\left(t_{n+1}\right)$ from (15) as $y_{n+1}$. Then, with (12) and (15), our predictor–corrector method for Problem (1) can be derived as follows:

$$\left\{\begin{array}{c}{y}_{n+1}^P=y_0+{\displaystyle \frac{1}{\mathsf{\Gamma }\left(\alpha \right)}}\left({\displaystyle \sum _{j=0}^n}{d}_j^{n+1}{f}_j+c_{n,-1}^{n+1}{f}_{n-2}+c_{n,0}^{n+1}{f}_{n-1}+c_{n,1}^{n+1}{f}_n\right),\hfill \\ y_{n+1}=y_0+{\displaystyle \frac{1}{\mathsf{\Gamma }\left(\alpha \right)}}\left({\displaystyle \sum _{j=0}^n}{d}_j^{n+1}{f}_j+b_{n,-1}^{n+1}{f}_{n-1}+b_{n,0}^{n+1}{f}_n+b_{n,1}^{n+1}{f}_{n+1}^P\right),\hfill \end{array}\right.$$

(17)

where $f_j:=f(t_j,y_j)$ and $f_j^P:=f(t_j,y_j^P)$.

Remark 1.

We use the same approximation of integral ${\int }_{s=t_0}^{t_n}{(t_{n+1}-s)}^{\alpha -1}{f}_y\left(s\right)$ ds for the calculation of predictor Formula (12) and corrector Formula (15), which had the greatest computational burden. Thus, this reduces the overall cost of the predictor–corrector method. In addition, even though our predictor–corrector method (17) can be viewed as a generalization of the predictor–corrector method presented in [21], unlike their method, we did not need to use the values of $y\left(t_{1/4}\right)$ and $y\left(t_{1/2}\right)$ to start up the scheme.

3. Error Estimates of the Predictor–Corrector Method

In this section, we study the error analysis of the predictor–corrector method (17). For this, we first introduce some lemmas that are used in analysis.

Lemma 2

([11], Lemma 3.3). Assume that $k_{j,n}\le C{\tau }_{j+1}{(t_n-t_j)}^{\alpha -1}$ with $0\le j\le n-1,1\le n\le N$. Let ${\psi }_0\ge 0$. Assume also that sequence ${\left\{{\varphi }_n\right\}}_{n=0}^N$ satisfies

$$\left\{\begin{array}{c}{\varphi }_0\le {\psi }_0,\hfill \\ {\varphi }_n\le {\psi }_0+{\displaystyle \sum _{j=0}^{n-1}}{k}_{j,n}{\varphi }_j\mathit{for}1\le n\le N.\hfill \end{array}\right.$$

Then, one has

$${\varphi }_n\le C{\psi }_0\mathit{for}1\le n\le N.$$

Lemma 3.

Terms $d_j^{n+1}$, $\left\{b_{j,-1}^{n+1},b_{j,0}^{n+1},b_{j,1}^{n+1}\right\}$ and $\left\{c_{j,-1}^{n+1},c_{j,0}^{n+1},c_{j,1}^{n+1}\right\}$ in (11), (13), (14) and (16) satisfy the following estimates:

$$|d_j^{n+1}|\le C{\tau }_{j+1}{(t_{n+1}-t_j)}^{\alpha -1}\mathit{for}0\le j\le n,0\le n\le N-1,$$

$$|c_{n,-1}^{n+1}|\le C{\tau }_{n-1}{(t_{n+1}-t_{n-2})}^{\alpha -1}\mathit{for}2\le n\le N-1,$$

$$\left\{|c_{n,0}^{n+1}|,|b_{n,-1}^{n+1}|\right\}\le C{\tau }_n{(t_{n+1}-t_{n-1})}^{\alpha -1}\mathit{for}1\le n\le N-1,$$

$$\left\{|c_{n,1}^{n+1}|,|b_{n,0}^{n+1}|,|b_{n,1}^{n+1}|\right\}\le C{\tau }_{n+1}^{\alpha }\mathit{for}0\le n\le N-1.$$

Proof. 

A simple deduction from the expression of $L_{j,\theta }(\theta =0\mathrm{or}1)$ and $Q_{j,\theta }(\theta =-1,0\mathrm{or}1)$ in (9) and (10) gives

$$|L_{j,\theta }|\le C\mathrm{for}\theta =0\mathrm{or}1,|Q_{j,\theta }|\le C\mathrm{for}\theta =-1,0\mathrm{or}1.$$

Then, from (11), we have for $0\le j\le n$ and $\theta =0\mathrm{or}1$ that

$$\begin{array}{cc}\hfill |a_{j,\theta }^{n+1}|& \le C{\int }_{s=t_j}^{t_{j+1}}{(t_{n+1}-s)}^{\alpha -1}ds\hfill \\ \hfill & \le C\left[{(t_{n+1}-t_j)}^{\alpha }-{(t_{n+1}-t_{j+1})}^{\alpha }\right]\hfill \\ \hfill & \le C{\tau }_{j+1}{(t_{n+1}-t_j)}^{\alpha -1}{\left(\frac{t_{n+1}-t_j}{t_{n+1}-t_{j+1}}\right)}^{1-\alpha }\hfill \\ \hfill & \le C{\tau }_{j+1}{(t_{n+1}-t_j)}^{\alpha -1}{\left(1+\frac{{\tau }_{j+1}}{{\tau }_{n+1}+{\tau }_n+\cdots +{\tau }_{j+2}}\right)}^{1-\alpha }\hfill \\ \hfill & \le C{\tau }_{j+1}{(t_{n+1}-t_j)}^{\alpha -1}.\hfill \end{array}$$

Again, one can obtain that

$$|b_{j,\theta }^{n+1}|\le C{\tau }_{j+1}{(t_{n+1}-t_j)}^{\alpha -1}\mathrm{with}\theta =-1,1\mathrm{or}1,j=0,1,\dots ,n,$$

(18)

$$|c_{j,\theta }^{n+1}|\le C{\tau }_{j+1}{(t_{n+1}-t_j)}^{\alpha -1}\mathrm{with}\theta =-1,1\mathrm{or}1,j=0,1,\dots ,n.$$

(19)

Moreover,

$$\begin{array}{cc}\hfill {\tau }_{j+2}{(t_{n+1}-t_{j+1})}^{\alpha -1}& ={\tau }_{j+1}{(t_{n+1}-t_j)}^{\alpha -1}\frac{{\tau }_{j+2}}{{\tau }_{j+1}}{\left(\frac{t_{n+1}-t_j}{t_{n+1}-t_{j+1}}\right)}^{1-\alpha }\hfill \\ \hfill & \le C{\tau }_{j+1}{(t_{n+1}-t_j)}^{\alpha -1}\frac{{\tau }_2}{{\tau }_1}{\left(1+\frac{{\tau }_{j+1}}{{\tau }_{n+1}+{\tau }_n+\cdots +{\tau }_{j+2}}\right)}^{1-\alpha }\hfill \\ \hfill & \le C{\tau }_{j+1}{(t_{n+1}-t_j)}^{\alpha -1}.\hfill \end{array}$$

(20)

Hence, for $2\le j\le n-2,n\ge 3$, one has from (14) that

$$\begin{array}{cc}\hfill |d_j^{n+1}|& \le |b_{j-1,1}^{n+1}|+|b_{j,0}^{n+1}|+|b_{j+1,-1}^{n+1}|\hfill \\ \hfill & \le C{\tau }_j{(t_{n+1}-t_{j-1})}^{\alpha -1}+C{\tau }_{j+1}{(t_{n+1}-t_j)}^{\alpha -1}+C{\tau }_{j+2}{(t_{n+1}-t_{j+1})}^{\alpha -1}\hfill \\ \hfill & \le C{\tau }_{j+1}{(t_{n+1}-t_j)}^{\alpha -1}.\hfill \end{array}$$

Similar to the above inequalities, we can obtain other cases of the bound of $|d_j^{n+1}|$; that is,

$$|d_j^{n+1}|\le C{\tau }_{j+1}{(t_{n+1}-t_j)}^{\alpha -1}\mathrm{for}j=0,1,\dots ,n,n=0,1,\dots ,N-1.$$

In addition, by using (18)–(20), we obtain

$$\begin{array}{cc}\hfill |c_{n,-1}^{n+1}|& \le C{\tau }_{n+1}{(t_{n+1}-t_n)}^{\alpha -1}\le C{\tau }_n{(t_{n+1}-t_{n-1})}^{\alpha -1}\hfill \\ \hfill & \le C{\tau }_{n-1}{(t_{n+1}-t_{n-2})}^{\alpha -1}\mathrm{for}2\le n\le N-1,\hfill \end{array}$$

$$\left\{|c_{n,0}^{n+1}|,|b_{n,-1}^{n+1}|\right\}\le C{\tau }_{n+1}{(t_{n+1}-t_n)}^{\alpha -1}\le C{\tau }_n{(t_{n+1}-t_{n-1})}^{\alpha -1}\mathrm{for}1\le n\le N-1,$$

$$\left\{|c_{n,1}^{n+1}|,|b_{n,0}^{n+1}|,|b_{n,1}^{n+1}|\right\}\le C{\tau }_{n+1}^{\alpha }\mathrm{for}0\le n\le N-1.$$

Therefore, the proof is now completed. □

For $r\ge 1$ and $0<\alpha <1$. Define

$$\mathsf{\Phi }(N,r,\alpha ):=\left\{\begin{array}{cc}{N}^{-2r\alpha }\hfill & \mathrm{for}1\le r<\frac{3}{2\alpha },\hfill \\ N^{-3}lnN\hfill & \mathrm{for}r=\frac{3}{2\alpha },\hfill \\ N^{-3}\hfill & \mathrm{for}r>\frac{3}{2\alpha }.\hfill \end{array}\right.$$

(21)

Lemma 4.

Let $w\in C[0,T]\cap C^3(0,T]$. Suppose that $|w^{\left(k\right)}\left(t\right)|\le C(1+t^{\alpha -k})$ for $k=0,1,2,3,$$t\in (0,T]$. For $n\ge 0$, we define

$$I_1^{n+1}=\left|{\int }_{s=t_0}^{t_1}{(t_{n+1}-s)}^{\alpha -1}(w-{\mathsf{\Pi }}_{1,0}w)\left(s\right)ds+\sum _{j=1}^n{\int }_{s=t_j}^{t_{j+1}}{(t_{n+1}-s)}^{\alpha -1}(w-{\mathsf{\Pi }}_{2,j}w)\left(s\right)ds\right|,$$

and

$$\begin{array}{cc}\hfill I_2^{n+1}& =\left|{\int }_{s=t_0}^{t_1}{(t_{n+1}-s)}^{\alpha -1}(w-{\mathsf{\Pi }}_{1,0}w)\left(s\right)ds+\sum _{j=1}^{n-1}{\int }_{s=t_j}^{t_{j+1}}{(t_{n+1}-s)}^{\alpha -1}(w-{\mathsf{\Pi }}_{2,j}w)\left(s\right)ds\right.\hfill \\ \hfill & \left.+{\int }_{s=t_n}^{t_{n+1}}{(t_{n+1}-s)}^{\alpha -1}(w-{\mathsf{\Pi }}_{2,n-1}w)\left(s\right)ds\right|.\hfill \end{array}$$

Then, we have

$$I_1^{n+1}+I_2^{n+1}\le C\mathsf{\Phi }(N,r,\alpha )\mathit{for}0\le n\le N-1.$$

The proof of the above lemma is a bit lengthy. For the detailed proof, see Appendix A. Set

$$e_j=y\left(t_j\right)-y_j,e_j^P=y\left(t_j\right)-y_j^P\mathrm{for}j=0,1,\dots ,N.$$

On the basis of the above preliminaries, a convergence criterion of the predictor–corrector method (17) can be stated as follows.

Theorem 1.

Suppose that $y\left(t_j\right)$ and ${\left\{y_j\right\}}_{j=0}^N$ are the solutions of (8) and (17), respectively. Suppose also that (5) holds true. Then, we have

$$|e_j|\le C\mathsf{\Phi }(N,r,\alpha )\mathit{for}1\le j\le N.$$

Proof. 

We can obtain from (8), (12), (15) and (17) that

$$\begin{array}{cc}\hfill e_{n+1}^P& =\frac{1}{\mathsf{\Gamma }\left(\alpha \right)}[{\int }_{s=t_0}^{t_1}{(t_{n+1}-s)}^{\alpha -1}(f_y-{\mathsf{\Pi }}_{1,0}{f}_y)\left(s\right)ds\hfill \\ \hfill & +\sum _{j=1}^{n-1}{\int }_{s=t_j}^{t_{j+1}}{(t_{n+1}-s)}^{\alpha -1}(f_y-{\mathsf{\Pi }}_{2,j}{f}_y)\left(s\right)ds\hfill \\ \hfill & +{\int }_{s=t_n}^{t_{n+1}}{(t_{n+1}-s)}^{\alpha -1}(f_y-{\mathsf{\Pi }}_{2,n-1}{f}_y)\left(s\right)ds]\hfill \\ \hfill & +\frac{1}{\mathsf{\Gamma }\left(\alpha \right)}[\sum _{j=0}^n{d}_j^{n+1}\left(f_y\left(t_j\right)-f_j\right)+c_{n,-1}^{n+1}\left(f_y\left(t_{n-2}\right)-f_{n-2}\right)\hfill \\ \hfill & +c_{n,0}^{n+1}\left(f_y\left(t_{n-1}\right)-f_{n-1}\right)+c_{n,1}^{n+1}(f_y\left(t_n\right)-f_n)]\hfill \\ \hfill & :=R_{1,1}+R_{1,2},\hfill \end{array}$$

(22)

and

$$\begin{array}{cc}\hfill e_{n+1}& =\frac{1}{\mathsf{\Gamma }\left(\alpha \right)}[{\int }_{s=t_0}^{t_1}{(t_{n+1}-s)}^{\alpha -1}(f_y-{\mathsf{\Pi }}_{1,0}{f}_y)\left(s\right)ds\hfill \\ \hfill & +\sum _{j=1}^n{\int }_{s=t_j}^{t_{j+1}}{(t_{n+1}-s)}^{\alpha -1}(f_y-{\mathsf{\Pi }}_{2,j}{f}_y)\left(s\right)ds]\hfill \\ \hfill & +\frac{1}{\mathsf{\Gamma }\left(\alpha \right)}\left[\sum _{j=0}^n{d}_j^{n+1}\left(f_y\left(t_j\right)-f_j\right)+b_{n,-1}^{n+1}\left(f_y\left(t_{n-1}\right)-f_{n-1}\right)+b_{n,0}^{n+1}\left(f_y\left(t_n\right)-f_n\right)\right]\hfill \\ \hfill & +\frac{1}{\mathsf{\Gamma }\left(\alpha \right)}{b}_{n,1}^{n+1}\left(f_y\left(t_{n+1}\right)-f_{n+1}^P\right)\hfill \\ \hfill & :=R_{2,1}+R_{2,2}+R_{2,3}.\hfill \end{array}$$

(23)

By using (1), (5), (6) and Lemma 4, we have

$$|R_{1,1}|+|R_{2,1}|\le C\mathsf{\Phi }(N,r,\alpha ).$$

(24)

It follows from (3) and Lemma 3 that

$$|R_{1,2}|\le CL\sum _{j=0}^n|d_j^{n+1}\left|\right|e_j|+CL\left(|c_{n,-1}^{n+1}\left|\right|e_{n-2}|+|c_{n,0}^{n+1}\left|\right|e_{n-1}|+|c_{n,1}^{n+1}\left|\right|e_n|\right),$$

(25)

$$|R_{2,2}|\le CL\sum _{j=0}^n|d_j^{n+1}\left|\right|e_j|+CL(|b_{n,-1}^{n+1}\left|\right|e_{n-1}|+|b_{n,0}^{n+1}\left|\right|e_n\left|\right),$$

(26)

and

$$|R_{2,3}|\le CL{\tau }_{n+1}^{\alpha }\left|e_{n+1}^P\right|.$$

(27)

Then, we obtain from (22)–(27) that

$$\begin{array}{cc}\hfill |e_{n+1}^P|& \le C\mathsf{\Phi }(N,r,\alpha )+CL\sum _{j=0}^n|d_j^{n+1}\left|\right|e_j|\hfill \\ \hfill & +CL\left(|c_{n,-1}^{n+1}\left|\right|e_{n-2}|+|c_{n,0}^{n+1}\left|\right|e_{n-1}|+|c_{n,1}^{n+1}\left|\right|e_n|\right),\hfill \end{array}$$

(28)

and

$$\begin{array}{cc}\hfill |e_{n+1}|& \le C\mathsf{\Phi }(N,r,\alpha )+CL\sum _{j=0}^n|d_j^{n+1}\left|\right|e_j|\hfill \\ \hfill & +CL\left(|b_{n,-1}^{n+1}\left|\right|e_{n-1}|+|b_{n,0}^{n+1}\left|\right|e_n|\right)+CL{\tau }_{n+1}^{\alpha }\left|e_{n+1}^P\right|.\hfill \end{array}$$

(29)

Substituting (28) into (29) gives

$$\begin{array}{cc}\hfill |e_{n+1}|& \le C\mathsf{\Phi }(N,r,\alpha )+C\sum _{j=0}^n|d_j^{n+1}\left|\right|e_j|+C\left(|c_{n,-1}^{n+1}\left|\right|e_{n-2}|+|c_{n,0}^{n+1}\left|\right|e_{n-1}|+|c_{n,1}^{n+1}\left|\right|e_n|\right)\hfill \\ \hfill & +C\left(|b_{n,-1}^{n+1}\left|\right|e_{n-1}|+|b_{n,0}^{n+1}\left|\right|e_n|\right)\hfill \\ \hfill & \le C_1\mathsf{\Phi }(N,r,\alpha )+C_1\sum _{j=0}^n{\tau }_{j+1}{(t_{n+1}-t_j)}^{\alpha -1}\left|e_j\right|\hfill \end{array}$$

(30)

for a fixed constant $C_1$ with the use of Lemma 3. Invoking Lemma 2 to (30) gives

$$|e_{n+1}|\le C\mathsf{\Phi }(N,r,\alpha )\mathrm{for}0\le n\le N-1.$$

The proof is, thus, complete. □

Remark 2.

Our predictor–corrector method (17) can easily be generalized to solve (1) with $\alpha \ge 1$. The corresponding convergence order is

$$|e_j|\le C\left\{\begin{array}{cc}{N}^{-3}lnN\hfill & \mathit{for}2r\alpha =3,\hfill \\ N^{-3}\hfill & \mathit{otherwise},\hfill \end{array}\right.\mathit{with}1\le j\le N.$$

4. Construction of the Fast Algorithm

Due to the nonlocality of the fractional derivatives, our predictor–corrector method (17) also needed high computational work and storage. In order to overcome this difficulty, inspired by Jiang [31], in this section we consider the corresponding sum-of-exponentials (SOE) technique to improve the computational efficiency of the predictor–corrector method (17). Before deriving the fast predictor–corrector method, we give the following lemma for the SOE approximation.

Lemma 5

([31], Section 2.1). For the given $\beta \in (0,2)$, an absolute tolerance error ϵ, a cut-off time $\mathsf{\Delta }t:={min}_{1\le n\le N}{\tau }_n$ and a final time T, there exist a positive integer $N_{exp}$, positive quadrature nodes $s_i$, and corresponding positive weights ${\varpi }_i$ ($i=1,2,\dots ,N_{exp}$) such that

$$|t^{-\beta }-\sum _{i=1}^{N_{exp}}{\varpi }_i{e}^{-s_{i}t}|\le ϵ\mathit{for}t\in [\mathsf{\Delta }t,T],$$

where

$$N_{exp}=O\left(\left(log\frac{1}{ϵ}\right)\left(loglog\frac{1}{ϵ}+log\frac{T}{\mathsf{\Delta }t}\right)+\left(log\frac{1}{\mathsf{\Delta }t}\right)\left(loglog\frac{1}{ϵ}+log\frac{1}{\mathsf{\Delta }t}\right)\right).$$

Now, we describe the fast predictor–corrector method, and we obtain from (12) that

$$\begin{array}{cc}\hfill y\left(t_{n+1}\right)& \approx y_0+\frac{1}{\mathsf{\Gamma }\left(\alpha \right)}[{\int }_{s=t_0}^{t_1}{\mathsf{\Pi }}_{1,0}{f}_y\left(s\right)\sum _{i=1}^{N_{exp}}{\varpi }_i{e}^{-s_i(t_{n+1}-s)}ds\hfill \\ \hfill & +\sum _{j=1}^{n-1}{\int }_{s=t_j}^{t_{j+1}}{\mathsf{\Pi }}_{2,j}{f}_y\left(s\right)\sum _{i=1}^{N_{exp}}{\varpi }_i{e}^{-s_i(t_{n+1}-s)}ds]\hfill \\ \hfill & +\frac{1}{\mathsf{\Gamma }\left(\alpha \right)}{\int }_{s=t_n}^{t_{n+1}}{(t_{n+1}-s)}^{\alpha -1}{\mathsf{\Pi }}_{2,n-1}{f}_y\left(s\right)ds\hfill \\ \hfill & =y_0+\frac{1}{\mathsf{\Gamma }\left(\alpha \right)}\sum _{i=1}^{N_{exp}}{\varpi }_i[{\int }_{s=t_0}^{t_1}{e}^{-s_i(t_{n+1}-s)}{\mathsf{\Pi }}_{1,0}{f}_y\left(s\right)ds\hfill \\ \hfill & +\sum _{j=1}^{n-1}{\int }_{s=t_j}^{t_{j+1}}{e}^{-s_i(t_{n+1}-s)}{\mathsf{\Pi }}_{2,j}{f}_y\left(s\right)ds]\hfill \\ \hfill & +\frac{1}{\mathsf{\Gamma }\left(\alpha \right)}{\int }_{s=t_n}^{t_{n+1}}{(t_{n+1}-s)}^{\alpha -1}{\mathsf{\Pi }}_{2,n-1}{f}_y\left(s\right)ds\hfill \\ \hfill & =y_0+\frac{1}{\mathsf{\Gamma }\left(\alpha \right)}\left(\sum _{i=1}^{N_{exp}}{\varpi }_i{P}_i^n+c_{n,-1}^{n+1}{f}_y\left(t_{n-2}\right)+c_{n,0}^{n+1}{f}_y\left(t_{n-1}\right)+c_{n,1}^{n+1}{f}_y\left(t_n\right)\right),\hfill \end{array}$$

(31)

where $P_i^0=0$ for $i=1,2,\dots ,N_{exp}$ and

$$\begin{array}{cc}\hfill P_i^n& ={\int }_{s=t_0}^{t_1}{e}^{-s_i(t_{n+1}-s)}{\mathsf{\Pi }}_{1,0}{f}_y\left(s\right)ds+\sum _{j=1}^{n-1}{\int }_{s=t_j}^{t_{j+1}}{e}^{-s_i(t_{n+1}-s)}{\mathsf{\Pi }}_{2,j}{f}_y\left(s\right)ds\hfill \\ \hfill & \mathrm{for}i=1,2,\dots ,N_{exp},n=1,2,\dots ,N-1.\hfill \end{array}$$

By using a recursive relation, one has that

$$\begin{array}{cc}\hfill P_i^n& ={\int }_{s=t_0}^{t_1}{e}^{-s_i(t_n+{\tau }_{n+1}-s)}{\mathsf{\Pi }}_{1,0}{f}_y\left(s\right)ds+\sum _{j=1}^{n-2}{\int }_{s=t_j}^{t_{j+1}}{e}^{-s_i(t_n+{\tau }_{n+1}-s)}{\mathsf{\Pi }}_{2,j}{f}_y\left(s\right)ds\hfill \\ \hfill & +{\int }_{s=t_{n-1}}^{t_n}{e}^{-s_i(t_{n+1}-s)}{\mathsf{\Pi }}_{2,n-1}{f}_y\left(s\right)ds\hfill \\ \hfill & =e^{-s_i{\tau }_{n+1}}\left[{\int }_{s=t_0}^{t_1}{e}^{-s_i(t_n-s)}{\mathsf{\Pi }}_{1,0}{f}_y\left(s\right)ds+\sum _{j=1}^{n-2}{\int }_{s=t_j}^{t_{j+1}}{e}^{-s_i(t_n-s)}{\mathsf{\Pi }}_{2,j}{f}_y\left(s\right)ds\right]\hfill \\ \hfill & +{\int }_{s=t_{n-1}}^{t_n}{e}^{-s_i(t_{n+1}-s)}{\mathsf{\Pi }}_{2,n-1}{f}_y\left(s\right)ds\hfill \\ \hfill & =e^{-s_i{\tau }_{n+1}}{P}_i^{n-1}+A_{i,-1}^{n+1}{f}_y\left(t_{n-2}\right)+A_{i,0}^{n+1}{f}_y\left(t_{n-1}\right)+A_{i,1}^{n+1}{f}_y\left(t_n\right)\hfill \\ \hfill & \mathrm{for}n=2,3,\dots ,N-1,\hfill \end{array}$$

(32)

where

$$\begin{array}{cc}\hfill A_{i,\theta }^{n+1}& :={\int }_{s=t_{n-1}}^{t_n}{e}^{-s_i(t_{n+1}-s)}{Q}_{n-1,\theta }\left(s\right)ds\mathrm{with}\theta =-1,0\mathrm{or}1,n=2,3,\dots ,N-1.\hfill \end{array}$$

Similarly, we have from (15) that

$$y\left(t_{n+1}\right)\approx y_0+\frac{1}{\mathsf{\Gamma }\left(\alpha \right)}\left(\sum _{i=1}^{N_{exp}}{\varpi }_i{P}_i^n+b_{n,-1}^{n+1}{f}_y\left(t_{n-1}\right)+b_{n,0}^{n+1}{f}_y\left(t_n\right)+b_{n,1}^{n+1}{f}_y\left(t_{n+1}\right)\right).$$

(33)

The prediction and correction stages approximations of $y\left(t_{n+1}\right)$ are denoted with ${\overline{y}}_{n+1}^P$ and ${\overline{y}}_{n+1}$, respectively. Set ${\overline{f}}_j=f(t_j,{\overline{y}}_j)$ and ${\overline{f}}_j^P:=f(t_j,{\overline{y}}_j^P)$. Then, we obtain the fast predictor–corrector method for Problem (1) from (31)–(33):

$$\left\{\begin{array}{c}{\overline{y}}_{n+1}^P=y_0+{\displaystyle \frac{1}{\mathsf{\Gamma }\left(\alpha \right)}}\left({\displaystyle \sum _{i=1}^{N_{exp}}}{\varpi }_i{\overline{p}}_i^n+c_{n,-1}^{n+1}{\overline{f}}_{n-2}+c_{n,0}^{n+1}{\overline{f}}_{n-1}+c_{n,1}^{n+1}{\overline{f}}_n\right),\hfill \\ {\overline{y}}_{n+1}=y_0+{\displaystyle \frac{1}{\mathsf{\Gamma }\left(\alpha \right)}}\left({\displaystyle \sum _{i=1}^{N_{exp}}}{\varpi }_i{\overline{p}}_i^n+b_{n,-1}^{n+1}{\overline{f}}_{n-1}+b_{n,0}^{n+1}{\overline{f}}_n+b_{n,1}^{n+1}{\overline{f}}_{n+1}^P\right),\hfill \\ {\overline{p}}_i^0=0,{\overline{p}}_i^1={\int }_{s=t_0}^{t_1}{e}^{-s_i(t_{n+1}-s)}(L_{0,0}{\overline{f}}_0+L_{0,1}{\overline{f}}_1)ds\mathrm{for}i=1,2,\dots ,N_{exp},\hfill \\ {\overline{p}}_i^n=e^{-s_i{\tau }_{n+1}}{\overline{p}}_i^{n-1}+A_{i,-1}^{n+1}{\overline{f}}_{n-2}+A_{i,0}^{n+1}{\overline{f}}_{n-1}+A_{i,1}^{n+1}{\overline{f}}_n\hfill \\ \mathrm{for}i=1,2,\dots ,N_{exp},n=2,3,\dots ,N.\hfill \end{array}\right.$$

(34)

The next result is the fundamental convergence bound for our fast predictor–corrector method (34).

Lemma 6.

Let $w\in C[0,T]\cap C^3(0,T]$. Suppose that $|w^{\left(k\right)}\left(t\right)|\le C(1+t^{\alpha -k})$ for $k=0,1,2,3,$$t\in (0,T]$. For $n\ge 0$, we define

$$\begin{array}{cc}\hfill I_3^{n+1}& =|{\int }_{s=t_0}^{t_{n+1}}{(t_{n+1}-s)}^{\alpha -1}w\left(s\right)ds-{\int }_{s=t_0}^{t_1}{\mathsf{\Pi }}_{1,0}w\left(s\right)\sum _{i=1}^{N_{exp}}{\varpi }_i{e}^{-s_i(t_{n+1}-s)}ds\hfill \\ \hfill & -\sum _{j=1}^{n-1}{\int }_{s=t_j}^{t_{j+1}}{\mathsf{\Pi }}_{2,j}w\left(s\right)\sum _{i=1}^{N_{exp}}{\varpi }_i{e}^{-s_i(t_{n+1}-s)}ds-{\int }_{s=t_n}^{t_{n+1}}{(t_{n+1}-s)}^{\alpha -1}{\mathsf{\Pi }}_{2,n}w\left(s\right)ds|\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill I_4^{n+1}& =|{\int }_{s=t_0}^{t_{n+1}}{(t_{n+1}-s)}^{\alpha -1}w\left(s\right)ds-{\int }_{s=t_0}^{t_1}{\mathsf{\Pi }}_{1,0}w\left(s\right)\sum _{i=1}^{N_{exp}}{\varpi }_i{e}^{-s_i(t_{n+1}-s)}ds\hfill \\ \hfill & -\sum _{j=1}^{n-1}{\int }_{s=t_j}^{t_{j+1}}{\mathsf{\Pi }}_{2,j}w\left(s\right)\sum _{i=1}^{N_{exp}}{\varpi }_i{e}^{-s_i(t_{n+1}-s)}ds-{\int }_{s=t_n}^{t_{n+1}}{(t_{n+1}-s)}^{\alpha -1}{\mathsf{\Pi }}_{2,n-1}w\left(s\right)ds|.\hfill \end{array}$$

Then, we have

$$I_3^{n+1}+I_4^{n+1}\le C\mathsf{\Phi }(N,r,\alpha )+Cϵ\mathit{for}0\le n\le N-1.$$

Proof. 

We can obtain that

$$\begin{array}{cc}\hfill I_3^{n+1}& \le I_1^{n+1}+|{\int }_{s=t_0}^{t_1}{\mathsf{\Pi }}_{1,0}w\left(s\right)\left[{(t_{n+1}-s)}^{\alpha -1}-\sum _{i=1}^{N_{exp}}{\varpi }_i{e}^{-s_i(t_{n+1}-s)}\right]ds\hfill \\ \hfill & +\sum _{j=1}^{n-1}{\int }_{s=t_j}^{t_{j+1}}{\mathsf{\Pi }}_{2,j}w\left(s\right)\left[{(t_{n+1}-s)}^{\alpha -1}-\sum _{i=1}^{N_{exp}}{\varpi }_i{e}^{-s_i(t_{n+1}-s)}ds\right]ds|\hfill \\ \hfill & \le I_1^{n+1}+ϵ|{\int }_{s=t_0}^{t_1}{\mathsf{\Pi }}_{1,0}w\left(s\right)ds+\sum _{j=1}^{n-1}{\int }_{s=t_j}^{t_{j+1}}{\mathsf{\Pi }}_{2,j}w\left(s\right)ds|\hfill \\ \hfill & \le I_1^{n+1}+Cϵt_n\underset{t_0\le t\le t_n}{max}\left|w\left(t\right)\right|\hfill \\ \hfill & \le C\mathsf{\Phi }(N,r,\alpha )+Cϵ,\hfill \end{array}$$

where we used Lemmas 4 and 5. The proof of the bound of $I_4^{n+1}$ is similar. □

The following theorem can easily be obtained by repeating the proof of Theorem 1.

Theorem 2.

Suppose that $y\left(t_j\right)$ and ${\left\{{\overline{y}}_j\right\}}_{j=0}^N$ are the solutions of (8) and (34), respectively. Suppose also that (5) holds true. Then, we have

$$|y\left(t_j\right)-{\overline{y}}_j|\le C\mathsf{\Phi }(N,r,\alpha )+Cϵ\mathit{for}1\le j\le N.$$

5. Numerical Examples

We present some numerical examples to check the convergence orders and the efficiency of the proposed predictor–corrector method (17) and fast predictor–corrector method (34). For convenience, we denote these two methods as PCM and fPCM, respectively.

Example 1.

Consider the following FDEs with $\alpha \in (0,1)$:

$${}^C{D}_0^{\alpha }y\left(t\right)=-y\left(t\right),t\in (0,1];y\left(0\right)=1.$$

(35)

The exact solution of (35) is $y\left(t\right)=E_{\alpha }(-t^{\alpha })$, where

$$E_{\alpha }\left(s\right)=\sum _{k=0}^{\infty }\frac{s^k}{\mathsf{\Gamma }(\alpha k+1)}$$

is the Mittag-Leffler function.

Since

$${}^C{D}_0^{\alpha }y\left(t\right)=-1-\frac{-t^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}-\frac{{(-t^{\alpha })}^2}{\mathsf{\Gamma }(2\alpha +1)}-\dots ,$$

that is, ${}^C{D}_0^{\alpha }y\left(t\right)$ behaves as $C(1+t^{\alpha })$. Set ${\mathrm{err}}_N:={max}_{0\le j\le N}\left\{|y\left(t_j\right)-y_j|\right\}$ and ${\mathrm{err}}_N^f:={max}_{0\le j\le N}\left\{|y\left(t_j\right)-{\overline{y}}_j|\right\}$. Through Theorems 1 and 2, we have

$${\mathrm{err}}_N\le C{N}^{-min\left\{2r\alpha ,3\right\}}\mathrm{and}{\mathrm{err}}_N^f\le C{N}^{-min\left\{2r\alpha ,3\right\}}+Cϵ,$$

(36)

for PCM (17) and fPCM (34), respectively.

In our calculation, for fPCM, we take $ϵ={10}^{-12}$. In addition, to present the results, we define $p:={log}_2\left(E_N/E_{2N}\right)$ to measure the convergence order of the methods, where $E_N$ can be ${\mathrm{err}}_N$ or ${\mathrm{err}}_N^f$. Applying PCM and fPCM to Problem (35) with different $\alpha$ and r, a series of numerical solutions can be obtained. For simplicity, in

Table 1. Maximal nodal errors, convergence orders, and CPU times of PCM and fPCM for Problem (35) with $\alpha =0.5$.

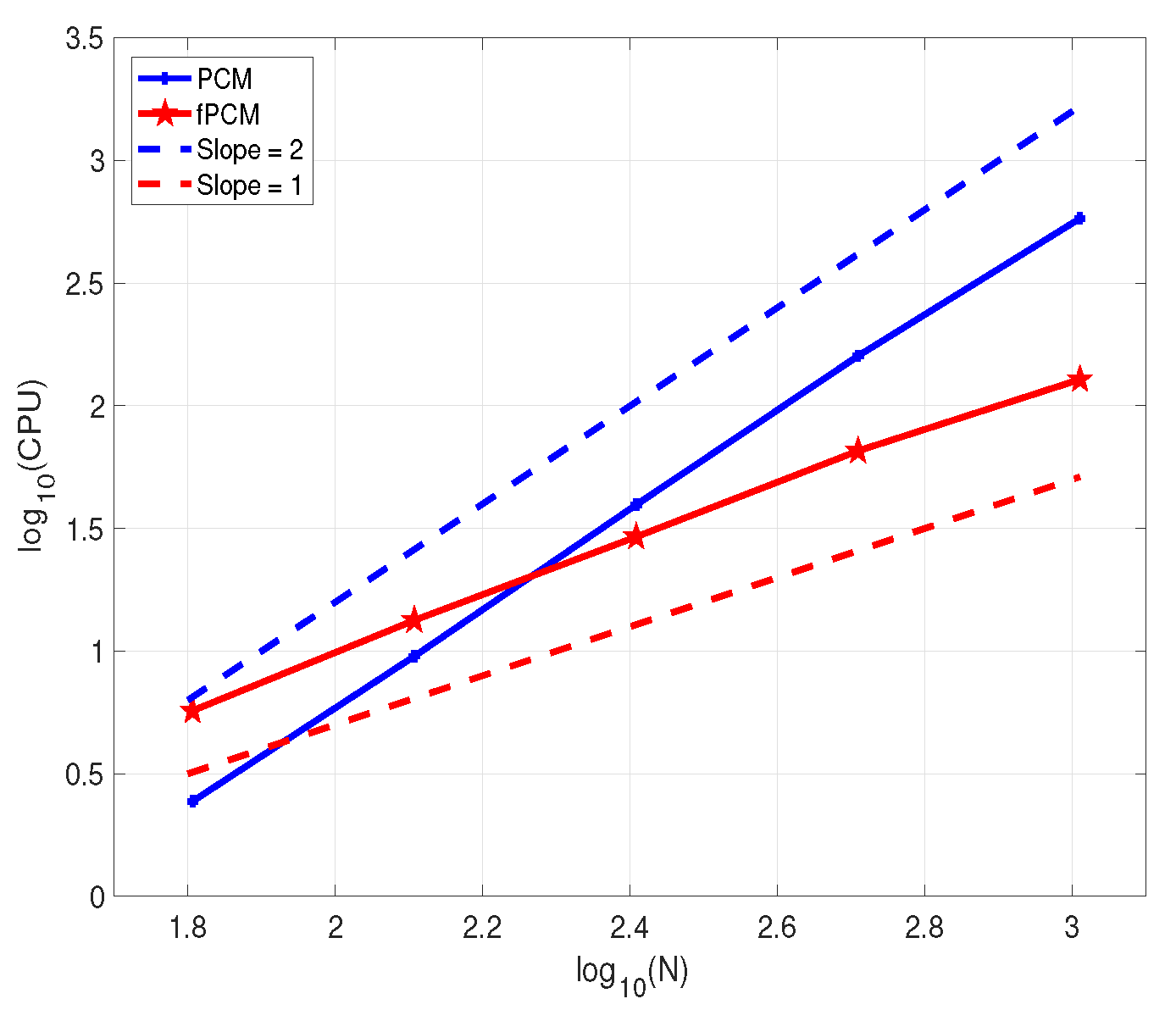
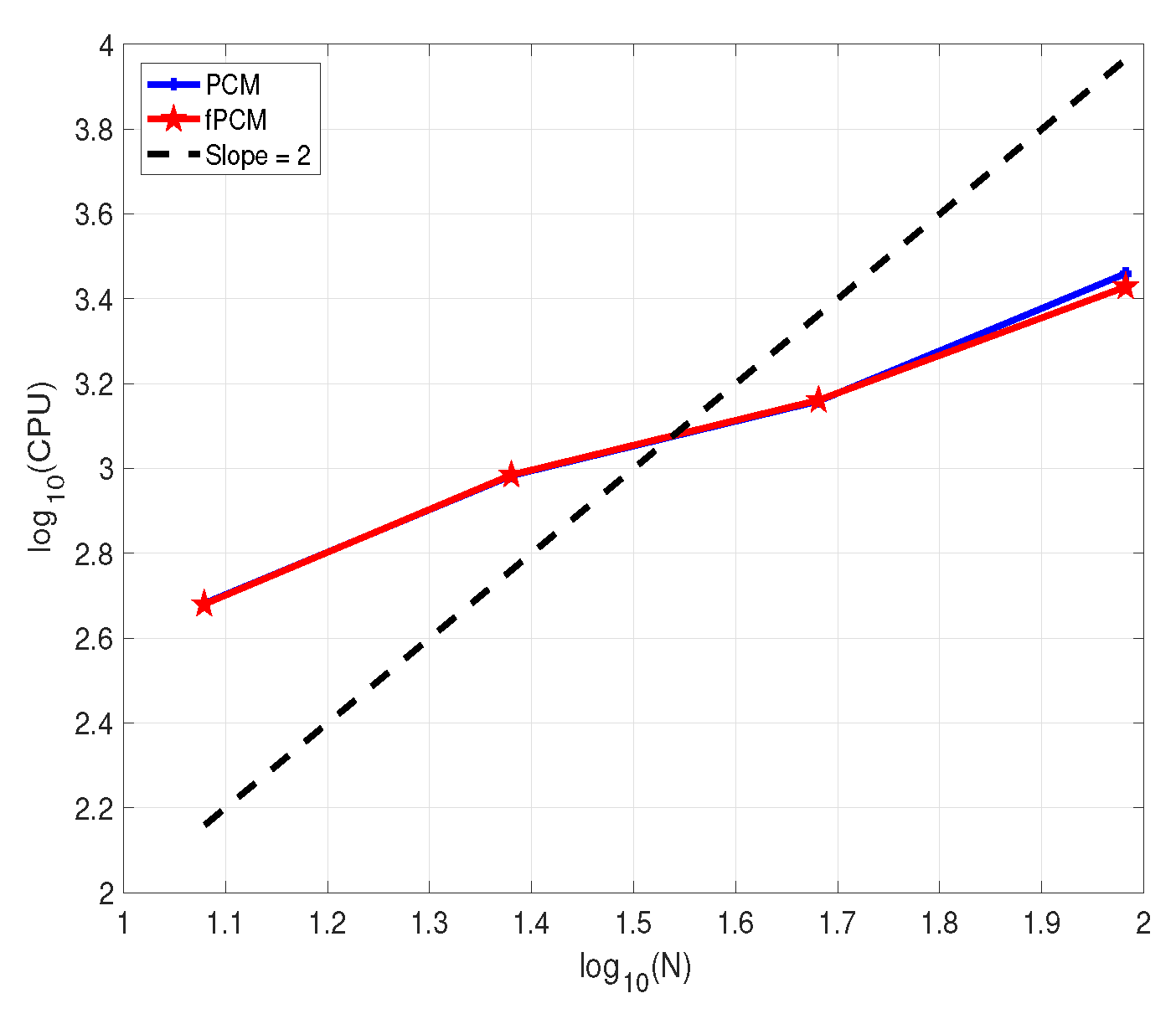
		PCM				fPCM
N	r	${\mathbf{err}}_{\mathit{N}}$	p	CPU		${\mathbf{err}}_{\mathit{N}}^{\mathit{f}}$	p	CPU
64	1	$1.1732\times {10}^{-3}$	–	2.58		$1.1732\times {10}^{-3}$	–	3.34
128		$6.9056\times {10}^{-4}$	0.7646	9.51		$6.9056\times {10}^{-4}$	0.7646	6.95
256		$4.1422\times {10}^{-4}$	0.7374	39.85		$4.1422\times {10}^{-4}$	0.7374	14.99
512		$2.3219\times {10}^{-4}$	0.8351	162.84		$2.3219\times {10}^{-4}$	0.8351	32.26
1024		$1.2514\times {10}^{-4}$	0.8917	638.56		$1.2514\times {10}^{-4}$	0.8917	67.66
EOC			1				1
64	$r=\frac{2}{2\alpha }$	$1.0150\times {10}^{-4}$	–	2.41		$1.0150\times {10}^{-4}$	–	4.68
128		$1.8584\times {10}^{-5}$	2.4493	9.61		$1.8584\times {10}^{-5}$	2.4493	9.97
256		$4.2737\times {10}^{-6}$	2.1205	39.23		$4.2737\times {10}^{-6}$	2.1205	22.57
512		$1.0898\times {10}^{-6}$	1.9715	157.12		$1.0898\times {10}^{-6}$	1.9715	48.61
1024		$2.7510\times {10}^{-7}$	1.9860	639.94		$2.7510\times {10}^{-7}$	1.9860	107.74
EOC			2				2
64	$r=\frac{3}{2\alpha }$	$8.3324\times {10}^{-6}$	–	2.44		$8.3324\times {10}^{-6}$	–	5.71
128		$8.1803\times {10}^{-7}$	3.3485	9.53		$8.1803\times {10}^{-7}$	3.3485	13.35
256		$9.6599\times {10}^{-8}$	3.0821	39.48		$9.6599\times {10}^{-8}$	3.0821	29.22
512		$1.2096\times {10}^{-8}$	2.9975	159.67		$1.2096\times {10}^{-8}$	2.9975	65.48
1024		$1.5129\times {10}^{-9}$	2.9991	580.18		$1.5129\times {10}^{-9}$	2.9991	128.07
EOC			3				3
64	$r=\frac{4}{2\alpha }$	$3.5974\times {10}^{-6}$	–	2.41		$3.5974\times {10}^{-6}$	–	6.95
128		$3.6817\times {10}^{-7}$	3.2885	8.71		$3.6817\times {10}^{-7}$	3.2885	15.04
256		$4.1714\times {10}^{-8}$	3.1418	35.14		$4.1714\times {10}^{-8}$	3.1418	33.36
512		$4.9751\times {10}^{-9}$	3.0677	142.50		$4.9751\times {10}^{-9}$	3.0677	73.69
1024		$6.0885\times {10}^{-10}$	3.0306	568.88		$6.0883\times {10}^{-10}$	3.0306	159.33
EOC			3				3

, we just display the maximal nodal errors, convergence orders, and CPU times in seconds of PCM and fPCM for Problem (35) with $\alpha =0.5$. “EOC” in each column of p denotes the expected order of convergence presented in (36). “CPU" denotes the total CPU time in seconds for used methods to solve (35). As one may infer from Table 1, both PCM and fPCM almost had the same maximal nodal errors and convergence orders because, as shown in (36), the influence of the SOE approximation error $ϵ$ could be negligible when it is chosen to be very small. In terms of CPU times, Figure 1 shows that fPCM took less time than PCM did, and this advantage is becoming more obvious with the increase in time steps N. When N was rather small compared to PCM, the fPCM was no longer efficient. Moreover, Figure 1 shows that the scales of PCM were like $O\left(N^2\right)$, but the scales of fPCM were just like $O\left(N\right)$.

Example 2.

Consider the following Benjamin–Bona–Mahony–Burgers equation:

$$\begin{array}{cc}\hfill & {}^C{D}_0^{\alpha }(u-u_{xx})+u{u}_x-u_{xx}=f(x,t)\mathit{for}(x,t)\in (0,1)\times (0,1],\hfill \end{array}$$

(37a)

$$\begin{array}{cc}\hfill & u(x,0)=sin\left(\pi x\right)\mathit{for}x\in [0,1],u(0,t)=u(1,t)=0\mathit{for}t\in (0,1],\hfill \end{array}$$

(37b)

the function f, the initial-boundary value conditions are determined by exact solution $u(x,t)=(1+t^{\alpha }+t^{2\alpha })sin\left(\pi x\right)$.

Similarly to (4), Equation (37) can be rewritten as the following integrodifferential equation.

$$\begin{array}{cc}\hfill u(x,t)-u_{xx}(x,t)& =Q\left(x\right)+\frac{1}{\mathsf{\Gamma }\left(\alpha \right)}{\int }_{s=0}^t{(t-s)}^{\alpha -1}F(x,s,u)ds\hfill \\ \hfill & \mathrm{for}(x,t)\in (0,1)\times (0,1],\hfill \end{array}$$

(38)

where

$$Q\left(x\right):=u(x,0)-u_{xx}(x,0)=(1+{\pi }^2)sin\left(\pi x\right),$$

$$F(x,t,u):=u_{xx}(x,t)-u(x,t)u_x(x,t)+f(x,t).$$

Let M be a positive integer. Set $h=(x_R-x_L)/M,x_i=x_L+ih$ for $0\le i\le M$. By applying the centered difference schemes ${\delta }_x^2{v}_i=\frac{v_{i+1}-2v_i+v_{i-1}}{h^2}$ and ${\mathsf{\Delta }}_x{v}_i=\frac{v_{i+1}-v_{i-1}}{2h}$ to numerically approximate $u_{xx}$ and $u_x$, respectively, we can obtain the corresponding PCM and fPCM for (37).

One can check that

$${}^C{D}_0^{\alpha }(u-u_{xx})(x,t)=\left[\mathsf{\Gamma }(\alpha +1)+\frac{2\alpha \mathsf{\Gamma }\left(2\alpha \right)}{\mathsf{\Gamma }(1+\alpha )}{t}^{\alpha }\right](1+{\pi }^2)sin\left(\pi x\right)$$

behaves as $C(1+t^{\alpha })$. For $0\le n\le N,0\le i\le M$, set $e_i^n=u(x_i,t_n)-u_i^n,{\overline{e}}_i^n=u(x_i,t_n)-{\overline{u}}_i^n$, where $u_i^n$ and ${\overline{u}}_i^n$ are the predictor–corrector method solution and the fast predictor–corrector method solution of (37). Set $e^n={\left(e_1^n,e_2^n,\dots ,e_{M-1}^n\right)}^T$ and ${\overline{e}}^n={\left({\overline{e}}_1^n,{\overline{e}}_2^n,\dots ,{\overline{e}}_{M-1}^n\right)}^T$. Similarly to [22], we use discrete $H^1$ norm to calculate the errors. Let $E(M,N):={max}_{0\le j\le N}{\parallel e^j\parallel }_{H^1}$ and $E{(M,N)}^f:={max}_{0\le j\le N}{\parallel {\overline{e}}^j\parallel }_{H^1}$. Then, one has

$$E(M,N)\le C(N^{-min\left\{2r\alpha ,3\right\}}+h^2)\mathrm{and}E{(M,N)}^f\le C(N^{-min\left\{2r\alpha ,3\right\}}+h^2+ϵ)$$

(39)

for PCM and fPCM, respectively.

The numerical results are given in

Table 2. Maximal nodal errors and convergence orders of PCM and fPCM for Problem (37) with $r=3/\left(2\alpha \right)$ and $M=8000$.

		$\mathit{\alpha }=0.4$			$\mathit{\alpha }=0.6$			$\mathit{\alpha }=0.8$
Scheme	N	${\mathit{E}}_{\mathit{M},\mathit{N}}$	${\mathit{p}}_{\mathit{t}}$		${\mathit{E}}_{\mathit{M},\mathit{N}}$	${\mathit{p}}_{\mathit{t}}$		${\mathit{E}}_{\mathit{M},\mathit{N}}$	${\mathit{p}}_{\mathit{t}}$
PCM	12	$6.4472\times {10}^{-2}$	–		$3.8631\times {10}^{-3}$	–		$4.8683\times {10}^{-4}$	–
	24	$3.1108\times {10}^{-3}$	4.3733		$2.5987\times {10}^{-4}$	3.8939		$4.4781\times {10}^{-5}$	3.4425
	48	$1.7218\times {10}^{-4}$	4.1753		$2.2876\times {10}^{-5}$	3.5058		$5.7787\times {10}^{-6}$	2.9541
	96	$1.1986\times {10}^{-5}$	3.8445		$2.4634\times {10}^{-6}$	3.2151		$7.9723\times {10}^{-7}$	2.8577
EOC			3			3			3
fPCM	12	$6.4472\times {10}^{-2}$	–		$3.8631\times {10}^{-3}$	–		$4.8683\times {10}^{-4}$	–
	24	$3.1108\times {10}^{-3}$	4.3733		$2.5987\times {10}^{-4}$	3.8939		$4.4781\times {10}^{-5}$	3.4425
	48	$1.7218\times {10}^{-4}$	4.1753		$2.2876\times {10}^{-5}$	3.5058		$5.7787\times {10}^{-6}$	2.9541
	96	$1.1986\times {10}^{-5}$	3.8445		$2.4634\times {10}^{-6}$	3.2151		$7.9723\times {10}^{-7}$	2.8577
EOC			3			3			3

and

Table 3. Maximal nodal errors, convergence orders, and CPU times of PCM and fPCM for Problem (37) with $\alpha =0.8$, $r=3/\left(2\alpha \right)$ and $N=2000$.

	PCM				fPCM
M	$\mathit{E}(\mathit{M},\mathit{N})$	${\mathit{p}}_{\mathit{x}}$	CPU		$\mathit{E}{(\mathit{M},\mathit{N})}^{\mathit{f}}$	${\mathit{p}}_{\mathit{x}}$	CPU
8	$8.9024\times {10}^{-2}$	1.9377	2141.30		$8.9024\times {10}^{-2}$	1.9377	134.57
16	$2.2690\times {10}^{-2}$	1.9722	2131.37		$2.2690\times {10}^{-2}$	1.9722	133.85
32	$5.7260\times {10}^{-3}$	1.9864	2164.59		$5.7260\times {10}^{-3}$	1.9864	132.92
64	$1.4382\times {10}^{-3}$	1.9932	2158.93		$1.4382\times {10}^{-3}$	1.9933	137.41
EOC		2				2

, where the convergence orders in time and space are calculated with

$$p_t:={log}_2\left(\frac{E_{M,N}}{E_{M,2N}}\right),p_x:={log}_2\left(\frac{E_{M,N}}{E_{2M,N}}\right),$$

respectively, and $E_{M,N}$ can be $E(M,N)$ or $E{(M,N)}^f$. In the fPCM, we set $ϵ={10}^{-8}$. Table 2 and Table 3 show that PCM and fPCM almost had the same accuracy. In terms of CPU time, Table 3 and Figure 2 show that the fPCM offered no advantage when N was small, but when N was larger, the advantage of fPCM was obvious.

6. Concluding Remarks

A fast high-order predictor–corrector method was constructed for solving fractional differential equations. Graded meshes were used for time discretization to deal with the weak singularity of the solution near the initial time. Several numerical examples were presented to support our theoretical analysis. Since the predictor–corrector method failed to solve the stiff problem (see [6], Section 5), our fast high-order predictor–corrector method also had the same property. In future work, we will try to construct implicit–explicit methods by using the technique of our predictor–corrector method to solve the stiff fractional differential equations or time-fractional partial differential equations.