Switching-Jumps-Dependent Quasi-Synchronization Criteria for Fractional-Order Memrisive Neural Networks
Abstract
:1. Introduction
2. Preliminaries and Model Description
3. Main Results
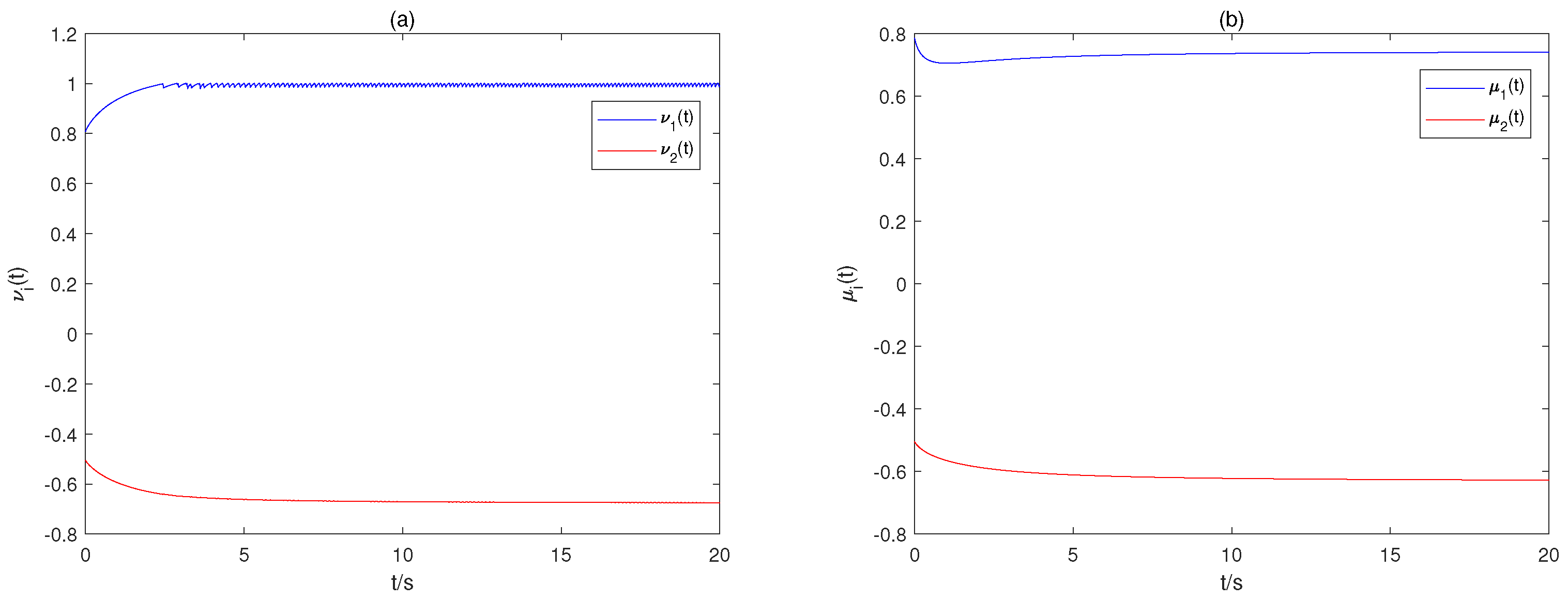
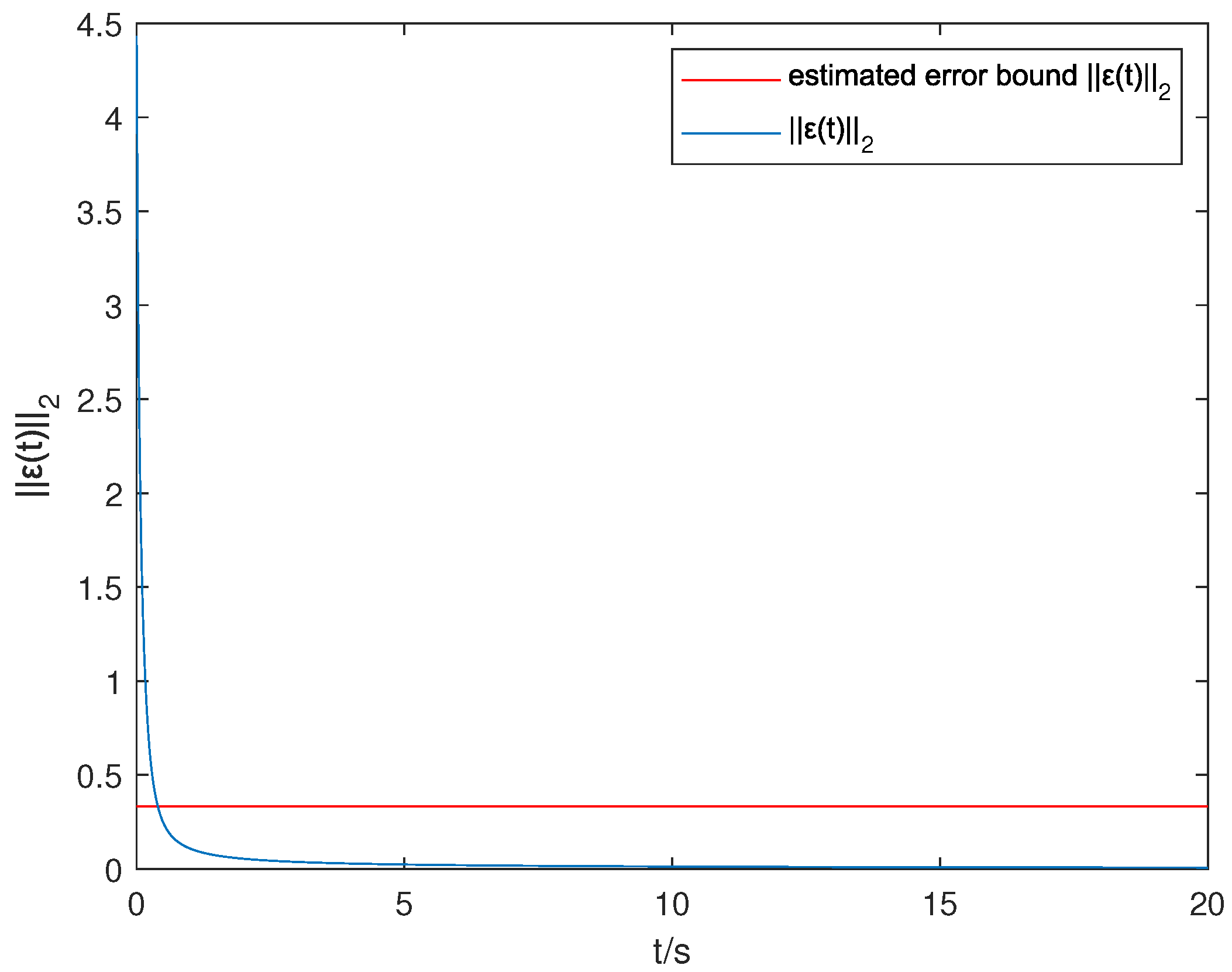
4. Numerical Examples
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ASTI | asynchronous switching time interval |
| FMNNs | fractional-order memristive neural networks |
| SSTI | asynchronous switching time interval |
| LMI | linear matrix inequality |
References
- Xu, X.; Tan, M.; Corcoran, B.; Wu, J.; Boes, A.; Nguyen, T.G.; Chu, S.T.; Little, B.E.; Hicks, D.G.; Morotti, R.; et al. 11 TOPS photonic convolutional accelerator for optical neural networks. Nature 2021, 589, 44–51. [Google Scholar] [CrossRef]
- Xu, X.; Cao, D.; Zhou, Y.; Gao, J. Application of neural network algorithm in fault diagnosis of mechanical intelligence. Mech. Syst. Signal Process. 2020, 141, 106625. [Google Scholar] [CrossRef]
- Yao, Q.; Wang, R.; Fan, X.; Liu, J.; Li, Y. Multi-class arrhythmia detection from 12-lead varied-length ECG using attention-based time-incremental convolutional neural network. Inf. Fusion 2020, 53, 174–182. [Google Scholar] [CrossRef]
- Wang, M.; Yan, Z.; Wang, T.; Cai, P.; Gao, S.; Zeng, Y.; Wan, C.; Wang, H.; Pan, L.; Yu, J.; et al. Gesture recognition using a bioinspired learning architecture that integrates visual data with somatosensory data from stretchable sensors. Nat. Electron. 2020, 3, 563–570. [Google Scholar] [CrossRef]
- Raissi, M.; Yazdani, A.; Karniadakis, G.E. Hidden fluid mechanics: Learning velocity and pressure fields from flow visualizations. Science 2020, 367, 1026–1030. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Xue, B.; Zhang, M.; Yen, G.G. Evolving deep convolutional neural networks for image classification. IEEE Trans. Evol. Comput. 2020, 24, 394–407. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Wang, J.; Han, Q. Multivehicle task assignment based on collaborative neurodynamic optimization with discrete hopfield networks. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 5274–5286. [Google Scholar] [CrossRef]
- Kim, B.; Lee, S.; Kim, J. Inverse design of porous materials using artificial neural networks. Sci. Adv. 2020, 6, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Cao, B.; Zhao, J.; Lv, Z.; Gu, Y.; Yang, P.; Halgamuge, S.K. Multiobjective evolution of fuzzy rough neural network via distributed parallelism for stock prediction. IEEE Trans. Fuzzy Syst. 2020, 28, 939–952. [Google Scholar] [CrossRef]
- Zhang, X.; Zhuo, Y.; Luo, Q.; Wu, Z.; Midya, R.; Wang, Z.; Song, W.; Wang, R.; Upadhyay, N.K.; Fang, Y.; et al. An artificial spiking afferent nerve based on Mott memristors for neurorobotics. Nat. Commun. 2020, 11, 51. [Google Scholar] [CrossRef] [PubMed]
- Si, X.; Wang, Z.; Song, Z.; Zhang, Z. Asymptotic Stabilization of Delayed Linear Fractional-Order Systems Subject to State and Control Constraints. Fractal Fract. 2022, 6, 67. [Google Scholar] [CrossRef]
- Yousefpour, A.; Jahanshahi, H.; Munoz-Pacheco, J.M.; Bekiros, S.; Wei, Z. A fractional-order hyper-chaotic economic system with transient chaos. Chaos Solitons Fractals 2020, 130, 109400. [Google Scholar] [CrossRef]
- Tuan, L.A. Neural observer and adaptive fractional-order back-stepping fast terminal sliding mode control of RTG cranes. IEEE Trans. Ind. Electron. 2021, 68, 434–442. [Google Scholar] [CrossRef]
- Chua, L. Memristor-The missing circuit element. IEEE Trans. Circuit Theory 1971, 18, 507–519. [Google Scholar] [CrossRef]
- Strukov, D.B.; Snider, G.S.; Stewart, D.R.; Williams, R.S. The missing memristor found. Nature 2008, 453, 80–83. [Google Scholar] [CrossRef]
- Chen, C.; Zhu, S.; Wei, Y.; Chen, C. Finite-Time stability of delayed memristor-based fractional-order neural networks. IEEE Trans. Cybern. 2020, 50, 1607–1616. [Google Scholar] [CrossRef]
- Chen, L.; Huang, T.; Machado, J.; Lopes, M.; Chai, Y.; Wu, R. Delay-dependent criterion for asymptotic stability of a class of fractional-order memristive neural networks with time-varying delays. Neural Netw. 2019, 118, 289–299. [Google Scholar] [CrossRef]
- Song, C.; Cao, J.; Abdel-Aty, M. New Results on Robust Synchronization for Memristive Neural Networks with Fractional Derivatives via Linear Matrix Inequality. Fractal Fract. 2022, 6, 585. [Google Scholar] [CrossRef]
- Chen, J.; Chen, B.; Zeng, Z. Global asymptotic stability and adaptive ultimate Mittag-Leffler synchronization for a fractional-order complex-valued memristive neural networks with delays. IEEE Trans. Syst. Man Cybern. Syst. 2019, 49, 2519–2535. [Google Scholar] [CrossRef]
- Jia, J.; Zeng, Z.; Wang, F. Pinning synchronization of fractional-order memristor-based neural networks with multiple time-varying delays via static or dynamic coupling. J. Frankl. Inst. 2021, 358, 895–933. [Google Scholar] [CrossRef]
- Ali, M.S.; Hymavathi, M.; Senan, S.; Shekher, V.; Arik, S. Global asymptotic synchronization of impulsive fractional-order complex-valued memristor-based neural networks with time varying delays. Commun. Nonlinear Sci. Numer. Simul. 2019, 78, 104869. [Google Scholar]
- Gu, Y.; Yu, Y.; Wang, H. Projective synchronization for fractional-order memristor-based neural networks with time delays. Neural Comput. Appl. 2019, 31, 6039–6054. [Google Scholar] [CrossRef]
- Xiong, P.; Jahanshahi, H.; Alcaraz, R.; Chu, Y.; Gómez-Aguilar, J.F.; Alsaadi, F.E. Spectral entropy analysis and synchronization of a multi-stable fractional-order chaotic system using a novel neural network-based chattering-free sliding mode technique. Chaos Solitons Fractals 2021, 144, 110576. [Google Scholar] [CrossRef]
- Fan, Y.; Huang, X.; Wang, Z.; Li, Y. Global dissipativity and quasi-synchronization of asynchronous updating fractional-order memristor-based neural networks via interval matrix method. J. Frankl. Inst. 2018, 355, 5998–6025. [Google Scholar] [CrossRef]
- Liu, S.; Yu, Y.; Zhang, S. Robust synchronization of memristor-based fractional-order Hopfield neural networks with parameter uncertainties. Neural Comput. Appl. 2019, 31, 3533–3542. [Google Scholar] [CrossRef]
- Wu, A.; Zeng, Z. Global Mittag-Leffler stabilization of fractional-order memristive neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 206–217. [Google Scholar] [CrossRef] [PubMed]
- Bao, H.; Park, J.H.; Cao, J. Adaptive synchronization of fractional-order memristor-based neural networks with time delay. Nonlinear Dyn. 2015, 82, 1343–1354. [Google Scholar] [CrossRef]
- Chen, L.; Cao, J.; Wu, R.; Machado, J.T.; Lopes, A.M.; Yang, H. Stability and synchro- nization of fractional-order memristive neural networks with multiple delays. Neural Netw. 2017, 94, 76–85. [Google Scholar] [CrossRef]
- Zhang, L.; Yang, Y. Lag synchronization for fractional-order memristive neural networks via period intermittent control. Nonlinear Dyn. 2017, 89, 367–381. [Google Scholar] [CrossRef]
- Huang, T.; Li, C.; Yu, W.; Chen, G. Synchronization of delayed chaotic systems with parameter mismatches by using intermittent linear state feedback. Nonlinearity 2009, 22, 569–584. [Google Scholar] [CrossRef]
- Filippov, A.F. Differential Equations with Discontinuous Righthand Sides; Kluwer Academic Publishers: Boston, MA, USA, 1988. [Google Scholar]
- Henderson, J.; Ouahab, A. Fractional functional differential inclusions with finite delay. Nonlinear Anal. 2009, 70, 2091–2105. [Google Scholar] [CrossRef]
- Aubin, J.P.; Cellina, A. Differential Inclusions: Set-Valued Maps and Viability Theory; Springer: Berlin, Germany, 1984. [Google Scholar]
- Shen, J.; Lam, J. Non-existence of finite-time stable equilibria in fractional-order nonlinear systems. Automatica 2014, 50, 547–551. [Google Scholar] [CrossRef]
- Fan, Y.; Huang, X.; Wang, Z. Local Stabilization of Delayed Fractional-Order Neural Networks Subject to Actuator Saturation. Fractal Fract. 2022, 6, 451. [Google Scholar] [CrossRef]
- Zhang, S.; Yu, Y.; Wang, H. Mittag-Leffler stability of fractional-order Hopfield neural networks. Nonlinear Anal. Hybrid Syst. 2015, 16, 104–121. [Google Scholar] [CrossRef]
- Duarte-Mermoud, M.A.; Aguila-Camacho, N.; Gallegos, J.A.; Castro-Linares, R. Using general quadratic Lyapunov functions to prove Lyapunov uniform stability for fractional order systems. Commun. Nonlinear Sci. Numer. Simul. 2015, 22, 650–659. [Google Scholar] [CrossRef]
- Clarke, F.H.; Ledyaev, Y.S.; Stern, R.J.; Wolenski, P.R. Nonsmooth Analysis and Control Theory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Wang, D.; Xiao, A.; Liu, H. Dissipativity and stability analysis for fractional functional differential equations. Fract. Calc. Appl. Anal. 2015, 18, 1399–1422. [Google Scholar] [CrossRef]



| Notation | Description |
|---|---|
| the maximum eigenvalue of matrix Q | |
| transpose (or inverse) of matrix Q | |
| * | the symmetric element |
| Q is a positive | |
| (or | definite (or semi-definite) matrix |
| diag(…) | a block diagonal matrix |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, Y.; Wei, Z.; Li, M. Switching-Jumps-Dependent Quasi-Synchronization Criteria for Fractional-Order Memrisive Neural Networks. Fractal Fract. 2023, 7, 12. https://doi.org/10.3390/fractalfract7010012
Fan Y, Wei Z, Li M. Switching-Jumps-Dependent Quasi-Synchronization Criteria for Fractional-Order Memrisive Neural Networks. Fractal and Fractional. 2023; 7(1):12. https://doi.org/10.3390/fractalfract7010012
Chicago/Turabian StyleFan, Yingjie, Zhongliang Wei, and Meixuan Li. 2023. "Switching-Jumps-Dependent Quasi-Synchronization Criteria for Fractional-Order Memrisive Neural Networks" Fractal and Fractional 7, no. 1: 12. https://doi.org/10.3390/fractalfract7010012





