High-Tracking-Precision Sensorless Control of PMSM System Based on Fractional Order Model Reference Adaptation
Abstract
:1. Introduction
2. Fractional-Order Calculus Fundamentals
2.1. Mathematical Model of FOPMSM
2.2. Miscellaneous Concepts
- (1)
- Feed-forward gain of the system must be real-positive. In other words, the transfer function of the feed-forward linear time invariant block must be strictly positive real.
- (2)
- The error should converge asymptotically, i.e., the nonlinear time varying block satisfies Popov’s integral inequality:
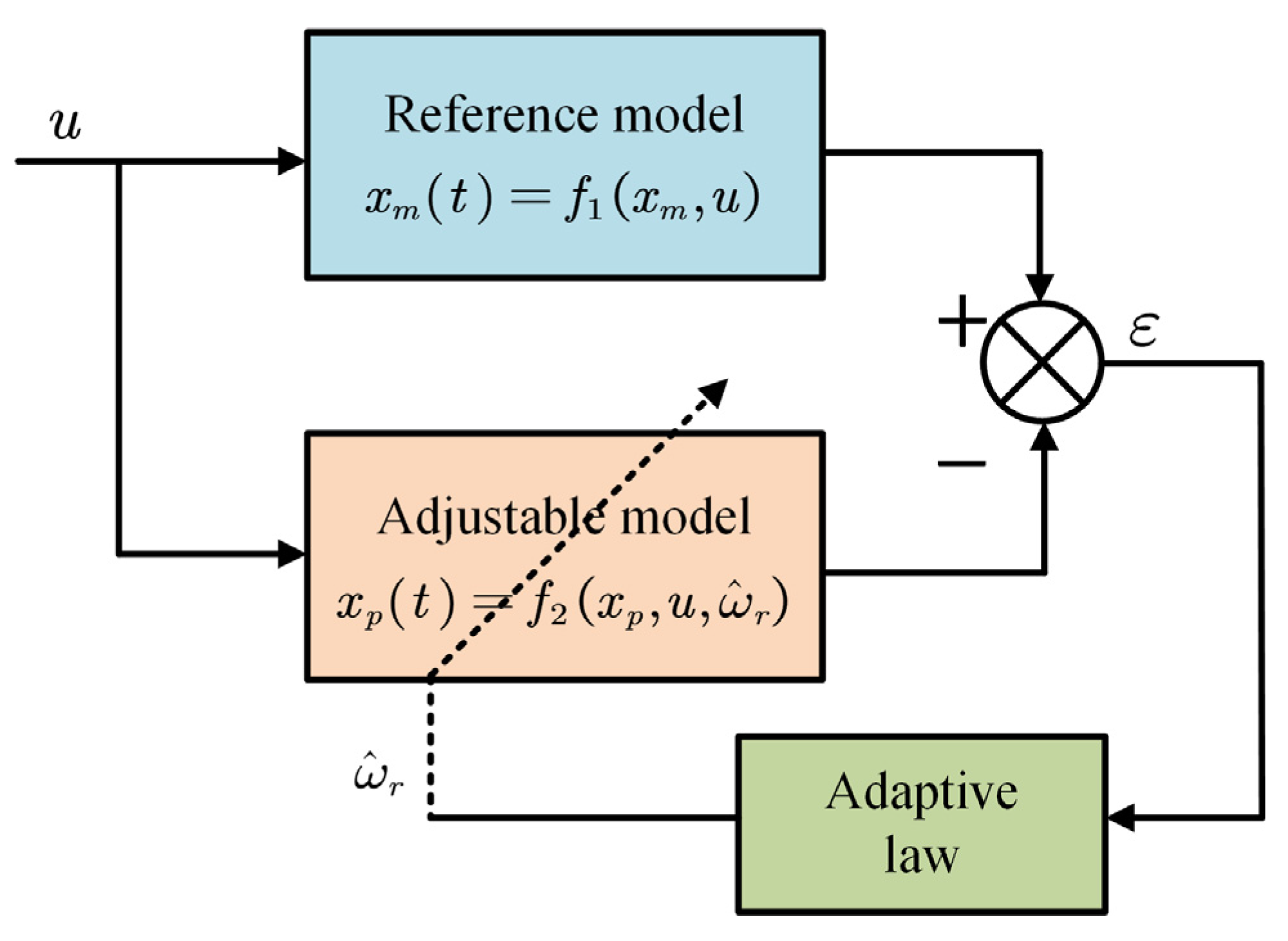
3. Speed-Estimation-Based MRAO
3.1. Design of the MRAO
3.2. Adaptation Mechanism
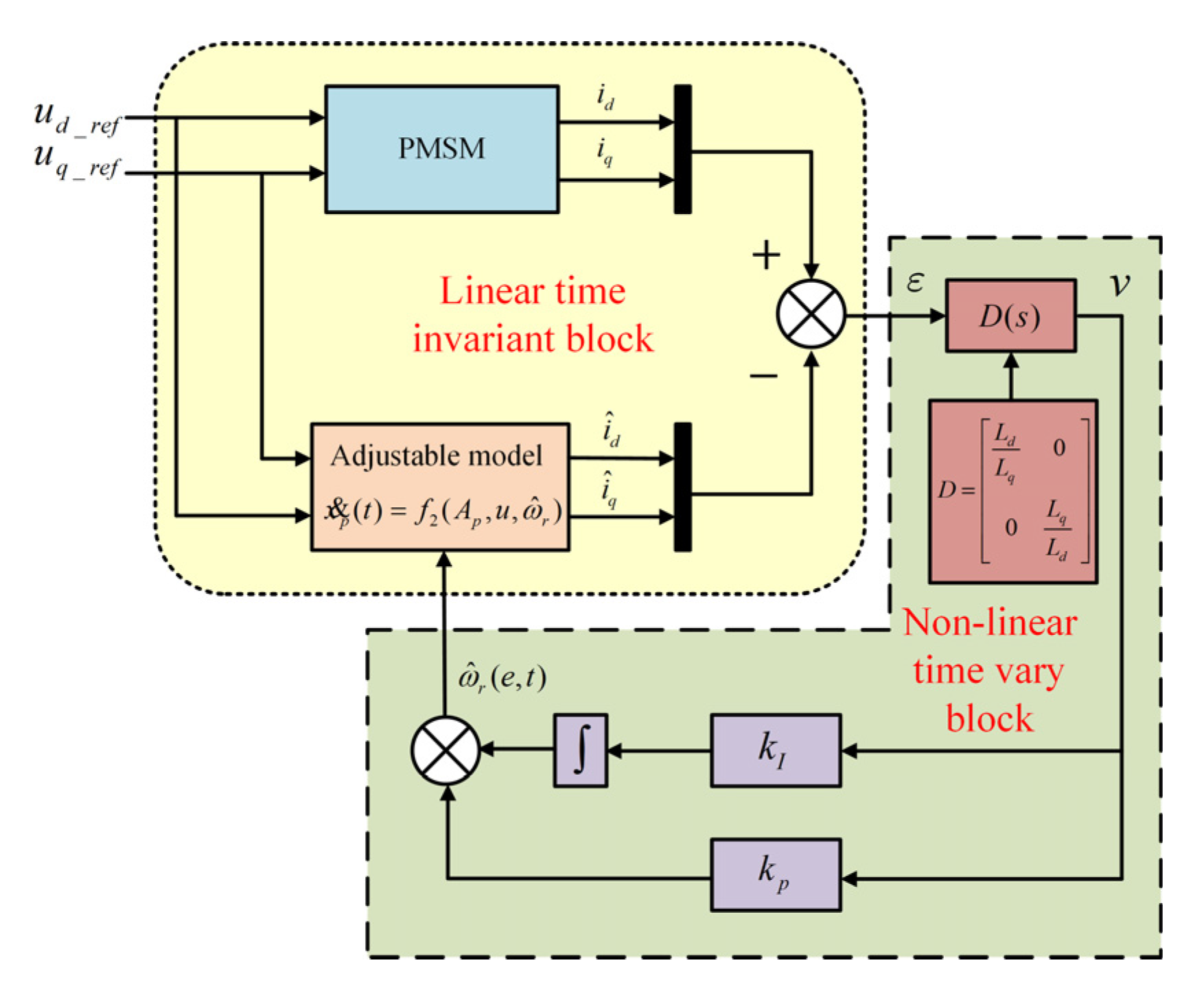
4. Design of the FOMRAC
4.1. Convergence Analysis
4.2. Controller Stabilization
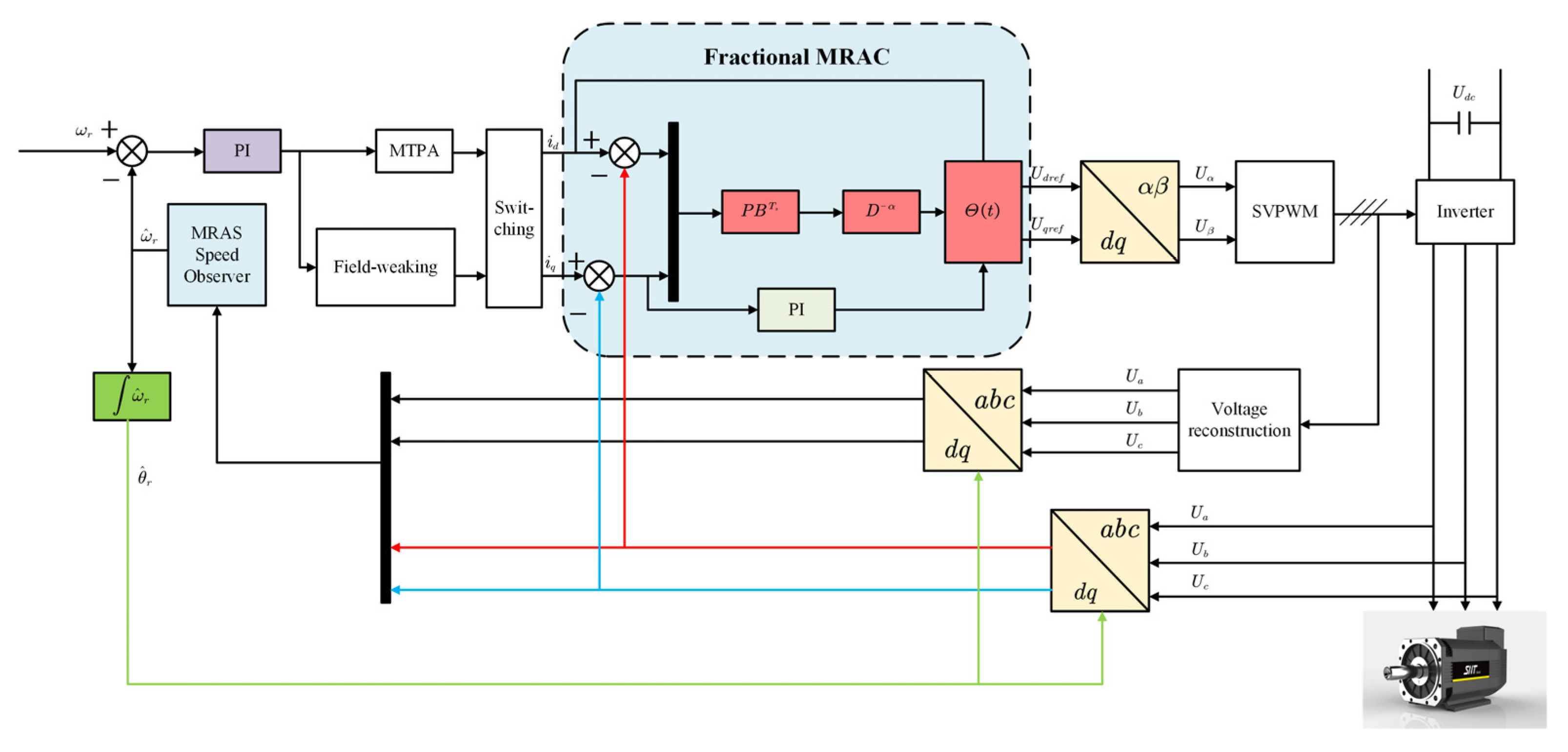
5. Simulation
5.1. Control Analysis in Order α = 1
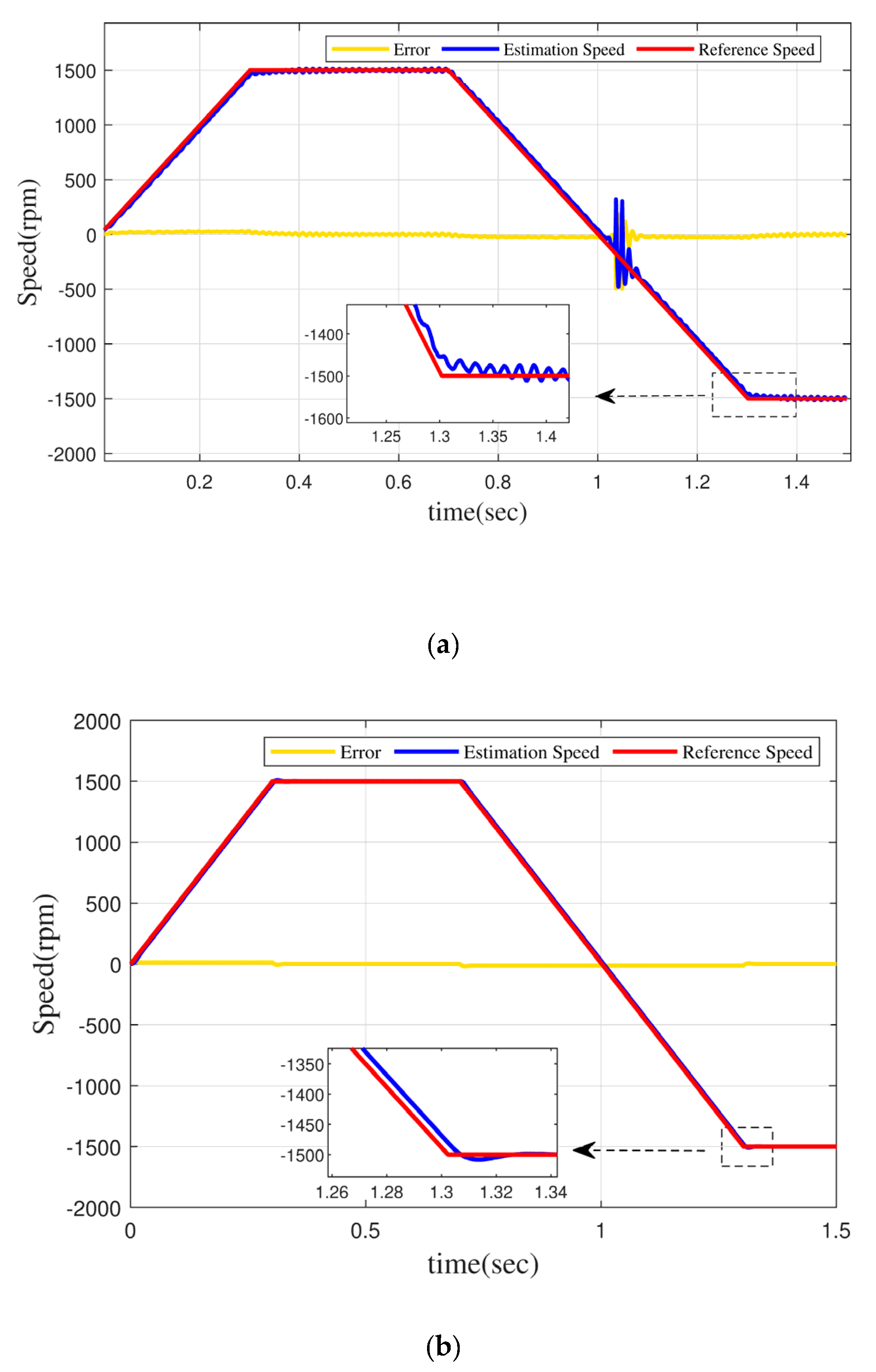
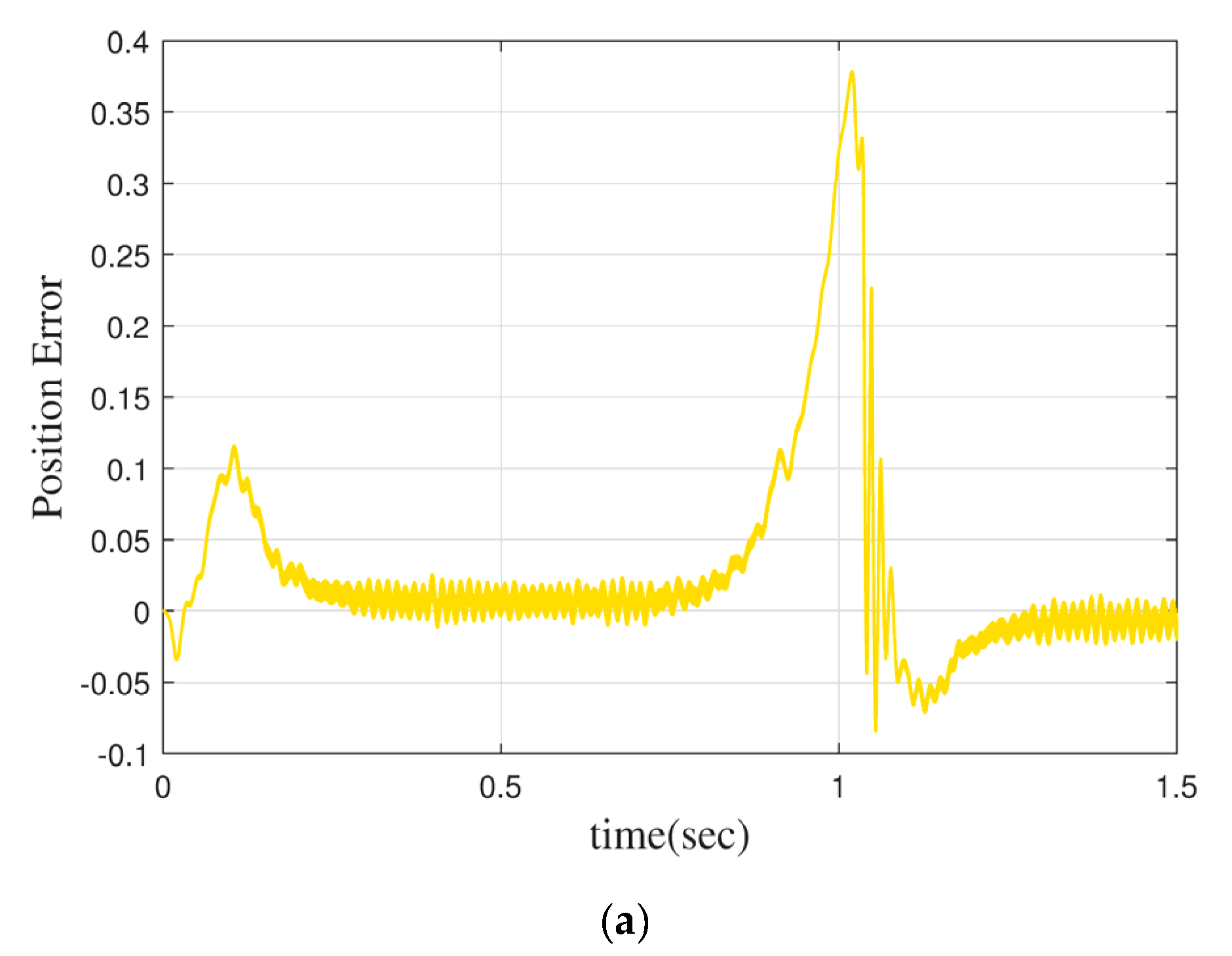
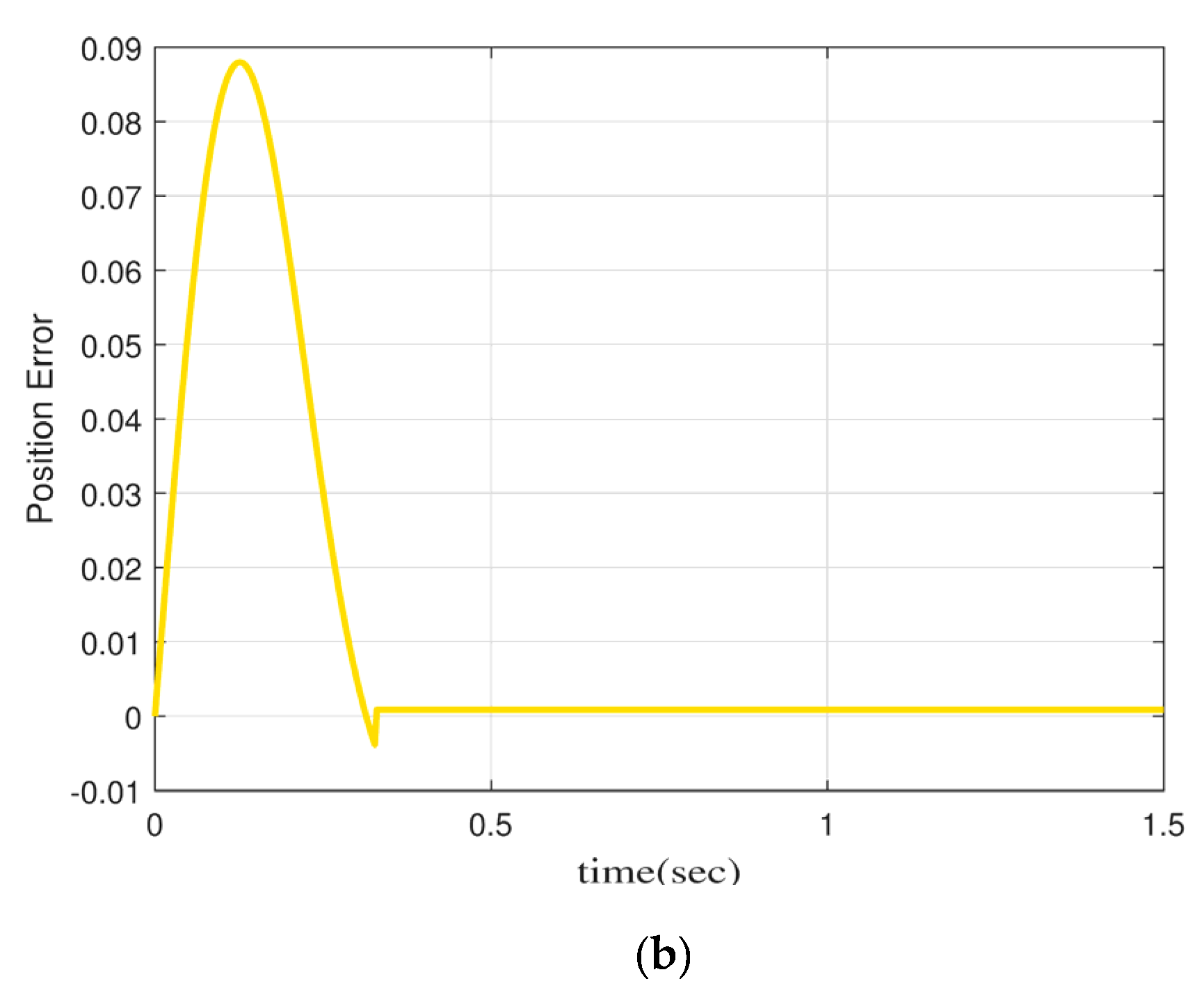
5.1.1. Dynamic Performance
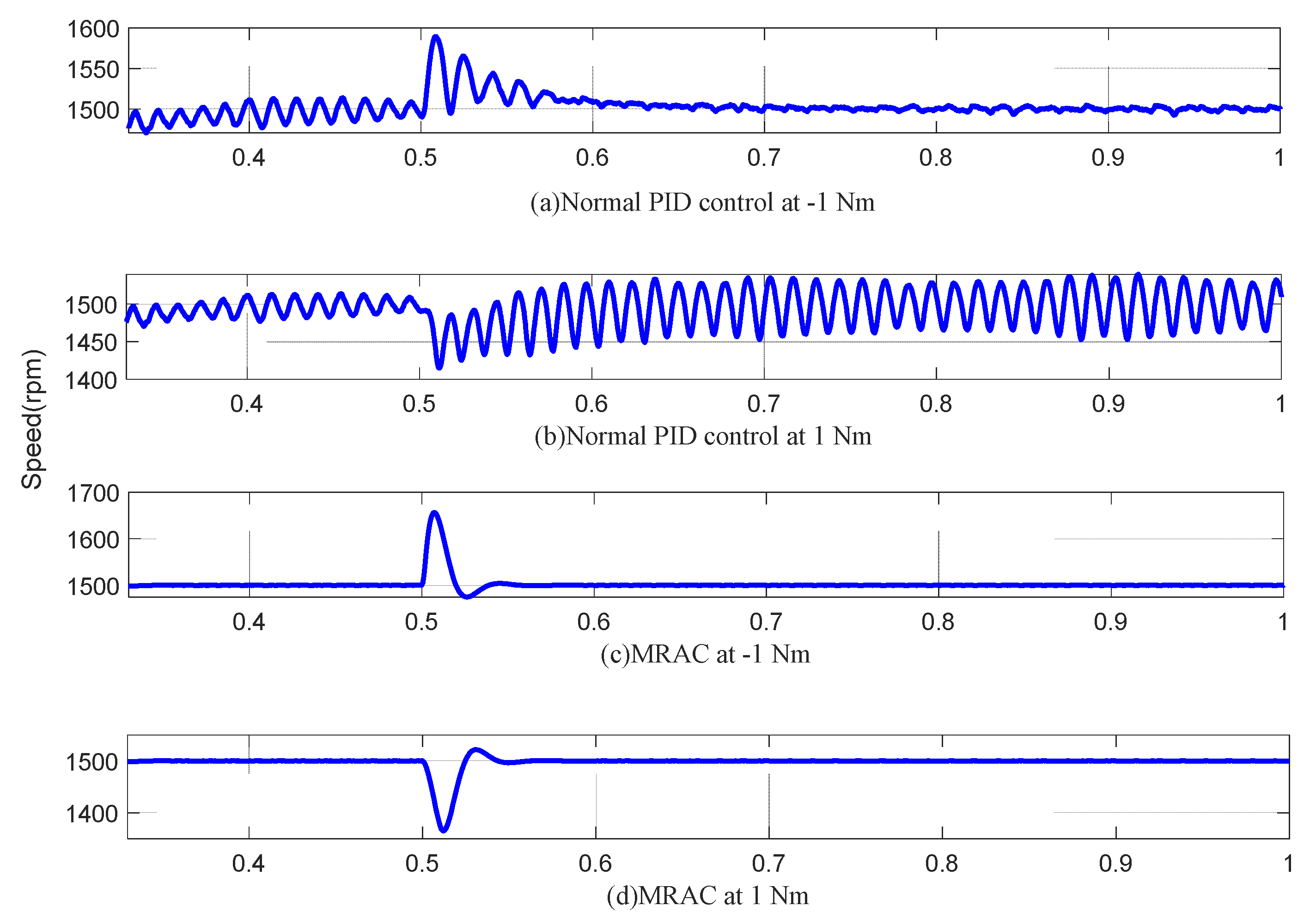
5.1.2. Steady-State Performance
5.1.3. Low-Speed Performance
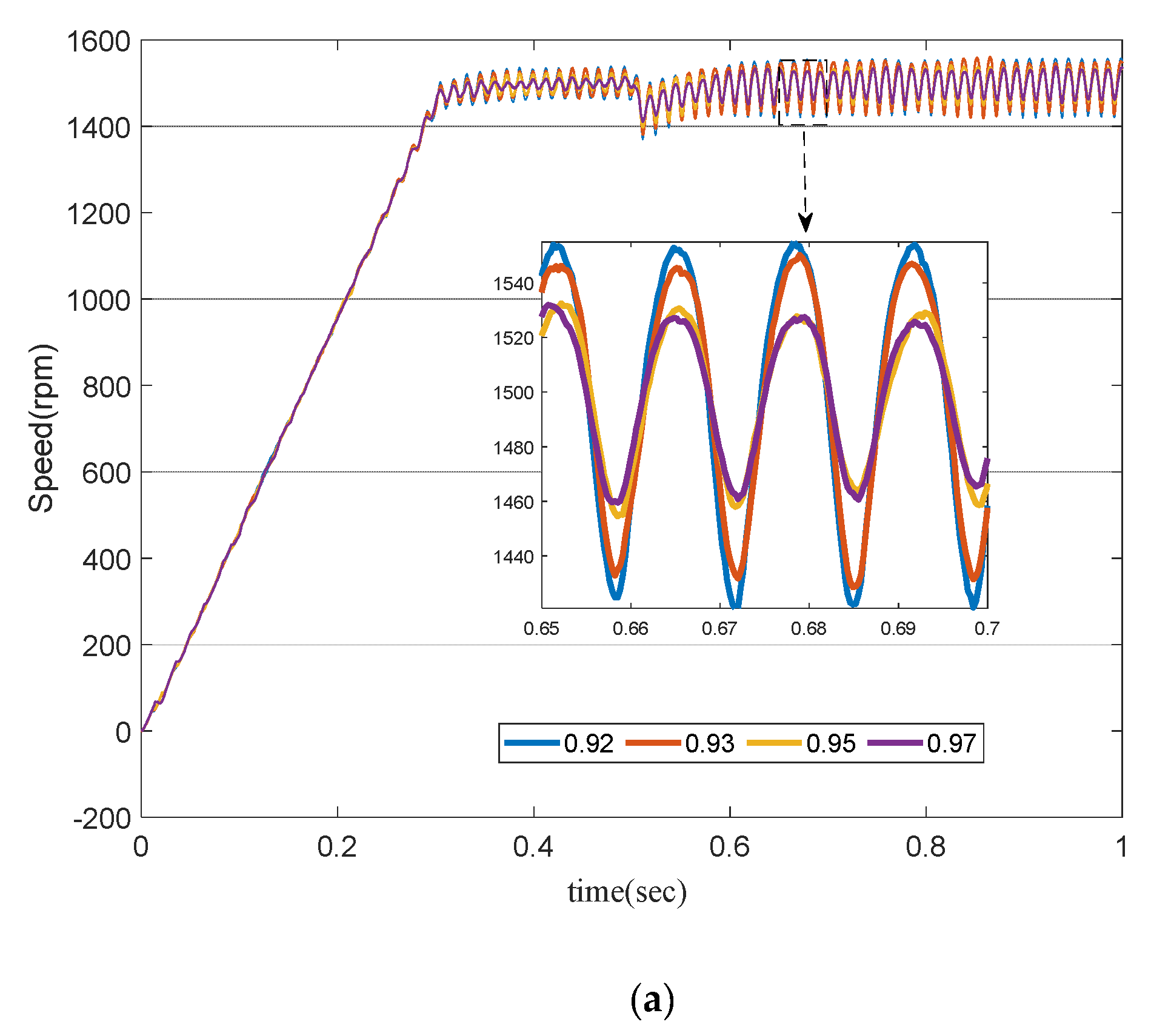
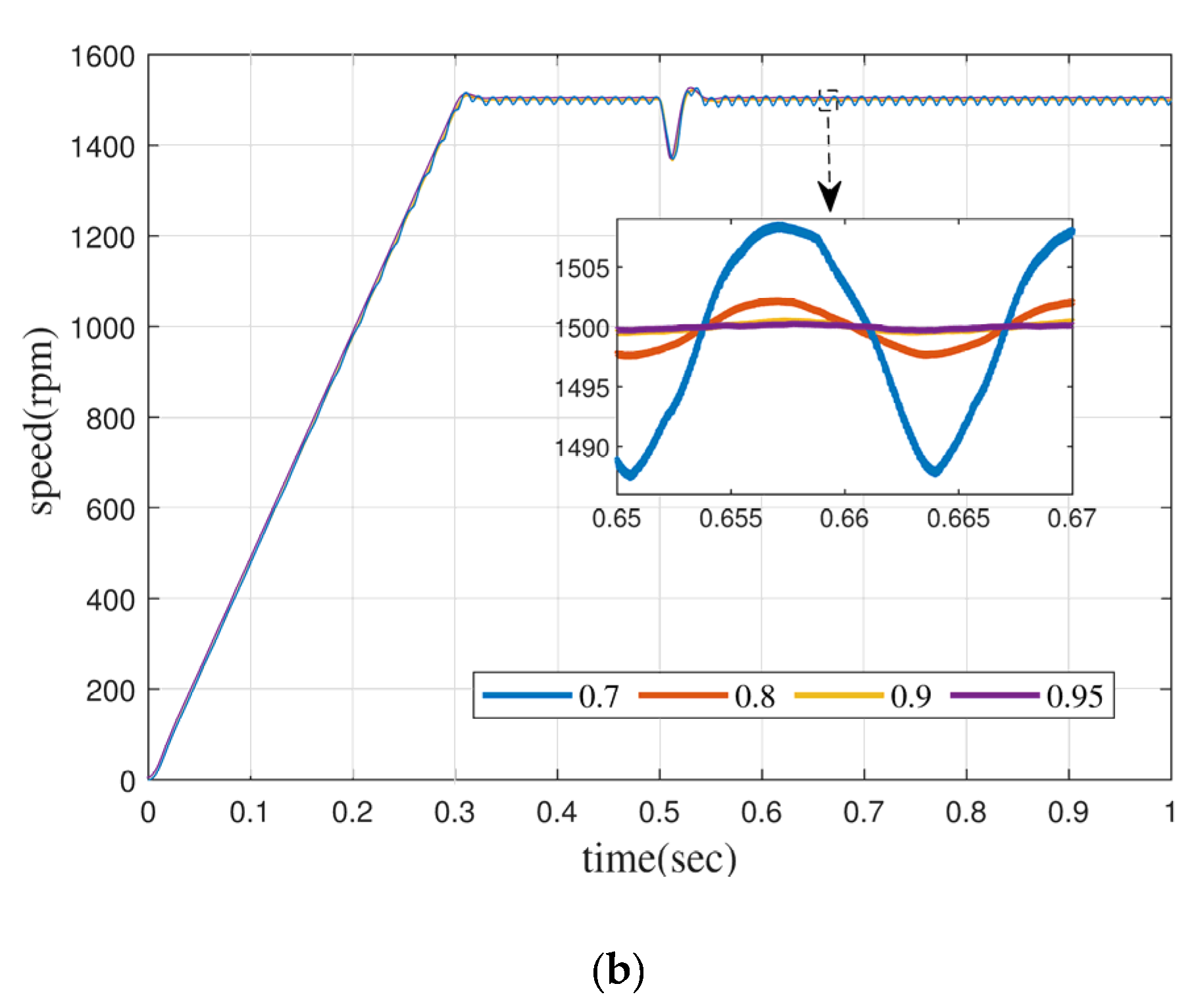
5.2. Control Analysis in Fractional Order
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Dai, C.; Guo, T.; Yang, J.; Li, S. A disturbance observer-based current-constrained controller for speed regulation of PMSM systems subject to unmatched disturbances. IEEE Trans. Ind. Electron. 2021, 68, 767–775. [Google Scholar] [CrossRef]
- Dong-Woo, S.; Bak, Y.; Lee, K. An improved rotating restart method for a sensorless permanent-magnet synchronous motor drive system using repetitive zero voltage vectors. IEEE Trans. Ind. Electron. 2020, 67, 3496–3504. [Google Scholar]
- Li, L.; Pei, G.; Liu, J.; Du, P.; Pei, L.; Zhong, C. 2-DOF robust h∞ control for permanent-magnet synchronous motor with disturbance observer. IEEE Trans. Power Electron. 2021, 36, 3462–3472. [Google Scholar] [CrossRef]
- Yeam, T.; Lee, D.C. Design of sliding-mode speed controller with active damping control for single-inverter dual-PMSM drive systems. IEEE Trans. Power Electron. 2021, 36, 5794–5801. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Y.; Wang, C.; Su, C.Y.; Li, Z.; Chen, X. Adaptive estimated inverse output-feedback quantized control for piezoelectric positioning stage. IEEE Trans. Cybern. 2019, 49, 2106–2118. [Google Scholar] [CrossRef] [PubMed]
- El-Sousy, F.F.M.; Amin, M.M.; Aziz, G.A.A.; Al-Durra, A. Adaptive neural-network optimal tracking control for permanent-magnet synchronous motor drive system via adaptive dynamic programming. In Proceedings of the 2020 IEEE Industry Applications Society Annual Meeting, Detroit, MI, USA, 10–16 October 2020; pp. 1–8. [Google Scholar]
- Deng, W.; Xu, J.; Zhao, H.; Song, Y. A novel gate resource allocation method using improved PSO-based QEA. IEEE Trans. Intell. Transp. Syst. 2022, 23, 1737–1745. [Google Scholar] [CrossRef]
- Chen, Y. Impulse Response Invariant Discretization of Frac-Tional Order Integrators/Differentiators, Filter Design and Analysis, MA TLAB Central. Available online: https://www.mathworks.com/matlabcentral/fileexchange/21342-impulse-response-invariant-discretization-of-fractionalorder-integrators-differentiators (accessed on 24 March 2012).
- Luo, Y.; Zhang, T.; Lee, B.; Kang, C.; Chen, Y. Fractional order proportional derivative controller synthesis and implementation for hard-disk-drive servo system. IEEE Trans. Control Syst. Technol. 2014, 22, 281–289. [Google Scholar] [CrossRef] [Green Version]
- Zeng, G.Q.; Chen, J.; Dai, Y.X.; Li, L.M.; Zheng, C.W.; Chen, M.R. Design of fractional order PID controller for automatic regulator voltage system based on multi-objective extremal optimization. Neurocomputing 2015, 160, 173–184. [Google Scholar] [CrossRef]
- Zhang, B.T.; Pi, Y.G.; Luo, Y. Fractional order sliding-mode control based on parameters auto-tuning for velocity control of permanent-magnet synchronous motor. ISA Trans. 2012, 51, 649–656. [Google Scholar] [CrossRef]
- Mujumdar, A.; Tamhane, B.; Kurode, S. Observer-based sliding-mode control for a class of noncommensurate fractional order systems. IEEE/ASME Trans. Mechatr. 2015, 20, 2504–2512. [Google Scholar] [CrossRef]
- Singh, S.; Tiwari, A.N.; Singh, S.N. Performance evaluation of MRAS and SMO based sensorless PMSM drives. World J. Eng. 2020, 17, 347–355. [Google Scholar] [CrossRef]
- Suman, M.; Chandan, C.; Sabyasachi, S. Simulation studies on model reference adaptive controller based speed estimation technique for the vector controlled permanent-magnet synchronous motor drive. Simul. Model. Pract. Theory 2009, 17, 4. [Google Scholar]
- He, Y.; Wang, J.; Wang, Z.; Wang, H.; Wang, Q.; Wei, D.; Zeng, Z. Speed observation for high-speed permanent-magnet synchronous motor with model reference adaptive system. Electr. Drive 2020, 50, 16–22. [Google Scholar]
- Wu, G.; Xiao, X. Speed controller of servo system based on MRAS method. In Proceedings of the IEEE International Conference on Industrial Technology, Churchill, Australia, 10–13 February 2009; pp. 1–5. [Google Scholar]
- Ayten, K.K. Real-Time Speed Control of an Electrically Powered Wheelchair by Using Fractional Order Model Reference Adaptive System Control. Elektron. Ir Elektrotechnika 2018, 24, 24–35. [Google Scholar] [CrossRef] [Green Version]
- Duarte-Mermoud, A.M.; Aguila-Camacho, N. Some Useful Results in Fractional Adaptive Control. In Proceedings of the Sixteenth Yale Workshop on Adaptive and Learning Systems, New Haven, CT, USA, 5–7 June 2013; pp. 51–56. [Google Scholar]
- Vinagre, B.M.; Petrás, I.; Podlubny, I.; Chen, Y. Using fractional order adjustment rules and fractional order reference models in model-reference adaptive control. Nonlinear Dyn. 2002, 29, 269–279. [Google Scholar] [CrossRef]
- Nain, A.; Vats, R.; Kumar, A. Coupled fractional differential equations involving Caputo-Hadamard derivative with nonlocal boundary conditions. Math. Methods Appl. Sci. 2021, 44, 4192–4204. [Google Scholar] [CrossRef]
- Bin, D.; Yiheng, W.; Shu, L.; Yong, W. Estimation of exact initial states of fractional order systems. Nonlinear Dyn. 2016, 86, 2061–2070. [Google Scholar]
- Shi, B.; Yuan, J.; Dong, C. On fractional model reference adaptive control. Sci. World J. 2014, 9. [Google Scholar] [CrossRef]
- Singh, A.; Shukla, A.; Vijayakumar, V.; Udhayakumar, R. Asymptotic stability of fractional order (1, 2] stochastic delay differential equations in Banach spaces. Chaos Solit. Fract. 2021, 150. [Google Scholar] [CrossRef]
- Damaren, C.J. Optimal strictly positive real controllers using direct optimization. J. Frankl. Inst. 2006, 343. [Google Scholar] [CrossRef]
- Larbi, M.; Roufaida, A.; Nawal, A.A.M. Sensorless control of PMSM with fuzzy model reference adaptive system. Int. J. Power Electr. Drive Syst. 2019, 10. [Google Scholar]
- Hu, B.; Kang, L.; Cheng, J.; Linghu, J.; Zhang, Z. Integrated dead-time compensation and elimination approach for model predictive power control with fixed switching frequency. IET Power Electr. 2019, 12, 1220–1228. [Google Scholar] [CrossRef]
- Zerdali, E.; Menguc, E.C. Novel Complex-Valued Stator Current-Based MRAS Estimators With Different Adaptation Mechanisms. IEEE Trans. Inst. Meas. 2019, 68, 3793–3795. [Google Scholar] [CrossRef]
- Sun, X.; Meng, L.; Liu, Y.; Wang, K. Research on PMSM Direct Torque Speed Control System with Speed Sensorless. In Proceedings of the 14th IEEE Conference on Industrial Electronics and Applications ( ICIEA), Xi’an, China, 19–21 June 2019. [Google Scholar]
- Qiao, G.; Mingqiao, W.; Liu, L.; Liu, Y.; Zheng, P.; Sui, Y. Analysis of Magnetic Properties of Al Ni Co and Magnetization State Estimation in Variable-Flux PMSMs. IEEE Trans. Mag. 2019, 55, 1–6. [Google Scholar]
- Yang, Y.; Chen, J.; Chu, Y.; Wang, Y.; Liang, Q. Fractional order adaptive sliding mode controller for permanent-magnet synchronous motor. In Proceedings of the 35th IEE Chinese Control Conference (CCC), Chengdu, China, 27–29 July 2016. [Google Scholar]



| Parameters | Values |
|---|---|
| Reference speed (N) | 1500 rpm |
| Stator resistance (Rs) | 0.93 Ω |
| Stator inductance (Ld) | 4.13 mH |
| Stator inductance (Lq) | 5.77 mH |
| Rotor magnet flux (φr) | 0.07 Wb |
| Pole-pair (Pn) | 5 |
| Rotor inertia (Jm) | 1.71 kg·cm2 |
| Friction coefficient (Br) | 0.025 Nm/rad/s |
| For Dynamic State | |
| 0~0.3 s | Accelerating from 0 to 1500 rpm |
| 0.3~0.7 s | 1500 rpm |
| 0.7~1.3 s | Turning from 1500 to −1500 rpm |
| 1.3~1.5 s | −1500 rpm |
| For steady state | |
| 0~0.5 s | 1500 rpm |
| For low-speed operation | |
| 0~0.05 s | 0 rpm |
| 0.05~0.5 s | Accelerating from 0 to 100 rpm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niu, H.; Liu, L.; Jin, D.; Liu, S. High-Tracking-Precision Sensorless Control of PMSM System Based on Fractional Order Model Reference Adaptation. Fractal Fract. 2023, 7, 21. https://doi.org/10.3390/fractalfract7010021
Niu H, Liu L, Jin D, Liu S. High-Tracking-Precision Sensorless Control of PMSM System Based on Fractional Order Model Reference Adaptation. Fractal and Fractional. 2023; 7(1):21. https://doi.org/10.3390/fractalfract7010021
Chicago/Turabian StyleNiu, Hongjie, Ling Liu, Dongsong Jin, and Siyuan Liu. 2023. "High-Tracking-Precision Sensorless Control of PMSM System Based on Fractional Order Model Reference Adaptation" Fractal and Fractional 7, no. 1: 21. https://doi.org/10.3390/fractalfract7010021
APA StyleNiu, H., Liu, L., Jin, D., & Liu, S. (2023). High-Tracking-Precision Sensorless Control of PMSM System Based on Fractional Order Model Reference Adaptation. Fractal and Fractional, 7(1), 21. https://doi.org/10.3390/fractalfract7010021





