On the Variable Order Fractional Calculus Characterization for the Hidden Variable Fractal Interpolation Function
Abstract
:1. Introduction
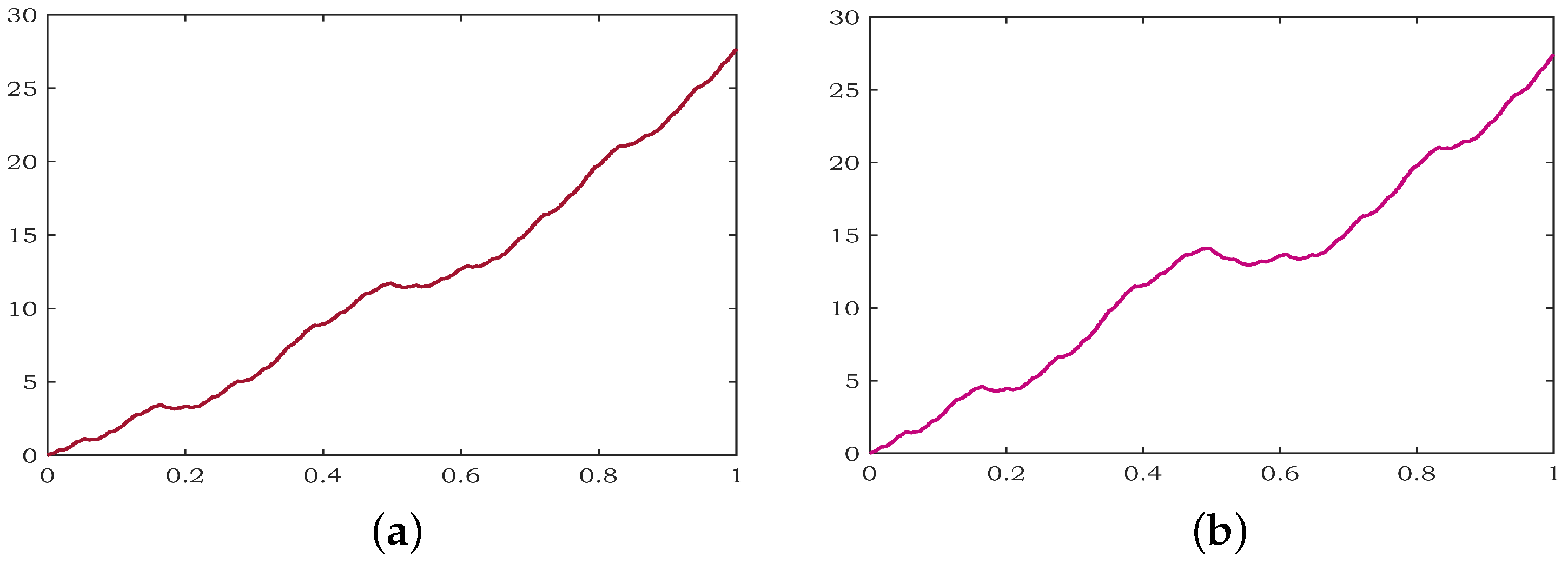
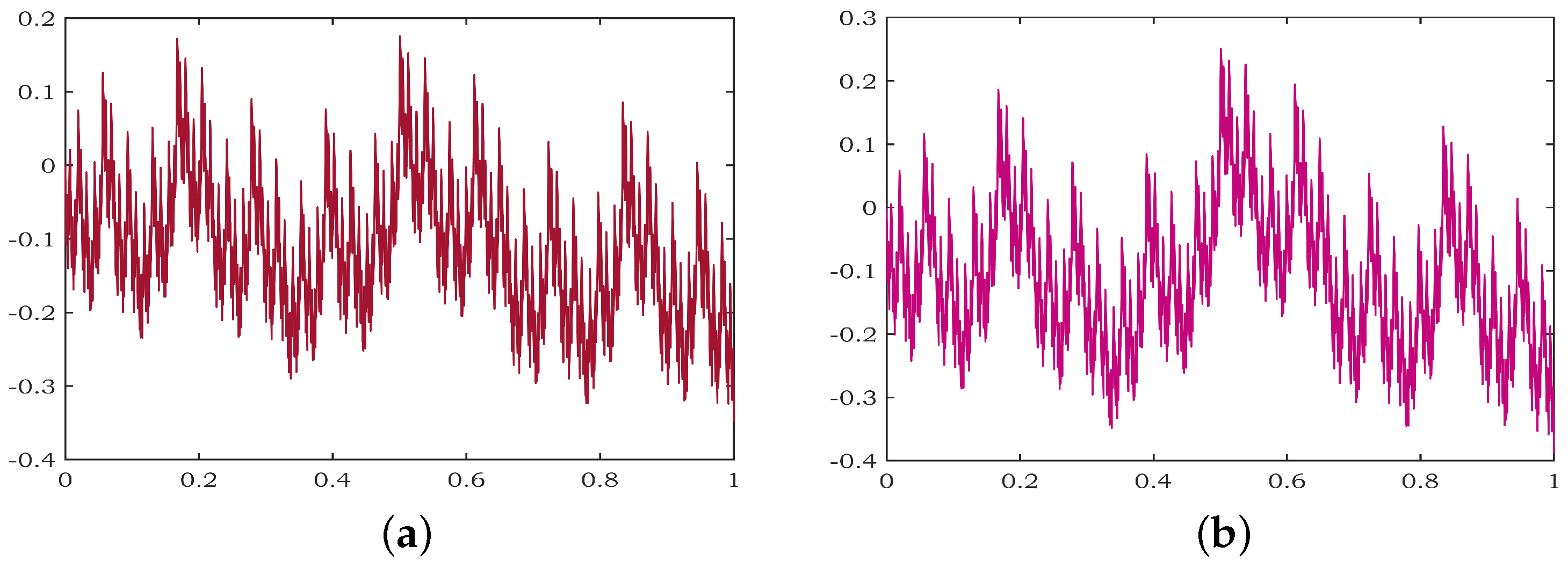
2. Brief of the Hidden Variable Fractal Interpolation Function
3. Main Results
4. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Barnsley, M.F. Fractal functions and interpolation. Constr. Approx. 1986, 2, 303–329. [Google Scholar] [CrossRef]
- Hutchinson, J.E. Fractals and self similarity. Indiana Univ. Math. J. 1981, 30, 713–747. [Google Scholar] [CrossRef]
- Easwaramoorthy, D.; Uthayakumar, R. Analysis on fractals in fuzzy metric spaces. Fractals 2011, 19, 379–386. [Google Scholar] [CrossRef]
- Banerjee, S.; Easwaramoorthy, D.; Gowrisankar, A. Fractal Functions, Dimensions and Signal Analysis; Springer: Cham, Switzerland, 2021. [Google Scholar]
- Banerjee, S.; Hassan, M.K.; Mukherjee, S.; Gowrisankar, A. Fractal Patterns in Nonlinear Dynamics and Applications; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar]
- Ruan, H.J.; Su, W.Y.; Yao, K. Box dimension and fractional integral of linear fractal-interpolation functions. J. Approx. Theory 2009, 161, 187–197. [Google Scholar] [CrossRef] [Green Version]
- Balasubramani, N. Affine recurrent fractal-interpolation functions. Eur. Phys. J. Spec. Top. 2021, 230, 3765–3779. [Google Scholar] [CrossRef]
- Barnsley, M.F.; Elton, J.; Hardin, D.; Massopust, P. Hidden variable fractal interpolation functions. Siam J. Math. Anal. 1989, 20, 1218–1242. [Google Scholar] [CrossRef]
- Chand, A.K.B.; Kapoor, G.P. Hidden variable bivariate fractal interpolation surfaces. Fractals 2003, 11, 277–288. [Google Scholar] [CrossRef]
- Bouboulis, P.; Dalla, L. Hidden variable vector valued fractal-interpolation functions. Fractals-London 2003, 13, 227. [Google Scholar] [CrossRef]
- Bouboulis, P.; Dalla, L.; Drakopoulos, V. Construction of recurrent bivariate fractal interpolation surfaces and computation of their box-counting dimension. J. Approx. Theory 2006, 141, 99–117. [Google Scholar] [CrossRef] [Green Version]
- Chand, A.K.B.; Kapoor, G.P. Cubic spline coalescence fractal interpolation through moments. Fractals 2007, 15, 41–53. [Google Scholar] [CrossRef]
- Kapoor, G.P.; Prasad, S.A. Smoothness of hidden variable bivariate coalescence fractal interpolation surfaces. Int. J. Bifurcat. Chaos 2009, 19, 2321–2333. [Google Scholar] [CrossRef] [Green Version]
- Prasad, S.A. Fractional calculus of coalescence hidden variable fractal interpolation functions. Fractals 2009, 25, 1750019. [Google Scholar] [CrossRef]
- Priyanka, T.M.C.; Gowrisankar, A. Analysis on Weyl–Marchaud Fractional Derivative for Types of fractal-interpolation function with Fractal Dimension. Fractals 2021, 29, 2150215. [Google Scholar] [CrossRef]
- Ri, M.G.; Yun, C.H.; Kim, M.H. Construction of cubic spline hidden variable recurrent fractal-interpolation function and its fractional calculus. Chaos Solitons Fractals 2021, 150, 111177. [Google Scholar] [CrossRef]
- Ri, M.G.; Yun, C.H. Smoothness and fractional integral of hidden variable recurrent fractal-interpolation function with function vertical scaling factors. Fractals 2021, 29, 2150136. [Google Scholar] [CrossRef]
- Gowrisankar, A.; Uthayakumar, R. Fractional calculus on fractal interpolation for a sequence of data with countable iterated function system. Mediterr. J. Math. 2016, 13, 3887–3906. [Google Scholar] [CrossRef]
- Gowrisankar, A.; Khalili Golmankhaneh, A.; Serpa, C. Fractal Calculus on fractal-interpolation functions. Fractal Fract. 2021, 5, 157. [Google Scholar] [CrossRef]
- Yao, K.; Su, W.Y.; Zhou, S.P. The fractional derivatives of a fractal function. Acta Math. Sin. 2006, 22, 719–722. [Google Scholar] [CrossRef]
- Ri, M.G.; Yun, C.H. Riemann–Liouville fractional integral of hidden variable fractal interpolation function. Chaos Solitons Fractals 2020, 140, 110126. [Google Scholar] [CrossRef]
- Liang, Y.S.; Su, W.Y. Fractal dimensions of fractional integral of continuous functions. Acta Math. Sin.-Engl. Ser. 2016, 32, 1494–1508. [Google Scholar] [CrossRef]
- Zhang, Q. Some remarks on one-dimensional functions and their Riemann–Liouville fractional calculus. Acta Math. Sin.-Engl. Ser. 2014, 30, 517–524. [Google Scholar] [CrossRef]
- Gowrisankar, A.; Prasad, M. Riemann–Liouville calculus on quadratic fractal-interpolation function with variable scaling factors. J. Anal. 2019, 27, 347–363. [Google Scholar] [CrossRef]
- Peng, W.L.; Yao, K.; Zhang, X.; Yao, J. Box dimension of Weyl–Marchaud fractional derivative of linear fractal-interpolation functions. Fractals 2019, 27, 1950058. [Google Scholar] [CrossRef]
- Ferrari, F. Weyl and Marchaud derivatives: A forgotten history. Mathematics 2018, 6, 6. [Google Scholar] [CrossRef] [Green Version]
- Priyanka, T.M.C.; Gowrisankar, A. Riemann–Liouville fractional integral of non-affine fractal-interpolation function and its fractional operator. Eur. Phys. J. Spec. Top. 2021, 230, 3789–3805. [Google Scholar] [CrossRef]
- Ri, M.G.; Yun, C.H. Riemann–Liouville fractional derivatives of hidden variable recurrent fractal-interpolation functions with function scaling factors and box dimension. Chaos Solitons Fractals 2022, 156, 111793. [Google Scholar] [CrossRef]
- Samko, S.G.; Ross, B. Integration and differentiation to a variable fractional order. Integr. Transform. Spec. Funct. 1993, 1, 277–300. [Google Scholar] [CrossRef]
- Samko, S.G. Fractional integration and differentiation of variable order. Anal. Math. 1995, 21, 213–236. [Google Scholar] [CrossRef]
- Zhao, X.; Sun, Z.Z.; Karniadakis, G.E. Second-order approximations for variable order fractional derivatives: Algorithms and applications. J. Comput. Phys. 2015, 293, 184–200. [Google Scholar] [CrossRef]
- Garrappa, R.; Giusti, A.; Mainardi, F. variable order fractional calculus: A change of perspective. Commun. Nonlinear Sci. Numer. Simul. 2021, 102, 105904. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Raja, V.; Gowrisankar, A. On the Variable Order Fractional Calculus Characterization for the Hidden Variable Fractal Interpolation Function. Fractal Fract. 2023, 7, 34. https://doi.org/10.3390/fractalfract7010034
Raja V, Gowrisankar A. On the Variable Order Fractional Calculus Characterization for the Hidden Variable Fractal Interpolation Function. Fractal and Fractional. 2023; 7(1):34. https://doi.org/10.3390/fractalfract7010034
Chicago/Turabian StyleRaja, Valarmathi, and Arulprakash Gowrisankar. 2023. "On the Variable Order Fractional Calculus Characterization for the Hidden Variable Fractal Interpolation Function" Fractal and Fractional 7, no. 1: 34. https://doi.org/10.3390/fractalfract7010034




