Relationships between Reference Evapotranspiration and Meteorological Variables in the Middle Zone of the Guadalquivir River Valley Explained by Multifractal Detrended Cross-Correlation Analysis
Abstract
1. Introduction
2. Materials and Methods
2.1. Data
2.2. Seasonal Detrending
2.3. Multifractal Detrending Analysis Algorithms
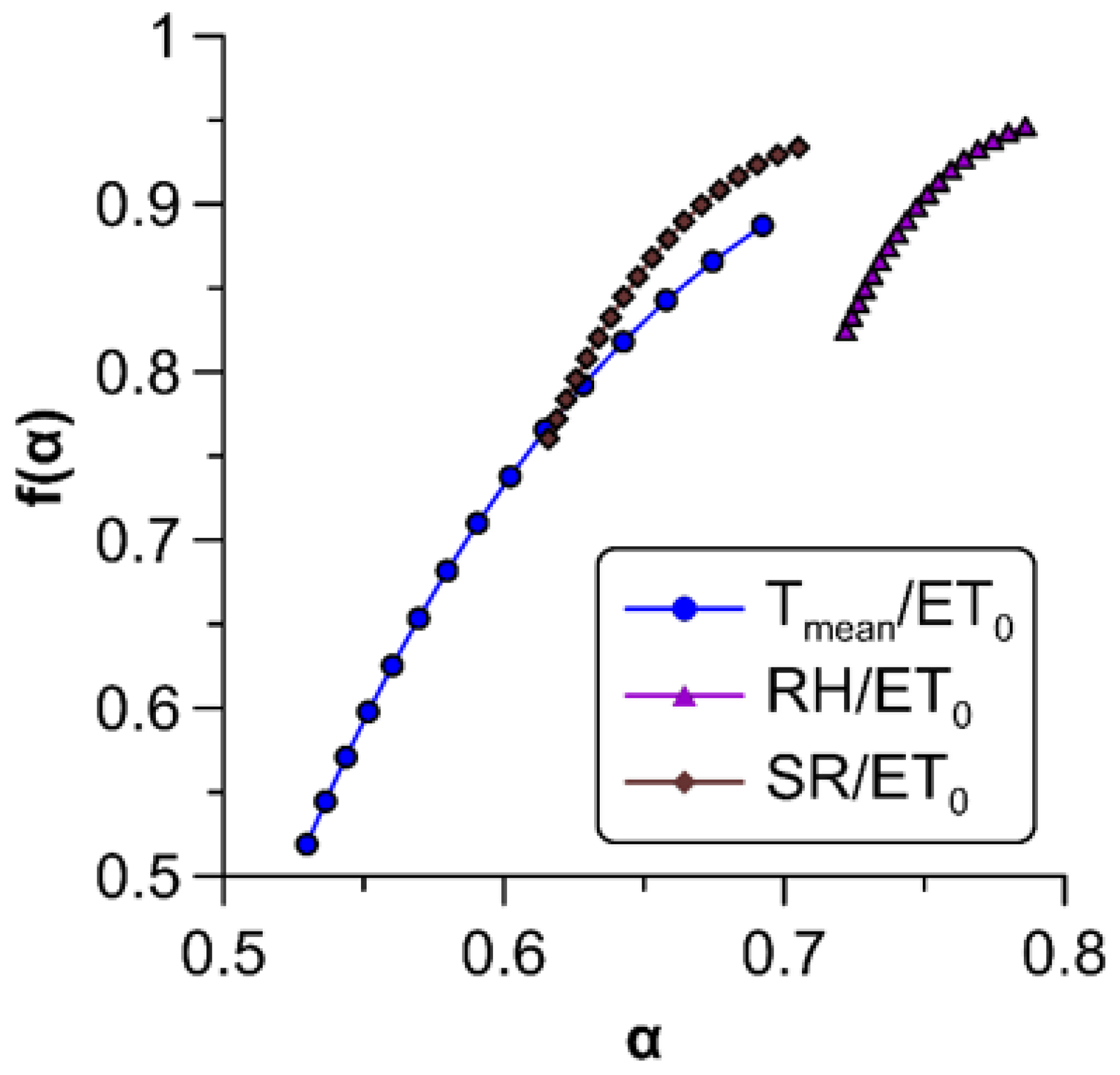
3. Results
3.1. MFDFA of Agro-Meteorological Times Series
3.2. MFCCA of Meteorological Times Series with
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tabari, H.; Hosseinzadeh Talaee, P. Sensitivity of Evapotranspiration to Climatic Change in Different Climates. Glob. Planet. Change 2014, 115, 16–23. [Google Scholar] [CrossRef]
- Ariza-Villaverde, A.B.; Pavón-Domínguez, P.; Carmona-Cabezas, R.; Gutiérrez de Ravé, E.; Jiménez-Hornero, F.J. Joint Multifractal Analysis of Air Temperature, Relative Humidity and Reference Evapotranspiration in the Middle Zone of the Guadalquivir River Valley. Agric. For. Meteorol. 2019, 278, 107657. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration—Guidelines for Computing Crop Water Requirements—FAO Irrigation and Drainage Paper 56. Fao Rome 1998, 300, D05109. [Google Scholar]
- Doorenbos, J.; Pruitt, W.O. Guidelines for Predicting Crop Water Requirements. Irrig. Drain. Pap. (FAO) 1975, 24, 1–179. [Google Scholar]
- Gong, L.; Xu, C.; Chen, D.; Halldin, S.; Chen, Y.D. Sensitivity of the Penman–Monteith Reference Evapotranspiration to Key Climatic Variables in the Changjiang (Yangtze River) Basin. J. Hydrol. 2006, 329, 620–629. [Google Scholar] [CrossRef]
- Li, Y.; Qin, Y.; Rong, P. Evolution of Potential Evapotranspiration and Its Sensitivity to Climate Change Based on the Thornthwaite, Hargreaves, and Penman–Monteith Equation in Environmental Sensitive Areas of China. Atmos. Res. 2022, 273, 106178. [Google Scholar] [CrossRef]
- Jensen, M.E.; Burman, R.D.; Allen, R.G. Evapotranspiration and Irrigation Water Requirements. ASCE Manuals and Reports on Engineering Practices (USA) No. 70; American Society of Civil Engineers: New York, NY, USA, 1990; p. 332. [Google Scholar]
- López-Urrea, R.; Olalla, F.M.d.S.; Fabeiro, C.; Moratalla, A. An Evaluation of Two Hourly Reference Evapotranspiration Equations for Semiarid Conditions. Agric. Water Manag. 2006, 86, 277–282. [Google Scholar] [CrossRef]
- Nam, W.-H.; Hong, E.-M.; Choi, J.-Y. Has Climate Change Already Affected the Spatial Distribution and Temporal Trends of Reference Evapotranspiration in South Korea? Agric. Water Manag. 2015, 150, 129–138. [Google Scholar] [CrossRef]
- Sun, J.; Wang, G.; Sun, X.; Hu, Z.; Lin, S.; Wang, F.; Yang, Y. New Cognition on the Response of Reference Evapotranspiration to Climate Change in China Using an Independent Climatic Driver System. Agric. Water Manag. 2022, 262, 107445. [Google Scholar] [CrossRef]
- Yassen, A.N.; Nam, W.-H.; Hong, E.-M. Impact of Climate Change on Reference Evapotranspiration in Egypt. CATENA 2020, 194, 104711. [Google Scholar] [CrossRef]
- Oteros, J.; García-Mozo, H.; Vázquez, L.; Mestre, A.; Domínguez-Vilches, E.; Galán, C. Modelling Olive Phenological Response to Weather and Topography. Agric. Ecosyst. Environ. 2013, 179, 62–68. [Google Scholar] [CrossRef]
- Zhan, C.; Liang, C.; Zhao, L.; Zhang, Y.; Cheng, L.; Jiang, S.; Xing, L. Multifractal Characteristics Analysis of Daily Reference Evapotranspiration in Different Climate Zones of China. Phys. A Stat. Mech. Its Appl. 2021, 583, 126273. [Google Scholar] [CrossRef]
- Feder, J. Fractals; Springer US: Boston, MA, USA, 1988; ISBN 978-1-4899-2126-0. [Google Scholar]
- Mandelbrot, B.B. The Fractal Geometry of Nature; W.H. Freeman: San Francisco, CA, USA, 1982; ISBN 978-0-7167-1186-5. [Google Scholar]
- Gómez-Gómez, J.; Carmona-Cabezas, R.; Sánchez-López, E.; Gutiérrez de Ravé, E.; Jiménez-Hornero, F.J. Multifractal Fluctuations of the Precipitation in Spain (1960–2019). Chaos Solitons Fractals 2022, 157, 111909. [Google Scholar] [CrossRef]
- Adarsh, S.; Nityanjaly, L.J.; Pham, Q.B.; Sarang, R.; Ali, M.; Nandhineekrishna, P. Multifractal Characterization and Cross Correlations of Reference Evapotranspiration Time Series of India. Eur. Phys. J. Spec. Top. 2021, 230, 3845–3859. [Google Scholar] [CrossRef]
- Adarsh, S.; Sanah, S.; Murshida, K.K.; Nooramol, P. Scale Dependent Prediction of Reference Evapotranspiration Based on Multi-Variate Empirical Mode Decomposition. Ain Shams Eng. J. 2018, 9, 1839–1848. [Google Scholar] [CrossRef]
- Sankaran, A.; Krzyszczak, J.; Baranowski, P.; Devarajan Sindhu, A.; Kumar, N.; Lija Jayaprakash, N.; Thankamani, V.; Ali, M. Multifractal Cross Correlation Analysis of Agro-Meteorological Datasets (Including Reference Evapotranspiration) of California, United States. Atmosphere 2020, 11, 1116. [Google Scholar] [CrossRef]
- Sreedevi, V.; Adarsh, S.; Nourani, V. Multiscale Coherence Analysis of Reference Evapotranspiration of North-Western Iran Using Wavelet Transform. J. Water Clim. Change 2022, 13, 505–521. [Google Scholar] [CrossRef]
- Kantelhardt, J.W.; Zschiegner, S.A.; Koscielny-Bunde, E.; Havlin, S.; Bunde, A.; Stanley, H.E. Multifractal Detrended Fluctuation Analysis of Nonstationary Time Series. Phys. A 2002, 316, 87–114. [Google Scholar] [CrossRef]
- Plocoste, T.; Pavón-Domínguez, P. Multifractal Detrended Cross-Correlation Analysis of Wind Speed and Solar Radiation. Chaos 2020, 30, 113109. [Google Scholar] [CrossRef]
- Wątorek, M.; Drożdż, S.; Oświȩcimka, P.; Stanuszek, M. Multifractal Cross-Correlations between the World Oil and Other Financial Markets in 2012–2017. Energy Econ. 2019, 81, 874–885. [Google Scholar] [CrossRef]
- Zhang, C.; Ni, Z.; Ni, L. Multifractal Detrended Cross-Correlation Analysis between PM2.5 and Meteorological Factors. Phys. A Stat. Mech. Its Appl. 2015, 438, 114–123. [Google Scholar] [CrossRef]
- Oświȩcimka, P.; Drożdż, S.; Forczek, M.; Jadach, S.; Kwapień, J. Detrended Cross-Correlation Analysis Consistently Extended to Multifractality. Phys. Rev. E 2014, 89, 023305. [Google Scholar] [CrossRef]
- Podobnik, B.; Stanley, H.E. Detrended Cross-Correlation Analysis: A New Method for Analyzing Two Nonstationary Time Series. Phys. Rev. Lett. 2008, 100, 084102. [Google Scholar] [CrossRef] [PubMed]
- Kwapień, J.; Oświęcimka, P.; Drożdż, S. Detrended Fluctuation Analysis Made Flexible to Detect Range of Cross-Correlated Fluctuations. Phys. Rev. E 2015, 92, 052815. [Google Scholar] [CrossRef] [PubMed]
- Jiménez-Hornero, F.J.; Jiménez-Hornero, J.E.; Gutiérrez de Ravé, E.; Pavón-Domínguez, P. Exploring the Relationship between Nitrogen Dioxide and Ground-Level Ozone by Applying the Joint Multifractal Analysis. Environ. Monit. Assess. 2010, 167, 675–684. [Google Scholar] [CrossRef] [PubMed]
- Plocoste, T.; Pavón-Domínguez, P. Temporal Scaling Study of Particulate Matter (PM10) and Solar Radiation Influences on Air Temperature in the Caribbean Basin Using a 3D Joint Multifractal Analysis. Atmos. Environ. 2020, 222, 117115. [Google Scholar] [CrossRef]
- Zeleke, T.B.; Si, B.C. Characterizing Scale-Dependent Spatial Relationships between Soil Properties Using Multifractal Techniques. Geoderma 2006, 134, 440–452. [Google Scholar] [CrossRef]
- Gavilán, P.; Lorite, I.J.; Tornero, S.; Berengena, J. Regional Calibration of Hargreaves Equation for Estimating Reference ET in a Semiarid Environment. Agric. Water Manag. 2006, 81, 257–281. [Google Scholar] [CrossRef]
- García-Marín, A.P.; Jiménez-Hornero, F.J.; Ayuso-Muñoz, J.L. Multifractal Analysis as a Tool for Validating a Rainfall Model. Hydrol. Process. 2008, 22, 2672–2688. [Google Scholar] [CrossRef]
- Hu, K.; Ivanov, P.C.; Chen, Z.; Carpena, P.; Eugene Stanley, H. Effect of Trends on Detrended Fluctuation Analysis. Phys. Rev. E 2001, 64, 011114. [Google Scholar] [CrossRef]
- Kantelhardt, J.W.; Koscielny-Bunde, E.; Rybski, D.; Braun, P.; Bunde, A.; Havlin, S. Long-Term Persistence and Multifractality of Precipitation and River Runoff Records. J. Geophys. Res. 2006, 111, D01106. [Google Scholar] [CrossRef]
- Gong, H.; Fu, Z. Beyond Linear Correlation: Strong Nonlinear Structures in Diurnal Temperature Range Variability over Southern China. Chaos Solitons Fractals 2022, 164, 112737. [Google Scholar] [CrossRef]
- Rybski, D.; Bunde, A.; von Storch, H. Long-Term Memory in 1000-Year Simulated Temperature Records. J. Geophys. Res. 2008, 113, D02106. [Google Scholar] [CrossRef]
- Xavier Júnior, S.F.A.; Stosic, T.; Stosic, B.; Jale, J.D.S.; Xavier, É.F.M. A Brief Multifractal Analysis of Rainfall Dynamics in Piracicaba, São Paulo, Brazil. Acta Sci. Technol. 2018, 40, 35116. [Google Scholar] [CrossRef]
- Peng, C.-K.; Buldyrev, S.V.; Havlin, S.; Simons, M.; Stanley, H.E.; Goldberger, A.L. Mosaic Organization of DNA Nucleotides. Phys. Rev. E 1994, 49, 1685–1689. [Google Scholar] [CrossRef]
- Kantelhardt, J.W.; Rybski, D.; Zschiegner, S.A.; Braun, P.; Koscielny-Bunde, E.; Livina, V.; Havlin, S.; Bunde, A. Multifractality of River Runoff and Precipitation: Comparison of Fluctuation Analysis and Wavelet Methods. Phys. A 2003, 330, 240–245. [Google Scholar] [CrossRef]
- Zhang, Q.; Xu, C.-Y.; Chen, Y.D.; Yu, Z. Multifractal Detrended Fluctuation Analysis of Streamflow Series of the Yangtze River Basin, China. Hydrol. Process. 2008, 22, 4997–5003. [Google Scholar] [CrossRef]
- Baranowski, P.; Krzyszczak, J.; Slawinski, C.; Hoffmann, H.; Kozyra, J.; Nieróbca, A.; Siwek, K.; Gluza, A. Multifractal Analysis of Meteorological Time Series to Assess Climate Impacts. Clim. Res. 2015, 65, 39–52. [Google Scholar] [CrossRef]
- Gómez-Gómez, J.; Carmona-Cabezas, R.; Ariza-Villaverde, A.B.; Gutiérrez de Ravé, E.; Jiménez-Hornero, F.J. Multifractal Detrended Fluctuation Analysis of Temperature in Spain (1960–2019). Phys. A Stat. Mech. Its Appl. 2021, 578, 126118. [Google Scholar] [CrossRef]
- Kalamaras, N.; Tzanis, C.; Deligiorgi, D.; Philippopoulos, K.; Koutsogiannis, I. Distribution of Air Temperature Multifractal Characteristics Over Greece. Atmosphere 2019, 10, 45. [Google Scholar] [CrossRef]
- Sarker, A.; Mali, P. Detrended Multifractal Characterization of Indian Rainfall Records. Chaos Solitons Fractals 2021, 151, 111297. [Google Scholar] [CrossRef]
- Telesca, L.; Lovallo, M. Analysis of the Time Dynamics in Wind Records by Means of Multifractal Detrended Fluctuation Analysis and the Fisher–Shannon Information Plane. J. Stat. Mech. 2011, 2011, P07001. [Google Scholar] [CrossRef]
- Shimizu, Y.; Thurner, S.; Ehrenberger, K. Multifractal spectra as a measure of complexity in human posture. Fractals 2002, 10, 103–116. [Google Scholar] [CrossRef]
- Drożdż, S.; Minati, L.; Oświȩcimka, P.; Stanuszek, M.; Wątorek, M. Signatures of the Crypto-Currency Market Decoupling from the Forex. Future Internet 2019, 11, 154. [Google Scholar] [CrossRef]
- Vassoler, R.T.; Zebende, G.F. DCCA Cross-Correlation Coefficient Apply in Time Series of Air Temperature and Air Relative Humidity. Phys. A Stat. Mech. Its Appl. 2012, 391, 2438–2443. [Google Scholar] [CrossRef]
- Oświęcimka, P.; Drożdż, S.; Kwapień, J.; Górski, A.Z. Effect of Detrending on Multifractal Characteristics. Acta Phys. Pol. A 2013, 123, 597–603. [Google Scholar] [CrossRef]
- Makowiec, D.; Fuliński, A. Multifractal Detrended Fluctuation Analysis as the Estimator of Long-Range Dependence. Acta Phys. Pol. B 2010, 41, 1025–1050. [Google Scholar]







| Variable | Maximum | Minimum | Mean | SD |
|---|---|---|---|---|
| 34.71 | 0.05 | 17.66 | 7.42 | |
| 100 | 21.12 | 64.03 | 18.38 | |
| 8.22 | 0.03 | 1.62 | 0.75 | |
| 33.25 | 0.58 | 17.85 | 8.43 | |
| 10.25 | 0.38 | 3.86 | 2.41 |
| Variables | H | w | AI | |||
|---|---|---|---|---|---|---|
| 0.764 | 0.137 | 0.794 | 0.265 | 0.364 | −0.333 | |
| 0.831 | 0.112 | 0.857 | 0.199 | 0.264 | −0.363 | |
| 0.668 | 0.089 | 0.688 | 0.176 | 0.219 | −0.193 | |
| 0.729 | 0.238 | 0.771 | 0.479 | 0.800 | −0.540 | |
| 0.707 | 0.067 | 0.725 | 0.127 | 0.134 | 0.094 |
| w | AI | |||||||
|---|---|---|---|---|---|---|---|---|
| / | 0.732 | 0.736 | −0.003 | 0.692 | 0.163 | 0.368 | 1 | 0.399 |
| / | 0.798 | 0.769 | 0.029 | 0.786 | 0.064 | 0.122 | 1 | −0.651 |
| / | - | - | - | - | - | - | - | 0.251 |
| / | 0.719 | 0.718 | 0.001 | 0.705 | 0.089 | 0.173 | 1 | 0.618 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gómez-Gómez, J.; Ariza-Villaverde, A.B.; Gutiérrez de Ravé, E.; Jiménez-Hornero, F.J. Relationships between Reference Evapotranspiration and Meteorological Variables in the Middle Zone of the Guadalquivir River Valley Explained by Multifractal Detrended Cross-Correlation Analysis. Fractal Fract. 2023, 7, 54. https://doi.org/10.3390/fractalfract7010054
Gómez-Gómez J, Ariza-Villaverde AB, Gutiérrez de Ravé E, Jiménez-Hornero FJ. Relationships between Reference Evapotranspiration and Meteorological Variables in the Middle Zone of the Guadalquivir River Valley Explained by Multifractal Detrended Cross-Correlation Analysis. Fractal and Fractional. 2023; 7(1):54. https://doi.org/10.3390/fractalfract7010054
Chicago/Turabian StyleGómez-Gómez, Javier, Ana B. Ariza-Villaverde, Eduardo Gutiérrez de Ravé, and Francisco J. Jiménez-Hornero. 2023. "Relationships between Reference Evapotranspiration and Meteorological Variables in the Middle Zone of the Guadalquivir River Valley Explained by Multifractal Detrended Cross-Correlation Analysis" Fractal and Fractional 7, no. 1: 54. https://doi.org/10.3390/fractalfract7010054
APA StyleGómez-Gómez, J., Ariza-Villaverde, A. B., Gutiérrez de Ravé, E., & Jiménez-Hornero, F. J. (2023). Relationships between Reference Evapotranspiration and Meteorological Variables in the Middle Zone of the Guadalquivir River Valley Explained by Multifractal Detrended Cross-Correlation Analysis. Fractal and Fractional, 7(1), 54. https://doi.org/10.3390/fractalfract7010054









