A New Perspective on the Exact Solutions of the Local Fractional Modified Benjamin–Bona–Mahony Equation on Cantor Sets
Abstract
:1. Introduction
2. Basic Theory
3. Construct of the NLFODEs
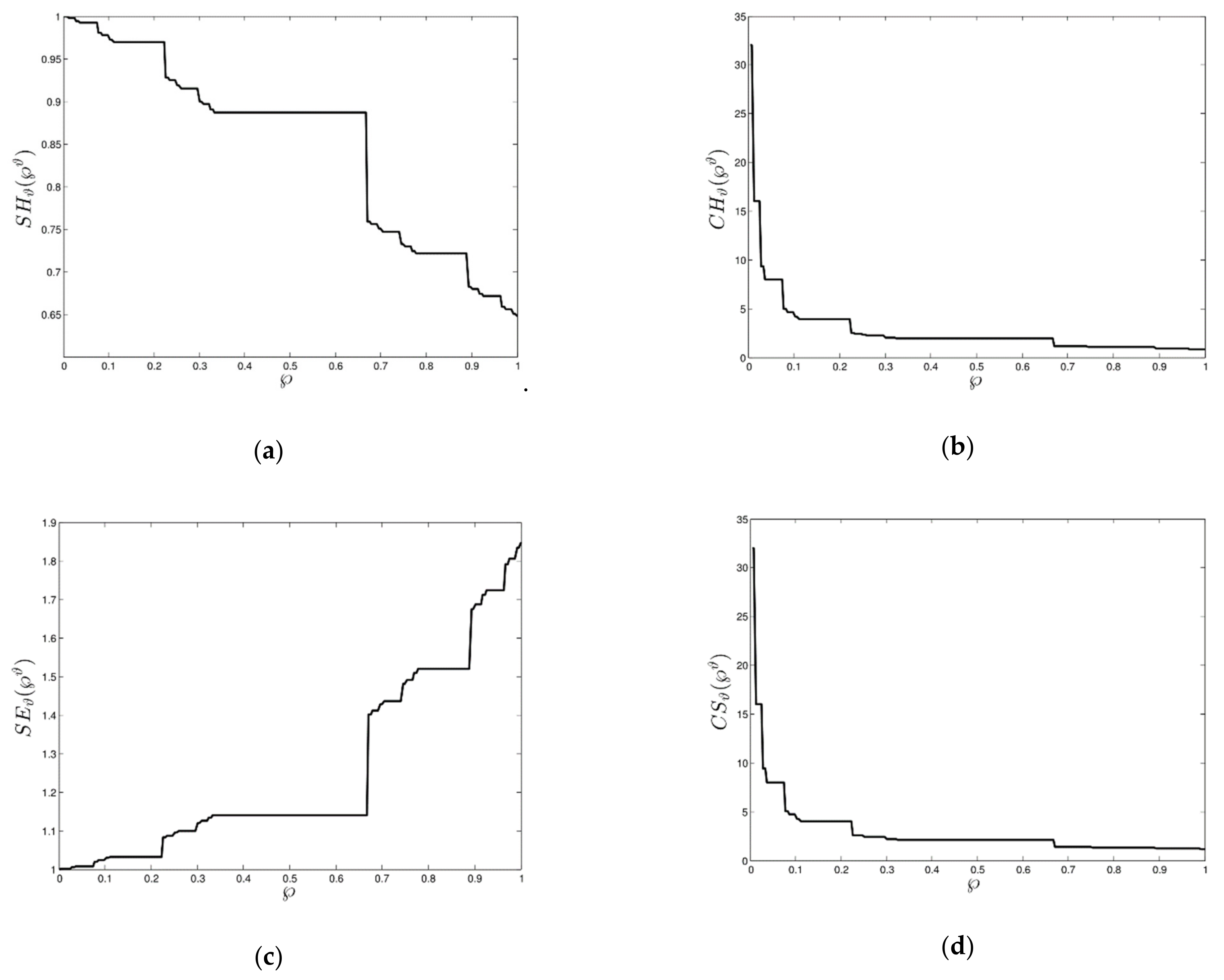
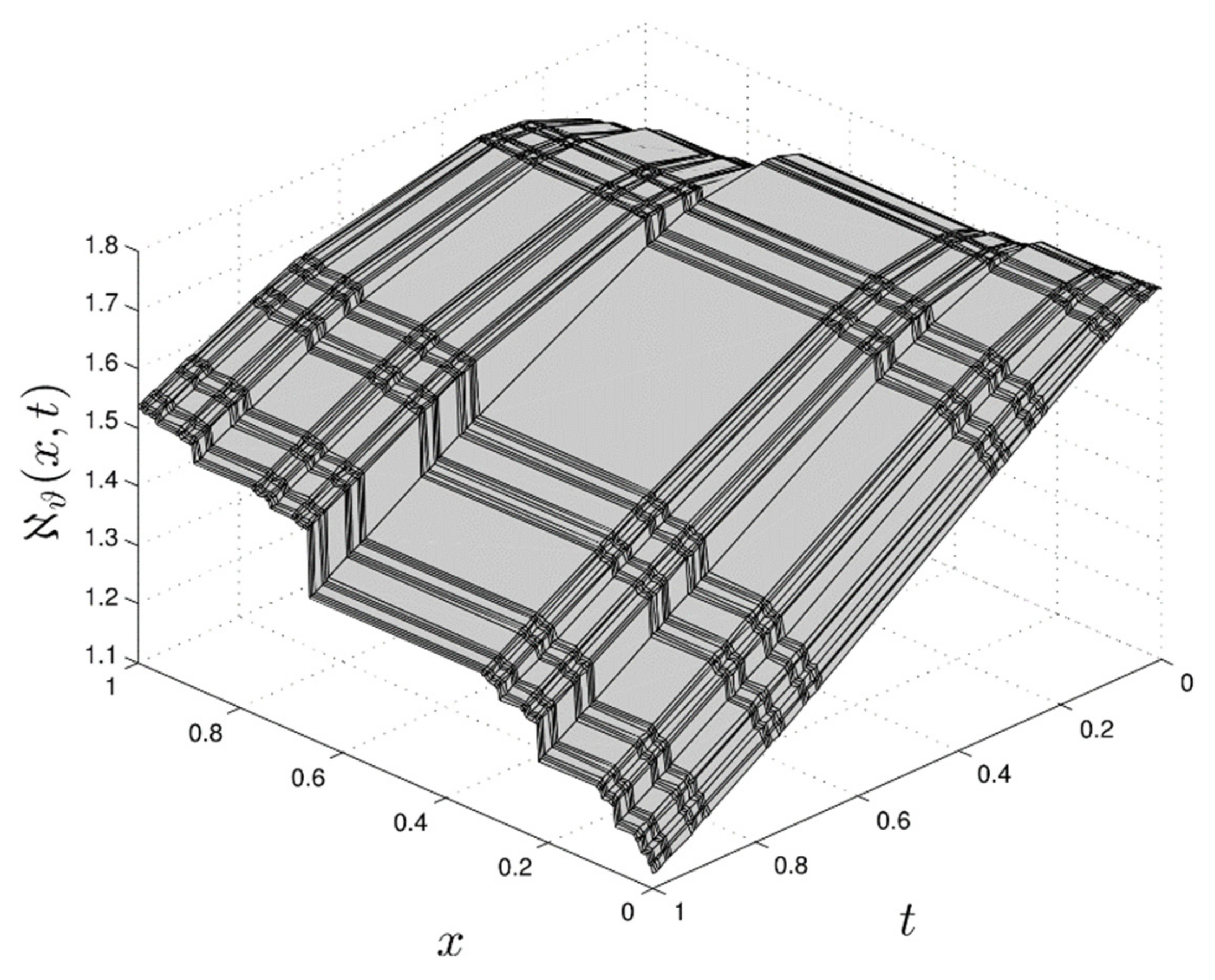
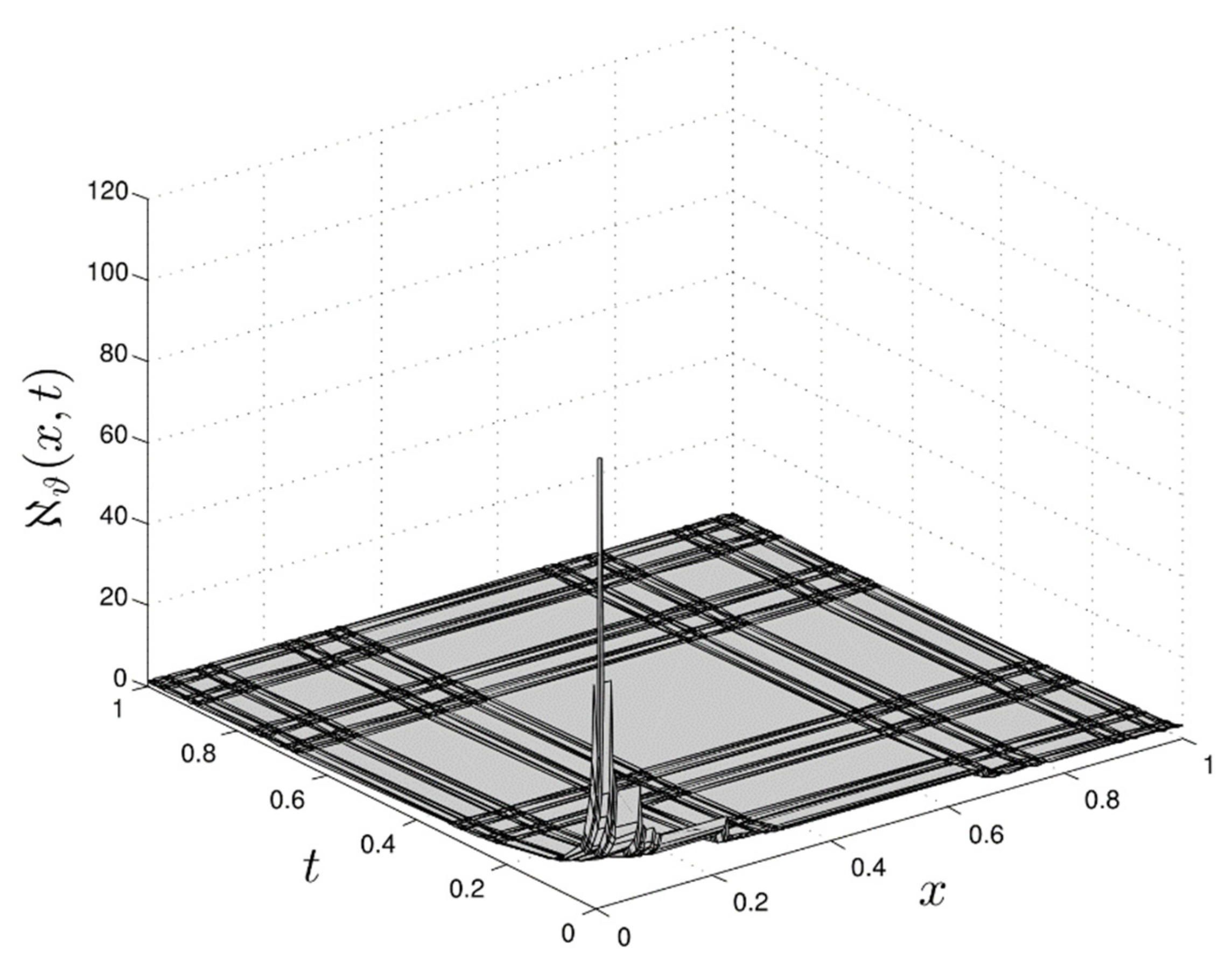
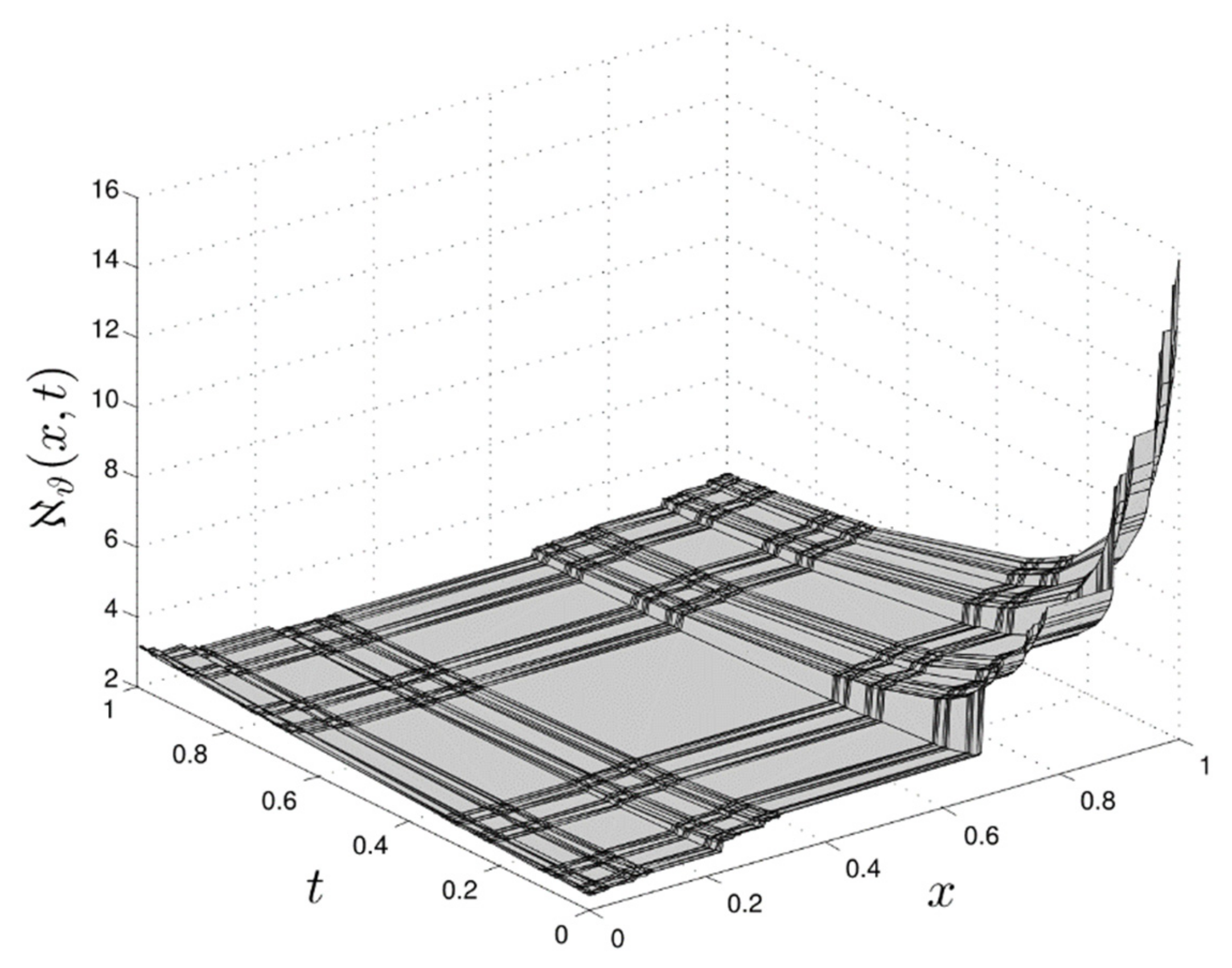
4. Yang’s Special Function Method
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Biswas, A.; Milovic, D.; Koh, R. Optical soliton perturbation in a log-law medium with full nonlinearity by He’s semi-inverse variational principle. Inverse Probl. Sci. Eng. 2021, 20, 227–232. [Google Scholar] [CrossRef]
- Wang, K.J.; Liu, J.-H. Diverse optical soliton solutions to the Kundu-Mukherjee-Naskar equation via two novel techniques. Optik 2023, 273, 170403. [Google Scholar] [CrossRef]
- Muniyappan, A.; Sahasraari, L.N.; Anitha, S.; Ilakiya, S.; Biswas, A.; Yıldırım, Y.; Triki, H.; Alshehri, H.M.; Belic, M.R. Family of optical solitons for perturbed Fokas–Lenells equation. Optik 2022, 249, 168224. [Google Scholar] [CrossRef]
- Wang, K.J. Diverse soliton solutions to the Fokas system via the Cole-Hopf transformation. Optik 2023, 272, 170250. [Google Scholar] [CrossRef]
- Lü, X.; Chen, S.-J. New general interaction solutions to the KPI equation via an optional decoupling condition approach. Commun. Nonlinear Sci. Numer. Simul. 2021, 103, 105939. [Google Scholar] [CrossRef]
- Qie, N.; Houa, W.F.; He, J.H. The fastest insight into the large amplitude vibration of a string. Rep. Mech. Eng. 2021, 2, 1–5. [Google Scholar] [CrossRef]
- He, C.H.; Tian, D.; Salman, H.F.; Zekry, M.H. Hybrid Rayleigh-Van der Pol-Duffing Oscillator (HRVD): Stability Analysis and Controller. J. Low Freq. Noise Vib. Act. Control. 2022, 41, 244–268. [Google Scholar] [CrossRef]
- Guo, A.; Ding, X.; Zhong, F.; Cheng, Q.; Huang, C. Predicting the future chinese population using shared socioeconomic pathways, the sixth national population census, and a PDE model. Sustainability 2019, 11, 3686. [Google Scholar] [CrossRef] [Green Version]
- Sohail, M.; Naz, R.; Shah, Z.; Kumam, P.; Thounthong, P. Exploration of temperature dependent thermophysical characteristics of yield exhibiting non-Newtonian fluid flow under gyrotactic microorganisms. AIP Adv. 2019, 9, 125016. [Google Scholar] [CrossRef] [Green Version]
- Abdelsalam, S.I.; Sohail, M. Numerical approach of variable thermophysical features of dissipated viscous nanofluid comprising gyrotactic micro-organisms. Pramana 2020, 94, 1–12. [Google Scholar] [CrossRef]
- Dashraath, P.; Wong, J.L.; Lim, M.X.; Lim, L.M.; Li, S.; Biswas, A.; Choolani, M.; Mattar, C.; Su, L.L. Coronavirus disease 2019 (COVID-19) pandemic and pregnancy. Am. J. Obstet. Gynecol. 2020, 222, 521–531. [Google Scholar] [CrossRef]
- Wang, K.J. Variational principle and diverse wave structures of the modified Benjamin-Bona-Mahony equation arising in the optical illusions field. Axioms 2022, 11, 445. [Google Scholar] [CrossRef]
- Singh, A.P.; Biswas, A.; Shukla, A.; Maiti, P. Targeted therapy in chronic diseases using nanomaterial-based drug delivery vehicles. Signal Transduct. Target. Ther. 2019, 4, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.-G.; Yang, X.-J.; Geng, L.-L.; Yu, X.-J. On fractional symmetry group scheme to the higher dimensional space and time fractional dissipative Burgers equation. Int. J. Geom. Methods Mod. Phys. 2022, 19, 2250173. [Google Scholar] [CrossRef]
- Wang, K.J. Bäcklund transformation and diverse exact explicit solutions of the fractal combined KdV-mKdV equation. Fractals 2022, 30, 2250189. [Google Scholar] [CrossRef]
- Muhammad, S.; Mohyud-Din, S.T. Reduced differential transform method for time-fractional heat equations. Int. J. Mark. Trade Policy 2012, 1, 13–22. [Google Scholar]
- Wang, K.L. New perspective to the fractal Konopelchenko-Dubrovsky equations with M-truncated fractional derivative. Int. J. Geom. Methods Mod. Phys. 2023, 2023, 2350072. [Google Scholar] [CrossRef]
- Xiao, B.; Huang, Q.; Chen, H.; Chen, X.; Long, G. A fractal model for capillary flow through a single tortuous capillary with roughened surfaces in fibrous porous media. Fractals 2021, 29, 2150017. [Google Scholar] [CrossRef]
- Baleanu, D.; Abadi, M.H.; Jajarmi, A.; Vahid, K.Z.; Nieto, J.J. A new comparative study on the general fractional model of COVID-19 with isolation and quarantine effects. Alex. Eng. J. 2022, 61, 4779–4791. [Google Scholar] [CrossRef]
- Zhang, Y.; Yu, X.; Sun, H.; Tick, G.R.; Wei, W.; Jin, B. Applicability of time fractional derivative models for simulating the dynamics and mitigation scenarios of COVID-19. Chaos Solitons Fractals 2020, 138, 109959. [Google Scholar] [CrossRef]
- Ghanbari, B.; Kumar, S.; Kumar, R. A study of behaviour for immune and tumor cells in immunogenetic tumour model with non-singular fractional derivative. Chaos Solitons Fractals 2020, 133, 109619. [Google Scholar] [CrossRef]
- He, J.H. A simple approach to one-dimensional convection-diffusion equation and its fractional modification for E reaction arising in rotating disk electrodes. J. Electroanal. Chem. 2019, 854, 113565. [Google Scholar] [CrossRef]
- Singh, H.; Srivastava, H.M. Numerical simulation for fractional-order Bloch equation arising in nuclear magnetic resonance by using the Jacobi polynomials. Appl. Sci. 2020, 10, 2850. [Google Scholar] [CrossRef] [Green Version]
- Kumar, S.; Kumar, A.; Momani, S.; Aldhaifallah, M.; Nisar, K.S. Numerical solutions of nonlinear fractional model arising in the appearance of the strip patterns in two-dimensional systems. Adv. Differ. Equ. 2019, 2019, 1–19. [Google Scholar] [CrossRef]
- Patnaik, S.; Sidhardh, S.; Semperlotti, F. Towards a unified approach to nonlocal elasticity via fractional-order mechanics. Int. J. Mech. Sci. 2021, 189, 105992. [Google Scholar] [CrossRef]
- Wang, G.; Liu, Y.; Wu, Y.; Su, X. Symmetry analysis for a seventh-order generalized KdV equation and its fractional version in fluid mechanics. Fractals 2020, 28, 2050044. [Google Scholar] [CrossRef]
- Raja, M.A.; Manzar, M.A.; Shah, S.M.; Chen, Y. Integrated intelligence of fractional neural networks and sequential quadratic programming for Bagley-Torvik systems arising in fluid mechanics. J. Comput. Nonlinear Dyn. 2020, 15, 051003. [Google Scholar] [CrossRef]
- Kiani-B, A.; Fallahi, K.; Pariz, N.; Leung, H. A chaotic secure communication scheme using fractional chaotic systems based on an extended fractional Kalman filter. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 863–879. [Google Scholar] [CrossRef]
- Tian, X.; Sun, X.; Yu, X.; Li, X. Modulation pattern recognition of communication signals based on fractional low-order Choi-Williams distribution and convolutional neural network in impulsive noise environment. In Proceedings of the 2019 IEEE 19th International Conference on Communication Technology (ICCT), Xi’an, China, 16–19 October 2019; IEEE: New York, NY, USA, 2019; pp. 188–192. [Google Scholar]
- Kalikulov, N.; Zhussip, D.; Zhexenov, N.; Kizilirmak, R.C. Multipath diversity for OFDM based visible light communication systems Through fractional sampling. Wirel. Pers. Commun. 2020, 112, 2715–2724. [Google Scholar] [CrossRef]
- Dimitrov, D.; Abdo, H. Tight independent set neighborhood union condition for fractional critical deleted graphs and ID deleted graphs. Discret. Contin. Dyn. Syst. S 2019, 12, 711. [Google Scholar] [CrossRef] [Green Version]
- Xiao, B.; Wang, W.; Zhang, X.; Long, G.; Fan, J.; Chen, H.; Deng, L. A novel fractal solution for permeability and Kozeny-Carman constant of fibrous porous media made up of solid particles and porous fibers. Powder Technol. 2019, 349, 92–98. [Google Scholar] [CrossRef]
- Stojiljković, V.; Ramaswamy, R.; Abdelnaby, O.A.A.; Radenović, S. Some Novel Inequalities for LR-(k,h-m)-p Convex Interval Valued Functions by Means of Pseudo Order Relation. Fractal Fract. 2022, 6, 726. [Google Scholar] [CrossRef]
- Singh, J.; Ahmadian, A.; Rathore, S.; Kumar, D.; Baleanu, D.; Salimi, M.; Salahshour, S. An efficient computational approach for local fractional Poisson equation in fractal media. Numer. Methods Part. Differ. Equ. 2021, 37, 1439–1448. [Google Scholar] [CrossRef]
- Singh, J.; Jassim, H.K.; Kumar, D. An efficient computational technique for local fractional Fokker Planck equation. Phys. A: Stat. Mech. Its Appl. 2020, 555, 124525. [Google Scholar] [CrossRef]
- Yang, X.J.; Gao, F.; Srivastava, H.M. A new computational approach for solving nonlinear local fractional PDEs. J. Comput. Appl. Math. 2018, 339, 285–296. [Google Scholar] [CrossRef]
- Ziane, D.; Baleanu, D.; Belghaba, K.; Cherif, M.H. Local fractional Sumudu decomposition method for linear partial differential equations with local fractional derivative. J. King Saud Univ. Sci. 2019, 31, 83–88. [Google Scholar] [CrossRef]
- Wang, K.J.; Si, J. On the non-differentiable exact solutions of the (2+1)-dimensional local fractional breaking soliton equation on Cantor sets. Math. Methods Appl. Sci. 2023, 46, 1456–1465. [Google Scholar] [CrossRef]
- Yang, X.J.; Baleanu, D. Fractal heat conduction problem solved by local fractional variation iteration method. Therm. Sci. 2013, 17, 625–628. [Google Scholar] [CrossRef]
- Wang, K.J. Investigation to the local fractional Fokas system on Cantor set by a novel technology. Fractals 2022, 30, 2250112. [Google Scholar] [CrossRef]
- Yang, Y.J.; Baleanu, D.; Yang, X.J. Analysis of fractal wave equations by local fractional Fourier series method. Adv. Math. Phys. 2013, 2013, 632309. [Google Scholar] [CrossRef] [Green Version]
- Wang, K.L. A novel perspective to the local fractional bidirectional wave model on Cantor sets. Fractals 2022, 30, 2250107. [Google Scholar] [CrossRef]
- Wang, K.L. A novel perspective to the local fractional Zakharov-Kuznetsov-modified equal width dynamical model on Cantor sets. Math. Methods Appl. Sci. 2022, 46, 622–630. [Google Scholar] [CrossRef]
- Dubey, V.P.; Singh, J.; Alshehri, A.M.; Dubey, S.; Kumar, D. A comparative analysis of two computational schemes for solving local fractional Laplace equations. Math. Methods Appl. Sci. 2021, 44, 13540–13559. [Google Scholar] [CrossRef]
- Su, W.H.; Yang, X.J.; Jafari, H.; Baleanu, D. Fractional complex transform method for wave equations on Cantor sets within local fractional differential operator. Adv. Differ. Equ. 2013, 2013, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Sang, X.; Zhang, Z.; Yang, H.; Han, X. Exact Traveling Wave Solutions of the Local Fractional Bidirectional Propagation System Equations. Fractal Fract. 2022, 6, 653. [Google Scholar] [CrossRef]
- Yang, X.J.; Baleanu, D.; Srivastava, H.M. Local Fractional Integral Transforms and Their Applications; Academic Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Yang, X.J.; Gao, F.; Srivastava, H.M. Non-differentiable exact solutions for the nonlinear ODEs defined on fractal sets. Fractals 2017, 25, 1740002. [Google Scholar] [CrossRef] [Green Version]
- Ghanbari, B. Abundant exact solutions to a generalized nonlinear Schrödinger equation with local fractional derivative. Math. Methods Appl. Sci. 2021, 44, 8759–8774. [Google Scholar] [CrossRef]
- Yang, X.J.; Gasimov, Y.S.; Gao, F.; Allahverdiyeva, N. Travelling-wave solutions for Klein-Gordon and Helmholtz equations on cantor sets. Proc. Inst. Math. Mechanics. 2017, 43, 123–131. [Google Scholar]
- Ghanbari, B. On novel nondifferentiable exact solutions to local fractional Gardner’s equation using an effective technique. Math. Methods Appl. Sci. 2021, 44, 4673–4685. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, K.-J.; Shi, F. A New Perspective on the Exact Solutions of the Local Fractional Modified Benjamin–Bona–Mahony Equation on Cantor Sets. Fractal Fract. 2023, 7, 72. https://doi.org/10.3390/fractalfract7010072
Wang K-J, Shi F. A New Perspective on the Exact Solutions of the Local Fractional Modified Benjamin–Bona–Mahony Equation on Cantor Sets. Fractal and Fractional. 2023; 7(1):72. https://doi.org/10.3390/fractalfract7010072
Chicago/Turabian StyleWang, Kang-Jia, and Feng Shi. 2023. "A New Perspective on the Exact Solutions of the Local Fractional Modified Benjamin–Bona–Mahony Equation on Cantor Sets" Fractal and Fractional 7, no. 1: 72. https://doi.org/10.3390/fractalfract7010072
APA StyleWang, K.-J., & Shi, F. (2023). A New Perspective on the Exact Solutions of the Local Fractional Modified Benjamin–Bona–Mahony Equation on Cantor Sets. Fractal and Fractional, 7(1), 72. https://doi.org/10.3390/fractalfract7010072






