Proportional-Integral-Derivative Controller Based-Artificial Rabbits Algorithm for Load Frequency Control in Multi-Area Power Systems

Abstract

A major problem in power systems is achieving a match between the load demand and generation demand, where security, dependability, and quality are critical factors that need to be provided to power producers. This paper proposes a proportional–integral–derivative (PID) controller that is optimally designed using a novel artificial rabbits algorithm (ARA) for load frequency control (LFC) in multi-area power systems (MAPSs) of two-area non-reheat thermal systems. The PID controller incorporates a filter with such a derivative coefficient to reduce the effects of the accompanied noise. In this regard, single objective function is assessed based on time-domain simulation to minimize the integral time-multiplied absolute error (ITAE). The proposed ARA adjusts the PID settings to their best potential considering three dissimilar test cases with different sets of disturbances, and the results from the designed PID controller based on the ARA are compared with various published techniques, including particle swarm optimization (PSO), differential evolution (DE), JAYA optimizer, and self-adaptive multi-population elitist (SAMPE) JAYA. The comparisons show that the PID controller’s design, which is based on the ARA, handles the load frequency regulation in MAPSs for the ITAE minimizations with significant effectiveness and success where the statistical analysis confirms its superiority. Considering the load change in area 1, the proposed ARA can acquire significant percentage improvements in the ITAE values of 1.949%, 3.455%, 2.077% and 1.949%, respectively, with regard to PSO, DE, JAYA and SAMPE-JAYA. Considering the load change in area 2, the proposed ARA can acquire significant percentage improvements in the ITAE values of 7.587%, 8.038%, 3.322% and 2.066%, respectively, with regard to PSO, DE, JAYA and SAMPE-JAYA. Considering simultaneous load changes in areas 1 and 2, the proposed ARA can acquire significant improvements in the ITAE values of 60.89%, 38.13%, 55.29% and 17.97%, respectively, with regard to PSO, DE, JAYA and SAMPE-JAYA.

1. Introduction

The primary goal of multi-area power systems (MAPSs) is to balance production with a connected load, whereas electrical power security, stability, and reliability are important factors that power producers must be made aware of. How to deal with the ongoing rise in demands and the complexities of the MAPSs structure, which includes a variety of power station designs, is a significant difficulty. Typically, MAPSs experience numerous system load variations and perturbations that have an immediate impact on the frequency for each area in MAPSs as well as the tie links power transfer among several regions [1,2]. Therefore, it is vital to maintain the frequency and tie lines’ power transfer below the prescribed levels before the protection schemes start working. These data indicate that the load frequency control (LFC), which regulates the generator’s output, is crucial in achieving the major goals. A supplementary goal on the economical operational aspect is to divide the required generating change among units to reduce their operational costs [3].

Since evolutionary optimization techniques can manage technical challenges such as uncertainties, non-linearities, and complexity, there have been significant attempts over a number of years to implement various optimizers to optimize the controllers’ settings. Therefore, in a two-area power system with the non-reheat thermal generation, genetic algorithms (GA) were used to optimize the parameters of the automatic generation control (AGC) [4]. GA were combined with the Taguchi technique to determine the optimal gains of the AGC controller to improve GA resilient due to a higher standard error of the obtained objective ratings [4]. In [5], the PID controller in MAPSs of three equal thermal electrical networks was tuned using a flower pollination mechanism, which takes advantage of the natural patterns of flower pollination. In [6], a particle swarm optimizer (PSO) with constriction factor and craziness-based PSO was used to enhance the transient response’s undershoot, overshoot, and settling time. Additionally, the differential evolution (DE) method was used to adjust the PI controller to address the LFC issue in a linked power system [7].

For the LFC of linear and non-linear linked MAPSs, a bacterial foraging algorithm was combined with a PSO depending on the PI controller under both traditional and modified fitness functions considering two areas of a non-reheat thermal system [8]. In [9], JAYA optimization was contrasted versus a modified JAYA version based on a self-adapted multi-population elitist (SAMPE) JAYA strategy to fine-tune the PID settings or linked MAPSs with two non-reheat thermal zones. Additionally, the bacterial foraging strategy was expanded to determine the optimal settings of the PID besides the integral plus double derivative controllers for MAPSs with nonlinear LFC problems, accordingly, in [10,11]. In addition, the LFC issue in both a two-area non-reheat thermal MPAS and a single-area combined cycle gas turbine plant have been tackled via the Firefly algorithm (FA), accordingly, in [12,13]. In order to optimize the overshoot and minimize the settling time of the operating frequency, the artificial bee colony method was implemented in coordination with the weighted sum method [14]. For minimizing a mono-objective goal that incorporates several performance measurements of the ITAE, a PID controller relying on the optimization method was deployed in a two-area linked MAPS [15]. In order to regulate the overshoot, undershoot, and settling time of the fuzzified PID controller, a teaching learning-based optimization method was used [16]. Grey wolf optimization applications for the AGC in three MAPS with and without solar thermal power plants are described in [17]. Additionally, the cuckoo search method was applied to handle the LFC challenge in three-area linked systems by optimal tuning of the PI controller in [18] and the integral plus double derivative controller based on two degrees of freedom based in [19].

Moreover, in [20], a fuzzy logic system depending on a fault-tolerant compensation (FTC) control approach was presented against simultaneous additive, multiplicative actuator faults, and nonlinearity in Markov jump systems. In [21], the neural network (NN)-based FTC issue was illustrated for Markovian jump systems. In [22], a gorilla troops algorithm was employed for optimal control of the power network flow with integration of the thyristor-controlled series capacitor (TCSC) devices to improve the voltage stability, reduce fuel costs, and eliminate emissions of power networks. In [23], a cascaded proportional integral–proportional integral (PI–PI) and proportional–derivative with filter-PI was designed using a coyote optimization algorithm to handle the load frequency control in MAPSs. In [24], an intelligent type II fuzzy PID (T2-FPID) controller was combined with a water cycle algorithm (WCA) and applied on a MAPS with generation rate constraints. In [25], an arithmetic optimization algorithm (AOA) was investigated to fine-tune a fuzzy PID controller taking into consideration the effect of the high voltage direct current link to eliminate the AC transmission disadvantages. In [26], a gravitational search technique was integrated with a firefly algorithm to improve the tuning of the controller parameter and applied on a two-area hydrothermal power systems. In [27], a bees algorithm (BA) was employed to tune the parameters of the Fuzzy PID with filtered derivative, and implemented on a dual-area interconnected power system.

Recently, a novel artificial rabbits algorithm (ARA) was proposed by Wang et al. [28] that draws inspiration from rabbit survival tactics in nature, such as detour foraging and haphazard hiding. This fundamental motivation for the ARA stresses the effectiveness of its features to address a variety of optimization issues. The rabbit is forced to eat the grasses next to neighboring nests of others as part of the detour foraging technique, which can keep attackers from finding its nest. Moreover, a rabbit may use the randomized hiding technique to pick at arbitrary any of its own shelters to hide in, which might lessen the likelihood that it will be taken by its adversaries. In addition, the rabbits’ energy would decrease, which will cause them to switch from the detour foraging method to the haphazard hiding strategy. The main contributions of this paper can be summarized as follows:

▪

In contrast to the scenario employed by the other methods, a unique model is utilized in the ARA.

▪

Given the distinctive characteristics of the ARA, this paper’s focus is on optimizing the PID controller settings for the LFC problems.

▪

The simulation techniques make use of a two-area non-reheat thermal MAPS.

▪

The suggested ARA is used in comparison to the particle swarm optimization (PSO), differential evolution (DE), JAYA optimizer, and self-adaptive multi-population elitist (SAMPE) JAYA optimizers in three distinct test situations with different sets of disturbances.

▪

The outcomes produced by the ARA-based PID controller design are evaluated against a number of published methods.

▪

These simulated results demonstrate that the developed PID controller relying on the ARA is efficient and excellent at managing load frequency management in multiple-area power grids.

▪

It is reliable and produces superior outcomes when compared to other indices and instances.

The structure of this article is as follows. The design of the integral-based objective features is covered in Section 2, along with a summary of the LFC optimization issue taking into account the power system model, its components, and the applied PID model. Section 3 presents the suggested ARA method and its phases; Section 4 presents the results and discussion; and Section 5 presents the findings.

2. Problem Formulation

2.1. MAPS Model

In this study, the power system model is modified to include two non-reheat thermal power plants. As shown in Figure 1, the primary parts consist of the speed-governing device, turbine, and generator for each region, which has two outputs and three inputs. The reheat thermal unit/turbine referenced is treated as a whole in this instance, together with numerous other reheat thermal units as indicated in Ref. [29]. In Appendix A, the baseline model parameters for the system under investigation are displayed. From Figure 1, the inputs are addressed by the controller signals (u₁ and u₂), the power change in the tie-line (∆P_TIE), and the power change in the demands (∆P_D1 and ∆P_D2). The outputs are the area control errors (ACE₁ and ACE₂), and the deviations in system frequencies (∆f₁ and ∆f₂) [15].

One of the most effective controllers for highly dynamic states of the system is the PID controller [30,31,32]. As a result, the PID controller is used in both parts of the model under consideration. In Figure 2, the PID design is illustrated. The derivative component is given a filter to reduce the impact of noise on the input signal. The transfer function of the PID (TF_PIDn) is mathematically denoted as:

$${{\displaystyle TF}}_{PIDn}=\left({{\displaystyle K}}_p+{{\displaystyle K}}_i\left(\frac{1}{s}\right)+{{\displaystyle K}}_d\left(\frac{1}{\frac{1}{n}+\frac{1}{s}}\right)\right)$$

(1)

The controllers’ inputs are the corresponding area control errors (ACE₁ and ACE₂) that come from:

$${{\displaystyle ACE}}_1={{\displaystyle B}}_1\Delta {{\displaystyle f}}_1+\Delta {{\displaystyle P}}_{TIE}$$

(2)

$${{\displaystyle ACE}}_2={{\displaystyle B}}_2\Delta {{\displaystyle f}}_2+{{\displaystyle a}}_{12}\Delta {{\displaystyle P}}_{TIE}$$

(3)

Figure 1. Block diagram for a two-area power system model [15,33].

Figure 1. Block diagram for a two-area power system model [15,33].

Figure 2. PID controller diagram containing a derivative filter component.

Figure 2. PID controller diagram containing a derivative filter component.

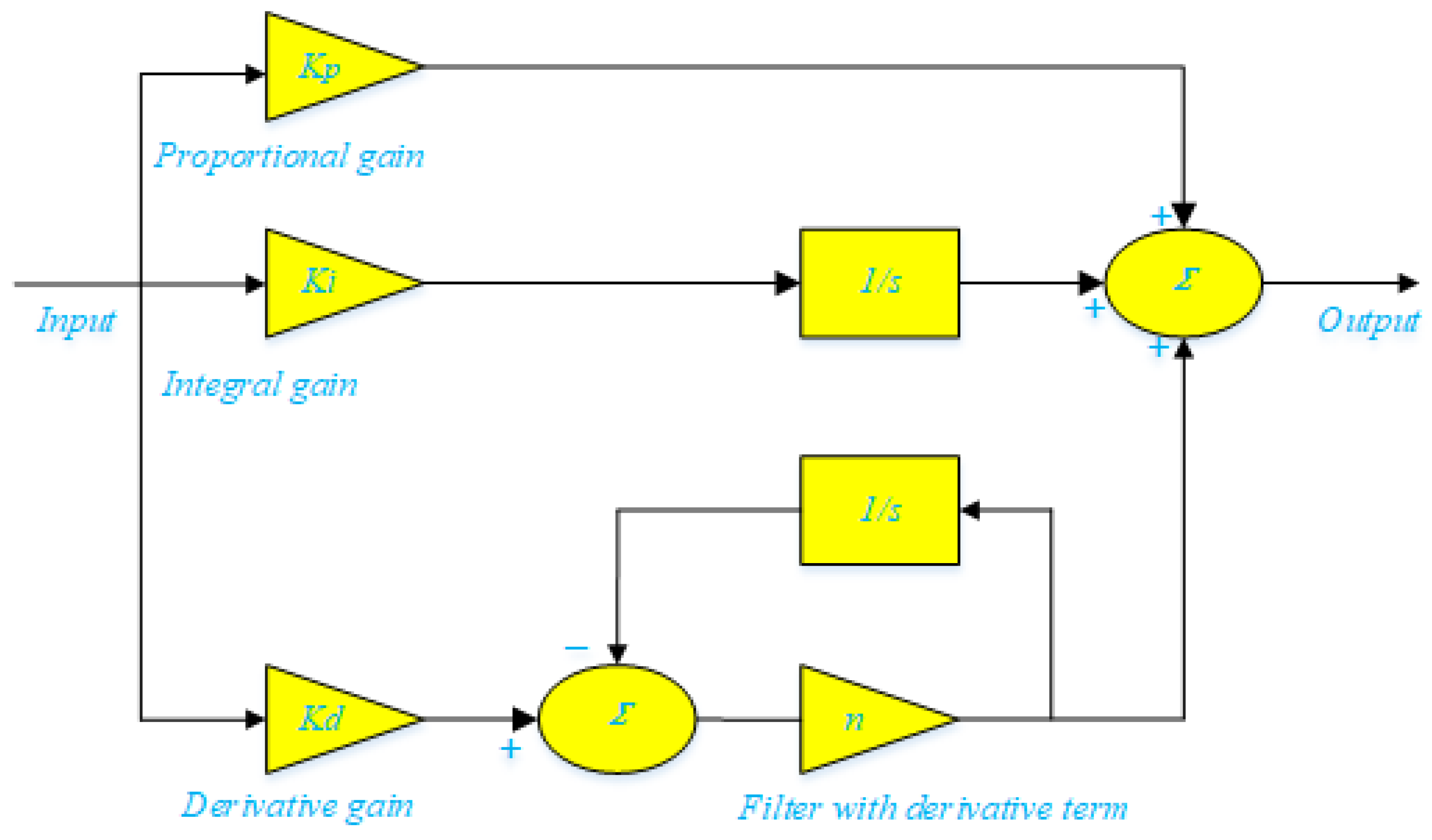
2.2. Objective Function

The objective function is taken into consideration to expose the demands and restrictions of the system to construct the PID controller as efficiently as possible.

The following are some instances of practical control needs for the AGC:

• The frequency variation should recover to zero once the load is altered.
• The integral of the frequency error must have the lowest feasible value.
• The control loop needs to be sufficiently stable.
• Each region shall carry out its load under normal circumstances, and after a load disruption, the power exchange between areas should be quickly restored to its planned value. A time-domain goal function is modified using integral criteria to determine the best PID controller gains as follows:

$$J_2=ITAE={\displaystyle \underset{0}{\overset{t_{sim}}{\int }}\left(\left|\Delta f_1\right|+\left|\Delta f_2\right|+\left|\Delta P_{TIE}\right|\right)}.t.dt$$

(4)

Additionally, J₂ may be easily advanced to take into account reducing the peak-overshoots of the frequency variations for both regions and in the tie-line power transfer. This evolution of the fitness form benefits from obtaining a sufficient damping ratio to provide a certain level of stability [15]. The limits of the controller parameter settings are the problem limitations. As a result, the design issue might be described as the subsequent optimization issue problem.

Minimize J

(5)

Subject to
                        For PID controller: Kp_min ≤ Kp ≤ Kp_max,
                                 Ki_min ≤ Ki ≤ Ki_max,
                                 Kd_min ≤ Kd ≤ Kd_max,
                               n_min ≤ n ≤ n_max

(6)

where J might either be J₁ or J₂. Every controller parameter’s lowest and maximum values are denoted by the subscripts “min” and “max.” The relative quantities are determined to be 0 and 3, and the border of the filter factor n is selected to be between 0 and 500 [15].

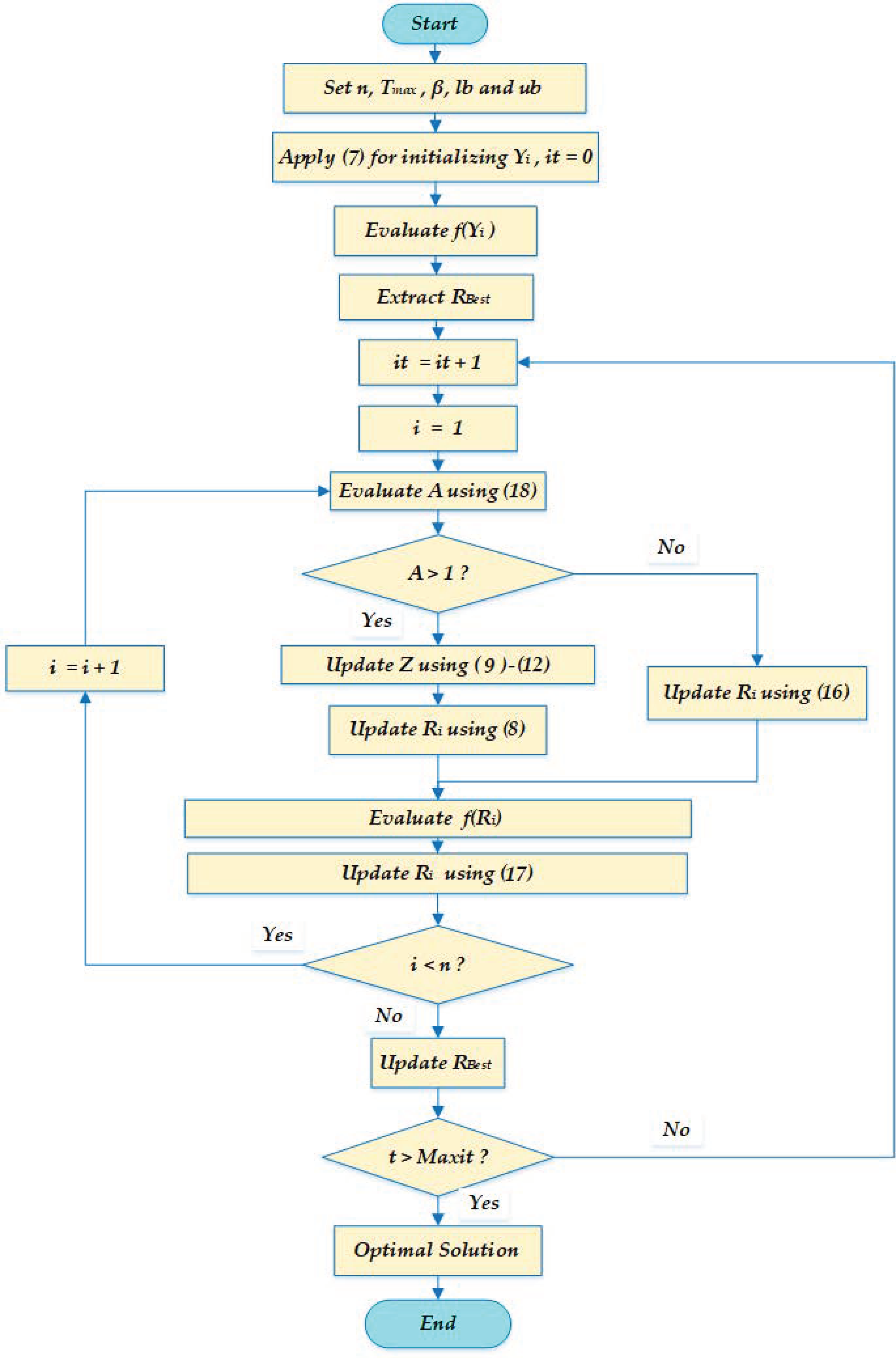
3. Mathematical Model of the Proposed Artificial Rabbits Algorithm (ARA)

In the proposed ARA, the rabbit survival tactics in nature are mathematically modeled into an efficient optimization framework. In this way, two simulated strategies are handled, which are detour foraging and haphazard hiding. The rabbit is forced to eat the grasses next to the neighboring nests of others as part of the detour foraging technique, which can keep attackers from finding its nest. Moreover, a rabbit may use the randomized hiding technique to pick at arbitrary any of its own shelters to hide in, which might lessen the likelihood that it will be taken by its adversaries. In addition, the rabbits’ energy would decrease, which will cause them to switch from the detour foraging method to the haphazard hiding strategy [28].

The suggested algorithm’s rules are applied for each iteration to update each population rabbit’s location, which is then evaluated by the fitness function. The solutions grow finer as the process is continued. Each location of the starting population is assigned based on Equation (7) to a random location inside the search area:

$$Y_i=lb+[ub-lb]\times rand(1,\dim )i=1,2,\dots ,n$$

(7)

where Y_i indicates the position of the rabbit, lb and ub refer to the lower and upper limits of the considered variables, n and dim are, respectively, the population size and the number of control variables of the problem.

3.1. Detour Foraging

According to the ARA’s detour foraging behavior, every searching individual prefers to change its relative position to another searching individual selected at random from the swarming and join perturbation. The following is the envisaged mathematical description of the rabbits’ detour foraging:

$$R_i\left(it+1\right)=Y_j\left(it\right)+Z\times \left(Y_i\left(it\right)-Y_j\left(it\right)\right)+round\left(0.5\times \left(0.05+v_1\right)\right)\times SND, i,j=1,\dots ,j\ne i$$

(8)

$$Z=c\times L$$

(9)

$$c\left(k\right)=\{\begin{array}{c}1 if k=g\left(l\right)\\ 0 else \end{array} k=1,\dots ,dim and l=1,\dots ,\left[v_2,dim\right]$$

(10)

$$g=randperm\left(d\right), n_1~N\left(0,1\right)$$

(11)

$$L=\sin \left(2\pi v_3\right)\times \left(e-e^{{\left(\left(it-1\right)/T_{max}\right)}^2}\right)$$

(12)

where it refers to the current time; R_i and Y_i are the new and old positions of rabbit (i); SND is governed by the standard normal distribution; L is the traveling distance, which reflects the movement rate; round and randperm are functions for rounding the value into the closest integer and randomizing permutation of the integers from 1 to dim; $v$₁, $v$₂ and $v$₃ indicate three randomized values within range [0, 1], and T_max indicates the highest number of iterations.

3.2. Randomized Hiding

A rabbit often digs several burrows close to its nest to use as cover when fleeing from enemies. In this respect, the following equation is provided.

$$b_{i,j}\left(it\right)=Y_i\left(it\right)+H.G.Y_i\left(it\right), i=1,\dots ,n and j=1,\dots ,dim$$

(13)

$$H=\frac{T_{max}+1-it}{T_{max}}.v_4$$

(14)

$$G\left(k\right)=\{\begin{array}{c}1 if k=j\\ 0 else \end{array} k=1,\dots ,dim$$

(15)

where b_i,j is the jth burrow of the rabbit (i); H is the concealing parameter and gradually decreases from 1 to 1/T_max with a random perturbation over the course of iterations; $v$₄ is a randomized value within range [0, 1]. Based on this characteristic, those burrows are first created in a rabbit’s larger neighborhood. This neighborhood shrinks as the iterations grow more numerous.

Rabbits must locate a secure place to hide in order to survive. They are therefore discouraged from picking a hole arbitrarily among those they have to hide in to avoid being discovered. This method of random concealment may be mathematically characterized as follows:

$$R_i\left(it+1\right)=Y_i\left(it\right)+Z\times \left(v_5\times b_{i,j}\left(t\right)-Y_i\left(it\right)\right) i=1,\dots ,n$$

(16)

When one of detour foraging or randomized hiding is successful, the ith rabbit’s position is updated as follows:

$$Y_i\left(it+1\right)=\{\begin{array}{c}{Y}_i\left(it\right) f(Y_i\left(it\right) \le f\left(R_i\left(it+1\right) \right)\\ R_i\left(it+1\right) f(Y_i\left(it\right)>f\left(R_i\left(it+1\right) \right) \end{array}$$

(17)

3.3. Energy Shrink (Switch from Exploration to Exploitation)

Modeling the transition from the discovery phase related to detour foraging to the exploiting phase represented by randomized hiding considers an energy component. The following definitions apply to the energy factor in this algorithm:

$$A\left(it\right)=4\left(1-\frac{it}{T_{max}}\right)\ln \frac{1}{r}$$

(18)

The above-mentioned tactics can be gathered in Figure 3 to illustrate the main steps of the proposed ARA technique.

4. Simulation Results and Discussions

The proposed ARA (Figure 3) is used in this section to minimize the target function of the ITAE, which is described in Equation (4). For comparison, the PSO, DE, JAYA, and SAMPE-JAYA optimization techniques are also used. Three different test scenarios with different sets of perturbations are performed. The entire simulation procedure is performed in MATLAB. The data from the power systems under study are identical to those from the references [7,12]. In every simulation run, a population number of 10 is used, and a maximum of 100 repetitions is specified. All tests are conducted depending upon the equivalent amount of function executions to allow for a valid assessment of the competing methods (1000 evaluations). In Appendix B, the quantities of the relevant parameters for each method under comparison are listed. The algorithms are carried out 20 times while considering these model parameters, and the best ultimate result from each is then obtained. Three cases are investigated depending on the considered objective function and the placement of the step change as summarized:

• Case study 1: Step load perturbation in area 1 only.
• Case study 2: Step load perturbation in area 2 only.
• Case study 3: Step load perturbation in area 1 and area 2.

4.1. Simulation of Case Study 1

In this scenario, area 2 remains unchanged, while a step load increment of 0.1 p.u. in area 1 is considered.

Table 1. Simulation results under Case Study 1.

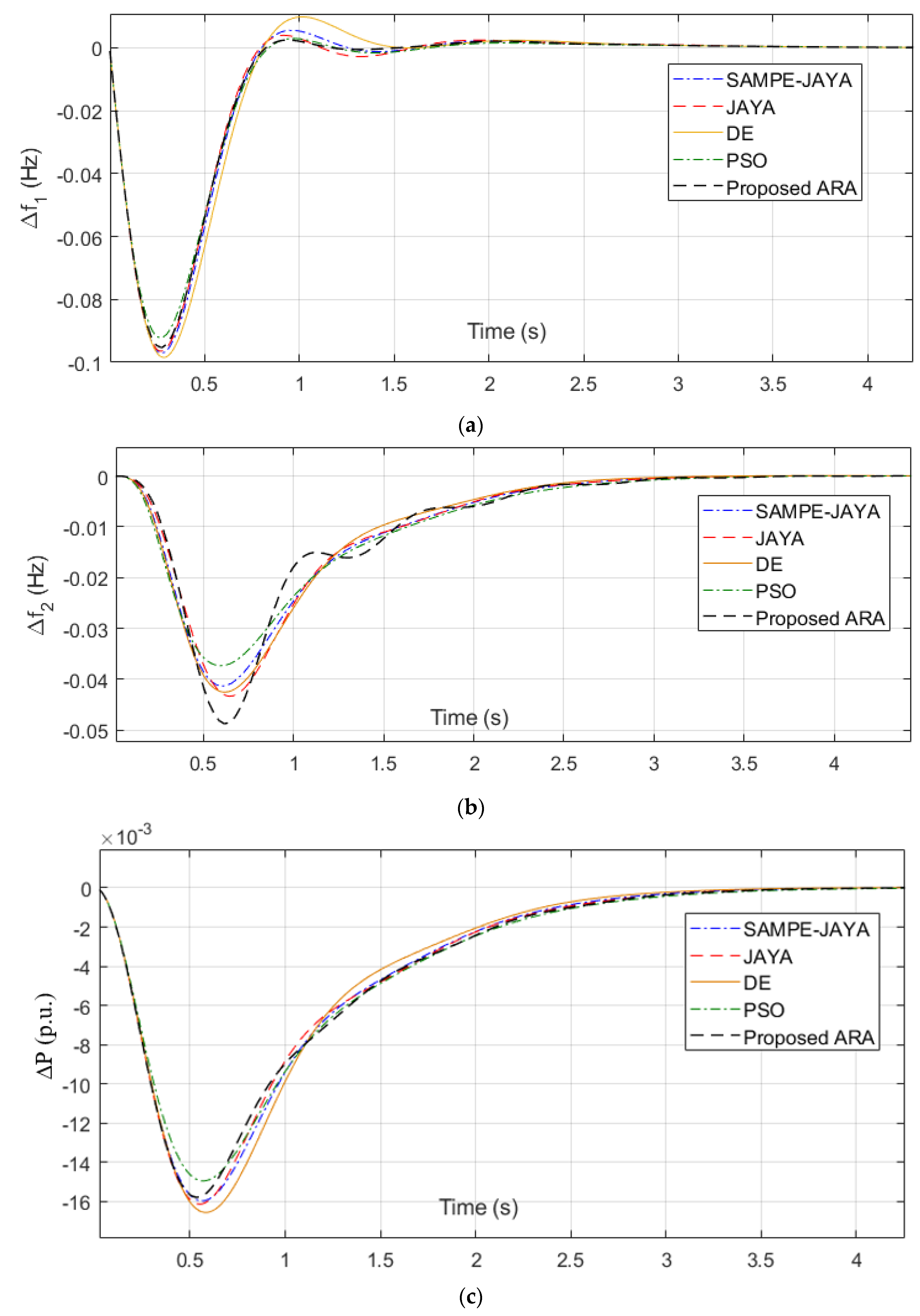
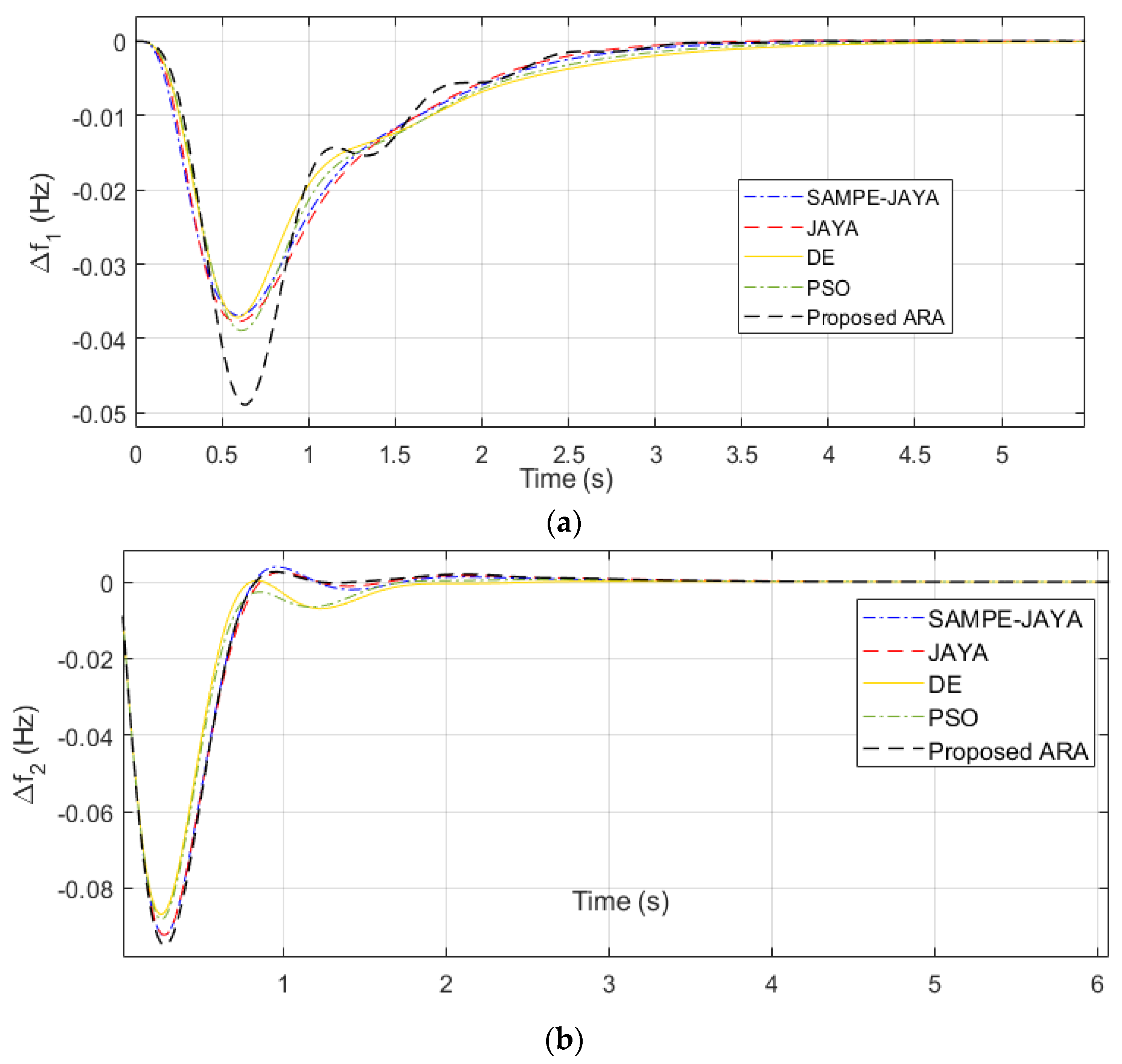
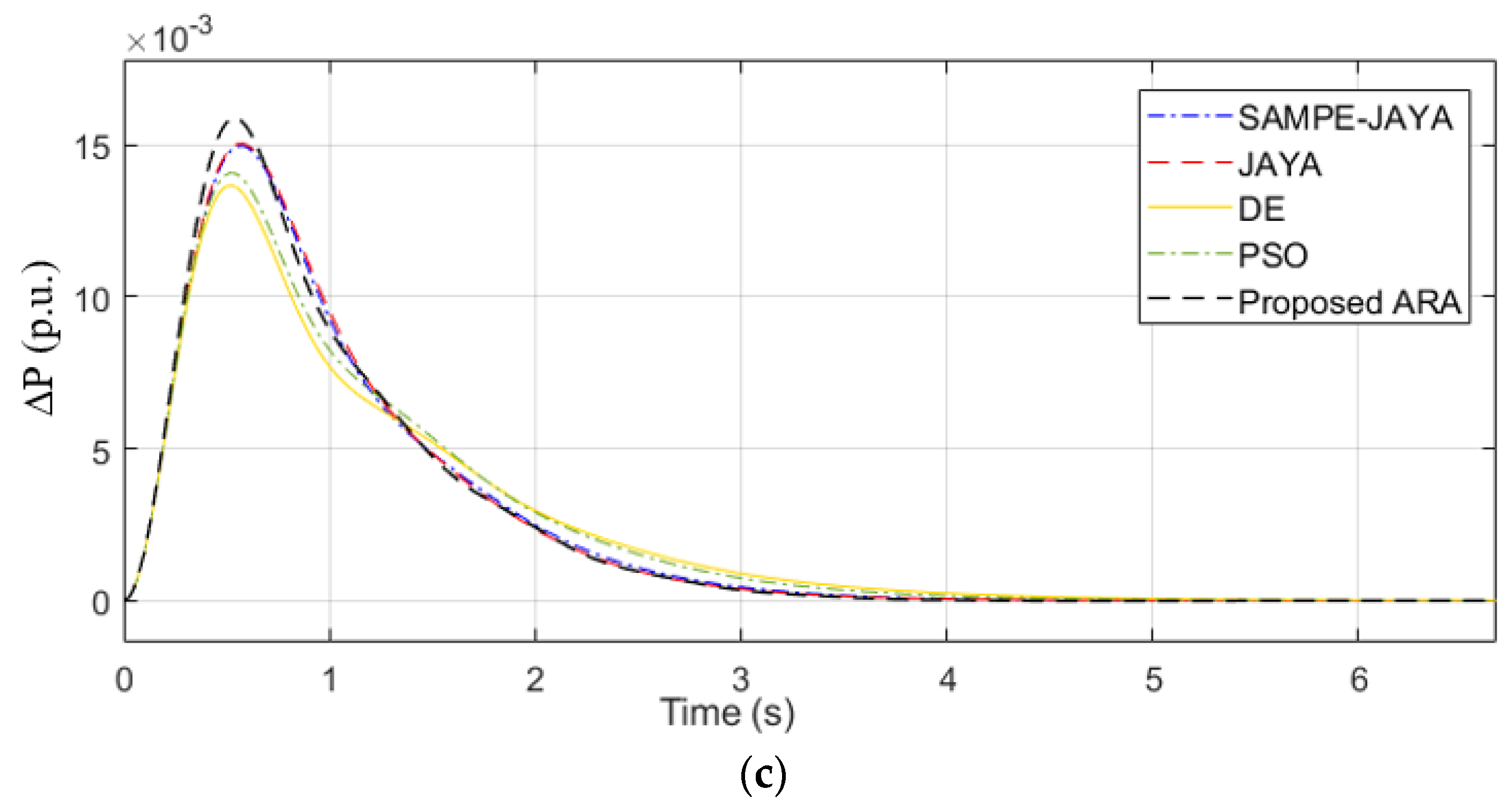
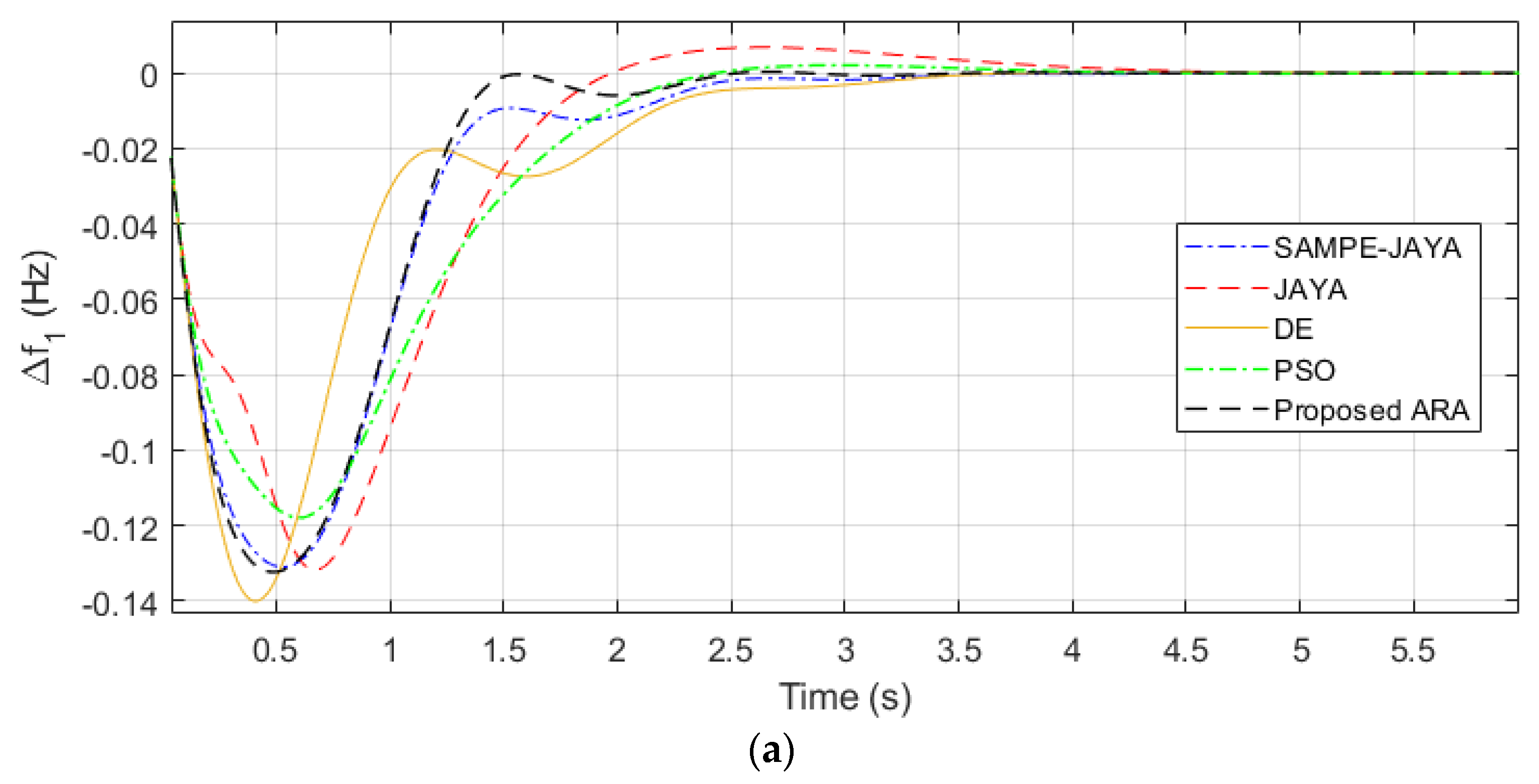
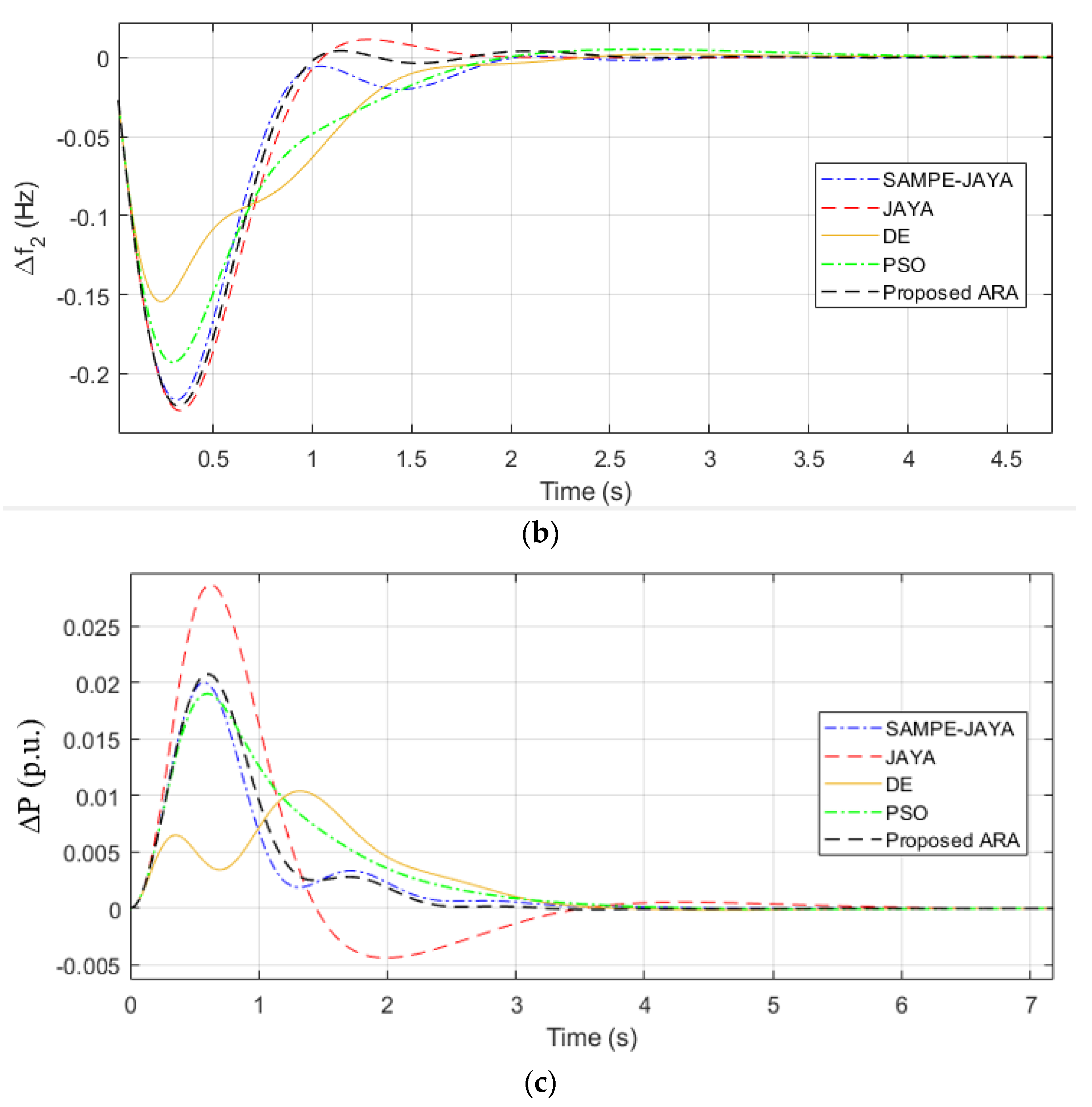
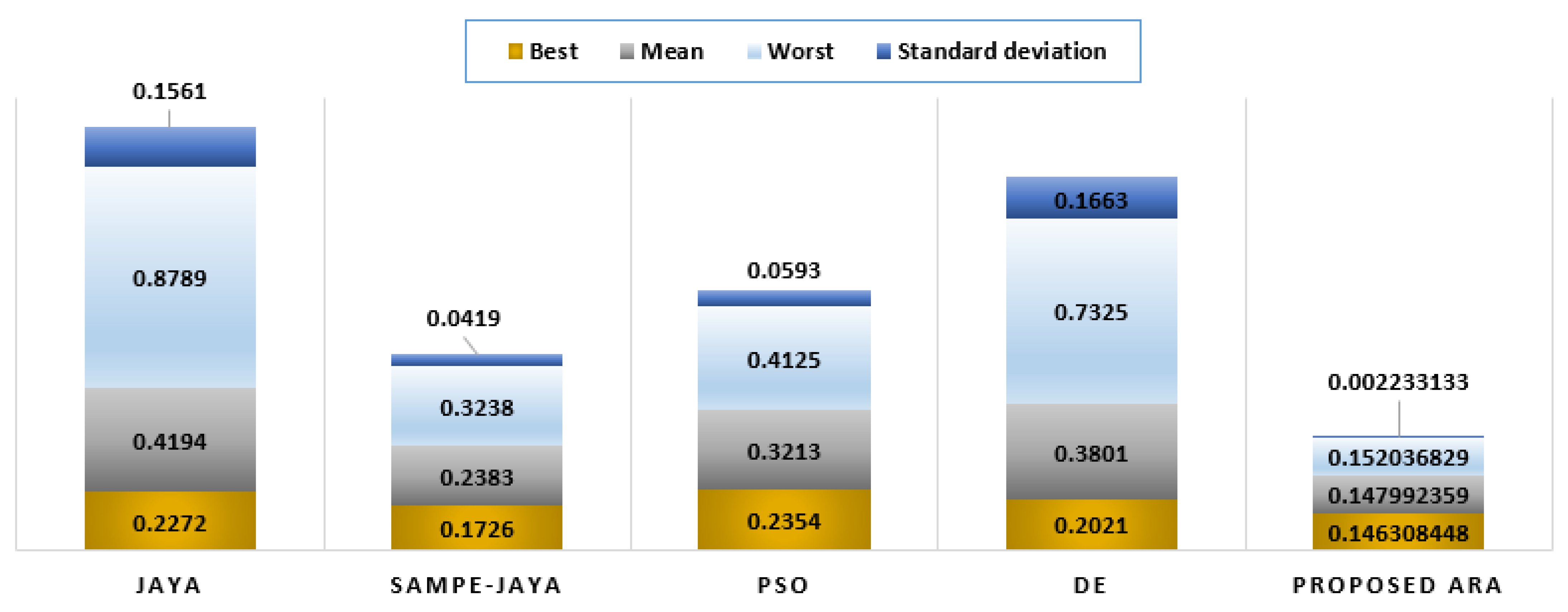
Algorithm		SAMPE-JAYA	JAYA	DE	PSO	Proposed ARA
Controller parameters	KP1	1.8066	1.8394	1.7101	1.9602	1.875133
	Ki1	2.9895	3	3	3	2.997462
	Kd1	0.5654	0.5806	0.5284	0.6083	0.578319
	n1	88.111	72.985	372.86	385.58	115.132
	KP2	2.1364	1.4843	2.8899	2.9756	2.979045
	Ki2	0.4187	0.4306	1.0332	1.5561	0.729651
	Kd2	1.7534	1.0095	1.9478	2.6638	1.050161
	n2	146.04	425.37	332.02	497.92	15.40281
ITAE Value		0.0769	0.077	0.0781	0.0769	0.075401
ITAE Improvement % compared to the proposed ARA		1.949	2.077	3.455	1.949	-

shows the relevant simulation findings for the evaluated ITAE minimization techniques that are concerning. The tabulated data are presented together with the ITAE objective values, as well as the optimal controller parameter settings of K_p, K_i, K_d, and n throughout every area. In comparison to PSO, DE, JAYA, and SAMPE-JAYA, which had minimum ITAE values of 0.0769, 0.0781, 0.077, and 0.0769, respectively, the proposed ARA achieved a minimum value of 0.0754. As shown, the proposed ARA can acquire significant improvements in the ITAE value of 1.949, 3.455, 2.077, and 1.949 %, respectively, compared to PSO, DE, JAYA and SAMPE-JAYA.

Furthermore, the dynamic responses for the frequency deviations in each area and the tie-line power are displayed in Figure 4. As shown in Figure 4, the proposed ARA has the edge over PSO, DE, JAYA, and SAMPE-JAYA in minimizing the fitness function. On the other hand, the peak overshoot that is acquired by the proposed ARA is the smallest for the frequency change in area 1 as illustrated in Figure 4a where it records 0.00246 Hz, while the change in frequency in area 1 is 0.00556, 0.00394, 0.00984 and 0.00295 based on SAMPE-JAYA, JAYA, DE and PSO, respectively. On the other side, the frequency change in area 2 has higher overshooting and oscillations by the proposed ARA as shown in Figure 4b. However, in general, the judgment is the considered ITAE fitness value where the proposed ARA finds the minimum value compared to PSO, DE, JAYA, and SAMPE-JAYA.

To show a statistical comparison between SAMPE-JAYA, JAYA, DE, PSO and the proposed ARA, Figure 5 displays the evaluated four indices of the minimum, mean, maximum, and standard deviation of the obtained ITAE under the different separate runs. As shown, the least indices are derived using the proposed ARA. It finds the least minimum, mean, maximum, and standard deviation with 0.0754, 0.07587, 0.0764, and 0.00034, respectively. This table declares the high effectiveness and capacity of the suggested ARA compared to SAMPE-JAYA, JAYA, DE and PSO.

In terms of ITAE and settling time,

Table 2. Comparative performance of various algorithms in terms of ITAE and settling time.

Controller	Optimization Technique	Reference	Settling Times(s)			Objective Value
			∆PTIE	∆F2	∆F1	ITAE
PI	Conventional	[12]	28.27	45.01	45	3.5795
PI	GA	[12]	9.37	11.39	10.59	2.7475
PI	BFOA	[12]	6.35	7.09	5.52	1.8379
PI	DE	[7]	5.75	8.16	8.96	0.9911
PI	PSO	[8]	5.0	7.82	7.37	1.2142
PI	BFOA-PSO	[8]	5.73	7.65	7.39	1.1865
PI	FA	[12]	5.62	7.22	7.11	0.8695
PID	FA	[12]	4.78	5.49	4.25	0.4714
PID	Proposed ARA	Presented	3.059294	2.901341	2.195834	0.075401

compares the effectiveness of the suggested ARA-based PID controller with a number of previously reported control systems. As shown, the proposed ARA obtains the minimum ITAE of 0.0754 where the conventional PI, PI-based-GA, PI-based-BFOA, PI-based-DE, PI-based-PSO, PI-based-BFOA-PSO, PI-based-FA, and PID-based-FA finds 3.5795, 2.7475, 1.8379, 0.9911, 1.2142, 1.1865, 0.8695, and 0.4714, respectively. This table declares how the suggested ARA-based PID controller outperforms other previously reported optimization techniques in terms of minimal ITAE value, frequency settling time, and tie-line power deviations.

4.2. Simulation of Case Study 2

In this scenario, without affecting area 1, a step load rise of 0.1 p.u. in area 2 is taken into account.

Table 3. Simulation results under Case Study 2.

Algorithm		SAMPE-JAYA	JAYA	DE	PSO	Proposed ARA
Controller parameters	KP1	2.7421	2.017	2.5822	2.2948	2.794512
	Ki1	0.3762	1.9978	0.4092	1.1983	0.509808
	Kd1	3	2.403	1.2792	1.0794	0.995084
	n1	307.57	57.928	409.97	500	15.03582
	KP2	1.9881	1.9102	2.4546	2.2328	1.865161
	Ki2	2.9963	3	3	2.9705	2.997782
	Kd2	0.5997	0.6106	0.6618	0.6757	0.576527
	n2	500	372.48	410.78	136.77	166.8088
ITAE Value		0.077	0.078	0.082	0.0816	0.075409
ITAE Improvement % compared to the proposed ARA		2.066566	3.322123	8.038117	7.587323	-

shows the relevant simulation findings for the evaluated ITAE minimization techniques that are concerning. This table illustrates the optimal controller parameter settings of K_p, K_i, K_d, and n throughout every area. As shown, the proposed ARA achieved a minimum value of 0.0754. On the other side, PSO, DE, JAYA, and SAMPE-JAYA records minimum ITAE values of 0.0816, 0.082, 0.078, and 0.077, respectively. As shown, the proposed ARA can acquire significant improvements in the ITAE value of 7.587, 8.038, 3.322, and 2.066%, respectively, compared to PSO, DE, JAYA, and SAMPE-JAYA.

Furthermore, the dynamic responses for frequency deviations in each area and tie-line power under ITAE are displayed in Figure 6. As shown, the proposed ARA has the edge over PSO, DE, JAYA and SAMPE-JAYA in minimization the fitness function. On the other hand, it provides a small settling time of 2.93 and 2.231 s for the frequency change in areas 1 and 2. In addition, it records the smallest settling time of 3.034 s in the tie-line power variations as illustrated in Figure 6c where SAMPE-JAYA, JAYA, DE and PSO record 3.208, 3.125, 3.911 and 3.631, respectively. The frequency change in area 1 has higher overshooting and oscillations in the proposed ARA as shown in Figure 6a. However, in general, the ITAE fitness value considers the three responses of frequencies in areas 1 and 2 and the power change in the tie lines where the proposed ARA finds the best performance.

To show a statistical comparison between SAMPE-JAYA, JAYA, DE, PSO and the proposed ARA, Figure 7 displays the evaluated four indices of the minimum, mean, maximum, and standard deviation of the obtained ITAE under different separate runs. As shown, the least indices are derived using the proposed ARA. It finds the least minimum, mean, maximum, and standard deviation with 0.0754, 0.07568, 0.0763, and 0.0003, respectively. This table declares the high effectiveness and capacity of the suggested ARA compared to SAMPE-JAYA, JAYA, DE, and PSO.

4.3. Simulation of Case Study 3

In this scenario, a simultaneous variation in both areas is simulated where step load increments of 0.1 p.u. in area 1 and 0.2 p.u. in area 2 are taken into consideration.

Table 4. Simulation results under Case Study 3.

Algorithm		SAMPE-JAYA	JAYA	DE	PSO	Proposed ARA
Controller parameters	KP1	1.8022	2.1068	1.5717	1.7764	1.820495
	Ki1	2.6685	2.9333	2.7589	3	2.994891
	Kd1	0.6436	1.4944	0.3809	0.9385	0.577278
	n1	138.3	85.067	147.82	392.86	67.01898
	KP2	1.7795	1.1472	2.3342	1.562	1.565437
	Ki2	2.859	2.9487	2.9998	2.5835	2.989529
	Kd2	0.4627	0.4789	0.9962	0.6575	0.462035
	n2	340.75	489.58	332.55	500	448.9027
ITAE Value		0.1726	0.2272	0.2021	0.2354	0.146308
ITAE Improvement % compared to the proposed ARA		17.97	55.29	38.13	60.89	-

shows the relevant simulation findings for the evaluated ITAE minimization techniques that are concerning. In comparison to PSO, DE, JAYA, and SAMPE-JAYA, which had minimum ITAE values of 0.2354, 0.2021, 0.2272 and 0.1726, respectively, the proposed ARA achieved a minimum value of 0.146308. As shown, the proposed ARA can acquire significant improvements in the ITAE value of 60.89, 38.13, 55.29 and 17.97%, respectively, compared to PSO, DE, JAYA and SAMPE-JAYA.

Furthermore, the dynamic responses for frequency deviations in each area and tie-line power under ITAE are displayed in Figure 8. As shown in Figure 8, the proposed ARA has the edge over PSO, DE, JAYA, and SAMPE-JAYA in minimizing the fitness function. In this regard, the settling times of the frequency deviations in areas 1 and 2 and tie-line power are displayed in

Table 5. Settling times (s) under Case Study 3.

Change	SAMPE-JAYA	JAYA	DE	PSO	Proposed ARA
∆F1	2.4343	3.6834	3.0722	2.2596	2.2967
∆F2	1.8693	1.6293	2.0993	3.1665	0.9804
∆PTIE	3.1625	3.2571	3.4722	3.5186	2.2305

. This table shows the high effectiveness of the proposed ARA in achieving the least settling times of 0.9804 and 2.2305 s for the frequency deviation in area 2 and tie-line power where it finds, at the same time, a very low settling time of 2.2967 s compared to the others.

To show a statistical comparison between SAMPE-JAYA, JAYA, DE, PSO and the proposed ARA, Figure 9 displays the evaluated four indices of the minimum, mean, maximum, and standard deviation of the obtained ITAE under different separate runs. As shown, the least indices are derived using the proposed ARA. It finds the least minimum, mean, maximum, and standard deviation with 0.1463, 0.1480, 0.1520, and 0.0022, respectively. This table declares the high effectiveness and capacity of the suggested ARA compared to SAMPE-JAYA, JAYA, DE, and PSO.

5. Conclusions

In this paper, a novel meta-heuristic optimization technique called the Artificial Rabbits Algorithm (ARA) is developed and employed on optimizing the parameters of the proportional–integral–derivative (PID) controller for the load frequency control (LFC) in multi-area power systems (MAPSs) of two-area non-reheat thermal systems. The PID controller with a filter is successfully designed using the proposed ARA to minimize the integral time-multiplied absolute error (ITAE). Three cases of disturbances in the step load increases in areas 1/2 are handled. The proposed ARA is compared with various published techniques, including particle swarm optimization (PSO), differential evolution (DE), JAYA optimizer, and self-adaptive multi-population elitist (SAMPE) JAYA. The comparisons show that the PID controller’s design, which is based on the ARA, handles the load frequency regulation in MAPSs for the ITAE minimizations with significant effectiveness and success where the statistical analysis confirms its superiority.