Multifractal Characteristics of Uranium Grade Distribution and Spatial Regularities in a Sandstone-Type Uranium Deposit in Xinjiang, China
Abstract
:1. Introduction
2. Preliminaries and Method
2.1. Fractal Theory
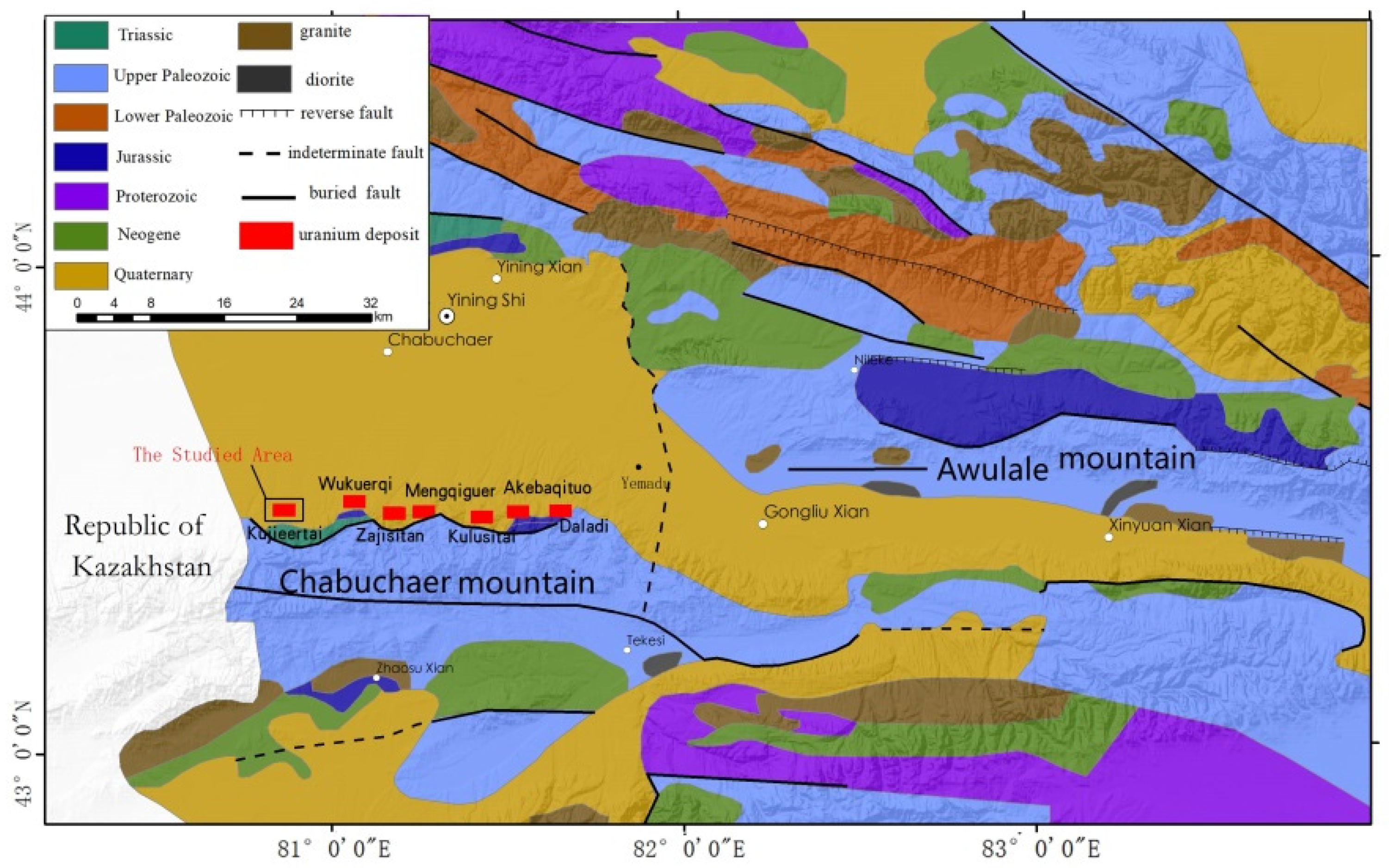
2.2. Overview of the Ore Deposit
3. Results and Discussion
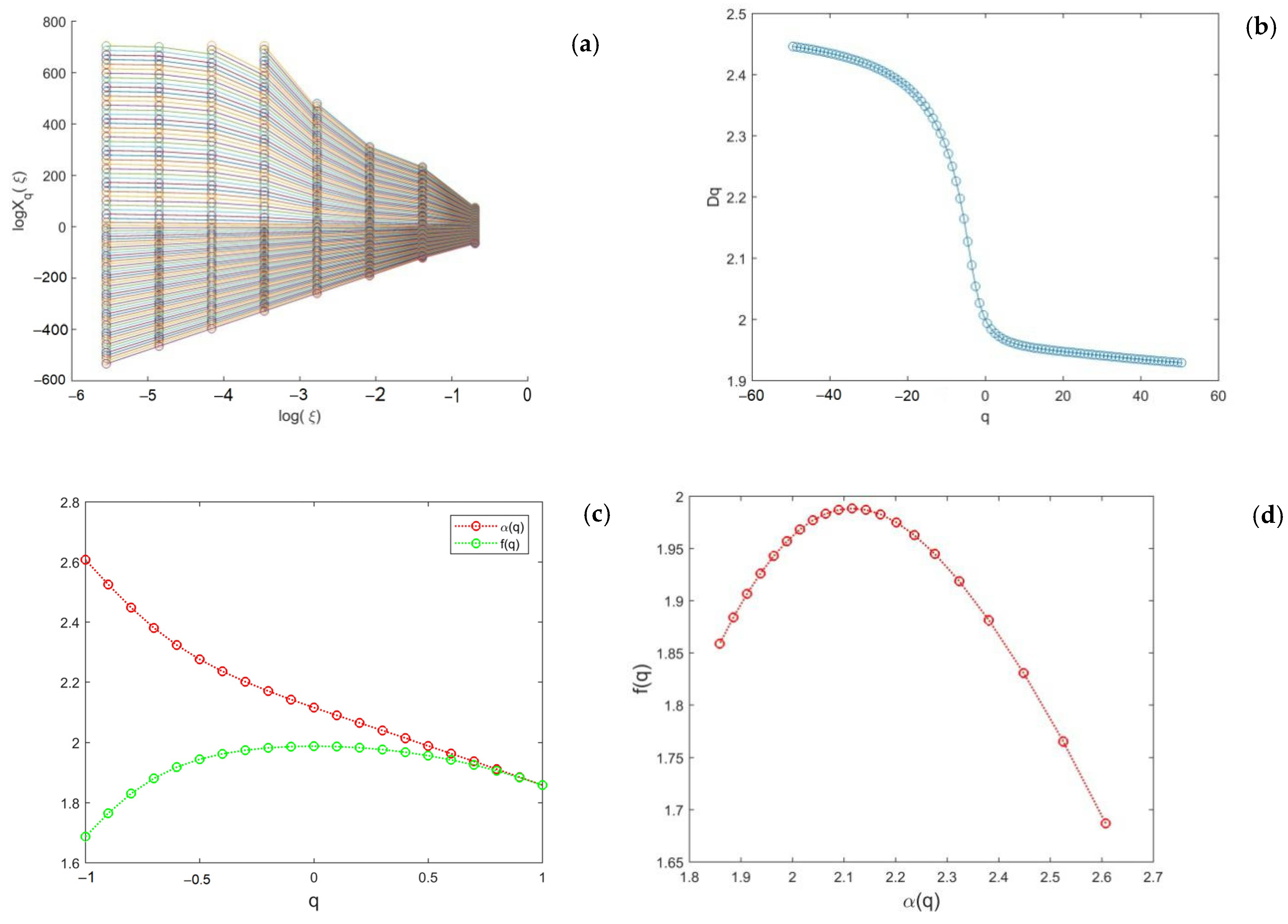
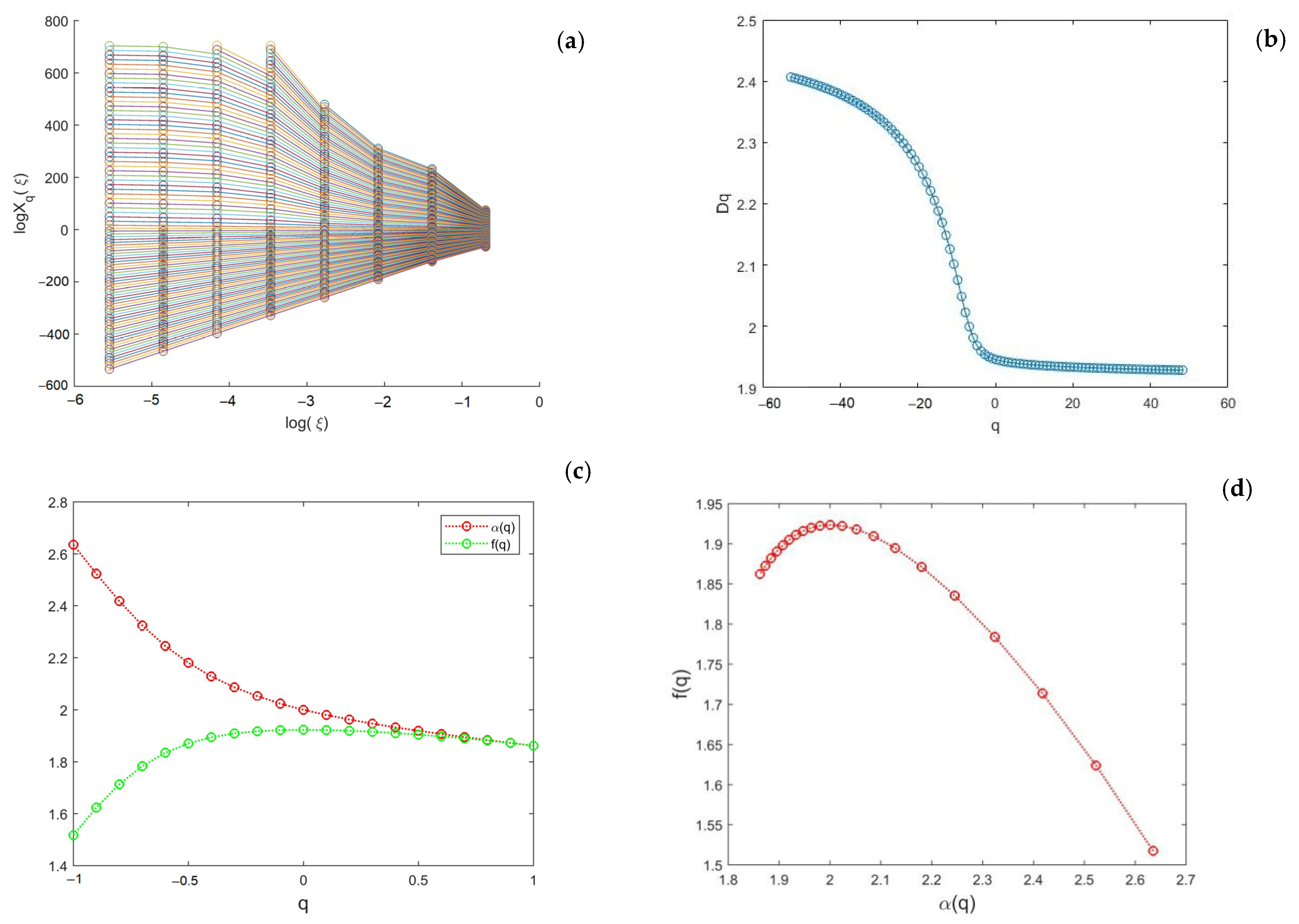
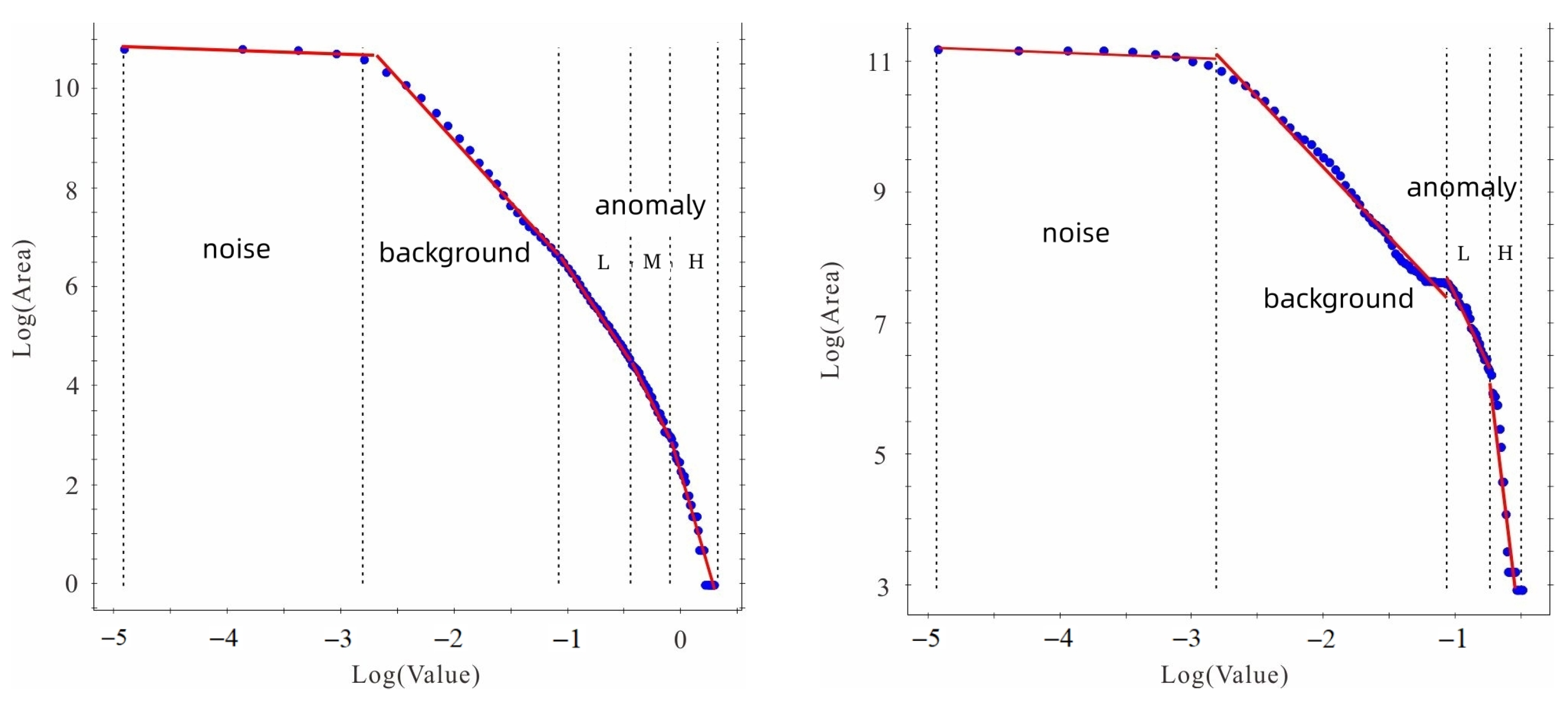
3.1. Multifractal Spectrum and Multifractal Parameters
3.2. Multifractal Spectrum Parameters Analysis of Uranium Grade
3.2.1. The Opening Width of Multifractal Spectrum ()
3.2.2. The Width of the Left Half and the Width of the Right Half of the Curve
3.2.3. The Spectral Height Difference of the Curve
3.2.4. The Skew Coefficient R of the Multifractal Spectrum
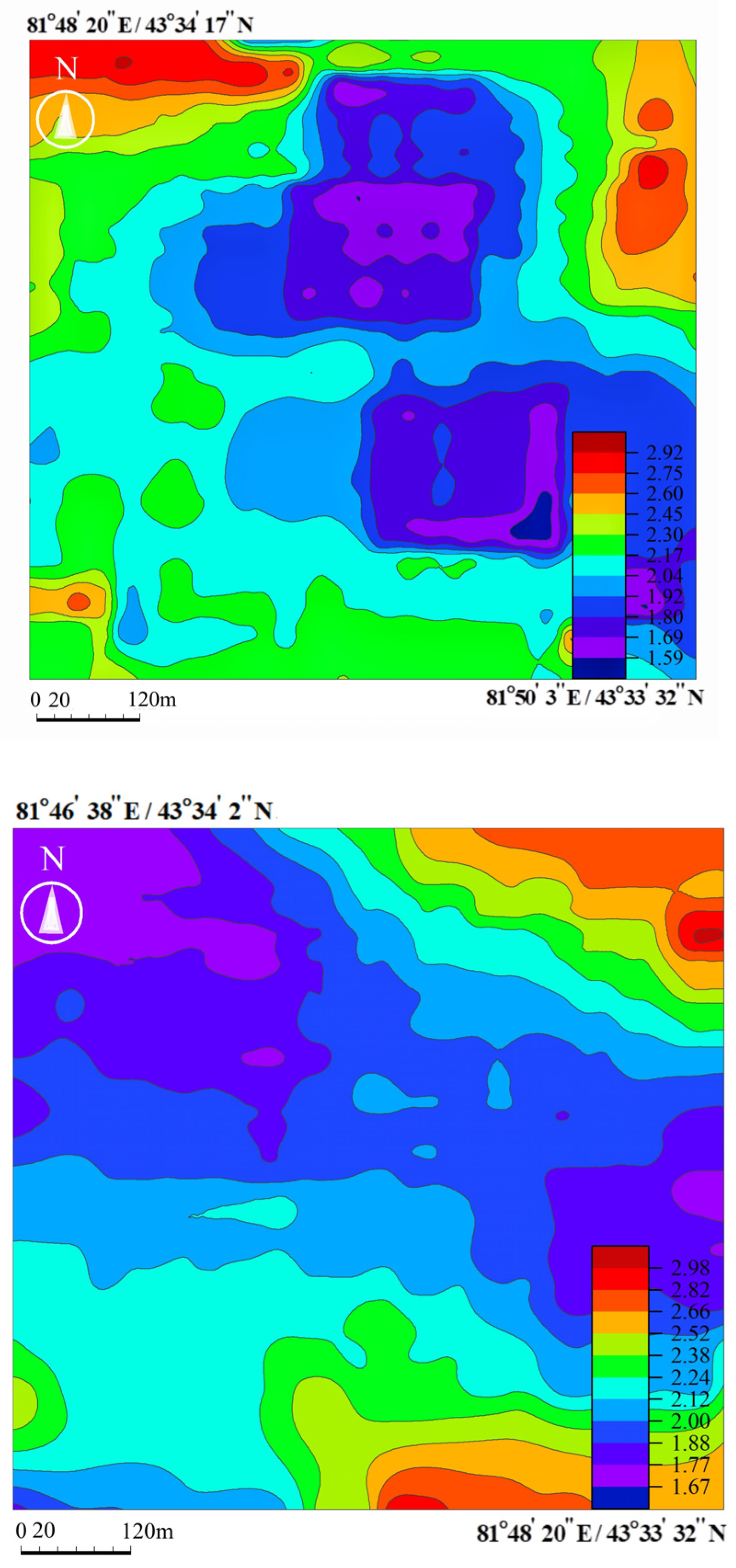
3.3. Uranium Distribution Information by Multifractal Local Singularity Exponent
4. Conclusions
- (1)
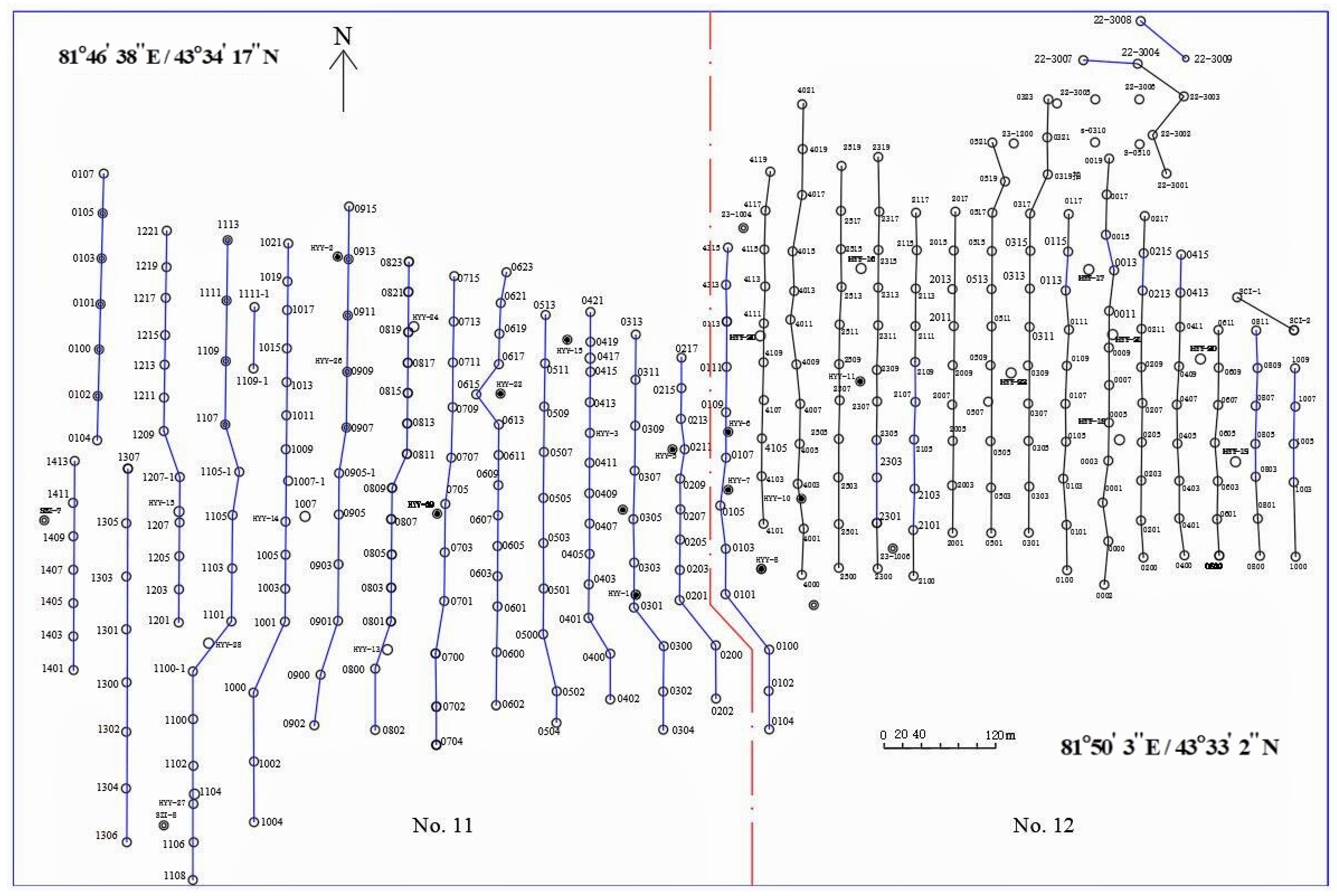
- A group of uranium-grade values and their plane distribution maps are obtained from the ore deposit, the uranium-grade grid data covering the area are formed by interpolating the uranium-grade values at these points, the data are processed by ash and the macroscopic distribution problem of geochemical elements is reduced to a microscopic distribution problem.
- (2)
- A multifractal model of uranium ore distribution is established, and the multifractal spectra and multifractal parameters of uranium grade in two stopes (No. 11 and No. 12 stopes) are obtained by numerical calculation. These spectral function images are almost parabolic shapes. Fractal dimension D0 and information dimension D1 of the uranium-grade distribution of stope No. 11 are 1.98 and 1.97, respectively, and fractal dimension D0 and information dimension D1 of the uranium grade distribution of stope No. 12 are 1.92 and 1.91. The skew coefficient R of the uranium-grade fractal spectrum of the two stopes is −0.30 and −0.56, respectively. The relationship between , and parameters shows that the average grade distribution of uranium ore in the two stopes has multifractal characteristics, and the differences in the multifractal parameters between the two areas are compared. After comparison, fractal dimension D0 and information dimension D1 of mining area No. 11 are both larger than the corresponding values of mining area No. 12. Similarly, the spectral width and the left-half spectrum width values of stope No. 11 are also larger than those of stope No. 12. Moreover, the skew coefficient R of the two stopes satisfies , indicating that the uranium-ore-grade distribution in stope No. 11 is more densely distributed than that in stope No. 12. The results after comparison all show that the singularity of uranium-grade distribution in the No. 11 stope is greater, the internal structure of uranium ore in this stope is more complex and the uranium ore is easier to enrich. The multifractal method can effectively indicate the local anomalies in the geochemical elements.
- (2)
- Singularity exponent distribution maps of uranium grade in the two stopes are obtained using the element content–area method. The spatial distribution region of the calculated singularity exponent () has a strong correlation with the uranium-grade enrichment region, and the singularity exponent can be used to accurately decompress and identify uranium-grade anomalies and background information. This is indicative for element content estimation, deposit reserve prediction and mineral resource information acquisition.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mandelbrot, B.B. The Fractal Geometry of Nature. Am. J. Phys. 1983, 51, 286–287. [Google Scholar] [CrossRef]
- Kenneth, F.; Xiong, J. Dimension conservation for self-similar sets and fractal percolation. Int. Math. Res. Not. 2015, 24, 13260–13289. [Google Scholar]
- Albeverio, S.; Torbin, G. Fractal properties of singular probability distributions with independent Q*-digits. Bull. Des Sci. Mathématiques 2005, 129, 356–367. [Google Scholar] [CrossRef]
- Hall, P.; Roy, R. On the relationship between fractal dimension and fractal index for stationary stochastic processes. Ann. Stat. 1994, 4, 241–253. [Google Scholar] [CrossRef]
- Yang, S.; Liang, M.; Yu, B.; Zou, M. Permeability model for fractal porous media with rough surfaces. Microfluid. Nanofluid. 2015, 18, 1085–1093. [Google Scholar] [CrossRef]
- Zhao, J.; Chen, S.; Zuo, R.; Zhao, M. Controls on and prospectivity mapping of volcanic-type uranium mineralization in the Pucheng district, NW Fujian, China. Ore Geol. Rev. J. Compr. Stud. Ore Genes. Ore Explor. 2019, 112, 103028. [Google Scholar] [CrossRef]
- Lovejoy, S.; Schertzer, D.; Ladoy, P. Fractal characterization of inhomogeneous geophysical measuring net-works. Nature 1987, 319, 43–44. [Google Scholar] [CrossRef]
- Salat, H.; Murcio, R.; Arcaute, E. Multifractal methodology. Phys. A Stat. Mech. Its Appl. 2017, 473, 467–487. [Google Scholar] [CrossRef]
- Zhang, J.; Hu, Q.; Wu, H.; Su, J.; Zhao, P. Application of Fractal Dimension of Terrestrial Laser Point Cloud in Classification of Independent Trees. Fractal Fract. 2021, 5, 14. [Google Scholar] [CrossRef]
- Cai, J.; Hu, X.; Xiao, B.; Zhou, Y.; Wei, W. Recent developments on fractal-based approaches to nanofluids and nanoparticle aggregation. J. Int. J. Heat. Mass. Transfer. 2017, 105, 623–637. [Google Scholar] [CrossRef]
- Ma, D.; Duan, H.; Liu, J. The role of gangue on the mitigation of mining-induced hazards and environmental pollution: An experimental investigation. Sci. Total Environ. 2019, 664, 436–448. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Liu, D.; Cai, Y.; Zhou, Y.; Yin, T. Investigation on the Methane Adsorption Capacity in Coals: Considerations from Nanopores by Multifractal Analysis. Energ. Fuel. 2021, 35, 6633–6643. [Google Scholar] [CrossRef]
- Mahamud, M.M.; Novo, M.F. The use of fractal analysis in the textural characterization of coals. Fuel 2008, 87, 222–231. [Google Scholar] [CrossRef]
- Wang, F.; Zeng, F.; Wang, L.; Hou, X.; Cheng, H.; Gao, J. Fractal analysis of tight sandstone petrophysical properties in unconventional oil reservoirs with NMR and rate-controlled porosimetry. Energy Fuels 2021, 35, 3753–3765. [Google Scholar] [CrossRef]
- Makevi, V.; Milovanovich, I.D.; Popovac, N.; Jankovi, R.; Trajkovi, J.; Vukovi, A.; Milosevi, B.; Jevti, J.; de Luka, S.R.; Ili, A. Fractal Parameters as Independent Biomarkers in the Early Diagnosis of Pediatric Onset Inflammatory Bowel Disease. Fractal Fract. 2023, 7, 619. [Google Scholar] [CrossRef]
- Lai, J.; Wang, S.; Wang, G.; Shi, Y.; Zhao, T.; Pang, X.; Fan, X.; Qin, Z.; Fan, X. Pore structure and fractal characteristics of Ordovician Majiagou carbonate reservoirs in Ordos Basin, China. AAPG Bull. 2019, 103, 2573–2596. [Google Scholar] [CrossRef]
- Dou, W.; Liu, L.; Xu, Z.; Wang, M.; Chen, Y.; Wang, X. Surface fractal analysis of pore structure of tight sandstones: Comparison of different models based on mercury intrusion porosimetry. AAPG Bull. 2021, 105, 1491–1509. [Google Scholar] [CrossRef]
- Agterberg, F.P. Multifractal modelling of the sizes and grades of giant and supergiant deposits. Int. Geol. Rev. 1995, 37, 1–8. [Google Scholar] [CrossRef]
- Nazarpour, A.; Omran, N.R.; Paydar, G.R. Application of multifractal models to identify geochemical anomalies in Zarshuran Au deposit, NW Iran. Arab. J. Geosci. 2015, 8, 877–889. [Google Scholar] [CrossRef]
- Monecke, T.; Gemmell, J.B.; Monecke, J. Fractal distributions of veins in drill core from the Hellyer VHMS deposit, Australia: Constraints on the origin and evolution of the Mineralising system. Miner Deposita. 2001, 36, 406–415. [Google Scholar] [CrossRef]
- Behnam, S.; Parviz Moarefvand, P.A.; Amir, B.Y.; Lili, D.S. Application of fractal models to outline mineralized zones in the Zaghia iron ore deposit, Central Iran. J. Geochem. Explor. 2012, 122, 9–19. [Google Scholar]
- Shen, B.; Shen, Y. Fractal characteristics of a gold deposit in Xinjiang and its geological significance. Sci. China Ser. B 1993, 23, 297–302. [Google Scholar]
- Wang, Q.F.; Deng, J.; Wan, L.; Zhao, J.; Gong, Q.J.; Yang, L.Q.; Zhou, L.; Zhang, Z.J. Multifractal Analysis of Element Distribution in Skarn-type Deposits in the Shizishan Orefield, Tongling Area, Anhui Province. Acta Geol. Sin. 2008, 82, 896–905. [Google Scholar]
- Zhao, J.; Chen, S.; Zuo, R. Identification and mapping of lithogeochemical signatures using staged factor analysis and fractal multifractal model. Geochem.-Explor. Environ. A 2017, 17, 239–251. [Google Scholar] [CrossRef]
- Seyedrahimi-Niaraq, M.; Hekmatnejad, A. The efficiency and accuracy of probability diagram, spatial statistic and fractal methods in the identification of shear zone gold mineralization: A case study of the Saqqez gold ore district, NW. Chin. J. Geochem. 2021, 40, 78–88. [Google Scholar] [CrossRef]
- Sun, T.; Liu, L. Delineating the complexity of Cu–Mo mineralization in a porphyry intrusion by computational and fractal modeling: A case study of the Chehugou deposit in the Chifeng district, inner Mongolia, China. J. Geochem. Explor. 2014. [CrossRef]
- Zuo, R.; Cheng, Q.; Xia, Q. Application of fractal models to characterization of vertical distribution of geochemical element concentration. J. Geochem. Explor. 2009, 102, 37–43. [Google Scholar] [CrossRef]
- Peyman, A.; Younes, F.A.; Parviz, M.; Nematolah, R.O.; Haroni, H.A. Application of power-spectrum–volume fractal method for detecting hypogene, supergene enrichment, leached and barren zones in Kahang Cu porphyry deposit, Central Iran. J. Geochem. Explor. 2012, 112, 131–138. [Google Scholar]
- Ahad, N.; Behnam, S.; Martiya, S. Application of fractal models to characterization and evaluation of vertical distribution of geochemical data in Zarshuran gold deposit, NW Iran. J. Geochem. Explor. 2015, 148, 60–70. [Google Scholar]
- Asadi, H.H.; Kianpouryan, S.; Lu, Y.J.; Mccuaig, T.C. Exploratory data analysis and c-a fractal model applied in mapping multi-element soil anomalies for drilling: A case study from the sari Gunay epithermal gold deposit, NW Iran. J. Geochem. Explor. 2014, 145, 233–241. [Google Scholar] [CrossRef]
- Deng, J.; Wang, Q.; Wan, L.; Yang, L.; Gong, Q.; Zhao, J. Self-similar fractal analysis of gold mineralization of Dayingezhuang disseminated-veinlet deposit in Jiaodong gold province, China. J. Geochem. Explor. 2009, 102, 95–102. [Google Scholar] [CrossRef]
- Cheng, Q. Multifractal and Geostatistic methods for characterizing local structure and singularity properties of exploration geochemical anomalies. J. Earth Sci. China 2001, 26, 161–164. [Google Scholar]
- Shen, B. Fractal structure factor and its application in geology. Acta Petrol. Sin. 1993, 9, 267–276. [Google Scholar]
- Kusk, M. Application of fractal and multifractal analysis on Blue Nile drainage patterns in the Morphostructural analysis of the Ethiopian highlands, Ethiopia. Prog. Phys. Geog. 2022, 46, 357–370. [Google Scholar] [CrossRef]
- Liu, Y.; Cheng, Q.; Zhou, K. New Insights into Element Distribution Patterns in Geochemistry: A Perspective from Fractal Density. Nat. Resour. Res. 2019, 28, 5–29. [Google Scholar] [CrossRef]
- Xiao, F.; Chen, Z.; Chen, J.; Zhou, Y. A batch sliding window method for local singularity mapping and its application for geochemical anomaly identification. Comput. Geosci. UK 2016, 90, 189–201. [Google Scholar] [CrossRef]
- Wang, W.; Zhu, M.; Zhao, J.; Chen, Z.; Cheng, Q. Joint Modeling Based on Singularity Mapping and U-statistical Methods for Geo-Anomaly Characterization. Nat. Resour. Res. 2022, 31, 1909–1923. [Google Scholar] [CrossRef]
- Liu, Y.; Carranza, E.M. Uncertainty Analysis of Geochemical Anomaly by Combining Sequential Indicator Co-simulation and Local Singularity Analysis. Nat. Resour. Res. 2022, 31, 1889–1908. [Google Scholar] [CrossRef]
- Xu, S.; Hu, X.; Carranza, E.M.; Wang, G.W. Multi-parameter Analysis of Local Singularity Mapping and Its Application to Identify Geochemical Anomalies in the Xishan Gold Deposit, North China. Nat. Resour. Res. 2020, 29, 3425–3442. [Google Scholar] [CrossRef]
- Mohammadi, N.M.; Hezarkhani, A.; Saljooghi, B.S. Separation of a geochemical anomaly from background by fractal and U-statistic methods, a case study: Khooni district, Central Iran. Geochem. Interdiscip. J. Chem. Probl. Geosci. Geoecol. 2016, 76, 491–499. [Google Scholar] [CrossRef]
- Wen, Z.; Liu, H.; Gao, X. Geochemical and Geophysical anomaly separation and anomaly analyses based on multifractal. Chin. J. Prog. Geophys. 2007, 22, 972–978. [Google Scholar]
- Shang, D.; Geissler, B.; Mew, M.; Satalkina, L.; Haneklaus, N. Unconventional uranium in China’s phosphate rock: Review and outlook. Renew. Sustain. Energy Rev. 2021, 140, 110740. [Google Scholar] [CrossRef]
- Zeng, S.; Shen, Y.; Sun, B.; Zhang, N.; Zhang, S.W.; Feng, S. Pore structure evolution characteristics of sandstone uranium ore during acid leaching. Nucl. Eng. Technol. 2021, 53, 4033–4041. [Google Scholar] [CrossRef]
- Sun, B.; Hou, S.; Zeng, S. 3D characterization of porosity and minerals of low-permeability uranium-bearing sandstone based on multi-resolution image fusion. Nucl. Technol. 2020, 31, 115–134. [Google Scholar] [CrossRef]
- Liu, X.; Yuan, S.; Bai, X.; Jiang, J.; Li, Y.; Liu, J. Tectonic uplift of the Tianshan mountains since quaternary: Evidence from Magnetostratigraphy of the Yili basin, northwestern China. Int. J. Earth Sci. 2023, 112, 855–865. [Google Scholar] [CrossRef]
- de Benicio, R.B.; Stošić, T.; de Figueirêdo, P.H.; Stošić, B.D. Multifractal behavior of wild-land and forest fire time series in Brazil. Phys. A Stat. Mech. Its Appl. 2013, 392, 6367–6374. [Google Scholar] [CrossRef]


| 2.60 | 0 | 2.60 | ||
| 0 | −1.98 | 2.12 | 1.98 | 1.98 |
| 1 | 0 | 1.87 | 1.87 | 1.97 |
| 1.68 | 0 | 1.68 |
| 2.64 | 0 | 2.64 | ||
| 0 | −1.92 | 2.05 | 1.92 | 1.92 |
| 1 | 0 | 1.86 | 1.86 | 1.91 |
| 1.52 | 0 | 1.52 |
| Stope | α0 | Δα | Δf | ΔαR | ΔαL | R |
|---|---|---|---|---|---|---|
| NO. 11 | 2.12 | 0.74 | 0.19 | 0.48 | 0.26 | −0.30 |
| NO. 12 | 2.05 | 0.72 | 0.34 | 0.56 | 0.16 | −0.56 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, Q.; Tan, K.; Zhu, J.; Zeng, S. Multifractal Characteristics of Uranium Grade Distribution and Spatial Regularities in a Sandstone-Type Uranium Deposit in Xinjiang, China. Fractal Fract. 2023, 7, 704. https://doi.org/10.3390/fractalfract7100704
Cai Q, Tan K, Zhu J, Zeng S. Multifractal Characteristics of Uranium Grade Distribution and Spatial Regularities in a Sandstone-Type Uranium Deposit in Xinjiang, China. Fractal and Fractional. 2023; 7(10):704. https://doi.org/10.3390/fractalfract7100704
Chicago/Turabian StyleCai, Qiue, Kaixuan Tan, Junjie Zhu, and Sheng Zeng. 2023. "Multifractal Characteristics of Uranium Grade Distribution and Spatial Regularities in a Sandstone-Type Uranium Deposit in Xinjiang, China" Fractal and Fractional 7, no. 10: 704. https://doi.org/10.3390/fractalfract7100704
APA StyleCai, Q., Tan, K., Zhu, J., & Zeng, S. (2023). Multifractal Characteristics of Uranium Grade Distribution and Spatial Regularities in a Sandstone-Type Uranium Deposit in Xinjiang, China. Fractal and Fractional, 7(10), 704. https://doi.org/10.3390/fractalfract7100704






