Abstract
This article studies the convolutional kernel function of fractal operators in bone fibers. On the basis of the micro-nano composite structure of compact bone, we abstracted the physical fractal space of bone fibers and derived the fractal operators. The article aims to construct the convolutional analytical expression of bone fractal operators and proves that the error function is the core component of the convolution kernel function in the fractal operators. In other words, bone mechanics is the fractional mechanics controlled by error function.
1. Introduction
The property of biological composite materials has always been a hot topic of concern, and related research has promoted the close integration of multiple disciplines, such as biology, materials, chemistry, and mechanics. Natural biological composites, including hard bones, teeth, spider silk, shells, soft tendons, etc., all possess excellent mechanical properties [1,2,3,4,5]. Compared with their constituent materials, biological composite materials have one to several orders of magnitude higher strength and toughness [6,7,8]. Taking bone as an example [9,10,11,12,13,14], at the micro scale, low-toughness mineral crystals are staggered in the low-modulus collagen matrix, forming the nanocomposite structure of bone. After functional self-assembly at different scales, a multi-level structure is formed, which has high elastic modulus and strong fracture toughness at the macro scale [15], as shown in Figure 1. The exquisite, ordered, and complex multi-level structure design of biomaterials is currently difficult to achieve in artificial composite materials, and its mechanical mechanism can provide theoretical guidance for the development of new nanocomposites.
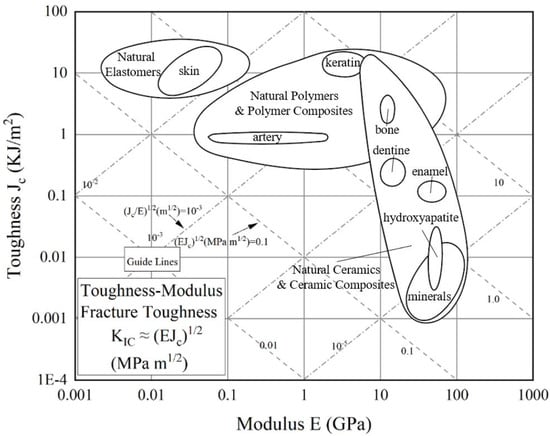
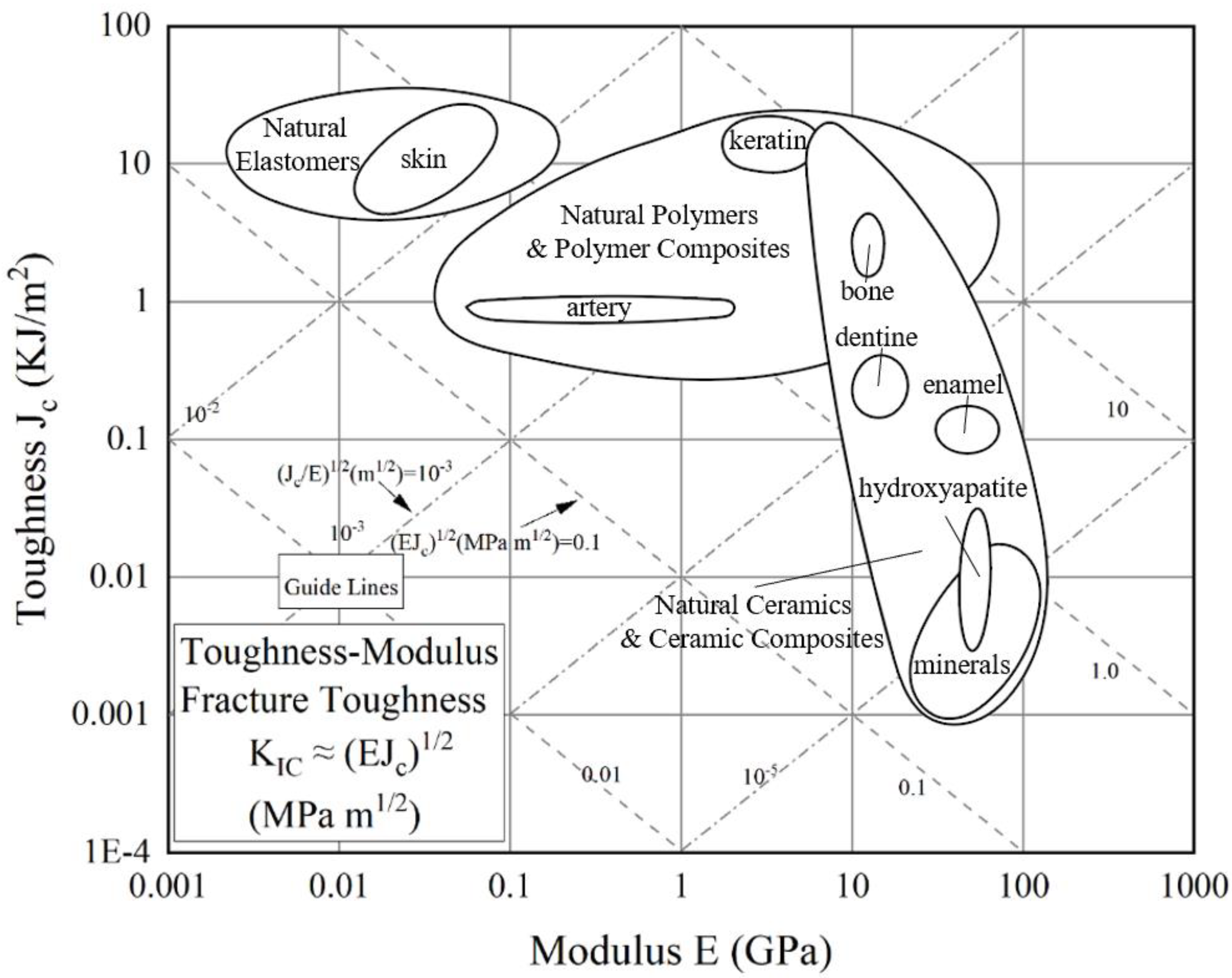
Figure 1.
Ashby map for elastic modulus and toughness of natural biological materials [15].
In biology, “structure determines function” is a research paradigm commonly followed by researchers. On the basis of this, as the inherent structural invariant feature of biomaterials, the multi-level self-similarity characteristics inevitably affect the mechanical response. However, most researchers directly extend the continuity assumption to biomaterials, ignoring the discrete properties of the actual structure, thus resulting in limitations in functional fitting. On the other hand, the emergence of fractional calculus provides a powerful mathematical tool for characterizing the properties of organisms. In recent years, we have abstracted the multi-level chainlike topology from muscle/ligament fibers [16] and nerve fibers [17] and set up a multi-level micro elastic cavity topology from arterial blood flows [18]. Furthermore, we extended the multi-level chainlike topology and multi-level micro-elastic cavity topology to infinite levels and abstracted the physical fractal space composed of physical components. We confirmed that there must be fractal operators in the physical fractal space. These fractal operators accurately characterize the mechanical behaviors of muscles/ligaments, nerves, and blood flow. This is in contrast to the characterization found in traditional bone mechanics models. Because the above fractal operators possess a fractional order of 1/2 order, we can say that the mechanics in organisms are mostly fractional-order mechanics of 1/2 order [19,20,21].
The above ideas and methods were once again confirmed in bone mechanics. On the basis of the micro-nano composite structure of compact bone, we abstracted the fractal cell of chain-like microfibers. On the basis of the Heaviside operational calculus, we established the fractional order constitutive equation of the fractal cell and derived a highly general 1/2-order fractal operator to characterize the fractional order mechanics of compact bone in the physical fractal space. The chain-like topological abstraction of biological fibers with fractal characteristics [19] is a new attempt in biomechanics, which brings the following enlightenment to bionics: by selecting the basic components of organisms, the idea of fractalization can be effectively utilized to study the overall intrinsic response of multi-level bionic systems. Abstracting biological fibers into physical fractals provides a new approach for artificial design: by regulating the intrinsic properties of physical components, multifunctional fractal operators can be effectively designed. Once the operator is controllable, the fundamental mechanical equations of the biomaterials possess designability [20,21].
Operational calculus theory is mainly used to solve differential equations, but in practical problems, it usually focuses on the functional form of the solution and often ignores the physical connotation of the operator [22,23,24]. The Heaviside symbol method provides a method for the convolutional construction of operators and a new perspective for explaining the inherent correlation between fractional order time and fractional dimensional space. We know that the mechanical response of physical components can be characterized by operators. Similarly, the total stiffness of fractal cells can also be characterized by fractal operators. Different from the algebraic structure of pure abstraction, fractal operators possess both a clear spatial form and a clear mechanical background, which also provide the possibility for the promotion of operational calculus in the fields of fractal and fractional order mechanics. What are the basic connotations of bone fractal operators in physical fractal space? This article aims to answer a fundamental question: is there an analytical convolutional construction for the fractal operators of bones? If the answer is positive, then what are the characteristics of convolutional kernel functions? This paper will prove that the fractal operator of bone does have a convolution structure. Furthermore, the convolution kernel function has an internal correlation with the error function; The mechanics of bone is 1/2-order fractional mechanics controlled by the error function.
2. Algebraic Expression of Bone Fractal Operators
For convenience, we first provide the algebraic expressions of bone fractal operators. When the stress is applied to bone fibers and the strain is generated, then we have:
where is the fractal operator on the physical fractal space of the bone. This is a stiffness operator [21]. The differential operator is defined as:
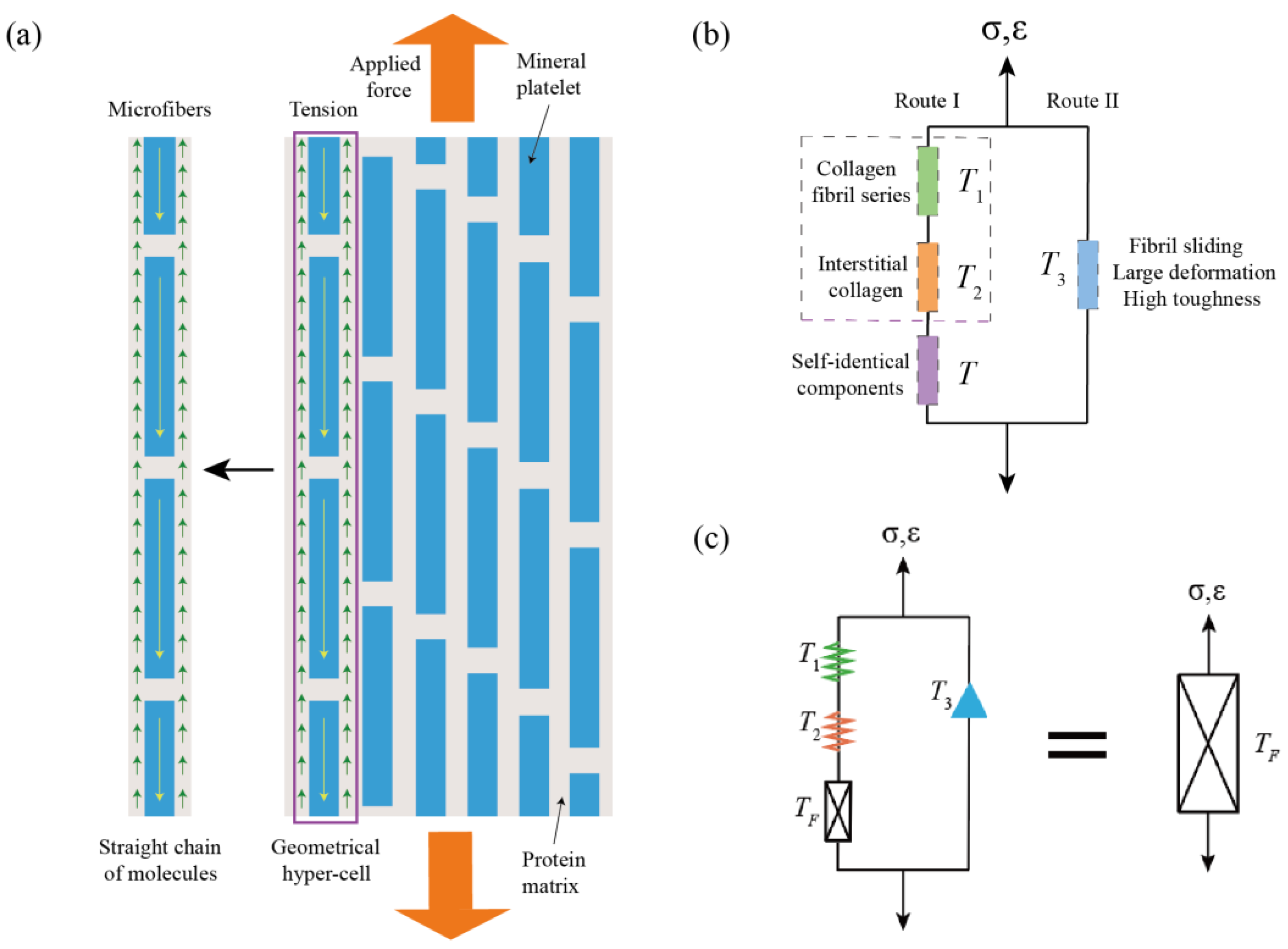
Next, we abstract the physical fractal space and fractal cell of compact bone. Unlike conventional methods, our selected research object was a microfiber, as shown in Figure 2a. In one of the situations, hydroxyapatite is equivalent to spring with the operator , the protein between hydroxyapatite is equivalent to spring with the operator , and the surrounding protein matrix is equivalent to dashpot with the operator . The reasons for the above abstraction are as follows: the stiffness of single hydroxyapatite is usually 10 times the bone’s macro modulus [11]. Therefore, it is necessary to concatenate a spring in order to reduce the global stiffness. Since parallel connection always increases the stiffness, when the dashpot model is paralleled, the fractal tree of self-identical components abstracted from a straight chain can be extended infinitely, as shown in Figure 2b. According to reference [21], the invariance described by the “=” sign is still valid in the operator fractal space, as shown in Figure 2c.
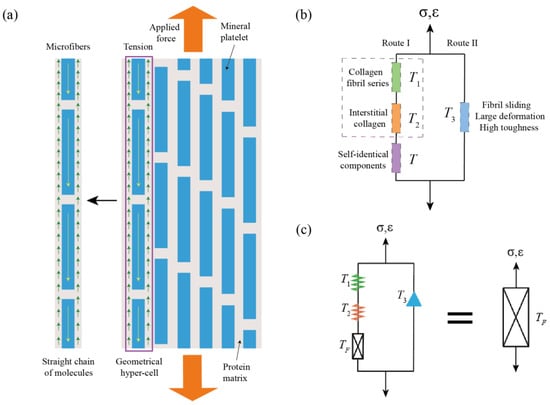
Figure 2.
Fractal cell abstraction from collagen fibrils: (a) straight chain-like duplicated structure of the peripheral fibrils; (b) parallel mechanical routes obtained in the fractal cell; (c) invariance of the operator fractal space.
Therefore, the bone fractal operator needs to satisfy the following algebraic equation:
In mechanics, the right-hand side of Equation (3) can be regarded as the stiffness of the fractal component, and the left-hand side can be regarded as the stiffness of the fractal cell. It is further deduced that:
Specifically, the fractal operator for compact bone is:
When or is equal to 0, can degenerate into Guo’s model [16,17], and the fractal operators of ligament/tendon can be abbreviated as :
Therefore, it can be said that the fractal operator of the ligaments/tendons is a special case of the bone fractal operator.
Once the operators , , and of the physical components are determined, the specific algebraic expression of the bone fractal operator can be determined.
In the bone fractal operator , the non-trivial term is a quadratic radical , which is particularly noted as:
Apparently, the operator is a 1/2-order fractional operator. In previous research [21], we called it the “apparent fractional order operator”. Of course, its specific order also depends on the order of the physical component operator.
In fact, as long as the properties of the operator are clarified, the properties of the bone fractal operator are clear. The following content will focus on the fractional order operator .
3. Convolutional Expressions for Apparent Fractional Order Operators
The algebraic expression of the operator alone is insufficient to characterize the mechanical responses of the bones. We also need to introduce a convolutional expression for the operator .
Mikusinski [25] and Courant and Hilbert [26] systematically summarized the Heaviside operational calculus and provided a universal theory for the convolutional representation of operators.
The Heaviside “unit function” is defined as:
Using the Carson–Laplace inverse transformation, the convolutional kernel function of the operator can be defined as:
Equation (9) given by Courant and Hilbert [26] depicts the kernel function for the operator . Once the algebraic expression of the operator is clarified, the convolutional kernel function in the time domain can be derived using Equation (9).
For the input signal (strain) , the output signal (stress) is:
Equations (9) and (10) provide a general convolution construction for the operators. In this model, the convolution kernel function is the key.
However, previous research has shown that it is difficult to directly obtain the convolutional kernel function for the fractal operator or apparent the fractional order operator .
How do we overcome the above obstacles? One effective method is to use operator multiplication. By multiplication decomposition, the complicated operator may be decomposed into the product of simple operators.
4. Multiplication Decomposition of Fractional Order Operators
This section discusses the multiplication decomposition of the apparent fractional order operator . Suppose that all physical components are of integer orders. We examine the following three representative scenarios with the elastic modulus and the viscous coefficient ().
In the first case, the physical component operators are taken as:
where is elastic component and and are both viscous components. By introducing physical constants and , using the multiplication decomposition of operators, the characteristic term in can be transformed into the following form:
The operator can be decomposed into the product of the classical differential operator , the 1/2-order integral operator , and the 1/2-order differential operator .
In Equation (11), the material constants are taken as and in order to facilitate various expansions. For example, if one takes , then may be transformed into .
In the second case, the physical component operators are taken as:
where is the elastic component, is the viscous component, and is the elastic component. Then the fractional order term can be transformed into the following form:
The operator can be decomposed into the product of the 1/2-order integral operator and the 1/2-order differential operator .
By comparing Formulas (12) and (10), we find that the only difference between them is the classical differential operator .
In the third case, the physical component operators are taken as:
where and are both elastic components and is the viscous component. The fractional order term can be transformed into the following form:
The operator can be decomposed into the product of the 1/2-order differential operator and the 1/2-order differential operator .
At this point, in all representative cases, operators are decomposed into the products of simple operators. Among them, the classical derivative is the simplest integer order differential operator, and is the simplest fractional order differential operator.
In the above multiplicative decomposition for the apparent fractional order operator , the 1/2-order integral operator and the 1/2-order differential operator appear repeatedly, so it is worth studying them separately. Although these two fractional order operators already have a simple form, they can still be expressed in their simplest form using the displacement theorem. It should be noted that the fractal operator of real bone usually satisfies Equation (13). The Equations (11) and (12) are intended to derive multiplicative decomposition and illustrate the frequent occurrence and universality of the 1/2-order differential operator .
5. The Displacement Theorem of Fractal Operators (or Apparent Fractional Order Operators)
The displacement theorem can be expressed as follows: if is an operator function and is a constant operator, then the operator function can be given as:
By the displacement theorem, the operator can be expressed by the operator , and thereby, calculations may be simplified. The displacement theorem remains valid for operators with integer orders as well as for fractal operators with fractional orders.
For the 1/2-order differential operator , the displacement theorem is applied as follows:
In this way, the operator can be characterized by the simplest operator .
For the 1/2-order integral operators , the displacement theorem is applied as follows:
In this way, the operator can be characterized by the simplest operator .
6. Error Function in 1/2-Order Differential Operators
The 1/2-order differential operator can be reduced to the operator . The convolutional kernel function of the operator is:
The output signal of the operator is:
Combining Equations (15) and (18) leads to the following result. When the operator acts on the Heaviside unit function under the definition of Courant and Hilbert, its convolutional kernel function can be obtained:
Due to the universal existence of the operator in bone mechanics, the integral term on the right-hand side of Equation (19) will also repeatedly appear in the convolutional kernel function of bone fractal operators. Therefore, it is necessary to study this integral term separately. Using variable substitution, we obtain:
Finally, we can export:
Introduce the error function :
Therefore, Equation (20) can be transformed into:
Equation (19) is rewritten as:
Note the following differential properties of the error function:
In Equation (22), the convolutional kernel function of the operator can finally be derived as follows:
The error function appears in the convolution kernel function of the 1/2-order differential operator . This is quite unexpected.
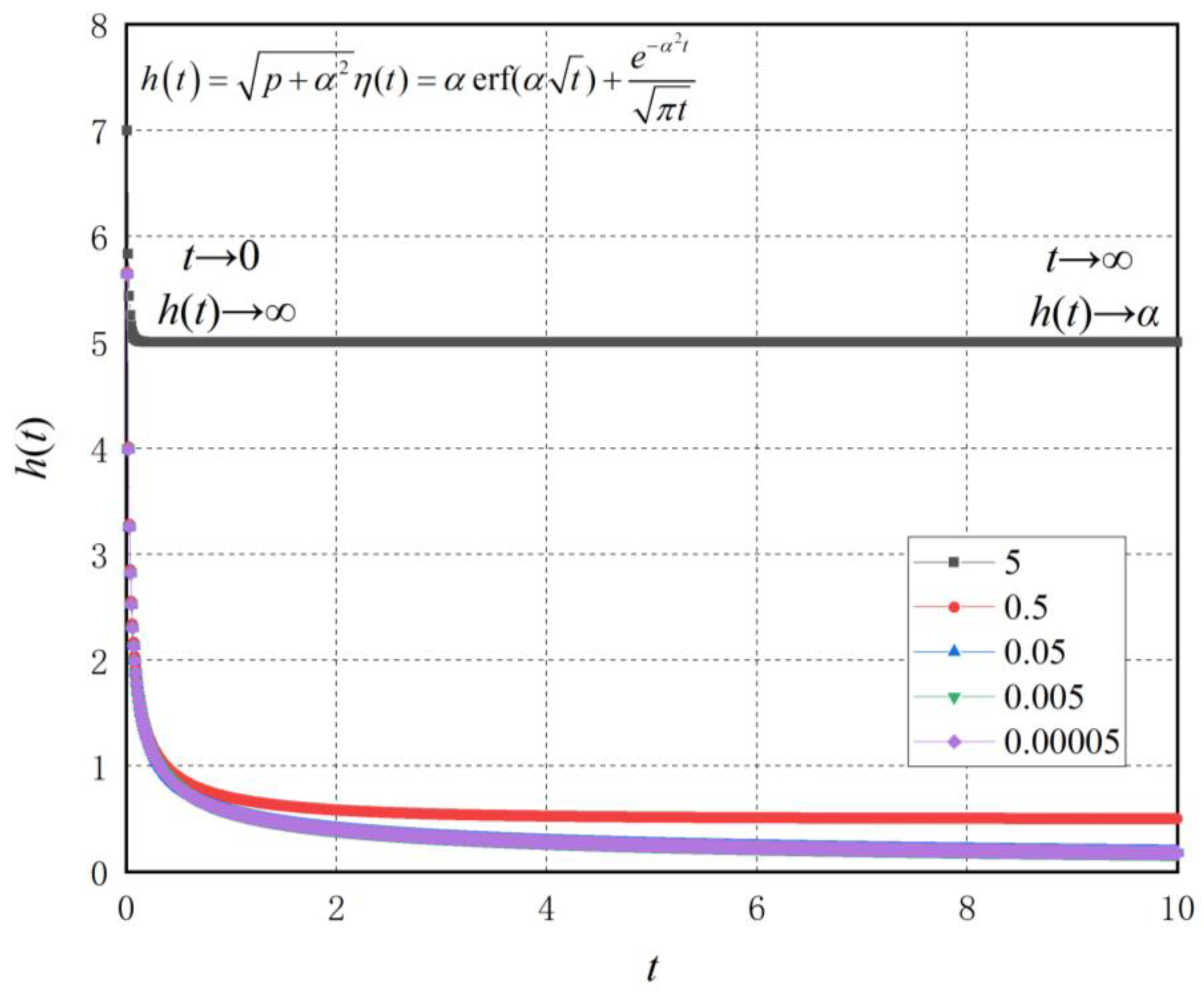
It should be noted that the kernel function exhibits singularity at . In Equation (24), , is the relaxation time constant. In general, the time term entered by the system is not negative, i.e., . In real bones, is usually within the range of 200–4000 s [11,12]. When , i.e., , the function image of Equation (24) is shown in Figure 3.
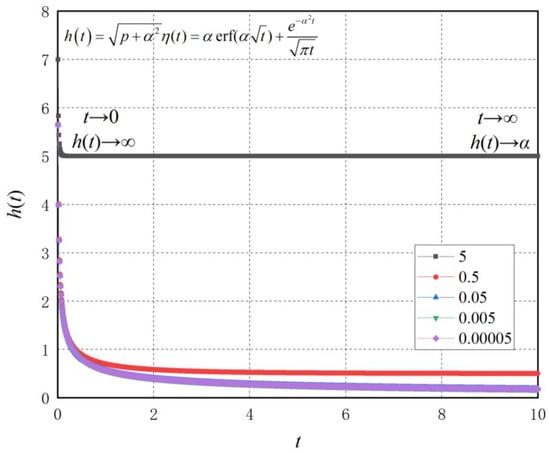
Figure 3.
Convolution analytic expression of 1/2-order differential operator with changes in relaxation time constant .
It can be seen in Figure 3 that when , . When , . In other words, as the relaxation time constant increases, decreases, and the corresponding convolutional kernel function also decays at . Therefore, Equation (24) is essentially an analytical function that continuously decays over time , and the core parameter determining decay is the relaxation time constant . In Equation (13), the quadratic radical operator is decomposed into the product of two 1/2-order differential operators, and , in which is a classical fractional order operator, while the operator is widely present in heat conduction problems, viscoelastic problems, hemodynamics, and bone mechanics. From this, we can see that the most common convolutional analytical Formula (24) in bone fractal operators has a similar trend to the unit pulse function. This is a very interesting phenomenon that also explains the widespread existence of the operator in many disciplines. As mentioned above, the parameter in the fractional order operator is equivalent to the characteristic frequencies of the physical fractal space. It can be seen that parameter is ubiquitous, not only in error functions but also in negative exponential functions. It can be expected that parameter has a significant impact on the properties of fractal space. Although the operator only has one more parameter than the operator , its properties are much more complex than the latter.
In Ref. [26], the fractional differential operator in the heat conduction equation was specifically discussed by Courant and Hilbert. Babenko also calculated the fractional differential operator when solving the heat conduction equation [27]. Babenko expanded the binomial [27] and derived the series expression of the operator :
The right-hand side of Equation (25) contains both the fractional differential operator and the power series of the fractional integral operator . By comparing Equations (24) and (25), it can be seen that the right-hand sides of the two equations should be equal. In fact, at , expanding the right-hand side into a power series, we can obtain:
The two right-hand sides of Equations (24) and (25) are indeed equal. The power series in Equation (26) is of uniform convergence, which directly shows that the analytical formula in Equation (24) is correct.
Historically, is a classical fractional operator. The error function is a classical special function. Now it seems that the operator actually depends on the error function . This is an interesting correlation. In the past, people never realized the existence of this correlation.
When the operator acts on a function , there are two paths pointing toward the output signal. One is to apply the displacement theorem:
is the most common integral term in the convolution operation of bone fractal operators.
The second path is to directly use Equations (10) and (24):
In theory, Equations (27) and (28) are equivalent.
By utilizing the symmetry of convolution operations, Equation (28) can also be written in a more concise form:
Equations (28) and (29) confirm the following fact: as long as the differential operator exists, the output signal is controlled by the error function.
7. Error Function in 1/2-Order Integral Operators
As mentioned above, in addition to the 1/2-order differential operator , the 1/2-order integral operator also appears in the bone fractal operator. Studying the properties of the operator can take different paths.
One path is to derive the properties of the operator from the properties of the operator by the displacement theorem (Equation (16)). However, this path has high complexity.
The second path is to derive the properties of the operator from the properties of the operator by the derivative operation of parameter variable:
Therefore, by simply taking the derivative of the parameter variable on both sides of Equations (28) and (29), we can obtain the convolutional kernel function of the operator .
The third path is to refer to the literature [25]. From a historical perspective, the operator first appeared in Mikusinski’s work [25]. When introducing non-integer order operators , Mikusinski utilized the properties of the Gamma function to derive:
So, there is:
Therefore, there is:
represents the Dirac function.
Note that the relationship between the Dirac function and the Heaviside unit function is:
So, Equation (31) is rewritten as:
That is to say, the convolution kernel function of the fractional integral operator also contains the error function .
When the operator acts on the input signal , the output signal is as follows:
By utilizing the symmetry of convolution operations, Equation (34) can also be written in a more concise form:
Equations (34) and (35) confirm the following fact: as long as the 1/2-order integral operator exists, the output signal is bound by the error function.
The integral operator and the differential operator are reciprocal operators. The convolution kernels of the two reciprocal operators both contain the error function , which is a wonderful and profound correlation.
8. Error Function in Bone Fractal Operators
By clarifying the convolution construction of the integral operator and the differential operator , the convolution kernel function of the bone fractal operators can be constructed. Three representative bone fractal operators can be used to write the convolutional kernel functions as follows:
Up to now, the bone mechanics described by the fractal operators possessed a complete mathematical foundation.
Equations (36)–(38) show the following fact: it is difficult for one single operator to describe bone mechanics. In other words, structured fractal operators are indispensable.
Bone mechanics, characterized by fractal operators, are fractional order mechanics. In Formula (36), and are both 1/2-order differential operators, but the product of them, is not a 1-order differential operator but a double 1/2-order differential operator. In Equations (37) and (38), is a 1/2-order integral operator, and is a 1/2-order differential operator, but the product is not a 0-order operator but a double 1/2-order differential and integral operator. Note that is essentially a 1/2-order irrational fraction-type operator, which includes both the fractional order differential and fractional order integral. Therefore, it can be said that bone mechanics is characterized by multiple fractional order operators.
9. Correlation between Error Function and Bessel Function from the Perspective of Bone Fractal Operator
In fact, the fractal operator in Equation (36) is the most essential operator for describing the mechanical properties of bone. Similarly, we find that it is also a basic fractal operator in arteriole hemodynamics [18]. Its property deserves our careful exploration.
If we directly solve the right-end integral of Equation (36) and assume that on the basis of actual biomechanical properties, there is:
where and is the first modified Bessel function of orders 0 and 1, respectively. This is the result of first calculating and then calculating the operator . The limit of this formula at is: .
On the other hand, if we exchange the operation order of the operator multiplicative decomposition, apply the displacement theorem, and assume that , there is:
Or, if we use the Courant’s kernel function of the operator and assume that , there is:
Based on the above formula, we can see that there is a correlation between the error function and the Bessel function:
Furthermore, we find that the Equation (42) is the Courant’s kernel function of the operator , that is:
Surprisingly, we find that the 1/2-order fractional differential of the error function , which means that it has acted on the operator , is the Bessel function weighted by negative power exponent. We establish a strong correlation between the error function, the fractional differential, and the Bessel function, which are seemingly unrelated. This exploration of scientific problems, such as physical mechanics and mathematics problems, provides important mathematical theoretical insights.
In addition, we find that under the Courant and Hilbert system, the Courant’s kernel function of the operator specifies that the initial value of the function affected by differential operator should be zero. Therefore, in order to meet this condition, when applying the differential operator to the above results in , we need to subtract the initial value at the zero point from the results, that is, . Therefore, the kernel function of the operator is written as follows:
This result shows that if we derivate Courant’s kernel function of the operator again, it can be consistent with the convolution kernel function of the physical fractal model in the arteriole [18].
So far, bone mechanics, characterized by fractal operators, possess a complete foundation of mathematical logic. On the basis of the micro-nano composite structure of compact bone, we derived the fractal operator in the physical fractal space. According to the representative bone fractal operator, we proved that the error function is the core component of its convolution kernel function. Through further mathematical transformation, we established a strong correlation between the error function, the fractional differential, and the Bessel function, which are seemingly unrelated. The above results deepen our understanding of special functions, and the correlation between biological fractal and fractional order mechanics is clearer. Therefore, it can be said that bone mechanics is fractional mechanics controlled by the error function, and fractional mechanics is also controlled by the Bessel function. Under certain conditions, there is a profound internal correlation between bone mechanics and hemodynamics.
10. Conclusions
The analysis in this article is based on the physical fractal space of the bone. Without physical fractal space, there would be no fractional order bone mechanics in this article.
The physical background of this article is the mechanical behavior in dense bone fibers. However, the research results are universal. As mentioned above, the fractal operator of dense bones is more general than the fractal operator of tendons/ligaments. Therefore, we can say that bone mechanics is more general mechanics than tendon/ligament fiber mechanics. The operators and their convolutional kernel functions in this article are applicable not only to bone mechanics but also to tendon/ligament fiber mechanics. The excellent unity between bone mechanics and tendon/ligament fiber mechanics is due to their completely unified physical fractal spatial form.
This article used the simplest physical components, namely elastic and viscous components. Both are the fundamental components with an integer order. However, through the regulation of the physical fractal space, integer order components generate fractional order mechanical systems. In addition, the mechanical behavior of this fractional order system is strongly constrained by the error function.
Error function generally exists in organism mechanics. This is a very interesting phenomenon. This also shows that the error function is an essential part of the modulation mechanism in organisms.
Author Contributions
Conceptualization, Z.J., D.L., G.P., X.Y. and Y.Y.; methodology, Z.J., D.L., G.P., X.Y. and Y.Y.; software, Z.J. and Y.Y.; validation, Z.J., G.P. and Y.Y.; formal analysis, Z.J., G.P. and Y.Y.; investigation, Z.J., G.P. and Y.Y.; writing—original draft preparation, Y.Y. and Z.J.; writing—review and editing, Y.Y. and Z.J. All authors have read and agreed to the published version of the manuscript.
Funding
This study was funded by the National Natural Science Foundation of China, grant number 12050001.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest related to this study.
References
- Fratzl, P.; Weinkamer, R. Nature’s hierarchical materials. Prog. Mater. Sci. 2007, 52, 1263–1334. [Google Scholar] [CrossRef]
- Weiner, S.; Veis, A.; Beniash, E.; Arad, T.; Dillon, J.W.; Sabsay, B.; Siddiqui, F. Peritubular dentin formation: Crystal organization and the macromolecular constituents in human teeth. J. Struct. Biol. 1999, 126, 27–41. [Google Scholar] [CrossRef]
- Shao, Y.; Zhao, H.P.; Feng, X.Q.; Gao, H. Discontinuous crack-bridging model for fracture toughness analysis of nacre. J. Mech. Phys. Solids 2012, 60, 1400–1419. [Google Scholar] [CrossRef]
- Menig, R.; Meyers, M.H.; Meyers, M.A.; Vecchio, K.S. Quasi-static and dynamic mechanical response of Strombus gigas (conch) shells. Mater. Sci. Eng. A 2001, 297, 203–211. [Google Scholar] [CrossRef]
- Huang, X.P.; Liu, G.Q.; Wang, X.W. New Secrets of Spider Silk: Exceptionally High Thermal Conductivity and Its Abnormal Change under Stretching. Adv. Mater. 2012, 24, 1482–1486. [Google Scholar] [CrossRef]
- Kamat, S.; Su, X.; Heuer, A.H.; Ballarini, R. Structural basis for the fracture toughness of the shell of the conch Strombus gigas. Nature 2000, 405, 1036–1040. [Google Scholar] [CrossRef]
- Jäger, I.; Fratzl, P. Mineralized collagen Mbrils: A mechanical model with a staggered arrangement of mineral particles. Biophys. J. 2000, 79, 1737–1746. [Google Scholar] [CrossRef]
- Gao, H.J.; Ji, B.H.; Fratzl, P.; Arzt, E. Materials become insensitive to flaws at nanoscale: Lessons from nature. Proc. Natl. Acad. Sci. USA 2003, 100, 5597–5600. [Google Scholar] [CrossRef]
- Wolff, J. The “law of bonetransformation”. Biol. Rev. 1991, 66, 245–273. [Google Scholar]
- Landis, W.J. The strength of a calcified tissue depends in part on the molecular structure and organization of its constituent mineral crystals in their organic matrix. Bone 1995, 16, 533–544. [Google Scholar] [CrossRef]
- Ji, B.H.; Gao, H.J. Mechanical properties of nanostructure of biological materials. J. Mech. Phys. Solids. 2004, 52, 1963–1990. [Google Scholar] [CrossRef]
- Gao, H.J. Application of fracture mechanics concepts to hierarchical biomechanics of bone and bone-like materials. Int. J. Fracture 2006, 138, 101–137. [Google Scholar] [CrossRef]
- Zhang, Z.Q.; Liu, B.; Huang, Y.; Hwang, K.C.; Gao, H. Mechanical properties of unidirectional nanocomposites with non-uniformly or randomly staggered platelet distribution. J. Mech. Phys. Solids 2010, 58, 1646–1660. [Google Scholar] [CrossRef]
- Reznikov, N.; Bilton, M.; Lari, L.; Stevens, M.M.; Kröger, R. Fractal-like hierarchical organization of bone begins at the nanoscale. Science 2018, 360, eaao2189. [Google Scholar] [CrossRef] [PubMed]
- Wegst, U.G.K.; Ashby, M.F. The mechanical efficiency of natural materials. Philos. Mag. 2004, 84, 2167–2181. [Google Scholar] [CrossRef]
- Guo, J.Q.; Yin, Y.J.; Ren, G.X. Abstraction and operator characterization of fractal ladder viscoelastic hyper-cell for ligaments and tendons. Appl. Math. Mech.-Engl. Ed. 2019, 40, 1429–1448. [Google Scholar] [CrossRef]
- Guo, J.; Yin, Y.; Hu, X.; Ren, G. Self-similar network model for fractional-order neuronal spiking: Implications of dendritic spine functions. Nonlin. Dyn. 2020, 100, 921–935. [Google Scholar] [CrossRef]
- Peng, G.; Guo, J.Q.; Yin, Y.J. Self-Similar functional circuit models of arteries and deterministic fractal operators: Theoretical revelation for biomimetic materials. Int. J. Mol. Sci. 2021, 22, 12897. [Google Scholar] [CrossRef]
- Guo, J.Q.; Yin, Y.J.; Peng, G. Fractional-order viscoelastic model of musculoskeletal tissues: Correlation with fractals. Proc. R. Soc. A 2021, 477, 20200990. [Google Scholar] [CrossRef]
- Yin, Y.J.; Peng, G.; Yu, X.B. Algebraic equations and non-integer orders of fractal operators abstracted from biomechanics. Acta Mech. Sin. 2022, 38, 521488. [Google Scholar] [CrossRef]
- Yin, Y.; Guo, J.; Peng, G.; Yu, X.; Kong, Y. Fractal Operators and Fractional Dynamics with 1/2 Order in Biological Systems. Fractal Fract. 2022, 6, 378. [Google Scholar] [CrossRef]
- Jiang, X.X.; Yang, X.H.; Zhang, H.X.; Tian, Q. An Implicit Difference Scheme for the Fourth-Order Nonlinear Evolution Equation with Multi-Term Riemann–Liouvile Fractional Integral Kernels. Fractal Fract. 2022, 6, 443. [Google Scholar] [CrossRef]
- Kukushkin, M.V. On Solvability of the Sonin–Abel Equation in the Weighted Lebesgue Space. Fractal Fract. 2021, 5, 77. [Google Scholar] [CrossRef]
- Michelitsch, T.M.; Polito, F.; Riascos, A.P. Biased Continuous-Time Random Walks with Mittag-Leffler Jumps. Fractal Fract. 2020, 4, 51. [Google Scholar] [CrossRef]
- Mikusinski, J. Operational Calculus, 2nd ed.; Pergamon Press: Oxford, UK, 1983. [Google Scholar]
- Courant, R.; Hilbert, D. Methods of Mathematical Physics; Interscience Publishers: New York, NY, USA, 1962. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999; pp. 1–198. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).