Long-Term Side Effects: A Mathematical Modeling of COVID-19 and Stroke with Real Data
Abstract
:1. Introduction
2. Preliminaries
- (1)
- Asymptomatically stable ⇔ the eigenvalues of the Jacobian matrix satisfy that ,
- (2)
- Stable ⇔ is asymptomatically stable or the eigenvalues of that satisfy if have the same geometric and algebraic multiplicity.
- (3)
- Unstable ⇔ such that the corresponding eigenvalue of satisfy
3. Mathematical Modeling
4. Existence and Uniqueness
- (1)
- whereare constants.
- (2)
- X(t) satisfies (5).
5. Equilibria and Stability
5.1. Positivity and Boundedness (P&B)
5.2. Stability of the Equilibria
5.3. Basic Reproduction Number
6. Sensitivity Analysis
7. Parameter Estimation (PE)
- Find coefficients c that solve the problem given input data , and the observed output , where and are matrices or vectors, and is a matrix-valued or vector-valued function of the same size as .
- When dealing with boundaries, lower and upper bounds ( and ) can be established accordingly. The parameters c, , and can take the form of vectors or matrices.
- To fit the actual data, we employ the MATLAB code lsqcurvefit, wherein the user defines a function to compute the function using the given vector value as follows:
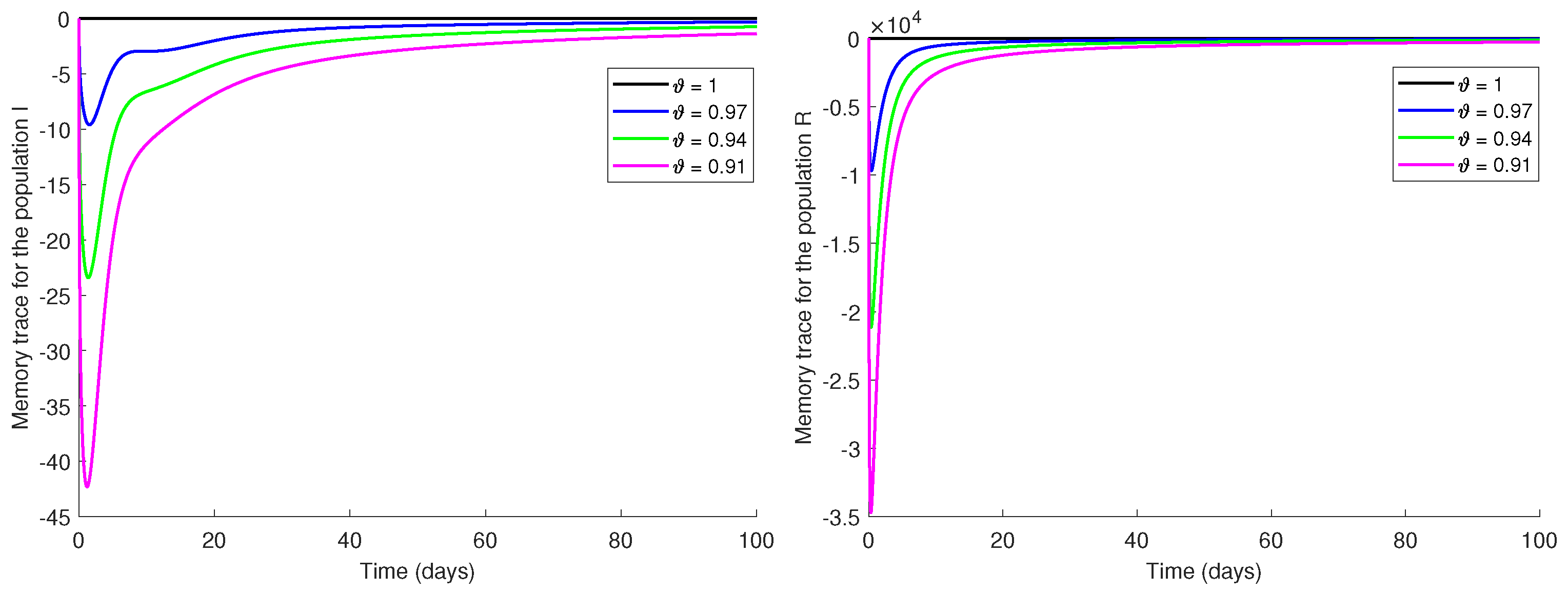
8. Memory Trace and Hereditary Traits
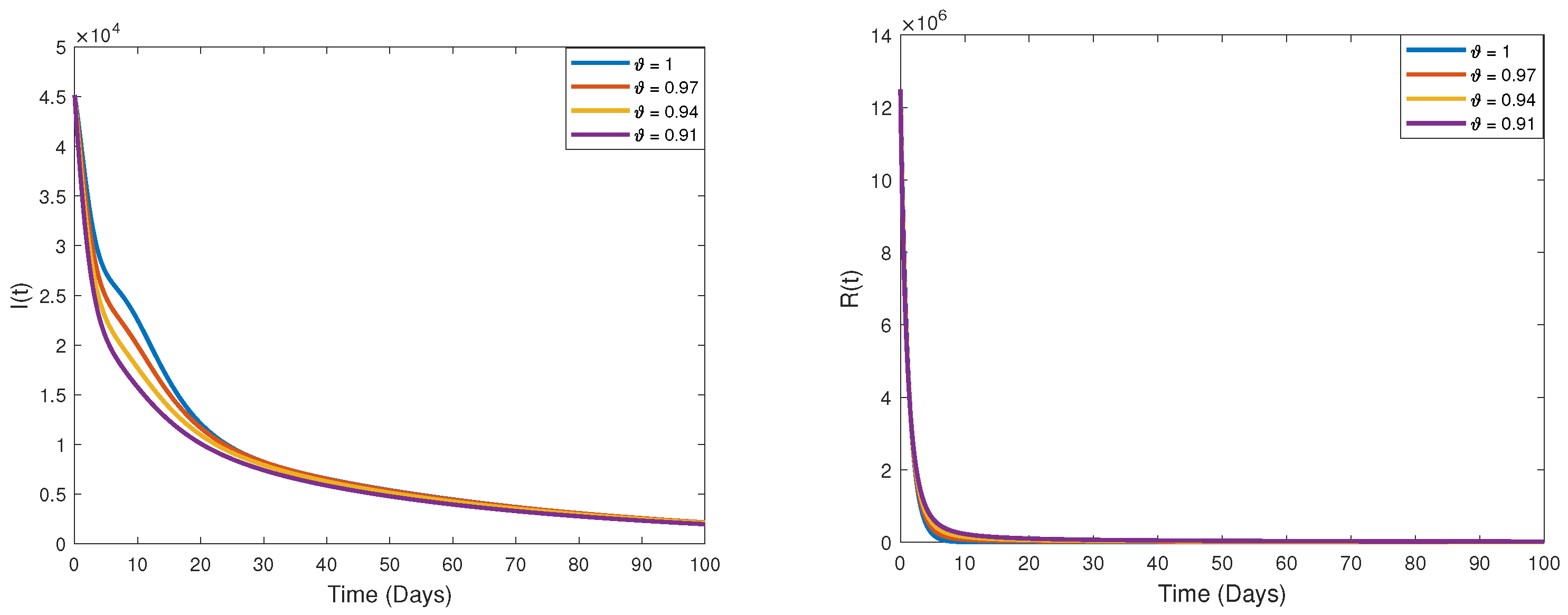
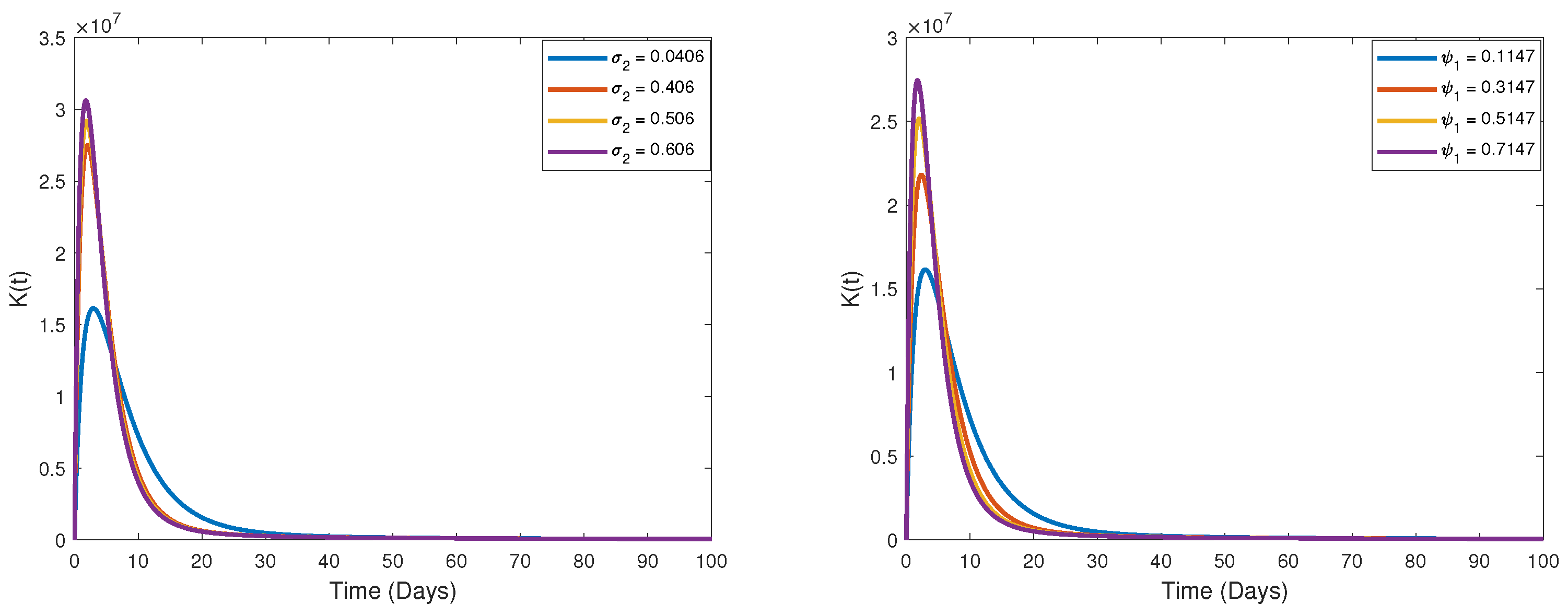
9. Some Numerical Simulations and Biological Interpretations
Measurement of Memory Trace
10. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
References
- Koh, J.S.; Hoe, R.H.M.; Chen, G.J.; Goh, Y.; Tan, B.Y.; Yong, M.H.; Hui, A.C.F.; Tu, T.M.; Yong, K.P.; Angon, J.; et al. Low incidence of neurological recurrent side-effects following COVID-19 reimmunization. QJM Int. J. Med. 2023, 116, 221–226. [Google Scholar] [CrossRef] [PubMed]
- Gill, C.; Cho, T.A. Neurologic complications of COVID-19. CONTINUUM Lifelong Learn. Neurol. 2023, 29, 946–965. [Google Scholar] [CrossRef] [PubMed]
- Rawat, M.; Ng, C.; Khan, E.; Shah, R.A.; Ashfaq, S.; Bahader, G.A.; Shah, Z.A. Use of mesenchymal stem cell therapy in COVID-19 related strokes. Neural Regen. Res. 2023, 18, 1881. [Google Scholar] [PubMed]
- Qureshi, A.I.; Baskett, W.I.; Huang, W.; Shyu, D.; Myers, D.; Raju, M.; Lobanova, I.; Suri, M.F.K.; Naqvi, S.H.; French, B.R.; et al. Acute ischemic stroke and COVID-19: An analysis of 27 676 patients. Stroke 2021, 52, 905–912. [Google Scholar] [CrossRef]
- Rivera, R.; Amudio, C.; Cruz, J.P.; Brunetti, E.; Catalan, P.; Sordo, J.G.; Echeverria, D.; Badilla, L.; Chamorro, A.; Gonzalez, C.; et al. The impact of a two-year long COVID-19 public health restriction program on mechanical thrombectomy outcomes in a stroke network. J. Stroke Cerebrovasc. Dis. 2023, 32, 107138. [Google Scholar] [CrossRef]
- Nalaini, F.; Salehi Zahabi, S.; Abdoli, M.; Kazemi, E.; Mehrbakhsh, M.; Khaledian, S.; Fatahian, R. COVID-19 and Brain complications in adult and pediatric patients: A review on neuroimaging findings. Cell. Mol. Biomed. Rep. 2023, 3, 212–221. [Google Scholar] [CrossRef]
- Shama, M.; Mahmood, A.; Mehmood, S.; Zhang, W. Pathological Effects of SARS-CoV-19 Associated With Hematological Abnormalities. Preprints 2023. [Google Scholar] [CrossRef]
- Mahmoudi, H.; Vardanjani, A.E. Blood Clotting Disorders and Thrombosis: An Important Complication of COVID-19. Acta Microbiol. Bulg. 2023, 39, 12–15. [Google Scholar] [CrossRef]
- Özköse, F.; Yavuz, M. Investigation of interactions between COVID-19 and diabetes with hereditary traits using real data: A case study in Turkey. Comput. Biol. Med. 2022, 141, 105044. [Google Scholar] [CrossRef]
- Evirgen, F.; Uçar, S.; Özdemir, N.; Hammouch, Z. System response of an alcoholism model under the effect of immigration via non-singular kernel derivative. Discret. Contin. Dyn. Syst.-S 2021, 14, 2199. [Google Scholar]
- Naik, P.A.; Zu, J.; Owolabi, K.M. Modeling the mechanics of viral kinetics under immune control during primary infection of HIV-1 with treatment in fractional order. Phys. A Stat. Mech. Its Appl. 2020, 545, 123816. [Google Scholar] [CrossRef]
- Özköse, F.; Yavuz, M.; Şenel, M.T.; Habbireeh, R. Fractional order modelling of omicron SARS-CoV-2 variant containing heart attack effect using real data from the United Kingdom. Chaos Solitons Fractals 2022, 157, 111954. [Google Scholar] [CrossRef] [PubMed]
- Öztürk, I.; Özköse, F. Stability analysis of fractional order mathematical model of tumor-immune system interaction. Chaos Solitons Fractals 2020, 133, 109614. [Google Scholar] [CrossRef]
- Naik, P.A.; Owolabi, K.M.; Zu, J.; Naik MU, D. Modeling the transmission dynamics of COVID-19 pandemic in Caputo type fractional derivative. J. Multiscale Model. 2021, 12, 2150006. [Google Scholar] [CrossRef]
- Özköse, F.; Şenel, M.T.; Habbireeh, R. Fractional-order mathematical modelling of cancer cells-cancer stem cells-immune system interaction with chemotherapy. Math. Model. Numer. Simul. Appl. 2021, 1, 67–83. [Google Scholar] [CrossRef]
- Haq, I.U.; Ali, N.; Nisar, K.S. An optimal control strategy and Grünwald-Letnikov finite-difference numerical scheme for the fractional-order COVID-19 model. Math. Model. Numer. Simul. Appl. 2022, 2, 108–116. [Google Scholar] [CrossRef]
- Allegretti, S.; Bulai, I.M.; Marino, R.; Menandro, M.A.; Parisi, K. Vaccination effect conjoint to fraction of avoided contacts for a Sars-Cov-2 mathematical model. Math. Model. Numer. Simul. Appl. 2021, 1, 56–66. [Google Scholar] [CrossRef]
- Evirgen, F. Transmission of Nipah virus dynamics under Caputo fractional derivative. J. Comput. Appl. Math. 2023, 418, 114654. [Google Scholar] [CrossRef]
- Özköse, F.; Yılmaz, S.; Yavuz, M.; Öztürk, İ.; Şenel, M.T.; Bağcı, B.Ş.; Doğan, M.; Önal, Ö. A fractional modeling of tumor–immune system interaction related to Lung cancer with real data. Eur. Phys. J. Plus 2022, 137, 40. [Google Scholar] [CrossRef]
- Özköse, F.; Habbireeh, R.; Şenel, M.T. A novel fractional order model of SARS-CoV-2 and Cholera disease with real data. J. Comput. Appl. Math. 2023, 423, 114969. [Google Scholar] [CrossRef]
- Naik, P.A.; Eskandari, Z.; Yavuz, M.; Zu, J. Complex dynamics of a discrete-time Bazykin–Berezovskaya prey-predator model with a strong Allee effect. J. Comput. Appl. Math. 2022, 413, 114401. [Google Scholar] [CrossRef]
- Sadek, L.; Sadek, O.; Alaoui, H.T.; Abdo, M.S.; Shah, K.; Abdeljawad, T. Fractional order modeling of predicting covid-19 with isolation and vaccination strategies in morocco. CMES-Comput. Model. Eng. Sci. 2023, 136, 1931–1950. [Google Scholar] [CrossRef]
- Karaagac, B.; Owolabi, K.M.; Pindza, E. A computational technique for the Caputo fractal-fractional diabetes mellitus model without genetic factors. Int. J. Dyn. Control 2023, 11, 2161–2178. [Google Scholar] [CrossRef] [PubMed]
- Alkahtani, B.S. Mathematical Modeling of COVID-19 Transmission Using a Fractional Order Derivative. Fractal Fract. 2022, 7, 46. [Google Scholar] [CrossRef]
- Hadi, M.S.; Bilgehan, B. Fractional COVID-19 modeling and analysis on successive optimal control policies. Fractal Fract. 2022, 6, 533. [Google Scholar] [CrossRef]
- Sun, T.C.; DarAssi, M.H.; Alfwzan, W.F.; Khan, M.A.; Alqahtani, A.S.; Alshahrani, S.S.; Muhammad, T. Mathematical Modeling of COVID-19 with Vaccination Using Fractional Derivative: A Case Study. Fractal Fract. 2023, 7, 234. [Google Scholar] [CrossRef]
- Dababneh, A.; Djenina, N.; Ouannas, A.; Grassi, G.; Batiha, I.M.; Jebril, I.H. A new incommensurate fractional-order discrete COVID-19 model with vaccinated individuals compartment. Fractal Fract. 2022, 6, 456. [Google Scholar] [CrossRef]
- Khedr, E.M.; Abdelwarith, A.; Moussa, G.M.; Saber, M. Recombinant tissue plasminogen activator (rTPA) management for first onset acute Ischemic Stroke with COVID-19 and non-COVID-19 patients. J. Stroke Cerebrovasc. Dis. 2023, 32, 107031. [Google Scholar] [CrossRef]
- Massoud, G.P.; Hazimeh, D.H.; Amin, G.; Mekary, W.; Khabsa, J.; Araji, T.; Fares, S.; Mericskay, M.; Booz, G.W.; Zouein, F.A. Risk of thromboembolic events in non-hospitalized COVID-19 patients: A systematic review. Eur. J. Pharmacol. 2023, 941, 175501. [Google Scholar] [CrossRef]
- Zuin, M.; Mazzitelli, M.; Rigatelli, G.; Bilato, C.; Cattelan, A.M. Risk of ischemic stroke in patients recovered from COVID-19 infection: A systematic review and meta-analysis. Eur. Stroke J. 2023. [Google Scholar] [CrossRef]
- Van Dusen, R.A.; Abernethy, K.; Chaudhary, N.; Paudyal, V.; Kurmi, O. Association of the COVID-19 pandemic on stroke admissions and treatment globally: A systematic review. BMJ Open 2023, 13, e062734. [Google Scholar] [CrossRef] [PubMed]
- Ferrone, S.R.; Sanmartin, M.X.; Ohara, J.; Jimenez, J.C.; Feizullayeva, C.; Lodato, Z.; Shahsavarani, S.; Lacher, G.; Demissie, S.; Vialet, J.M.; et al. Acute ischemic stroke outcomes in patients with COVID-19: A systematic review and meta-analysis. J. NeuroInterventional Surg. 2023. [Google Scholar] [CrossRef] [PubMed]
- Sasmal, S.K. Population dynamics with multiple Allee effects induced by fear factors—A mathematical study on prey-predator interactions. Appl. Math. Model. 2018, 64, 1–14. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Ghaziani, R.K.; Alidousti, J.; Eshkaftaki, A.B. Stability and dynamics of a fractional order Leslie–Gower prey–predator model. Appl. Math. Model. 2016, 40, 2075–2086. [Google Scholar] [CrossRef]
- Petráš, I. Fractional-Order Nonlinear Systems: Modeling, Analysis and Simulation; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Lin, W. Global existence theory and chaos control of fractional differential equations. J. Math. Anal. Appl. 2007, 332, 709–726. [Google Scholar] [CrossRef]
- Odibat, Z.M.; Shawagfeh, N.T. Generalized Taylor’s formula. Appl. Math. Comput. 2007, 186, 286–293. [Google Scholar] [CrossRef]
- Odibat, Z.; Baleanu, D. Numerical simulation of initial value problems with generalized Caputo-type fractional derivatives. Appl. Numer. Math. 2020, 156, 94–105. [Google Scholar] [CrossRef]
- Van den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Diekmann, O.; Heesterbeek, J.A.P.; Roberts, M.G. The construction of next-generation matrices for compartmental epidemic models. J. R. Soc. Interface 2010, 7, 873–885. [Google Scholar] [CrossRef]
- Breda, D.; Florian, F.; Ripoll, J.; Vermiglio, R. Efficient numerical computation of the basic reproduction number for structured populations. J. Comput. Appl. Math. 2021, 384, 113165. [Google Scholar] [CrossRef]
- Breda, D.; Kuniya, T.; Ripoll, J.; Vermiglio, R. Collocation of next-generation operators for computing the basic reproduction number of structured populations. J. Sci. Comput. 2020, 85, 1–33. [Google Scholar] [CrossRef]
- Chitnis, N.; Hyman, J.M.; Cushing, J.M. Determining important parameters in the spread of malaria through the sensitivity analysis of a mathematical model. Bull. Math. Biol. 2008, 70, 1272. [Google Scholar] [CrossRef]
- Vargas-De-León, C. Volterra-type Lyapunov functions for fractional-order epidemic systems. Commun. Nonlinear Sci. Numer. Simul. 2015, 24, 75–85. [Google Scholar] [CrossRef]
- Naik, P.A.; Yavuz, M.; Zu, J. The role of prostitution on HIV transmission with memory: A modeling approach. Alex. Eng. J. 2020, 59, 2513–2531. [Google Scholar] [CrossRef]
- Jin, B.; Lazarov, R.; Zhou, Z. An analysis of the L1 scheme for the subdiffusion equation with nonsmooth data. IMA J. Numer. Anal. 2016, 36, 197–221. [Google Scholar] [CrossRef]
- Du, M.; Wang, Z. Correcting the initialization of models with fractional derivatives via history-dependent conditions. Acta Mech. Sin. 2016, 32, 320–325. [Google Scholar] [CrossRef]
- Magin, R.L. Fractional Calculus in Bioengineering; Begell House Publishers Redding: Redding, CT, USA, 2006. [Google Scholar]
- van Baarle, D.; Tsegaye, A.; Miedema, F.; Akbar, A. Significance of senescence for virus-specific memory T cell responses: Rapid ageing during chronic stimulation of the immune system. Immunol. Lett. 2005, 97, 19–29. [Google Scholar] [CrossRef]
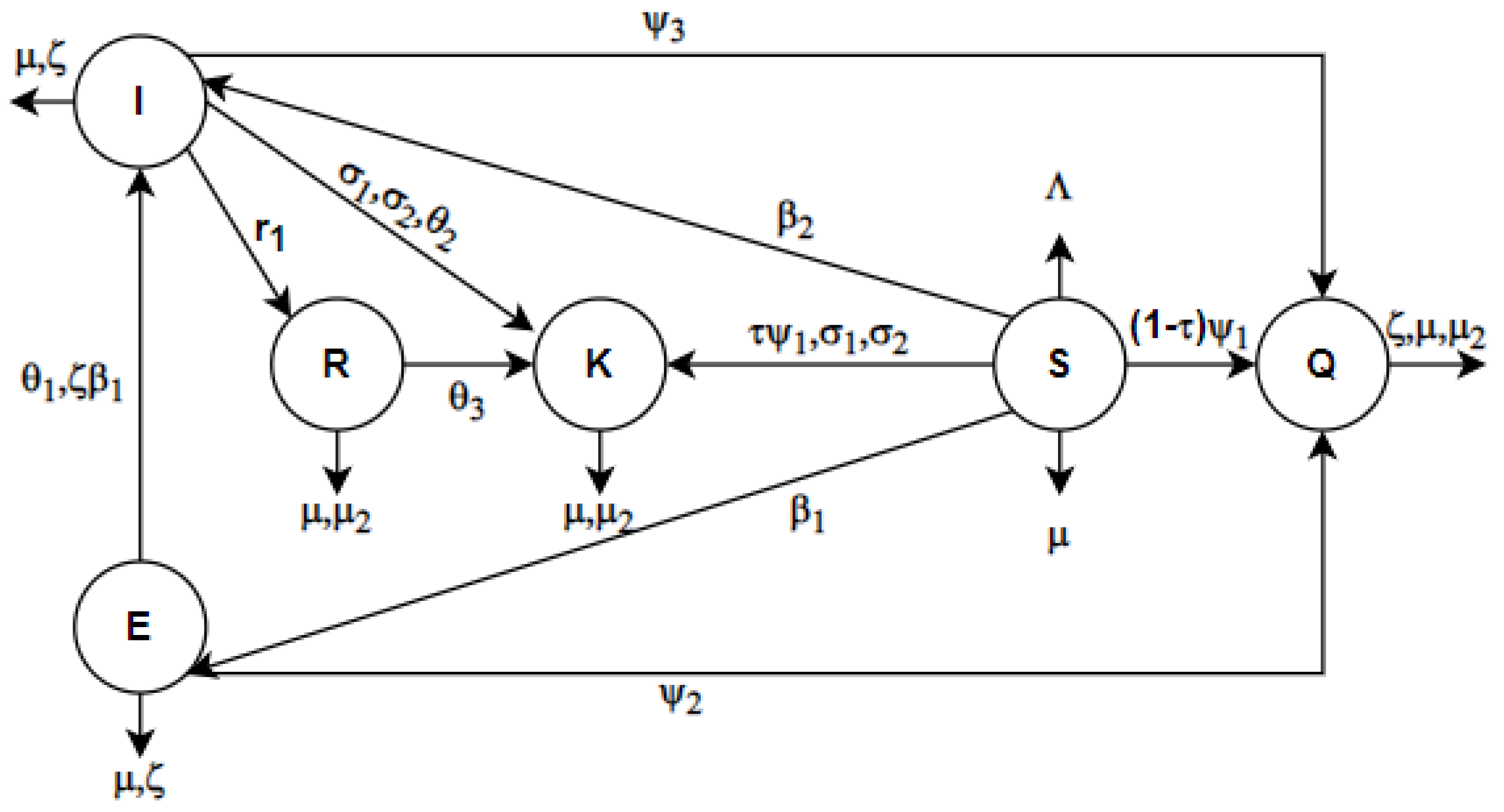








| Parameters | Parameter Description |
|---|---|
| Recruitment rate | |
| Natural death probability | |
| Death rate from stroke | |
| Transmission rate for E class | |
| Transmission rate for I class | |
| Growth rate | |
| Level of the fear to be infected with COVID-19 | |
| Carrying capacity of S | |
| Rate of susceptible individuals undergoing quarantine | |
| Rate of infected individuals without symptoms who have undergone quarantine | |
| Rate of infected individuals exhibiting symptoms who have been placed in quarantine | |
| Recovered rate from COVID-19 | |
| Mortality rate due to complications | |
| Screening rate | |
| Rates of developing stroke of infected individuals | |
| Probability rate of developing stroke of recovered people | |
| Rates of having a stroke due to heredity (genetic disorders) | |
| Rates of having a stroke due to a chronic disease such as high | |
| blood pressure | |
| Probability of individuals in the susceptible S class developing a stroke due to quarantine | |
| The appearance of symptoms of COVID-19 on the infected person |
| Par. | Meaning | Value | Source |
|---|---|---|---|
| Recruitment rate | Calculated | ||
| The natural death rate | Calculated | ||
| The death rate from stroke | Fitted | ||
| Rate of disease transmission through contact with E class | Fitted | ||
| Rate of disease transmission through contact with I class | Fitted | ||
| The growth rate | Fitted | ||
| Level of the fear to be infected with COVID-19 | Fitted | ||
| Carrying capacity of S | Fitted | ||
| Rate of susceptible individuals undergoing quarantine | Fitted | ||
| Rate of infected individuals without symptoms who have undergone quarantine | Fitted | ||
| Rate of infected individuals exhibiting symptoms | Fitted | ||
| who have been placed in quarantine | Fitted | ||
| Recovered rate from COVID-19 | Fitted | ||
| The mortality rate due to complications | Fitted | ||
| Screening rate | Fitted | ||
| Probability of developing stroke of infected individuals | Fitted | ||
| Probability rate of developing stroke of recovered people | Fitted | ||
| probability of having a stroke due to heredity (genetic disorders) | Fitted | ||
| Probability of having a stroke due to a chronic disease such as high | Fitted | ||
| blood pressure | Fitted | ||
| Probability of individuals in S class developing a stroke due to quarantine | Fitted | ||
| The appearance of symptoms of COVID-19 on the infected person | Fitted |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Özköse, F. Long-Term Side Effects: A Mathematical Modeling of COVID-19 and Stroke with Real Data. Fractal Fract. 2023, 7, 719. https://doi.org/10.3390/fractalfract7100719
Özköse F. Long-Term Side Effects: A Mathematical Modeling of COVID-19 and Stroke with Real Data. Fractal and Fractional. 2023; 7(10):719. https://doi.org/10.3390/fractalfract7100719
Chicago/Turabian StyleÖzköse, Fatma. 2023. "Long-Term Side Effects: A Mathematical Modeling of COVID-19 and Stroke with Real Data" Fractal and Fractional 7, no. 10: 719. https://doi.org/10.3390/fractalfract7100719
APA StyleÖzköse, F. (2023). Long-Term Side Effects: A Mathematical Modeling of COVID-19 and Stroke with Real Data. Fractal and Fractional, 7(10), 719. https://doi.org/10.3390/fractalfract7100719





