On Ikeda-Based Memristor Map with Commensurate and Incommensurate Fractional Orders: Bifurcation, Chaos, and Entropy
Abstract
:1. Introduction
2. Discrete Memristor Mathematical Model
3. Fractional-Order Ikeda-Based Memristor Map
4. Nonlinear Dynamics of the Fractional-Order Ikeda-Based Memristor Map
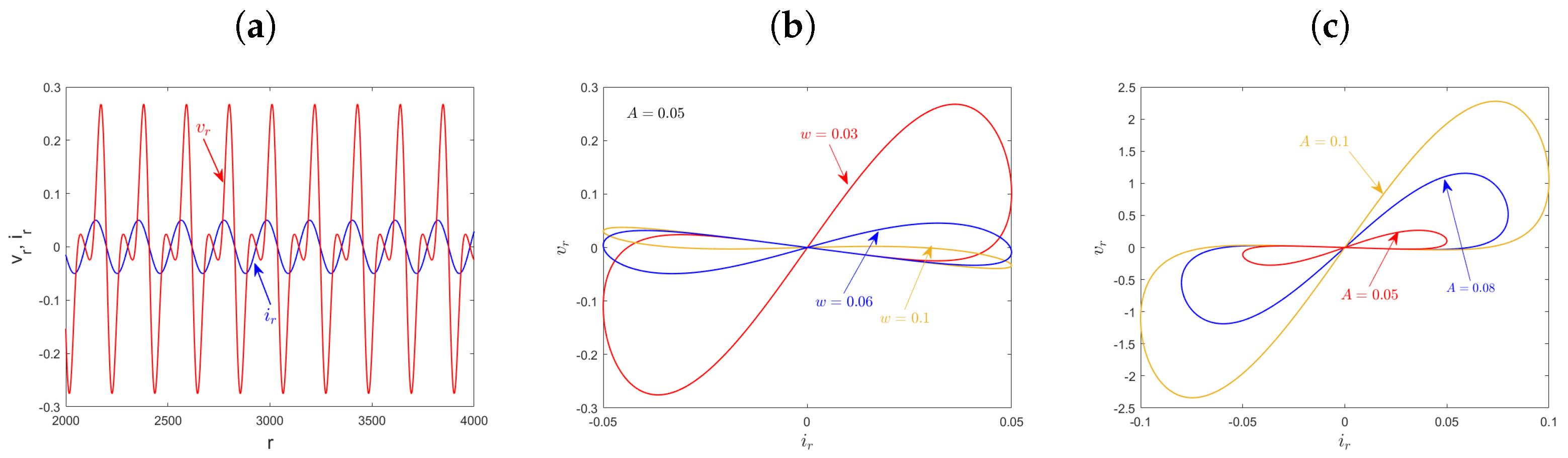
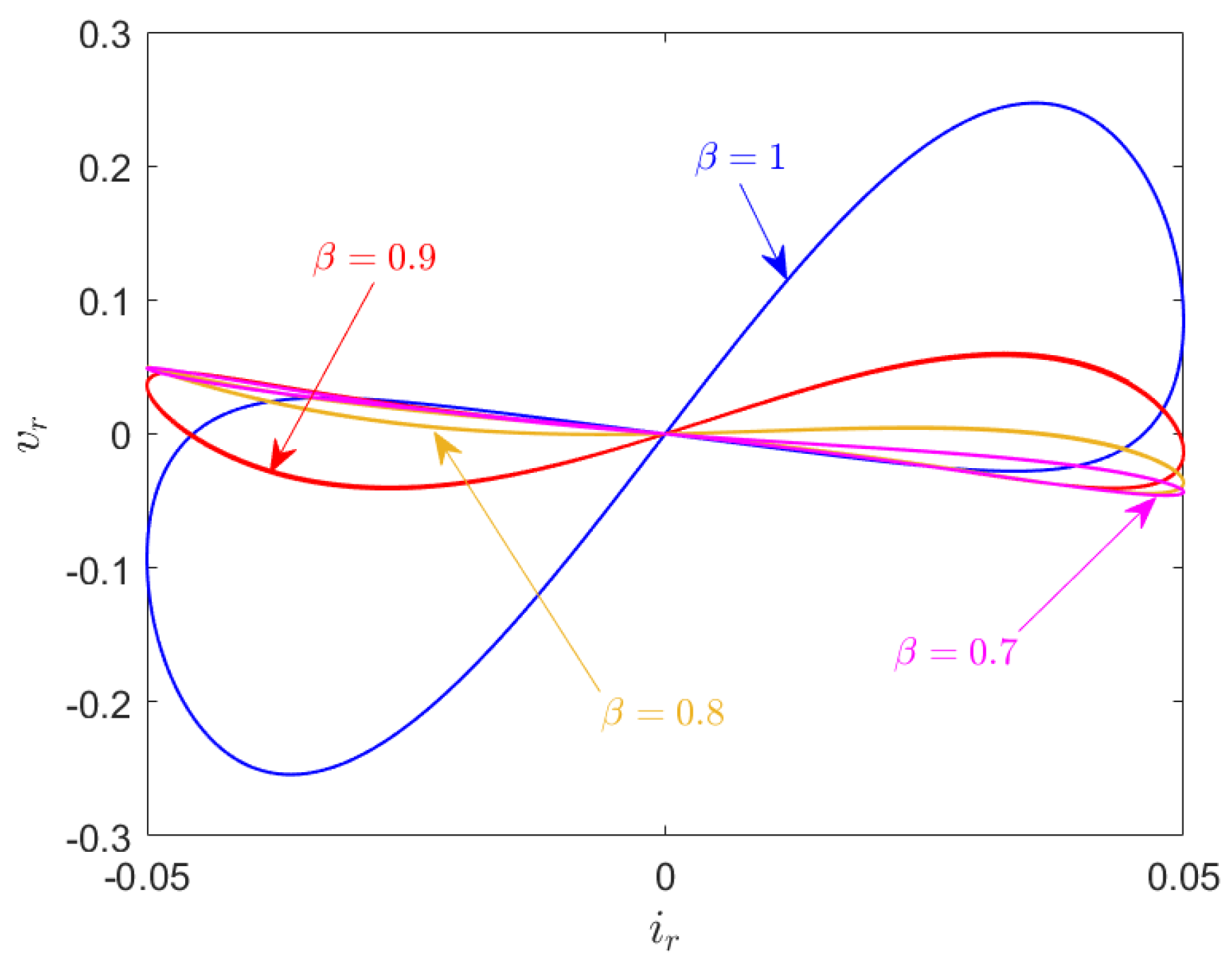
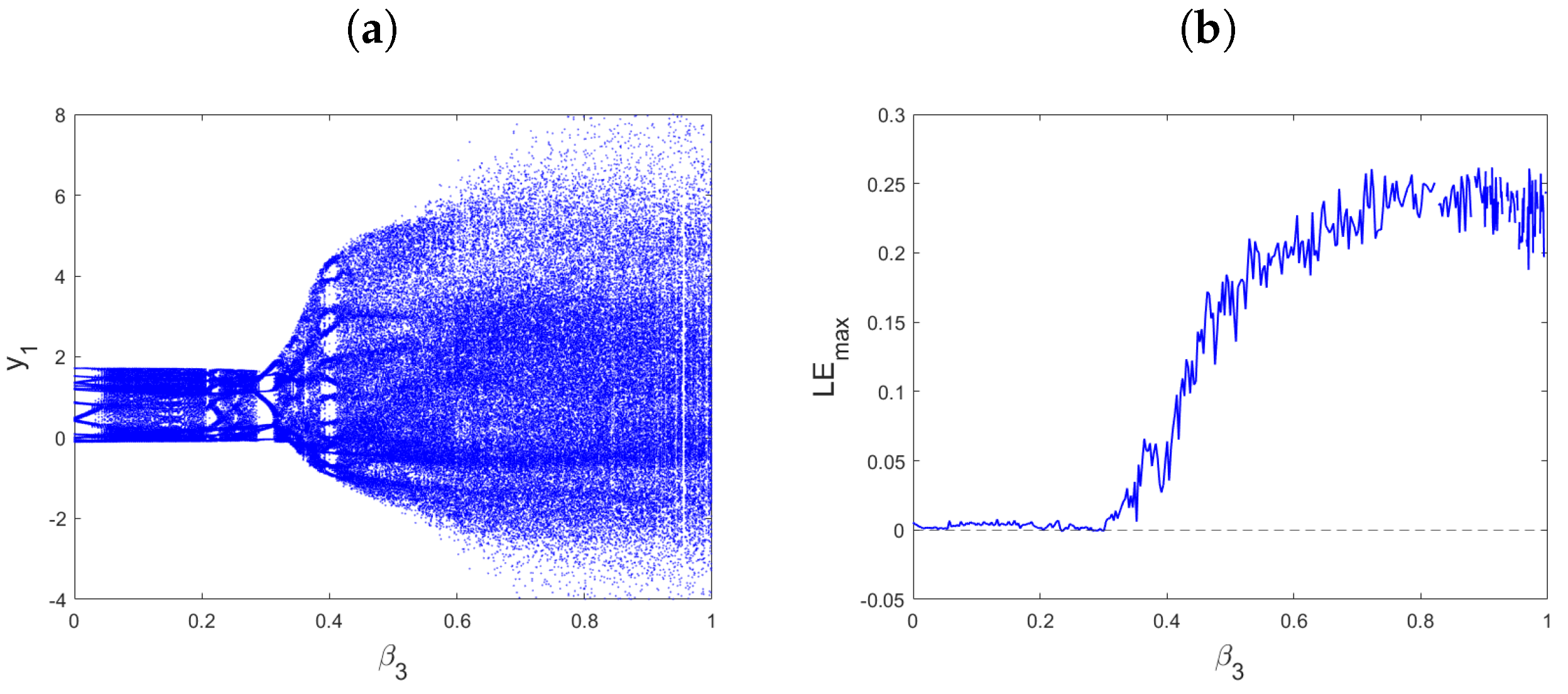
4.1. Commensurate-Order Fractional Ikeda-Based Memristor Map
4.2. Incommensurate-Order Fractional Ikeda-Based Memristor Map
- Case 1.
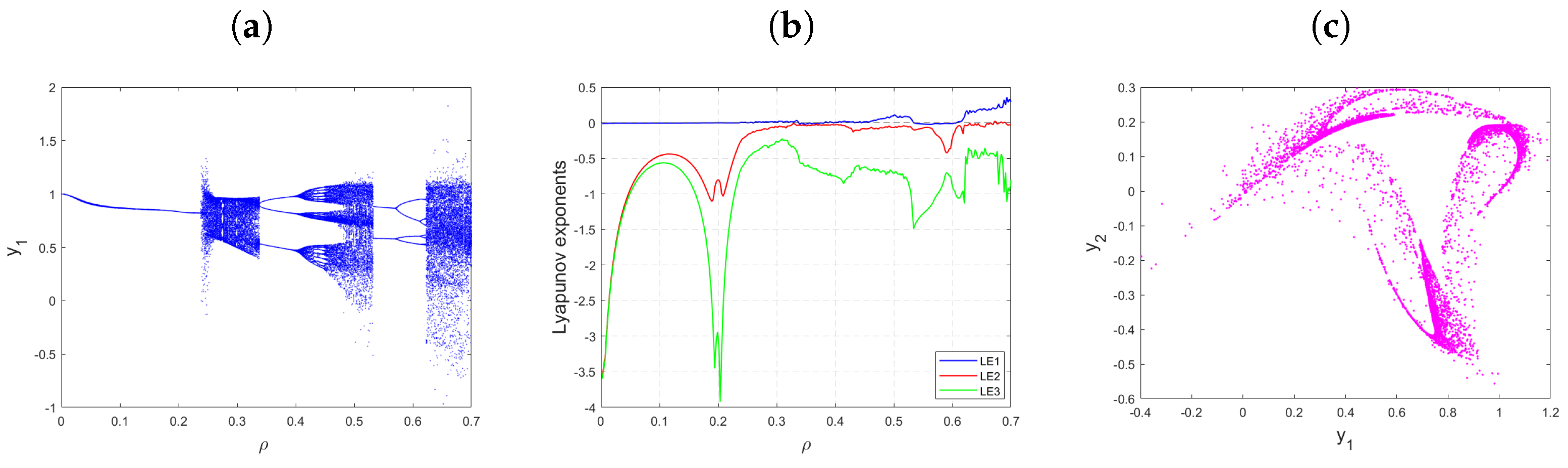
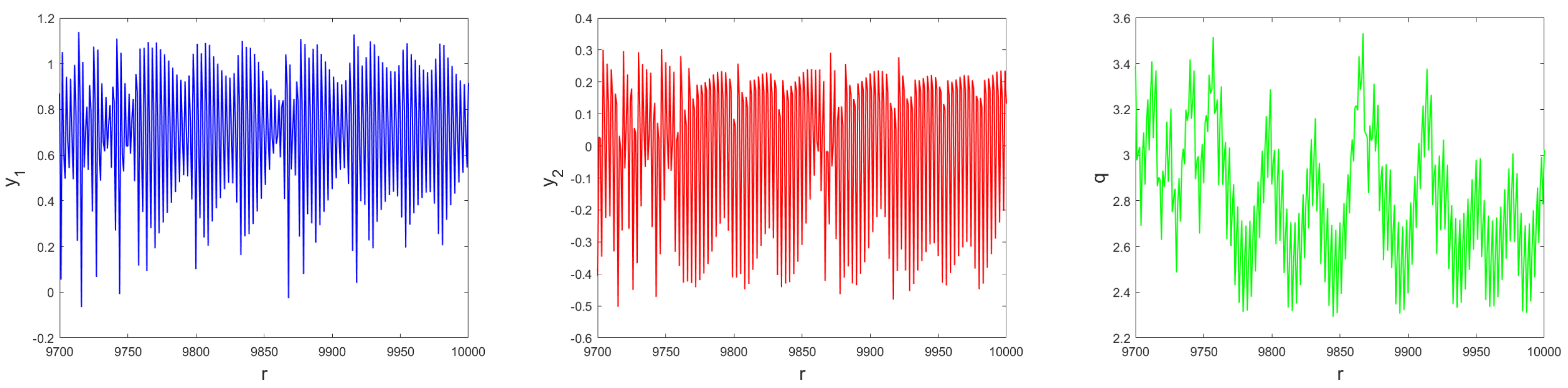
- In Figure 9a,b, we observe the variation of the order from 0 to 1 with a step size of . These figures illustrate the bifurcation and its corresponding Lyapunov exponent of the incommensurate-order fractional Ikeda-based memristor map (21) for , the parameter value , , and the initial conditions =. From Figure 9a, it is evident that the state of the incommensurate Ikeda-based memristor map (21) exhibits chaotic behavior for smaller values of , as evidenced by positive , as shown in Figure 9b. The Lyapunov exponent () displayed in Figure 9b fluctuates between positive and negative values when lies within the region (0.24, 0.36). This outcome indicates the presence of chaotic behavior with the emergence of periodic windows. As the incommensurate order increases further, the trajectories transition from chaotic to regular motion, characterized by two-period orbits where the states of the incommensurate order fractional Ikeda-based memristor map (21) become stable.
- Case 2.
- The bifurcation diagram and its () are plotted to investigate the dynamic behaviors of the incommensurate order fractional Ikeda-based memristor map (21), with being an adjustable parameter, as depicted in Figure 10. The simulations are conducted by varying in the range , while keeping the incommensurate orders , initial conditions , and parameter values unchanged. From the figure, it can be observed that as the order increases to larger values, the trajectories become more stable. On the other hand, as decreases, chaotic behaviors emerge with positive values of , along with the appearance of small periodic regions exhibiting negative values of . Additionally, as decreases even further and approaches 0, the maximum Lyapunov exponent values decrease until they reach zero. This indicates that periodic trajectories appear and signifies that the incommensurate fractional Ikeda-based memristor map (21) undergoes a transition from chaotic to regular behavior. The observed changes in the and the corresponding dynamic patterns illustrate the system’s sensitivity to variations in the parameter , highlighting the complexity and versatility of the incommensurate-order fractional Ikeda-based memristor map.
- Case 3.
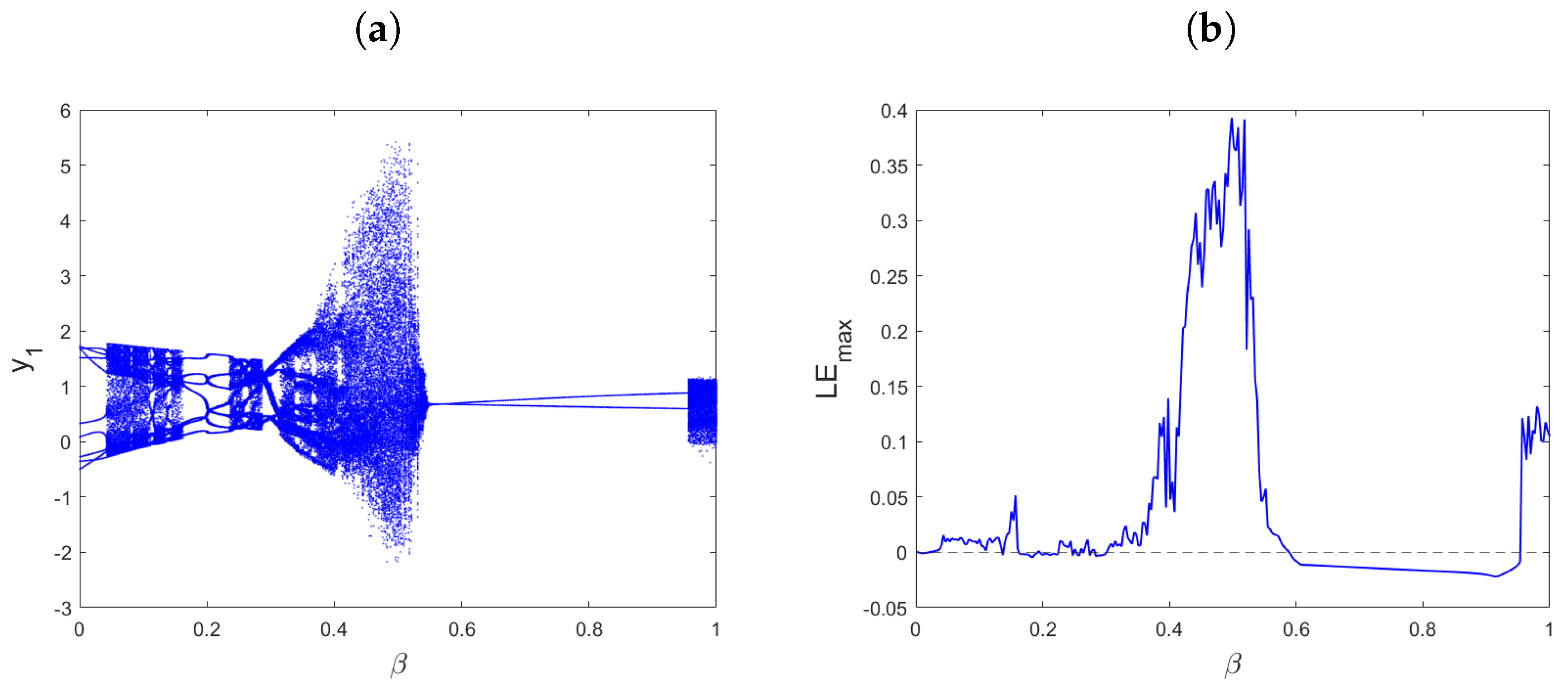
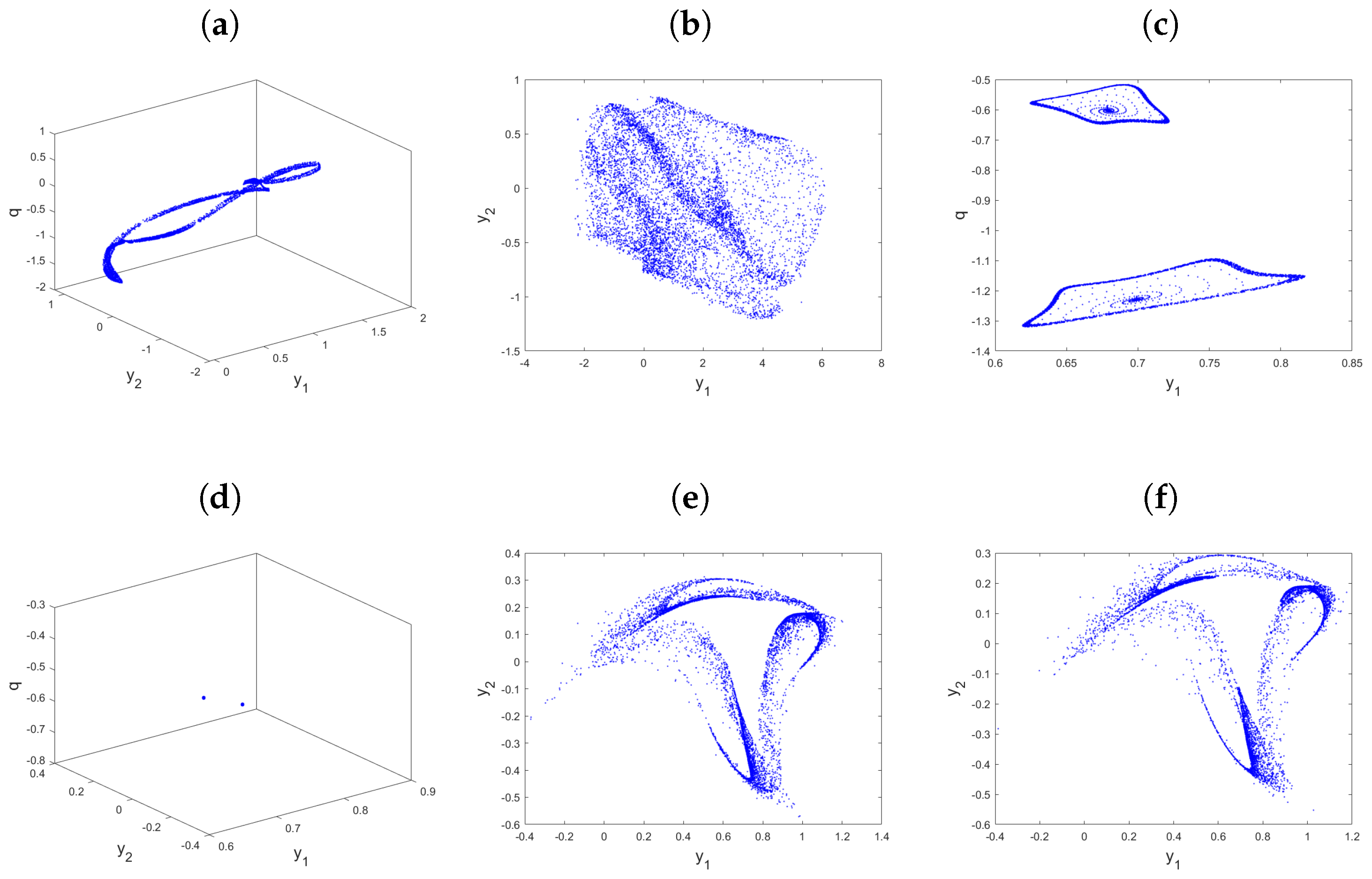
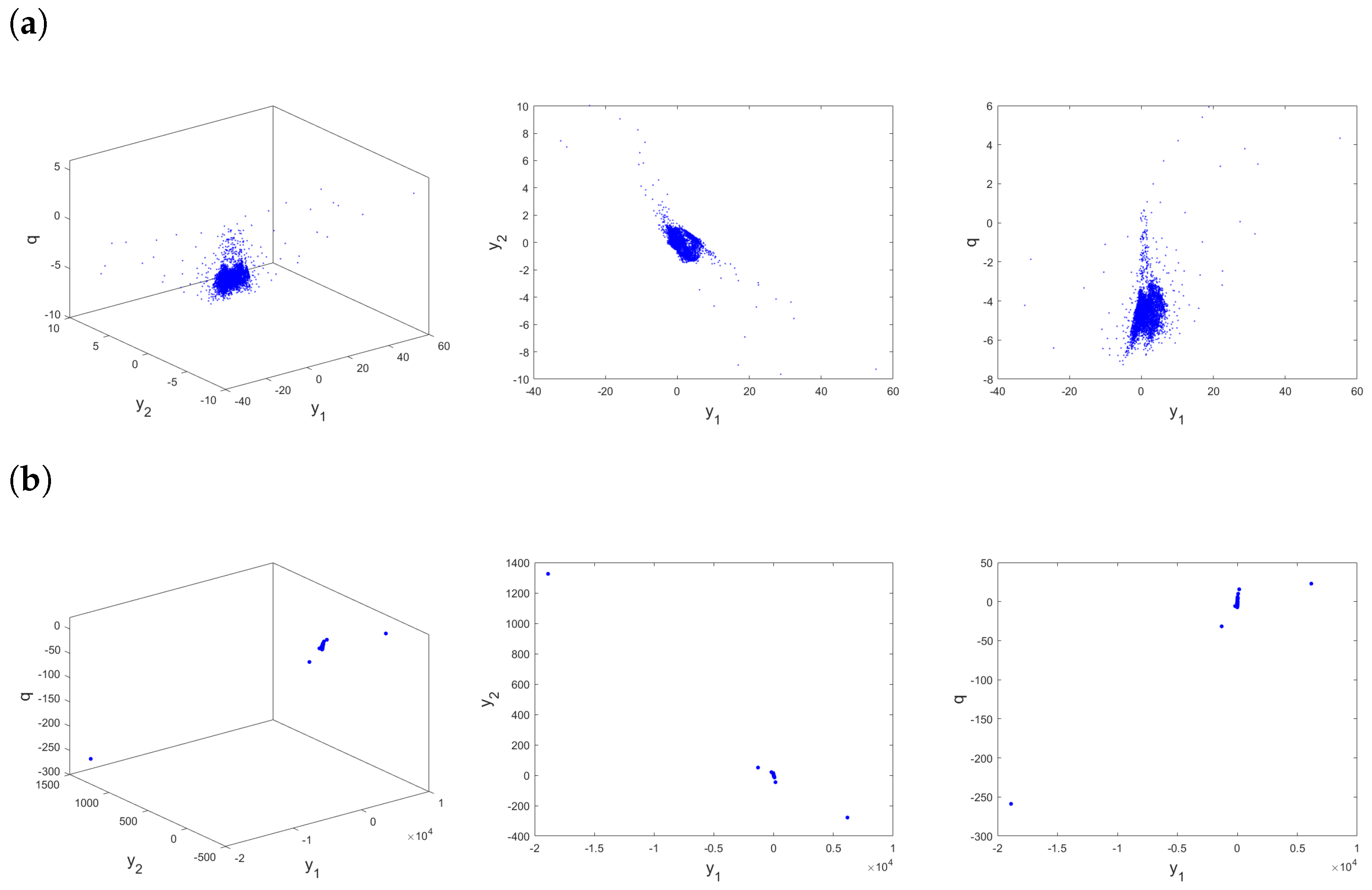
- The bifurcation chart and its corresponding of the proposed new incommensurate-order fractional Ikeda-based memristor map (21) are presented in Figure 11, where the parameter is varied within the range . In this analysis, we maintain the incommensurate orders as . From Figure 11, it is evident that unlike the previous cases, the trajectories of the incommensurate model exhibit chaotic behavior when the order takes larger values, as indicated by the higher values of . We see also see that when approaches 1, the map shows transition states and the trajectories go to infinity, for example, when and after some number of iterations, especially , the trajectories diverge toward infinity, as presented in Figure 12. As continues to decrease, the starts decreasing as well, reaching its smallest value, leading to a reduction in chaos and, consequently, the behavior of the map’s states becomes more stable. These results emphasize the sensitivity of the incommensurate fractional Ikeda-based memristor map (21) to changes in the order , resulting in a diverse range of dynamic behaviors, including chaotic and periodic motion. This highlights the significance of incommensurate orders in shaping the system’s dynamics. Additionally, the phase portraits of the state variables of the incommensurate fractional Ikeda-based memristor map (21), as shown in Figure 13, further support the notion that incommensurate orders more accurately represent the system’s behaviors. Overall, the study emphasizes the intricate and diverse nature of the incommensurate-order fractional Ikeda-based memristor map and the significance of the choice of fractional orders in modeling and characterizing its dynamics.
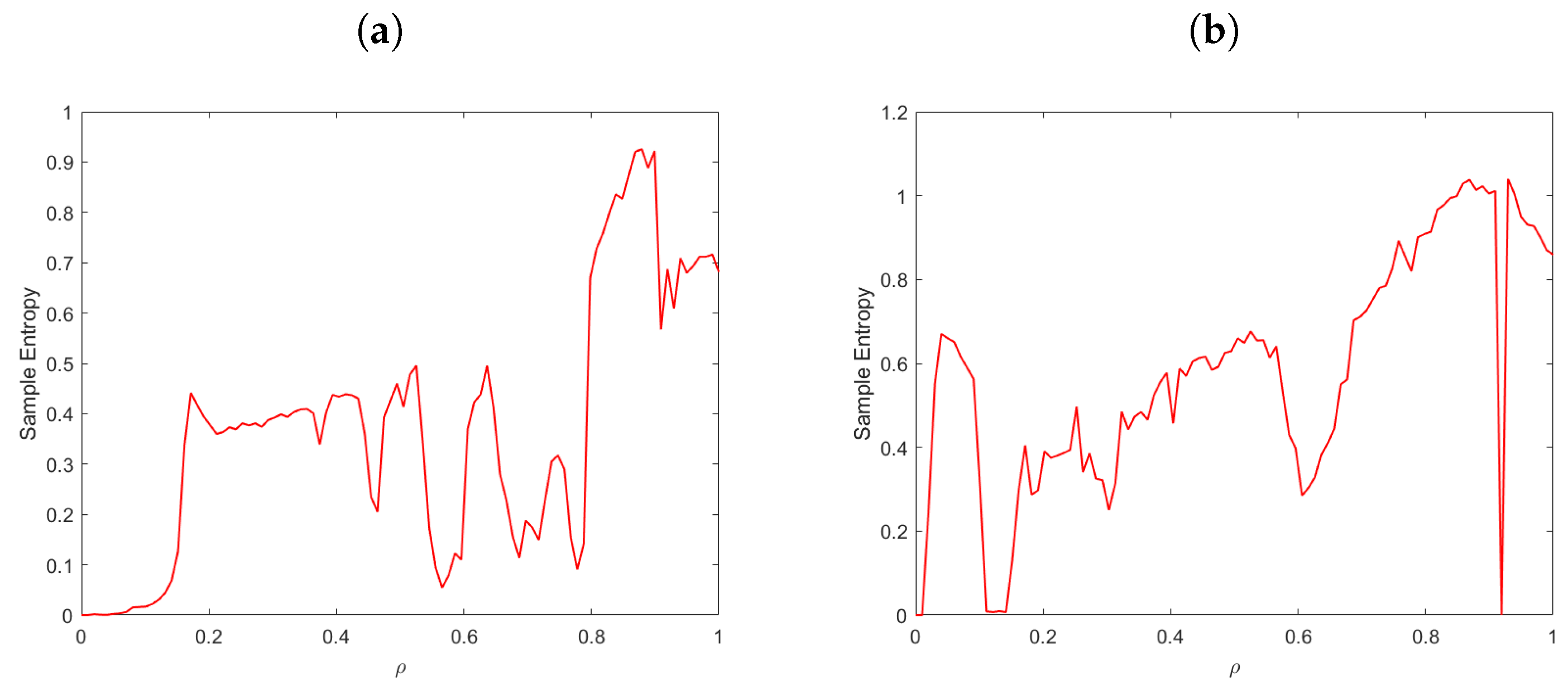
5. The Sample Entropy Test (SampEn)
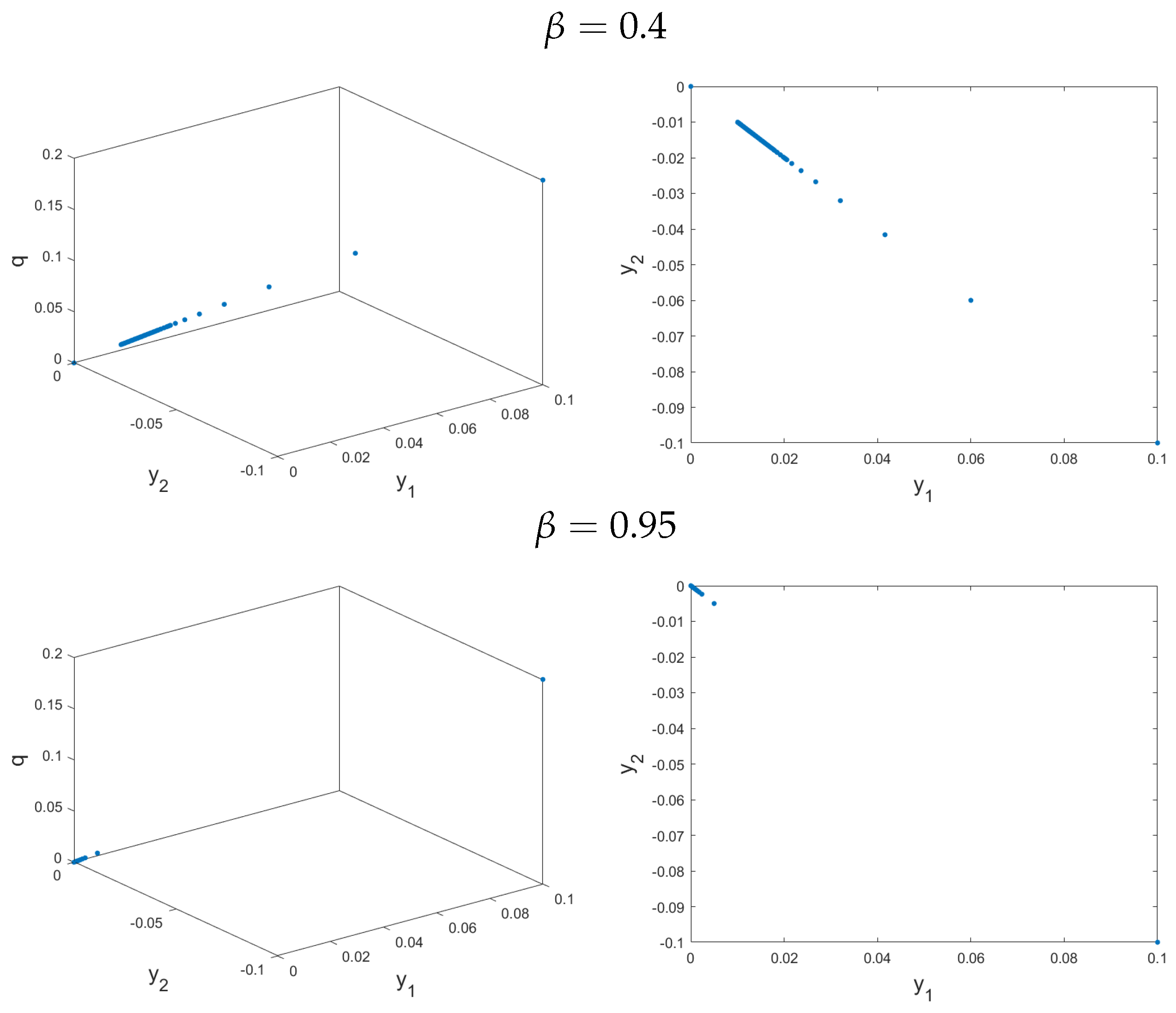
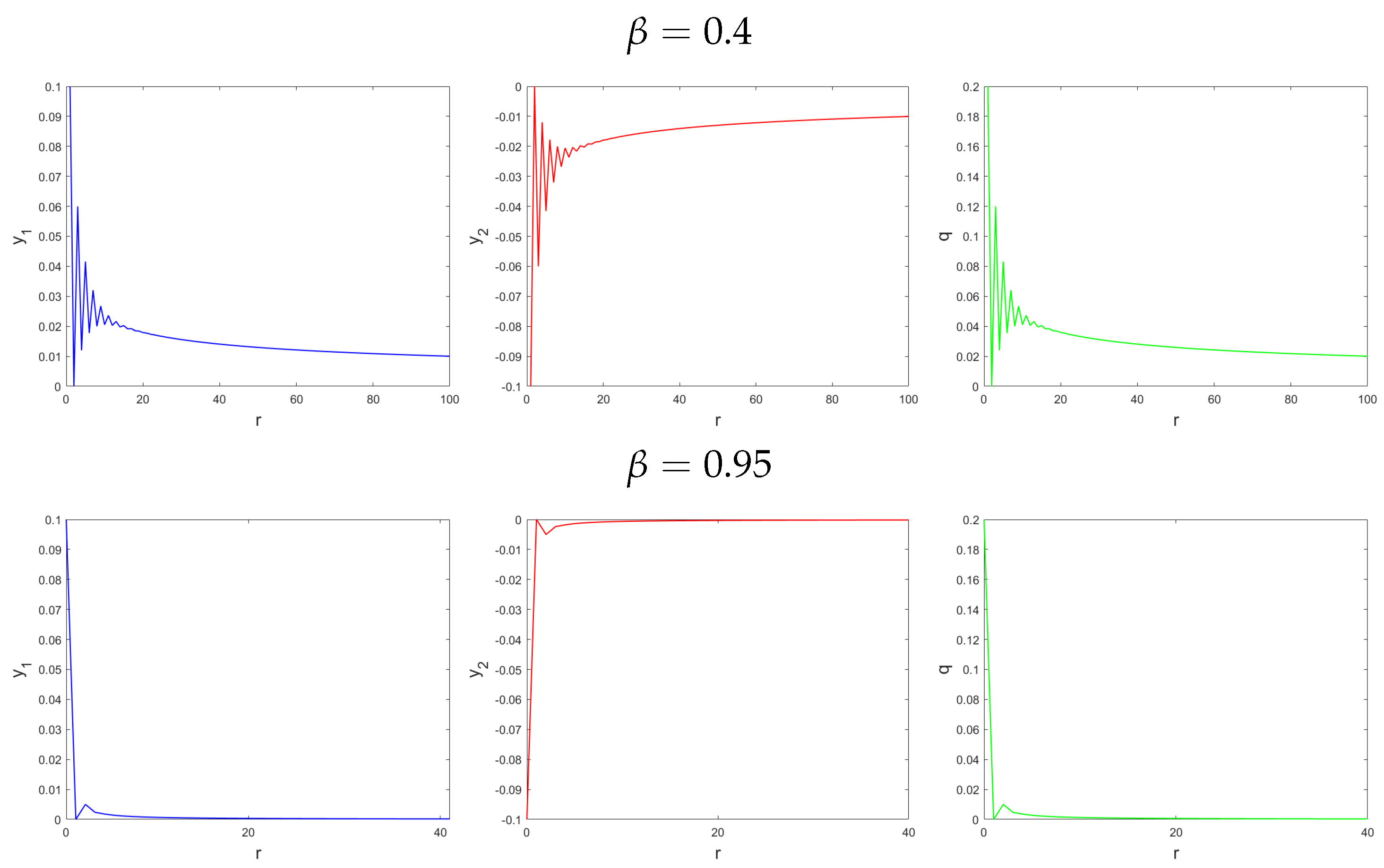
6. Control of Fractional Ikeda-Based Memristor Map
6.1. Stabilisation of Fractional Ikeda-Based Memristor Map
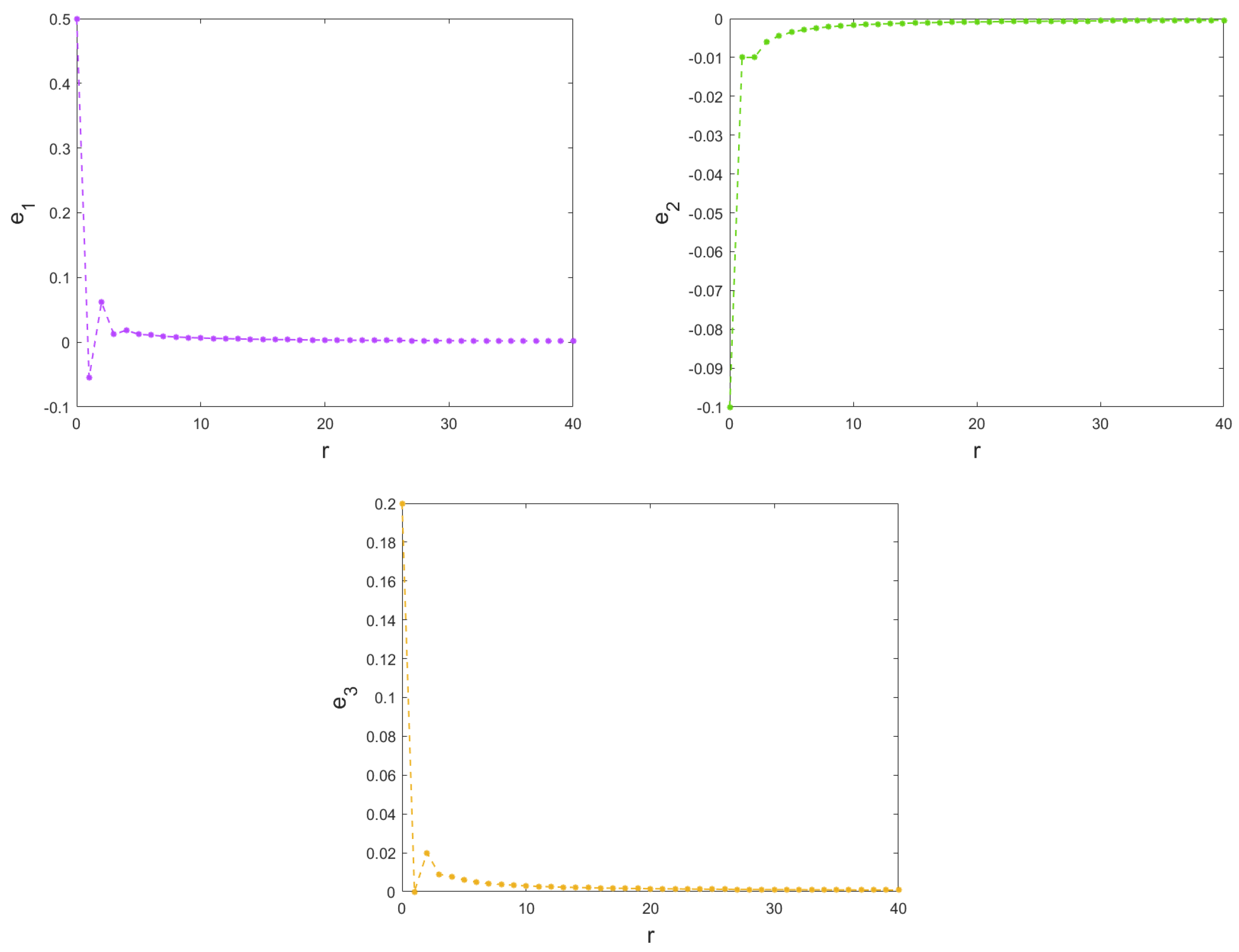
6.2. Synchronization Scheme of Fractional Ikeda-Based Memristor Map
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pecora, L.M.; Carroll, T.L.; Johnson, G.A.; Mar, D.J.; Heagy, J.F. Fundamentals of synchronization in chaotic systems, concepts, and applications. Chaos Interdiscip. J. Nonlinear Sci. 1997, 7, 520–543. [Google Scholar] [CrossRef]
- Yang, D.; Liu, Z.; Zhou, J. Chaos optimization algorithms based on chaotic maps with different probability distribution and search speed for global optimization. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 1229–1246. [Google Scholar] [CrossRef]
- Chai, X.; Zheng, X.; Gan, Z.; Han, D.; Chen, Y. An image encryption algorithm based on chaotic system and compressive sensing. Signal Process. 2018, 148, 124–144. [Google Scholar] [CrossRef]
- Xu, Q.; Sun, K.; Cao, C.; Zhu, C. A fast image encryption algorithm based on compressive sensing and hyperchaotic map. Opt. Lasers Eng. 2019, 121, 203–214. [Google Scholar] [CrossRef]
- Ditto, W.; Munakata, T. Principles and applications of chaotic systems. Commun. ACM 1995, 38, 96–102. [Google Scholar] [CrossRef]
- Vaidyanathan, S.; Volos, C. (Eds.) Advances and Applications in Chaotic Systems; Springer: Berlin, Germany, 2016; Volume 636, p. 445. [Google Scholar]
- Zang, X.; Iqbal, S.; Zhu, Y.; Liu, X.; Zhao, J. Applications of chaotic dynamics in robotics. Int. J. Adv. Robot. Syst. 2016, 13, 60. [Google Scholar] [CrossRef]
- Wang, X.; Su, Y.; Luo, C.; Nian, F.; Teng, L. Color image encryption algorithm based on hyperchaotic system and improved quantum revolving gate. Multimed. Tools Appl. 2022, 81, 13845–13865. [Google Scholar] [CrossRef]
- Chua, L.O. Memristor-The missing circuit element. IEEE Trans. Circuit. Theory 1971, 18, 507–519. [Google Scholar] [CrossRef]
- Strukov, D.B.; Snider, G.S.; Stewart, D.R.; Williams, R.S. The missing memristor found. Nature 2008, 453, 80–83. [Google Scholar] [CrossRef]
- Ma, X.; Mou, J.; Liu, J.; Ma, C.; Yang, F.; Zhao, X. A novel simple chaotic circuit based on memristor—Memcapacitor. Nonlinear Dyn. 2020, 100, 2859–2876. [Google Scholar] [CrossRef]
- Lin, T.C.; Huang, F.Y.; Du, Z.; Lin, Y.C. Synchronization of fuzzy modeling chaotic time delay memristor-based Chua’s circuits with application to secure communication. Int. J. Fuzzy Syst. 2015, 17, 206–214. [Google Scholar] [CrossRef]
- Sun, J.; Kang, K.; Sun, Y.; Hong, Q.; Wang, C. A multi-value 3D crossbar array nonvolatile memory based on pure memristors. Eur. Phys. J. Spec. Top. 2022, 231, 3119–3130. [Google Scholar] [CrossRef]
- Bao, B.; Rong, K.; Li, H.; Li, K.; Hua, Z.; Zhang, X. Memristor-coupled logistic hyperchaotic map. IEEE Trans. Circuits Syst. Regul. Pap. 2021, 68, 2992–2996. [Google Scholar] [CrossRef]
- Itoh, M.; Chua, L.O. Dynamics of memristor circuits. Int. J. Bifurc. Chaos 2014, 24, 1430015. [Google Scholar] [CrossRef]
- Li, C.; Feng, B.; Li, S.; Kurths, J.; Chen, G. Dynamic analysis of digital chaotic maps via state-mapping networks. IEEE Trans. Circuits Syst. Regul. Pap. 2019, 66, 2322–2335. [Google Scholar] [CrossRef]
- Rong, K.; Bao, H.; Li, H.; Hua, Z.; Bao, B. Memristive Hénon map with hidden Neimark–Sacker bifurcations. Nonlinear Dyn. 2022, 108, 4459–4470. [Google Scholar] [CrossRef]
- Ramakrishnan, B.; Mehrabbeik, M.; Parastesh, F.; Rajagopal, K.; Jafari, S. A new memristive neuron map model and its network’s dynamics under electrochemical coupling. Electronics 2022, 11, 153. [Google Scholar] [CrossRef]
- Almatroud, O.A.; Pham, V.T. Building Fixed Point-Free Maps with Memristor. Mathematics 2023, 11, 1319. [Google Scholar] [CrossRef]
- Chen, M.; Luo, X.; Suo, Y.; Xu, Q.; Wu, H. Hidden extreme multistability and synchronicity of memristor-coupled non-autonomous memristive Fitzhugh–Nagumo models. Nonlinear Dyn. 2023, 111, 7773–7788. [Google Scholar] [CrossRef]
- Zhang, L.P.; Liu, Y.; Wei, Z.C.; Jiang, H.B.; Lyu, W.P.; Bi, Q.S. Extremely hidden multi-stability in a class of two-dimensional maps with a cosine memristor. Chin. Phys. B 2022, 31, 100503. [Google Scholar] [CrossRef]
- Hilfer, R. (Ed.) Applications of Fractional Calculus in Physics; World Scientific: Singapore, 2000. [Google Scholar]
- Atici, F.M.; Eloe, P. Discrete fractional calculus with the nabla operator. Electron. J. Qual. Theory Differ. Equ. [Electron. Only] 2009, 2009, 3. [Google Scholar] [CrossRef]
- Anastassiou, G.A. Principles of delta fractional calculus on time scales and inequalities. Math. Comput. Model. 2010, 52, 556–566. [Google Scholar] [CrossRef]
- Abdeljawad, T. On Riemann and Caputo fractional differences. Comput. Math. Appl. 2011, 62, 1602–1611. [Google Scholar] [CrossRef]
- Wu, G.C.; Song, T.T.; Wang, S. Caputo—Hadamard fractional differential equations on time scales: Numerical scheme, asymptotic stability, and chaos. Chaos Interdiscip. J. Nonlinear Sci. 2022, 32, 093143. [Google Scholar] [CrossRef] [PubMed]
- Majhi, S.; Perc, M.; Ghosh, D. Dynamics on higher-order networks: A review. J. R. Soc. Interface 2022, 19, 20220043. [Google Scholar] [CrossRef]
- Wu, G.C.; Baleanu, D. Discrete fractional logistic map and its chaos. Nonlinear Dyn. 2014, 75, 283–287. [Google Scholar] [CrossRef]
- Abbes, A.; Ouannas, A.; Shawagfeh, N.; Khennaoui, A.A. Incommensurate fractional discrete neural network: Chaos and complexity. Eur. Phys. J. Plus 2022, 137, 235. [Google Scholar] [CrossRef]
- Shatnawi, M.T.; Abbes, A.; Ouannas, A.; Batiha, I.M. A new two-dimensional fractional discrete rational map: Chaos and complexity. Phys. Scr. 2022, 98, 015208. [Google Scholar] [CrossRef]
- Hamadneh, T.; Abbes, A.; Falahah, I.A.; AL-Khassawneh, Y.A.; Heilat, A.S.; Al-Husban, A.; Ouannas, A. Complexity and Chaos Analysis for Two-Dimensional Discrete-Time Predator–Prey Leslie–Gower Model with Fractional Orders. Axioms 2023, 12, 561. [Google Scholar] [CrossRef]
- Abbes, A.; Ouannas, A.; Shawagfeh, N. An incommensurate fractional discrete macroeconomic system: Bifurcation, chaos, and complexity. Chin. Phys. B 2023, 32, 030203. [Google Scholar] [CrossRef]
- Khennaoui, A.A.; Ouannas, A.; Bendoukha, S.; Grassi, G.; Lozi, R.P.; Pham, V.T. On fractional–order discrete–time systems: Chaos, stabilization and synchronization. Chaos Solitons Fractals 2019, 119, 150–162. [Google Scholar] [CrossRef]
- Saadeh, R.; Abbes, A.; Al-Husban, A.; Ouannas, A.; Grassi, G. The Fractional Discrete Predator–Prey Model: Chaos, Control and Synchronization. Fractal Fract. 2023, 7, 120. [Google Scholar] [CrossRef]
- Ouannas, A.; Khennaoui, A.A.; Batiha, I.M.; Pham, V.T. Synchronization between fractional chaotic maps with different dimensions. In Fractional-Order Design; Academic Press: Cambridge, MA, USA, 2022; pp. 89–121. [Google Scholar]
- Peng, Y.; He, S.; Sun, K. Chaos in the discrete memristor-based system with fractional-order difference. Results Phys. 2021, 24, 104106. [Google Scholar] [CrossRef]
- Lu, Y.M.; Wang, C.H.; Deng, Q.L.; Xu, C. The dynamics of a memristor-based Rulkov neuron with the fractional-order difference. Chin. Phys. B 2022, 31, 060502. [Google Scholar] [CrossRef]
- Ma, M.; Lu, Y.; Li, Z.; Sun, Y.; Wang, C. Multistability and phase synchronization of Rulkov neurons coupled with a locally active discrete memristor. Fractal Fract. 2023, 7, 82. [Google Scholar] [CrossRef]
- Peng, Y.; Liu, J.; He, S.; Sun, K. Discrete fracmemristor-based chaotic map by Grunwald–Letnikov difference and its circuit implementation. Chaos Solitons Fractals 2023, 171, 113429. [Google Scholar] [CrossRef]
- Shatnawi, M.T.; Abbes, A.; Ouannas, A.; Batiha, I.M. Hidden multistability of fractional discrete non-equilibrium point memristor based map. Phys. Scr. 2023, 98, 035213. [Google Scholar]
- Lai, Q.; Lai, C.; Kuate, P.D.K.; Li, C.; He, S. Chaos in a simplest cyclic memristive neural network. Int. J. Bifurc. Chaos 2022, 32, 2250042. [Google Scholar] [CrossRef]
- Ramadoss, J.; Natiq, H.; Nazarimehr, F.; He, S.; Rajagopal, K.; Jafari, S. A novel chaotic map with a shifting parameter and stair-like bifurcation diagram: Dynamical analysis and multistability. Phys. Scr. 2023, 98, 025212. [Google Scholar] [CrossRef]
- Wang, J.; Gu, Y.; Rong, K.; Xu, Q.; Zhang, X. Memristor-based Lozi map with hidden hyperchaos. Mathematics 2022, 10, 3426. [Google Scholar] [CrossRef]
- Bao, H.; Hua, Z.; Li, H.; Chen, M.; Bao, B. Discrete memristor hyperchaotic maps. IEEE Trans. Circuits Syst. Regul. Pap. 2021, 68, 4534–4544. [Google Scholar] [CrossRef]
- Bao, B.C.; Li, H.; Wu, H.; Zhang, X.; Chen, M. Hyperchaos in a second-order discrete memristor-based map model. Electron. Lett. 2020, 56, 769–770. [Google Scholar] [CrossRef]
- Kong, S.; Li, C.; He, S.; Çiçek, S.; Lai, Q. A memristive map with coexisting chaos and hyperchaos. Chin. Phys. B 2021, 30, 110502. [Google Scholar] [CrossRef]
- Ikeda, K. Multiple-valued stationary state and its instability of the transmitted light by a ring cavity system. Opt. Commun. 1979, 30, 257–261. [Google Scholar] [CrossRef]
- Ikeda, K.; Daido, H.; Akimoto, O. Optical turbulance: Chaotic behavior of transmitted light from a ring cavity. Phys. Rev. Lett. 1980, 45, 709–712. [Google Scholar] [CrossRef]
- Laskaridis, L.; Volos, C.; Munoz-Pacheco, J.; Stouboulos, I. Study of the dynamical behavior of an Ikeda-based map with a discrete memristor. Integration 2023, 89, 168–177. [Google Scholar] [CrossRef]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J.-Physiol.-Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef]
- Li, Y.; Wang, X.; Liu, Z.; Liang, X.; Si, S. The entropy algorithm and its variants in the fault diagnosis of rotating machinery: A review. IEEE Access 2018, 6, 66723–66741. [Google Scholar] [CrossRef]
- Čermák, J.; Győri, I.; Nechvátal, L. On explicit stability conditions for a linear fractional difference system. Fract. Calc. Appl. Anal. 2015, 18, 651–672. [Google Scholar] [CrossRef]





| 0.1 | 0.1 | 0.4 | 0.4 | 1 | 0.8 | 1 | |
| 0.1 | 0.5 | 0.1 | 0.4 | 0.1 | 0.8 | 1 | |
| 0.1 | 0.1 | 0.1 | 0.4 | 0.1 | 0.8 | 1 | |
| of Ikeda memristor map | 0.4363 | 0.5188 | 0.7081 | 0.8150 | 0.0468 | 0.0029 | 0.4542 |
| of Ikeda map | 0.4066 | 0.1596 | 0.5909 | 0.4899 | 0.0602 | 0.0046 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alsayyed, O.; Abbes, A.; Gharib, G.M.; Abualhomos, M.; Al-Tarawneh, H.; Al Soudi, M.S.; Abu-Alkishik, N.; Al-Husban, A.; Ouannas, A. On Ikeda-Based Memristor Map with Commensurate and Incommensurate Fractional Orders: Bifurcation, Chaos, and Entropy. Fractal Fract. 2023, 7, 728. https://doi.org/10.3390/fractalfract7100728
Alsayyed O, Abbes A, Gharib GM, Abualhomos M, Al-Tarawneh H, Al Soudi MS, Abu-Alkishik N, Al-Husban A, Ouannas A. On Ikeda-Based Memristor Map with Commensurate and Incommensurate Fractional Orders: Bifurcation, Chaos, and Entropy. Fractal and Fractional. 2023; 7(10):728. https://doi.org/10.3390/fractalfract7100728
Chicago/Turabian StyleAlsayyed, Omar, Abderrahmane Abbes, Gharib Mousa Gharib, Mayada Abualhomos, Hassan Al-Tarawneh, Maha S. Al Soudi, Nabeela Abu-Alkishik, Abdallah Al-Husban, and Adel Ouannas. 2023. "On Ikeda-Based Memristor Map with Commensurate and Incommensurate Fractional Orders: Bifurcation, Chaos, and Entropy" Fractal and Fractional 7, no. 10: 728. https://doi.org/10.3390/fractalfract7100728
APA StyleAlsayyed, O., Abbes, A., Gharib, G. M., Abualhomos, M., Al-Tarawneh, H., Al Soudi, M. S., Abu-Alkishik, N., Al-Husban, A., & Ouannas, A. (2023). On Ikeda-Based Memristor Map with Commensurate and Incommensurate Fractional Orders: Bifurcation, Chaos, and Entropy. Fractal and Fractional, 7(10), 728. https://doi.org/10.3390/fractalfract7100728








