Dynamical Analysis of Rubella Disease Model in the Context of Fractional Piecewise Derivative: Simulations with Real Statistical Data
Abstract
:1. Introduction
2. Preliminaries
3. Existence and Uniqueness Results
- (C1)
- ∃ such that ∀, one may have
- (C2)
- ∃ & one have
4. Numerical Scheme
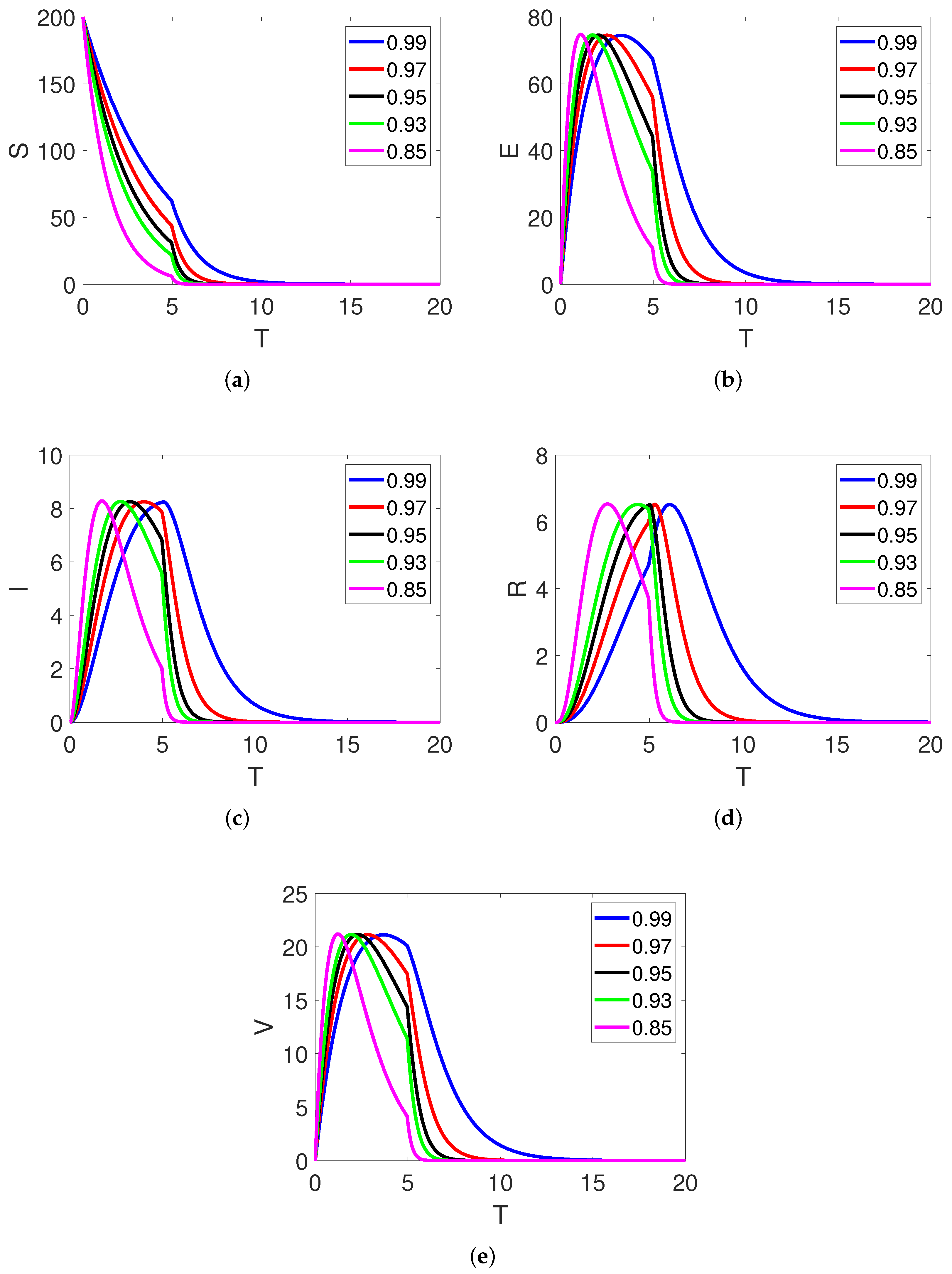
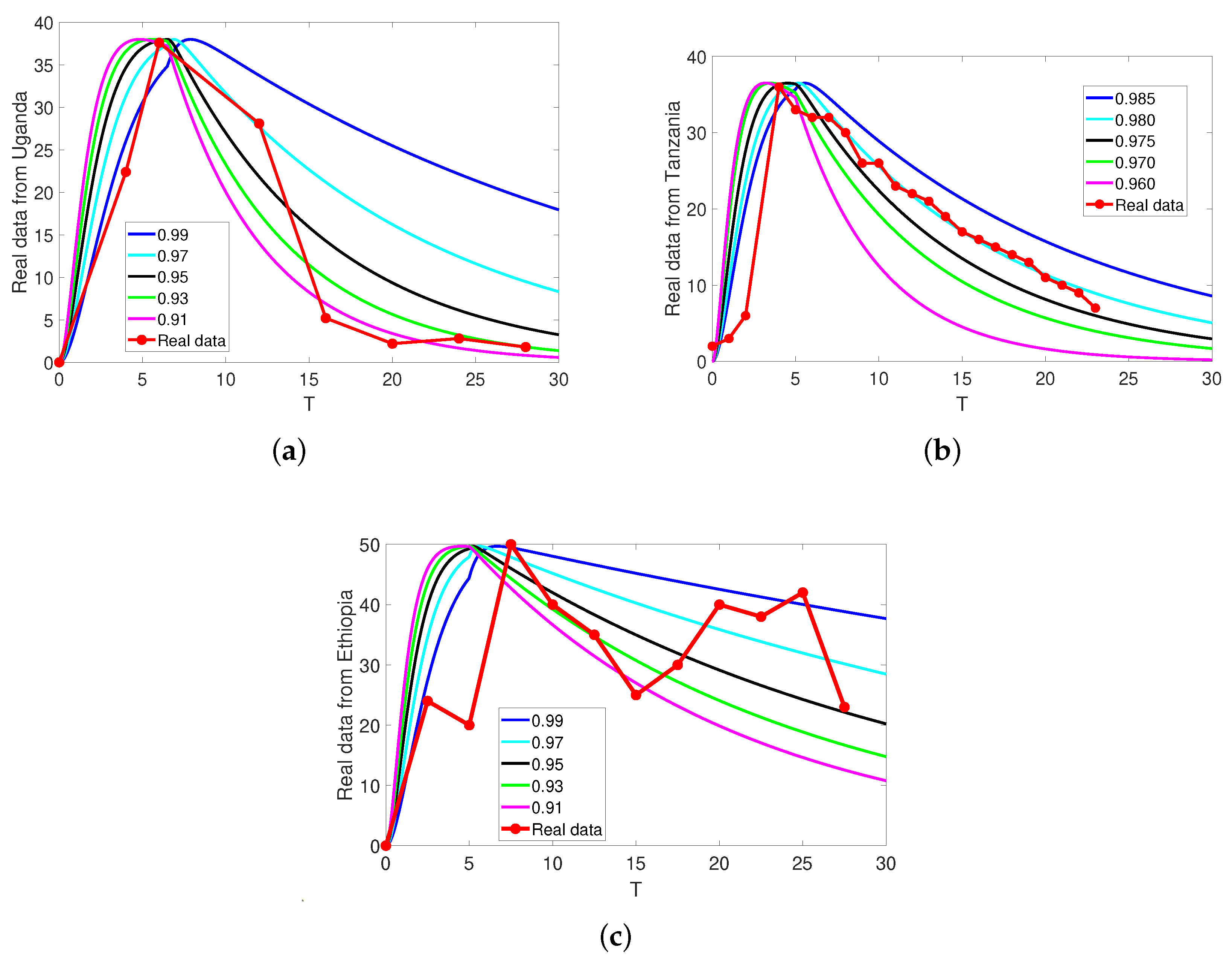
5. Graphical Analysis
6. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wesselhoeft, C. Rubella (German measles) and congenital deformities. N. Engl. J. Med. 1949, 240, 258–261. [Google Scholar] [CrossRef] [PubMed]
- Edlich, R.; Winters, K.L.; Long, W.B., III. Rubella and congenital rubella (German measles). J. Long-Term Eff. Med. Implant. 2005, 15, 3. [Google Scholar] [CrossRef] [PubMed]
- Neighbors, M.; Tannehill-Jones, R. Childhood diseases and disorders. In Human Diseases; Clifton Park: New York, NY, USA, 2010; pp. 457–479. [Google Scholar]
- Ackerknecht, E.H. A Short History of Medicine; JHU Press: Baltimore, MD, USA, 2016. [Google Scholar]
- Jajarmi, A.; Ghanbari, B.; Baleanu, D. A new and efficient numerical method for the fractional modeling and optimal control of diabetes and tuberculosis co-existence. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 9. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.; Wu, L.; Zhang, H. A space-time spectral order sinc-collocation method for the fourth-order nonlocal heat model arising in viscoelasticity. Appl. Math. Comput. 2023, 457, 128192. [Google Scholar] [CrossRef]
- Jiang, X.; Wang, J.; Wang, W.; Zhang, H. A Predictor–Corrector Compact Difference Scheme for a Nonlinear Fractional Differential Equation. Fractal Fract. 2023, 7, 521. [Google Scholar] [CrossRef]
- Iqbal, Z.; Ahmed, N.; Baleanu, D.; Adel, W.; Rafiq, M.; Rehman, M.A.U.; Alshomrani, A.S. Positivity and boundedness preserving numerical algorithm for the solution of fractional nonlinear epidemic model of HIV/AIDS transmission. Chaos Solitons Fractals 2020, 134, 109706. [Google Scholar] [CrossRef]
- Ameen, I.; Baleanu, D.; Ali, H.M. An efficient algorithm for solving the fractional optimal control of SIRV epidemic model with a combination of vaccination and treatment. Chaos Solitons Fractals 2020, 137, 109892. [Google Scholar] [CrossRef]
- Mahdy, A.M.S.; Mohamed, M.S.; Lotfy, K.; Alhazmi, M.; El-Bary, A.A.; Raddadi, M.H. Numerical solution and dynamical behaviors for solving fractional nonlinear Rubella ailment disease model. Results Phys. 2021, 24, 104091. [Google Scholar] [CrossRef]
- Atangana, A.; Qureshi, S. Modeling attractors of chaotic dynamical systems with fractal–fractional operators. Chaos Solitons Fractals 2019, 123, 320–337. [Google Scholar] [CrossRef]
- Atangana, A. Application of fractional calculus to epidemiology. Fract. Dyn. 2015, 2015, 174–190. [Google Scholar]
- Ahmed, N.; Rafiq, M.; Baleanu, D.; Alshomrani, A.S.; Rehman, M.A.U. Positive explicit and implicit computational techniques for reaction–diffusion epidemic model of dengue disease dynamics. Adv. Differ. Equ. 2020, 2020, 202. [Google Scholar] [CrossRef]
- Qureshi, S.; Atangana, A. Mathematical analysis of dengue fever outbreak by novel fractional operators with field data. Phys. A Stat. Mech. Its Appl. 2019, 526, 121127. [Google Scholar] [CrossRef]
- Ahmad, S.; Dong, Q.I.U.; Rahman, M.U. Dynamics of a fractional-order COVID-19 model under the nonsingular kernel of Caputo-Fabrizio operator. Math. Model. Numer. Simul. Appl. 2022, 2, 228–243. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D. New fractional derivatives with nonlocal and non-singular kernel: Theory and application to heat transfer model. arXiv 2016, arXiv:1602.03408. [Google Scholar] [CrossRef]
- Rahman, M.U.; Arfan, M.; Deebani, W.; Kumam, P.; Shah, Z. Analysis of time-fractional Kawahara equation under Mittag-Leffler power law. Fractals 2022, 30, 2240021. [Google Scholar] [CrossRef]
- Li, B.; Zhang, T.; Zhang, C. Investigation of financial bubble mathematical model under fractal-fractional Caputo derivative. FRACTALS 2023, 31, 1–13. [Google Scholar] [CrossRef]
- Li, B.; Eskandari, Z. Dynamical analysis of a discrete-time SIR epidemic model. J. Frankl. Inst. 2023, 360, 7989–8007. [Google Scholar] [CrossRef]
- Zhang, X.; Ding, Z.; Hang, J.; He, Q. How do stock price indices absorb the COVID-19 pan-demic shocks? N. Am. J. Econ. Financ. 2022, 60, 101672. [Google Scholar] [CrossRef]
- He, Q.; Zhang, X.; Xia, P.; Zhao, C.; Li, S. A Comparison Research on Dynamic Characteris-tics of Chinese and American Energy Prices. J. Glob. Inf. Manag. (JGIM) 2023, 31, 1–16. [Google Scholar]
- Zhang, X.; Yang, X.; He, Q. Multi-scale systemic risk and spillover networks of commodity markets in the bullish and bearish regimes. N. Am. J. Econ. Financ. 2022, 62, 101766. [Google Scholar] [CrossRef]
- Li, B.; Eskandari, Z.; Avazzadeh, Z. Strong resonance bifurcations for a discrete-time prey–predator model. J. Appl. Math. Comput. 2023, 69, 2421–2438. [Google Scholar] [CrossRef]
- Qurashi, M.M. Role of fractal-fractional operators in modeling of rubella epidemic with optimized orders. Open Phys. 2020, 18, 1111–1120. [Google Scholar] [CrossRef]
- Atangana, A.; Araz, S.İ. New concept in calculus: Piecewise differential and integral operators. Chaos Solitons Fractals 2021, 145, 110638. [Google Scholar] [CrossRef]
- Xu, C.; Alhejaili, W.; Saifullah, S.; Khan, A.; Khan, J.; El-Shorbagy, M.A. Analysis of Huanglongbing disease model with a novel fractional piecewise approach. Chaos Solitons Fractals 2022, 161, 112316. [Google Scholar] [CrossRef]
- Ahmad, S.; Haque, S.; Khan, K.A.; Mlaiki, N. The Evolution of COVID-19 Transmission with Superspreaders Class under Classical and Caputo Piecewise Operators: Real Data Perspective from India, France, and Italy. Fractal Fract. 2023, 7, 501. [Google Scholar] [CrossRef]
- Abdelmohsen, S.A.; Yassen, M.F.; Ahmad, S.; Abdelbacki, A.M.M.; Khan, J. Theoretical and numerical study of the rumours spreading model in the framework of piecewise derivative. Eur. Phys. J. Plus 2022, 137, 738. [Google Scholar] [CrossRef]
- Saifullah, S.; Ahmad, S.; Jarad, F. Study on the dynamics of a piecewise tumor–immune interaction model. Fractals 2022, 30, 2240233. [Google Scholar] [CrossRef]
- Naowarat, S.; Ahmad, S.; Saifullah, S.; De la Sen, M.; Akgül, A. Crossover dynamics of Rotavirus disease under fractional piecewise derivative with vaccination effects: Simulations with real data from Thailand, West Africa, and the US. Symmetry 2022, 14, 2641. [Google Scholar] [CrossRef]
- Gdawiec, K.; Kotarski, W.; Lisowska, A. Newton’s method with fractional derivatives and various iteration processes via visual analysis. Numer. Algorithms 2021, 86, 953–1010. [Google Scholar] [CrossRef]
- Koca, I. Analysis of rubella disease model with non-local and non-singular fractional derivatives. Int. J. Optim. Control Theor. Appl. (IJOCTA) 2018, 8, 17–25. [Google Scholar] [CrossRef]
- Xu, C.; Saifullah, S.; Ali, A. Theoretical and numerical aspects of Rubella disease model involving fractal fractional exponential decay kernel. Results Phys. 2022, 34, 105287. [Google Scholar] [CrossRef]
- Michael, F.; Mirambo, M.M.; Lyimo, D.; Kyesi, F.; Msanga, D.R.; Joachim, G.; Nyaki, H. Reduction in Rubella Virus Active Cases among Children and Adolescents after Rubella Vaccine Imple-mentation in Tanzania: A Call for Sustained High Vaccination Coverage. Vaccines 2022, 10, 1188. [Google Scholar] [CrossRef] [PubMed]
- Bagenda, F.; Mulogo, E.M.; Apecu, R.O.; Kisakye, A.; Opar, B.T. Rubella IgM epidemi-ology in the pre-rubella vaccination era in Uganda. BMC Infect. Dis. 2020, 20, 219. [Google Scholar] [CrossRef] [PubMed]
- Ou, W.; Xu, C.; Cui, Q.; Liu, Z.; Pang, Y.; Farman, M.; Ahmad, S.; Zeb, A. Analysis of Huanglongbing disease model with a novel fractional piecewise approach. Math. Methods Appl. Sci. 2023, 161, 112316. [Google Scholar]
- Xu, C.; Cui, Q.Y.; Liu, Z.X.; Pan, Y.L.; Cui, X.H.; Ou, W.; Rahman, M.; Farman, M.; Ahmad, S.; Zeb, A. Extended hybrid controller design of bifurcation in a delayed chemostat model. MATCH Commun. Math. Comput. Chem. 2023, 90, 609–648. [Google Scholar] [CrossRef]
- Doungmo Goufo, E.F. Application of the Caputo-Fabrizio fractional derivative without singular kernel to Korteweg-de Vries-Burgers equation. Math. Model. Anal. 2016, 21, 188–198. [Google Scholar] [CrossRef]
- Doungmo Goufo, E.F. A biomathematical view on the fractional dynamics of cellulose degradation. Fract. Calc. Appl. Anal. 2015, 18, 554–564. [Google Scholar] [CrossRef]
- Atangana, A. Extension of rate of change concept: From local to nonlocal operators with applications. Results Phys. 2020, 19, 103515. [Google Scholar] [CrossRef]
- Atangana, A.; Araz, S.İ. Nonlinear equations with global differential and integral operators: Existence, uniqueness with application to epidemiology. Results Phys. 2021, 20, 103593. [Google Scholar] [CrossRef]
- Kabunga, S.K.; Goufo, E.F. Analysis and simulation of a mathematical model of tuberculosis transmission in Democratic Republic of the Congo. Adv. Differ. Equ. 2020, 1, 642. [Google Scholar] [CrossRef]
- Xu, C.; Mu, D.; Pan, Y.; Aouiti, C.; Yao, L. Exploring Bifurcation in a Fractional-Order Predator-Prey System with Mixed Delays. J. Appl. Anal. Comput. 2023, 13, 1119–1136. [Google Scholar] [CrossRef]
- Xu, C.; Mu, D.; Liu, Z.; Pang, Y.; Aouiti, C.; Tunc, O.; Ahmad, S.; Zeb, A. Bifurcation dy-namics and control mechanism of a fractional–order delayed Brusselator chemical reaction model. Match 2023, 89, 1. [Google Scholar] [CrossRef]
- Xu, C.; Cui, X.; Li, P.; Yan, J.; Yao, L. Exploration on dynamics in a discrete predator–prey competitive model involving feedback controls. J. Biol. Dyn. 2023, 17, 2220349. [Google Scholar] [CrossRef] [PubMed]
- Li, P.; Lu, Y.; Xu, C.; Ren, J. Insight into Hopf Bifurcation and Control Methods in Fractional Order BAM Neural Networks Incorporating Symmetric Structure and Delay. Cogn. Comput. 2023, 1–43. [Google Scholar] [CrossRef]

| Parameter | Description | Value |
|---|---|---|
| Transmission rate | 0.8 | |
| Rate of infection | 0.4 | |
| Q | Immunized with vaccines | 0.3 |
| Natural death-rate | 0.1 | |
| Rate of recovery | 0.4 | |
| Rate of exposure to disease | 0.4 | |
| Rate of the second dose of vaccine | 0.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alkahtani, B.S.T. Dynamical Analysis of Rubella Disease Model in the Context of Fractional Piecewise Derivative: Simulations with Real Statistical Data. Fractal Fract. 2023, 7, 746. https://doi.org/10.3390/fractalfract7100746
Alkahtani BST. Dynamical Analysis of Rubella Disease Model in the Context of Fractional Piecewise Derivative: Simulations with Real Statistical Data. Fractal and Fractional. 2023; 7(10):746. https://doi.org/10.3390/fractalfract7100746
Chicago/Turabian StyleAlkahtani, Badr Saad T. 2023. "Dynamical Analysis of Rubella Disease Model in the Context of Fractional Piecewise Derivative: Simulations with Real Statistical Data" Fractal and Fractional 7, no. 10: 746. https://doi.org/10.3390/fractalfract7100746
APA StyleAlkahtani, B. S. T. (2023). Dynamical Analysis of Rubella Disease Model in the Context of Fractional Piecewise Derivative: Simulations with Real Statistical Data. Fractal and Fractional, 7(10), 746. https://doi.org/10.3390/fractalfract7100746






