Analysis of the Corneal Geometry of the Human Eye with an Artificial Neural Network
Abstract
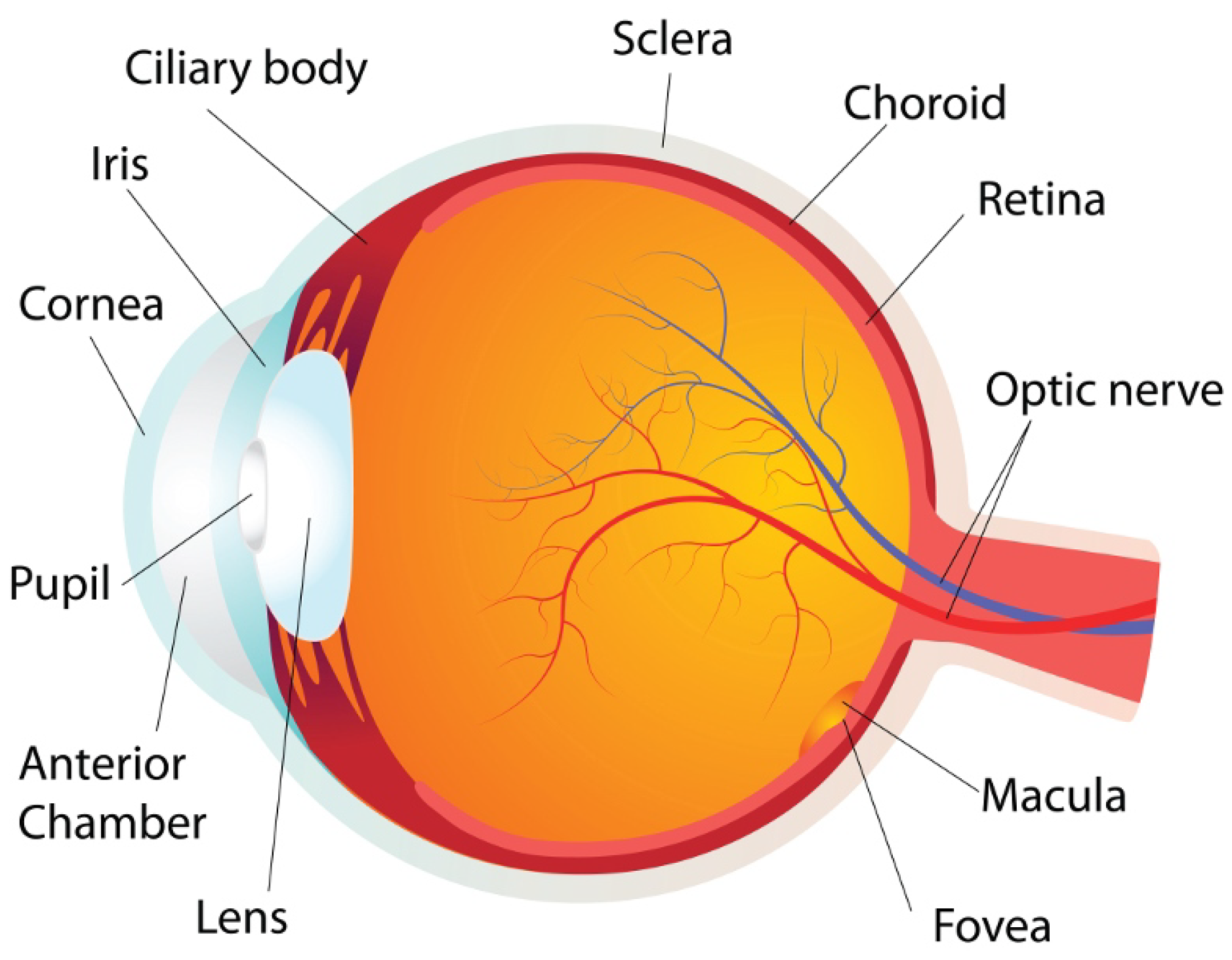
:1. Introduction
2. Our Contribution
- To the best of our knowledge, this is the first study to tackle the curvature model of the eye by using the hybrid cuckoo search with the neural network.
- The proposed BHCS-ANN is applied to six different corneal geometries to show the accuracy of the method.
- The proposed BHCS-ANN is more accurate as compared to other state-of-the-art.
- Based on statistical analysis performed, BHCS-ANN outperformed other techniques.
3. Mathematical Model
Neural Network Modeling for Differential Equations
4. Proposed Algorithm
4.1. Proposed BHCS Algorithm
4.2. Biogeography-Based Revelation Operator
5. Statistical Evaluation
6. Results and Discussions
7. Conclusions
- This approach effectively minimized the fitness function and provided the best approximation of the solution to the problem.
- The proposed approach demonstrated efficacy in all CSM scenarios and identified the optimum approximation for the CSM geometry in all scenarios.
- In figures, the results were compared with Adam’s numerical solution, where the BHCS-ANN showed a better trend.
- The statistical evaluations such as MAD, TIC, and ENSE were evaluated in 100 different runs, and the results showed that the proposed approach outperformed the current state of the art.
- The obtained results for the minimum approximated functions were compared with the FO-DPSO algorithm, where BHCS-ANN performed better in all the cases.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Corsato, C.; De Coster, C.; Omari, P. The Dirichlet problem for a prescribed anisotropic mean curvature equation: Existence, uniqueness and regularity of solutions. J. Differ. Equ. 2016, 260, 4572–4618. [Google Scholar] [CrossRef]
- Okrasiński, W.; Płociniczak, Ł. A nonlinear mathematical model of the corneal shape. Nonlinear Anal. Real World Appl. 2012, 13, 1498–1505. [Google Scholar] [CrossRef]
- Coelho, I.; Corsato, C.; Omari, P. A one-dimensional prescribed curvature equation modeling the corneal shape. Bound. Value Probl. 2014, 2014, 127. [Google Scholar] [CrossRef]
- Komai, Y.; Ushiki, T. The three-dimensional organization of collagen fibrils in the human cornea and sclera. Investig. Ophthalmol. Vis. Sci. 1991, 32, 2244–2258. [Google Scholar]
- Peh, G.S.; Beuerman, R.W.; Colman, A.; Tan, D.T.; Mehta, J.S. Human corneal endothelial cell expansion for corneal endothelium transplantation: An overview. Transplantation 2011, 91, 811–819. [Google Scholar] [CrossRef] [PubMed]
- Almubrad, T.; Akhtar, S. Structure of corneal layers, collagen fibrils, and proteoglycans of tree shrew cornea. Mol. Vis. 2011, 17, 2283. [Google Scholar]
- Płociniczak, Ł.; Okrasiński, W.; Nieto, J.J.; Dominguez, O. On a nonlinear boundary value problem modeling corneal shape. J. Math. Anal. Appl. 2014, 414, 461–471. [Google Scholar] [CrossRef]
- He, J.H. A remark on “A nonlinear mathematical model of the corneal shape”. Nonlinear Anal. Real World Appl. 2012, 13, 2863–2865. [Google Scholar] [CrossRef]
- Chen, C.L.; Liu, Y. Solution of two-point boundary-value problems using the differential transformation method. J. Optim. Theory Appl. 1998, 99, 23. [Google Scholar] [CrossRef]
- Abukhaled, M.; Khuri, S.; Sayfy, A. A numerical approach for solving a class of singular boundary value problems arising in physiology. Int. J. Numer. Anal. Model. 2011, 8, 353–363. [Google Scholar]
- Lu, J. Variational iteration method for solving two-point boundary value problems. J. Comput. Appl. Math. 2007, 207, 92–95. [Google Scholar] [CrossRef]
- Malekzadeh, P.; Golbahar Haghighi, M.; Atashi, M. Free vibration analysis of elastically supported functionally graded annular plates subjected to thermal environment. Meccanica 2011, 46, 893–913. [Google Scholar] [CrossRef]
- Płociniczak, Ł.; Griffiths, G.W.; Schiesser, W.E. ODE/PDE analysis of corneal curvature. Comput. Biol. Med. 2014, 53, 30–41. [Google Scholar] [CrossRef] [PubMed]
- Griffiths, G.W.; Płociniczak, Ł.; Schiesser, W. Analysis of cornea curvature using radial basis functions–Part I: Methodology. Comput. Biol. Med. 2016, 77, 274–284. [Google Scholar] [CrossRef]
- Abukhaled, M.; Khuri, S. A semi-analytical solution of amperometric enzymatic reactions based on Green’s functions and fixed point iterative schemes. J. Electroanal. Chem. 2017, 792, 66–71. [Google Scholar] [CrossRef]
- Abukhaled, M. Green’s function iterative method for solving a class of boundary value problems arising in heat transfer. Appl. Math. Inf. Sci 2017, 11, 229–234. [Google Scholar] [CrossRef]
- Kafri, H.; Khuri, S.A. Bratu’s problem: A novel approach using fixed-point iterations and Green’s functions. Comput. Phys. Commun. 2016, 198, 97–104. [Google Scholar] [CrossRef]
- Żur, K. Green’s function approach to frequency analysis of thin circular plates. Bull. Pol. Acad. Sciences. Tech. Sci. 2016, 64. [Google Scholar] [CrossRef]
- Żur, K.K. Free vibration analysis of elastically supported functionally graded annular plates via quasi-Green’s function method. Compos. Part B Eng. 2018, 144, 37–55. [Google Scholar] [CrossRef]
- Żur, K.K. Quasi-Green’s function approach to free vibration analysis of elastically supported functionally graded circular plates. Compos. Struct. 2018, 183, 600–610. [Google Scholar] [CrossRef]
- Andrade, F.M. Exact Green’s function for rectangular potentials and its application to quasi-bound states. Phys. Lett. A 2014, 378, 1461–1468. [Google Scholar] [CrossRef]
- Ahyoune, S.; Sieiro, J.; Carrasco, T.; Vidal, N.; Lopez-Villegas, J.M.; Roca, E.; Fernández, F.V. Quasi-static PEEC planar solver using a weighted combination of 2D and 3D analytical Green’s functions and a predictive meshing generator. Integration 2018, 63, 332–341. [Google Scholar] [CrossRef]
- Abukhaled, M. Green’s function iterative approach for solving strongly nonlinear oscillators. J. Comput. Nonlinear Dyn. 2017, 12, 051021. [Google Scholar] [CrossRef]
- Mehdi, H.M.; Azeem, M.K.; Ahmad, I. Artificial intelligence based nonlinear control of hybrid DC microgrid for dynamic stability and bidirectional power flow. J. Energy Storage 2023, 58, 106333. [Google Scholar] [CrossRef]
- Raja, M.A.Z.; Mehmood, A.; Niazi, S.A.; Shah, S.M. Computational intelligence methodology for the analysis of RC circuit modelled with nonlinear differential order system. Neural Comput. Appl. 2018, 30, 1905–1924. [Google Scholar] [CrossRef]
- Khan, J.A.; Raja, M.A.Z.; Rashidi, M.M.; Syam, M.I.; Wazwaz, A.M. Nature-inspired computing approach for solving non-linear singular Emden–Fowler problem arising in electromagnetic theory. Connect. Sci. 2015, 27, 377–396. [Google Scholar] [CrossRef]
- Raja, M.A.Z. Solution of the one-dimensional Bratu equation arising in the fuel ignition model using ANN optimised with PSO and SQP. Connect. Sci. 2014, 26, 195–214. [Google Scholar] [CrossRef]
- Ahmad, I.; Ahmad, F.; Raja, M.A.Z.; Ilyas, H.; Anwar, N.; Azad, Z. Intelligent computing to solve fifth-order boundary value problem arising in induction motor models. Neural Comput. Appl. 2018, 29, 449–466. [Google Scholar] [CrossRef]
- Sabir, Z.; Manzar, M.A.; Raja, M.A.Z.; Sheraz, M.; Wazwaz, A.M. Neuro-heuristics for nonlinear singular Thomas-Fermi systems. Appl. Soft Comput. 2018, 65, 152–169. [Google Scholar] [CrossRef]
- Silva, G.A. A new frontier: The convergence of nanotechnology, brain machine interfaces, and artificial intelligence. Front. Neurosci. 2018, 12, 843. [Google Scholar] [CrossRef] [PubMed]
- Raja, M.A.Z.; Khan, M.A.R.; Mahmood, T.; Farooq, U.; Chaudhary, N.I. Design of bio-inspired computing technique for nanofluidics based on nonlinear Jeffery–Hamel flow equations. Can. J. Phys. 2016, 94, 474–489. [Google Scholar] [CrossRef]
- Umar, M.; Sabir, Z.; Raja, M.A.Z. Intelligent computing for numerical treatment of nonlinear prey–predator models. Appl. Soft Comput. 2019, 80, 506–524. [Google Scholar] [CrossRef]
- Raja, M.A.Z.; Sabir, Z.; Mehmood, N.; Al-Aidarous, E.S.; Khan, J.A. Design of stochastic solvers based on genetic algorithms for solving nonlinear equations. Neural Comput. Appl. 2015, 26, 1–23. [Google Scholar] [CrossRef]
- Raja, M.A.Z. Stochastic numerical treatment for solving Troesch’s problem. Inf. Sci. 2014, 279, 860–873. [Google Scholar] [CrossRef]
- Motyl, J. Upper separated multifunctions in deterministic and stochastic optimal control. Appl. Math. Nonlinear Sci. 2017, 2, 479–484. [Google Scholar] [CrossRef]
- Azad, A.K.; Wang, L.; Guo, N.; Tam, H.Y.; Lu, C. Signal processing using artificial neural network for BOTDA sensor system. Opt. Express 2016, 24, 6769–6782. [Google Scholar] [CrossRef]
- Edelen, A.L.; Biedron, S.; Chase, B.; Edstrom, D.; Milton, S.; Stabile, P. Neural networks for modeling and control of particle accelerators. IEEE Trans. Nucl. Sci. 2016, 63, 878–897. [Google Scholar] [CrossRef]
- Pinsky, P.M.; Datye, D.V. A microstructurally-based finite element model of the incised human cornea. J. Biomech. 1991, 24, 907–922. [Google Scholar] [CrossRef]
- Pandolfi, A.; Manganiello, F. A model for the human cornea: Constitutive formulation and numerical analysis. Biomech. Model. Mechanobiol. 2006, 5, 237–246. [Google Scholar] [CrossRef]
- Ahmad, I.; Raja, M.A.Z.; Ramos, H.; Bilal, M.; Shoaib, M. Integrated neuro-evolution-based computing solver for dynamics of nonlinear corneal shape model numerically. Neural Comput. Appl. 2021, 33, 5753–5769. [Google Scholar] [CrossRef]
- Płociniczak, Ł.; Okrasiński, W. Nonlinear parameter identification in a corneal geometry model. Inverse Probl. Sci. Eng. 2015, 23, 443–456. [Google Scholar] [CrossRef]
- Erturk, V.S.; Ahmadkhanlu, A.; Kumar, P.; Govindaraj, V. Some novel mathematical analysis on a corneal shape model by using Caputo fractional derivative. Optik 2022, 261, 169086. [Google Scholar] [CrossRef]
- Sáez-Gutiérrez, F.L.; Velázquez, J.S.; del Barrio, J.A.; Alio, J.L.; Cavas, F. Novel Multivariable Evolutionary Algorithm-Based Method for Modal Reconstruction of the Corneal Surface from Sparse and Incomplete Point Clouds. Bioengineering 2023, 10, 989. [Google Scholar] [CrossRef] [PubMed]
- Jawad, K.; Mahto, R.; Das, A.; Ahmed, S.U.; Aziz, R.M.; Kumar, P. Novel Cuckoo Search-Based Metaheuristic Approach for Deep Learning Prediction of Depression. Appl. Sci. 2023, 13, 5322. [Google Scholar] [CrossRef]
- Aziz, R.M.; Desai, N.P.; Baluch, M.F. Computer vision model with novel cuckoo search based deep learning approach for classification of fish image. Multimed. Tools Appl. 2023, 82, 3677–3696. [Google Scholar] [CrossRef]
- Sahu, B.; Das, P.K.; Kumar, R. A modified cuckoo search algorithm implemented with SCA and PSO for multi-robot cooperation and path planning. Cogn. Syst. Res. 2023, 79, 24–42. [Google Scholar] [CrossRef]
- Liu, C.; Wang, J.; Zhou, L.; Rezaeipanah, A. Solving the multi-objective problem of IoT service placement in fog computing using cuckoo search algorithm. Neural Process. Lett. 2022, 54, 1823–1854. [Google Scholar] [CrossRef]
- Yang, Q.; Huang, H.; Zhang, J.; Gao, H.; Liu, P. A collaborative cuckoo search algorithm with modified operation mode. Eng. Appl. Artif. Intell. 2023, 121, 106006. [Google Scholar] [CrossRef]
- Figueiredo Camargo, R.; Chiacchio, A.O.; Capelas de Oliveira, E. Differentiation to fractional orders and the fractional telegraph equation. J. Math. Phys. 2008, 49, 033505. [Google Scholar] [CrossRef]
- Tenreiro Machado, J.; Silva, M.F.; Barbosa, R.S.; Jesus, I.S.; Reis, C.M.; Marcos, M.G.; Galhano, A.F. Some applications of fractional calculus in engineering. Math. Probl. Eng. 2010, 2010, 639801. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations, Mathematics in Science and Engineering; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Ding, X.; Xu, Z.; Cheung, N.J.; Liu, X. Parameter estimation of Takagi–Sugeno fuzzy system using heterogeneous cuckoo search algorithm. Neurocomputing 2015, 151, 1332–1342. [Google Scholar] [CrossRef]
- Cheung, N.J.; Ding, X.M.; Shen, H.B. A nonhomogeneous cuckoo search algorithm based on quantum mechanism for real parameter optimization. IEEE Trans. Cybern. 2016, 47, 391–402. [Google Scholar] [CrossRef] [PubMed]
- Waseem, W.; Sulaiman, M.; Alhindi, A.; Alhakami, H. A soft computing approach based on fractional order DPSO algorithm designed to solve the corneal model for eye surgery. IEEE Access 2020, 8, 61576–61592. [Google Scholar] [CrossRef]










| Case 1 | Case 2 | Case 3 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| t | Min | Mean | STD | Min | Mean | STD | Min | Mean | STD |
| 0.8 | |||||||||
| 0.9 | |||||||||
| 1 |
| Case 4 | Case 5 | Case 6 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| t | Min | Mean | STD | Min | Mean | STD | Min | Mean | STD |
| 0.0 | 4.38 | 2.31 | 5.42 | 1.18 | 2.76 | 2.51 | 7.58 | 1.10 | 4.87 |
| 0.1 | 1.11 | 2.43 | 4.17 | 7.68 | 6.28 | 7.52 | 8.78 | 1.41 | 3.69 |
| 0.2 | 8.43 | 1.59 | 3.37 | 9.67 | 3.68 | 3.47 | 6.58 | 1.09 | 2.58 |
| 0.3 | |||||||||
| 0.4 | |||||||||
| 0.5 | 4.59 | 1.52 | 2.53 | 1.72 | 2.81 | 7.58 | 5.12 | 1.00 | 2.41 |
| 0.6 | 4.69 | 9.18 | 1.72 | 1.62 | 1.98 | 7.18 | 1.32 | 7.34 | 1.81 |
| 0.7 | 3.34 | 1.38 | 2.88 | 1.09 | 3.84 | 6.41 | 3.19 | 1.41 | 2.10 |
| 0.8 | 4.12 | 3.04 | 4.13 | 7.11 | 3.00 | 5.69 | 2.87 | 2.32 | 5.06 |
| 0.9 | 6.45 | 1.59 | 2.09 | 1.41 | 4.91 | 2.39 | 1.62 | 7.31 | 1.69 |
| 1 | 4.57 | 4.79 | 7.69 | 7.09 | 4.38 | 2.08 | 1.43 | 4.81 | 1.11 |
| GTIC | GMAD | GFIT | GENSE | |||||
|---|---|---|---|---|---|---|---|---|
| Case | Mean | STD | Mean | STD | Mean | STD | Mean | STD |
| 1 | 2.63 | 2.00 | 3.19 | 2.92 | 3.68 | 1.45 | 1.17 | 3.71 |
| 2 | 4.59 | 1.58 | 3.19 | 2.21 | 7.69 | 7.19 | 2.30 | 2.31 |
| 3 | 1.20 | 2.09 | 1.39 | 2.58 | 1.88 | 3.37 | 1.31 | 3.48 |
| 4 | 2.24 | 1.48 | 5.68 | 4.11 | 2.02 | 9.41 | 6.71 | 1.84 |
| 5 | 1.81 | 2.59 | 9.16 | 1.29 | 3.62 | 1.73 | 2.39 | 5.38 |
| 6 | 2.38 | 5.39 | 9.18 | 1.29 | 5.68 | 9.60 | 1.81 | 2.59 |
| Execution Time | Generation | Function Counts | ||||
|---|---|---|---|---|---|---|
| Case | Mean | STD | Mean | STD | Mean | STD |
| 1 | 17.7791 | 3.0599 | 2000 | 0 | 200,010 | 0 |
| 2 | 27.5776 | 2.9333 | 2000 | 0 | 200,010 | 0 |
| 3 | 27.1637 | 2.448 | 2000 | 0 | 200,010 | 0 |
| 4 | 27.421 | 3.0261 | 2000 | 0 | 200,010 | 0 |
| 5 | 26.8823 | 3.2615 | 2000 | 0 | 200,010 | 0 |
| 6 | 27.0509 | 3.888 | 2000 | 0 | 200,010 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Waseem; Ullah, A.; Awwad, F.A.; Ismail, E.A.A. Analysis of the Corneal Geometry of the Human Eye with an Artificial Neural Network. Fractal Fract. 2023, 7, 764. https://doi.org/10.3390/fractalfract7100764
Waseem, Ullah A, Awwad FA, Ismail EAA. Analysis of the Corneal Geometry of the Human Eye with an Artificial Neural Network. Fractal and Fractional. 2023; 7(10):764. https://doi.org/10.3390/fractalfract7100764
Chicago/Turabian StyleWaseem, Asad Ullah, Fuad A. Awwad, and Emad A. A. Ismail. 2023. "Analysis of the Corneal Geometry of the Human Eye with an Artificial Neural Network" Fractal and Fractional 7, no. 10: 764. https://doi.org/10.3390/fractalfract7100764
APA StyleWaseem, Ullah, A., Awwad, F. A., & Ismail, E. A. A. (2023). Analysis of the Corneal Geometry of the Human Eye with an Artificial Neural Network. Fractal and Fractional, 7(10), 764. https://doi.org/10.3390/fractalfract7100764






