An Investigation on Fractal Characteristics of the Superposition of Fractal Surfaces
Abstract
:1. Introduction
2. Preliminaries
- (1)
- The smallest number of sets of diameter at most δ that cover X;
- (2)
- The smallest number of cubes of side δ that cover X;
- (3)
- The largest number of disjoint balls of radius δ with centres in X;
- (4)
- The smallest number of closed balls of radius δ that cover X.
- (1)
- If f is a Lipschitz map, that is,for and certain . Then
- (2)
- If f is a bi-Lipschitz map, that is,for and certain . Then
- (1)
- It holds
- (2)
- For a constant bivariate function on , we have
- (3)
- If , then
- (1)
- Assume that . On one hand, it follows from Lemma 2 thatThus by Definition 1,On the other hand, it is observed thatSo by Definition 1, we can getObviously, we can assert from Definition 1 that , which leads to the conclusion of (1).
- (2)
- Note that when on . Consequently,At this time, we obtainCombining (1) of Proposition 1,That is,finishing the proof of (2).
- (3)
- Let us define a mapping byfor . By using the simple properties of norm, one can show thatandfor . With Lemma 1, we can claim that is a bi-Lipschitz mapping and then the result of (3) holds.
3. Main Results
- (1)
- Let be the space of all bivariate continuous functions whose box dimension exists and is equal to d on as . Namely, is the space of d-dimensional bivariate continuous functions on .
- (2)
- Let as the space of all bivariate continuous functions whose box dimension does not exist on . Here are the lower and upper box dimensions of the function on as , respectively.
- (1)
- If ,
- (2)
- If ,
- (1)
- If ,
- (2)
- If ,
4. Examples
5. Conclusions
5.1. Conclusions and Remarks
- (1)
- .
- (2)
- .
- (3)
- Whenwe prove that
- (4)
- Whenwe prove that
- (5)
- It has been proven that the superposition of two continuous surfaces cannot keep the fractal dimensions invariable unless both of them are two-dimensional.
- (6)
- It has been proven that the fractal dimensions of the graph of the sum of a bivariate continuous function and a bivariate Lipschitz function equal the fractal dimensions of the graph of the former. That is, a bivariate Lipschitz function can be absorbed by any other bivariate continuous function in the sense of fractal dimensions.
5.2. Applications in Other Fields
5.3. Further Research
- (1)
- This work only deals with cases when the two bivariate continuous functions have a different upper box dimension and the lower box dimension of one function is larger than the upper box dimension of the other one. People could further explore the other situations later.Question 1. Suppose that , . What is when and what is when ?
- (2)
- In the present paper, we only focus on the box dimension of the graph of the sum of two bivariate continuous functions. Therefore, other kinds of fractal dimensions, such as the packing dimension, the Hausdorff dimension, and the Assouad dimension, could be further considered for this problem.Question 2. Let be continuous. What can , and be, respectively?
- (3)
- This study is only about bivariate continuous functions, which could be generalized to continuous functions of n variables in the future.Question 3. Let be continuous. What can the fractal dimensions of be?
- (4)
- Apart from this, people could further investigate the fractal dimensions of the graph of bivariate continuous functions under other operations.Question 4. Let be continuous. What can the fractal dimensions of be?
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mandelbrot, B.B. The Fractal Geometry of Nature; Freeman: Sanfrancisco, CA, USA, 1982. [Google Scholar]
- Mandelbrot, B.B.; Passoja, D.E.; Paullay, A.J. Fractal character of fracture surfaces of metals. Nature 1984, 308, 721–722. [Google Scholar] [CrossRef]
- Turcotte, D.L. Fractals in geology and geophysics. Pure Appl. Geophys. 1989, 131, 171–196. [Google Scholar] [CrossRef]
- Kube, P.; Pentland, A. On the imaging of fractal surfaces. IEEE Trans. Pattern Anal. Mach. Intell. 1988, 10, 704–707. [Google Scholar] [CrossRef]
- Massopust, P.R. Fractal Functions, Fractal Surfaces, and Wavelets, 2nd ed.; Academic Press: San Diego, CA, USA, 2016. [Google Scholar]
- Pardo-Igúzquiza, E.; Dowd, P.A. Fractal analysis of karst landscapes. Math. Geosci. 2020, 52, 543–563. [Google Scholar] [CrossRef]
- Massopust, P.R. Fractal surfaces. J. Math. Anal. Appl. 1990, 151, 275–290. [Google Scholar] [CrossRef]
- Malysz, R. The Minkowski dimension of the bivariate fractal interpolation surfaces. Chaos Solitons Fractals 2006, 27, 1147–1156. [Google Scholar] [CrossRef]
- Ruan, H.J.; Xu, Q. Fractal interpolation surfaces on rectangular grids. Bull. Aust. Math. Soc. 2015, 91, 435–446. [Google Scholar] [CrossRef]
- Feng, Z.; Feng, Y.; Yuan, Z. Fractal interpolation surfaces with function vertical scaling factors. Appl. Math. Lett. 2012, 25, 1896–1900. [Google Scholar] [CrossRef]
- Barnsley, M.F. Fractal functions and interpolation. Constr. Approx. 1986, 2, 303–329. [Google Scholar] [CrossRef]
- Ruan, H.J.; Su, W.Y.; Yao, K. box dimension and fractional integral of linear fractal interpolation functions. J. Approx. Theory 2009, 161, 187–197. [Google Scholar] [CrossRef]
- Verma, M.; Priyadarshi, A.; Verma, S. Analytical and dimensional properties of fractal interpolation functions on the Sierpiński gasket. Fract. Calc. Appl. Anal. 2023, 26, 1294–1325. [Google Scholar] [CrossRef]
- Yu, B.Y.; Liang, Y.S. Construction of monotonous approximation by fractal interpolation functions and fractal dimensions. Fractals 2023, 31, 2440006. [Google Scholar]
- Cui, X.X.; Xiao, W. What is the effect of the Weyl fractional integral on the Hölder continuous functions? Fractals 2021, 29, 2150026. [Google Scholar] [CrossRef]
- Wu, J.R. The effects of the Riemann-Liouville fractional integral on the box dimension of fractal graphs of Hölder continuous functions. Fractals 2020, 28, 2050052. [Google Scholar] [CrossRef]
- Bedford, T.J. The box dimension of self-affine graphs and repellers. Nonlinearity 1989, 2, 53–71. [Google Scholar] [CrossRef]
- Liang, Y.S.; Su, W.Y. Von Koch curve and its fractional calculus. Acta Math. Sin. Chin. Ser. 2011, 54, 227–240. [Google Scholar]
- Berry, M.V.; Lewis, Z.V. On the Weierstrass-Mandelbrot fractal function. Proc. R. Soc. Lond. A 1980, 370, 459–484. [Google Scholar]
- Hunt, B.R. The Hausdorff dimension of graphs of Weierstrass functions. Proc. Am. Math. Soc. 1998, 126, 791–800. [Google Scholar] [CrossRef]
- Sun, D.C.; Wen, Z.Y. The Hausdorff dimension of graphs of a class of Weierstrass functions. Prog. Nat. Sci. 1996, 6, 547–553. [Google Scholar]
- Barański, K. On the dimension of graphs of Weierstrass-type functions with rapidly growing frequencies. Nonlinearity 2012, 25, 193–209. [Google Scholar] [CrossRef]
- Shen, W.X. Hausdorff dimension of the graphs of the classical Weierstrass functions. Math. Z. 2018, 289, 223–266. [Google Scholar] [CrossRef]
- He, G.L.; Zhou, S.P. What is the exact condition for fractional integrals and derivatives of Besicovitch functions to have exact box dimension? Chaos Solitons Fractals 2005, 26, 867–879. [Google Scholar] [CrossRef]
- Wang, B.; Ji, W.L.; Zhang, L.G.; Li, X. The relationship between fractal dimensions of Besicovitch function and the order of Hadamard fractional integral. Fractals 2020, 28, 2050128. [Google Scholar] [CrossRef]
- Liang, Y.S.; Su, W.Y. The relationship between the box dimension of the Besicovitch functions and the orders of their fractional calculus. Appl. Math. Comput. 2008, 200, 297–307. [Google Scholar] [CrossRef]
- Wang, X.F.; Zhao, C.X.; Yuan, X. A review of fractal functions and applications. Fractals 2022, 30, 2250113. [Google Scholar] [CrossRef]
- Chandra, S.; Abbas, S. box dimension of mixed Katugampola fractional integral of two-dimensional continuous functions. Fract. Calc. Appl. Anal. 2022, 25, 1022–1036. [Google Scholar] [CrossRef]
- Verma, M.; Priyadarshi, A. Dimensions of new fractal functions and associated measures. Numer. Algorithms 2023, 2301521. [Google Scholar] [CrossRef]
- Liang, Y.S. Progress on estimation of fractal dimensions of fractional calculus of continuous functions. Fractals 2019, 27, 1950084. [Google Scholar] [CrossRef]
- Verma, M.; Priyadarshi, A.; Verma, S. Vector-valued fractal functions: Fractal dimension and fractional calculus. Indag. Math. 2023, 2303005. [Google Scholar] [CrossRef]
- Verma, S.; Massopust, P.R. Dimension preserving approximation. Aequationes Math. 2022, 96, 1233–1247. [Google Scholar] [CrossRef]
- Falconer, K.J. Fractal Geometry: Mathematical Foundations and Applications; John Wiley Sons Inc.: New York, NY, USA, 1990. [Google Scholar]
- Yu, B.Y.; Liang, Y.S. On the lower and upper box dimensions of the sum of two fractal functions. Fractal Fract. 2022, 6, 398. [Google Scholar] [CrossRef]
- Verma, M.; Priyadarshi, A. Graphs of continuous functions and fractal dimensions. Chaos Solitons Fractals 2023, 173, 2311351. [Google Scholar] [CrossRef]
- Yu, B.Y.; Liang, Y.S. Estimation of the fractal dimensions of the linear combination of continuous functions. Mathematics 2022, 10, 2154. [Google Scholar] [CrossRef]
- Wen, Z.Y. Mathematical Foundations of Fractal Geometry; Science Technology Education Publication House: Shanghai, China, 2000. [Google Scholar]
- Wang, X.F.; Zhao, C.X. Fractal dimensions of linear combination of continuous functions with the same box dimension. Fractals 2020, 28, 2050139. [Google Scholar] [CrossRef]
- Yu, B.Y.; Liang, Y.S. Fractal dimension variation of continuous functions under certain operations. Fractals 2023, 31, 2350044. [Google Scholar] [CrossRef]
- Yu, B.Y.; Liang, Y.S. Approximation with continuous functions preserving fractal dimensions of the Riemann-Liouville operators of fractional calculus. Fract. Calc. Appl. Anal. 2023, 26, 2300215. [Google Scholar] [CrossRef]
- Verma, S.; Viswanathan, P. Bivariate functions of bounded variation: Fractal dimension and fractional integral. Indag. Math. 2020, 31, 294–309. [Google Scholar] [CrossRef]
- Falconer, K.J. Techniques in Fractal Geometry; John Wiley Sons Inc.: New York, NY, USA, 1997. [Google Scholar]
- Yu, B.Y.; Liang, Y.S. On two special classes of fractal surfaces with certain Hausdorff and box dimensions. Appl. Math. Comput. 2023; submitted. [Google Scholar]
- Wu, J.; Jin, X.; Mi, S.; Tang, J. An effective method to compute the box-counting dimension based on the mathematical definition and intervals. Results Eng. 2020, 6, 100106. [Google Scholar] [CrossRef]
- Hussain Hashmi, M.; Saeid Rahimian Koloor, S.; Foad Abdul-Hamid, M.; Nasir Tamin, M. Exploiting fractal features to determine fatigue crack growth rates of metallic materials. Eng. Fract. Mech. 2022, 308, 108589. [Google Scholar] [CrossRef]
- Macek, W. Correlation between fractal dimension and areal surface parameters for fracture analysis after bending-torsion fatigue. Metals 2021, 11, 1790. [Google Scholar] [CrossRef]
- Chen, S.S.; Keller, J.M.; Crownover, R.M. On the calculation of fractal features from images. IEEE Trans. Pattern Anal. Mach. Intell. 1993, 15, 1087–1090. [Google Scholar] [CrossRef]
- Chan, K.L. Quantitative characterization of electron micrograph image using fractal feature. IEEE Trans. Biomed. Eng. 1995, 42, 1033–1037. [Google Scholar] [CrossRef] [PubMed]
- Martino, G.D.; Riccio, D.; Zinno, I. SAR imaging of fractal surfaces. IEEE Trans. Geosci. Remote Sens. 2012, 50, 630–644. [Google Scholar] [CrossRef]
- Riccio, D.; Ruello, G. Synthesis of fractal surfaces for remote-sensing applications. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3803–3814. [Google Scholar] [CrossRef]
- Yan, Y. Back scattering from fractal surface of sea. Int. J. Infrared Millimetre Waves 2000, 21, 979–985. [Google Scholar] [CrossRef]
- Gaci, S.; Nicolis, O. A Grey System Approach for Estimating the Hölderian Regularity with an Application to Algerian Well Log Data. Fractal Fract. 2021, 5, 86. [Google Scholar] [CrossRef]
- Karydas, C.G. Unified Scale Theorem: A Mathematical Formulation of Scale in the Frame of Earth Observation Image Classification. Fractal Fract. 2021, 5, 27. [Google Scholar] [CrossRef]
- Zhang, X.; Li, D.; Li, J.; Liu, B.; Jiang, Q.; Wang, J. Signal-Noise Identification for Wide Field Electromagnetic Method Data Using Multi-Domain Features and IGWO-SVM. Fractal Fract. 2021, 5, 80. [Google Scholar] [CrossRef]

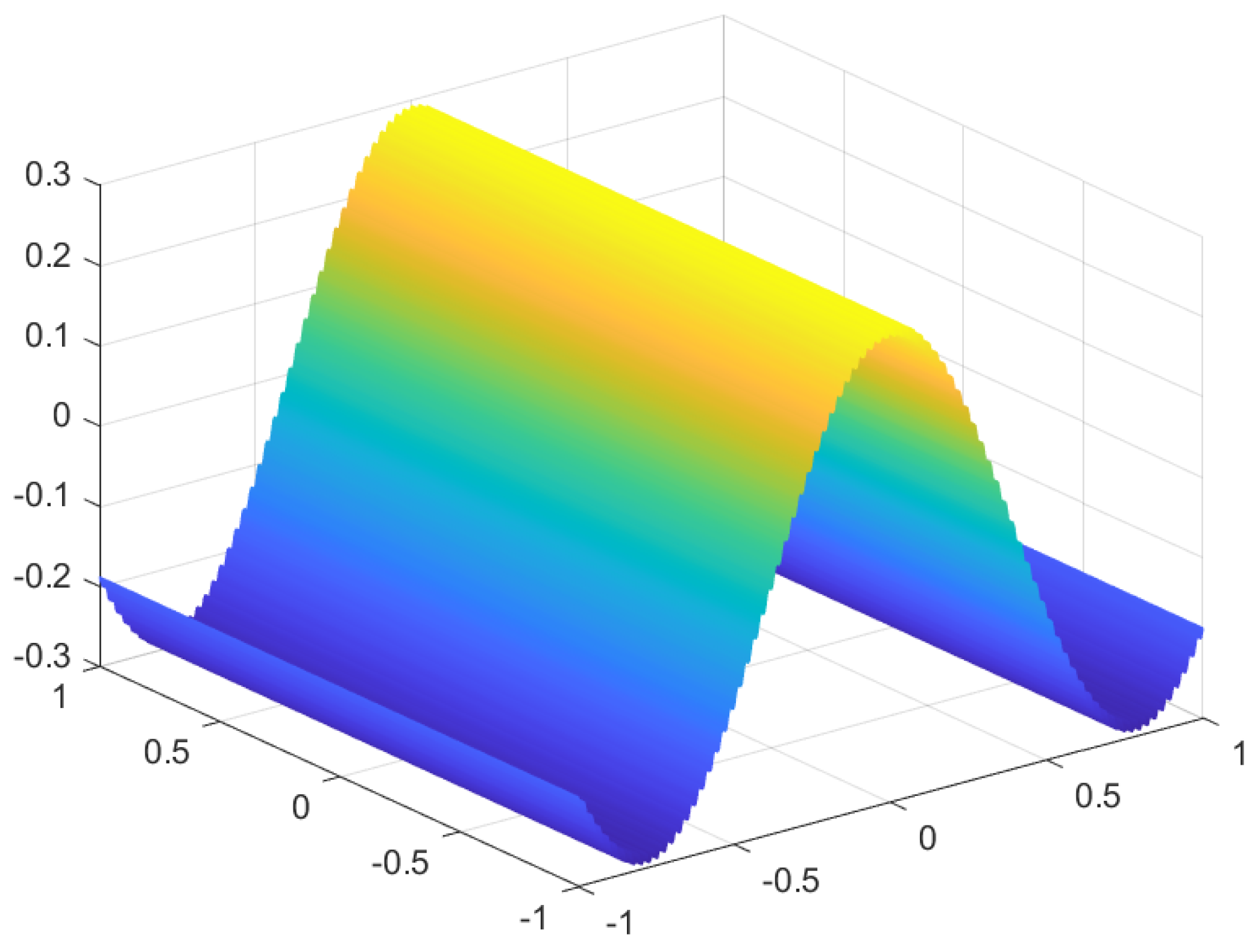
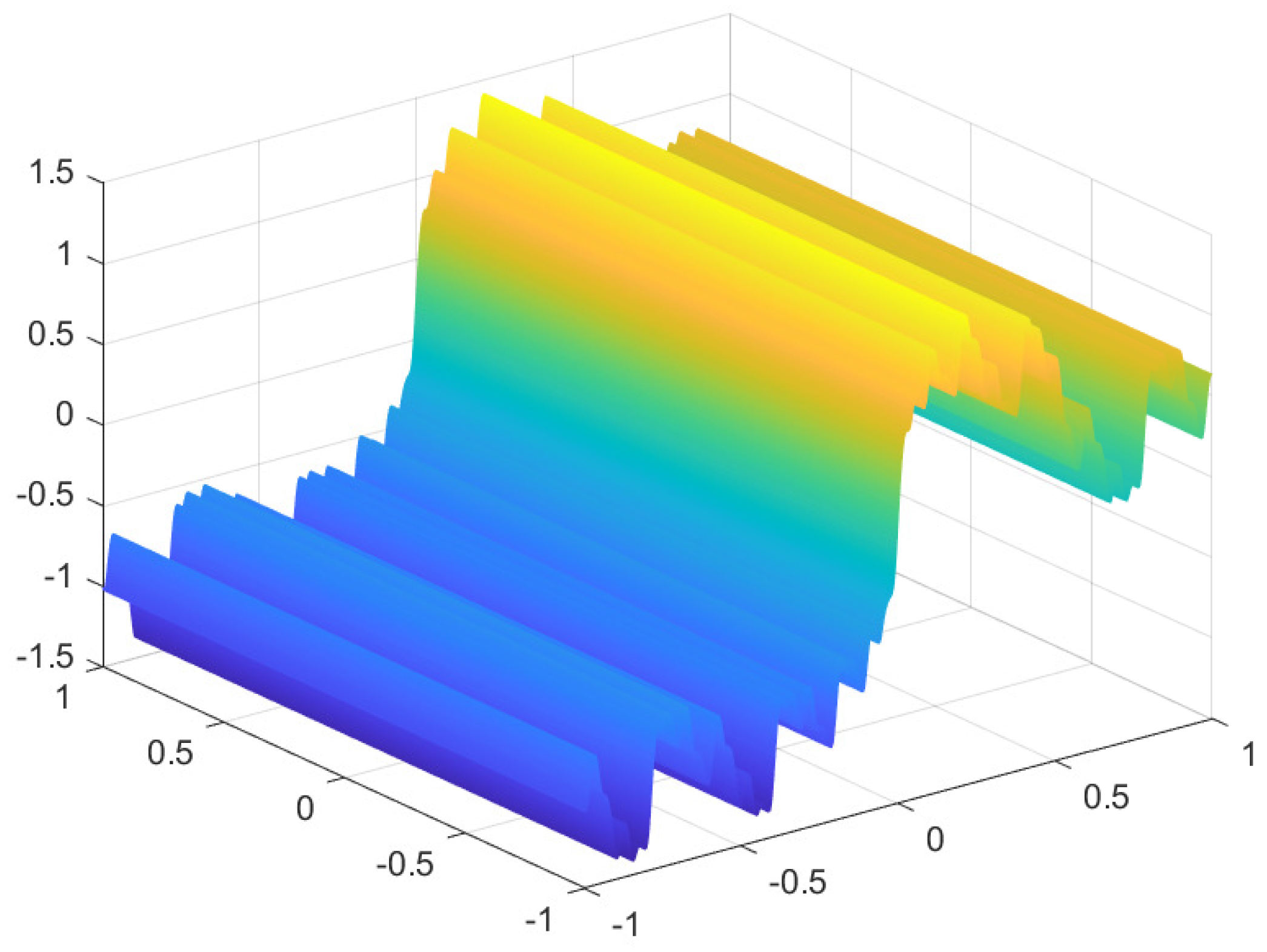
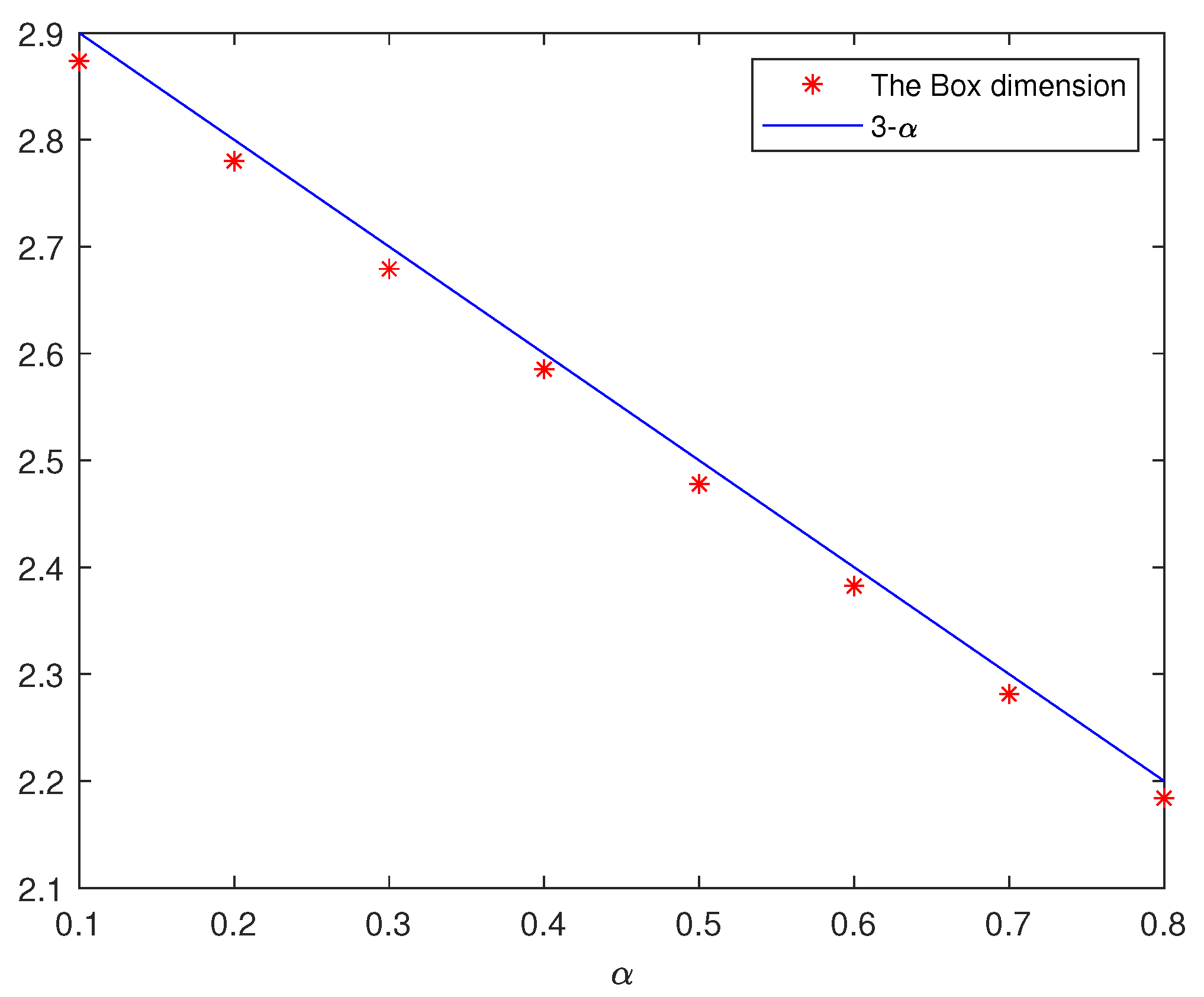
| 0.1 | 2.8736 |
| 0.2 | 2.7801 |
| 0.3 | 2.6792 |
| 0.4 | 2.5853 |
| 0.5 | 2.4779 |
| 0.6 | 2.3825 |
| 0.7 | 2.2814 |
| 0.8 | 2.1840 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X. An Investigation on Fractal Characteristics of the Superposition of Fractal Surfaces. Fractal Fract. 2023, 7, 802. https://doi.org/10.3390/fractalfract7110802
Wang X. An Investigation on Fractal Characteristics of the Superposition of Fractal Surfaces. Fractal and Fractional. 2023; 7(11):802. https://doi.org/10.3390/fractalfract7110802
Chicago/Turabian StyleWang, Xuefei. 2023. "An Investigation on Fractal Characteristics of the Superposition of Fractal Surfaces" Fractal and Fractional 7, no. 11: 802. https://doi.org/10.3390/fractalfract7110802
APA StyleWang, X. (2023). An Investigation on Fractal Characteristics of the Superposition of Fractal Surfaces. Fractal and Fractional, 7(11), 802. https://doi.org/10.3390/fractalfract7110802






