Qualitative Analysis of RLC Circuit Described by Hilfer Derivative with Numerical Treatment Using the Lagrange Polynomial Method
Abstract
1. Introduction
- The existence, uniqueness, and stability of the solution of the Hilfer fractional integro-differential equation for the RLC circuit model has been investigated via the fixed point approach.
- We apply a novel hypothesis to verify the existence, uniqueness, and Ulam–Hyers stability of the solution to the RLC circuit Equation (3). Additionally, we illustrate numerical results using the two step Lagrangian polynomial approach, in order to validate the theoretical outcomes.
2. Auxiliary Results
- 1.
- The operator can be written as
- 2.
- The Hilfer fractional derivative can be interpolated between the R-L fractional derivative and the Caputo fractional derivative as:
3. Main Results
Problem Formulation
4. Ulam Stability Results
- 1.
- , ,
- 2.
- , .
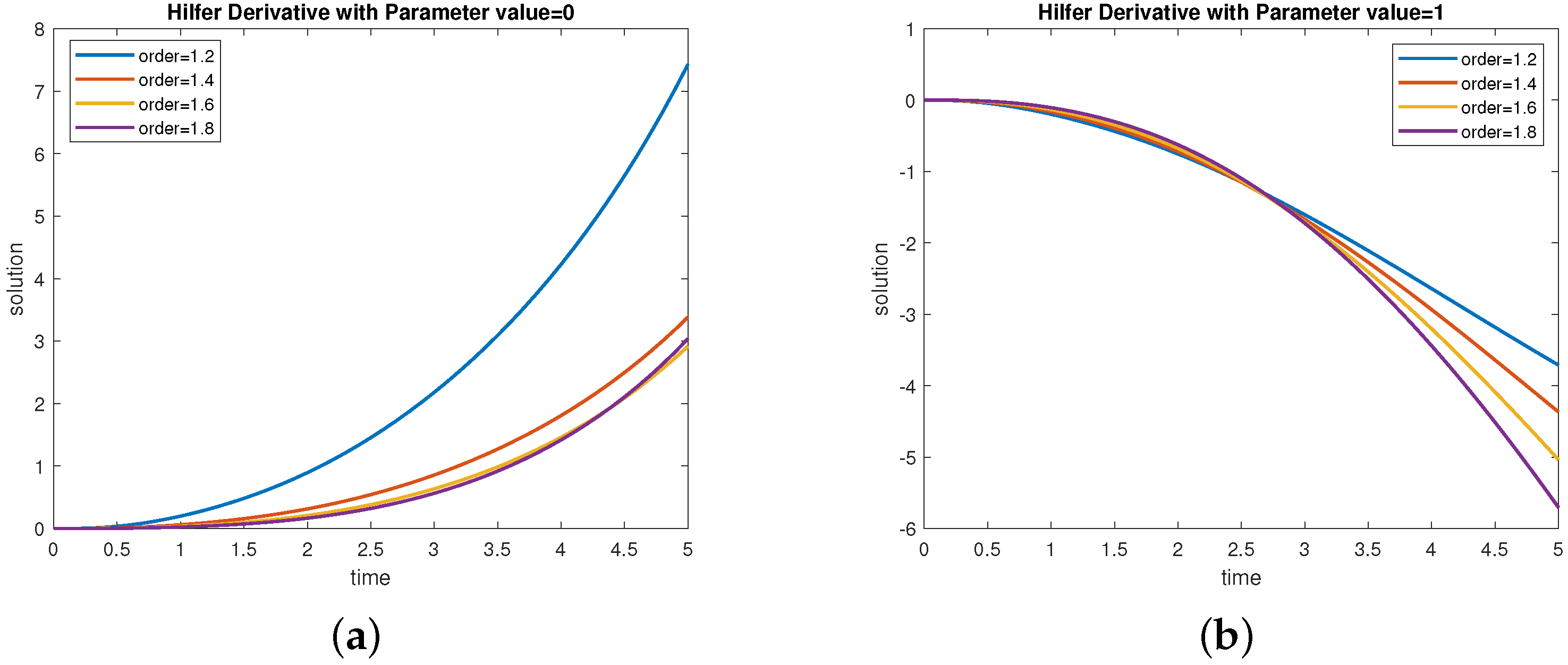
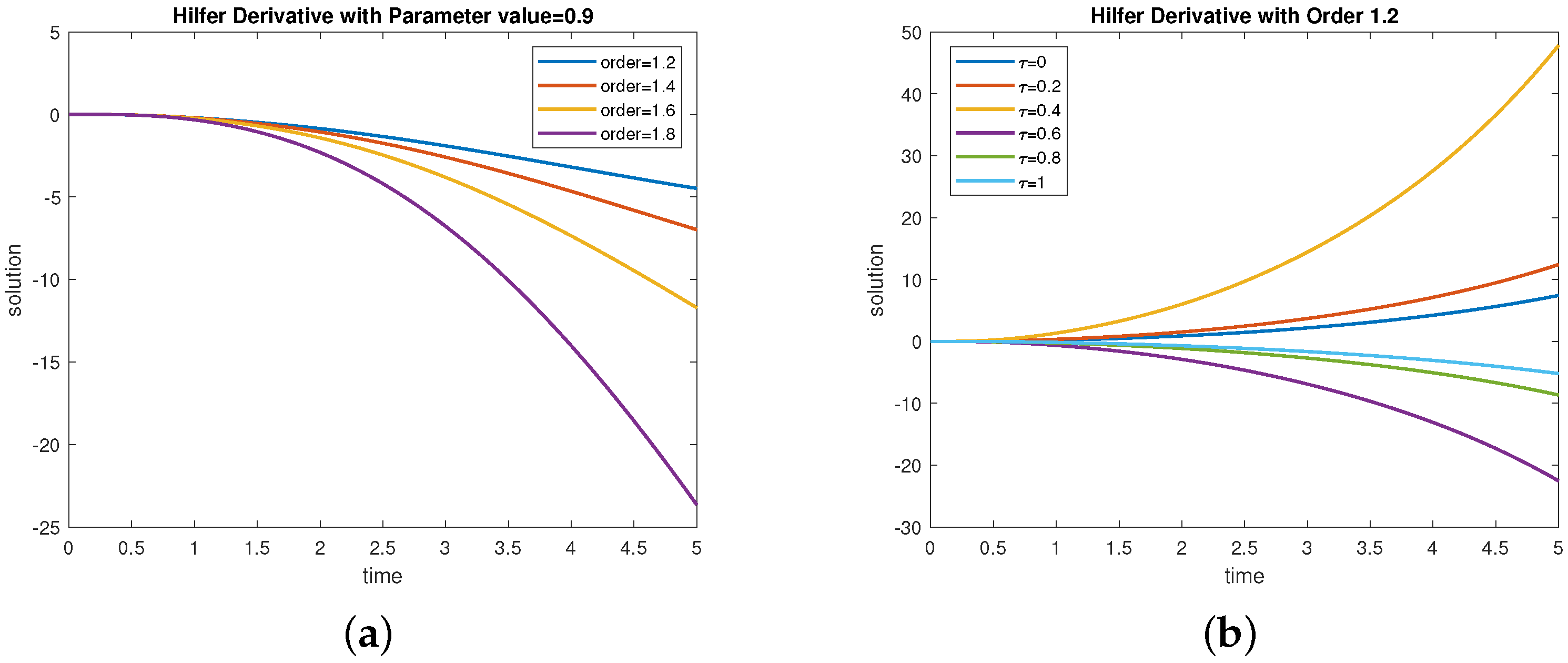
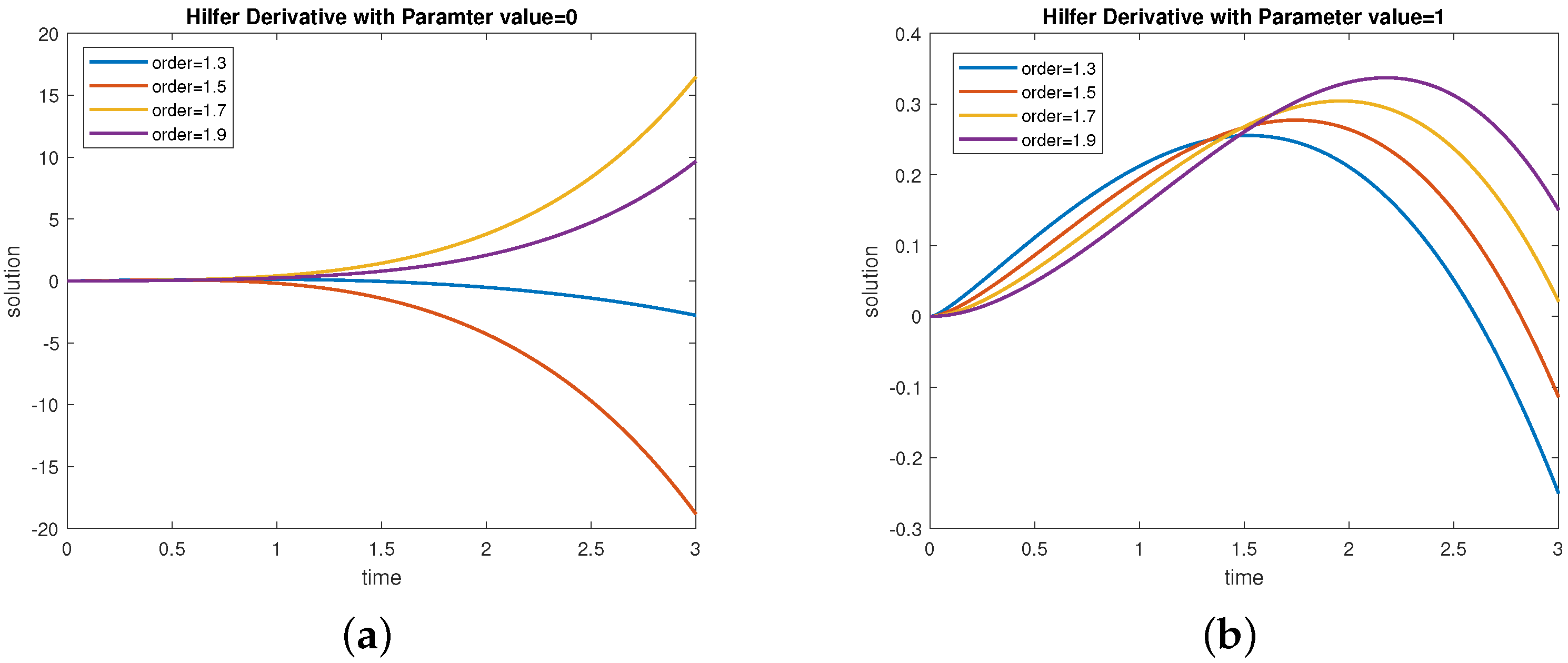
5. Examples
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Notations
| Current | |
| charge at t | |
| Supplied source (volt) | |
| Capacitance (farad) | |
| Resistance (ohms) | |
| t | time |
References
- Diethelm, K.; Ford, N.J. Analysis of fractional differential equations. J. Math. Anal. Appl. 2002, 265, 229–248. [Google Scholar] [CrossRef]
- Gupta, V.; Dabas, J.; Fečkan, M. Existence results of solutions for impulsive fractional differential equations. Nonautonomous Dyn. Syst. 2018, 5, 35–51. [Google Scholar] [CrossRef][Green Version]
- Hilfer, R. Applications of Fractional Calculus in Physics; World Scientific: Singapore, 2000. [Google Scholar]
- Podlubny, I. Fractional differential equations. In Mathematics in Science and Engineering; Elsevier: Amsterdam, The Netherlands, 1999. [Google Scholar]
- Zhou, Y. Basic Theory of Fractional Differential Equations; World Scientific Publishing Co., Pte. Ltd.: Hackensack, NJ, USA, 2014. [Google Scholar]
- Ahmad, B.; Nieto, J.J. Riemann-Liouville fractional integro-differential equations with fractional nonlocal integral boundary conditions. Bound. Value Probl. 2011, 2011, 36. [Google Scholar] [CrossRef]
- Borisut, P.; Kumam, P.; Ahmed, I.; Jirakitpuwapat, W. Existence and uniqueness for ψ-Hilfer fractional differential equation with nonlocal multi-point condition. Math. Methods Appl. Sci. 2021, 44, 2506–2520. [Google Scholar] [CrossRef]
- Furati, K.M.; Kassim, M.D. Existence and uniqueness for a problem involving Hilfer fractional derivative. Comput. Math. Appl. 2012, 64, 1616–1626. [Google Scholar] [CrossRef]
- Gu, H.; Trujillo, J.J. Existence of mild solution for evolution equation with Hilfer fractional derivative. Appl. Math. Comput. 2015, 257, 344–354. [Google Scholar] [CrossRef]
- Asawasamrit, S.; Kijjathanakorn, A.; Ntouyas, S.K.; Tariboon, J. Nonlocal boundary value problems for Hilfer fractional differential equations. Bull. Korean Math. Soc. 2018, 55, 1639–1657. [Google Scholar]
- Vivek, D.; M Elsayed, E.; Kanagarajan, K. Nonlocal Initial Value Problems for Nonlinear Neutral Pantograph Equations with Hilfer-Hadamard Fractional Derivative. Inf. Sci. Lett. 2021, 10, 111–119. [Google Scholar]
- Wang, J.; Zhang, Y. Nonlocal initial value problems for differential equations with Hilfer fractional derivative. Appl. Math. Comput. 2015, 266, 850–859. [Google Scholar] [CrossRef]
- Gholami, Y. Existence and uniqueness criteria for the higher-order Hilfer fractional boundary value problems at resonance. Adv. Differ. Equ. 2020, 2020, 482. [Google Scholar] [CrossRef]
- Naveen, S.; Srilekha, R.; Suganya, S.; Parthiban, V. Controllability of damped dynamical systems modelled by Hilfer fractional derivatives. J. Taibah Univ. Sci. 2022, 16, 1254–1263. [Google Scholar] [CrossRef]
- Owolabi, K.M. Numerical Analysis and Pattern Formation Process for Space-Fractional Superdiffusive Systems. Discret. Contin. Dyn.-Syst.-Ser. 2019, 12, 543–566. [Google Scholar] [CrossRef]
- Gómez-Aguilar, J. Fundamental solutions to electrical circuits of non-integer order via fractional derivatives with and without singular kernels. Eur. Phys. J. Plus 2018, 133, 197. [Google Scholar] [CrossRef]
- Sabir, Z.; Saoud, S.; Raja, M.A.Z.; Wahab, H.A.; Arbi, A. Heuristic computing technique for numerical solutions of nonlinear fourth order Emden-Fowler equation. Math. Comput. Simul. 2020, 178, 534–548. [Google Scholar] [CrossRef]
- Sabir, Z.; Raja, M.A.Z.; Arbi, A.; Altamirano, G.C.; Cao, J. Neuro-swarms intelligent computing using Gudermannian kernel for solving a class of second order Lane-Emden singular nonlinear model. AIMS Math 2021, 6, 2468–2485. [Google Scholar] [CrossRef]
- Gómez-Aguilar, J.; Atangana, A. New insight in fractional differentiation: Power, exponential decay and Mittag-Leffler laws and applications. Eur. Phys. J. Plus 2017, 132, 13. [Google Scholar] [CrossRef]
- Sene, N.; Abdelmalek, K. Analysis of the fractional diffusion equations described by Atangana-Baleanu-Caputo fractional derivative. Chaos Solitons Fractals 2019, 127, 158–164. [Google Scholar] [CrossRef]
- Aguilar, J.F.G. Behavior characteristics of a cap-resistor, memcapacitor, and a memristor from the response obtained of RC and RL electrical circuits described by fractional differential equations. Turk. J. Electr. Eng. Comput. Sci. 2016, 24, 1421–1433. [Google Scholar] [CrossRef]
- Morales-Delgado, V.F.; Gómez-Aguilar, J.F.; Taneco-Hernández, M.A.; Escobar-Jiménez, R.F. Fractional operator without singular kernel: Applications to linear electrical circuits. Int. J. Circuit Theory Appl. 2018, 46, 2394–2419. [Google Scholar] [CrossRef]
- Morales-Delgado, V.; Gómez-Aguilar, J.; Taneco-Hernandez, M. Analytical solutions of electrical circuits described by fractional conformable derivatives in Liouville-Caputo sense. AEU Int. J. Electron. Commun. 2018, 85, 108–117. [Google Scholar] [CrossRef]
- Gómez-Aguilar, J.; Escobar-Jiménez, R.; Olivares-Peregrino, V.; Taneco-Hernandez, M.; Guerrero-Ramírez, G. Electrical circuits RC and RL involving fractional operators with bi-order. Adv. Mech. Eng. 2017, 9, 1687814017707132. [Google Scholar] [CrossRef]
- Gómez-Aguilar, J.F.; Atangana, A.; Morales-Delgado, V.F. Electrical circuits RC, LC, and RL described by Atangana-Baleanu fractional derivatives. Int. J. Circuit Theory Appl. 2017, 45, 1514–1533. [Google Scholar] [CrossRef]
- Radwan, A.G.; Salama, K.N. Fractional-order RC and RL circuits. Circuits Syst. Signal Process. 2012, 31, 1901–1915. [Google Scholar] [CrossRef]
- Sene, N.; Gómez-Aguilar, J. Analytical solutions of electrical circuits considering certain generalized fractional derivatives. Eur. Phys. J. Plus 2019, 134, 260. [Google Scholar] [CrossRef]
- Gómez-Aguilar, J.; Córdova-Fraga, T.; Escalante-Martínez, J.; Calderón-Ramón, C.; Escobar-Jiménez, R. Electrical circuits described by a fractional derivative with regular kernel. Rev. Mex. De Física 2016, 62, 144–154. [Google Scholar]
- Arshad, U.; Sultana, M.; Ali, A.H.; Bazighifan, O.; Al-Moneef, A.A.; Nonlaopon, K. Numerical solutions of fractional-order electrical rlc circuit equations via three numerical techniques. Mathematics 2022, 10, 3071. [Google Scholar] [CrossRef]
- Malarvizhi, M.; Karunanithi, S.; Gajalakshmi, N. Numerical Analysis Using RK-4 In Transient Analysis Of RLC Circuit. Adv. Math. Sci. J. 2020, 9, 6115–6124. [Google Scholar] [CrossRef]
- Abbas, S.; Benchohra, M.; Sivasundaram, S. Dynamics and Ulam stability for Hilfer type fractional differential equations. Nonlinear Stud. 2016, 23, 627–637. [Google Scholar]
- András, S.; Kolumbán, J.J. On the Ulam-Hyers stability of first order differential systems with nonlocal initial conditions. Nonlinear Anal. Theory Methods Appl. 2013, 82, 1–11. [Google Scholar] [CrossRef]
- Harikrishnan, S.; Kanagarajan, K.; Vivek, D. Some Existence and Stability Results for Integro-Differential Equation by Hilfer-Katugampola Fractional Derivative. Palest. J. Math. 2020, 9, 254–262. [Google Scholar]
- Sudsutad, W.; Thaiprayoon, C.; Ntouyas, S.K. Existence and stability results for ψ-Hilfer fractional integro-differential equation with mixed nonlocal boundary conditions. AIMS Math 2021, 6, 4119–4141. [Google Scholar] [CrossRef]
- Wang, J.; Zhou, Y.; Medved, M. Existence and stability of fractional differential equations with Hadamard derivative. Topol. Methods Nonlinear Anal. 2013, 41, 113–133. [Google Scholar]
- Ibrahim, R.W. Generalized Ulam-Hyers stability for fractional differential equations. Int. J. Math. 2012, 23, 1250056. [Google Scholar] [CrossRef]
- Pachpatte, D.B. Existence and stability of some nonlinear ψ-Hilfer partial fractional differential equation. Partial Differ. Equ. Appl. Math. 2021, 3, 100032. [Google Scholar] [CrossRef]
- Rus, I.A. Ulam stabilities of ordinary differential equations in a Banach space. Carpathian J. Math. 2010, 26, 103–107. [Google Scholar]
- Wang, J.; Lv, L.; Zhou, Y. New concepts and results in stability of fractional differential equations. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 2530–2538. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
S., N.; V., P.; Abbas, M.I. Qualitative Analysis of RLC Circuit Described by Hilfer Derivative with Numerical Treatment Using the Lagrange Polynomial Method. Fractal Fract. 2023, 7, 804. https://doi.org/10.3390/fractalfract7110804
S. N, V. P, Abbas MI. Qualitative Analysis of RLC Circuit Described by Hilfer Derivative with Numerical Treatment Using the Lagrange Polynomial Method. Fractal and Fractional. 2023; 7(11):804. https://doi.org/10.3390/fractalfract7110804
Chicago/Turabian StyleS., Naveen, Parthiban V., and Mohamed I. Abbas. 2023. "Qualitative Analysis of RLC Circuit Described by Hilfer Derivative with Numerical Treatment Using the Lagrange Polynomial Method" Fractal and Fractional 7, no. 11: 804. https://doi.org/10.3390/fractalfract7110804
APA StyleS., N., V., P., & Abbas, M. I. (2023). Qualitative Analysis of RLC Circuit Described by Hilfer Derivative with Numerical Treatment Using the Lagrange Polynomial Method. Fractal and Fractional, 7(11), 804. https://doi.org/10.3390/fractalfract7110804








