New Approach to Quasi-Synchronization of Fractional-Order Delayed Neural Networks

Abstract

This article investigates quasi-synchronization for a class of fractional-order delayed neural networks. By utilizing the properties of the Laplace transform, the Caputo derivative, and the Mittag–Leffler function, a new fractional-order differential inequality is introduced. Furthermore, an adaptive controller is designed, resulting in the derivation of an effective criterion to ensure the aforementioned synchronization. Finally, a numerical illustration is provided to demonstrate the validity of the presented theoretical findings.

1. Introduction

With the rapid advancement of numerical algorithms, there has been significant interest in fractional calculus, which is an extension of classical integration and differentiation to arbitrary orders. Fractional-order systems offer distinct advantages over integer-order systems in capturing the memory and hereditary characteristics of numerous materials. For instance, they provide a more accurate description of the relationship between voltage and current in capacitors by utilizing the fractional properties of capacitor dielectrics [1,2]. Indeed, various real-world processes can be effectively described as fractional-order systems, including diffusion theory [3,4], electromagnetic theory [5], colored noise [6], happiness model [7], and dielectric relaxation [8]. The study of fractional-order systems is of paramount importance, offering valuable insights for both theoretical understanding and practical applications.

In recent decades, scholars have extensively studied neural networks due to their broad utility across various domains, including combinational optimization, automatic control, and signal processing [9,10,11,12,13,14]. The limited switching speed of amplifiers gives rise to time delays, which lead to oscillation, instability, and bifurcation [15,16]. Consequently, extensive research has been carried out to investigate the dynamic properties of neural networks incorporating time delays, focusing on aspects such as bifurcation [17], stability [18], and dissipativity [19]. The continuous-time integer-order Hopfield neural network [20] was introduced by Hopfield in 1984 and has garnered significant attention from scientists. In recent years, researchers have recognized the potential of fractional calculus in neural network studies and have extended the order of neural networks from integer-order to fractional-order. In fact, fractional calculus equips neurons with a fundamental and versatile computational capability, which plays a crucial role in enabling efficient information processing and anticipation of stimuli [21]. The integration of fractional calculus with neural networks reveals their true behavior, providing valuable insights into qualitative analysis and synchronization control. This integration has led numerous researchers to construct fractional models within neural networks, resulting in a wealth of findings in the field of fractional-order neural networks. These findings encompass the existence and uniqueness of nontrivial solutions, Mittag–Leffler stability, and synchronization control [22,23,24,25,26]. Anastassiou [27] highlighted the crucial role played by fractional-order recurrent neural networks in parameter estimation, noting their superior accuracy rates in approximations. Consequently, integrating fractional calculus into delayed neural networks and establishing fractional-order delayed neural networks represent a more precise and substantial approach. This approach enhances performance for optimization and complex computations, surpassing the capabilities of conventional integer-order neural networks.

The synchronization analysis of neural networks has been widely explored in the domains of neural networks and complex networks, leading to interesting findings in information science, signal processing, and secure communication [24,28,29,30]. Various forms of synchronization, including complete synchronization, exponential synchronization, and Mittag–Leffler synchronization, have been widely studied by researchers [25,26,31,32,33,34]. In the synchronization schemes mentioned above, it is typically assumed that the system error eventually converges to zero. However, in practical applications, the electronic components used in the construction of artificial neural networks often feature threshold voltages. When these threshold voltages are triggered, they can cause changes in the connection weights, resulting in unforeseen errors in the dynamical system. This, in turn, makes it challenging for the error system to reach a state of complete equilibrium at zero [35]. To address this issue, the concept of quasi-synchronization is employed, signifying that synchronization errors may not necessarily approach zero. Instead, they gradually converge within a confined range around zero as time progresses [36]. It is noteworthy that significant research on the quasi-synchronization of delayed neural networks has emerged in recent years [36,37,38,39]. Adaptive control [24,30], which automatically adjusts its control parameters according to an adaptive law, offers the distinct advantages of cost-effectiveness and ease of operation. Consequently, it is imperative and of considerable significance to study quasi-synchronization in fractional-order delayed neural networks utilizing adaptive control.

In [40], a finite-time synchronization criterion was established for fractional-order delayed fuzzy cellular neural networks by the utilization of a fractional-order Gronwall inequality. It was observed that the estimated value function within this inequality exhibited non-decreasing behavior over a finite time interval, potentially amplifying the disparity between the estimated synchronization error and the actual error. To minimize this difference, another study [41] focused on adaptive finite-time synchronization of the same neural networks. By designing an adaptive controller and proposing a new fractional-order differential inequality, the estimated error bound was shown to exhibit a declining trend over a finite time interval. These studies raise an intriguing question: can we determine a decreasing estimated value function that accurately captures the synchronization error in an infinite-time scenario? If such a function exists, how can we derive the corresponding synchronization criterion? It is worth noting that this problem has not been extensively investigated in the existing literature, indicating a need for further study and exploration in this area. Motivated by the problem, this article presents a criterion for achieving infinite-time synchronization of the considered fractional-order systems. The main results of this article are as follows:

(i)

A new fractional-order differential inequality has been developed on an unbounded time interval. This inequality can be utilized to investigate the quasi-synchronization of fractional-order complex networks or neural networks.

(ii)

Utilizing the proposed inequality in combination with an adaptive controller, a novel criterion for the quasi-synchronization of fractional-order delayed neural networks has been derived.

(iii)

The validity of the developed results is substantiated through a numerical analysis, offering sufficient evidence in support of the obtained synchronization criterion.

Here is an outline of this article. In Section 2, some preliminaries and a model description are provided to lay the foundation for the subsequent analysis. In Section 3, the key fractional-order differential inequality and a new approach to quasi-synchronization are established. In Section 4, connections between mathematical treatment and numerical simulation are outlined, establishing a theoretical foundation for subsequent numerical analysis. Section 5 presents a numerical result, highlighting the significance of the obtained findings in a practical context.

Notations: Suppose that r is a real number, and m is a natural number. Then, ${\mathbb{N}}_r=\{r,r+1,r+2,\cdots \}$ and ${\mathbb{N}}_r^{r+m}=\{r,r+1,\cdots ,r+m\}$. Let ${\mathcal{L}}_1([t_0,t],\mathbb{R})$ denote the set of measurable functions from $[t_0,t]$ to $\mathbb{R}$, where $\mathbb{R}$ is the set of real numbers. For each n-dimensional real vector $\xi ={({\xi }_1,{\xi }_2,\cdots ,{\xi }_n)}^{\mathrm{T}}\in {\mathbb{R}}^n$, let $\parallel \xi \parallel ={\displaystyle \sum _{i=1}^n}|{\xi }_i|$.

2. Preliminaries and Model Formulation

2.1. Preliminaries

In this subsection, we review some fundamental knowledge that will be used later.

Definition 1

([42]). Let $\alpha ,\beta \in (0,+\infty )$. A Mittag–Leffler function with two parameters, denoted by $E_{\alpha ,\beta }\left(t\right)$, is defined as

$$E_{\alpha ,\beta }\left(t\right)={\displaystyle \sum _{\mu =0}^{\infty }}\frac{t^{\mu }}{\Gamma (\mu \alpha +\beta )},t\in \mathbb{R}.$$

In particular, let $\beta =1$. Then, its one-parameter form is

$$E_{\alpha }\left(t\right)=E_{\alpha ,1}\left(t\right)={\displaystyle \sum _{\mu =0}^{\infty }}\frac{t^{\mu }}{\Gamma (\mu \alpha +1)}.$$

Lemma 1

([42,43,44,45]). Let $\alpha \in (0,1)$ and $\omega \in (0,+\infty )$. Then:

(i) 

$E_{\alpha }(-\omega {(t-t_0)}^{\alpha })$ is monotonically non-increasing for $t\in [t_0,+\infty )$.

(ii) 

$0<E_{\alpha }(-\omega {(t-t_0)}^{\alpha })\le 1$.

(iii) 

$E_{\alpha ,\alpha }(-\omega {(t-t_0)}^{\alpha })>0$.

Lemma 2

([46]). The following equality holds for the Mittag–Leffler function $E_{\alpha ,\alpha }(·)$

$${\int }_{t_0}^t{(t-\zeta )}^{\alpha -1}{E}_{\alpha ,\alpha }(-\omega {(t-\zeta )}^{\alpha })\mathrm{d}\zeta =\frac{1}{\omega }\left(1-E_{\alpha }(-\omega {(t-t_0)}^{\alpha })\right).$$

(1)

We next recall from [47] (§ 3) the definition and some basic properties of the one-parameter Laplace transform.

Definition 2

([47]). Given a function $f:[t_0,+\infty )\to \mathbb{R}$, its Laplace transform with parameter $t_0$ is defined by

$${\mathcal{L}}_{t_0}\left\{f\left(t\right)\right\}\left(s\right)={\int }_{t_0}^{+\infty }f\left(t\right)e^{-s(t-t_0)}\mathrm{d}t.$$

Lemma 3

([47]). Given two piecewise continuous functions f and g on $[t_0,+\infty )$ of exponential order $\breve{\epsilon }$, the following equation holds:

$${\mathcal{L}}_{t_0}\{f\left(t\right)\ast g\left(t\right)\}\left(s\right)={\mathcal{L}}_{t_0}\left\{f\left(t\right)\right\}\left(s\right)·{\mathcal{L}}_{t_0}\left\{g\left(t\right)\right\}\left(s\right),$$

where $\mathcal{R}e\left(s\right)>\breve{\epsilon }$ and the convolution is given by

$$f\left(t\right)\ast g\left(t\right)={\int }_{t_0}^{t}f\left(\zeta \right)g(t+t_0-\zeta )\mathrm{d}\zeta .$$

(2)

Lemma 4

([41,43]). Let $E_{\alpha ,\beta }\left(\kappa {(t-t_0)}^{\alpha }\right)$ be the Mittag–Leffler function. Then,

$${\mathcal{L}}_{t_0}\left\{{(t-t_0)}^{\beta -1}{E}_{\alpha ,\beta }\left(\kappa {(t-t_0)}^{\alpha }\right)\right\}\left(s\right)=\frac{s^{\alpha -\beta }}{s^{\alpha }-\kappa },$$

where $\mathcal{R}e\left(s\right)>{|\kappa |}^{\frac{1}{\alpha }}.$

Definition 3

([42]). Let $\alpha \in (0,+\infty )$ and $u\in {\mathcal{L}}_1([t_0,t],\mathbb{R})$. The α-order integral of u is given by

$${}_{t_0}{D}_t^{-\alpha }u\left(t\right)={\int }_{t_0}^t\frac{{(t-\zeta )}^{\alpha -1}}{\Gamma \left(\alpha \right)}u\left(\zeta \right)\mathrm{d}\zeta .$$

Definition 4

([42]). Let $\alpha \in (0,1)$ and $v\in {\mathcal{C}}^1([t_0,t],\mathbb{R})$. The α-order Caputo derivative of v is given by

$${}_{t_0}^c{D}_t^{\alpha }v\left(t\right)={\int }_{t_0}^t\frac{{(t-\zeta )}^{-\alpha }}{\Gamma (1-\alpha )}{v}^{\prime }\left(\zeta \right)\mathrm{d}\zeta .$$

Lemma 5

([48]). Let $\alpha \in (0,1)$ and $w\in {\mathcal{C}}^1([t_0,t],\mathbb{R})$. Then,

$${}_{t_0}{D}_t^{-\alpha }{}_{t_0}^c{D}_t^{\alpha }w\left(t\right)=w\left(t\right)-w\left(t_0\right).$$

(3)

Lemma 6

([49]). Let $\alpha \in (0,1)$ and $v\in {\mathcal{C}}^1([t_0,t],\mathbb{R})$. Then,

$${}_{t_0}^c{D}_t^{\alpha }|v\left(t\right)|\le \mathrm{sign}{\left(v\left(t\right)\right)}_{t_0}^c{D}_t^{\alpha }v\left(t\right)$$

holds almost everywhere.

Lemma 7

([41]). Let $w\in {\mathcal{C}}^1([t_0,t],\mathbb{R})$ and of exponential order $\breve{\epsilon }$. Then,

$${\mathcal{L}}_{t_0}{\{}_{t_0}^c{D}_t^{\alpha }w\left(t\right)\}\left(s\right)=s^{\alpha }W\left(s\right)-s^{\alpha -1}w\left(t_0\right),$$

where $\alpha \in (0,1),\mathcal{R}e\left(s\right)>\breve{\epsilon }$, and $W\left(s\right)={\mathcal{L}}_{t_0}\left\{w\left(t\right)\right\}\left(s\right)$.

Lemma 8

([50]). Let $\alpha \in (0,1)$ and $\omega \in (0,+\infty )$. Assume that $h_1$ and $h_2$ are two non-negative differentiable functions, and satisfy

$${}_{t_0}^c{D}_t^{\alpha }(h_1\left(t\right)+h_2\left(t\right))\le -\omega h_1\left(t\right),t\ge t_0.$$

(4)

For arbitrary positive constant λ, there exists a non-negative constant T satisfying $T\ge {\left(\frac{\lambda \Gamma (\alpha +1)}{\omega (h_1\left(t_0\right)+h_2\left(t_0\right)+\lambda )}\right)}^{\frac{1}{\alpha }}$ such that

$$h_1\left(t\right)\le \left(h_1\left(t_0\right)+h_2\left(t_0\right)+\lambda \right)E_{\alpha }(-\omega {(t-t_0)}^{\alpha }),t\in [t_0,t_0+T].$$

(5)

Lemma 9

([41]). Let $\alpha \in (0,1)$, $\omega \in (0,+\infty )$, and $\kappa \in (-\infty ,0].$ Suppose that two non-negative differentiable functions $h_1$ and $h_2$ satisfy

$${}_{t_0}^c{D}_t^{\alpha }(h_1\left(t\right)+h_2\left(t\right))\le -\omega h_1\left(t\right)+\kappa ,t\ge t_0.$$

(6)

Then, for arbitrary positive constant λ, there exists a non-negative constant $\overline{T}$ such that

$$h_1\left(t\right)\le \left(h_1\left(t_0\right)+h_2\left(t_0\right)+\lambda \right)E_{\alpha }(-\omega {(t-t_0)}^{\alpha })+\frac{\kappa }{\omega }\left(1-E_{\alpha }(-\omega {(t-t_0)}^{\alpha })\right),$$

(7)

where $t\in [t_0,\overline{T}]$ and $\overline{T}$ are the solutions of the equation

$$E_{\alpha }(-\omega {(t-t_0)}^{\alpha })-\frac{h_1\left(t_0\right)+h_2\left(t_0\right)}{h_1\left(t_0\right)+h_2\left(t_0\right)+\lambda }=0.$$

Lemma 10

([13]). Let $\alpha \in (0,1)$, $\omega \in (0,+\infty )$, and $\kappa \in (0,+\infty )$. Suppose that $h_1$ and $h_2$ are two non-negative differentiable functions satisfying

$${}_{t_0}^c{D}_t^{\alpha }(h_1\left(t\right)+h_2\left(t\right))\le -\omega h_1\left(t\right)+\kappa ,t\ge t_0.$$

Then,

$$h_1\left(t\right)\le \left(h_1\left(t_0\right)+h_2\left(t_0\right)-\frac{\kappa }{\omega }\right)E_{\alpha }(-\omega {(t-t_0)}^{\alpha })+\frac{\kappa }{\omega },t\ge t_0+{\left(\frac{\Gamma \left(\alpha \right)}{\omega }\right)}^{\frac{1}{1-\alpha }}.$$

Lemma 11

([51]). Let $\alpha \in (0,1]$, $h\in {\mathcal{C}}^1([t_0,t],\mathbb{R})$, $g\in \mathcal{C}([t_0,t],\mathbb{R})$, and γ be a fixed constant. If

$${}_{t_0}^c{D}_t^{\alpha }h\left(t\right)\le \gamma h\left(t\right)+g\left(t\right),t\ge t_0,$$

(8)

then for any $t\ge t_0$,

$$h\left(t\right)\le h\left(t_0\right)E_{\alpha }\left(\gamma {(t-t_0)}^{\alpha }\right)+{\int }_{t_0}^t{(t-s)}^{\alpha -1}{E}_{\alpha ,\alpha }\left(\gamma {(t-s)}^{\alpha }\right)g\left(s\right)\mathrm{d}s.$$

If we let $g\left(t\right)\equiv c\in \mathbb{R}$, then

$$h\left(t\right)\le h\left(t_0\right)E_{\alpha }\left(\gamma {(t-t_0)}^{\alpha }\right)-\frac{c}{\gamma }\left(1-E_{\alpha }\left(\gamma {(t-t_0)}^{\alpha }\right)\right),t\ge t_0.$$

(9)

2.2. Model Description

We revisit the fractional-order delayed neural network presented in [13], which is commonly referred to as the driving system:

$$\left\{\begin{array}{cc}\hfill {}_{t_0}^c{D}_t^{\alpha }{q}_i\left(t\right)=& -c_i{q}_i\left(t\right)+{\displaystyle \sum _{j=1}^m}{w}_{ij}{f}_j\left(q_j\left(t\right)\right)\hfill \\ \hfill & +{\displaystyle \sum _{j=1}^m}{w}_{ij}^{\iota }{f}_j\left(q_j(t-\iota )\right)+I_i\left(t\right),t\ge t_0,\hfill \\ \hfill q_i\left(s\right)=& {\phi }_i\left(s\right),i\in {\mathbb{N}}_1^m,s\in [t_0-\iota ,t_0],\hfill \end{array}\right.$$

(10)

where $0<\alpha <1$, $c_i\in \mathbb{R}$, $\iota >0$ is a constant delay, $q_i\left(t\right)\in \mathbb{R}$ is the state variable of the ith neuron, $I_i$ is the external input, and $w_{ij},w_{ij}^{\iota }\in \mathbb{R}$ represent the connection weight and delayed connection weight, respectively; $f_j\left(q_j\left(t\right)\right)$ and $f_j\left(q_j(t-\iota )\right)$ are the activation functions without delay and with delay, respectively.

The corresponding response system is defined as

$$\left\{\begin{array}{cc}\hfill {}_{t_0}^c{D}_t^{\alpha }{p}_i\left(t\right)=& -c_i{p}_i\left(t\right)+{\displaystyle \sum _{j=1}^m}{w}_{ij}{f}_j\left(p_j\left(t\right)\right)\hfill \\ \hfill & +{\displaystyle \sum _{j=1}^m}{w}_{ij}^{\iota }{f}_j\left(p_j(t-\iota )\right)+I_i\left(t\right)+u_i\left(t\right),t\ge t_0,\hfill \\ \hfill p_i\left(s\right)=& {\varphi }_i\left(s\right),i\in {\mathbb{N}}_1^m,s\in [t_0-\iota ,t_0],\hfill \end{array}\right.$$

(11)

where $p_i\left(t\right)\in \mathbb{R}$ is the state variable of the ith neuron of (11), and $u_i\left(t\right)$ is a control input.

Let $r_i\left(t\right)=p_i\left(t\right)-q_i\left(t\right)$ and $r\left(t\right)={(r_1\left(t\right),r_2\left(t\right),\cdots ,r_m\left(t\right))}^{\mathrm{T}}$. Then, we obtain the following error system

$$\begin{array}{cc}\hfill {}_{t_0}^c{D}_t^{\alpha }{r}_i\left(t\right)& =-c_i{r}_i\left(t\right)+{\displaystyle \sum _{j=1}^m}{w}_{ij}\left(f_j\left(p_j\left(t\right)\right)-f_j\left(q_j\left(t\right)\right)\right)\hfill \\ \hfill & +{\displaystyle \sum _{j=1}^m}{w}_{ij}^{\iota }\left(f_j\left(p_j(t-\iota )\right)-f_j\left(q_j(t-\iota )\right)\right)+u_i\left(t\right),t\ge t_0,\hfill \end{array}$$

(12)

where the adaptive controller is given by

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{u}_i\left(t\right)=\left\{\begin{array}{c}-{\sigma }_i\left(t\right)r_i\left(t\right)-\xi \frac{r_i\left(t\right)}{|r_i\left(t\right)|}|r_i(t-\iota )|-\eta \frac{r_i\left(t\right)}{|r_i\left(t\right)|},|r_i\left(t\right)|\ne 0,\hfill \\ 0,|r_i\left(t\right)|=0,\hfill \end{array}\right.\hfill \\ {}_{t_0}^c{D}_t^{\alpha }{\sigma }_i\left(t\right)={\rho }_i|r_i\left(t\right)|,i\in {\mathbb{N}}_1^m,\hfill \end{array}\right.\end{array}$$

(13)

where $\xi$, $\eta$, ${\rho }_i$ are tunable positive constants, and ${\sigma }_i\left(t\right)$ is the time-varying feedback strength.

Definition 5

([36]). System (10) is quasi-synchronized with system (11) if there exists a small error bound $ϵ>0$ and a compact set $M=\{r\left(t\right)\in {\mathbb{R}}^n|\parallel r\left(t\right)\parallel \le ϵ\}$ such that when $t\to \infty$, the error signal $r\left(t\right)$ converges into M.

Assumption 1

([41]). For any $r_1,r_2\in \mathbb{R},$ and $i\in {\mathbb{N}}_1^m$, there exists a positive real number $l_i$ satisfying

$$\begin{array}{cc}\hfill & |f_i\left(r_1\right)-f_i\left(r_2\right)|\le l_i|r_1-r_2|.\hfill \end{array}$$

(14)

3. Main Results

In [41], for the inequality ${}_{t_0}^c{D}_t^{\alpha }(h_1\left(t\right)+h_2\left(t\right))\le -\omega h_1\left(t\right)+\kappa$, where $\alpha \in (0,1)$, $\omega \in (0,+\infty )$, and $\kappa \in (-\infty ,0]$, the finite-time dynamic behaviors of $h_1\left(t\right)$ were established to study the finite-time synchronization of fractional-order delayed systems. Naturally, one may consider whether this inequality can also be used to investigate the case of infinite time. The purpose of the following Theorem 1 is to address this problem.

Theorem 1.

Let $\alpha \in (0,1)$, $\omega \in (0,+\infty )$, and $\kappa \in (-\infty ,0]$. Suppose that $h_1$ and $h_2$ are two non-negative differentiable functions satisfying $h_1\left(t_0\right)+h_2\left(t_0\right)+\frac{\kappa }{\omega }>0$ and

$${}_{t_0}^c{D}_t^{\alpha }(h_1\left(t\right)+h_2\left(t\right))\le -\omega h_1\left(t\right)+\kappa ,t\ge t_0.$$

(15)

Then, we obtain

$$h_1\left(t\right)\le h_1\left(t_0\right)+h_2\left(t_0\right)+\frac{\kappa }{\omega }\left(1-E_{\alpha }(-\omega {(t-t_0)}^{\alpha })\right),t\ge t_0.$$

(16)

Proof. 

By (15), there exists a non-negative function $h\left(t\right)$ satisfying

$${}_{t_0}^c{D}_t^{\alpha }(h_1\left(t\right)+h_2\left(t\right))+h\left(t\right)=-\omega h_1\left(t\right)+\kappa .$$

(17)

Then, the following equation holds:

$${\mathcal{L}}_{t_0}\left\{{}_{t_0}^c{D}_t^{\alpha }(h_1\left(t\right)+h_2\left(t\right))\right\}\left(s\right)+{\mathcal{L}}_{t_0}\left\{h\left(t\right)\right\}\left(s\right)=-\omega {\mathcal{L}}_{t_0}\left\{h_1\left(t\right)\right\}\left(s\right)+\frac{\kappa }{s}.$$

Using Lemma 7, we obtain

$$s^{\alpha }\left(H_1\left(s\right)+H_2\left(s\right)\right)-s^{\alpha -1}\left(h_1\left(t_0\right)+h_2\left(t_0\right)\right)+H\left(s\right)=-\omega H_1\left(s\right)+\frac{\kappa }{s},$$

(18)

where $H_1\left(s\right)={\mathcal{L}}_{t_0}\left\{h_1\left(t\right)\right\}\left(s\right)$, $H_2\left(s\right)={\mathcal{L}}_{t_0}\left\{h_2\left(t\right)\right\}\left(s\right)$ and $H\left(s\right)={\mathcal{L}}_{t_0}\left\{h\left(t\right)\right\}\left(s\right)$. Thus,

$$H_1\left(s\right)=\frac{s^{\alpha -1}}{s^{\alpha }+\omega }\left(h_1\left(t_0\right)+h_2\left(t_0\right)\right)-\left(1-\frac{\omega }{s^{\alpha }+\omega }\right)H_2\left(s\right)-\frac{H\left(s\right)}{s^{\alpha }+\omega }+\frac{s^{-1}}{s^{\alpha }+\omega }\kappa .$$

(19)

By the Equation (19) and Lemma 3, we have

$$\begin{array}{cc}\hfill h_1\left(t\right)& ={\mathcal{L}}_{t_0}^{-1}\left\{H_1\left(s\right)\right\}=\left(h_1\left(t_0\right)+h_2\left(t_0\right)\right){\mathcal{L}}_{t_0}^{-1}\left\{\frac{s^{\alpha -1}}{s^{\alpha }+\omega }\right\}\hfill \\ \hfill & -{\mathcal{L}}_{t_0}^{-1}\left\{H_2\left(s\right)\right\}+{\mathcal{L}}_{t_0}^{-1}\left\{\frac{\omega }{s^{\alpha }+\omega }\right\}\ast {\mathcal{L}}_{t_0}^{-1}\left\{H_2\left(s\right)\right\}\hfill \\ \hfill & -{\mathcal{L}}_{t_0}^{-1}\left\{H\left(s\right)\right\}\ast {\mathcal{L}}_{t_0}^{-1}\left\{\frac{1}{s^{\alpha }+\omega }\right\}+\kappa {\mathcal{L}}_{t_0}^{-1}\left\{\frac{s^{-1}}{s^{\alpha }+\omega }\right\}\hfill \\ \hfill & \stackrel{\mathrm{Lem}.4}{=}\left(h_1\left(t_0\right)+h_2\left(t_0\right)\right)E_{\alpha }(-\omega {(t-t_0)}^{\alpha })\hfill \\ \hfill & -h_2\left(t\right)+\left(\omega {(t-t_0)}^{\alpha -1}{E}_{\alpha ,\alpha }(-\omega {(t-t_0)}^{\alpha })\right)\ast h_2\left(t\right)\hfill \\ \hfill & -h\left(t\right)\ast \left({(t-t_0)}^{\alpha -1}{E}_{\alpha ,\alpha }(-\omega {(t-t_0)}^{\alpha })\right)+\kappa {(t-t_0)}^{\alpha }{E}_{\alpha ,\alpha +1}(-\omega {(t-t_0)}^{\alpha })\hfill \\ \hfill & \stackrel{\mathrm{Lem}.2}{=}\left(h_1\left(t_0\right)+h_2\left(t_0\right)\right)E_{\alpha }(-\omega {(t-t_0)}^{\alpha })\hfill \\ \hfill & -h_2\left(t\right)+\underset{v_1\left(t\right)}{\underbrace{\left(\omega {(t-t_0)}^{\alpha -1}{E}_{\alpha ,\alpha }(-\omega {(t-t_0)}^{\alpha })\right)\ast h_2\left(t\right)}}\hfill \\ \hfill & \underset{v_2\left(t\right)}{\underbrace{-h\left(t\right)\ast \left({(t-t_0)}^{\alpha -1}{E}_{\alpha ,\alpha }(-\omega {(t-t_0)}^{\alpha })\right)}}+\frac{\kappa }{\omega }\left(1-E_{\alpha }(-\omega {(t-t_0)}^{\alpha })\right).\hfill \end{array}$$

(20)

Applying (3), we obtain

$${}_{t_0}{D}_t^{-\alpha }{}_{t_0}^c{D}_t^{\alpha }(h_1\left(t\right)+h_2\left(t\right))=(h_1\left(t\right)+h_2\left(t\right))-(h_1\left(t_0\right)+h_2\left(t_0\right))\le 0.$$

Also by the non-negativity of the functions $h_1$ and $h_2$, the following inequalities hold:

$$0\le h_2\left(t\right)\le h_1\left(t\right)+h_2\left(t\right)\le h_1\left(t_0\right)+h_2\left(t_0\right).$$

(21)

Based on the convolution given in (2), we obtain

$$\begin{array}{cc}\hfill v_1\left(t\right)& :=\left(\omega {(t-t_0)}^{\alpha -1}{E}_{\alpha ,\alpha }(-\omega {(t-t_0)}^{\alpha })\right)\ast h_2\left(t\right)\hfill \\ & ={\int }_{t_0}^t\left(\omega {(t-\zeta )}^{\alpha -1}{E}_{\alpha ,\alpha }(-\omega {(t-\zeta )}^{\alpha })\right)h_2\left(\zeta \right)\mathrm{d}\zeta \hfill \\ & \stackrel{\left(21\right)}{\le }\left(h_1\left(t_0\right)+h_2\left(t_0\right)\right){\int }_{t_0}^t\omega {(t-\zeta )}^{\alpha -1}{E}_{\alpha ,\alpha }(-\omega {(t-\zeta )}^{\alpha })\mathrm{d}\zeta \hfill \\ & \stackrel{\left(1\right)}{=}\left(h_1\left(t_0\right)+h_2\left(t_0\right)\right)\left(1-E_{\alpha }(-\omega {(t-t_0)}^{\alpha })\right).\hfill \end{array}$$

(22)

By $h\left(t\right)\ge 0$ and $E_{\alpha ,\alpha }(-\omega {(t-\zeta )}^{\alpha })>0$ given in Lemma 1i,

$$\begin{array}{cc}\hfill v_2\left(t\right):=& -h\left(t\right)\ast \left({(t-t_0)}^{\alpha -1}{E}_{\alpha ,\alpha }(-\omega {(t-t_0)}^{\alpha })\right)\hfill \\ \hfill =& -{\int }_{t_0}^{t}h\left(\zeta \right){(t-\zeta )}^{\alpha -1}{E}_{\alpha ,\alpha }(-\omega {(t-\zeta )}^{\alpha })\mathrm{d}\zeta \le 0.\hfill \end{array}$$

(23)

Furthermore, by (20), (22), (23), and the non-negativity of $h_2\left(t\right)$, we have

$$\begin{array}{cc}\hfill h_1\left(t\right)\le & \left(h_1\left(t_0\right)+h_2\left(t_0\right)\right)E_{\alpha }(-\omega {(t-t_0)}^{\alpha })\hfill \\ \hfill & +\left(h_1\left(t_0\right)+h_2\left(t_0\right)\right)\left(1-E_{\alpha }(-\omega {(t-t_0)}^{\alpha })\right)+\frac{\kappa }{\omega }\left(1-E_{\alpha }(-\omega {(t-t_0)}^{\alpha })\right)\hfill \\ \hfill =& h_1\left(t_0\right)+h_2\left(t_0\right)+\frac{\kappa }{\omega }\left(1-E_{\alpha }(-\omega {(t-t_0)}^{\alpha })\right),t\ge t_0.\hfill \end{array}$$

□

Remark 1.

Theorem 1 will play a pivotal role in deriving the quasi-synchronization criteria for systems, specifically in the context of various types of fractional-order complex networks or neural networks. It serves as a fundamental tool that enables the analysis of quasi-synchronization phenomena within these interconnected systems.

Remark 2.

The inequality ${}_{t_0}^c{D}_t^{\alpha }(h_1\left(t\right)+h_2\left(t\right))\le -\omega h_1\left(t\right)+\kappa$ is employed in both Lemma 10 and Theorem 1 to explore the asymptotic synchronization of fractional-order neural networks. In Lemma 10, the sign of ${}_{t_0}^c{D}_t^{\alpha }(h_1\left(t\right)+h_2\left(t\right))$ is indefinite, whereas in Theorem 1, the sign is non-positive.

Remark 3.

Let $\widehat{h_1}\left(t\right):=h_1\left(t_0\right)+h_2\left(t_0\right)+\frac{\kappa }{\omega }\left(1-E_{\alpha }(-\omega {(t-t_0)}^{\alpha })\right)$ for $t\ge t_0$. Then, the inequality (16) in Theorem 1 becomes $h_1\left(t\right)\le \widehat{h_1}\left(t\right)$. By Lemma 1, $\widehat{h_1}\left(t\right)$ is monotonically non-increasing for $t\ge t_0,$$\widehat{h_1}\left(t_0\right)=h_1\left(t_0\right)+h_2\left(t_0\right)>0$, and ${\displaystyle \underset{t\to \infty }{lim}}\widehat{h_1}\left(t\right)=h_1\left(t_0\right)+h_2\left(t_0\right)+\frac{\kappa }{\omega }>0$. Thus, we obtain $\widehat{h_1}\left(t\right)>0$ for $t\ge t_0$, which guarantees that the obtained inequality (16) makes sense.

Remark 4.

Even though Theorem 1 and Lemma 9 utilize the same Caputo-derivative inequality, they provide the function estimates on an infinite interval and a finite interval, respectively. In addition, the inverse Laplace techniques of $\left(1-\frac{\omega }{s^{\alpha }+\omega }\right)H_2\left(s\right)$ employed for Theorem 1 and Lemma 9 are different. Notably, the Dirac delta function $\delta (·)$ is not used in Theorem 1, resulting in a simplification of the proof process. Finally, the estimate inequality (16) in Theorem 1 can be used to study quasi-synchronization of fractional-order systems in Theorem 2.

Remark 5.

When $\kappa =0$ in Theorem 1, the obtained inequality (16) will be reduced to

$$h_1\left(t\right)\le h_1\left(t_0\right)+h_2\left(t_0\right),t\ge t_0,$$

(24)

which can be also given by (21). In this case, the inequality (15) is reduced to the inequality (4) in Lemma 8.

In addition, as another special case of Theorem 1, let $h_2\left(t\right)\equiv 0$, and then we have

Corollary 1.

Let $\alpha \in (0,1)$, $\omega \in (0,+\infty )$, and $\kappa \in (-\infty ,0]$. Assume that $h_1$ is a non-negative differentiable function satisfying $h_1\left(t_0\right)+\frac{\kappa }{\omega }>0$, and

$${}_{t_0}^c{D}_t^{\alpha }{h}_1\left(t\right)\le -\omega h_1\left(t\right)+\kappa ,t\ge t_0.$$

(25)

Then,

$$h_1\left(t\right)\le h_1\left(t_0\right)+\frac{\kappa }{\omega }\left(1-E_{\alpha }(-\omega {(t-t_0)}^{\alpha })\right),t\ge t_0.$$

(26)

Remark 6.

The inequality (25) in Corollary 1 can be obtained by the differential inequality (8) in Lemma 11, where $h\left(t\right):=h_1\left(t\right)$, $\gamma :=-\omega$, and $g\left(t\right):=\kappa$. Then,

$$\begin{array}{cc}\hfill h_1\left(t\right)& \stackrel{\left(9\right)}{\le }{h}_1\left(t_0\right)E_{\alpha }(-\omega {(t-t_0)}^{\alpha })-\frac{\kappa }{-\omega }\left(1-E_{\alpha }(-\omega {(t-t_0)}^{\alpha })\right)\hfill \\ \hfill & \stackrel{\mathrm{Lem}.1\left(i\right)}{\le }{h}_1\left(t_0\right)+\frac{\kappa }{\omega }\left(1-E_{\alpha }(-\omega {(t-t_0)}^{\alpha })\right),t\ge t_0.\hfill \end{array}$$

(27)

Consequently, the inequality (27) is consistent with (26).

Theorem 2.

Following Assumption 1 and applying the adaptive controller (13), system (10) is quasi-synchronized with system (11) if

$$W_1\left(t_0\right)+W_2\left(t_0\right)+\frac{\kappa }{\omega }>0,$$

(28)

where $W_1\left(t\right)={\displaystyle \sum _{i=1}^m}|r_i\left(t\right)|$, $W_2\left(t\right)={\displaystyle \sum _{i=1}^m}\frac{{({\sigma }_i\left(t\right)-{\sigma }^{\ast })}^2}{2{\rho }_i}$, $\kappa =-m\eta$,

$$\omega =\underset{1\le i\le m}{min}\left\{c_i-{\displaystyle \sum _{j=1}^m}|w_{ji}|l_i+{\sigma }^{\ast }\right\},$$

(29)

and ${\sigma }^{\ast },\xi$ are two real numbers satisfying

$${\sigma }^{\ast }>\underset{1\le i\le m}{max}\left\{-c_i+{\displaystyle \sum _{j=1}^m}|w_{ji}|l_i\right\},$$

(30)

$$\xi >\underset{1\le i\le m}{max}\left\{{\displaystyle \sum _{j=1}^m}|w_{ji}^{\iota }|l_i\right\}.$$

(31)

Proof. 

We construct a Lyapunov function $W\left(t\right):=W_1\left(t\right)+W_2\left(t\right).$ Then,

$$\begin{array}{cc}\hfill {}_{t_0}^c{D}_t^{\alpha }W\left(t\right)& ={}_{t_0}^c{D}_t^{\alpha }\left({\displaystyle \sum _{i=1}^m}|r_i\left(t\right)|+{\displaystyle \sum _{i=1}^m}\frac{{({\sigma }_i\left(t\right)-{\sigma }^{\ast })}^2}{2{\rho }_i}\right)\hfill \\ \hfill & \stackrel{\mathrm{Lem}.6}{\le }{\displaystyle \sum _{i=1}^m}\mathrm{sign}{\left(r_i\left(t\right)\right)}_{t_0}^c{D}_t^{\alpha }{r}_i\left(t\right)+{\displaystyle \sum _{i=1}^m}\frac{({\sigma }_i\left(t\right)-{\sigma }^{\ast })}{{\rho }_i}{}_{t_0}^c{D}_t^{\alpha }{\sigma }_i\left(t\right)\hfill \\ \hfill & \underset{\left(13\right)}{\stackrel{\left(12\right)}{=}}{\displaystyle \sum _{i=1}^m}\mathrm{sign}\left(r_i\left(t\right)\right)\{-c_i{r}_i\left(t\right)+{\displaystyle \sum _{j=1}^m}{w}_{ij}\left(f_j\left(p_j\left(t\right)\right)-f_j\left(q_j\left(t\right)\right)\right)\hfill \\ \hfill & +{\displaystyle \sum _{j=1}^m}{w}_{ij}^{\iota }\left(f_j\left(p_j(t-\iota )\right)-f_j\left(q_j(t-\iota )\right)\right)-{\sigma }_i\left(t\right)r_i\left(t\right)\hfill \\ \hfill & -\xi \frac{r_i\left(t\right)}{|r_i\left(t\right)|}|r_i(t-\iota )|-\eta \frac{r_i\left(t\right)}{|r_i\left(t\right)|}\}+{\displaystyle \sum _{i=1}^m}({\sigma }_i\left(t\right)-{\sigma }^{\ast })|r_i\left(t\right)|\hfill \\ \hfill & \le {\displaystyle \sum _{i=1}^m}\{-c_i|r_i\left(t\right)|+{\displaystyle \sum _{j=1}^m}|w_{ij}|l_j|r_j\left(t\right)|+{\displaystyle \sum _{j=1}^m}|w_{ij}^{\iota }|l_j|r_j(t-\iota )|\hfill \\ \hfill & -{\sigma }_i\left(t\right)|r_i\left(t\right)|-\xi |r_i(t-\iota )|-\eta \}+{\displaystyle \sum _{i=1}^m}({\sigma }_i\left(t\right)-{\sigma }^{\ast })|r_i\left(t\right)|\hfill \\ \hfill & ={\displaystyle \sum _{i=1}^m}\left(-c_i+{\displaystyle \sum _{j=1}^m}|w_{ji}|l_i-{\sigma }^{\ast }\right)|r_i\left(t\right)|-m\eta +{\displaystyle \sum _{i=1}^m}\left(-\xi +{\displaystyle \sum _{j=1}^m}|w_{ji}^{\iota }|l_i\right)|r_i(t-\iota )|.\hfill \end{array}$$

Also by (29)–(31), and $\kappa =-m\eta$, we have

$${}_{t_0}^c{D}_t^{\alpha }W\left(t\right)={}_{t_0}^c{D}_t^{\alpha }(W_1\left(t\right)+W_2\left(t\right))\le -\omega W_1\left(t\right)+\kappa .$$

Furthermore, applying Theorem 1,

$$\begin{array}{c}\hfill \parallel r\left(t\right)\parallel =W_1\left(t\right)\stackrel{\left(16\right)}{\le }{W}_1\left(t_0\right)+W_2\left(t_0\right)+\frac{\kappa }{\omega }\left(1-E_{\alpha }(-\omega {(t-t_0)}^{\alpha })\right).\end{array}$$

Then, by (28) and ${\displaystyle \underset{t\to \infty }{lim}}{E}_{\mu }(-\omega {(t-t_0)}^{\mu })=0$, there exists a small error bound

$$ϵ:=W_1\left(t_0\right)+W_2\left(t_0\right)+\frac{\kappa }{\omega }>0$$

satisfying

$$\parallel r\left(t\right)\parallel \le ϵ,t\to \infty ,$$

which shows that system (10) is quasi-synchronized with system (11) with error bound $W_1\left(t_0\right)+W_2\left(t_0\right)+\frac{\kappa }{\omega }$. □

Remark 7.

Quasi-synchronization techniques, as utilized in Theorem 2, find applications in various domains. For instance, they can be employed in traffic networks to optimize traffic flow and alleviate congestion. By achieving partial synchronization among traffic signals or regulating the behavior of individual vehicles, overall traffic efficiency can be enhanced. Furthermore, these techniques can also be utilized in financial networks to analyze and forecast market behaviors. By examining synchronized patterns or deviations in the interconnections between financial entities, it becomes feasible to identify systemic risks and make well-informed investment choices.

4. Connections between the Mathematical Treatment and the Numerical Simulation

In this section, we present a modified version of the Adams–Bashforth–Moulton algorithm [52] specifically designed to solve fractional-order differential equations with time delay. This modification serves as a theoretical basis for the subsequent numerical simulation in Section 5.

Consider the following system:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{}_{t_0}^c{D}_t^{\alpha }h\left(t\right)=\Psi (t,h\left(t\right),h(t-\iota )),t\in [t_0,t_0+S],\alpha \in (0,1),\hfill \\ h\left(t\right)=z\left(t\right),t\in [t_0-\iota ,t_0].\hfill \end{array}\right.\end{array}$$

(32)

Fix a uniform grid as follows:

$$\left\{t_0-\tilde{N}d,t_0-(\tilde{N}-1)d,\cdots ,t_0-d,t_0,t_0+d,\cdots ,t_0+\widehat{N}d\right\},$$

where $\tilde{N}$ is a fixed integer, $d=\frac{\iota }{\tilde{N}}$, and $\widehat{N}=\left[\frac{S}{d}\right]$ is also an integer. For each integer k satisfying $-\tilde{N}\le k\le \widehat{N}$, let $t_k=t_0+kd$. Then, for $-\tilde{N}\le k\le 0$, $h_d\left(t_k\right)$ is the approximation to $z\left(t_k\right)$. In addition, $h_d(t_k-\iota )=h_d(t_0+kd-\tilde{N}d)=h_d\left(t_{k-\tilde{N}}\right)$ holds for $0\le k\le \widehat{N}$.

Suppose that the approximation $h_d\left(t_k\right)\approx h\left(t_k\right)$ holds for $-\tilde{N}\le k\le \widehat{N}$. Then, by Definition 3, (3) and (32), we have

$$h\left(t_{k+1}\right)=z\left(t_0\right)+\frac{1}{\Gamma \left(\alpha \right)}{\int }_{t_0}^{t_{k+1}}{(t_{k+1}-\zeta )}^{\alpha -1}\Psi (\zeta ,h\left(\zeta \right),h(\zeta -\iota ))\mathrm{d}\zeta .$$

Furthermore, we utilize the product trapezoidal quadrature method and obtain the corrector formula as follows:

$$\begin{array}{cc}{h}_d\left(t_{k+1}\right)\hfill & =z\left(t_0\right)+\frac{d^{\alpha }}{\Gamma (\alpha +2)}\Psi (t_{k+1},h_d\left(t_{k+1}\right),h_d(t_{k+1}-\iota ))\hfill \\ \hfill & +\frac{d^{\alpha }}{\Gamma (\alpha +2)}{\displaystyle \sum _{s=0}^k}{e}_{s,k+1}\Psi (t_s,h_d\left(t_s\right),h_d(t_s-\iota ))\hfill \\ \hfill & =z\left(t_0\right)+\frac{d^{\alpha }}{\Gamma (\alpha +2)}\Psi (t_{k+1},h_d\left(t_{k+1}\right),h_d\left(t_{k+1-\tilde{N}}\right))\hfill \\ \hfill & +\frac{d^{\alpha }}{\Gamma (\alpha +2)}{\displaystyle \sum _{s=0}^k}{e}_{s,k+1}\Psi (t_s,h_d\left(t_s\right),h_d\left(t_{s-\tilde{N}}\right)),\hfill \end{array}$$

(33)

where

$$\begin{array}{c}\hfill e_{s,k+1}=\left\{\begin{array}{c}{k}^{\alpha +1}-(k-\alpha ){(k+1)}^{\alpha },\mathrm{if}s=0,\hfill \\ {(k-s+2)}^{\alpha +1}+{(k-s)}^{\alpha +1}-2{(k-s+1)}^{\alpha +1},\mathrm{if}1\le s\le k,\hfill \\ 1,\mathrm{if}s=k+1.\hfill \end{array}\right.\end{array}$$

Because the Equation (33) contains the unknown term $h_d\left(t_{k+1}\right)$ on both sides and involves the nonlinear function $\Psi$, it is not possible to find an explicit solution for $h_d\left(t_{k+1}\right)$. To address this issue, we introduce a preliminary approximation called a predictor, denoted as $h_d^p\left(t_{k+1}\right)$. We then modify (33) by substituting $h_d^p\left(t_{k+1}\right)$ for $h_d\left(t_{k+1}\right)$ on the right-hand side, resulting in the following redefined equation:

$$\begin{array}{cc}\hfill h_d\left(t_{k+1}\right)=& z\left(t_0\right)+\frac{d^{\alpha }}{\Gamma (\alpha +2)}\Psi (t_{k+1},h_d^p\left(t_{k+1}\right),h_d\left(t_{k+1-\tilde{N}}\right))\hfill \\ \hfill & +\frac{d^{\alpha }}{\Gamma (\alpha +2)}{\displaystyle \sum _{s=0}^k}{e}_{s,k+1}\Psi (t_s,h_d\left(t_s\right),h_d\left(t_{s-\tilde{N}}\right)).\hfill \end{array}$$

(34)

In addition, in order to compute the predictor term, we apply the product rectangle rule in (34). Then, we have

$$\begin{array}{cc}\hfill h_d^p\left(t_{k+1}\right)& =z\left(t_0\right)+\frac{1}{\Gamma \left(\alpha \right)}{\displaystyle \sum _{s=0}^k}{f}_{s,k+1}\Psi (t_s,h_d\left(t_s\right),h_d(t_s-\iota ))\hfill \\ \hfill & =z\left(t_0\right)+\frac{1}{\Gamma \left(\alpha \right)}{\displaystyle \sum _{s=0}^k}{f}_{s,k+1}\Psi (t_s,h_d\left(t_s\right),h_d\left(t_{s-\tilde{N}}\right)),\hfill \end{array}$$

where $f_{s,k+1}=\frac{d^{\alpha }}{\alpha }({(k+1-s)}^{\alpha }-{(k-s)}^{\alpha }).$

In this method, the error can be expressed as

$$\underset{-\tilde{N}\le k\le \widehat{N}}{max}|h\left(t_k\right)-h_d\left(t_k\right)|=O\left(d^m\right),$$

where $m=min\{2,1+\alpha \}.$

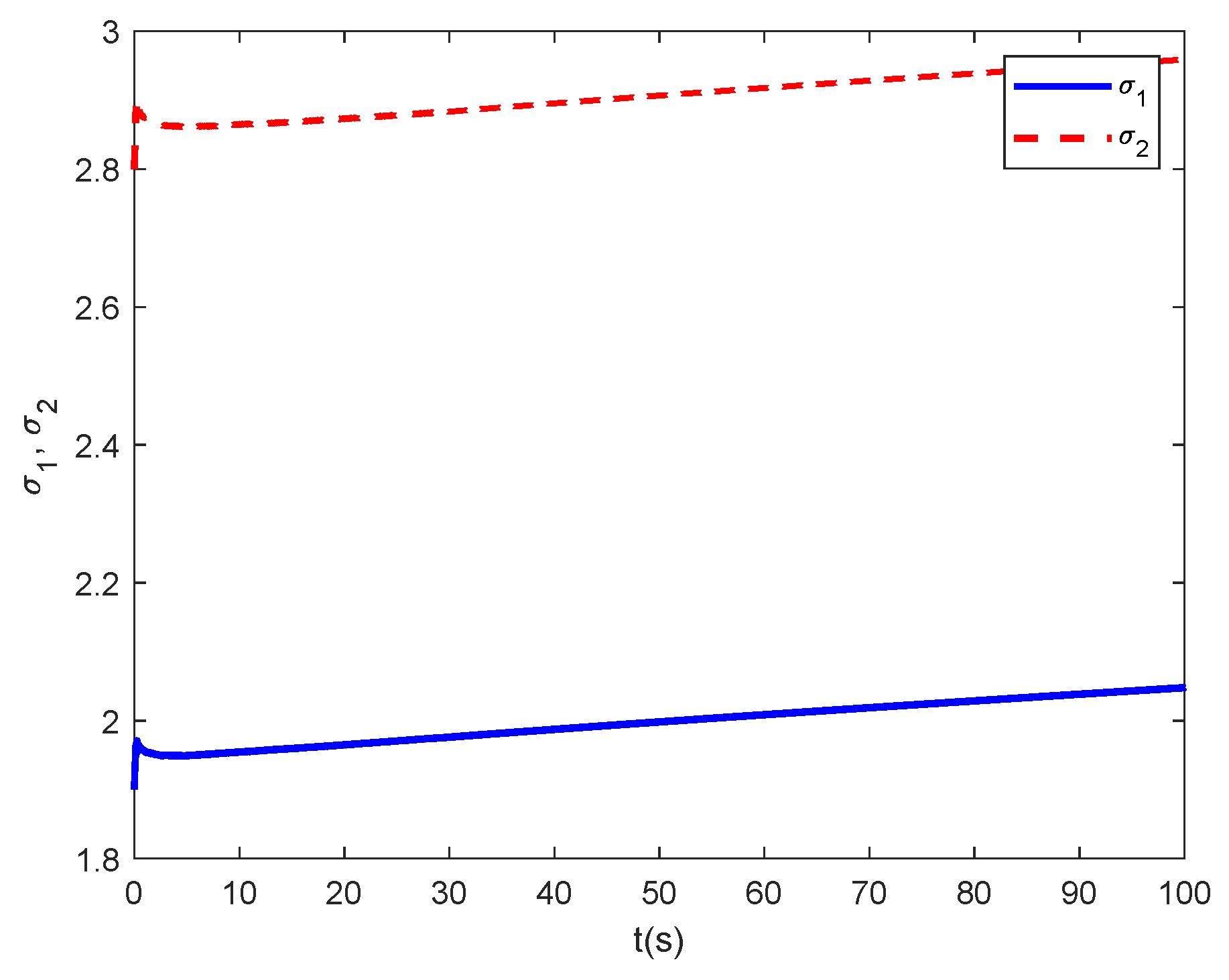
5. Numerical Simulation

To demonstrate the practical applicability of the key results, we provide a numerical illustration as follows.

Example 1.

Suppose that the parameters in the systems (10) and (11) are given: $\alpha =0.8$, $f_j\left(x\right)=tanh\left(x\right)$, $c_1=0.3$, $c_2=0.2$, $\iota =0.3$, $W={\left(w_{ij}\right)}_{2\times 2}=\left(\begin{array}{c}-1.40.3\\ 0.9-1.5\end{array}\right)$, $W^{\iota }={\left(w_{ij}^{\iota }\right)}_{2\times 2}=\left(\begin{array}{c}-2.6-0.2\\ -0.4-1.6\end{array}\right)$, $I=\left(\begin{array}{c}0\\ 0\end{array}\right)$, $\phi \left(t\right)=\left(\begin{array}{c}0.4\\ -0.3\end{array}\right)$, $\varphi \left(t\right)=\left(\begin{array}{c}-0.2\\ 0.4\end{array}\right)$, $\sigma \left(t_0\right)=\left(\begin{array}{c}1.9\\ 2.8\end{array}\right)$.

It is evident that Assumption 1 holds for $l_1=l_2=1$. Then, we let $t_0=0$, ${\sigma }^{\ast }=2.1$, $\xi =3.1$, $\eta =0.075$, ${\rho }_i=1$, $i=1,2$ to demonstrate the correctness of Theorem 2. By performing straightforward calculations, we obtain $\omega =0.1$, $\kappa =-0.15$, $W_1\left(t_0\right)=1.3$, $W_2\left(t_0\right)=0.2650$, and $ϵ=W_1\left(t_0\right)+W_2\left(t_0\right)+\frac{\kappa }{\omega }=0.065$.

The time-varying feedback strengths ${\sigma }_i\left(t\right)$ are depicted in Figure 1. The evolution of synchronization error is presented in Figure 2. Furthermore, Figure 3 displays the magnitude of the synchronization error, which serves as further validation for the effectiveness of Theorem 2.

6. Conclusions

The quasi-synchronization for a class of fractional-order delayed neural networks has been studied in this paper. To obtain the quasi-synchronization criterion, the properties of the Laplace transform, the Caputo derivative, and the Mittag–Leffler function have been employed. In addition, a new fractional-order differential inequality has been constructed. Finally, a numerical example has been provided to demonstrate the validity of the proposed results. It is worth noting that when simulating continuous-time neural networks on a computer, it is necessary to discretize them to generate corresponding discrete-time networks. However, this discretization process may not fully preserve the dynamics exhibited by the original continuous networks. Therefore, future research will focus on discrete-time fractional order neural networks based on q-exponential and q-calculus.