Exploring Integral ϝ-Contractions with Applications to Integral Equations and Fractional BVPs

Abstract

In this article, two types of contractive conditions are introduced, namely extended integral $\mathsf{Ϝ}$-contraction and $(\varkappa ,\Omega$-$\mathsf{Ϝ})$-contraction. For the case of two mappings and their coincidence point theorems, a variant of $(\varkappa ,\Omega$-$\mathsf{Ϝ})$-contraction has been introduced, which is called $(\varkappa ,{\Gamma }_{1,2},\Omega$-$\mathsf{Ϝ})$-contraction. In the end, the applications of an extended integral $\mathsf{Ϝ}$-contraction and $(\varkappa ,\Omega$-$\mathsf{Ϝ})$-contraction are given by providing an existence result in the solution of a fractional order multi-point boundary value problem involving the Riemann–Liouville fractional derivative. An interesting existence result for the solution of the nonlinear Fredholm integral equation of the second kind using the $(\varkappa ,{\Gamma }_{1,2},\Omega$-$\mathsf{Ϝ})$-contraction has been proven. Herein, an example is established that explains how the Picard–Jungck sequence converges to the solution of the nonlinear integral equation. Examples are given for almost all the main results and some graphs are plotted where required.

1. Introduction

An integral-type contractive inequality is an inequality that relates the integral of a function over a certain domain to the value of the function at some point within that domain. Integral-type contractive inequalities are important in the analysis of various mathematical problems, including differential equations, dynamical systems, and optimization. They provide a powerful tool for proving the existence, uniqueness, and stability of solutions to these problems. Integral-type contractive inequality was first introduced and related fixed-point results were proved by Branciari [1] in 2002. Ozturk and Turkoglu [2] established remarkable results using partial metric space, satisfying integral-type contractive conditions. In 1993, Czerwik [3] uncovered the novel concept of b-metric spaces and proved the fixed-point theorem of contractive-type mappings. The b-metric space is a generalization of metric spaces that weakens one of the axioms of a metric space, namely the triangle inequality, by replacing it with a weaker condition called the b-metric inequality. Therefore, b-metric spaces are important in mathematics as they provide a more flexible framework for studying distance-based structures that do not necessarily satisfy the triangle inequality. This allows the study of a wide range of phenomena that cannot captured by classical metric spaces, including certain types of fractals, non-Euclidean geometries, and various types of networks and graphs. b-metric spaces are especially used in the study of fixed-point theory, and they provide a generalization of the Banach fixed-point theorem to non-metric spaces.

In 1998, Czerwik [4] proved the fixed-point result for set-valued mappings in the context of b-metric space. Suzuki [5] proved basic inequality related to b-metric and proved important fixed-point theorems by using the basic inequality in [5]. Neetu [6], proved the fixed-point result of contractive functions in cone b-metric spaces without a normality condition. Kanwal et al. [7], introduced a new type of contractive condition for contractive mappings to prove the fixed-point theorems in the settings of b-metric space. More articles related to this study are in [8,9,10,11,12,13,14,15] and the references therein.

In 2012, Wardowksi [16] gave the idea of $\mathsf{Ϝ}$-contraction and proved new remarkable results. Parvaneh et al. [17] introduced $\left(\alpha \text{-}\beta \right)$-$FG$-contractions and generalized the result of the Wardowski fixed-point theorem in ordered b-metric spaces. In 2015, Sarwar et al. [18] proved the results for weakly compatible mappings which satisfy integral-type contractions. Some other important results related to $\mathsf{Ϝ}$-contraction are in [16,19,20]. Cosentino and Vetro [21] in 2014 derived some new results for the fixed points of mapping satisfying Hardy Roger-type $\mathsf{Ϝ}$-contractions. Some other results related to integral $\mathsf{Ϝ}$-integral contraction are in [22,23]. In 2020, Carić et al. [24] presented simpler proofs for recent significant results in generalized $\mathsf{Ϝ}$-Suzuki-contractions in b-metric spaces. Hammad and Sen [25] presented the generalized almost $(s,q)$-Jaggi $\mathsf{Ϝ}$-contraction in b-metric-like spaces, discussing its properties and exploring fixed-point results. The article also demonstrates applications in solving electric circuit equations and second-order differential equations. In 2021, Carić et al. [26] introduced $\mathsf{Ϝ}$-integral contraction and present new results of fixed points and common fixed points. Huang et al. [27] introduced and studied the generalized $\mathsf{Ϝ}$-contractions in b-metric-like spaces, along with the establishment of fixed-point theorems for these contractions. This article also explores the application of these theorems in finding the existence and uniqueness of solutions to integral equations in the context of b-metric-like spaces.

This article basically combine three ideas, namely the Banach contraction principle; F-contraction (in which F satisfies three conditions, defined below) given by Wardowksi [16] in 2002; and Integral contraction given by Branciari [1] in 2002. It has already been explored to some extent by Carić et al. [26], namely integral $\mathsf{Ϝ}$-contraction. Here, we extend the integral $\mathsf{Ϝ}$-contraction by generalizing the contractive condition and only using the first conditions of F-contraction by Wardowksi [16] and naming it extended integral $\mathsf{Ϝ}$-contraction. Furthermore, we also generalized the integral contraction with the class of functions denoted by $\Omega .$ We further generalize the extended integral $\mathsf{Ϝ}$-contraction using this class $\Omega ,$ and named the resulting contraction $(\varkappa ,\Gamma ,\Omega$-$\mathsf{Ϝ})$-contraction, but space remains the metric space. In this way, we explore $\mathsf{Ϝ}$-contraction and the integral contraction. In the next paragraph, a clearer picture of our work has been explained.

The article introduces new types of the contractions that are more general than the existing ones. In Section 2, extended integral $\mathsf{Ϝ}$-contractions are introduced. In Section 3, the notion of $(\varkappa ,\Gamma ,\Omega$-$\mathsf{Ϝ})$-contraction has been introduced. Furthermore, for two mappings and their coincidence/common fixed-point results, and a variant of $(\varkappa ,\Gamma ,\Omega$-$\mathsf{Ϝ})$-contraction is introduced called $(\varkappa ,{\Gamma }_{1,2},\Omega$-$\mathsf{Ϝ})$-contraction. The whole Section 4 is devoted to the applications of the contractions. These applications include existence results for a given nonlinear fractional order boundary value problem. This has been performed using both extended integral $\mathsf{Ϝ}$-contraction and $(\varkappa ,\Gamma ,\Omega$-$\mathsf{Ϝ})$-contraction. An existence result for a nonlinear integral equation has also been proved using $(\varkappa ,{\Gamma }_{1,2},\Omega$-$\mathsf{Ϝ})$-contraction. This is well explained in a given example using the Picard–Jungck sequence, which converges to the solution of the integral equation. Some nontrivial examples at the end of all main theorems are given, and the graphs are plotted if required.

In this article, for the main results, the following preliminaries are required.

Definition 1 

([17]). Let S be a non-empty set. A mapping $d:S\times S\to \left[0,\infty \right)$ satisfying

• (B${}_1)$. $d(b_1,b_2)=0$ ⇔ $b_1=b_2$ for all $b_1,b_2\in S$,
• (B${}_2)$. $d(b_1,b_2)=d(b_2,b_1)$for all $b_1,b_2\in S$,
• (B${}_3)$. for all $b_1,b_2,b_3\in S$ and $k\ge 1$

$$d(b_1,b_2)\le k\left\{d(b_1,b_3)+d(b_3,b_2)\right\},\left(b\text{-}\mathit{metric}\mathit{inequality}\right)$$

is called the b-metric and the pair $(S,d)$ is called a b-metric space with a constant k. A b-metric space is a metric space provided that $k=1$.

Definition 2 

([26]). Suppose that ${\Gamma }_1,{\Gamma }_2:S⟶S$ are two mappings, a point $b\in S$ is called a point of coincidence of ${\Gamma }_1$ and ${\Gamma }_2$ if there exists an element $a\in S$ such that $b={\Gamma }_{1}a={\Gamma }_{2}a$.

Definition 3 

([26]). A pair of maps ${\Gamma }_1,{\Gamma }_2:S⟶S$ is said to be compatible in a metric space $(S,d)$ if

$$\underset{n⟶+\infty }{lim}d\left({\Gamma }_1{\Gamma }_2{a}_{{}_n},{\Gamma }_2{\Gamma }_1{a}_{{}_n}\right)=0$$

for every sequence $\left\{a_n\right\}\subseteq S$ such that

$$\underset{n⟶+\infty }{lim}{\Gamma }_1{a}_{{}_n}=\underset{n⟶+\infty }{lim}{\Gamma }_2{a}_{{}_n}=\ell$$

for some $\ell \in S$.

Definition 4 

([26]). A pair of mappings ${\Gamma }_1,{\Gamma }_2:S⟶S$ is said to be weakly compatible if ${\Gamma }_{1}a={\Gamma }_{2}a$ implies ${\Gamma }_1{\Gamma }_{2}a={\Gamma }_2{\Gamma }_{1}a$, for all $a\in S$.

Proposition 1 

([26]). If ${\Gamma }_1,{\Gamma }_2:S⟶S$ are weakly compatible mappings and have a unique point of coincidence $b={\Gamma }_{1}a={\Gamma }_{2}a$, then b is a unique common fixed point of ${\Gamma }_1$ and ${\Gamma }_2$.

Definition 5 

([26]). Suppose a pair of mappings ${\Gamma }_1,{\Gamma }_2:S⟶S$. A sequence $\left\{a_n\right\}$ in $S$is said to be a Picard–Jungck sequence of the pair $({\Gamma }_1,{\Gamma }_2)$ if

$${\Gamma }_1{a}_{n+1}={\Gamma }_2{a}_n=b_n,\forall n\in \mathbb{N}\cup \left\{0\right\}.$$

Lemma 1 

([23]). Assume a sequence ${\left(a_n\right)}_{n\in \mathbb{N}}$ in a metric space $(S,d)$ which satisfies

$$\underset{n⟶+\infty }{lim}d(a_n,a_{n+1})=0$$

and a sequence ${\left(a_n\right)}_{n\in \mathbb{N}}$ is not Cauchy. Then, there exist the $\epsilon >0$ and sequences of positive integers ($n_{\hslash })$ and $\left(m_{\hslash }\right)$ where $n_{\hslash }>m_{\hslash }>\hslash$ such that the sequences

$$\begin{array}{cc}\hfill & \left\{d(a_{m_{{}_{{}_{\hslash }}}},a_{n_{{}_{\hslash }}})\right\},\left\{d(a_{m_{{}_{{}_{\hslash }}}},a_{n_{{}_{\hslash }}+1})\right\},\left\{d(a_{m_{{}_{{}_{\hslash }}}-1},a_{n_{{}_{\hslash }}})\right\},\hfill \\ \hfill & \left\{d(a_{m_{{}_{{}_{\hslash }}}-1},a_{n_{{}_{\hslash }}+1})\right\},\left\{d(a_{m_{{}_{{}_{\hslash }}}+1},a_{n_{{}_{\hslash }}+1})\right\}⟶\epsilon \hfill \end{array}$$

when $\hslash ⟶+\infty$.

Let $\Psi$ be the class of all Lebesgue integrable, summable (finite integral) functions $\xi :[0,+\infty )⟶[0,+\infty )$ and $\underset{0}{\stackrel{\epsilon }{\int }}\xi \left(\tau \right)d\tau >0$, for all$\epsilon >0$.

In [12], Mocanu et al. proved the following useful lemmas.

Lemma 2 

([12]). Let ${\left({\ell }_n\right)}_{n\in \mathbb{N}}$ be a non-negative sequence of real numbers, then ${\displaystyle \underset{n⟶+\infty }{lim}}\underset{0}{\stackrel{{\ell }_n}{\int }}\xi \left(\tau \right)d\tau =0$ if and only if ${\displaystyle \underset{n⟶+\infty }{lim}}{\ell }_n=0$.

Lemma 3 

([12]). Let ${\left({\ell }_n\right)}_{n\in \mathbb{N}}$ be a non-negative sequence of real numbers with ${\displaystyle \underset{n⟶+\infty }{lim}}{\ell }_n=\ell$. Then ${\displaystyle \underset{n⟶+\infty }{lim}}\underset{0}{\stackrel{{\ell }_n}{\int }}\xi \left(\tau \right)d\tau =\underset{0}{\stackrel{\ell }{\int }}\xi \left(\tau \right)d\tau .$

In 2002, Branciari [1] proved the following fixed-point theorem for the self-mapping satisfying the integral type contractive condition.

Theorem 1 

([1]). Let $(S,d)$ be a complete metric space and $\Gamma :S\to S$ be a mapping such that

$$\stackrel{d\left(\Gamma a,\Gamma b\right)}{\underset{0}{{\displaystyle \int }}}\xi \left(\tau \right)d\tau \le \zeta \stackrel{d\left(a,b\right)}{\underset{0}{{\displaystyle \int }}}\xi \left(\tau \right)d\tau ,$$

for all $a,b\in S$, $\zeta \in \left(0,1\right)$, $\xi \in \Psi$ and for each $\epsilon >0$, $\stackrel{\epsilon }{\underset{0}{{\displaystyle \int }}}\xi \left(\tau \right)d\tau >0$. Then, Γ has a unique fixed-point $c\in S$ such that ${\displaystyle \underset{n⟶+\infty }{lim}}{\Gamma }^{n}a=c$ for all $a\in S$.

In 2012, Wardowski [16] gave the idea of a new contraction called an $\mathsf{Ϝ}$-contraction as follows.

Definition 6 

([16]). Let F be a set of mappings $\mathsf{Ϝ}:[0,\infty )\to \mathbb{R}$ satisfying

• (F${}_1)$. Ϝ is strictly increasing,
• (F${}_2)$. If ${\left\{t_n\right\}}_{{}_{n\in \mathbb{N}}}$ in $[0,\infty )$, then ${\displaystyle \underset{n\to +\infty }{lim}}{t}_{{}_n}=0\iff {\displaystyle \underset{n⟶+\infty }{lim}}\mathsf{Ϝ}\left(t_n\right)=-\infty$,
• (F${}_3)$. There exist some $\varrho \in (0,1)$ such that ${\displaystyle \underset{t⟶0^{+}}{lim}}{t}^{{}^{\varrho }}\mathsf{Ϝ}\left(t\right)=0$.
• Let $\left(S,d\right)$ be a metric space and mapping $\Gamma :S⟶S$ is called Ϝ-contraction if there exists $\varrho >0$. Where $\mathsf{Ϝ}\in F$ and $d(\Gamma a,\Gamma b)>0$implies

  $$\varrho +\mathsf{Ϝ}\left(d(\Gamma a,\Gamma b)\right)\le \mathsf{Ϝ}\left(d(a,b)\right),\forall a,b\in S.$$

Now and onwards, assume that $F^{*}$ is the class of all $\mathsf{Ϝ}\in F$, which only follows $\left(F_1\right)$, i.e., it is the collection of all strictly increasing mappings.

Remark 1 

([23]). Denote ${\displaystyle \underset{r⟶s^{-}}{lim}}\mathsf{Ϝ}\left(r\right)=\mathsf{Ϝ}(s-0)$ and ${\displaystyle \underset{r⟶s^{+}}{lim}}\mathsf{Ϝ}\left(r\right)=\mathsf{Ϝ}(s+0)$, also any $\mathsf{Ϝ}\in F^{*}$ has at most countable point of discontinuities.

In 2012, Wardowski [16] proved the following fixed-point result using the notion of $\mathsf{Ϝ}$-contraction.

Theorem 2 

([16]). Suppose that $(S,d)$ is a complete metric space and a mapping $\Gamma :S⟶S$ is a Ϝ-contraction with a property. Assume there exists $\varrho >0$ such that

$$\varrho +\mathsf{Ϝ}\left(d\right(\Gamma a,\Gamma b\left)\right)\le \mathsf{Ϝ}\left(d\right(a,b\left)\right)$$

for all $a,b\in S$ with $\Gamma a\ne \Gamma b.$ Then, there exists a unique fixed-point $c$of $\Gamma$and sequence $\left({\Gamma }^{n}a\right)$converges to $c,\forall n\in \mathbb{N}$.

In 2021, Carić et al. [26] introduced integral $\mathsf{Ϝ}$-contraction, and using (F${}_1)$ proved the fixed-point theorem for the self-mapping, satisfying the integral $\mathsf{Ϝ}$-contraction as follows.

Definition 7 

([26]). Let $(S,d)$ be metric space and $\mathsf{Ϝ}\in F^{*}$. A mapping $\Gamma :S\to S$ is called integral Ϝ-contraction on $(S,d)$ if $\varrho >0 exists,$ such that

$$\varrho +\mathsf{Ϝ}\left(\underset{0}{\stackrel{d(\Gamma a,\Gamma b)}{\int }}\xi \left(\tau \right)d\tau \right)\le \mathsf{Ϝ}\left(\underset{0}{\stackrel{d(a,b)}{\int }}\xi \left(\tau \right)d\tau \right),$$

for all $a,b\in S,$ with $d(\Gamma a,\Gamma b)>0$ and $\xi \in \Psi$.

Theorem 3 

([26]). Let $(S,d)$ be a complete metric space and $\Gamma :S\to S$ be an integral F-contraction. Then, there exists a unique $a\in S$ such that $\Gamma a=a$.

To generalize the above notions, we need the following class of functions.

Let $\Lambda$be a class of mapping $\varrho :(0,+\infty )⟶(0,+\infty )$ satisfying

$$\underset{c⟶{\theta }^{+}}{lim}inf\varrho \left(c\right)>0,\forall \theta >0.$$

Using this class $\Lambda ,$ the following generalized definition was given in [26].

Definition 8 

([26]). Let $(S,d)$ be a metric space and mappings ${\Gamma }_1,{\Gamma }_2:S⟶S$. A mapping ${\Gamma }_1$ is a $\left(\varrho ,\xi ,\mathsf{Ϝ},{\Gamma }_2\right)$-integral contraction if a mapping $\varrho \in \Lambda$ exists. Let $\xi \in \Psi$ be a function $\mathsf{Ϝ}\in F^{*}$ such that for all $a,b\in S$ with ${\Gamma }_{2}a\ne {\Gamma }_{2}b$ and ${\Gamma }_{1}a\ne {\Gamma }_{1}b$ one has

$$\varrho \left(\underset{0}{\stackrel{d({\Gamma }_{2}a,{\Gamma }_{2}b)}{\int }}\xi \left(\tau \right)d\tau \right)+\mathsf{Ϝ}\left(\underset{0}{\stackrel{d({\Gamma }_{1}a,{\Gamma }_{1}b)}{\int }}\xi \left(\tau \right)d\tau \right)\le \mathsf{Ϝ}\left(\underset{0}{\stackrel{d({\Gamma }_{2}a,{\Gamma }_{2}b)}{\int }}\xi \left(\tau \right)d\tau \right).$$

Theorem 4 

([26]). Let $(S,d)$ be a complete metric space and mappings ${\Gamma }_1,{\Gamma }_2:S⟶S$. A mapping ${\Gamma }_1$ is a $\left(\varrho ,\xi ,\mathsf{Ϝ},{\Gamma }_2\right)$-integral contraction. Assume that there exists a Picard–Jungck sequence ${\left(a_n\right)}_{{}_{n\in \mathbb{Z}/{\mathbb{Z}}^{-}}}$of $({\Gamma }_1,{\Gamma }_2)$and following condition hold,

• (A${}_1)$$({\Gamma }_{2}S,d)$ is complete,
• (A${}_2)$${\Gamma }_2$ is a continuous, and $({\Gamma }_1,{\Gamma }_2)$ is compatible.
• Then, ${\Gamma }_1$ and ${\Gamma }_2$ have a unique point of coincidence.

2. Extended Integral Ϝ-Contraction

In this section, we introduce the concepts of extended integral $\mathsf{Ϝ}$-contraction, as a generalization of extended integral contraction, and extended $\mathsf{Ϝ}$-contraction. The first result will be about the existence of fixed point of extended integral $\mathsf{Ϝ}$-contraction, in the setting of b-metric spaces. To achieve our goal for defining extended integral $\mathsf{Ϝ}$-contraction, first we need to define the two new following contractions.

Definition 9 

(Extended $\mathsf{Ϝ}$-contraction). Let $\left(S,d\right)$ be a b-metric space and mapping $\Gamma :S⟶S$ is called extended Ϝ-contraction if $\varrho \in \Lambda$ and $\mathsf{Ϝ}\in F^{*}$ exist, if $d(\Gamma a,\Gamma b)>0$implies

$$\varrho \left(M\left(a,b\right)\right)+\mathsf{Ϝ}\left(d(\Gamma a,\Gamma b)\right)\le \mathsf{Ϝ}\left(M(a,b)\right),$$

(1)

for all $a,b\in S$, where

$$M(a,b)=\eta max\left\{d(a,b),d(a,\Gamma a),d(b,\Gamma b),\left(\frac{d(a,\Gamma b)+d(b,\Gamma a)}{k\left[1+d(a,\Gamma a)+d(b,\Gamma b)\right]}\right)d(a,b)\right\},$$

for some $\eta \in \left(0,\frac{1}{k}\right)$ and $k\ge 1$.

Definition 10 

(Extended integral contraction). Let $\left(S,d\right)$ be a b-metric space and mapping $\Gamma :S⟶S$ is called extended integral type contraction if Γ satisfies

$$\underset{0}{\stackrel{d(\Gamma a,\Gamma b)}{\int }}\xi \left(\tau \right)d\tau \le \zeta \underset{0}{\stackrel{M(a,b)}{\int }}\xi \left(\tau \right)d\tau ,$$

(2)

for all $a,b\in S$, $\zeta \in \left(0,1\right)$, $\xi \in \Psi$, where

$$M(a,b)=\eta max\left\{d(a,b),d(a,\Gamma a),d(b,\Gamma b),\left(\frac{d(a,\Gamma b)+d(b,\Gamma a)}{k\left[1+d(a,\Gamma a)+d(b,\Gamma b)\right]}\right)d(a,b)\right\},$$

(3)

for some $\eta \in \left(0,\frac{1}{k}\right)$ and $k\ge 1$.

Now, as a generalization of two above contraction, we define extended integral $\mathsf{Ϝ}$-contraction as follows.

Definition 11 

(Extended integral $\mathsf{Ϝ}$-contraction). Let $(S,d)$ be a b-metric space and mapping $\mathsf{Ϝ}\in F^{*}$. A mapping $\Gamma :S⟶S$ satisfies the extended integral Ϝ-contraction, if $\varrho \in \Lambda$ exists such that

$$\varrho \left(\underset{0}{\stackrel{M(a,b)}{\int }}\xi \left(\tau \right)d\tau \right)+\mathsf{Ϝ}\left(\underset{0}{\stackrel{d(\Gamma a,\Gamma b)}{\int }}\xi \left(\tau \right)d\tau \right)\le \mathsf{Ϝ}\left(\underset{0}{\stackrel{M(a,b)}{\int }}\xi \left(\tau \right)d\tau \right),$$

(4)

for all $a,b\in S,d(\Gamma a,\Gamma b)>0$, where

$$M(a,b)=\eta max\left\{d(a,b),d(a,\Gamma a),d(b,\Gamma b),\left(\frac{d(a,\Gamma b)+d(b,\Gamma a)}{k\left[1+d(a,\Gamma a)+d(b,\Gamma b)\right]}\right)d(a,b)\right\},$$

(5)

for some $\eta \in \left(0,\frac{1}{k}\right)$ and $k\ge 1$.

Remark 2. 

If $\xi \left(\tau \right)=1$, then the extended integral Ϝ-contraction becomes an extended Ϝ-contraction.

Proof. 

As $\xi \left(\tau \right)=1$, then from $\left(2\right)$

$$\begin{array}{cc}\hfill \varrho \left(M\left(a,b\right)\right)+\mathsf{Ϝ}\left(\underset{0}{\stackrel{d(\Gamma a,\Gamma b)}{\int }}1d\tau \right)& \le \mathsf{Ϝ}\left(\underset{0}{\stackrel{M(a,b)}{\int }}1d\tau \right),\hfill \\ \hfill \varrho \left(M\left(a,b\right)\right)+\mathsf{Ϝ}\left(d(\Gamma a,\Gamma b)\right)& \le \mathsf{Ϝ}\left(M(a,b)\right).\hfill \end{array}$$

□

Remark 3. 

Extended integral Ϝ-contraction becomes an extended integral contraction if $\mathsf{Ϝ}a=lna$.

Proof. 

Assume that $\Gamma$ satisfies the extended integral $\mathsf{Ϝ}$-contraction. Then,

$$\varrho \left(M\left(a,b\right)\right)+\mathsf{Ϝ}\left(\underset{0}{\stackrel{d(\Gamma a,\Gamma b)}{\int }}\xi \left(\tau \right)d\tau \right)\le \mathsf{Ϝ}\left(\underset{0}{\stackrel{M(a,b)}{\int }}\xi \left(\tau \right)d\tau \right).$$

By using $\mathsf{Ϝ}a=lna$, the above inequality becomes

$$\varrho \left(M\left(a,b\right)\right)+ln\left(\underset{0}{\stackrel{d(\Gamma a,\Gamma b)}{\int }}\xi \left(\tau \right)d\tau \right)\le ln\left(\underset{0}{\stackrel{M(a,b)}{\int }}\xi \left(\tau \right)d\tau \right),$$

$$ln\left(\underset{0}{\stackrel{d(\Gamma a,\Gamma b)}{\int }}\xi \left(\tau \right)d\tau \right)\le ln\left(\underset{0}{\stackrel{M(a,b)}{\int }}\xi \left(\tau \right)d\tau \right)-\varrho \left(M\left(a,b\right)\right)$$

As $\varrho \left(M\left(a,b\right)\right)>0$, then we can write $\varrho \left(M\left(a,b\right)\right)=-ln{e}^{-\varrho \left(M\left(a,b\right)\right)}$. Then, the above inequality gives

$$\begin{array}{cc}\hfill ln\left(\underset{0}{\stackrel{d(\Gamma a,\Gamma b)}{\int }}\xi \left(\tau \right)d\tau \right)& \le ln\left(\underset{0}{\stackrel{M(a,b)}{\int }}\xi \left(\tau \right)d\tau \right)-ln{e}^{\varrho \left(M\left(a,b\right)\right)},\hfill \\ \hfill ln\left(\underset{0}{\stackrel{d(\Gamma a,\Gamma b)}{\int }}\xi \left(\tau \right)d\tau \right)& \le ln\left(\frac{1}{e^{\varrho \left(M\left(a,b\right)\right)}}\underset{0}{\stackrel{M(a,b)}{\int }}\xi \left(\tau \right)d\tau \right).\hfill \end{array}$$

which gives

$$\underset{0}{\stackrel{d(\Gamma a,\Gamma b)}{\int }}\xi \left(\tau \right)d\tau \le e^{-\varrho \left(M\left(a,b\right)\right)}\underset{0}{\stackrel{M(a,b)}{\int }}\xi \left(\tau \right)d\tau .$$

Clearly, $\Gamma$ satisfies an extended integral contraction only if $\mathsf{Ϝ}a=lna$. □

To prove our main result for the fixed point of the mapping defined in Definition 11, we need the following lemma.

Lemma 4. 

Let $\left(S,d\right)$ be a complete b-metric space and ${\left\{a_n\right\}}_{n\in \mathbb{N}\cup \left\{0\right\}}$ be the sequence such that

$$d\left(a_n,a_{n+1}\right)\le M\left(a_{n-1},a_n\right),$$

(6)

for all $n=0,1,2,\dots$, where

$$M\left(a_{n-1},a_n\right)=\eta max\left\{d(a_{n-1},a_n),d(a_n,a_{n+1}),\frac{d(a_{n-1},a_{n+1})d(a_{n-1},a_n)}{k\left[1+d(a_{n-1},a_n)+d(a_n,a_{n+1})\right]}\right\},$$

for some $\eta \in \left(0,\frac{1}{k}\right)$ and $k\ge 1$. Then, ${\left\{a_n\right\}}_{n\in \mathbb{N}\cup \left\{0\right\}}$ is a Cauchy sequence in $\left(S,d\right)$. Moreover, ${\displaystyle \underset{n\to \infty }{lim}}d\left(a_n,a_{n+1}\right)=0$.

Proof. 

For the values of $M\left(a_{n-1},a_n\right)$, there are three following cases

Case-1. If $max\left\{d(a_{n-1},a_n),d(a_n,a_{n+1}),\frac{d(a_{n-1},a_{n+1})d(a_{n-1},a_n)}{k\left[1+d(a_{n-1},a_n)+d(a_n,a_{n+1})\right]}\right\}=d(a_{n-1},a_n),$ then

$$M\left(a_{n-1},a_n\right)=\eta d(a_{n-1},a_n)$$

for all $n=0,1,2,\dots$, then (6) implies

$$d\left(a_n,a_{n+1}\right)\le \eta d(a_{n-1},a_n).$$

Case-2. If $max\left\{d(a_{n-1},a_n),d(a_n,a_{n+1}),\frac{d(a_{n-1},a_{n+1})d(a_{n-1},a_n)}{k\left[1+d(a_{n-1},a_n)+d(a_n,a_{n+1})\right]}\right\}=d(a_n,a_{n+1}),$ then

$$M\left(a_{n-1},a_n\right)=\eta d(a_n,a_{n+1})$$

for all $n=0,1,2,\dots$, then (6) implies

$$\begin{array}{cc}\hfill d\left(a_n,a_{n+1}\right)& \le \eta d(a_n,a_{n+1}),\hfill \\ \hfill & <d(a_n,a_{n+1}),\hfill \end{array}$$

which is not possible.

Case-3. If $max\left\{d(a_{n-1},a_n),d(a_n,a_{n+1}),\frac{d(a_{n-1},a_{n+1})d(a_{n-1},a_n)}{k\left[1+d(a_{n-1},a_n)+d(a_n,a_{n+1})\right]}\right\}=\frac{d(a_{n-1},a_{n+1})d(a_{n-1},a_n)}{k\left[1+d(a_{n-1},a_n)+d(a_n,a_{n+1})\right]},$ then

$$M\left(a_{n-1},a_n\right)=\eta \left(\frac{d(a_{n-1},a_{n+1})d(a_{n-1},a_n)}{k\left[1+d(a_{n-1},a_n)+d(a_n,a_{n+1})\right]}\right)$$

for all $n=0,1,2,\dots$, then (6) implies

$$d\left(a_n,a_{n+1}\right)\le \eta \left(\frac{d(a_{n-1},a_{n+1})d(a_{n-1},a_n)}{k\left[1+d(a_{n-1},a_n)+d(a_n,a_{n+1})\right]}\right),$$

using $\left(B_3\right),$ we have

$$\begin{array}{cc}\hfill & \le \eta \left(\frac{k\left(d(a_{n-1},a_n)+d(a_n,a_{n+1})\right)}{k\left[1+d(a_{n-1},a_n)+d(a_n,a_{n+1})\right]}\right)d(a_{n-1},a_n),\hfill \\ \hfill & =\eta \left(\frac{d(a_{n-1},a_n)+d(a_n,a_{n+1})}{1+d(a_{n-1},a_n)+d(a_n,a_{n+1})}\right)d(a_{n-1},a_n)\hfill \\ \hfill & =\eta d(a_{n-1},a_n),\because \left(\frac{d(a_{n-1},a_n)+d(a_n,a_{n+1})}{1+d(a_{n-1},a_n)+d(a_n,a_{n+1})}\right)\le 1.\hfill \end{array}$$

Consequently, for all $n=1,2,3,\dots ,$ we have

$$\begin{array}{cc}\hfill d\left(a_n,a_{n+1}\right)& \le \eta d(a_{n-1},a_n),\hfill \\ \hfill & \le {\eta }^{2}d(a_{n-2},a_{n-1}),\hfill \\ \hfill & ⋮\hfill \\ \hfill d\left(a_n,a_{n+1}\right)& \le {\eta }^{n}d(a_0,a_1).\hfill \end{array}$$

(7)

For $m,n\in ,\mathbb{N}$ with $m<n$ and by using (B${}_3)$

$$\begin{array}{cc}\hfill d\left(a_m,a_n\right)& \le k\left\{d\left(a_m,a_{m+1}\right)+d\left(a_{m+1},a_n\right)\right\},\hfill \\ \hfill & \le kd\left(a_m,a_{m+1}\right)+k^2\left\{d\left(a_{m+1},a_{m+2}\right)+d\left(a_{m+2},a_n\right)\right\},\hfill \\ \hfill & ⋮\hfill \\ \hfill & \le kd\left(a_m,a_{m+1}\right)+k^{2}d\left(a_{m+1},a_{m+2}\right)+k^{3}d\left(a_{m+2},a_{m+3}\right)\hfill \\ \hfill & +\cdots +k^{n-m-1}d\left(a_{n-2},a_{n-1}\right)+k^{n-m}d\left(a_{n-1},a_n\right),\hfill \\ \hfill & \le k{\eta }^{m}d\left(a_0,a_1\right)+k^2{\eta }^{m+1}d\left(a_0,a_1\right)+k^3{\eta }^{m+2}d\left(a_0,a_1\right)\hfill \\ \hfill & +\cdots +k^{n-m-1}{\eta }^{n-2}d\left(a_0,a_1\right)+k^{n-m}{\eta }^{n-1}d\left(a_0,a_1\right),\hfill \\ \hfill & <\frac{k{\eta }^m}{1-k\eta }d\left(a_0,a_1\right)\to 0,\mathrm{when}m,n\to \infty .\hfill \end{array}$$

It follows that the sequence ${\left\{a_n\right\}}_{n\in \mathbb{N}\cup \left\{0\right\}}$ is a Cauchy sequence in $\left(S,d\right)$. Also, from (7) and using $n\to \infty$ gives

$$\underset{n\to \infty }{lim}d\left(a_n,a_{n+1}\right)=0.$$

□

Theorem 5. 

Let $\left(S,d\right)$ be a complete b-metric space and the mapping $\Gamma :S⟶S$ be extended integral Ϝ-contraction. Then, Γ has a unique fixed point in S.

Proof. 

Let us consider an arbitrary element $a_0\in S$ and construct a sequence $a_{n+1}=\Gamma a_n$ for $n=0,1,2,3,\dots$. If $a_n=a_{n+1}$, for some $n\in \mathbb{N}\cup \left\{0\right\}$ then $a_n$ is fixed point of self-mapping $\Gamma$. We assume $a_n\ne a_{n+1}$ for all $n=0,1,2,3,\dots$. As $\Gamma :S⟶S$ is extended integral $\mathsf{Ϝ}$-contraction, therefore

$$\varrho \left(\underset{0}{\stackrel{M(a_{n-1},a_n)}{\int }}\xi \left(\tau \right)d\tau \right)+\mathsf{Ϝ}\left(\underset{0}{\stackrel{d(\Gamma a_{n-1},\Gamma a_n)}{\int }}\xi \left(\tau \right)d\tau \right)\le \left(\underset{0}{\stackrel{M(a_{n-1},a_n)}{\int }}\xi \left(\tau \right)d\tau \right),$$

which implies

$$\mathsf{Ϝ}\left(\underset{0}{\stackrel{d(\Gamma a_{n-1},\Gamma a_n)}{\int }}\xi \left(\tau \right)d\tau \right)\le \left(\underset{0}{\stackrel{M(a_{n-1},a_n)}{\int }}\xi \left(\tau \right)d\tau \right)-\varrho \left(\underset{0}{\stackrel{M(a_{n-1},a_n)}{\int }}\xi \left(\tau \right)d\tau \right)$$

furthermore, we have

$$\mathsf{Ϝ}\left(\underset{0}{\stackrel{d(a_n,a_{n+1})}{\int }}\xi \left(\tau \right)d\tau \right)<\mathsf{Ϝ}\left(\underset{0}{\stackrel{M(a_{n-1},a_n)}{\int }}\xi \left(\tau \right)d\tau \right).$$

As $\mathsf{Ϝ}\in F^{*}$, i.e., $\mathsf{Ϝ}$ is strictly increasing, therefore

$$\underset{0}{\stackrel{d(a_n,a_{n+1})}{\int }}\xi \left(\tau \right)d\tau <\underset{0}{\stackrel{M(a_{n-1},a_n)}{\int }}\xi \left(\tau \right)d\tau ,$$

(8)

which implies

$$d(a_n,a_{n+1})<M(a_{n-1},a_n),$$

By utilizing (8) and Lemma 4, we can conclude that the sequence ${\left\{a_n\right\}}_{n\in \mathbb{N}\cup \left\{0\right\}}$ is a Cauchy sequence. Since S is complete, there exists an element $a\in S$ such that

$$\underset{n\to +\infty }{lim}d\left(a_n,a\right)=0$$

(9)

To verify this, we need to show that $a\in S$ is a fixed point of the mapping $\Gamma$, using (4)

$$\underset{0}{\stackrel{d(a_n,\Gamma a)}{\int }}\xi \left(\tau \right)d\tau <\underset{0}{\stackrel{M(a_{n-1},a)}{\int }}\xi \left(\tau \right)d\tau ,$$

Calculating the values of $M(a_{n-1},a_n),$ it has been concluded that either $M(a_{n-1},a_n)=0,$ which gives

$$\underset{n\to +\infty }{lim}d(a_n,\Gamma a)=0$$

(10)

or $M(a_{n-1},a_n)=$$\eta d\left(a,\Gamma a\right),$ which implies

$$\underset{n\to +\infty }{lim}d(a_n,\Gamma a)\le \eta d\left(a,\Gamma a\right).$$

(11)

Now, consider

$$d\left(a,\Gamma a\right)\le k\left\{d\left(a,a_n\right)+d\left(a_n,\Gamma a\right)\right\},$$

using $\left(10\right)$, we have

$$d\left(a,\Gamma a\right)\le 0$$

which implies that a is a fixed point of $\Gamma .$ Now, for the case when $\left(11\right)$ holds, we have

$$d\left(a,\Gamma a\right)\le k\left\{d\left(a,a_n\right)+d\left(a_n,\Gamma a\right)\right\}$$

implies

$$d\left(a,\Gamma a\right)\le k\left\{0+\eta d\left(a,\Gamma a\right)\right\}=k\eta d\left(a,\Gamma a\right)$$

or

$$\left(1-k\eta \right)d\left(a,\Gamma a\right)\le 0$$

gives $d\left(a,\Gamma a\right)=0$, as $k\eta <1.$ Hence, $a\in S$ is the fixed point of mapping $\Gamma$. The uniqueness of the fixed point can be proved using the contradiction method along with the inequality $\left(5\right).$ □

Corollary 1. 

Let $\left(S,d\right)$ be a complete b-metric space and mapping $\Gamma :S⟶S$ be extended Ϝ-contraction or extended integral contraction. Then, Γ has a unique fixed point in S.

Proof. 

Proof followed by Remarks 1 and 2. □

In the next example, we have shown the validity of our main Theorem 4.

Example 1. 

Let $S=\left[0,1\right]$ and $d\left(a,b\right)={\left|a-b\right|}^2$ for all $a,b\in S$ and $a\le b$. Clearly, $\left(S,d\right)$ is a complete b-metric space. Define $\Gamma :S\to S$ as $\Gamma a=\frac{1}{a+1}$ for all $a\in S$. Also, define $\xi \in \Psi$, $\mathsf{Ϝ}\in F^{*}$ and $\varrho \in \Lambda$ as $\xi \left(t\right)=t$, $\mathsf{Ϝ}\left(r\right)=50lnr$ and $\varrho \left(u\right)=\frac{1}{100+u}$ respectively. Assume that $X=\varrho \left(M(a,b)\right)$, $Y=\mathsf{Ϝ}\left(\underset{0}{\stackrel{d(\Gamma a,\Gamma b)}{\int }}\xi \left(\tau \right)d\tau \right)$ and $Z=\mathsf{Ϝ}\left(\underset{0}{\stackrel{M(a,b)}{\int }}\xi \left(\tau \right)d\tau \right)$, then consider

$$\begin{array}{cc}\hfill Z-Y& =\mathsf{Ϝ}\left(\underset{0}{\stackrel{M(a,b)}{\int }}\xi \left(\tau \right)d\tau \right)-\mathsf{Ϝ}\left(\underset{0}{\stackrel{d(\Gamma a,\Gamma b)}{\int }}\xi \left(\tau \right)d\tau \right),\hfill \\ \hfill & =50ln\left(\underset{0}{\stackrel{M(a,b)}{\int }}\tau d\tau \right)-50ln\left(\underset{0}{\stackrel{d(\Gamma a,\Gamma b)}{\int }}\tau d\tau \right),\hfill \\ \hfill & =50ln\left(\frac{{\left(M\left(a,b\right)\right)}^2}{2}-0\right)-50ln\left(\frac{{\left(d(\Gamma a,\Gamma b)\right)}^2}{2}-0\right),\hfill \\ \hfill & =100ln\frac{M\left(a,b\right)}{d(\Gamma a,\Gamma b)},\hfill \end{array}$$

(12)

where,

$$M(a,b)=\eta max\left\{{\left|a-b\right|}^2,{\left|a-\frac{1}{a+1}\right|}^2,{\left|b-\frac{1}{b+1}\right|}^2,\left(\frac{{\left(a-\frac{1}{b+1}\right)}^2+{\left(b-\frac{1}{a+1}\right)}^2}{k\left(1+{\left(a-\frac{1}{a+1}\right)}^2+{\left(b-\frac{1}{b+1}\right)}^2\right)}\right){\left(a-b\right)}^2\right\},$$

possible determined real values for $d(\Gamma a,\Gamma b)$ and $M(a,b)$ for all $a,b\in \left[0,1\right]$ are

$$d(\Gamma a,\Gamma b)=\left\{\begin{array}{cc}0,& \mathit{when}a=b\\ \frac{1}{4},& \mathit{when}a=0,b=1\\ \frac{1}{4},& \mathit{when}a=1,b=0\\ 0<l_2<1,& \mathit{when}a,b\in \left(0,1\right)\mathrm{and}a\ne b\end{array}\right.,$$

for some $\eta \in \left(0,\frac{1}{k}\right)$ and $k\ge 1$, and

$$M(a,b)=\eta max\left\{0,1,0<l_1\le \frac{1}{3k}\right\}=1.$$

From the above values of $M(a,b)$ and $d(\Gamma a,\Gamma b)$, it is obvious that $d(\Gamma a,\Gamma b)<M(a,b)\Rightarrow \frac{M(a,b)}{d(\Gamma a,\Gamma b)}>1$. Also, assume

$$\begin{array}{cc}\hfill X& =\varrho \left(M(a,b)\right),\hfill \\ \hfill & =\frac{1}{100+M(a,b)}.\hfill \end{array}$$

(13)

As, $100ln\frac{M\left(a,b\right)}{d(\Gamma a,\Gamma b)}\ge \frac{1}{100+M\left(a,b\right)}>0$, then from $\left(C_3\right)$ and $\left(C_4\right)$

$$\begin{array}{cc}\hfill Z-Y& =100ln\frac{M\left(a,b\right)}{d(\Gamma a,\Gamma b)},\hfill \\ \hfill & \ge \frac{1}{100+M(a,b)},\hfill \\ \hfill Z-Y& \ge X,\hfill \\ \hfill X+Y& \le Z,\hfill \end{array}$$

this implies that

$$\varrho \left(M(a,b)\right)+\mathsf{Ϝ}\left(\underset{0}{\stackrel{d(\Gamma a,\Gamma b)}{\int }}\xi \left(\tau \right)d\tau \right)\le \mathsf{Ϝ}\left(\underset{0}{\stackrel{M(a,b)}{\int }}\xi \left(\tau \right)d\tau \right).$$

Hence, mapping Γ satisfies all the conditions of Theorem 4. Thus, Γ has unique fixed-point $\frac{\sqrt{5}-1}{2}\in S$.

3. $(\mathbf{\varkappa },$Ω-Ϝ)-Contraction

In the first part of this section, we introduced $(\varkappa ,\Omega$-$\mathsf{Ϝ})$-contraction and related fixed-point results in the complete metric spaces. The second part introduced the notions of $(\varkappa ,{\Gamma }_{1,2},\Omega$-$\mathsf{Ϝ})$-contraction, the addition ${\Gamma }_{1,2}$, in $(\varkappa ,\Omega$-$\mathsf{Ϝ})$-contraction indicates two mappings, so that we will discuss the coincidence and common fixed points of two mappings satisfying the $(\varkappa ,{\Gamma }_{1,2},\Omega$-$\mathsf{Ϝ})$ contraction. The notions has been generalized in some sense, but the considered space is a metric space, as it is essential to first go through metric spaces, then we will pose a question about their existence in b-metric space and other generalizations.

Definition 12. 

Let Ω denote the class of mappings $\Im :[0,\infty )\times [0,\infty )⟶\mathbb{R}$which fulfil the three following conditions

• $\left(a_1\right)$. $\Im (a,b)\ge 0$,
• $\left(a_2\right)$. $\Im (a,b)=0⟹a=b$,
• $\left(a_3\right)$. ℑ is continuous in the second variable.

Remark 4. 

It is worthy to note that a special case of above function ℑ can be considered as

$$\Im (0,a)=\stackrel{a}{\underset{0}{{\displaystyle \int }}}\xi \left(\tau \right)d\tau$$

for $\xi \in \Psi$ and for each $a>0$.

The next definition is our main definition which utilizes the above definition.

Definition 13. 

Let $\left(S,d\right)$ be a metric space, $\Im \in \Omega$ and $\mathsf{Ϝ}\in F^{*}$. A mapping $\Gamma :S⟶S$is called $(\varkappa ,\Omega$-$\mathsf{Ϝ})$-contraction, if there exists $\varkappa \in \Lambda$and for all $a,b\in S\Rightarrow d(\Gamma a,\Gamma b)>0$, such that

$$\varkappa \left(\Im \left(0,d\left(a,b\right)\right)\right)+\mathsf{Ϝ}\left(\Im (0,d(\Gamma a,\Gamma b\right)\left)\right)\le \mathsf{Ϝ}\left(\Im \left(0,d\left(a,b\right)\right)\right).$$

(14)

Theorem 6. 

Suppose that $(S,d)$ is a complete metric space, and let $\Gamma :S\to S$ be a $(\varkappa ,\Omega$-$\mathsf{Ϝ})$-contraction mapping. Then, there exists a unique element $a\in S$ such that $\Gamma \left(a\right)=a$.

Proof. 

Let $a_0\in S$ and construct a sequence, $a_{n+1}=\Gamma a_n$ for $n\in \mathbb{N}\cup \left\{0\right\}$. If $a_n=a_{n+1}$ for some $n\in \mathbb{N}\cup \left\{0\right\}$, then $a_n\in S$ is the fixed point of $\Gamma$. Therefore, we assume that $a_n\ne a_{n+1}$ for all $n\in \mathbb{N}\cup \left\{0\right\}$. As $\Gamma :S⟶S$ satisfies $\left(11\right),$ then

$$\begin{array}{cc}\hfill \varkappa \left(\Im \left(0,d\left(a_n,a_{n-1}\right)\right)\right)+\mathsf{Ϝ}\left(\Im \left(0,d\left(a_{n+1},a_n\right)\right)\right)& \le \mathsf{Ϝ}\left(\Im \left(0,d\left(a_n,a_{n-1}\right)\right)\right),\hfill \\ \hfill \mathsf{Ϝ}\left(\Im \left(0,d\left(a_{n+1},a_n\right)\right)\right)& <\mathsf{Ϝ}\left(\Im \left(0,d\left(a_n,a_{n-1}\right)\right)\right),\hfill \\ \hfill \Im \left(0,d\left(a_{n+1},a_n\right)\right)& <\Im \left(0,d\left(a_n,a_{n-1}\right)\right),\because \mathsf{Ϝ}\in F^{*},\hfill \end{array}$$

the sequence ${\left\{\Im \left(0,d\left(a_{n+1},a_n\right)\right)\right\}}_{n\in \mathbb{N}\cup \left\{0\right\}}$ can be observed to be both decreasing and bounded below by 0. Consequently, there exists a ${\wp }_1\ge 0$ such that

$$\underset{n⟶+\infty }{lim}\Im \left(0,d\left(a_{n+1},a_n\right)\right)={\wp }_1$$

or

$$\Im \left(0,\underset{n⟶+\infty }{lim}d\left(a_{n+1},a_n\right)\right)={\wp }_1.$$

(15)

Assuming that, ${\wp }_1>0$, from (14), consider

$$\begin{array}{cc}\hfill \mathsf{Ϝ}\left(\Im \left(0,d\left(a_{n+1},a_n\right)\right)\right)& <\varkappa \left(\Im \left(0,d\left(a_n,a_{n-1}\right)\right)\right)+\mathsf{Ϝ}\left(\Im \left(0,d\left(a_{n+1},a_n\right)\right)\right)\le \mathsf{Ϝ}\left(\Im \left(0,d\left(a_n,a_{n-1}\right)\right)\right),\hfill \\ \hfill \mathsf{Ϝ}\left(\Im \left(0,d\left(a_{n+1},a_n\right)\right)\right)& <\mathsf{Ϝ}\left(\Im \left(0,d\left(a_n,a_{n-1}\right)\right)\right),\hfill \\ \hfill \Im \left(0,d\left(a_{n+1},a_n\right)\right)& <\Im \left(0,d\left(a_n,a_{n-1}\right)\right),\because \mathsf{Ϝ}\in F^{*},\hfill \\ \hfill \underset{n⟶+\infty }{lim}\Im \left(0,d\left(a_{n+1},a_n\right)\right)& <\underset{n⟶+\infty }{lim}\Im \left(0,d\left(a_n,a_{n-1}\right)\right),\hfill \\ \hfill \Im \left(0,\underset{n⟶+\infty }{lim}d\left(a_{n+1},a_n\right)\right)& <\Im \left(0,\underset{n⟶+\infty }{lim}d\left(a_n,a_{n-1}\right)\right),\hfill \\ \hfill {\wp }_1& <{\wp }_1,\mathrm{using}\left(a_3\right),\hfill \end{array}$$

a contradiction, which implies that ${\wp }_1=0$. Moreover, Equation (15) gives

$$\underset{n⟶+\infty }{lim}\Im \left(0,d\left(a_{n+1},a_n\right)\right)=0$$

which, using $\left(a_2\right)$ and $\left(a_3\right)$, implies

$$\underset{n⟶+\infty }{lim}d\left(a_{n+1},a_n\right)=0.$$

(16)

To prove that the sequence ${\left\{a_n\right\}}_{n\in \mathbb{N}\cup \left\{0\right\}}$ is a Cauchy sequence, suppose on the contrary, that the sequence ${\left\{a_n\right\}}_{n\in \mathbb{N}\cup \left\{0\right\}}$ is not a Cauchy sequence. From (16), ${\displaystyle \underset{n⟶+\infty }{lim}}d\left(a_{n+1},a_n\right)=0$. Consequently, $\epsilon >0$ as well as positive integers $m_{\hslash }$ and $n_{\hslash }$ exist with $n_{\hslash }>m_{\hslash }>\hslash$. By substituting $a=a_{n_{\hslash }}$, $b=a_{m_{\hslash }}$ into (11), this gives

$$\begin{array}{cc}\hfill \varkappa \left(u\right)+\mathsf{Ϝ}\left(\Im \left(0,d(a_{n_{\hslash }+1},a_{m_{\hslash }+1})\right)\right)& \le \mathsf{Ϝ}\left(\Im \left(0,d(a_{n_{\hslash }},a_{m_{\hslash }})\right)\right),\hfill \\ \hfill \mathsf{Ϝ}\left(\Im \left(0,d(a_{n_{\hslash }+1},a_{m_{\hslash }+1})\right)\right)& <\mathsf{Ϝ}\left(\Im \left(0,d(a_{n_{\hslash }},a_{m_{\hslash }})\right)\right),\hfill \\ \hfill \Im \left(0,d(a_{n_{\hslash }+1},a_{m_{\hslash }+1})\right)& <\Im \left(0,d(a_{n_{\hslash }},a_{m_{\hslash }})\right),\because \mathsf{Ϝ}\in F^{*},\hfill \\ \hfill \underset{\hslash \to +\infty }{lim}\Im \left(0,d(a_{n_{\hslash }+1},a_{m_{\hslash }+1})\right)& <\underset{\hslash \to +\infty }{lim}\Im \left(0,d(a_{n_{\hslash }},a_{m_{\hslash }})\right),\hfill \\ \hfill \Im \left(0,\underset{\hslash \to +\infty }{lim}d(a_{n_{\hslash }+1},a_{m_{\hslash }+1})\right)& <\Im \left(0,\underset{\hslash \to +\infty }{lim}d(a_{n_{\hslash }},a_{m_{\hslash }})\right),\because \Im \mathrm{follows}\left(a_3\right),\hfill \end{array}$$

by Lemma 1, ${\displaystyle \underset{\hslash \to +\infty }{lim}}d(a_{n_{\hslash }+1},a_{m_{\hslash }+1})={\epsilon }^{+}$ and ${\displaystyle \underset{\hslash \to +\infty }{lim}}d(a_{n_{\hslash }},a_{m_{\hslash }})={\epsilon }^{+}$ gives

$$\Im \left(0,{\epsilon }^{+}\right)<\Im \left(0,{\epsilon }^{+}\right),$$

This leads to a contradiction, proving that the sequence ${\left\{a_n\right\}}_{n\in \mathbb{N}\cup \left\{0\right\}}$ is a Cauchy sequence. Since S is complete, there exists an element $a\in S$ such that ${\displaystyle \underset{n\to +\infty }{lim}}d\left(a_n,a\right)=0$. To verify that $a\in S$ is a fixed point of mapping $\Gamma$, using (14)

$$\begin{array}{cc}\hfill \mathsf{Ϝ}\left(\Im (0,d(a_n,\Gamma a\right)\left)\right)& <\varkappa +\mathsf{Ϝ}\left(\Im (0,d(a_n,\Gamma a\right)\left)\right)\le \mathsf{Ϝ}\left(\Im (0,d(a_{n-1},a\right)\left)\right),\hfill \\ \hfill \mathsf{Ϝ}\left(\Im (0,d(a_n,\Gamma a\right)\left)\right)& <\mathsf{Ϝ}\left(\Im \left(0,d(a_{n-1},a)\right)\right),\hfill \\ \hfill \Im \left(0,d(a_n,\Gamma a)\right)& <\Im \left(0,d(a_{n-1},a)\right),\because \mathsf{Ϝ}\in F^{*},\hfill \\ \hfill \underset{n⟶+\infty }{lim}\Im \left(0,d(a_n,\Gamma a)\right)& <\underset{n⟶+\infty }{lim}\Im \left(0,d(a_{n-1},a)\right),\hfill \\ \hfill \Im \left(0,\underset{n⟶+\infty }{lim}d(a_n,\Gamma a)\right)& <\Im \left(0,\underset{n⟶+\infty }{lim}d(a_{n-1},a)\right),\because \Im \mathrm{follows}\left(a_3\right),\hfill \\ \hfill \Im \left(0,\underset{n⟶+\infty }{lim}d(a_n,\Gamma a)\right)& <\Im \left(0,0\right),\hfill \\ \hfill \underset{n⟶+\infty }{lim}d(a_n,\Gamma a)& =0.\hfill \end{array}$$

(17)

Using ($B_3$) and (17)

$$\begin{array}{cc}\hfill d\left(a,\Gamma a\right)& \le k\left\{d\left(a,a_n\right)+d\left(a_n,\Gamma a\right)\right\},\hfill \\ \hfill & \le k\underset{n\to +\infty }{lim}\left\{d\left(a,a_n\right)+d\left(a_n,\Gamma a\right)\right\},\hfill \\ \hfill & =0,\hfill \\ \hfill \Gamma a& =a.\hfill \end{array}$$

Therefore, $a\in S$ is a fixed point of $\Gamma$. To verify the uniqueness of this fixed point, assume that there exists another fixed point of $\Gamma$. Suppose that $a,b\in S$ are the two distinct fixed points in S, $a\ne b$, $\Gamma a=a$ and $\Gamma b=b$. From (11),

$$\begin{array}{cc}\hfill \varkappa \left(u\right)+\mathsf{Ϝ}\left(\Im (0,d(\Gamma a,\Gamma b\right)\left)\right)& \le \mathsf{Ϝ}\left(\Im (0,d(a,b\right)\left)\right),\hfill \\ \hfill \mathsf{Ϝ}\left(\Im (0,d(\Gamma a,\Gamma b\right)\left)\right)& <\mathsf{Ϝ}\left(\Im (0,d(a,b\right)\left)\right),\hfill \\ \hfill \mathsf{Ϝ}\left(\Im (0,d(a,b\right)\left)\right)& <\mathsf{Ϝ}\left(\Im (0,d(a,b\right)\left)\right),\hfill \end{array}$$

which is not true; therefore, the fixed point of $\Gamma$ is unique. □

Using Remark 4, we have the following corollary.

Corollary 2. 

Let $\left(S,d\right)$ be a complete metric space, $\Im \in \Omega$ and $\mathsf{Ϝ}\in F^{*}$. Let $\Gamma :S⟶S$be given, if there exists $\varkappa \in \Lambda$and for all $a,b\in S\Rightarrow d(\Gamma a,\Gamma b)>0$, such that

$$\varkappa \left(\Im \left(\stackrel{d\left(a,b\right)}{\underset{0}{{\displaystyle \int }}}\xi \left(\tau \right)d\tau \right)\right)+\mathsf{Ϝ}\left(\Im \left(\stackrel{d\left(\Gamma a,\Gamma b\right)}{\underset{0}{{\displaystyle \int }}}\xi \left(\tau \right)d\tau \right)\right)\le \mathsf{Ϝ}\left(\Im \left(\stackrel{d\left(a,b\right)}{\underset{0}{{\displaystyle \int }}}\xi \left(\tau \right)d\tau \right)\right),$$

then Γ has a unique fixed point.

Now, we will define the $(\varkappa ,{\Gamma }_{1,2},\Omega$-$\mathsf{Ϝ})$-contraction and prove the coincidence and common fixed-point results.

Definition 14. 

Let $(S,d)$ be a metric space and mappings ${\Gamma }_1,{\Gamma }_2:S⟶S$. If functions exist $\varkappa \in \Lambda$ and $\mathsf{Ϝ}\in F^{*}$ such that, for all $a,b\in S$ with ${\Gamma }_{1}a\ne {\Gamma }_{1}b$ and ${\Gamma }_{2}a\ne {\Gamma }_{2}b$. Then, the pair of mappings ${\Gamma }_1,{\Gamma }_2$ is called a $(\varkappa ,{\Gamma }_{1,2},\Omega$-$\mathsf{Ϝ})$-contraction if

$$\varkappa \left(\Im \left(0,d\left({\Gamma }_{2}a,{\Gamma }_{2}b\right)\right)\right)+\mathsf{Ϝ}\left(\Im \left(0,d\left({\Gamma }_{1}a,{\Gamma }_{1}b\right)\right)\right)\le \mathsf{Ϝ}\left(\Im \left(0,d\left({\Gamma }_{2}a,{\Gamma }_{2}b\right)\right)\right).$$

(18)

for all $a,b\in S.$

Theorem 7. 

Let $(S,d)$ be a metric space and the pair ${\Gamma }_1,{\Gamma }_2:S⟶S$ be $(\varkappa ,{\Gamma }_{1,2},\Omega$-$\mathsf{Ϝ})$-contraction. Suppose that a Picard–Jungck sequence ${\left(a_n\right)}_{n\in \mathbb{N}\cup \left\{0\right\}}$ of the pair $({\Gamma }_1,{\Gamma }_2) exists.$Furthermore, assume that the following conditions hold,

• $\left(b_1\right)$. $({\Gamma }_{2}S,d)$ is complete,
• $\left(b_2\right)$. $(S,d)$ is complete, ${\Gamma }_2$ is a continuous, and $({\Gamma }_1,{\Gamma }_2)$ is a compatible pair,
• then ${\Gamma }_1$and ${\Gamma }_2$ have a unique point of coincidence.

Proof. 

Suppose that $\left(a_{{}_n}\right)$ in $S$ is a Picard–Jungck sequence such that ${\Gamma }_1{a}_{n-1}={\Gamma }_2{a}_n=b_n,\forall n\in \mathbb{N}\cup \left\{0\right\}$. If ${\Gamma }_1{b}_{n+1}=b_n={\Gamma }_2{b}_{n+1}$ for some $n\in \mathbb{N}\cup \left\{0\right\}$, then $b_n\in S$ is point of coincidence of ${\Gamma }_1$ and ${\Gamma }_2$. Thus, we assume $b_n\ne b_{n+1}$for all $n\in \mathbb{N}\cup \left\{0\right\}$ by using (18)

$$\begin{array}{cc}\hfill & \varkappa \left(\Im \left(0,d\left({\Gamma }_2{a}_n,{\Gamma }_2{a}_{n+1}\right)\right)\right)+\mathsf{Ϝ}\left(\Im \left(0,d\left({\Gamma }_1{a}_n,{\Gamma }_1{a}_{n+1}\right)\right)\right)\hfill \\ \hfill & \le \mathsf{Ϝ}\left(\Im \left(0,d\left({\Gamma }_2{a}_n,{\Gamma }_2{a}_{n+1}\right)\right)\right),\hfill \end{array}$$

$$\varkappa \left(\Im \left(0,d\left(b_n,b_{n+1}\right)\right)\right)+\mathsf{Ϝ}\left(\Im \left(0,d\left(b_{n-1},b_n\right)\right)\right)\le \mathsf{Ϝ}\left(\Im \left(0,d\left(b_n,b_{n+1}\right)\right)\right),$$

using the properties that $liminf\varkappa >0$ and $\mathsf{Ϝ}\in F^{*}$, then

$$\Im \left(0,d\left(b_{n-1},b_n\right)\right)<\Im \left(0,d\left(b_n,b_{n+1}\right)\right),$$

(19)

then ${\left\{\Im \left(0,d\left(b_n,b_{n+1}\right)\right)\right\}}_{n\in \mathbb{N}\cup \left\{0\right\}}$ is decreasing and bounded below the sequence, then a ${\wp }_2\ge 0$ exists such that

$$\underset{n⟶+\infty }{lim}\Im \left(0,d\left(b_n,b_{n+1}\right)\right)={\wp }_2$$

using $\left(a_3\right)$

$$\Im \left(0,\underset{n⟶+\infty }{lim}d\left(b_n,b_{n+1}\right)\right)={\wp }_2.$$

(20)

Suppose that ${\wp }_2>0$, then, using (19),

$$\begin{array}{cc}\hfill \Im \left(0,d\left(b_{n-1},b_n\right)\right)& <\Im \left(0,d\left(b_n,b_{n+1}\right)\right),\hfill \\ \hfill \underset{n⟶+\infty }{lim}\Im \left(0,d\left(b_{n-1},b_n\right)\right)& <\underset{n⟶+\infty }{lim}\Im \left(0,d\left(b_n,b_{n+1}\right)\right),\hfill \\ \hfill \Im \left(0,\underset{n⟶+\infty }{lim}d\left(b_{n-1},b_n\right)\right)& <\Im \left(0,\underset{n⟶+\infty }{lim}d\left(b_n,b_{n+1}\right)\right),\because \Im \mathrm{follows}\left(a_3\right),\hfill \\ \hfill {\wp }_2& <{\wp }_2,\hfill \end{array}$$

this leads to a contradiction, our supposition (i.e., ${\wp }_2>0$) is wrong. Hence, ${\wp }_2=0$ and (20) gives ${\displaystyle \underset{n⟶+\infty }{lim}}d\left(b_n,b_{n+1}\right)=0$ (using $\left(a_2\right)$). Now, to prove that the sequence ${\left\{b_n\right\}}_{n\in \mathbb{N}\cup \left\{0\right\}}$ is a Cauchy sequence, suppose, on the contrary, that the sequence ${\left\{b_n\right\}}_{n\in \mathbb{N}\cup \left\{0\right\}}$ is not a Cauchy sequence. Then, there exist $\epsilon >0$ and positive integers $m_{\hslash }$ and $n_{\hslash }$ such that $n_{\hslash }>m_{\hslash }>\hslash$. Putting $a=a_{n_{\hslash }+1}$, $b=a_{m_{\hslash }+1}$ in (18)

$$\begin{array}{cc}\hfill & \varkappa \left(\Im \left(0,d\left({\Gamma }_2{a}_{n_{\hslash }+1},{\Gamma }_2{a}_{m_{\hslash }+1}\right)\right)\right)+\mathsf{Ϝ}\left(\Im \left(0,d\left({\Gamma }_1{a}_{n_{\hslash }+1},{\Gamma }_1{a}_{m_{\hslash }+1}\right)\right)\right)\hfill \\ \hfill & \le \mathsf{Ϝ}\left(\Im \left(0,d\left({\Gamma }_2{a}_{n_{\hslash }+1},{\Gamma }_2{a}_{m_{\hslash }+1}\right)\right)\right),\hfill \end{array}$$

$$\varkappa \left(\Im \left(0,d\left(b_{n_{\hslash }+1},b_{m_{\hslash +1}}\right)\right)\right)+\mathsf{Ϝ}\left(\Im \left(0,d\left(b_{n_{\hslash }},b_{m_{\hslash }}\right)\right)\right)\le \mathsf{Ϝ}\left(\Im \left(0,d\left(b_{n_{\hslash }+1},b_{m_{\hslash +1}}\right)\right)\right),$$

using the properties that $\varkappa \in \Lambda$ and $\mathsf{Ϝ}\in F^{*}$, gives

$$\begin{array}{cc}\hfill \Im \left(0,d\left(b_{n_{\hslash }},b_{m_{\hslash }}\right)\right)& <\Im \left(0,d\left(b_{n_{\hslash }+1},b_{m_{\hslash +1}}\right)\right),\hfill \\ \hfill \underset{\hslash \to +\infty }{lim}\Im \left(0,d\left(b_{n_{\hslash }},b_{m_{\hslash }}\right)\right)& <\underset{\hslash \to +\infty }{lim}\Im \left(0,d\left(b_{n_{\hslash }+1},b_{m_{\hslash +1}}\right)\right),\hfill \end{array}$$

following, as ℑ follows $\left(a_3\right)$ and by Lemma 1, there exists ${\epsilon }^{+}>0,$ such that

$$\underset{\hslash \to +\infty }{lim}d\left(b_{n_{\hslash }},b_{m_{\hslash }}\right)=\underset{\hslash \to +\infty }{lim}d\left(b_{n_{\hslash }+1},b_{m_{\hslash +1}}\right)={\epsilon }^{+},$$

so we have

$$\begin{array}{cc}\hfill \Im \left(0,\underset{\hslash \to +\infty }{lim}d\left(b_{n_{\hslash }},b_{m_{\hslash }}\right)\right)& <\Im \left(0,\underset{\hslash \to +\infty }{lim}d\left(b_{n_{\hslash }+1},b_{m_{\hslash +1}}\right)\right),\hfill \\ \hfill \Im \left(0,{\epsilon }^{+}\right)& <\Im \left(0,{\epsilon }^{+}\right),\hfill \end{array}$$

a contradiction; therefore, the sequence ${\left\{b_n\right\}}_{n\in \mathbb{N}\cup \left\{0\right\}}$ is a Cauchy sequence. As the condition ($b_1$) holds, then there exists an element $c\in {\Gamma }_{2}S$ such that $b_n={\Gamma }_2{a}_n⟶{\Gamma }_{2}c$ as $n⟶+\infty$ or ${\displaystyle \underset{n\to \infty }{lim}}d\left(b_n,{\Gamma }_{2}c\right)=0$. To check, ${\Gamma }_{1}c={\Gamma }_{2}c$. Since $b_n\ne b_p$, whenever $n\ne p$. Now, suppose that ${\Gamma }_{1}c,{\Gamma }_{2}c\notin \left\{b_n:n\in \mathbb{N}\cup \left\{0\right\}\right\}$. From (18),

$$\begin{array}{cc}\hfill \varkappa \left(\Im \left(0,d\left({\Gamma }_2{a}_{n+1},{\Gamma }_{2}c\right)\right)\right)+\mathsf{Ϝ}\left(\Im \left(0,d\left(b_{n-1},{\Gamma }_{1}c\right)\right)\right)& \le \mathsf{Ϝ}\left(\Im \left(0,d\left({\Gamma }_2{a}_{n+1},{\Gamma }_{2}c\right)\right)\right),\hfill \\ \hfill \varkappa \left(\Im \left(0,d\left(b_{n+1},{\Gamma }_{2}c\right)\right)\right)+\mathsf{Ϝ}\left(\Im \left(0,d\left(b_n,{\Gamma }_{1}c\right)\right)\right)& \le \mathsf{Ϝ}\left(\Im \left(0,d\left(b_{n+1},{\Gamma }_{2}c\right)\right)\right),\hfill \\ \hfill \mathsf{Ϝ}\left(\Im \left(0,d\left(b_n,{\Gamma }_{1}c\right)\right)\right)& <\mathsf{Ϝ}\left(\Im \left(0,d\left(b_{n+1},{\Gamma }_{2}c\right)\right)\right),\hfill \end{array}$$

as $\mathsf{Ϝ}\in F^{*}$, then

$$\begin{array}{cc}\hfill \Im \left(0,d\left(b_n,{\Gamma }_{1}c\right)\right)& <\Im \left(0,d\left(b_{n+1},{\Gamma }_{2}c\right)\right),\hfill \\ \hfill \underset{n\to \infty }{lim}\Im \left(0,d\left(b_n,{\Gamma }_{1}c\right)\right)& <\underset{n\to \infty }{lim}\Im \left(0,d\left(b_{n+1},{\Gamma }_{2}c\right)\right),\hfill \\ \hfill \Im \left(0,\underset{n\to \infty }{lim}d\left(b_n,{\Gamma }_{1}c\right)\right)& <\Im \left(0,\underset{n\to \infty }{lim}d\left(b_{n+1},{\Gamma }_{2}c\right)\right),\hfill \\ \hfill \Im \left(0,\underset{n\to \infty }{lim}d\left(b_n,{\Gamma }_{1}c\right)\right)& <\Im \left(0,0\right),\hfill \\ \hfill \underset{n\to \infty }{lim}d\left(b_n,{\Gamma }_{1}c\right)& =0,\hfill \end{array}$$

Using ($B_3$)

$$\begin{array}{cc}\hfill d\left({\Gamma }_{1}c,{\Gamma }_{2}c\right)& \le k\left\{d\left({\Gamma }_{1}c,b_n\right)+d\left(b_n,{\Gamma }_{2}c\right)\right\},\hfill \\ \hfill & \le k\underset{n\to \infty }{lim}\left\{d\left({\Gamma }_{1}c,b_n\right)+d\left(b_n,{\Gamma }_{2}c\right)\right\},\hfill \\ \hfill & =0,\hfill \\ \hfill {\Gamma }_{1}c& ={\Gamma }_{2}c.\hfill \end{array}$$

Thus, ${\Gamma }_{1}c={\Gamma }_{2}c$ and $c\in S$ are points of coincidence of ${\Gamma }_1$and ${\Gamma }_2$. In another case, from ($b_2$), there exists $v\in S$ such that, for a Cauchy sequence ${\left\{b_n\right\}}_{n\in \mathbb{N}\cup \left\{0\right\}}$ in S, $b_n\to v$ if $n\to \infty$. Thus, ${\Gamma }_1{a}_n=b_{n-1}\to v$ if $n\to \infty$. Also, as ${\Gamma }_2$ is continuous, then ${\Gamma }_2{\Gamma }_1{a}_n={\Gamma }_2{b}_{n-1}\to {\Gamma }_{2}v$ if $n\to \infty$. Using (18) and continuity of ${\Gamma }_2$

$$\begin{array}{cc}\hfill & \varkappa \left(\Im \left(0,d\left({\Gamma }_2{\Gamma }_1{a}_n,{\Gamma }_{2}v\right)\right)\right)+\mathsf{Ϝ}\left(\Im \left(0,d\left({\Gamma }_1{\Gamma }_2{a}_n,{\Gamma }_{1}v\right)\right)\right)\hfill \\ \hfill & \le \mathsf{Ϝ}\left(\Im \left(0,d\left({\Gamma }_2{\Gamma }_1{a}_n,{\Gamma }_{2}v\right)\right)\right),\hfill \end{array}$$

$$\mathsf{Ϝ}\left(\Im \left(0,d\left({\Gamma }_1{\Gamma }_2{a}_n,{\Gamma }_{1}v\right)\right)\right)<\mathsf{Ϝ}\left(\Im \left(0,d\left({\Gamma }_2{\Gamma }_1{a}_n,{\Gamma }_{2}v\right)\right)\right),$$

as $\mathsf{Ϝ}\in F^{*}$, then

$$\begin{array}{cc}\hfill \Im \left(0,d\left({\Gamma }_1{\Gamma }_2{a}_n,{\Gamma }_{1}v\right)\right)& <\Im \left(0,d\left({\Gamma }_2{\Gamma }_1{a}_n,{\Gamma }_{2}v\right)\right),\hfill \\ \hfill \underset{n\to \infty }{lim}\Im \left(0,d\left({\Gamma }_1{\Gamma }_2{a}_n,{\Gamma }_{1}v\right)\right)& <\underset{n\to \infty }{lim}\Im \left(0,d\left({\Gamma }_2{\Gamma }_1{a}_n,{\Gamma }_{2}v\right)\right),\hfill \end{array}$$

using $\left(a_3\right)$

$$\begin{array}{cc}\hfill \Im \left(0,\underset{n\to \infty }{lim}d\left({\Gamma }_1{\Gamma }_2{a}_n,{\Gamma }_{1}v\right)\right)& <\left(0,\underset{n\to \infty }{lim}d\left({\Gamma }_2{\Gamma }_1{a}_n,{\Gamma }_{2}v\right)\right),\hfill \\ \hfill \Im \left(0,\underset{n\to \infty }{lim}d\left({\Gamma }_1{\Gamma }_2{a}_n,{\Gamma }_{1}v\right)\right)& <\left(0,0\right),\hfill \\ \hfill \underset{n\to \infty }{lim}d\left({\Gamma }_1{\Gamma }_2{a}_n,{\Gamma }_{1}v\right)& =0.\hfill \end{array}$$

Thus, ${\Gamma }_1{\Gamma }_2{a}_n\to {\Gamma }_{1}v$ as $n\to \infty$ and hence ${\Gamma }_1$ is also continuous. Now, by using ($B_3$) and the compatibility of ${\Gamma }_1$ and ${\Gamma }_2$, this gives

$$\begin{array}{cc}\hfill d\left({\Gamma }_{1}v,{\Gamma }_{2}v\right)& \le \left\{d\left({\Gamma }_{1}v,{\Gamma }_1{\Gamma }_2{a}_n\right)+d\left({\Gamma }_1{\Gamma }_2{a}_n,{\Gamma }_2{\Gamma }_1{a}_n\right)+d\left({\Gamma }_2{\Gamma }_1{a}_n,{\Gamma }_{2}v\right)\right\},\hfill \\ \hfill d\left({\Gamma }_{1}v,{\Gamma }_{2}v\right)& \le {\displaystyle \underset{n\to \infty }{lim}}\left\{\begin{array}{c}d\left({\Gamma }_{1}v,{\Gamma }_1{\Gamma }_2{a}_n\right)+d\left({\Gamma }_1{\Gamma }_2{a}_n,{\Gamma }_2{\Gamma }_1{a}_n\right)\\ +d\left({\Gamma }_2{\Gamma }_1{a}_n,{\Gamma }_{2}v\right)\end{array}\right\},\hfill \\ \hfill d\left({\Gamma }_{1}v,{\Gamma }_{2}v\right)& \le \left\{\begin{array}{c}{\displaystyle \underset{n\to \infty }{lim}}d\left({\Gamma }_{1}v,{\Gamma }_1{\Gamma }_2{a}_n\right)+{\displaystyle \underset{n\to \infty }{lim}}d\left({\Gamma }_1{\Gamma }_2{a}_n,{\Gamma }_2{\Gamma }_1{a}_n\right)\\ +{\displaystyle \underset{n\to \infty }{lim}}d\left({\Gamma }_2{\Gamma }_1{a}_n,{\Gamma }_{2}v\right)\end{array}\right\},\hfill \\ \hfill d\left({\Gamma }_{1}v,{\Gamma }_{2}v\right)& \le \left\{0+0+0\right\},\hfill \\ \hfill d\left({\Gamma }_{1}v,{\Gamma }_{2}v\right)& \le 0,\hfill \\ \hfill {\Gamma }_{1}v& ={\Gamma }_{2}v.\hfill \end{array}$$

In both cases, ${\Gamma }_1$and ${\Gamma }_2$ have a point of coincidence. Now, to prove that ${\Gamma }_1$and ${\Gamma }_2$ have a unique point of coincidence. Suppose, on the contrary, that there are $a_1,a_2,b_1,b_2\in S$, and $a_1$ and $a_2$ are the point of distinct and point of coincidence, respectively, and $b_1\ne b_2$ such that ${\Gamma }_1{b}_1={\Gamma }_2{b}_1=a_1$ and ${\Gamma }_1{b}_2={\Gamma }_2{b}_2=a_2$. From (16),

$$\begin{array}{cc}\hfill \varkappa \left(\Im \left(0,d\left({\Gamma }_2{b}_1,{\Gamma }_2{b}_2\right)\right)\right)+\mathsf{Ϝ}\left(\Im \left(0,d\left({\Gamma }_1{b}_1,{\Gamma }_1{b}_2\right)\right)\right)& \le \mathsf{Ϝ}\left(\Im \left(0,d\left({\Gamma }_2{b}_1,{\Gamma }_2{b}_2\right)\right)\right),\hfill \\ \hfill \varkappa \left(\Im \left(0,d\left(a_1,a_2\right)\right)\right)+\mathsf{Ϝ}\left(\Im \left(0,d\left(a_1,a_2\right)\right)\right)& \le \mathsf{Ϝ}\left(\Im \left(0,d\left(a_1,a_2\right)\right)\right),\hfill \\ \hfill \mathsf{Ϝ}\left(\Im \left(0,d\left(a_1,a_2\right)\right)\right)& <\mathsf{Ϝ}\left(\Im \left(0,d\left(a_1,a_2\right)\right)\right),\hfill \end{array}$$

which is a contradiction, and hence, $c\in S$ is a unique point of coincidence of ${\Gamma }_1$and ${\Gamma }_2$. □

Remark 5. 

$\left(R_1\right)$. If $\left(b_1\right)$ holds and mappings ${\Gamma }_1$and ${\Gamma }_2$ are weakly compatible, then using Proposition 1 proves that ${\Gamma }_1$and ${\Gamma }_2$ have unique common fixed point

$\left(R_2\right)$. If $\left(b_2\right)$ holds, ${\Gamma }_1$and ${\Gamma }_2$ have a unique common fixed point, and using Proposition 1 proves that every compatible mapping ${\Gamma }_1$and ${\Gamma }_2$ are also weakly compatible mappings.

In the next non-trivial example, we validate the above Theorem 7 and Remark 4 by showing that ${\Gamma }_1$ and ${\Gamma }_2$ are not contraction mappings.

Example 2. 

Let $S=\left\{a_n=1+4+7+\cdots +\left(3n-2\right)=\frac{n\left(3n-1\right)}{2}:n\in \mathbb{N}\right\}$ and $d(a,b)=\left|a-b\right|$, then $\left(S,d\right)$ is a complete metric space. Consider two self-mappings ${\Gamma }_1,{\Gamma }_2:S\to S$defined by ${\Gamma }_{1}t=\frac{1}{t^2}$and ${\Gamma }_{2}t=\frac{1}{t}$, respectively, for all $t\in S$. Define a mapping $\Im :[0,+\infty )\times [0,+\infty )⟶\mathbb{R}$ by $\Im (r_1,r_2)=r_2-r_1$ for all $(r_1,r_2)\in [0,+\infty )\times [0,+\infty )$. Also, define $\mathsf{Ϝ}\in F^{*}$ and $\tau \in \Lambda$ by $\mathsf{Ϝ}\left(t\right)=60lnt$ and $\tau \left(t\right)=\frac{1}{70t}$, respectively. It can be checked, respectively, that ${\Gamma }_1$ and ${\Gamma }_2$ does not follow a Banach contraction. For this, consider the Picard–Jungck sequence such that ${\Gamma }_1{a}_{n-1}={\Gamma }_2{a}_n=b_n,\forall n\in \mathbb{N}\cup \left\{0\right\}$ in S. For the ${\Gamma }_1$ mapping,

$$\begin{array}{cc}\hfill d({\Gamma }_1{a}_m,{\Gamma }_1{a}_n)& =\left|{\Gamma }_1{a}_m-{\Gamma }_1{a}_n\right|,\hfill \\ \hfill & =\left|b_{m+1}-b_{n+1}\right|,\hfill \\ \hfill & =\left|\frac{\left(m+1\right)\left(3m+2\right)}{2}-\frac{\left(n+1\right)\left(3n+2\right)}{2}\right|,\hfill \\ \hfill & >\left|\frac{m\left(3m-1\right)}{2}-\frac{\left(n+1\right)\left(3n+2\right)}{2}\right|,\hfill \\ \hfill & =\left|\frac{\left(n+1\right)\left(3n+2\right)}{2}-\frac{m\left(3m-1\right)}{2}\right|,\hfill \\ \hfill & >\left|\frac{n\left(3n-1\right)}{2}-\frac{m\left(3m-1\right)}{2}\right|,\hfill \\ \hfill & =\left|a_n-a_m\right|,\hfill \\ \hfill & =d(a_m,a_n).\hfill \end{array}$$

Thus, the mapping ${\Gamma }_1$ does not satisfy the Banach contraction. Now, for the ${\Gamma }_2$ mapping

$$\begin{array}{cc}\hfill d({\Gamma }_2{a}_m,{\Gamma }_2{a}_n)& =\left|{\Gamma }_2{a}_m-{\Gamma }_2{a}_n\right|,\hfill \\ \hfill & =\left|b_m-b_n\right|,\hfill \\ \hfill & =\left|\frac{m\left(3m-1\right)}{2}-\frac{n\left(3n-1\right)}{2}\right|,\hfill \\ \hfill & =\left|a_n-a_m\right|,\hfill \\ \hfill & =d(a_m,a_n).\hfill \end{array}$$

Thus, the mapping ${\Gamma }_2$ does not satisfy the Banach contraction. Suppose that $X_1=\mathsf{Ϝ}\left(\Im (0,d({\Gamma }_{2}a,{\Gamma }_{2}b))\right)$ and $Y_1=\mathsf{Ϝ}(\Im (0,d({\Gamma }_{1}a,{\Gamma }_{1}b)))$, then consider

$$\begin{array}{cc}\hfill X_1-Y_1& =\mathsf{Ϝ}\left(\Im (0,d({\Gamma }_{2}a,{\Gamma }_{2}b))\right)-\mathsf{Ϝ}(\Im (0,d({\Gamma }_{1}a,{\Gamma }_{1}b))),\hfill \\ \hfill & =\mathsf{Ϝ}\left(d({\Gamma }_{2}a,{\Gamma }_{2}b)\right)-\mathsf{Ϝ}\left(d({\Gamma }_{1}a,{\Gamma }_{1}b)\right),\hfill \\ \hfill & =60lnd({\Gamma }_{2}a,{\Gamma }_{2}b)-60lnd({\Gamma }_{1}a,{\Gamma }_{1}b),\hfill \\ \hfill & =60ln\frac{d({\Gamma }_{2}a,{\Gamma }_{2}b)}{d({\Gamma }_{1}a,{\Gamma }_{1}b)},\hfill \end{array}$$

(21)

As $\mathsf{Ϝ}\in F^{*}$, then $d({\Gamma }_{2}a,{\Gamma }_{2}b)>d({\Gamma }_{1}a,{\Gamma }_{1}b)$; this implies that $60ln\frac{d({\Gamma }_{2}a,{\Gamma }_{2}b)}{d({\Gamma }_{1}a,{\Gamma }_{1}b)}\ge \frac{1}{70d({\Gamma }_{2}a,{\Gamma }_{2}b)}>0$. Therefore, from $\left(21\right)$,

$$\begin{array}{cc}\hfill X_1-Y_1& =60ln\frac{d({\Gamma }_{2}a,{\Gamma }_{2}b)}{d({\Gamma }_{1}a,{\Gamma }_{1}b)},\hfill \\ \hfill & >\frac{1}{70d({\Gamma }_{2}a,{\Gamma }_{2}b)},\hfill \\ \hfill & =\tau \left(d({\Gamma }_{2}a,{\Gamma }_{2}b)\right),\hfill \\ \hfill \varkappa \left(d({\Gamma }_{2}a,{\Gamma }_{2}b)\right)+Y_1& <X_1\hfill \end{array}$$

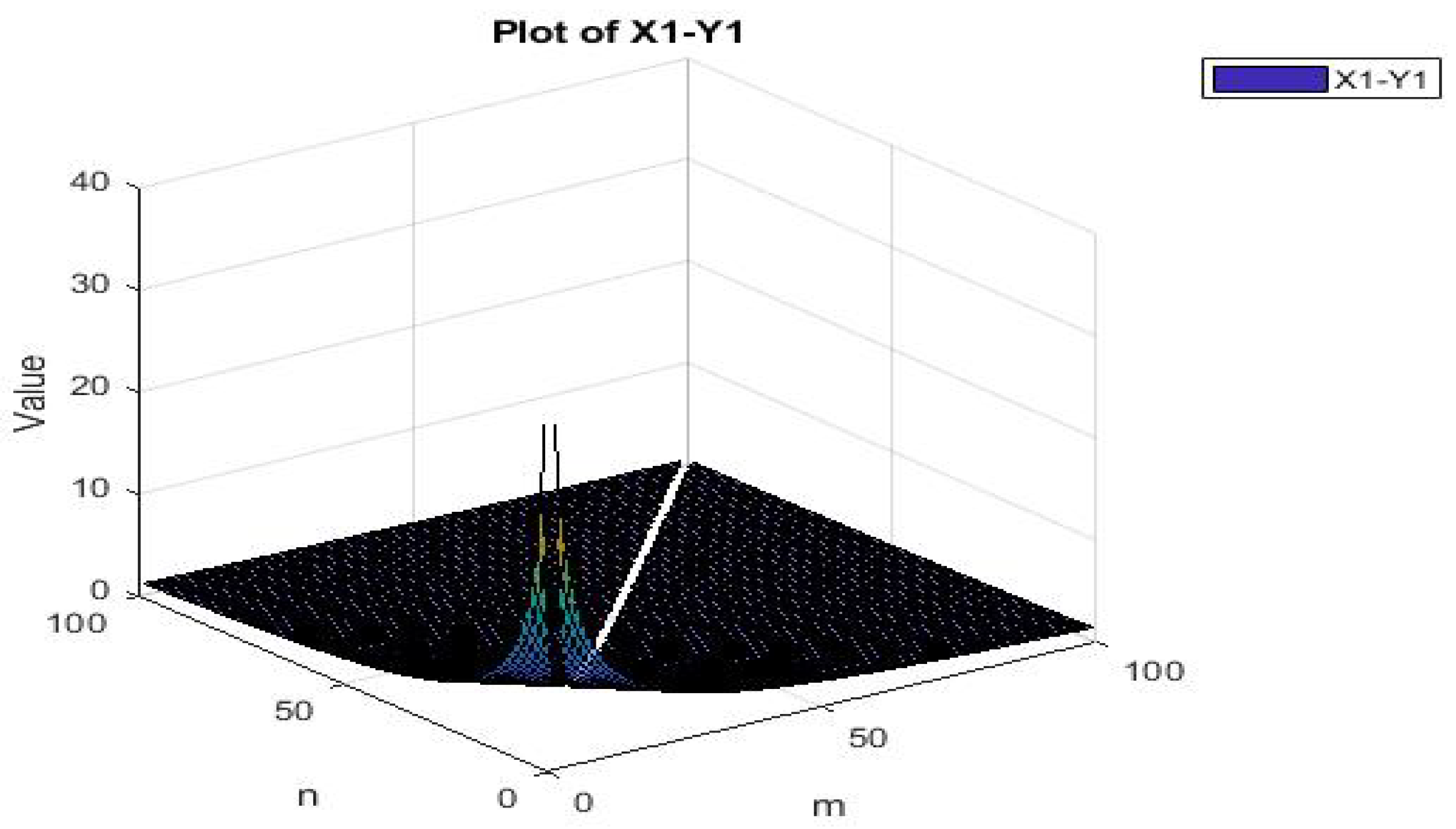
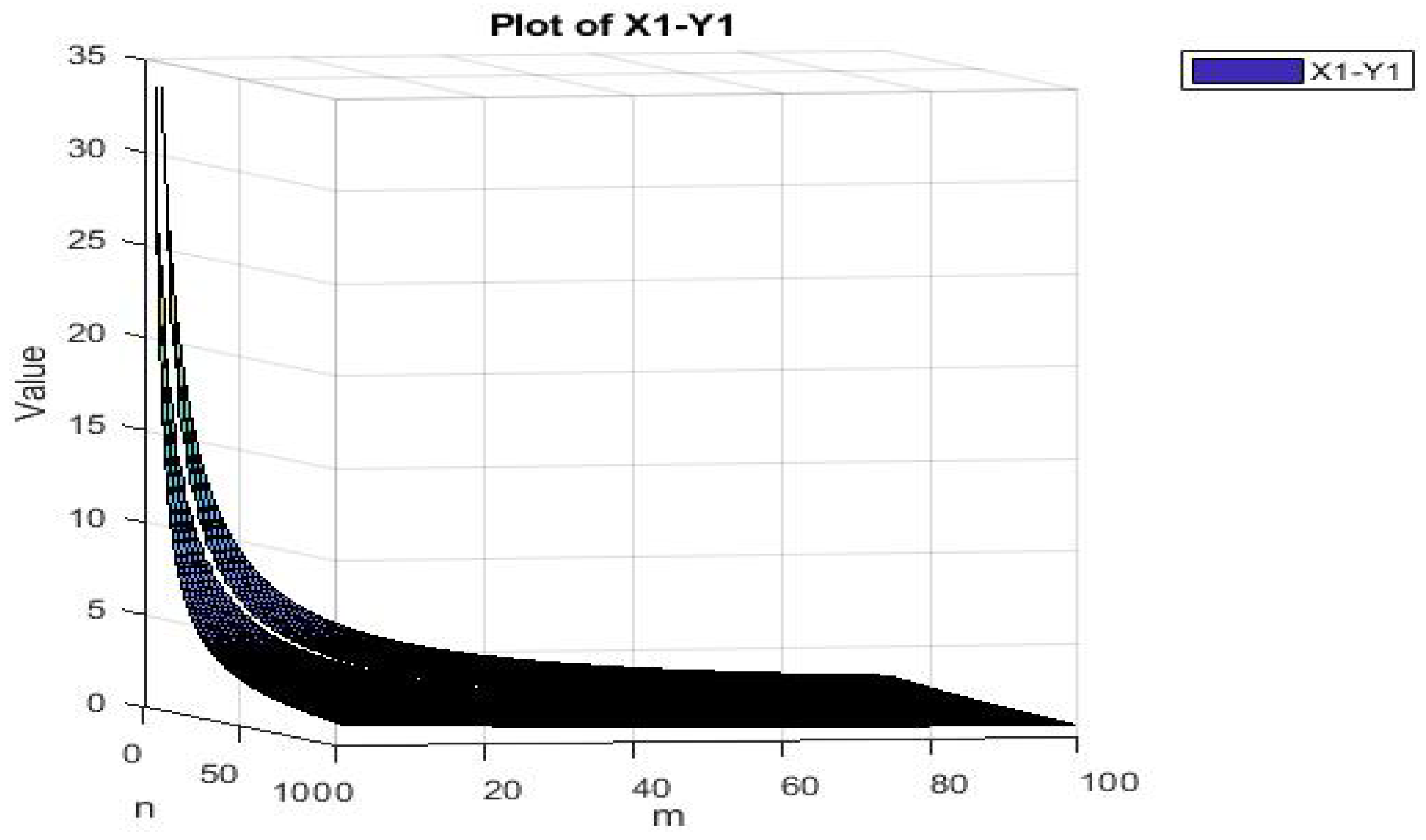
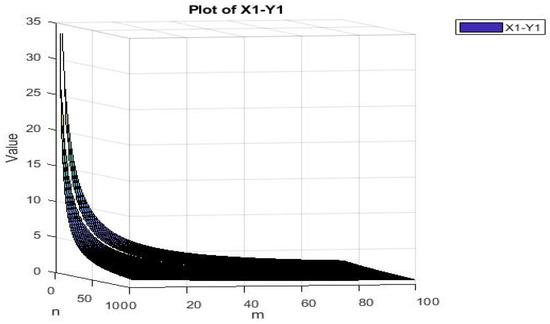
Consequently, it has been observed that, for $X_1-Y_1>0$ to reach some conclusion, this will allow us to choose and adjust the value of ϰ such that $X_1-Y_1>\varkappa >0.$ The following Figure 1 and Figure 2 show clearly that $X_1-Y_1>0.$

Figure 1. Graph of the difference X1–Y1.

Figure 2. Graph of the difference X1–Y1 from different angle.

Hence, all the conditions of the Theorem 7 are satisfied. Thus, the weakly compatible mappings ${\Gamma }_1$and ${\Gamma }_2$ have a unique point of coincidence and a common fixed point in S, i.e., ${\Gamma }_{1}1={\Gamma }_{2}1=1$.

In the above example, it can be seen that, in [28], only considering ${\Gamma }_1,$ with the same domain, the results of [16] are not valid, but here, ${\Gamma }_1$ has a unique fixed point ${\Gamma }_{1}1=1.$

4. Applications of Extended Integral Ϝ-Contraction and $(\mathit{\varkappa },$Ω-Ϝ)-Contraction

In this section, we explore some useful applications of our defined extended integral $\mathsf{Ϝ}$-contraction and $(\varkappa ,\Omega$-$\mathsf{Ϝ})$-contraction as well as its other variant for two mappings $(\varkappa ,{\Gamma }_{1,2},\Omega$-$\mathsf{Ϝ})$-contraction. Section 4 contains two subsections, namely Section 4.1 and Section 4.2. In Section 4.1, there two more subsections. In Section 4.1.1, we prove the existence result for a nonlinear the fractional boundary value problem involving Riemann–Liouville fractional order derivative of order $\sigma \in \left(1,2\right)$ using the extended integral $\mathsf{Ϝ}$-contraction. In Section 4.1.2, we prove the existence result for a nonlinear fractional boundary value problem using $(\varkappa ,\Omega$-$\mathsf{Ϝ})$ contraction. In Section 4.2, the existence result for the solution of a given nonlinear integral equation has been proven using the $(\varkappa ,{\Gamma }_{1,2},\Omega$-$\mathsf{Ϝ})$-contraction. An interesting example explaining the iterative procedure of the Picard–Jungck sequence is that of the convergence to the solution of the given integral equation.

4.1. Application in Nonlinear BVP

The existence theory for the solutions of the boundary value problems associated with fractional differential equations has been attracting numerous researchers in recent decades. Future research on multi-point boundary value problems for the Riemann–Liouville fractional order nonlinear differential equations can focus on developing efficient numerical methods, investigating the solution existence and uniqueness, analyzing the stability properties, and exploring interdisciplinary applications. For more comprehensive information and related sources on this subject, readers are referred to [29,30,31,32], as well as the recommended sources mentioned within those references. In the cited work [33], the study revolves around the utilization of classical fixed-point theory to explore the existence of at least one solution.

In this subsection, we explore the applications of extended integral $\mathsf{Ϝ}$-contraction and $(\varkappa ,\Omega$-$\mathsf{Ϝ})$-contraction to prove the existence results for multi-point boundary value problems of the Riemann–Liouville fractional order of the form

$$-{\mathcal{L}}_{0^{+}}^{\sigma }x\left(\top \right)=\mathbf{K}(x\left(\top \right),\top ),1<\sigma \le 2,0<\top <1$$

(22)

subjected to the boundary conditions $x\left(0\right)=0$ and $x\left(1\right)={\displaystyle {\displaystyle \sum }_{j=1}^{n-2}}{\lambda }_{j}x\left({\gamma }_j\right).$ Where ${\mathcal{L}}_{0^{+}}^{\sigma }$ is the Riemann–Liouville fractional order derivative and ${\lambda }_j,{\gamma }_j\in \left(0,1\right)$ with conditions $\delta ={\displaystyle \sum _{j=1}^{n-2}}{\lambda }_j{\gamma }_j^{\sigma -1}<1$ and $\mathbf{K}:[0,1]\times \left[0,\infty \right)⟶\mathbb{R}$ is a continuous function.

The integral form for the problem $\left(22\right)$ is given by

$$x(\top )=\underset{0}{\stackrel{1}{\int }}G\left(\top ,v\right)\mathbf{K}(x\left(v\right),v)dv.$$

where $G\left(t,v\right)$ is a Green function given by

$$G\left(\top ,v\right)=\frac{1}{\left(\sigma -1\right)!}\left\{\begin{array}{cc}\begin{array}{c}\frac{{\top }^{\sigma -1}}{1-\delta }\left({\left(1-v\right)}^{\sigma -1}-{\displaystyle {\displaystyle \sum }_{j=1}^{n-2}}{\lambda }_j{\left({\gamma }_j-v\right)}^{\sigma -1}\right)\\ -{\left(v-\top \right)}^{\sigma -1};\end{array}& \begin{array}{c}v\le \top ,{\gamma }_{j-1}\le v\le {\gamma }_j,\\ j=1,2,3,\dots ,n-1,\end{array}\\ \frac{{\top }^{\sigma -1}}{1-\delta }\left({\left(1-v\right)}^{\sigma -1}-{\displaystyle {\displaystyle \sum }_{j=1}^{n-2}}{\lambda }_j{\left({\gamma }_j-v\right)}^{\sigma -1}\right);& \begin{array}{c}\top \le v,{\gamma }_{j-1}\le v\le {\gamma }_j,\\ j=1,2,3,\dots ,n-1.\end{array}\end{array}\right.$$

Let $S=C[0,1]$ and a function $\Gamma :S\to S$, where the $C[0,1]$space of all continuous functions defined on $[0,1]$with b-metric (with constant $k\ge 1$) is defined by

$$d(a,b)=\underset{v\in [0,1]}{max}{\left|a\left(v\right)-b\left(v\right)\right|}^2$$

for all $a,b\in S$. For the solution of the BVP $\left(22\right)$, define a mapping $\Gamma :S\to S$ by

$$\Gamma x(\top )=\underset{0}{\stackrel{1}{\int }}G\left(\top ,v\right)\mathbf{K}(x\left(v\right),v)dv.$$

(23)

Assume that $\left|G\left(\top ,v\right)\right|\le \stackrel{’}{N}$ for some real positive number $\stackrel{’}{N}$.

4.1.1. Using the Extended Integral Ϝ-Contraction

First, the application of the extended integral $\mathsf{Ϝ}$-contraction to the existence result for the solution of the nonlinear BVP $\left(22\right)$ is given in the following theorem.

Theorem 8. 

Assume that $\mathbf{K}:\left[0,\infty \right)\times [0,1]⟶\mathbb{R}$ is a continuous function and

$$\left|\mathbf{K}(a\left(v\right),v)-\mathbf{K}(b\left(v\right),v)\right|\le \frac{1}{\stackrel{’}{N}}\sqrt{e^{-\varsigma \left(M\right(a\left(v\right),b\left(v\right)\left)\right)}M(a\left(v\right),b\left(v\right))}$$

(24)

for all $a,b\in S$,$e^{-\varsigma \left(u\right)}\ge 0$ for $\varsigma \in \Lambda$ and $v\in [0,1]$, where

$$M(a\left(v\right),b\left(v\right))=\eta \underset{t\in [0,1]}{max}\left\{\begin{array}{c}{\left|a\left(v\right)-b\left(v\right)\right|}^2,\left|a\left(v\right)-\Gamma a{\left(v\right)}^2\right|,{\left|b\left(v\right)-\Gamma b\left(v\right)\right|}^2,\\ \left(\frac{{\left|a\left(v\right)-\Gamma b\left(v\right)\right|}^2+{\left|b\left(v\right)-\Gamma a(t\setminus v)\right|}^2}{1+{\left|a\left(v\right)-\Gamma a\left(v\right)\right|}^2+{\left|b\left(v\right)-\Gamma b\left(v\right)\right|}^2}\right){\left|a\left(v\right)-b\left(v\right)\right|}^2\end{array}\right\},$$

where $\eta \in \left(0,\frac{1}{k^2}\right)$ and $k\ge 1$. Then, the BVP $\left(22\right)$ is subject to boundary conditions and has a unique solution in $C[0,1]$.

Proof. 

For $a,b\in S$, $v\in [0,1]$ and for the mapping $\Gamma :S\to S$, given in $\left(23\right),$ consider

$$\begin{array}{cc}\hfill {\left|\Gamma a\left(v\right)-\mathbf{\Gamma }b\left(v\right)\right|}^2& ={\left|\underset{0}{\stackrel{1}{\int }}G\left(t,v\right)\mathbf{K}(a\left(v\right),v)dv-\underset{0}{\stackrel{1}{\int }}G\left(t,v\right)\mathbf{K}(b\left(v\right),v)dv\right|}^2,\hfill \\ \hfill d(\Gamma a,\Gamma b)& =\underset{v\in [0,1]}{max}{\left|\underset{0}{\stackrel{1}{\int }}G\left(t,v\right)\left(\mathbf{K}\left(a\right(v),v)dv-\mathbf{K}\left(b\right(v),v)\right)dv\right|}^2,\hfill \\ \hfill & \le {\left(\underset{0}{\stackrel{1}{\int }}\underset{v\in [0,1]}{max}\left|G\left(t,v\right)\left(\mathbf{K}\left(a\right(v),v)-\mathbf{K}\left(b\right(v),v)\right)\right|dv\right)}^2,\hfill \\ \hfill & ={\left(\underset{0}{\stackrel{1}{\int }}\underset{v\in [0,1]}{max}\left|G\left(t,v\right)\right|\left|\left(\mathbf{K}\left(a\right(v),v)-\mathbf{K}\left(b\right(v),v)\right)\right|dv\right)}^2,\hfill \\ \hfill & \le {\left(\underset{0}{\stackrel{1}{\int }}\stackrel{’}{N}\underset{v\in [0,1]}{max}\left|\left(\mathbf{K}\left(a\right(v),v)-\mathbf{K}\left(b\right(v),v)\right)\right|dv\right)}^2,\hfill \end{array}$$

from $\left(24\right)$, we have

$$\begin{array}{cc}\hfill d(\Gamma a,\Gamma b)& \le {\left(\underset{0}{\stackrel{1}{\int }}\sqrt{e^{-\varsigma \left(M\right(a\left(v\right),b\left(v\right)\left)\right)}M(a\left(v\right),b\left(v\right))}dv\right)}^2,\hfill \\ \hfill & \le {\left(\sqrt{e^{-\varsigma \left(M\right(a\left(v\right),b\left(v\right)\left)\right)}M(a\left(v\right),b\left(v\right))}\underset{0}{\stackrel{1}{\int }}dv\right)}^2,\hfill \\ \hfill d(\Gamma a,\Gamma b)& \le e^{-\varsigma \left(M\right(a\left(v\right),b\left(v\right)\left)\right)}M(a\left(v\right),b\left(v\right)).\hfill \end{array}$$

(25)

Consider $\varrho \left(M\right(a\left(v\right),b\left(v\right)\left)\right)=\varsigma \left(M\right(a\left(v\right),b\left(v\right)\left)\right)\in \Lambda ,\mathsf{Ϝ}\left(r\right)=lnr$ such that $\mathsf{Ϝ}\in F^{*}$ and $\xi \left(\tau \right)=1$. Hence,

$$\begin{array}{cc}\hfill \varrho \left(M(a\left(v\right),b\left(v\right))\right)+\mathsf{Ϝ}\left(\underset{0}{\stackrel{d(\Gamma a,\Gamma b)}{\int }}\xi \left(\tau \right)d\tau \right)& =\varsigma \left(M(a\left(v\right),b\left(v\right))\right)+\mathsf{Ϝ}\left(\underset{0}{\stackrel{d(\Gamma a,\Gamma b)}{\int }}1d\tau \right),\hfill \\ \hfill & =\varsigma \left(M(a\left(v\right),b\left(v\right))\right)+\mathsf{Ϝ}\left(d\left(\Gamma a,\Gamma b\right)\right),\hfill \\ \hfill & =\varsigma \left(M(a\left(v\right),b\left(v\right))\right)+ln\left(d\left(\Gamma a,\Gamma b\right)\right),\hfill \\ \hfill & \le \varsigma \left(M\right(a\left(v\right),b\left(v\right)\left)\right)\hfill \\ \hfill & +ln\left(e^{-\varsigma \left(M\right(a\left(v\right),b\left(v\right)\left)\right)}M(M(a\left(v\right),b\left(v\right))\right),\mathrm{from}\left(25\right),\hfill \\ \hfill & =\varsigma \left(M\right(a\left(v\right),b\left(v\right)\left)\right)-\varsigma \left(M\right(a\left(v\right),b\left(v\right)\left)\right)\hfill \\ \hfill & +ln\left(M\left(a\right(v),b(v\left)\right)\right),\hfill \\ \hfill & =ln\left(M\left(a\right(v),b(v\left)\right)\right).\hfill \end{array}$$

(26)

Also, as

$$\begin{array}{cc}\hfill \mathsf{Ϝ}\left(\underset{0}{\stackrel{M\left(a\right(v),b(v\left)\right)}{\int }}\xi \left(\tau \right)d\tau \right)& =\mathsf{Ϝ}\left(\underset{0}{\stackrel{M\left(a\right(v),b(v\left)\right)}{\int }}1d\tau \right)\hfill \\ \hfill & =\mathsf{Ϝ}\left(M\left(a\right(v),b(v\left)\right)\right).\hfill \end{array}$$

(27)

From $\left(26\right)$ and $\left(27\right)$,

$$\varrho \left(M(a\left(v\right),b\left(v\right))\right)+\mathsf{Ϝ}\left(\underset{0}{\stackrel{d(\Gamma a,\Gamma b)}{\int }}\xi \left(\tau \right)d\tau \right)\le \mathsf{Ϝ}\left(\underset{0}{\stackrel{M\left(a\right(v),b(v\left)\right)}{\int }}\xi \left(\tau \right)d\tau \right).$$

Hence, the mapping $\Gamma$ satisfies the extended integral $\mathsf{Ϝ}$-contraction. Therefore, $\Gamma$ has a unique fixed point in $C[0,1]$ and which is the unique solution of BVP $\left(22\right)$. □

4.1.2. Using $(\varkappa ,\Omega$-$\mathsf{Ϝ})$-Contraction

Now, we will use our second main result related to the $(\varkappa ,\Omega$-$\mathsf{Ϝ})$-contraction to discuss the existence result for nonlinear BVP $\left(22\right)$ in the next theorem as follows.

Theorem 9. 

Assume $\mathbf{K}:[0,1]\times \left[0,\infty \right)⟶\mathbb{R}$ is a continuous function and

$$\left|\mathbf{K}(a\left(v\right),v)-\mathbf{K}(b\left(v\right),v)\right|\le \frac{1}{\stackrel{’}{N}}\sqrt{e^{-\varkappa \left(u\right)}d(a,b)},$$

(28)

for all $a,b\in S$, where $e^{-\varkappa \left(u\right)}\ge 0$ for $\varkappa \in \Lambda$, $d(a,b)={\left|a\left(v\right)-b\left(v\right)\right|}^2$ and $v\in [0,1]$. Then, the BVP $\left(22\right)$, subjected to boundary conditions, has a unique solution in $C\left[0,1\right]$.

Proof. 

For $a,b\in S$, $v\in [0,1]$ and mapping $\Gamma :S\to S$, consider

$$\begin{array}{cc}\hfill {\left|\Gamma a\left(v\right)-\Gamma b\left(v\right)\right|}^2& ={\left|\underset{0}{\stackrel{1}{\int }}G\left(t,v\right)\mathbf{K}(a\left(v\right),v)dv-\underset{0}{\stackrel{1}{\int }}G\left(t,v\right)\mathbf{K}(b\left(v\right),v)dv\right|}^2,\hfill \\ \hfill d(\Gamma a,\Gamma b)& =\underset{v\in [0,1]}{max}{\left|\underset{0}{\stackrel{1}{\int }}G\left(t,v\right)\left(\mathbf{K}\left(a\right(v),v)dv-\mathbf{K}\left(b\right(v),v)\right)dv\right|}^2,\hfill \\ \hfill & \le {\left(\underset{0}{\stackrel{1}{\int }}\underset{v\in [0,1]}{max}\left|G\left(t,v\right)\left(\mathbf{K}\left(a\right(v),v)dv-\mathbf{K}\left(b\right(v),v)\right)\right|dv\right)}^2,\hfill \\ \hfill & ={\left(\underset{0}{\stackrel{1}{\int }}\underset{v\in [0,1]}{max}\left|G\left(t,v\right)\right|\left|\mathbf{K}\left(a\right(v),v)-\mathbf{K}\left(b\right(v),v)\right|dv\right)}^2,\hfill \\ \hfill & <{\left(\underset{0}{\stackrel{1}{\int \stackrel{’}{N}}}\underset{v\in [0,1]}{max}\left|\mathbf{K}\left(a\right(v),v)-\mathbf{K}\left(b\right(v),v)\right|dv\right)}^2,\hfill \\ \hfill & \le {\left(\underset{0}{\stackrel{1}{\int }}\sqrt{e^{-\varkappa \left(u\right)}d(a,b)}dv\right)}^2,\mathrm{From}\left(25\right)\hfill \\ \hfill & ={\left(\sqrt{e^{-\varkappa \left(u\right)}d(a,b)}\underset{0}{\stackrel{1}{\int }}dv\right)}^2,\hfill \\ \hfill & =e^{-\varkappa \left(u\right)}d(a,b).\hfill \end{array}$$

(29)

Taking $\varkappa \left(u\right)=\frac{\varsigma \left(u\right)}{2}>0,\mathsf{Ϝ}\left(r\right)=lnr$ such that $\mathsf{Ϝ}\in F^{*}$,and $\Im (u,v)=u+\sqrt{v}$ gives

$$\begin{array}{cc}\hfill \varrho \left(u\right)+\mathsf{Ϝ}\left(\Im (0,d(\Gamma a,\Gamma b\left)\right)\right)& =\frac{\varsigma \left(u\right)}{2}+ln\left(\Im \left(0,\sqrt{d(\Gamma x,\Gamma y)}\right)\right),\hfill \\ \hfill & =\frac{\varsigma \left(u\right)}{2}+\frac{1}{2}lnd(\Gamma x,\Gamma y),\hfill \\ \hfill & \le \frac{\varsigma \left(u\right)}{2}+\frac{1}{2}ln{e}^{{}^{-\varsigma \left(u\right)}}d(a,b),\mathrm{from}\left(25a\right),\hfill \\ \hfill & =\frac{\varsigma \left(u\right)}{2}+\frac{1}{2}\left(-\varsigma \left(u\right)+lnd(a,b)\right),\hfill \\ \hfill & =\frac{\varsigma \left(u\right)}{2}-\frac{\varsigma \left(u\right)}{2}+\frac{1}{2}lnd(a,b),\hfill \\ \hfill & =ln\sqrt{d(a,b)},\hfill \\ \hfill & =\mathsf{Ϝ}\left(\sqrt{d(a,b)}\right),\hfill \\ \hfill & =\mathsf{Ϝ}\left(0+\sqrt{d(a,b)}\right),\hfill \\ \hfill & =\mathsf{Ϝ}\left(\Im (0,d(a,b\left)\right)\right),\hfill \\ \hfill \varrho \left(u\right)+\mathsf{Ϝ}\left(\Im (0,d(\Gamma a,\Gamma b\left)\right)\right)& \le \mathsf{Ϝ}\left(\Im (0,d(a,b\left)\right)\right).\hfill \end{array}$$

hence, $\Gamma$ satisfies the $(\Omega$-$\mathsf{Ϝ})$-contraction. Therefore, $\Gamma$ has a unique fixed point in $C[0,1]$ and it is also a unique solution of BVP $\left(22\right)$. □

4.2. Solution of Integral Equation Using $(\varkappa ,{\Gamma }_{1,2},\Omega$-$\mathsf{Ϝ})$-Contraction

To examine the existence and uniqueness of a solution within a broad category of Fredholm integral equations of the second kind, there are different assumptions concerning the functions at hand. In order to establish the outcome, Theorem 7 is employed in conjunction with a function space $S=\left(C[x,y],\mathbb{R}\right)$ and a contractive inequality. Let us consider the integral equation

$$ga\left(u\right)=f\left(u\right)+\mu \underset{x}{\stackrel{y}{{\displaystyle \int }}}K\left(u,v\right)ha\left(t\right)dt.$$

(30)

where $a:[x,y]\to \mathbb{R}$, given functions $f:[x,y]\to \mathbb{R}$, and $h,g:\mathbb{R}\to \mathbb{R}$, are all continuous and a parameter $\mu \in \mathbb{R}$. The integral equation’s kernel, denoted by K, is defined on the domain $[x,y]\times [x,y]$. In the specific case where both f and h correspond to the identity mapping I on $\mathbb{R}$, Equation $\left(30\right)$ is commonly referred to as a Fredholm integral equation of the second kind. Further details and relevant references on this subject can be found in [34,35,36,37], along with the cited sources therein.

The subsequent theorem provides a comprehensive methodology for solving Equation (30) utilizing the techniques used in Theorem 7.

Theorem 10. 

Assuming continuity of $K,f,g$, and h, and for all $t,u\in \left[x,y\right]$, $\left|K(u,t)\right|<c_{\circ }$. Moreover, for each $a\in S$, there exists $b\in S$ in satisfying the equation

$$\left(gb\right)\left(u\right)=f\left(u\right)+\mu \underset{x}{\stackrel{y}{{\displaystyle \int }}}K(u\left(t\right),t)\left(ha\right)\left(t\right)dt.$$

(31)

If g is an injective mapping, there exists $\pounds \in {\mathbb{R}}^{+}$ such that, for all $a,b\in \mathbb{R}$

$$|ha-hb|\le \pounds |ga-gb|.$$

Additionally, the set $\left\{ga:a\in S\right\}$ is complete. Then, for $\left|\mu \right|\le \frac{e^{-\tau \left(d\left(ga,gb\right)\right)}}{c_{\circ }\pounds \left(y-x\right)},$ where $\varkappa \in \Lambda$, defined by $\varkappa \left(t\right)=e^{-t}$ and $\mathsf{Ϝ}\left(r\right)=lnr$, such that $\mathsf{Ϝ}\in F^{*}$, for $a,b\in S$, there exists a function $c\in S$ such that, for $a_0\in S$, the functional integral equation

$$gc\left(u\right)=\underset{n\to \infty }{lim}g{a}_n\left(u\right)=\underset{n\to \infty }{lim}\left[f\left(u\right)+\mu \underset{x}{\stackrel{y}{{\displaystyle \int }}}K(u\left(t\right),t).h{a}_{n-1}\left(t\right)dt\right]$$

and c represents the unique solution of Equation $\left(30\right)$.

Proof. 

Consider the metric space $(S,d)$, where $d\left(a,b\right)=\underset{t\in \left[x,y\right]}{\max }\left|a\left(t\right)-b\left(t\right)\right|$ for all $a,b\in S$. Let ${\Gamma }_1$ and ${\Gamma }_2$ be self-mappings on S defined by

$$\left({\Gamma }_{1}a\right)\left(u\right)=f\left(u\right)+\mu \underset{x}{\stackrel{y}{{\displaystyle \int }}}K(u\left(t\right),t)\left(ha\right)\left(t\right)dt\mathrm{and}{\Gamma }_{2}a=ga.$$

Under the assumption that $({\Gamma }_{2}S,d)$ is a complete space, where ${\Gamma }_{2}S=\left\{{\Gamma }_{2}s:s\in S\right\}$. Let $a^{*}\in {\Gamma }_{1}S$, then there exists an element $a\in S$ such that $a^{*}={\Gamma }_{1}a$, implying that $a^{*}\left(t\right)={\Gamma }_{1}a\left(t\right)$. Using Equation $\left(31\right)$ and the mapping described above, we can observe that, for any $b\in S$, we have ${\Gamma }_{1}a\left(t\right)=gb\left(t\right)={\Gamma }_{2}b\left(t\right)$. Consequently, this implies that ${\Gamma }_{1}a={\Gamma }_{2}b\in {\Gamma }_{2}S$ and the inclusion ${\Gamma }_{1}S\subseteq {\Gamma }_{2}S$. Now

$$\begin{array}{cc}\hfill \left|\left({\Gamma }_{1}a\right)\left(u\right)-\left({\Gamma }_{1}b\right)\left(u\right)\right|& =\left|\mu \underset{x}{\stackrel{y}{{\displaystyle \int }}}K(u\left(t\right),t)\left(ha\right)\left(t\right)dt-\mu \underset{x}{\stackrel{y}{{\displaystyle \int }}}K(u\left(t\right),t)\left(hb\right)\left(t\right)dt\right|,\hfill \\ \hfill & =\left|\mu \right|\left|\underset{x}{\stackrel{y}{{\displaystyle \int }}}K(u\left(t\right),t)\left(ha\right)\left(t\right)dt-\underset{x}{\stackrel{y}{{\displaystyle \int }}}K(u\left(t\right),t)\left(hb\right)\left(t\right)dt\right|,\hfill \\ \hfill & =\left|\mu \right|\left|\underset{x}{\stackrel{y}{{\displaystyle \int }}}K(u\left(t\right),t)\left(\left(ha\right)\left(t\right)-\left(hb\right)\left(t\right)\right)dt\right|,\hfill \end{array}$$

which implies

$$\begin{array}{cc}\hfill \left|\left({\Gamma }_{1}a\right)\left(u\right)-\left({\Gamma }_{1}b\right)\left(u\right)\right|& \le \left|\mu \right|\underset{x}{\stackrel{y}{{\displaystyle \int }}}\left|K(u\left(t\right),t)\right|\left|\left(ha\right)\left(t\right)-\left(hb\right)\left(t\right)\right|dt,\hfill \\ \hfill & <\left|\mu \right|k{c}_{\circ }\left|\left(ha\right)\left(t\right)-\left(hb\right)\left(t\right)\right|\underset{x}{\stackrel{y}{{\displaystyle \int }}}dt,\hfill \\ \hfill d\left({\Gamma }_{1}a,{\Gamma }_{1}b\right)& <\left|\mu \right|c_{\circ }\left(y-x\right)\underset{t\in \left[x,y\right]}{max}\pounds \left|\left(ga\right)\left(t\right)-\left(gb\right)\left(t\right)\right|,\hfill \\ \hfill & =\left|\mu \right|c_{\circ }\pounds \left(y-x\right)d\left(ga,gb\right),\hfill \\ \hfill & =\left|\mu \right|c_{\circ }\pounds \left(y-x\right)d\left({\Gamma }_{2}a,{\Gamma }_{2}b\right),\hfill \\ \hfill & <\frac{e^{-\tau \left(d\left(ga,gb\right)\right)}}{c_{\circ }\pounds \left(y-x\right)}{c}_{\circ }\pounds \left(y-x\right)d\left({\Gamma }_{2}a,{\Gamma }_{2}b\right),\hfill \\ \hfill & =e^{-\tau \left(d\left(ga,gb\right)\right)}d\left({\Gamma }_{2}a,{\Gamma }_{2}b\right),\hfill \end{array}$$

$$\begin{array}{cc}\hfill lnd\left({\Gamma }_{1}a,{\Gamma }_{1}b\right)& <ln{e}^{-\tau \left(d\left(ga,gb\right)\right)}+lnd\left({\Gamma }_{2}a,{\Gamma }_{2}b\right),\hfill \\ \hfill \mathsf{Ϝ}\left(d\left({\Gamma }_{1}a,{\Gamma }_{1}b\right)\right)& <-\varkappa \left(d\left(ga,gb\right)\right)+\mathsf{Ϝ}\left(d\left({\Gamma }_{2}a,{\Gamma }_{2}b\right)\right),\hfill \\ \hfill \mathsf{Ϝ}\left(d\left({\Gamma }_{1}a,{\Gamma }_{1}b\right)-0\right)& <-\varkappa \left(d\left(ga,gb\right)-0\right)+\mathsf{Ϝ}\left(d\left({\Gamma }_{2}a,{\Gamma }_{2}b\right)-0\right),\hfill \\ \hfill \varkappa \left(\Im \left(0,d\left({\Gamma }_{2}a,{\Gamma }_{2}b\right)\right)\right)+\mathsf{Ϝ}\left(\Im \left(0,d\left({\Gamma }_{1}a,{\Gamma }_{1}b\right)\right)\right)& \le \mathsf{Ϝ}\left(\Im \left(0,d\left({\Gamma }_{2}a,{\Gamma }_{2}b\right)\right)\right).\hfill \end{array}$$

Hence, the mappings ${\Gamma }_1$ and ${\Gamma }_2$ satisfy all the conditions of Theorem 7. Thus, for $a_0\in S$, there exists a unique $c\in S$ such that

$$\begin{array}{cc}\hfill gc\left(t\right)& ={\Gamma }_{2}c\left(t\right)=\underset{n\to \infty }{lim}{\Gamma }_2{a}_n\left(t\right),(\mathrm{by}\mathrm{continuity}\mathrm{of}{\Gamma }_2),\hfill \\ \hfill gc\left(t\right)& =\underset{n\to \infty }{lim}{\Gamma }_1{a}_{n+1}\left(t\right),\hfill \\ \hfill gc\left(t\right)& =\underset{n\to \infty }{lim}\left[f\left(u\right)+\mu \underset{x}{\stackrel{y}{{\displaystyle \int }}}K(u\left(t\right),t).h{a}_{n-1}\left(t\right)dt\right],\hfill \\ \hfill gc\left(t\right)& =f\left(u\right)+\mu \underset{x}{\stackrel{y}{{\displaystyle \int }}}K(u\left(t\right),t).h\underset{n\to \infty }{lim}{a}_{n-1}\left(t\right)dt,\hfill \end{array}$$

$$\begin{array}{cc}\hfill gc\left(t\right)& =f\left(u\right)+\mu \underset{x}{\stackrel{y}{{\displaystyle \int }}}K(u\left(t\right),t).hc\left(t\right)dt,\hfill \\ \hfill gc\left(t\right)& ={\Gamma }_{1}c\left(t\right),\hfill \end{array}$$

which implies that $gc\left(t\right)={\Gamma }_{2}c\left(t\right)={\Gamma }_{1}c\left(t\right)$ for all $t\in \left[x,y\right]$ and $c\in S$ is a unique solution of $\left(30\right)$. □

The following example validates all the conditions of Theorem 10 to find the solution of a given nonlinear integral equation.

Example 3. 

Suppose

$$2a^2\left(u\right)=u+\mu \underset{0}{\stackrel{1}{{\displaystyle \int }}}ut.a^2\left(t\right)dt,$$

(32)

with $ga=2a^2$, $ha=a^2$, and $f\left(u\right)=u$. Let $S=\left(C\left[0,1\right],\mathbb{R}\right)$ and $d\left(a,b\right)={\displaystyle \underset{u\in \left[0,1\right]}{max}}\left|a\left(u\right)-b\left(u\right)\right|$ for all $a,b\in S$. Also, as $K(u\left(t\right),t)=ut\le 1$

$$\left|K(u\left(t\right),t)\right|\le 1,\mathit{for}\mathit{all}t,u\in \left[0,1\right].$$

Again, as

$$\begin{array}{cc}\hfill \left|hb-ha\right|& =\left|b^2-a^2\right|\hfill \\ \hfill & =\frac{1}{2}\left|2b^2-2a^2\right|,\hfill \\ \hfill \left|hb-ha\right|& =\frac{1}{2}\left|gb-ga\right|,\hfill \end{array}$$

$\forall a,b\in S$, $\pounds =\frac{1}{2}$ and $c_{\circ }=1$. Therefore, all the conditions of Theorem 10 are satisfied. Hence, there exists a unique solution for $\left(32\right)$, if, for $\tau \in \Lambda$, there exists μ such that

$$\left|\mu \right|\le \frac{e^{-\tau \left(d\left(ga,gb\right)\right)}}{c_{\circ }\pounds \left(y-x\right)}=\frac{2e^{-\tau \left(d\left(ga,gb\right)\right)}}{\left(1-0\right)}=\frac{2}{e^{\tau \left(d\left(ga,gb\right)\right)}},$$

where $\tau \left(d\left(ga,gb\right)\right)>0$ gives

$$\left|\mu \right|\le \frac{2}{e^{\tau \left(d\left(ga,gb\right)\right)}}<1$$

Hence, $\mu \in \left(-1,1\right)$. For the approximation of the solution of $\left(32\right)$, consider, for the self-mappings ${\Gamma }_1$ and ${\Gamma }_2$ defined on S, the iterative sequence of the form ${\Gamma }_1{a}_{n-1}={\Gamma }_2{a}_n$, where $a_0\in S$ and $n\in \mathbb{N}$. Define the mappings ${\Gamma }_1$, ${\Gamma }_2$ by

$${\Gamma }_{1}a\left(u\right)=u+\mu \underset{0}{\stackrel{1}{{\displaystyle \int }}}ut.a^2\left(t\right)dt,\mathit{and}{\Gamma }_{2}a\left(u\right)=2a^2\left(u\right).$$

Consider $a_0\in S$ such that $a_0\left(u\right)=0$ for $u\in \left[0,1\right]$. Then, for $n=1$

$$\begin{array}{cc}\hfill {\Gamma }_1{a}_0\left(u\right)& ={\Gamma }_2{a}_1\left(u\right),\hfill \\ \hfill u+\mu \underset{0}{\stackrel{1}{{\displaystyle \int }}}ut.a_0^2\left(t\right)dt& =2a_1^2\left(u\right),\hfill \\ \hfill a_1\left(u\right)& ={\left(\frac{u}{2}\right)}^{\frac{1}{2}}.\hfill \end{array}$$

For $n=2$,

$$\begin{array}{cc}\hfill {\Gamma }_1{a}_1\left(u\right)& ={\Gamma }_2{a}_2\left(u\right),\hfill \\ \hfill 2a_2^2\left(u\right)& =u+\mu \underset{0}{\stackrel{1}{{\displaystyle \int }}}ut.a_1^2\left(t\right)dt,\hfill \\ \hfill 2a_2^2\left(u\right)& =u+\mu \underset{0}{\stackrel{1}{{\displaystyle \int }}}\frac{u^2}{2}tdt=u+\frac{\mu u^2}{4},\hfill \\ \hfill a_2\left(u\right)& ={\left(\frac{u}{2}+\frac{\mu u^2}{2^3}\right)}^{\frac{1}{2}}={\left(\stackrel{2}{{\displaystyle \sum }_{i=1}}\frac{{\mu }^{i-1}{u}^i}{2^{2i-1}}\right)}^{\frac{1}{2}}.\hfill \end{array}$$

For $n=3$,

$$\begin{array}{cc}\hfill {\Gamma }_1{a}_2\left(u\right)& ={\Gamma }_2{a}_3\left(u\right),\hfill \\ \hfill 2a_3^2\left(u\right)& =u+\mu \underset{0}{\stackrel{1}{{\displaystyle \int }}}ut.a_2^2\left(t\right)dt,\hfill \\ \hfill 2a_3^2\left(u\right)& =u+\mu \underset{0}{\stackrel{1}{{\displaystyle \int }}}\left(\frac{u^2}{2}+\frac{\mu u^3}{2^3}\right)tdt=u+\frac{\mu u^2}{2^2}+\frac{{\mu }^2{u}^3}{2^4},\hfill \\ \hfill a_3\left(u\right)& ={\left(\frac{u}{2}+\frac{\mu u^2}{2^3}+\frac{{\mu }^2{u}^3}{2^5}\right)}^{\frac{1}{2}}={\left(\stackrel{3}{{\displaystyle \sum }_{i=1}}\frac{{\mu }^{i-1}{u}^i}{2^{2i-1}}\right)}^{\frac{1}{2}}.\hfill \end{array}$$

Inductively, continuing in the same way for $n\in \mathbb{N}$ gives $a_n\left(u\right)={\left({\displaystyle {\displaystyle \sum }_{i=1}^n}\frac{{\mu }^{i-1}{u}^i}{2^{2i-1}}\right)}^{\frac{1}{2}}$. Clearly, $a_n\left(u\right)$ is finite geometric progression with a common ration $\frac{\mu u}{2^2}<1$, $(\because -1<\mu <1$ and $0\le u\le 1$, which implies $0<\mu u<1\Rightarrow 0<\frac{\mu u}{2^2}<\frac{1}{2})$. Therefore,

$$a_n\left(u\right)={\left[\frac{\frac{u}{2}\left(1-{\left(\frac{\mu u}{2^2}\right)}^n\right)}{1-\frac{\mu u}{2^2}}\right]}^{\frac{1}{2}}={\left[\frac{2u}{2^2-\mu u}\left(1-{\left(\frac{\mu u}{2^2}\right)}^n\right)\right]}^{\frac{1}{2}}.$$

Hence,

$$\begin{array}{cc}\hfill {\Gamma }_1{a}_n\left(u\right)& =2a_n^2\left(u\right)={\Gamma }_2{a}_{n+1}\left(u\right),\hfill \\ \hfill {\Gamma }_1{a}_n\left(u\right)& =2\left[\frac{2u}{2^2-\mu u}\left(1-{\left(\frac{\mu u}{2^2}\right)}^n\right)\right]={\Gamma }_2{a}_{n+1}\left(u\right).\hfill \end{array}$$

As for $\mu \in \left(-1,1\right)$, the sequence ${\left\{a_n\left(u\right)\right\}}_{n\in \mathbb{N}}$ converges to $c\in S$ such that

$$\begin{array}{cc}\hfill \underset{n\to \infty }{lim}{\Gamma }_2{a}_{n+1}\left(u\right)& =\underset{n\to \infty }{lim}\frac{4u}{2^2-\mu u}\left(1-{\left(\frac{\mu u}{2^2}\right)}^n\right),\hfill \\ \hfill \underset{n\to \infty }{lim}{\Gamma }_{2}c\left(u\right)& =\frac{4u}{2^2-\mu u},\hfill \\ \hfill c\left(u\right)& =\frac{4u}{4-\mu u}\in \mathbb{R},\hfill \end{array}$$

which is the solution of $\left(32\right)$.

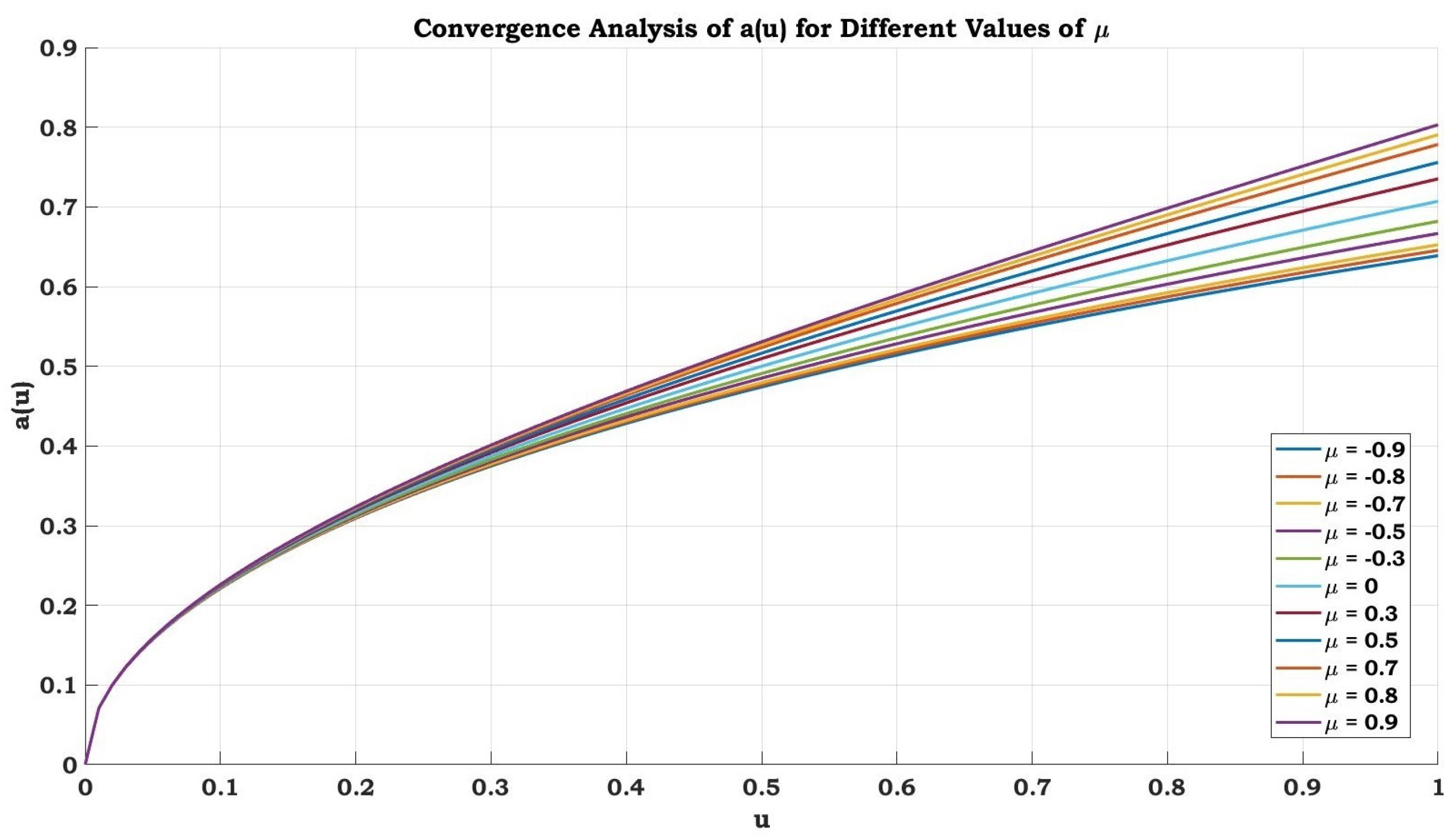
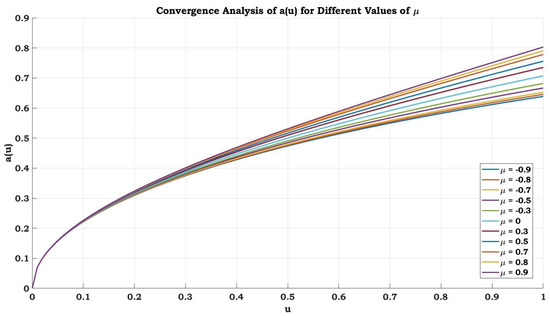
Figure 3 shows how $\mu \in \left(-1,1\right)$ affects the slope of $c\in S$ and its impact on the convergence of $c\in S$. As μ increases, the slopes of $c\in S$ become steeper, implying the faster convergence of $c\in S$. Conversely, decreasing μ leads to flatter slopes and the slower convergence of $c\in S$. The figure visually demonstrates the relationship between μ values, slope steepness, and the convergence behaviour of $c\in S$.

Figure 3. Graph of convergence.

Problem 1. 

Under what conditions Theorems 7 and 8 can be proved for the case of b-metric space? Equivalently, how we can define the $(\varkappa ,\Gamma ,\Omega$-$\mathsf{Ϝ})$-contraction and $(\varkappa ,{\Gamma }_{1,2},\Omega$-$\mathsf{Ϝ})$-contraction in the setting of the b-metric space to find the fixed point and coincidence point results?

5. Conclusions

The article introduces the novel concepts of the extended integral $\mathsf{Ϝ}$-contraction and $(\varkappa ,\Gamma ,\Omega$-$\mathsf{Ϝ})$-contraction. Furthermore, for two mappings and their coincidence/common fixed point results, a variant of the $(\varkappa ,\Gamma ,\Omega$-$\mathsf{Ϝ})$-contraction is introduced, called $(\varkappa ,{\Gamma }_{1,2},\Omega$-$\mathsf{Ϝ})$-contraction. Section 4, is devoted to the applications of these contractions. These applications include existence results for a given nonlinear fractional order boundary value problem. This was performed using both the extended integral $\mathsf{Ϝ}$-contraction and $(\varkappa ,\Gamma ,\Omega$-$\mathsf{Ϝ})$-contraction. An existence result for a nonlinear integral equation has also been proved using the $(\varkappa ,{\Gamma }_{1,2},\Omega$-$\mathsf{Ϝ})$-contraction. In this regard, a well-explained example has been established using the Picard–Jungck sequence, that converges to the solution of the integral equation. Some non-trivial examples at the end of all the main theorems are given, and the graphs are plotted if required. An open question is proposed for future directions.