A Multi-Task Learning Framework of Stable Q-Compensated Reverse Time Migration Based on Fractional Viscoacoustic Wave Equation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Fractional Laplacian Viscoacoustic Wave Equation
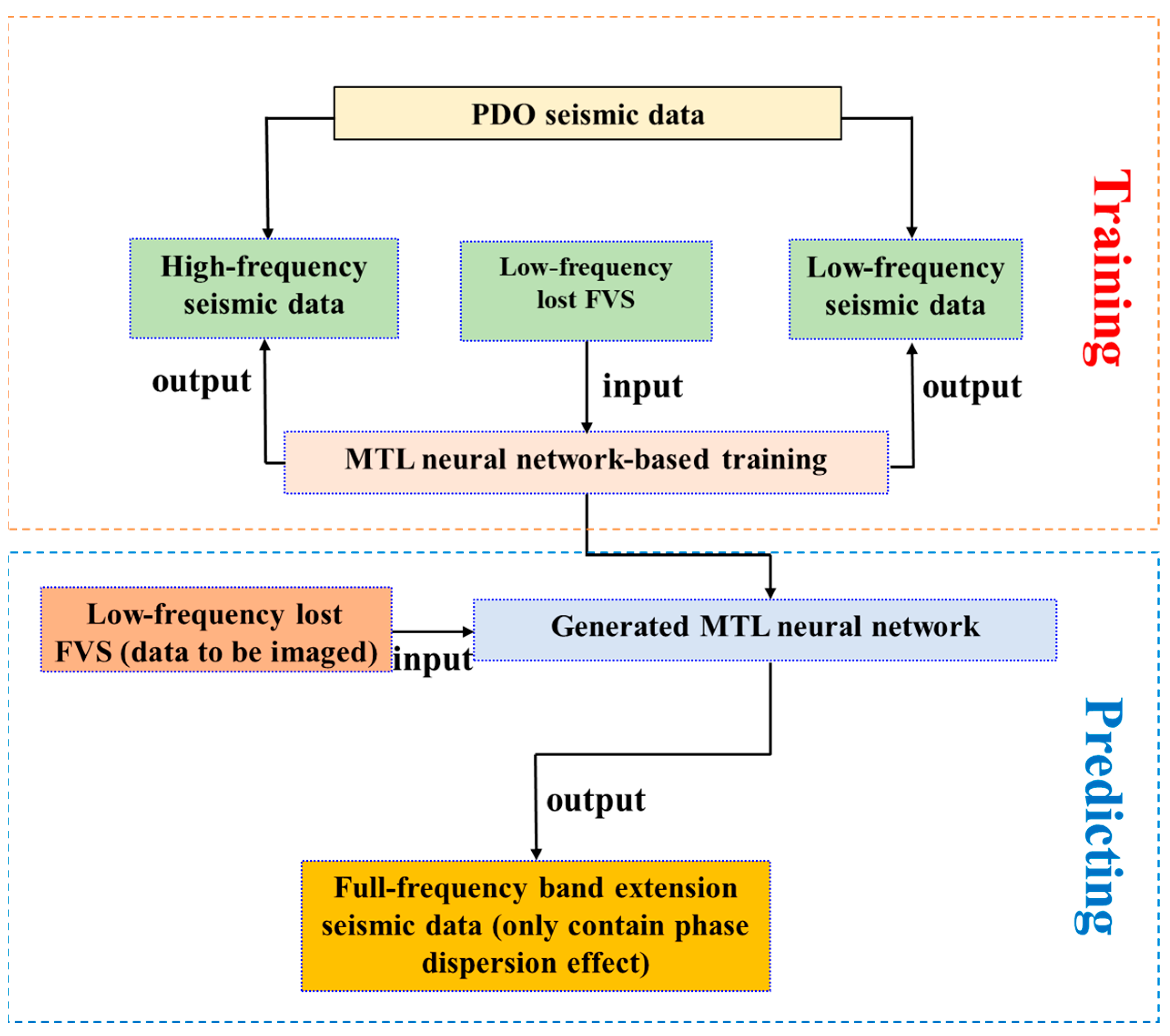
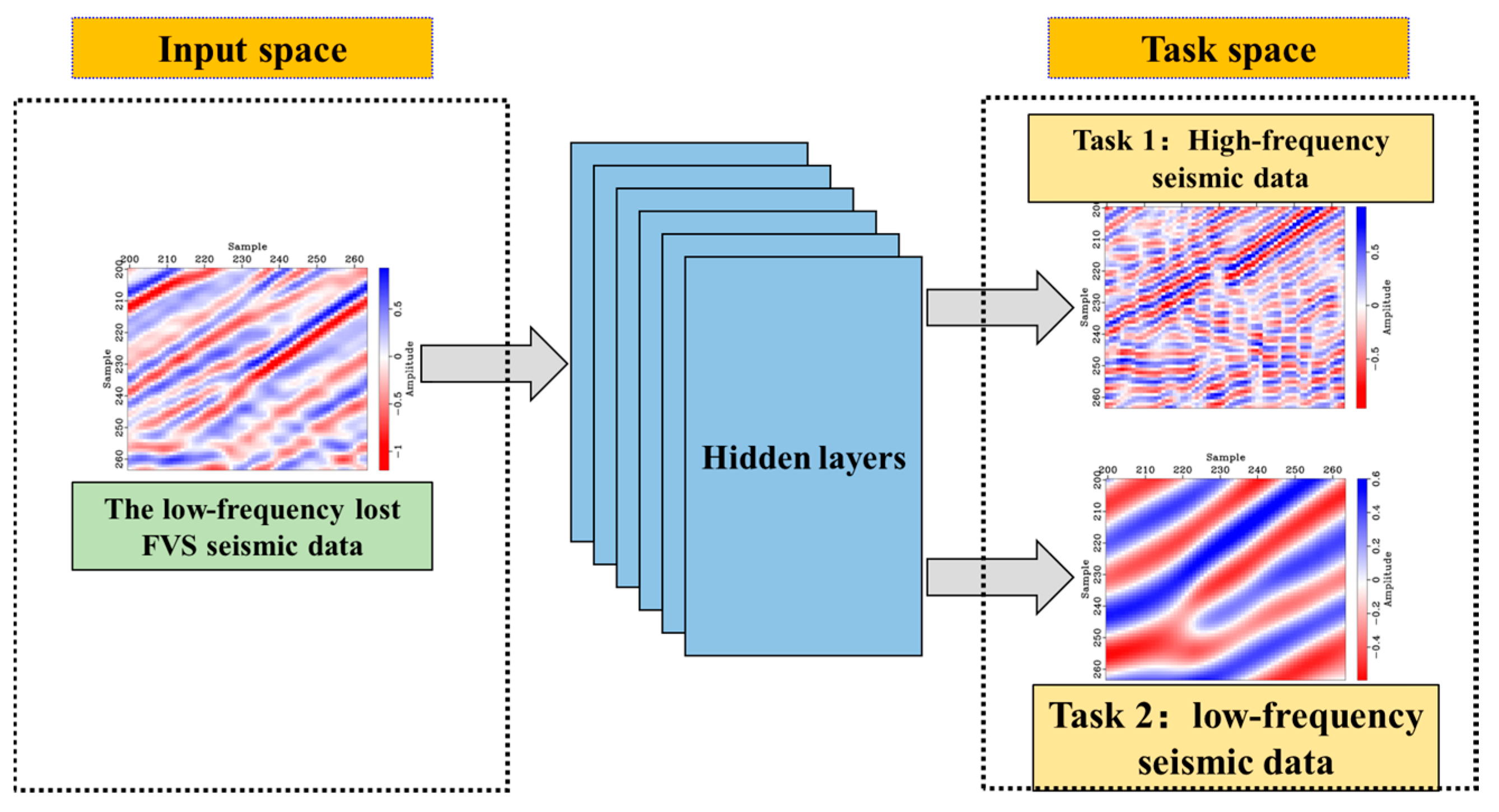
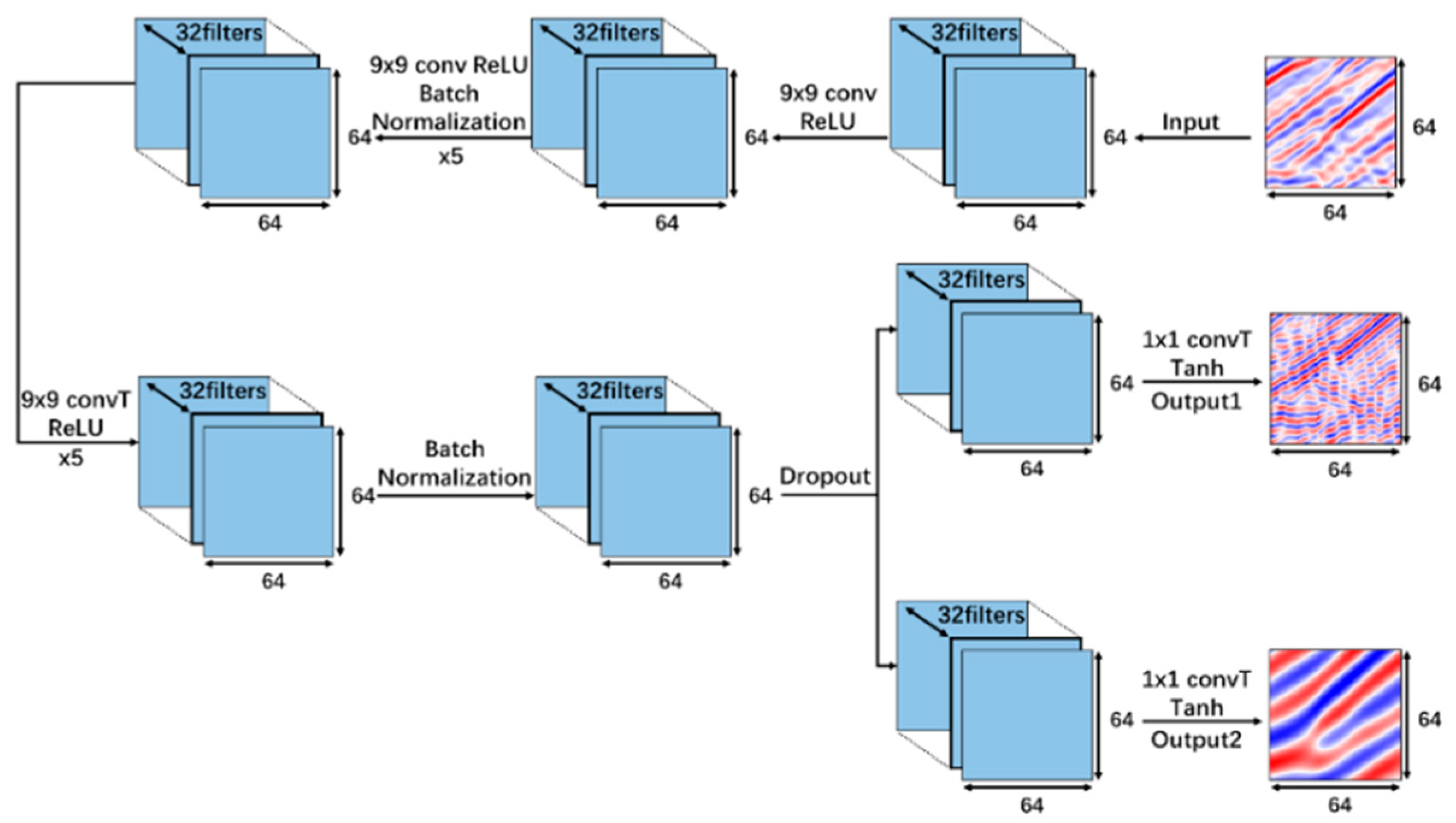
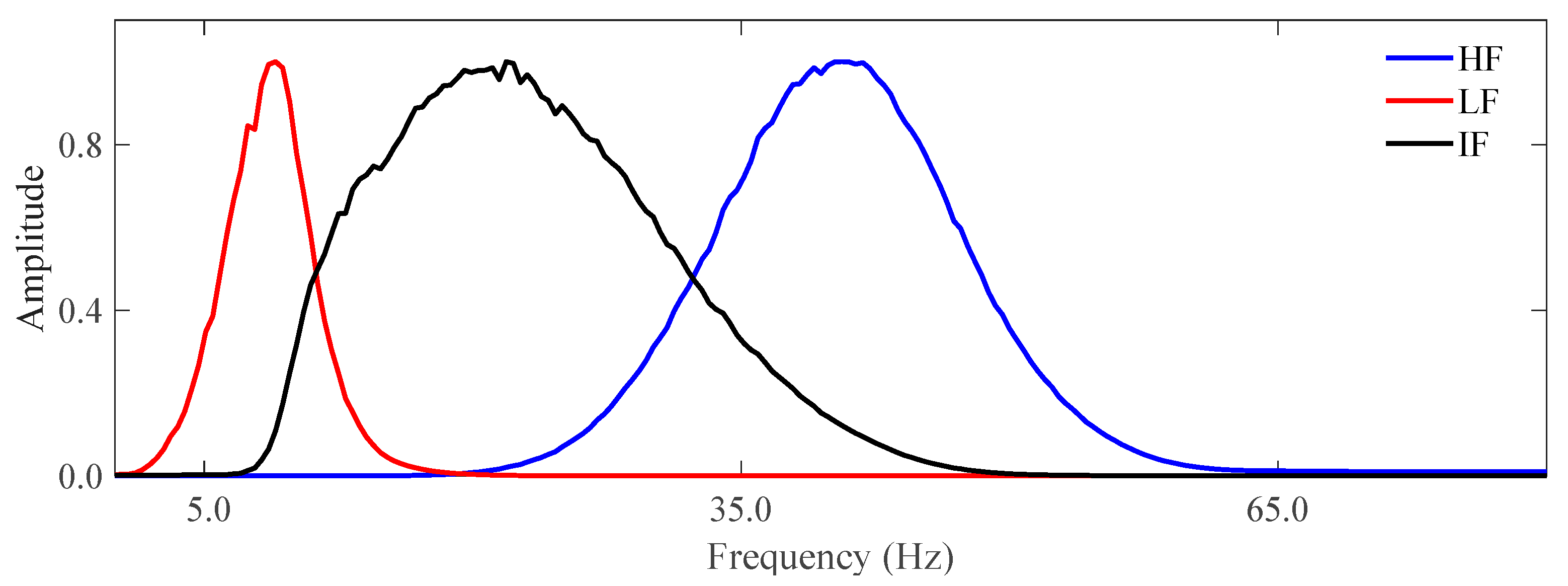
2.2. Network Architecture of Frequency Extension Based on MTL
2.3. Data Preparation
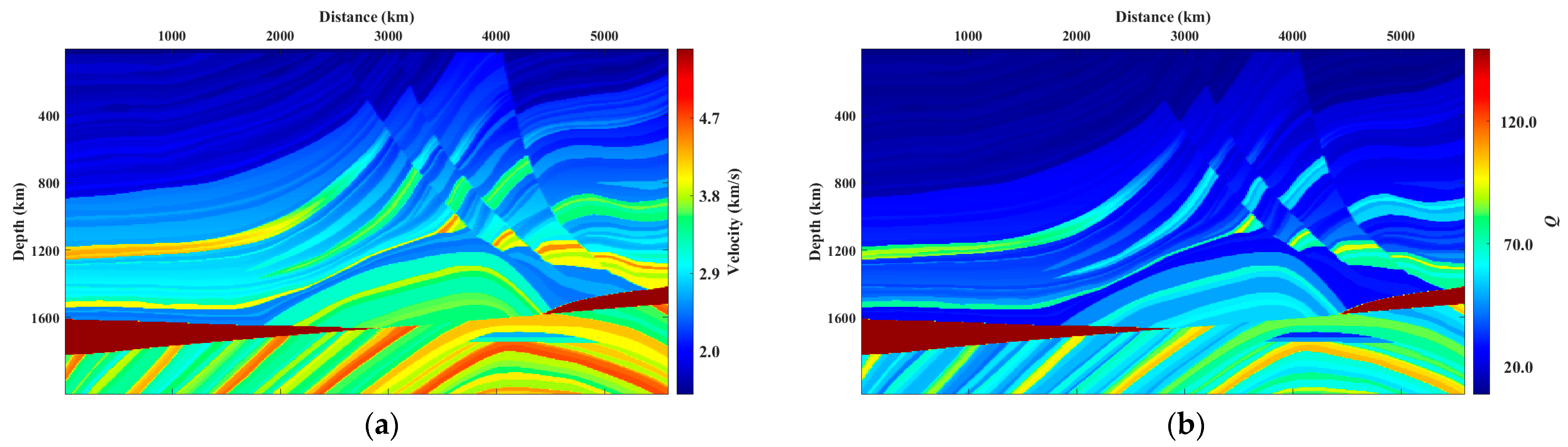
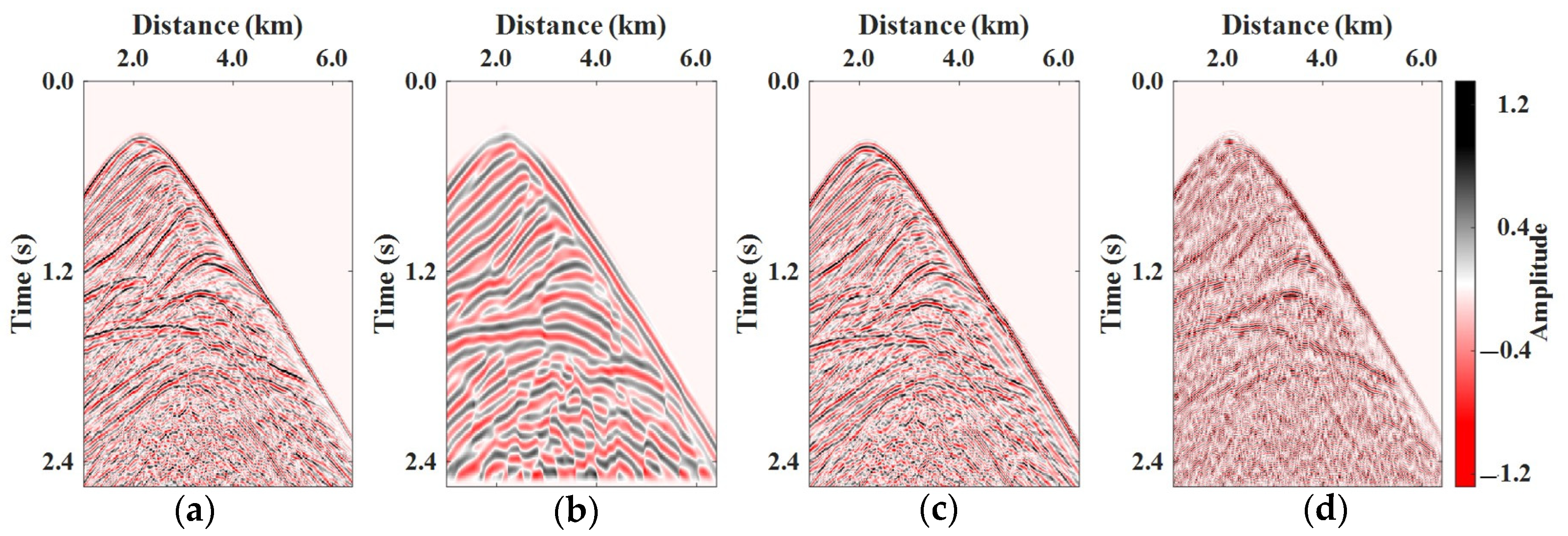
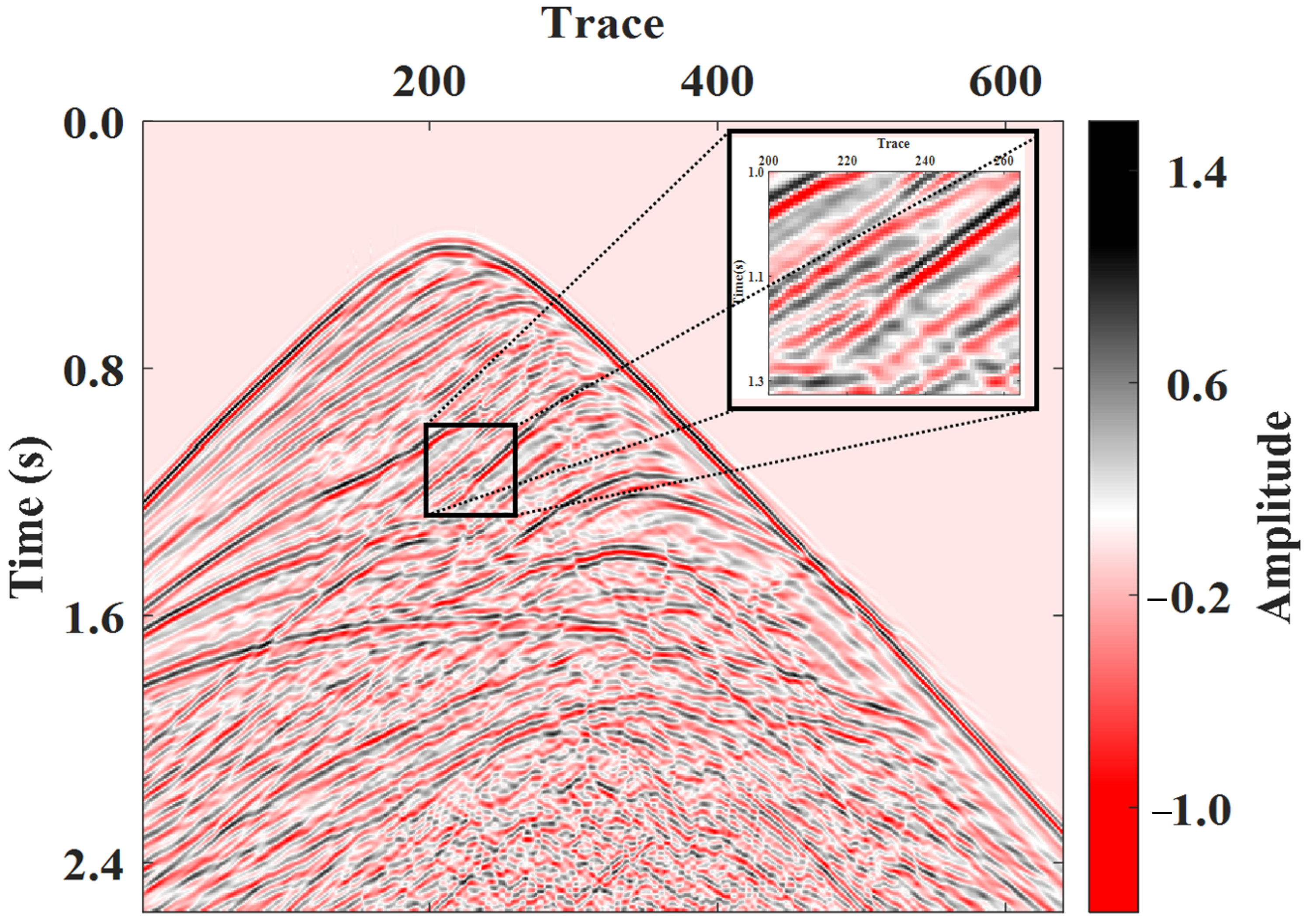
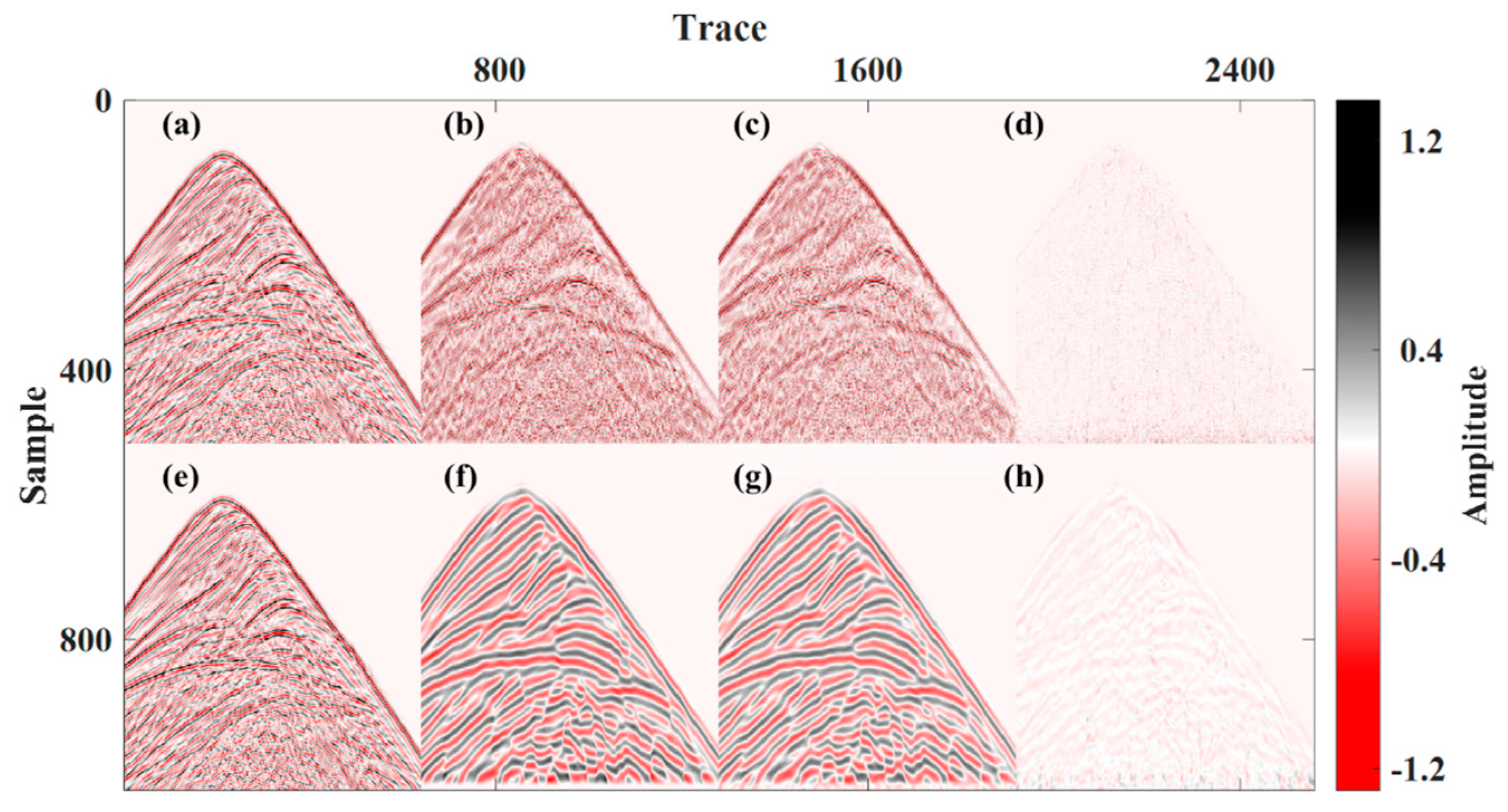
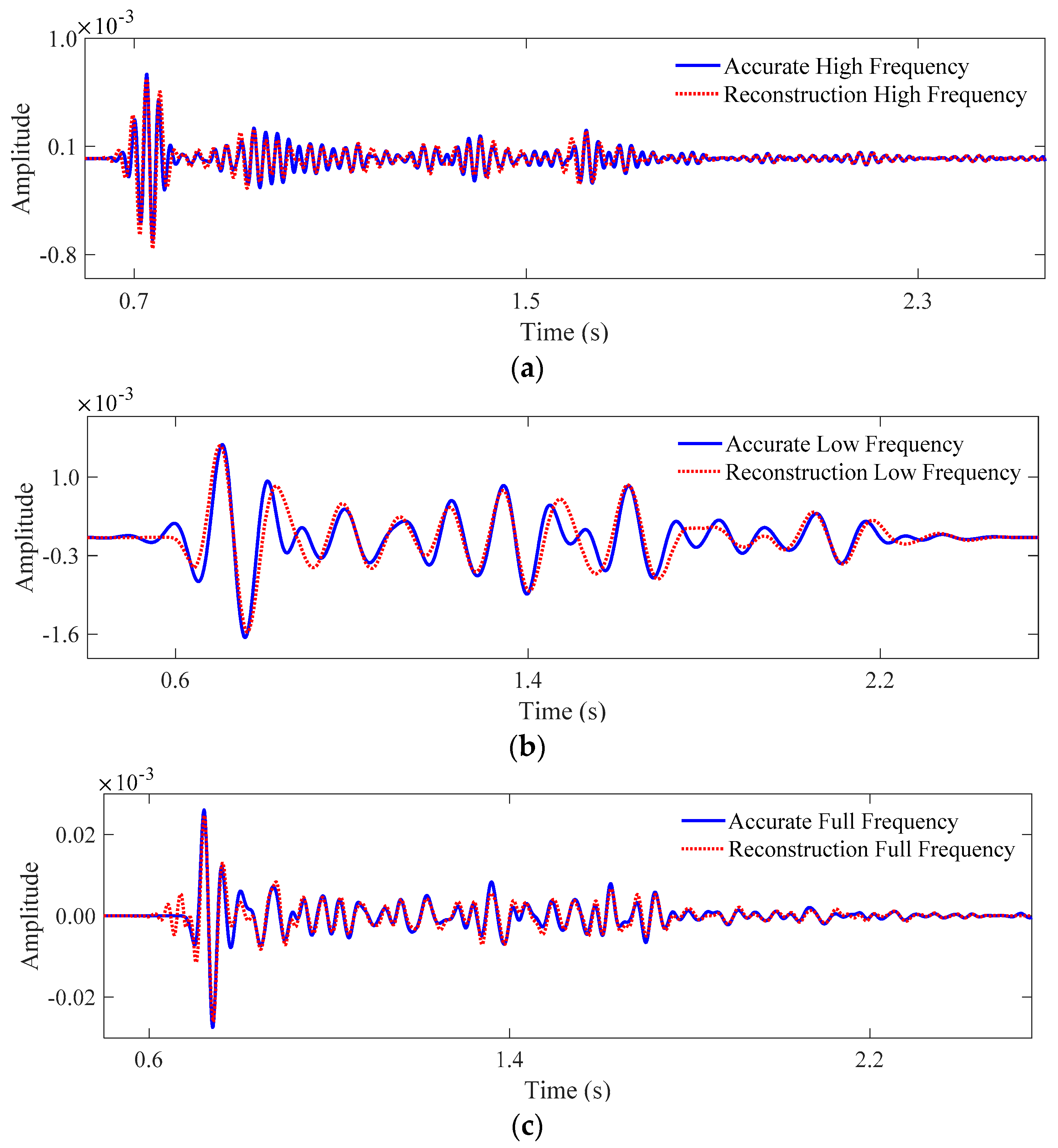
3. Examples
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Aki, K.; Richards, P. Quantitative Seismology, 2nd ed.; University Science Books: Melville, NY, USA, 1980. [Google Scholar]
- Wang, Y. A stable and efficient approach of inverse q filtering. Geophysics 2002, 67, 657–663. [Google Scholar] [CrossRef]
- Wang, Y. Inverse q-filter for seismic resolution enhancement. Geophysics 2006, 71, V51–V60. [Google Scholar] [CrossRef]
- Li, G.; Liu, Y.; Zheng, H.; Huang, W. Absorption decomposition and compensation via a two-step scheme. Geophysics 2015, 80, V145–V155. [Google Scholar] [CrossRef]
- Etgen, J.; Gray, S.H.; Zhang, Y. An overview of depth imaging in exploration Geophysics. Geophysics 2009, 74, WCA5–WCA17. [Google Scholar] [CrossRef]
- Deng, F.; McMechan, G.A. True-amplitude prestack depth migration. Geophysics 2007, 72, S155–S166. [Google Scholar] [CrossRef]
- Deng, F. Viscoelastic true-amplitude prestack reverse-time depth migration. Geophysics 2008, 73, S143–S155. [Google Scholar] [CrossRef]
- Zhu, T.; Harris, J.M. Modeling acoustic wave propagation in heterogeneous attenuating media using decoupled fractional laplacians. Geophysics 2014, 79, T105–T116. [Google Scholar] [CrossRef]
- Zhu, T.; Harris, J.M.; Biondi, B. Q-compensated reverse-time migration. Geophysics 2014, 79, S77–S87. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, P.; Zhang, H. Compensating for visco-acoustic effects in reverse time migration. In Seg Technical Program Expanded Abstracts; Society of Exploration Geophysicists: Houston, TX, USA, 2010; pp. 3160–3164. [Google Scholar]
- Li, Q.; Zhou, H.; Zhang, Q.; Chen, H.; Sheng, S. Efficient reverse time migration based on fractional laplacian viscoacoustic wave equation. Geophys. J. Int. 2016, 204, 488–504. [Google Scholar] [CrossRef]
- Chen, H.; Zhou, H.; Qu, S. Lowrank approximation for time domain viscoacoustic wave equation with spatially varying order fractional laplacians. In Proceedings of the 2014 SEG Annual Meeting, Denver, CO, USA, 26–31 October 2014; pp. 3400–3405. [Google Scholar]
- Sun, J.; Zhu, T. Stable attenuation compensation in reverse-time migration. In Seg Technical Program Expanded; Society of Exploration Geophysicists: Houston, TX, USA, 2015; pp. 3942–3947. [Google Scholar]
- Yan, H.; Liu, Y. Viscoacoustic prestack reverse-time migration based on the time-space domain adaptive high-order finite-difference method. Geophys. Prospect. 2013, 61, 941–954. [Google Scholar] [CrossRef]
- Yang, J.; Huang, J.; Zhu, H.; Li, Z.; Dai, N. Viscoacoustic reverse time migration with a robust space-wavenumber domain attenuation compensation operator. Geophysics 2021, 86, S339–S353. [Google Scholar] [CrossRef]
- Aghamiry, H.S.; Gholami, A. Interval-Q estimation and compensation: An adaptive dictionary-learning approach. Geophysics 2018, 83, V233–V242. [Google Scholar] [CrossRef]
- Shao, J.; Wang, Y. Simultaneous inversion of Q and reflectivity using dictionary learning. Geophysics 2021, 86, R763–R776. [Google Scholar] [CrossRef]
- Sun, H.; Demanet, L. Low-frequency extrapolation with deep learning. In SEG Technical Program Expanded Abstracts; Society of Exploration Geophysicists: Houston, TX, USA, 2018; pp. 2011–2015. [Google Scholar]
- Fang, J.; Zhou, H.; Elita Li, Y.; Zhang, Q.; Wang, L.; Sun, P.; Zhang, J. Data-driven low-frequency signal recovery using deep-learning predictions in full-waveform inversion. Geophysics 2020, 85, A37–A43. [Google Scholar] [CrossRef]
- Hu, W.; Jin, Y.; Wu, X.; Chen, J. Progressive transfer learning for low-frequency data prediction in full-waveform inversion. Geophysics 2021, 86, R369–R382. [Google Scholar] [CrossRef]
- Ovcharenko, O.; Kazei, V.; Kalita, M.; Peter, D.; Alkhalifah, T. Deep learning for low-frequency extrapolation from multioffset seismic data. Geophysics 2019, 84, R989–R1001. [Google Scholar] [CrossRef]
- Ovcharenko, O.; Kazei, V.; Plotnitskiy, P.; Peter, D.; Silvestrov, I.; Bakulin, A.; Alkhalifah, T. Extrapolating low-frequency prestack land data with deep learning. In Proceedings of the SEG International Exposition and Annual Meeting, Virtual, 11–16 October 2020; pp. 1546–1550. [Google Scholar]
- Ovcharenko, O.; Kazei, V.; Alkhalifah, T.A.; Peter, D.B. Multi-task learning for low-frequency extrapolation and elastic model building from seismic data. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–17. [Google Scholar] [CrossRef]
- Duong, L.; Cohn, T.; Bird, S.; Cook, P. Low resource dependency parsing: Cross-lingual parameter sharing in a neural network parser. In Proceedings of the 53rd Annual Meeting of the Association for Computational Linguistics and the 7th International Joint Conference on Natural Language Processing (Short Papers), Beijing, China, 26–31 July 2015; pp. 845–850. [Google Scholar]
- Yang, Y.; Hospedales, T.M. Trace norm regularised deep multi-task learning. arXiv 2016, arXiv:1606.04038. [Google Scholar]
- Caruana, R. Multitask learning: A knowledge-based source of inductive bias. In Proceedings of the Tenth International Conference on Machine Learning, San Francisco, CA, USA, 27–29 July 1993; pp. 27–29. [Google Scholar]
- Long, M.; Cao, Z.; Wang, J.; Yu, P.S. Learning multiple tasks with multilinear relationship networks. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]
- Bruggemann, D.; Kanakis, M.; Georgoulis, S.; Van Gool, L. Automated search for resource-efficient branched multi-task networks. arXiv 2020, arXiv:2008.10292. [Google Scholar]
- Liu, P.; Qiu, X.; Huang, X. Adversarial multi-task learning for text classification. arXiv 2017, arXiv:1704.05742. [Google Scholar]
- Zhao, X.; Li, H.; Shen, X.; Liang, X.; Wu, Y. A modulation module for multi-task learning with applications in image retrieval. In Proceedings of the European Conference on Computer Vision, Munich, Germany, 8–14 September 2018; pp. 401–416. [Google Scholar]
- Chen, Z.; Badrinarayanan, V.; Lee, C.Y.; Rabinovich, A. Gradnorm: Gradient normalization for adaptive loss balancing in deep multitask networks. In Proceedings of the 35th International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 794–803. [Google Scholar]
- Lin, X.; Zhen, H.L.; Li, Z.; Zhang, Q.F.; Kwong, S. Pareto multi-task learning. Adv. Neural Inf. Process. Syst. 2019, 32. [Google Scholar]
- Sener, O.; Koltun, V. Multi-task learning as multi-objective optimization. Adv. Neural Inf. Process. Syst. 2018, 31. [Google Scholar]
- Versteeg, R. The Marmousi experience: Velocity model determination on a synthetic complex data set. Lead. Edge 1994, 13, 927–936. [Google Scholar] [CrossRef]
- Rajagopalan, S.; Milligan, P. Image Enhancement of Aeromagnetic Data using Automatic Gain Control, Exploration. Geophysics 1994, 25, 173–178. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, Z.; Ma, Y.; Wang, S.; Hu, H.; Li, Q. A Multi-Task Learning Framework of Stable Q-Compensated Reverse Time Migration Based on Fractional Viscoacoustic Wave Equation. Fractal Fract. 2023, 7, 874. https://doi.org/10.3390/fractalfract7120874
Xue Z, Ma Y, Wang S, Hu H, Li Q. A Multi-Task Learning Framework of Stable Q-Compensated Reverse Time Migration Based on Fractional Viscoacoustic Wave Equation. Fractal and Fractional. 2023; 7(12):874. https://doi.org/10.3390/fractalfract7120874
Chicago/Turabian StyleXue, Zongan, Yanyan Ma, Shengjian Wang, Huayu Hu, and Qingqing Li. 2023. "A Multi-Task Learning Framework of Stable Q-Compensated Reverse Time Migration Based on Fractional Viscoacoustic Wave Equation" Fractal and Fractional 7, no. 12: 874. https://doi.org/10.3390/fractalfract7120874
APA StyleXue, Z., Ma, Y., Wang, S., Hu, H., & Li, Q. (2023). A Multi-Task Learning Framework of Stable Q-Compensated Reverse Time Migration Based on Fractional Viscoacoustic Wave Equation. Fractal and Fractional, 7(12), 874. https://doi.org/10.3390/fractalfract7120874





