Fractional Photoconduction and Nonlinear Optical Behavior in ZnO Micro and Nanostructures

Abstract

A fractional description for the optically induced mechanisms responsible for conductivity and multiphotonic effects in ZnO nanomaterials is studied here. Photoconductive, electrical, and nonlinear optical phenomena exhibited by pure micro and nanostructured ZnO samples were analyzed. A hydrothermal approach was used to synthetize ZnO micro-sized crystals, while a spray pyrolysis technique was employed to prepare ZnO nanostructures. A contrast in the fractional electrical behavior and photoconductivity was identified for the samples studied. A positive nonlinear refractive index was measured on the nanoscale sample using the z-scan technique, which endows it with a dominant real part for the third-order optical nonlinearity. The absence of nonlinear optical absorption, along with a strong optical Kerr effect in the ZnO nanostructures, shows favorable perspectives for their potential use in the development of all-optical switching devices. Fractional models for predicting electronic and nonlinear interactions in nanosystems could pave the way for the development of optoelectronic circuits and ultrafast functions controlled by ZnO photo technology.

1. Introduction

Zinc oxide (ZnO) is a fascinating semiconductor material which has gained particular interest in recent years due to its characteristic wide bandgap energy ($E_g$) that promotes an easy electron interchange between its conduction and valence band [1]. Also, due to its unique physical properties [2], and versatility in being designed by different processing routes [3], this material is suitable for applications in highly sensitive gas sensors, transparent electrodes, and a variety of optoelectronic and piezoelectric devices like solar cells [4]. Moreover, ZnO is a low-cost material that can be synthesized by hydrothermal effects, sol-gel methods, chemical vapor deposition (CVD), spray pyrolysis, and other techniques [5]. It is worth mentioning that the physico-chemical properties exhibited by the ZnO depend on their structure size, shape, and morphology, which are crucial for their successful application in various fields [6,7]. The high surface/volume ratio of ZnO nanomaterials has a significant impact on electrical features, compared to the bulk phase case. Defect structures present at grain boundaries of nanostructures, such as dangling bonds, vacancies, and micropores, significantly affect energy transport phenomena. A decrease in nanoscale size increases the defect ion concentration, which tends to segregate at grain boundaries and leads to grain boundary defect barrier formation [8,9]. On the other hand, considering that the morphology of ZnO nanostructures affects the amount of surface oxygen, it has been reported that oxygen vacancies in ZnO nanostructures can be responsible for an increase in electrical conductivity [10].

Diverse potential applications of ZnO nanostructures for optoelectronic, electronic, and biomedical functions have been pointed out [11]. High electron mobility and strong luminescence exhibited by ZnO nanostructures make them useful in light-emitting diodes (LEDs), while high biocompatibility makes them useful for drug delivery and tissue engineering [12].

Moreover, the ZnO exhibits UV-protection properties attractive for UV-blocking coatings with different low-cost nanofabrication processes, and in this direction, their photoconductive and nonlinear optical properties have been investigated for a wide range of applications. The design of opto-piezo-electronic materials like highly sensitive sensors [13] and energy collectors for both piezotronic logic nanodevices [14] and piezotronic transistors [15] has been demonstrated in ZnO. The photon absorption of ZnO for valence band excitations [16] and a decreased transmittance at shorter wavelengths [17] can be employed for developing ultrafast functions and nonlinear materials. A large nonlinear optical (NLO) response has the ability to manipulate light, which is the base for modern data transmission [18] and harmonic generation [19].

Regarding the vectorial nature of light and the physical mechanisms responsible for the optically induced electronic effects, NLO properties in ZnO nanosystems are dependent on wavelength, incident polarization, and pulse duration able to tune a variety of electronic excitations [20,21,22,23,24,25,26,27,28,29,30]. In this work, we report the modification of photoconductive, electrical, and NLO effects exhibited by ZnO-based materials prepared by two different processing routes. A fractional description allowed us to analyze electronic characteristics and photoinduced properties using nanosecond pulses that proved to be of interest as a base for the design and development of optoelectronic and all-optical devices.

2. Materials and Methods

2.1. Synthesis of the ZnO Samples and Morphology Characterization

For the preparation of the ZnO microstructures in film form, a combination of hydrothermal synthesis and intermittent spray was employed, similar to the procedure of Wang et al. [31]. For the synthesis, a mixture of 1.53 g of zinc acetate (Zn(O₂CCH₃)₂) and 12.47 g of sodium citrate (Na₃C₆H₅O₇) was dissolved in 70 mL of deionized water and stirred for 20 min to form a clear solution. Subsequently, a sodium hydroxide solution (1 mol/L) was added to the product and stirred for 30 min to adjust the pH to 14. Then, the solution was transferred to an autoclave and placed in an oven at 150 °C for 24 h. Subsequently, it was allowed to cool at room temperature and filtered using a vacuum pump. The resulting product was washed with deionized water and anhydrous ethanol twice and diluted in 10 mL of deionized water. The obtained product was ultrasonically cleaned for 20 min. Finally, the solution was sprayed intermittently every 10 s on a SiO₂ substrate, previously ultrasonically cleaned with ethanol, and then preheated to 320 °C, following the method of Ravichandran and Philominathan [32]. Also, the spray pyrolysis technique was used for the generation of nanostructures by depositing a total of 15 layers on preheated 10 × 25 × 1 mm³ SiO₂ substrates ultrasonically cleaned with ethanol for 20 min and then after with deionized water at 430 °C on a graphite surface over a tin bath.

For the fabrication of the ZnO nanostructures, a precursor solution of 2.65 g of zinc acetylacetone (Zn(C₅H₇O₂)₂), 12.54 mL of deionized water, 83.88 mL of methanol (CH₃OH), and 3.58 mL of acetic acid (C₂H₄O₂) was made and stirred for about 10 min. The deposition was performed by nebulizing the precursor solution on the substrates with a vapor exposition of 105 s, at an input pressure of 7 L/min and output of 3 L/min, with a stabilizing time of 10 min between each deposit. With this, multiple ZnO nanostructured thin films were obtained.

The ZnO samples were characterized using a Nova200 Nanolab, Dual Beam Microscope, Field Emission Scanning Electron Beam, Scanning Electron Microscope (SEM), which has 1.1 nm of resolution, and a Focused Ion Beam with 1.7 nm for obtaining high-resolution images for the analysis of a large portion of the surface and the characterization of its morphology. From SEM analysis, it was possible to achieve the visualization of the sample porosity and the orientation of the crystallization phase on the surface. Experimental data for the material thickness over the substrate were obtained by spectroscopic ellipsometry (Uvisel HORIBA Jobin Yvon ellipsometer model LT M200AGMS) with an incident angle of 70°, a 1200 μm spot, and a spectral range of 1.5 to 5.5 eV with increments of 0.0500 eV, and a high-pressure Xenon lamp of 75 W was used for both samples.

2.2. Optical and Electrical Properties Characterization

For the characterization of the optical properties, a UV spectrophotometer (Perkin Elmer XLS) was used to obtain the absorbance of the micro and nanostructured ZnO samples. Moreover, the electrical conductivity was evaluated using a two-probe ohmmeter model MUT-202 (Truper, Mexico); the measurement was carried out by applying copper electrodes over the samples with a separation distance of 1.5 cm. The electrical impedance ($Z$) as a function of electrical frequency was obtained with an Autolab potentiostat (Autolab/PGSTAT302N high-power potentiostat/galvanostat) connected to the same electrodes of the analyzed samples.

Photoconductivity under optical irradiation from a Nd:YVO₄ laser system (Spectra-Physics Explorer^® One™ XP) at 532 nm wavelength, linear polarization, and 50 KHz was also studied. In order to describe the buildup persistent photoconductivity ($\sigma$) for semiconductors, we consider [33]:

$$\sigma (I)={\sigma }_D+\left({\sigma }_{\max }-{\sigma }_D\right) (1-\exp (-{\alpha }_{1}I)),$$

(1)

where ${\sigma }_D$ is the initial material electrical current in darkness, and ${\sigma }_{max}$ is the maximum data value of photoconduction, which was assumed to be the value at maximum irradiance (100%) of the laser system employed. Also, ${\alpha }_1$ is described as a decay constant of the buildup process system.

In order to describe the fractional order photoconductivity, different values of the optical irradiance were systematically evaluated with fractional calculus. The implementation of this derivation was carried out to analyze the gradual fractional order contribution of the intensity and its relationship with the experimental photoconduction buildup process. For this, we found the best fitting for the study of the photoconduction effect with the Caputo fractional derivative. The following expression was employed [34]:

$$\frac{d^n}{d{x}^n}{[}_a^{RL}{I}_x^{\varphi }(f(t))]=\frac{d^n}{d{x}^n}\left[\frac{1}{\mathsf{\Gamma }(\varphi )}{\displaystyle {\int }_a^x{(x-t)}^{\varphi -1}}f(t)dt\right],$$

(2)

where $\varphi$ is the fractional order exponent that takes different fractional values ($0<\varphi <1)$, $x$ and $a$ are derivative limits, $\mathsf{\Gamma }\left(\varphi \right)$ is the gamma function. The understanding of this formula requires the obtention of the Riemann–Liouville fractional integral (${{}_a{}^{RL}I}_x^{\varphi }$) of the analyzed function.

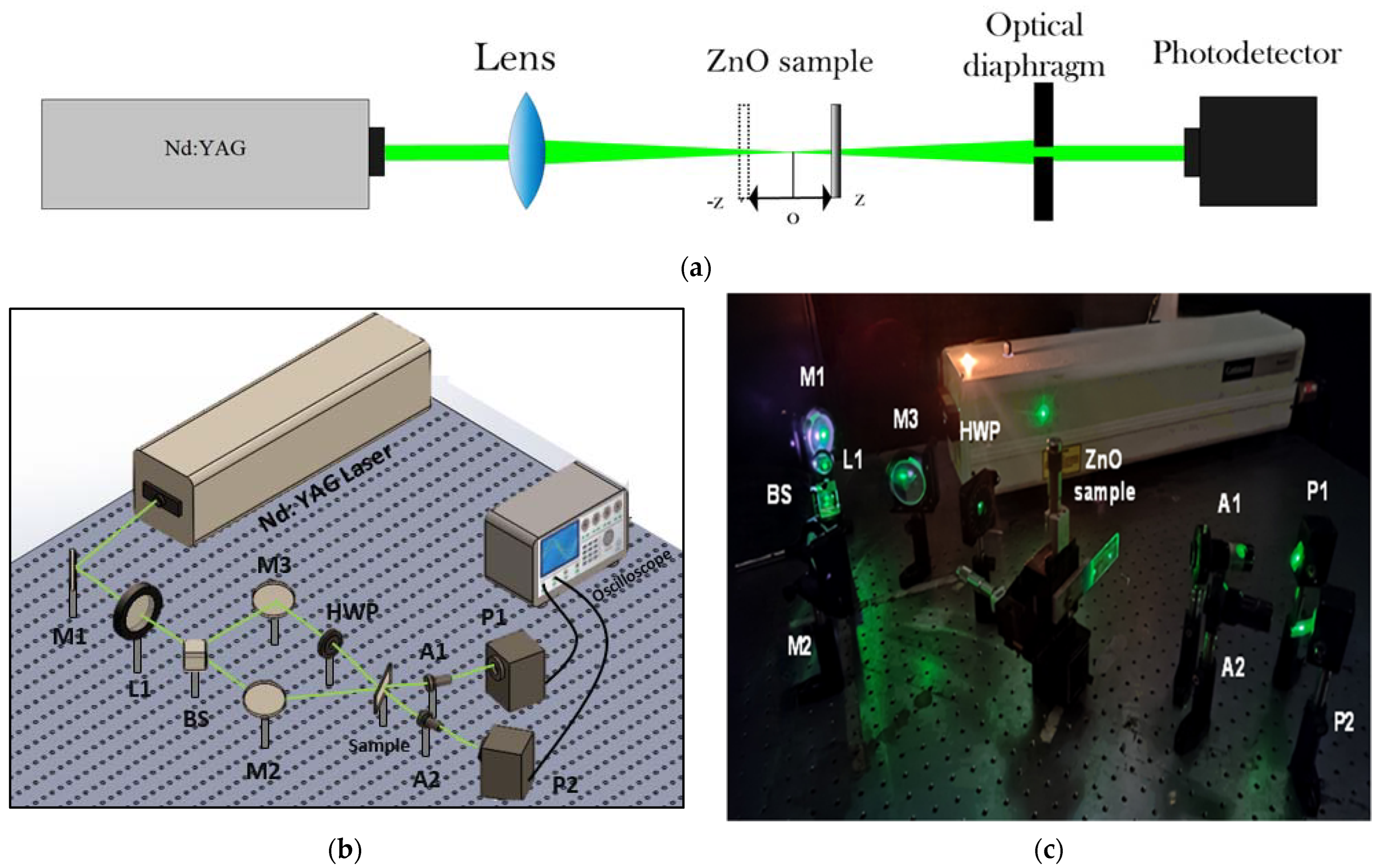
2.3. Experimental Setups for NLO Effects

The z-scan technique setup was used to characterize the NLO properties of the analyzed samples. With this technique, it is possible to determine the possible Kerr nonlinearity and nonlinear absorption effects by analyzing the closed and open aperture configurations, respectively. In this research, the experimental setup was designed for a range between −4 and 4 mm for the manifestation of the nonlinear optical transmittance. For both samples, an incident irradiance of 10.3 and 14.58 GW/cm² was used for open and closed configurations, under the same laboratory conditions provided by a 532 nm wavelength with 4 nanosecond pulses emitted by a Continuum SL II-10 Nd:YAG Laser system. The z-scan setup used for this work can be seen in Figure 1a. An approximation of the optical transmittance $T_o$ in the nonlinear media for the open aperture configuration of the z-scan can be obtained by considering the following equations [35]:

$$T_o(z,\Delta {\mathsf{\Phi }}_o)=1-\frac{(\beta I_o{L}_{e}ff)}{(2\sqrt{2}(1+z^2/z_o^2))},$$

(3)

$$L_{eff}=\frac{(1-e_{}^{(-{\alpha }_{o}L)})}{{\alpha }_o},$$

(4)

where z is the position, $z_0^{}=k{w}_o^2/2$, $k=2\pi /\lambda$, with $\lambda$ being the probe laser wavelength, $\beta$ represents the two-photon absorption coefficient, $L_{eff}$ is the effective length, $L$ is the sample length, $I_o$ is the peak irradiance at focus on the propagation axis, and ${\alpha }_o$ is the linear absorption coefficient. In a similar way, for the closed aperture configuration using a Gaussian beam with waist radius $w_o$ travelling in the propagation direction, the normalized transmittance $T_c$, as a function of the position ($z$), is given by [36]:

$$T_c(z,\Delta {\mathsf{\Phi }}_o)=1-\frac{(4\Delta {\mathsf{\Phi }}_o(z/z_o))}{(z^2/(z_o^2)+9)(z^2/(z_o^2)+1)},$$

(5)

$$\Delta {\mathsf{\Phi }}_o=k\Delta n_o{L}_{eff},$$

(6)

where $∆{\mathsf{\Phi }}_o$ is the optical phase change when the laser passes through the sample, and $\mathsf{\Delta }{n}_o$ is the refractive index change equal to the product of the nonlinear refractive index $n_2$ and $I_o$.

To further investigate the NLO effects, a two-wave-mixing (TWM) setup, shown in Figure 1b, was used to explore the vectorial nature of the nonlinear response. Irradiation at 532 nm wavelength with 4 nanosecond pulses was provided by a Continuum SL II-10 Nd:YAG Laser system, focused by a 50 mm optical lens. The results of the high optical irradiation of the sample were captured by a pair of photodetectors connected to an ADS1102CAL ATTEN, 100 MHz capacity digital oscilloscope. In order to numerically estimate the transmitted irradiance of the TWM interaction, an approximation of the wave equation [37] can be described as:

$${\nabla }^2{E}_{\pm }=-\frac{n_{\pm }^2{\omega }^2}{c^2}{E}_{\pm }$$

(7)

where $E_{\pm }$ represents the electric fields that propagate through the samples in their circular components as $E_{+}$ and $E_{-}$, while $\omega$ represents the optical frequency of the light. The refraction index is denoted by $n$, and $c$ is the speed of light.

The nonlinear refractive index for circular polarized light, being right-handed ($n_{+}$) or left-handed ($n_{-}$) can be considered:

$$n_{\pm }^2=n_o^2+4\pi ({\chi }_{1122}^{(3)}|E_{\pm }{|}^2+({\chi }_{1122}^{(3)}+{\chi }_{1212}^{(3)})|E_{\pm }{|}^2),$$

(8)

where $n_o$ is the refractive index at low irradiance, and ${\chi }_{1122}^{\left(3\right)}$ and ${\chi }_{1212}^{\left(3\right)}$ are the independent components of the third-order optical susceptibility tensor of the system.

Furthermore, to numerically estimate the contribution of different micro and nanostructures on the sample as a function of the volume fraction $\rho$, the nonlinear third-order susceptibility can be approximated as follows:

$${\chi }_{(n+m)}^{(3)}=(1-\rho ){\chi }_n^{(3)}+\rho {\chi }_m^{(3)},$$

(9)

The sum of the nonlinear third-order susceptibility of the integrated nanocrystals ${\chi }_n^{\left(3\right)}$ with microcrystals ${\chi }_m^{\left(3\right)}$ on the sample is represented as ${\chi }_{n+m}^{\left(3\right)}$. For further analysis, the mathematical expression used to obtain the transmitted irradiance $I$, as a function of the propagation distance $L$, the absorption coefficient ${\alpha }_o$, and the incident irradiance $I_0$ from a coherent optical source analyzed through a nonlinear optical absorptive medium is:

$$I(L)=\frac{I_0\exp \left(-{\alpha }_{o}L\right)}{1+\beta I_o{L}_{eff}},$$

(10)

3. Results and Discussion

3.1. Morphology Characterization

The results in Figure 2 show representative images of the surface of the ZnO thin films. It was possible to observe the morphology of the micro and nanostructures, obtaining micro-structured desert rose-like ZnO (RD-ZnO) crystals of about 6 μm in diameter which compose the thin film. In a similar way, from the images of the nanostructures, we observe nanoflake-like crystals which form the nanomaterial. The estimated flake thickness ranged from 30 to 150 nm. Furthermore, an ellipsometry test was carried out to determine the nanoscale thickness of the thin film, obtaining an approximate value of 688 nm. The material thickness was attributed to the spray pyrolysis technique utilized for both samples.

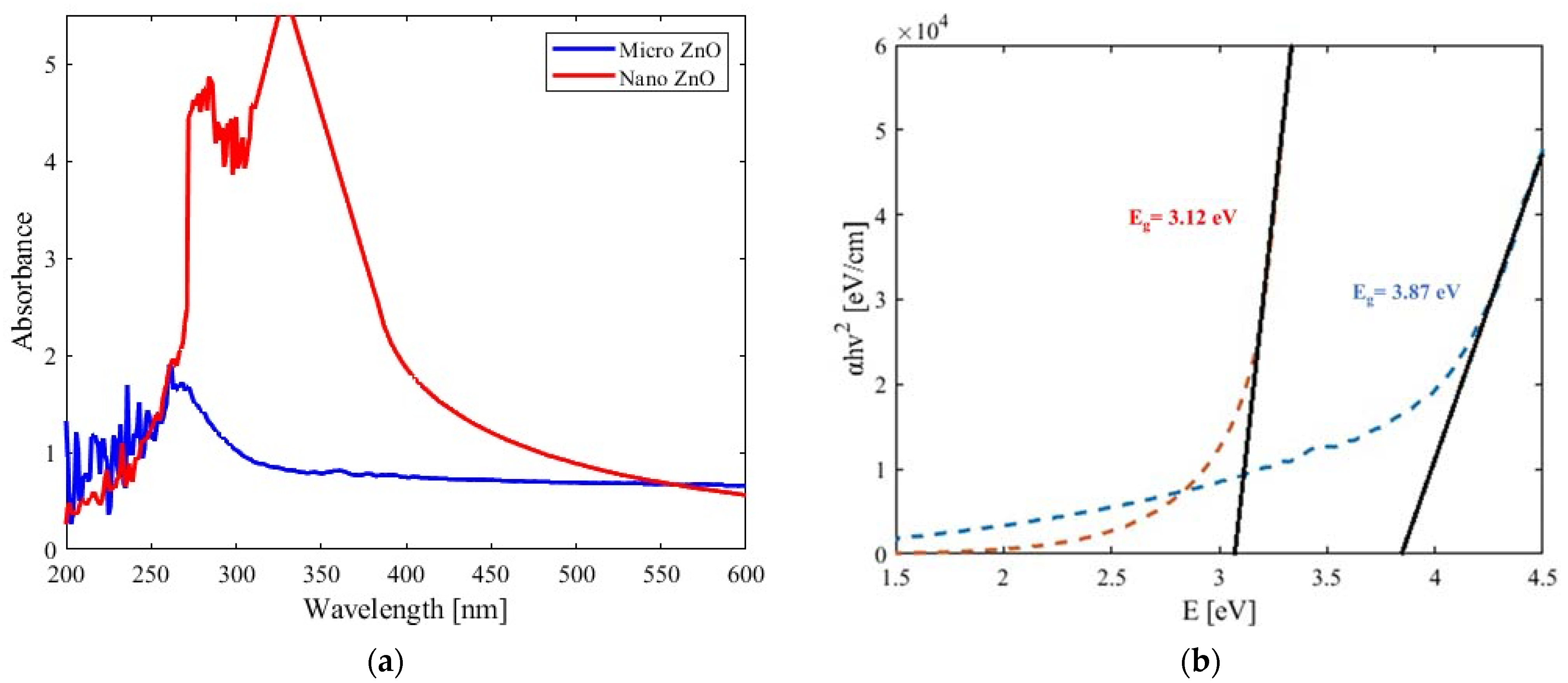
3.2. UV-VIS Observations

The absorbance of the analyzed ZnO is shown in Figure 3a. It was found that the absorbance spectra of the samples have a special preference for the UV low frequencies at wavelength regions from about 260 to 400 nm. The obtained Tauc plots for the absorbance spectra are shown in Figure 3b. It was determined that the binding energy was about 3.15 eV and 3.76 eV for the nano and microstructures, respectively. The nanoscale contribution of the petals in the microstructures seems to be responsible for a higher bandgap than the correspondent magnitude in the flake-like nanostructures studied.

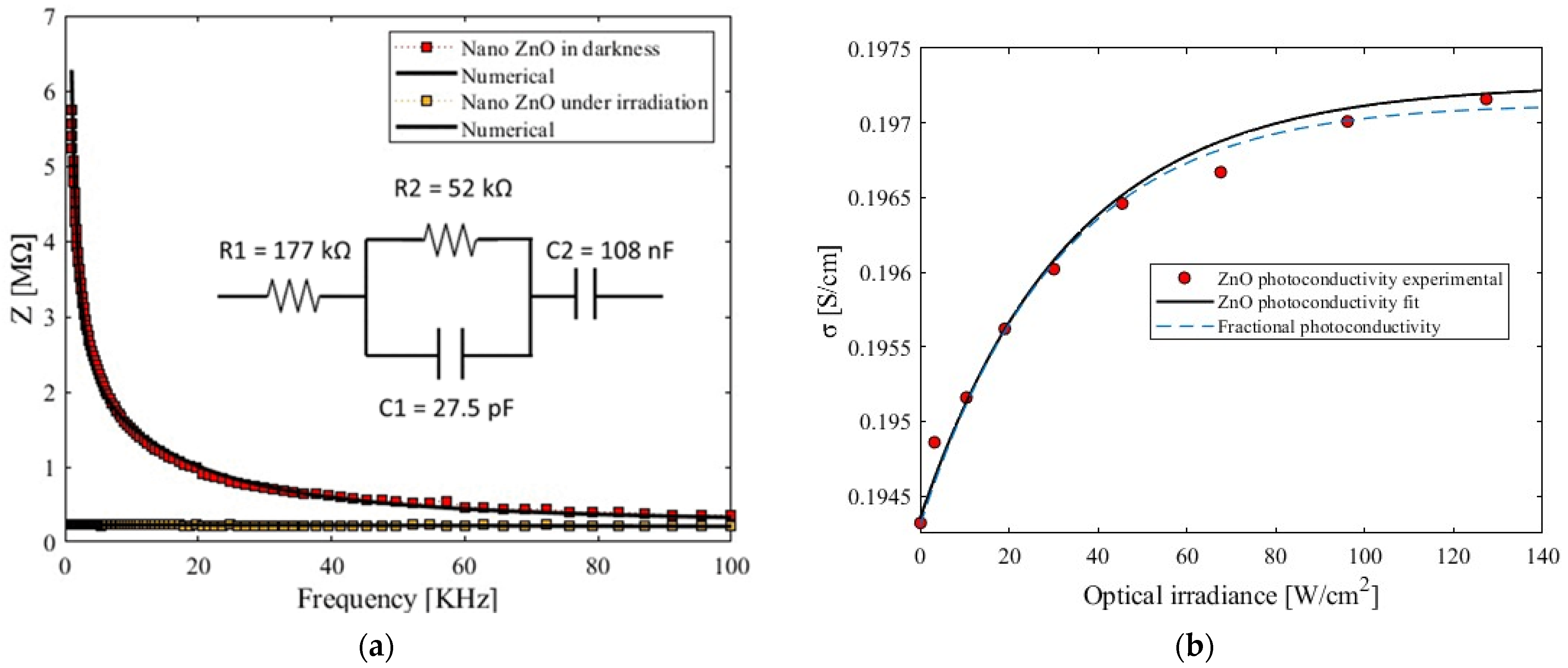
3.3. Photoconductivity Response

The electrical response under laser irradiation measured by an Autolab potentiostat indicated an impedance decrease as a function of the frequency, denoting an n-type semiconductor behavior in the ZnO nanostructured material when analyzing with Nova 1.1 software. The micro-structured sample presented high electrical resistivity, which cannot be measured when analyzing with the potentiostat; this behavior is in good agreement with similar works for other synthetized ZnO microstructures which reported low electrical conductivity values in a range of 1–100 S/cm. The best numerical simulation was obtained by considering a Resistor-Capacitor (RC) system that induced the impedance drop for the photoconductivity data results and their equivalent RC circuit showing capacitive behavior, presented in Figure 4a for the overall results.

Furthermore, experimentation to evaluate the photoconduction influenced by the light intensity on thin films was undertaken as shown in Figure 4b. The results indicated an exponential growth from the initial steady state (or current in darkness) to the irradiation state. The change from the initial darkness current on the semiconductors could be attributed to the excited charge carriers that change with the irradiation of the light, which makes them photoconductive. Also, it was assumed that the interface heating the mechanism behind the conduction phenomena modifies the velocity of the carriers. Such an amount of heat could be obtained from the high-intensity irradiation of the light beams, which produces multiphotonic effects. From these results, an exponential growth in photoconduction can be seen as a function of higher irradiances for both samples. An important aspect of the conductivity behavior in semiconductors is the temperature dependence; in this type of material, a large amount of temperature differential is required to induce a notable change in the charge carrier’s mobility. Thus, the numerical interpretation of some fractional values of the dependent variable was obtained by putting Equations (1) in (2) with different fractional order values of $I$.

A comparison was made between different fractional derivative theories to probe the effectiveness on these equations, like Grünwald–Letnikov and Riemann–Liouville, determining that the Caputo fractional derivative was the best for the fitting. The results of the Caputo fractional derivative can be observed in detail in Figure 4b, showing the relation of the conductivity as a function of the light intensity. Comparative results in ZnO nanostructures have been previously reported [38,39]. These are explained as the oxygen vacancies that directly affect the electron–hole interactions of the charge carriers, which permit the electrical conduction. The implications of this effect are investigated for uses in photodetectors, gas sensors, and other optoelectronic systems. It should be mentioned that optical absorbance effects are interesting for applications in a handful of solar cells systems, electronics, and optoelectronics [40]. In addition, ZnO micro and nanostructures have been compared in their photoconductive potential, which showed results that indicated an enhancement in photo response in nano ZnO materials [41], which also leads to an increase in NLO response.

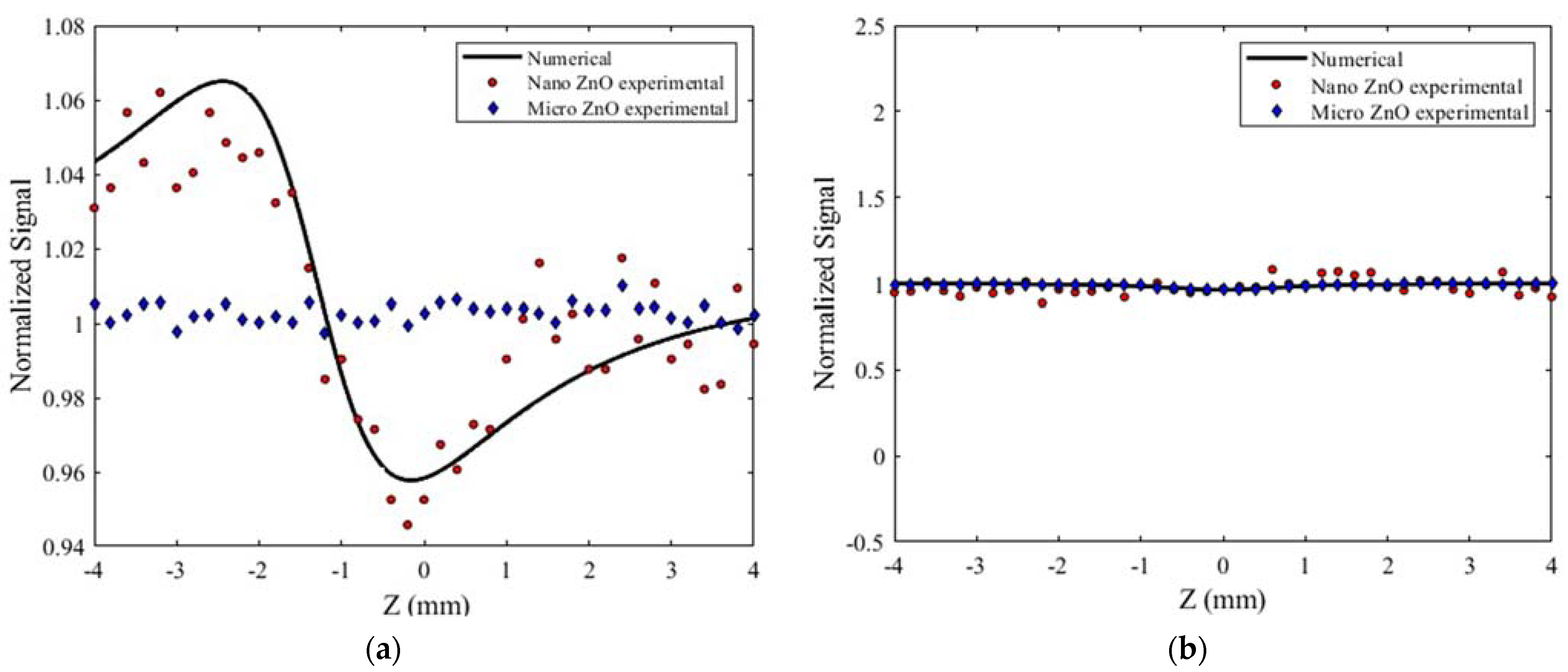
3.4. Results of the z-Scan Analysis

The z-scan traces for the open and closed apertures and the best numerical fitting for the ZnO nanostructured thin film are presented in Figure 5. A significant Kerr effect on the sample inducing a change in the refractive index at high irradiances was clearly observed. On the other side, the micro-structured ZnO was irradiated under the same conditions but showed a Kerr response with at least a decrease of one order of magnitude not far from the error bar ±15%. Also, a positive change in the nonlinear absorption index was found for the open aperture, which reveals the existence of a significant multiphonic effect in the nanostructures at high irradiances. In addition, the numerical interpretation of the overall results allows us to calculate the nonlinear refractive index and absorption coefficient of the samples. The approximated nonlinear refractive index value obtained was $n_2=1.36\times 10^{-11 }\mathrm{c}{\mathrm{m}}^2/\mathrm{W}$ for the ZnO nanostructured sample.

The z-scan results indicate a positive nonlinear refractive index in the nanosecond regime. The sign in the nonlinear refractive index might vary depending on many factors responsible for the physical mechanisms of nonlinearity [42], material thickness, incident irradiance, and different preparation techniques, like RF magnetron sputtering [43] or chemical vapor deposition [44]. Also, previous works have reported that the crystallization form of the ZnO could have influenced its optical and NLO response.

3.5. Nanosecond TWM Studies

Figure 6a depicts the transmitted optical irradiance obtained as a function angle of polarization for both ZnO samples in the TWM mixing experiments. The obtained curves show a clear relation between the optical properties and the crystal size that forms the ZnO structures, one of the principal factors that influence different physical properties of ZnO thin films. Thus, the overall results indicate a direct correlation between the two-sized structures and the optical response at a maximum angle of polarization. Complementarily, the nanosized crystals presented the stronger enhancement on transmittance at least three times larger than the microcrystals (at data ×100). In view of these considerations, it is possible to speculate a particle size dependence responsible for the variations in the Kerr transmittance that increased from the polarization of the light. The possibility of obtaining different optical signals with hybrid materials is rather attractive in optoelectronics in order to generate different nonlinearities and all-optical functions. The modulation of a normalized nonlinear refractive index in the ZnO nanostructures as a function of their volume fraction in respect to microstructures and the angle of polarization is illustrated in Figure 6b. The numerical data plotted in Figure 6b were estimated using Equations (7)–(10) and the finite difference method.

Third-order optical nonlinearities can be controlled by irradiance, polarization, and concentration of different sizes and morphologies of crystals in ZnO nanostructures [45]. In addition, it has been reported that ZnO nanocrystals, nanofilms, nanowires [46], and bulk structures can be used as nonlinear media to obtain higher-frequency conversion efficiencies from nonlinear effects [47,48]. Also, various ZnO-based nanohybrids have been examined for the enhancement of their nonlinear optical interactions [49,50,51,52,53,54,55,56]. In this work, we highlight the importance of describing a fractional model and optically induced electronic behavior with influence on photoconductivity and electronic mechanisms responsible for Kerr nonlinearity. We propose the tuning of ZnO systems via the combination of micro and nanostructures that can be assisted by a fractional description for predicting electronic and optically induced functions with potential applications for optoelectronics and all-optical devices.

4. Conclusions

Fractional electrical studies for describing conductivity effects in low-dimensional systems are reported. Photoconductive and capacitive behavior was identified in the nanostructured ZnO thin film studied, while inhibition of conductivity was obtained when the samples were in a micro-structured form. An enhancement in NLO effects and electrical conductivity was obtained via the preparation of ZnO in a nanostructured form. A red shift in the optical resonance of nanostructured ZnO was observed in respect to micro-structured ZnO. TWM experiments and z-scan explorations were conducted for the characterization of NLO response of the studied ZnO samples. The NLO effects revealed the existence of a nanosecond Kerr effect at 532 nm, which was attributed to an electronic physical mechanism responsible for the third-order optical nonlinearities. The results of the NLO nature demonstrate the potential to combine nano and microstructures to modulate electrical, electromagnetic, and NLO effects in ZnO circuits and optoelectronic platforms.