Fractional Criticality Theory and Its Application in Seismology
Abstract
:1. Introduction
2. Compound Fractional Poisson Process with Power-Law Distribution of Events Recurrence Frequencies
2.1. Compound Fractional Poisson Process
2.2. Distribution of Recurrence Frequencies of Events
3. Critical Indices and Process Instability
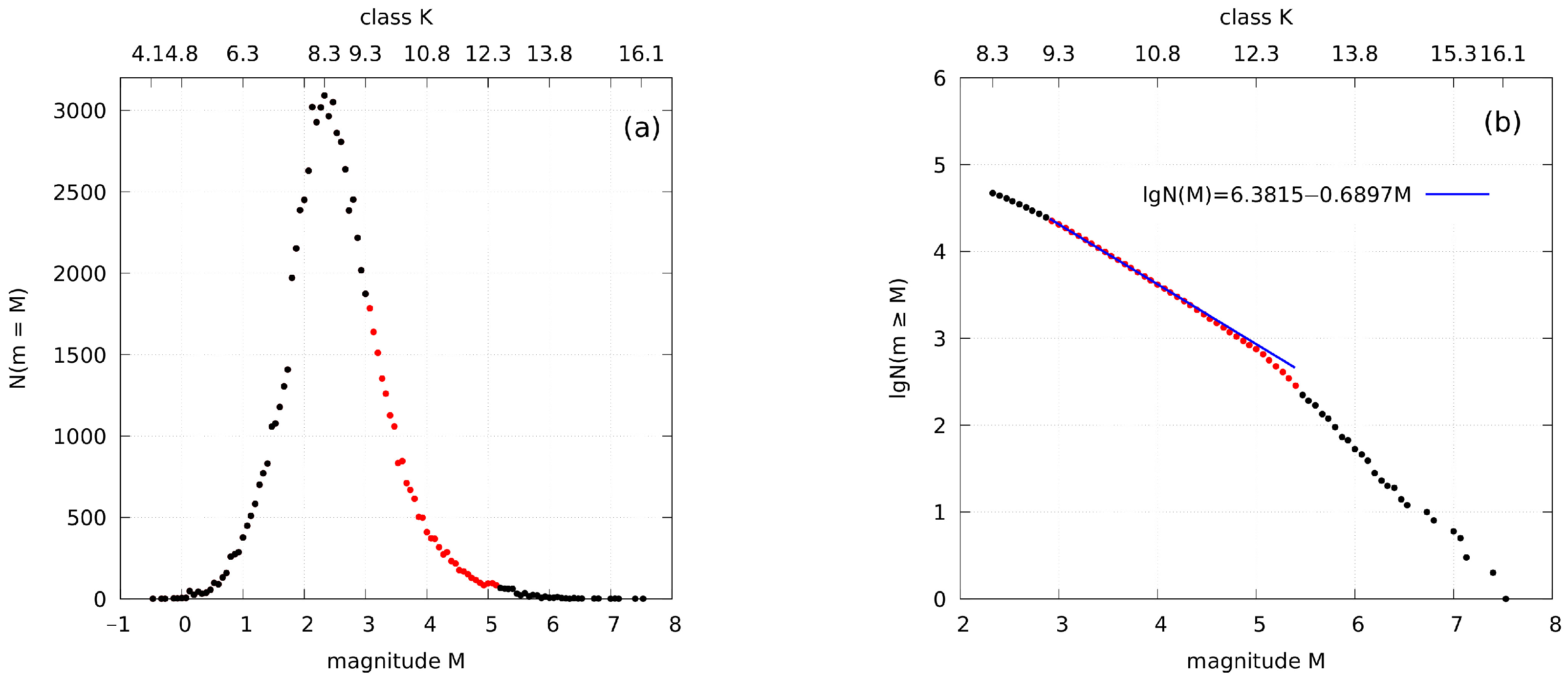
4. Calculation of the Distribution Parameters of the Events Recurrence Frequency Based on Seismic Data
4.1. Calculation of b-Value
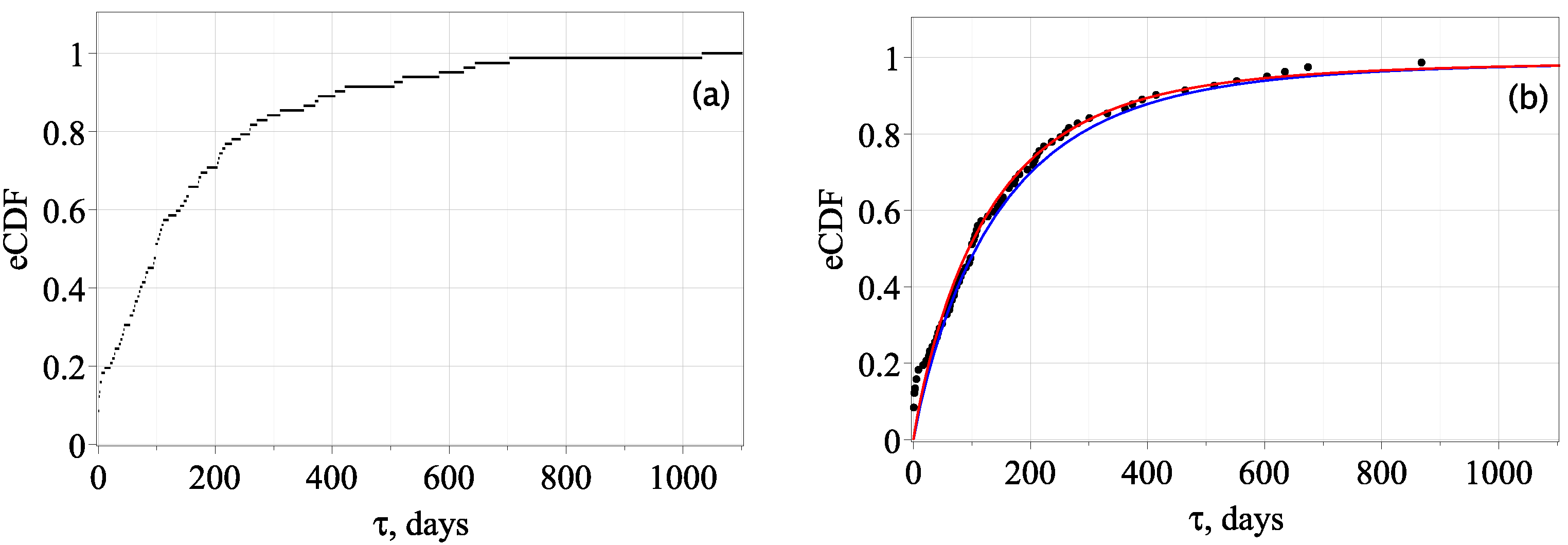
4.2. Distributions of the First-Passage Times
4.3. Approximation of the First-Passage Times Distributions
5. Results and Discussion
- The hereditarity parameter or the average of the exponent of the fractional derivative of the CFPP is calculated on the values in column 10 of the Table 2According to the value of this parameter, we can conclude that the considered seismic process has «memory», so random events of deformation changes cannot be considered independent.Since , the distributions (16) define the delayed relaxation of strains, which are associated with the hardening of the deformable medium and the accumulation of elastic energy, which may be the reason for the activation of the process.
- The fractional decay rate of CFPP states is determined by the parameter (13), (14), which is represented as follows:The -value equal to the zero moment is calculated on the values in column 9 of Table 2 and in item 1,
- The stability parameter of the CFPP takes the valuewhere the b-value is taken from Table 1. This parameter defines the multiplicative effect of the scaling and hereditarity on the critical indices.
- The values of the critical indices (23) are equal toA comparison of the -parameter (item 1) with the critical indices () shows that the seismic process is in a subcritical regime for the zero and first moments and in a supercritical regime for the second moment of distribution (13), which indicates the instability of deformation changes that can go into a non-stationary regime of the seismic process. The reason for this activation is indicated in item 1.This result means that the fractional decay rate of the seismic process, described by the parameters of the CFPP (14) and (18), and the average deformations (20), proportional to at , are finite, and the divergence in the dispersion growth (21) caused by at leads to the instability of the process and its transition to a non-stationary regime considered in papers [13,14].The anomalous growth of fluctuations caused by the hereditarity of the seismic process is represented in (21) by the second term, which is proportional to the square of the mean (20), which is different to the first term and proportional to the mean . If the first term in (21) describes an ordinary deformation, then the second term describes an anomalous one caused by the consolidation of scales. This is a collective or induced coherent effect, the analogue of which in quantum optics is superluminescence, and in phase transition physics is explosive boiling. In the absence of hereditarity, this effect disappears, because if we take , then the second term of in (21) will be zero based on the property of the gamma function .
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CFPP | Compound Fractional Poisson Process |
| LSM | Least Squares Method |
| eCDF | Empirical Cumulative Distribution Function |
References
- Janossy, L.; Renyi, A.; Aczel, J. On composed Poisson distributions I. Acta Math. Acad. Sci. Hungar. 1950, 1, 209–224. [Google Scholar] [CrossRef]
- Adelson, R.M. Compound Poisson distributions. Oper. Res. Quart. 1966, 17, 73–75. [Google Scholar] [CrossRef]
- Khandakar, M.; Kataria, K.K. Some Compound Fractional Poisson Processes. Fractal Fract. 2023, 7, 15. [Google Scholar] [CrossRef]
- Di Crescenzo, A.; Martinucci, B.; Meoli, A. A fractional counting process and its connection with the Poisson process. ALEA Lat. Am. J. Probab. Math. Stat. 2016, 13, 291–307. [Google Scholar] [CrossRef]
- Beghin, L.; Macci, C. Multivariate fractional Poisson processes and compound sums. Adv. Appl. Probab. 2016, 48, 691–711. [Google Scholar] [CrossRef]
- Gutenberg, B.; Richter, C.F. Frequency of Earthquakes in California. Bull. Seismol. Soc. Am. 1944, 34, 185–188. [Google Scholar] [CrossRef]
- Kanamori, H. The Energy Release in Great Earthquakes. J. Geophys. Res. 1977, 82, 2981–2987. [Google Scholar] [CrossRef]
- The Geophysical Service of the Russian Academy of Sciences. Available online: http://www.gsras.ru/new/eng/catalog/ (accessed on 27 February 2022).
- Marapulets, Y.; Senkevich, Y.; Lukovenkova, O.; Solodchuk, A. Method of Analysis and Classification of Acoustic Emission Signals to Identify Pre-Seismic Anomalies. ASTES J. 2020, 5, 894–903. [Google Scholar]
- Marapulets, Y.; Lukovenkova, O. Time-Frequency Analysis of Geoacoustic Data Using Adaptive Matching Pursuit. Acoust. Phys. 2021, 67, 312–319. [Google Scholar] [CrossRef]
- Lukovenkova, O.; Marapulets, Y.; Solodchuk, A. Adaptive Approach to Time-Frequency Analysis of AE Signals of Rocks. Sensors 2022, 22, 9798. [Google Scholar] [CrossRef] [PubMed]
- Gapeev, M.; Marapulets, Y. Modeling Locations with Enhanced Earth’s Crust Deformation during Earthquake Preparation near the Kamchatka Peninsula. Appl. Sci. 2023, 13, 290. [Google Scholar] [CrossRef]
- Sheremetyeva, O.; Shevtsov, B. Fractional Model of the Deformation Process. Fractal Fract. 2022, 6, 372. [Google Scholar] [CrossRef]
- Shevtsov, B.; Sheremetyeva, O. Fractional models of seismoacoustic and electromagnetic activity. E3S Web Conf. 2017, 20, 02013. [Google Scholar] [CrossRef]
- Baiesi, M.; Paczuski, M. Complex networks of earthquakes and aftershocks. Nonlinear Process. Geophys. 2005, 12, 1–11. [Google Scholar] [CrossRef]
- Shebalin, P.N. Increased correlation range of seismicity before large events manifested by earthquake chains. Tectonophysics 2006, 424, 335–349. [Google Scholar] [CrossRef]
- Shevtsov, B.M.; Sagitova, R.N. Statistical analysis of seismic processes on the basis of the diffusion approach. Dokl. Earth Sci. 2009, 426, 642–644. [Google Scholar] [CrossRef]
- Shevtsov, B.M.; Sagitova, R.N. A diffusion approach to the statistical analysis of Kamchatka seismicity. J. Volcanol. Seismol. 2012, 6, 116–125. [Google Scholar] [CrossRef]
- Shebalin, P.; Narteau, C. Depth Dependent Stress Revealed by Aftershocks. Nat. Commun. 2017, 8, 1317–1318. [Google Scholar] [CrossRef] [PubMed]
- Shebalin, P.N.; Narteau, C.; Baranov, S.V. Earthquake Productivity Law. Geophys. J. Int. 2020, 222, 1264–1269. [Google Scholar] [CrossRef]
| 1 | k | a | b | R | F | ||||
|---|---|---|---|---|---|---|---|---|---|
| 38 | 22,230 | 1233 99 |
| Approximation by a Function (16) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| One-Parameter | Two-Parameter | |||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 9.2 | 2.93 | 57 | 0.102 | 0.135 | 0.961 | 4.71 | 0.025 | 0.182 | 0.891 | 2.33 |
| 9.3 | 3.0 | 57 | 0.067 | 0.125 | 0.974 | 3.93 | 0.031 | 0.152 | 0.925 | 2.59 |
| 9.4 | 3.07 | 57 | 0.085 | 0.119 | 0.962 | 4.36 | 0.034 | 0.149 | 0.905 | 2.76 |
| 9.5 | 3.13 | 58 | 0.099 | 0.109 | 0.958 | 4.71 | 0.039 | 0.139 | 0.897 | 2.97 |
| 9.6 | 3.2 | 62 | 0.105 | 0.101 | 0.959 | 4.71 | 0.033 | 0.129 | 0.895 | 2.64 |
| 9.7 | 3.27 | 67 | 0.109 | 0.09 | 0.962 | 4.62 | 0.036 | 0.114 | 0.901 | 2.65 |
| 9.8 | 3.33 | 67 | 0.102 | 0.084 | 0.954 | 4.55 | 0.032 | 0.105 | 0.895 | 2.53 |
| 9.9 | 3.4 | 77 | 0.095 | 0.075 | 0.961 | 4.08 | 0.043 | 0.09 | 0.914 | 2.76 |
| 10.0 | 3.47 | 71 | 0.108 | 0.071 | 0.955 | 4.65 | 0.063 | 0.083 | 0.907 | 3.54 |
| 10.1 | 3.53 | 83 | 0.077 | 0.056 | 0.960 | 3.70 | 0.036 | 0.064 | 0.92 | 2.51 |
| 10.2 | 3.6 | 84 | 0.074 | 0.057 | 0.968 | 3.57 | 0.029 | 0.065 | 0.928 | 2.24 |
| 10.3 | 3.67 | 91 | 0.112 | 0.048 | 0.960 | 4.29 | 0.035 | 0.056 | 0.91 | 2.38 |
| 10.4 | 3.73 | 93 | 0.245 | 0.045 | 0.932 | 6.31 | 0.045 | 0.06 | 0.849 | 2.7 |
| 10.5 | 3.8 | 95 | 0.133 | 0.041 | 0.969 | 4.64 | 0.043 | 0.049 | 0.918 | 2.64 |
| 10.6 | 3.87 | 103 | 0.214 | 0.034 | 0.942 | 5.79 | 0.051 | 0.042 | 0.88 | 2.83 |
| 10.7 | 3.93 | 103 | 0.163 | 0.033 | 0.959 | 5.12 | 0.081 | 0.039 | 0.91 | 3.61 |
| 10.8 | 4.0 | 107 | 0.257 | 0.027 | 0.922 | 6.53 | 0.089 | 0.034 | 0.858 | 3.83 |
| 10.9 | 4.07 | 109 | 0.28 | 0.025 | 0.947 | 6.75 | 0.041 | 0.031 | 0.888 | 2.6 |
| 11.0 | 4.13 | 113 | 0.331 | 0.025 | 0.922 | 7.19 | 0.041 | 0.033 | 0.865 | 3.76 |
| 11.1 | 4.2 | 115 | 0.395 | 0.021 | 0.880 | 8.01 | 0.079 | 0.028 | 0.817 | 3.59 |
| 11.2 | 4.27 | 112 | 0.357 | 0.018 | 0.907 | 7.97 | 0.059 | 0.023 | 0.852 | 3.25 |
| 11.3 | 4.33 | 113 | 0.301 | 0.019 | 0.926 | 7.17 | 0.103 | 0.024 | 0.873 | 4.19 |
| 11.4 | 4.4 | 112 | 0.144 | 0.016 | 0.898 | 5.38 | 0.044 | 0.018 | 0.886 | 4.05 |
| 11.5 | 4.47 | 104 | 0.405 | 0.015 | 0.845 | 9.15 | 0.101 | 0.019 | 0.797 | 4.57 |
| 11.6 | 4.53 | 100 | 0.225 | 0.012 | 0.936 | 7.27 | 0.141 | 0.013 | 0.91 | 5.75 |
| 11.7 | 4.6 | 95 | 0.505 | 0.011 | 0.825 | 11.18 | 0.023 | 0.021 | 0.784 | 4.07 |
| 11.8 | 4.67 | 89 | 0.451 | 0.01 | 0.861 | 10.74 | 0.112 | 0.014 | 0.822 | 5.35 |
| 11.9 | 4.73 | 79 | 0.353 | 0.009 | 0.835 | 10.21 | 0.036 | 0.012 | 0.85 | 5.4 |
| 12.0 | 4.8 | 76 | 0.529 | 0.008 | 0.803 | 13.1 | 0.055 | 0.012 | 0.818 | 4.22 |
| 12.1 | 4.87 | 73 | 0.576 | 0.007 | 0.772 | 14.03 | 0.08 | 0.01 | 0.775 | 5.21 |
| 12.2 | 4.93 | 61 | 0.21 | 0.006 | 0.915 | 9.31 | 0.113 | 0.007 | 0.886 | 6.83 |
| 12.3 | 5.0 | 68 | 0.133 | 0.006 | 0.920 | 7.06 | 0.089 | 0.007 | 0.909 | 5.76 |
| 12.4 | 5.07 | 65 | 0.666 | 0.006 | 0.751 | 15.45 | 0.04 | 0.01 | 0.766 | 5.95 |
| 12.5 | 5.13 | 55 | 0.644 | 0.006 | 0.755 | 16.42 | 0.033 | 0.011 | 0.749 | 4.92 |
| 12.6 | 5.2 | 49 | 0.273 | 0.005 | 0.787 | 12.2 | 0.043 | 0.007 | 0.791 | 6.04 |
| 12.7 | 5.27 | 51 | 0.217 | 0.004 | 0.896 | 10.55 | 0.075 | 0.005 | 0.882 | 6.21 |
| 12.8 | 5.33 | 47 | 0.108 | 0.004 | 0.880 | 7.92 | 0.051 | 0.005 | 0.858 | 5.46 |
| 12.9 | 5.4 | 50 | 0.428 | 0.004 | 0.868 | 14.85 | 0.032 | 0.006 | 0.883 | 5.32 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shevtsov, B.; Sheremetyeva, O. Fractional Criticality Theory and Its Application in Seismology. Fractal Fract. 2023, 7, 890. https://doi.org/10.3390/fractalfract7120890
Shevtsov B, Sheremetyeva O. Fractional Criticality Theory and Its Application in Seismology. Fractal and Fractional. 2023; 7(12):890. https://doi.org/10.3390/fractalfract7120890
Chicago/Turabian StyleShevtsov, Boris, and Olga Sheremetyeva. 2023. "Fractional Criticality Theory and Its Application in Seismology" Fractal and Fractional 7, no. 12: 890. https://doi.org/10.3390/fractalfract7120890
APA StyleShevtsov, B., & Sheremetyeva, O. (2023). Fractional Criticality Theory and Its Application in Seismology. Fractal and Fractional, 7(12), 890. https://doi.org/10.3390/fractalfract7120890







