Explicit Soliton Structure Formation for the Riemann Wave Equation and a Sensitive Demonstration
Abstract
:1. Introduction
2. Structures of Analytical Solutions
2.1. New Extended Direct Algebraic Method
2.2. Application of the New Extended Direct Algebraic Method
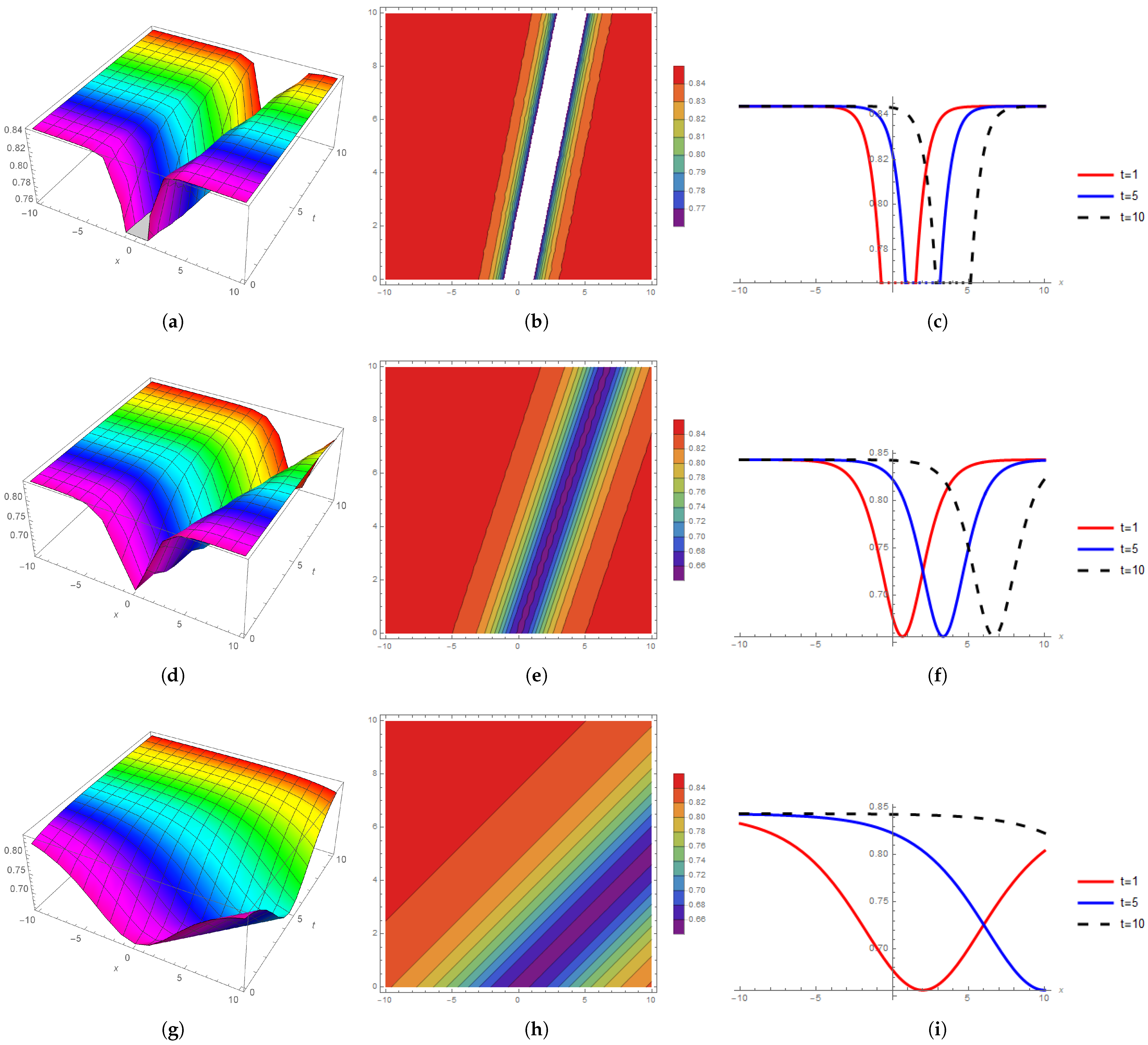
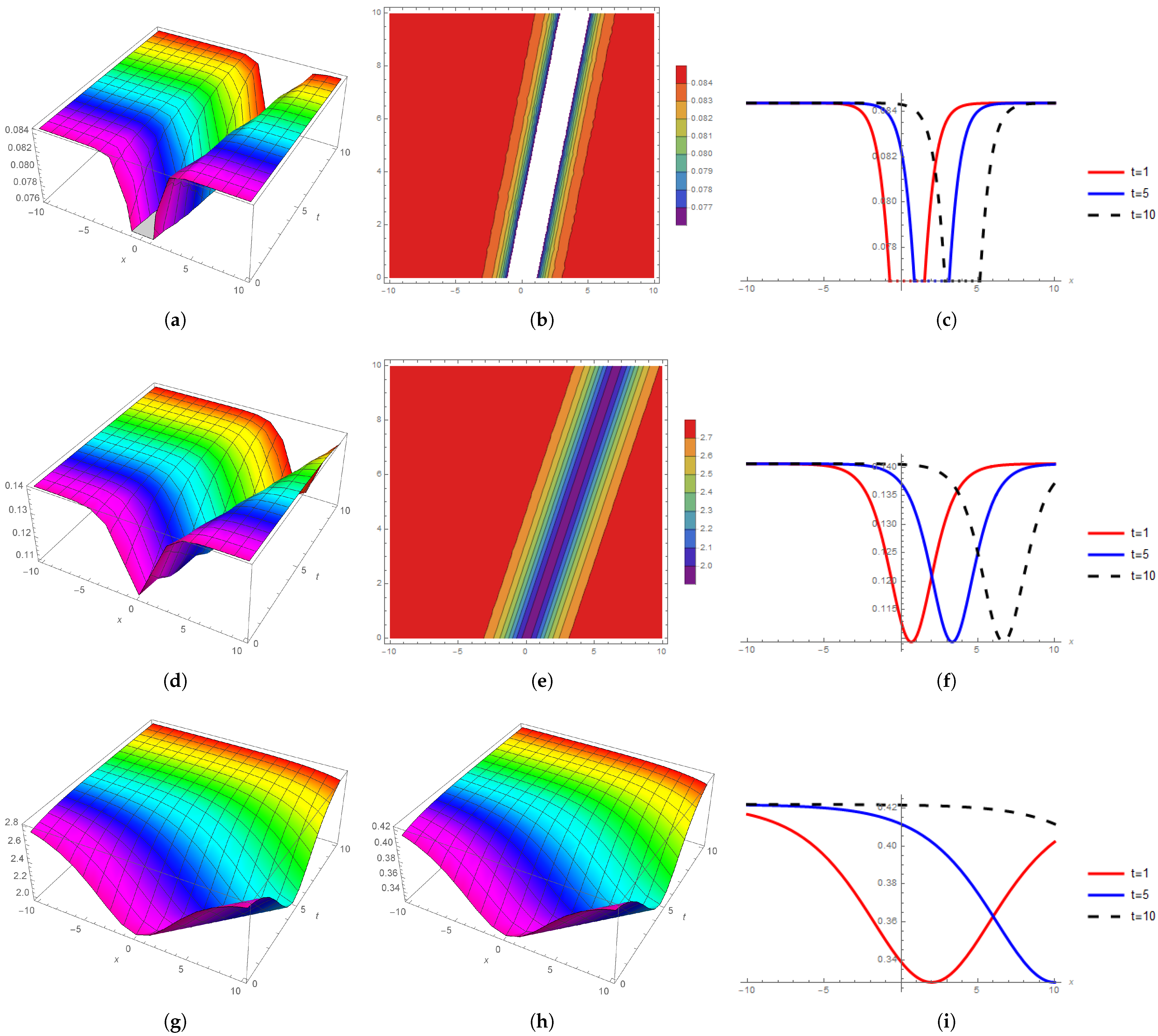
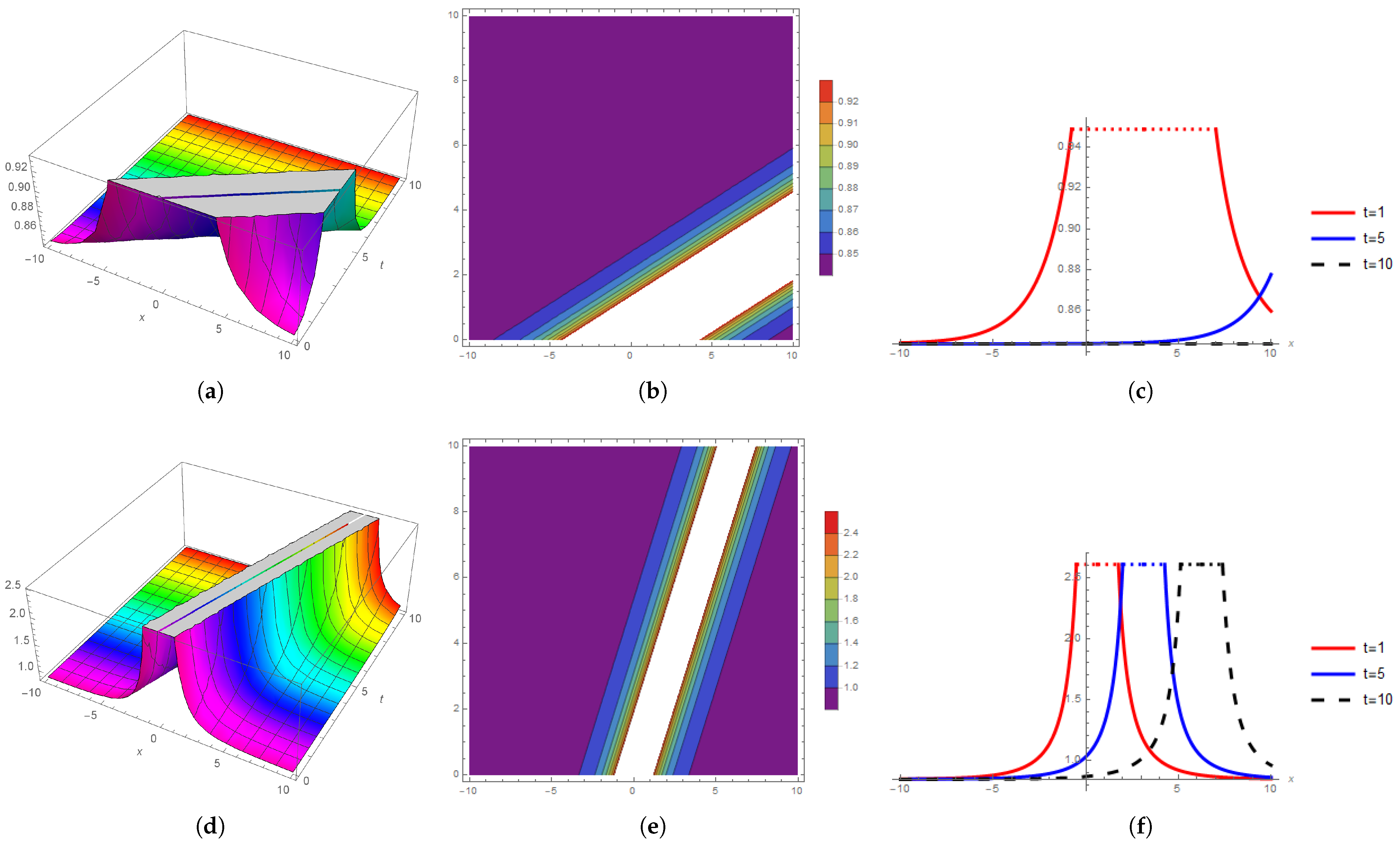
3. Graphical Representation
Graphical Discussion
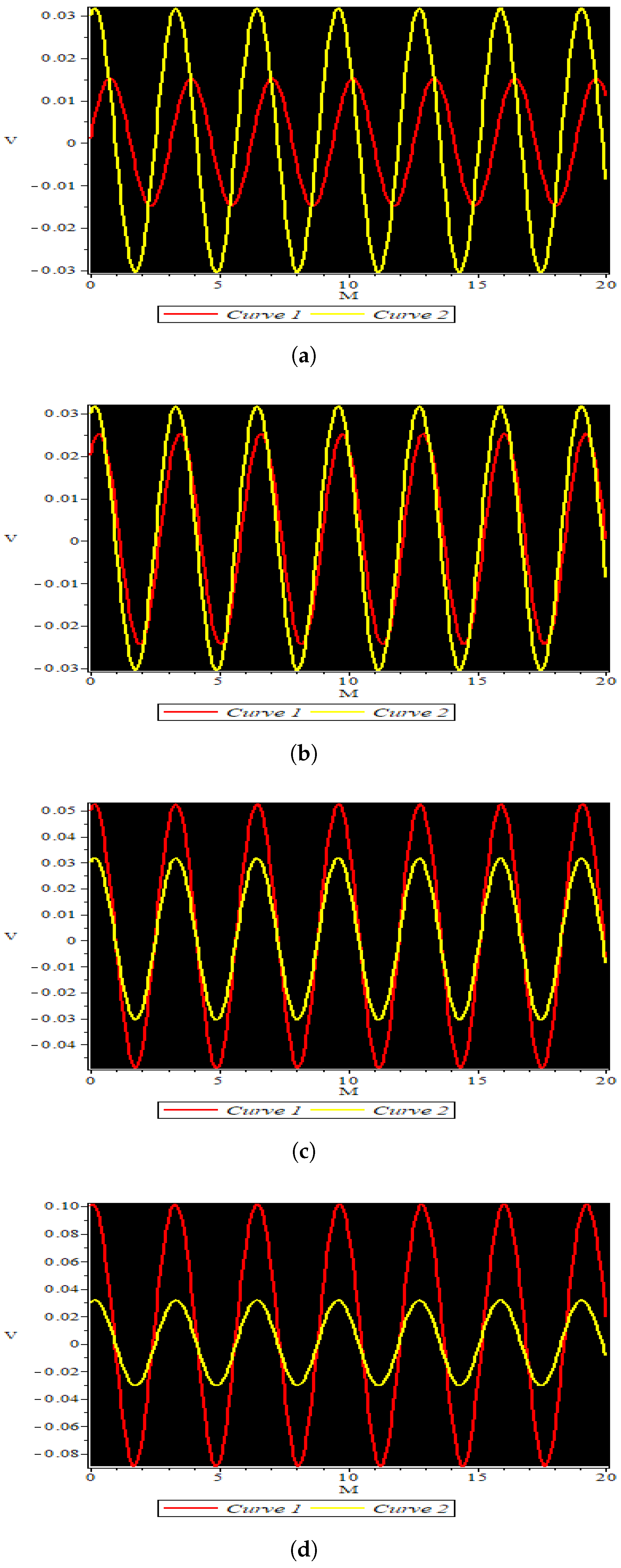
4. The Sensitivity Assessment
5. Conclusions
- We developed soliton solutions with twelve distinct families in which various newly different solutions were derived, such as the plane solution, mixed hyperbolic solution, trigonometry solution, mixed periodic and periodic solutions, shock solution, mixed singular solution, mixed trigonometric solution, mixed shock single solution, complex solitary shock solution, singular solution, and shock wave solutions.
- We displayed the 3D, 2D, and contour presentations of the obtained solutions with the appropriate values of involved parameters.
- A sensitivity analysis of the obtained system is displayed with the appropriate values of the involved parameters.
- The wave velocity and wave number parameters are responsible for controlling the singularity of the water waves.
- The new extended direct algebraic performance is reliable and effective, and it provides new solutions. The methodology utilized in this study will be used in future research to discover novel solutions for other nonlinear wave equations.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Faridi, W.A.; Asjad, M.I.; Jarad, F. Non-linear soliton solutions of perturbed Chen-Lee-Liu model by Φ6-model expansion approach. Opt. Quantum Electron. 2022, 54, 664. [Google Scholar] [CrossRef]
- Hosseini, K.; Mirzazadeh, M.; Salahshour, S.; Baleanu, D.; Zafar, A. Specific wave structures of a fifth-order nonlinear water wave equation. J. Ocean Eng. Sci. 2022, 7, 462–466. [Google Scholar] [CrossRef]
- Aziz, N.; Seadawy, A.R.; Ali, K.; Sohail, M.; Rizvi, S.T.R. The nonlinear Schrödinger equation with polynomial law nonlinearity: Localized chirped optical and solitary wave solutions. Opt. Quantum Electron. 2022, 54, 458. [Google Scholar] [CrossRef]
- Asjad, M.I.; Faridi, W.A.; Jhangeer, A.; Abu-Zinadah, H.; Ahmad, H. The fractional comparative study of the non-linear directional couplers in non-linear optics. Results Phys. 2021, 27, 104459. [Google Scholar]
- Nisar, K.S.; Ciancio, A.; Ali, K.K.; Osman, M.S.; Cattani, C.; Baleanu, D.; Azeem, M. On beta-time fractional biological population model with abundant solitary wave structures. Alex. Eng. J. 2022, 61, 1996–2008. [Google Scholar]
- Tariq, K.U.; Rezazadeh, H.; Zubair, M.; Osman, M.S.; Akinyemi, L. New Exact and Solitary Wave Solutions of Nonlinear Schamel–KdV Equation. Int. J. Appl. Comput. Math. 2022, 8, 114. [Google Scholar]
- Pan, C.; Bu, L.; Chen, S.; Mihalache, D.; Grelu, P.; Baronio, F. Omnipresent coexistence of rogue waves in a nonlinear two-wave interference system and its explanation by modulation instability. Phys. Rev. Res. 2021, 3, 033152. [Google Scholar]
- Bu, L.; Baronio, F.; Chen, S.; Trillo, S. Quadratic Peregrine solitons resonantly radiating without higher-order dispersion. Opt. Lett. 2022, 47, 2370–2373. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Xie, X.; Jin, C. Phase portraits and optical soliton solutions of coupled nonlinear Maccari systems describing the motion of solitary waves in fluid flow. Results Phys. 2022, 41, 105932. [Google Scholar] [CrossRef]
- Shen, Y.; Tian, B.; Gao, X.T. Bilinear auto-Bäcklund transformation, soliton and periodic-wave solutions for a (2+1)-dimensional generalized Kadomtsev–Petviashvili system in fluid mechanics and plasma physics. Chin. J. Phys. 2022, 77, 2698–2706. [Google Scholar]
- Faridi, W.A.; Asjad, M.I.; Jhangeer, A. The fractional analysis of fusion and fission process in plasma physics. Phys. Scr. 2021, 96, 104008. [Google Scholar] [CrossRef]
- Faridi, W.A.; Asjad, M.I.; Eldin, S.M. Exact Fractional Solution by Nucci’s Reduction Approach and New Analytical Propagating Optical Soliton Structures in Fiber-Optics. Fractal Fract. 2022, 6, 654. [Google Scholar] [CrossRef]
- Akinyemi, L.; Şenol, M.; Huseen, S.N. Modified homotopy methods for generalized fractional perturbed Zakharov–Kuznetsov equation in dusty plasma. Adv. Differ. Equ. 2021, 2021, 45. [Google Scholar] [CrossRef]
- Ali, K.K.; Cattani, C.; Gómez-Aguilar, J.F.; Baleanu, D.; Osman, M.S. Analytical and numerical study of the DNA dynamics arising in oscillator-chain of Peyrard-Bishop model. Chaos Solitons Fractals 2020, 139, 110089. [Google Scholar] [CrossRef]
- Aktar, M.S.; Akbar, M.A.; Osman, M.S. Spatio-temporal dynamic solitary wave solutions and diffusion effects to the nonlinear diffusive predator-prey system and the diffusion-reaction equations. Chaos Solitons Fractals 2022, 160, 112212. [Google Scholar] [CrossRef]
- Bruzzone, O.A.; Perri, D.V.; Easdale, M.H. Vegetation responses to variations in climate: A combined ordinary differential equation and sequential Monte Carlo estimation approach. Ecol. Inform. 2022, 73, 101913. [Google Scholar] [CrossRef]
- Zhou, T.Y.; Tian, B.; Zhang, C.R.; Liu, S.H. Auto-Bäcklund transformations, bilinear forms, multiple-soliton, quasi-soliton and hybrid solutions of a (3+1)-dimensional modified Korteweg-de Vries-Zakharov-Kuznetsov equation in an electron-positron plasma. Eur. Phys. J. Plus 2022, 137, 912. [Google Scholar] [CrossRef]
- Poguluri, S.K.; Kim, J.; George, A.; Cho, I.H. Wave interaction with horizontal multilayer porous plates. J. Waterw. Port Coast. Ocean. Eng. 2022, 148, 04022016. [Google Scholar] [CrossRef]
- Alabedalhadi, M. Exact traveling wave solutions for nonlinear system of spatiotemporal fractional quantum mechanics equations. Alex. Eng. J. 2022, 61, 1033–1044. [Google Scholar] [CrossRef]
- Akinyemi, L.; Rezazadeh, H.; Yao, S.W.; Akbar, M.A.; Khater, M.M.; Jhangeer, A.; Ahmad, H. Nonlinear dispersion in parabolic law medium and its optical solitons. Results Phys. 2021, 26, 104411. [Google Scholar] [CrossRef]
- Akinyemi, L.; Şenol, M.; Rezazadeh, H.; Ahmad, H.; Wang, H. Abundant optical soliton solutions for an integrable (2+1)-dimensional nonlinear conformable Schrödinger system. Results Phys. 2021, 25, 104177. [Google Scholar] [CrossRef]
- Fahim, M.R.A.; Kundu, P.R.; Islam, M.E.; Akbar, M.A.; Osman, M.S. Wave profile analysis of a couple of (3+1)-dimensional nonlinear evolution equations by sine-Gordon expansion approach. J. Ocean Eng. Sci. 2022, 7, 272–279. [Google Scholar] [CrossRef]
- Ozdemir, N.; Esen, H.; Secer, A.; Bayram, M.; Sulaiman, T.A.; Yusuf, A.; Aydin, H. Optical solitons and other solutions to the Radhakrishnan-Kundu-Lakshmanan equation. Optik 2021, 242, 167363. [Google Scholar] [CrossRef]
- Osman, M.S.; Almusawa, H.; Tariq, K.U.; Anwar, S.; Kumar, S.; Younis, M.; Ma, W.X. On global behavior for complex soliton solutions of the perturbed nonlinear Schrödinger equation in nonlinear optical fibers. J. Ocean Eng. Sci. 2022, 7, 431–443. [Google Scholar] [CrossRef]
- Kumar, S.; Dhiman, S.K.; Baleanu, D.; Osman, M.S.; Wazwaz, A.M. Lie symmetries, closed-form solutions, and various dynamical profiles of solitons for the variable coefficient (2+1)-dimensional KP equations. Symmetry 2022, 14, 597. [Google Scholar] [CrossRef]
- Mirzazadeh, M.; Akinyemi, L.; Şenol, M.; Hosseini, K. A variety of solitons to the sixth-order dispersive (3+1)-dimensional nonlinear time-fractional Schrödinger equation with cubic-quintic-septic nonlinearities. Optik 2021, 241, 166318. [Google Scholar] [CrossRef]
- Leventoux, Y.; Fabert, M.; Săpânţan, M.; Krupa, K.; Tonello, A.; Granger, G.; Couderc, V. Latest experimental advances in nonlinear multimode fiber optics. In Proceedings of the 2021 Conference on Lasers and Electro-Optics Europe & European Quantum Electronics Conference (CLEO/Europe-EQEC), Munich, Germany, 21–25 June 2021; p. 1. [Google Scholar]
- Zafar, A.; Shakeel, M.; Ali, A.; Akinyemi, L.; Rezazadeh, H. Optical solitons of nonlinear complex Ginzburg–Landau equation via two modified expansion schemes. Opt. Quantum Electron. 2022, 54, 1–15. [Google Scholar]
- Ali, K.K.; Wazwaz, A.M.; Osman, M.S. Optical soliton solutions to the generalized nonautonomous nonlinear Schrödinger equations in optical fibers via the sine-Gordon expansion method. Optik 2020, 208, 164132. [Google Scholar] [CrossRef]
- Zhang, R.; Bilige, S.; Chaolu, T. Fractal solitons, arbitrary function solutions, exact periodic wave and breathers for a nonlinear partial differential equation by using bilinear neural network method. J. Syst. Sci. Complex 2021, 34, 122–139. [Google Scholar] [CrossRef]
- Khater, M.; Jhangeer, A.; Rezazadeh, H.; Akinyemi, L.; Akbar, M.A.; Inc, M.; Ahmad, H. New kinds of analytical solitary wave solutions for ionic currents on microtubules equation via two different techniques. Opt. Quantum Electron. 2021, 53, 609. [Google Scholar] [CrossRef]
- Karaman, B. The use of improved-F expansion method for the time-fractional Benjamin–Ono equation. Rev. Real Acad. Cienc. Exactas Fis. Nat. Ser. Mat. 2021, 115, 128. [Google Scholar] [CrossRef]
- Zayed, E.M.; Gepreel, K.A.; Shohib, R.M.; Alngar, M.E.; Yıldırım, Y. Optical solitons for the perturbed Biswas-Milovic equation with Kudryashov’s law of refractive index by the unified auxiliary equation method. Optik 2021, 230, 166286. [Google Scholar] [CrossRef]
- Ismael, H.F.; Bulut, H.; Baskonus, H.M. Optical soliton solutions to the Fokas–Lenells equation via sine-Gordon expansion method and (m+(G′/G))(m+(G′/G))-expansion method. Pramana 2020, 94, 35. [Google Scholar] [CrossRef]
- Sulaiman, A.T.; Yusuf, A. Dynamics of lump-periodic and breather waves solutions with variable coefficients in liquid with gas bubbles. Waves Random Complex Media 2021, 6, 1–14. [Google Scholar] [CrossRef]
- Khodadad, F.S.; Mirhosseini-Alizamini, S.M.; Günay, B.; Akinyemi, L.; Rezazadeh, H.; Inc, M. Abundant optical solitons to the Sasa-Satsuma higher-order nonlinear Schrödinger equation. Opt. Quantum Electron. 2021, 53, 702. [Google Scholar] [CrossRef]
- Kumar, S.; Kumar, A.; Wazwaz, A.M. New exact solitary wave solutions of the strain wave equation in microstructured solids via the generalized exponential rational function method. Eur. Phys. J. Plus 2020, 135, 870. [Google Scholar] [CrossRef]
- Wazwaz, A.M. Optical bright and dark soliton solutions for coupled nonlinear Schrödinger (CNLS) equations by the variational iteration method. Optik 2020, 207, 164457. [Google Scholar] [CrossRef]
- Ghanbari, B.; Kumar, S.; Niwas, M.; Baleanu, D. The Lie symmetry analysis and exact Jacobi elliptic solutions for the Kawahara–KdV type equations. Results Phys. 2021, 23, 104006. [Google Scholar] [CrossRef]
- Rehman, S.U.; Yusuf, A.; Bilal, M.; Younas, U.; Younis, M.; Sulaiman, T.A. Application of (GG′-2)-expansion method to microstructured solids, magneto-electro-elastic circular rod and (2+1)-dimensional nonlinear electrical lines. Math. Eng. Sci. Aerosp. 2020, 11, 789–803. [Google Scholar]
- Rashed, A.S.; Mabrouk, S.M.; Wazwaz, A.M. Forward scattering for non-linear wave propagation in (3+1)-dimensional Jimbo-Miwa equation using singular manifold and group transformation methods. Waves Random Complex Media 2022, 32, 663–675. [Google Scholar] [CrossRef]
- Kumar, S.; Rani, S. Symmetries of optimal system, various closed-form solutions, and propagation of different wave profiles for the Boussinesq–Burgers system in ocean waves. Phys. Fluids 2022, 34, 037109. [Google Scholar] [CrossRef]
- Abdulwahhab, M.A. Hamiltonian structure, optimal classification, optimal solutions and conservation laws of the classical Boussinesq–Burgers system. Part. Differ. Equ. Appl. Math. 2022, 6, 100442. [Google Scholar] [CrossRef]
- Kumar, S.; Niwas, M.; Osman, M.S.; Abdou, M.A. Abundant different types of exact soliton solution to the (4+1)-dimensional Fokas and (2+1)-dimensional breaking soliton equations. Commun. Theor. Phys. 2021, 73, 105007. [Google Scholar] [CrossRef]
- Abdulwahhab, M.A. On the invariant solutions, third order multipliers and local conservation laws of the 3-dimensional Pavlov Equation. Optik 2022, 168852. [Google Scholar] [CrossRef]
- Pan, C.; Bu, L.; Chen, S.; Yang, W.X.; Mihalache, D.; Grelu, P.; Baronio, F. General rogue wave solutions under SU (2) transformation in the vector Chen–Lee–Liu nonlinear Schrödinger equation. Phys. D Nonlinear Phenom. 2022, 434, 133204. [Google Scholar] [CrossRef]
- Shakeel, M.; Ahmad, B.; Shah, N.A.; Chung, J.D. Solitons Solution of Riemann Wave Equation via Modified Exp Function Method. Symmetry 2022, 14, 2574. [Google Scholar]
- Spatschek, K.H.; Shukla, P.K. Nonlinear interaction of magneto-sound wave with whistler turbulence. Radio Sci. 1978, 13, 211–214. [Google Scholar] [CrossRef]
- Islam, M.E.; Akbar, M.A. Stable wave solutions to the Landau-Ginzburg-Higgs equation and the modified equal width wave equation using the IBSEF method. Arab. J. Basic Appl. Sci. 2020, 27, 270–278. [Google Scholar] [CrossRef]
- Barman, H.K.; Akbar, M.A.; Osman, M.S.; Nisar, K.S.; Zakarya, M.; Abdel-Aty, A.H.; Eleuch, H. Solutions to the Konopelchenko-Dubrovsky equation and the Landau-Ginzburg-Higgs equation via the generalized Kudryashov technique. Results Phys. 2021, 24, 104092. [Google Scholar] [CrossRef]
- Kundu, P.R.; Almusawa, H.; Fahim, M.R.A.; Islam, M.E.; Akbar, M.A.; Osman, M.S. Linear and nonlinear effects analysis on wave profiles in optics and quantum physics. Results Phys. 2021, 23, 103995. [Google Scholar] [CrossRef]
- Jhangeer, A.; Faridi, W.A.; Asjad, M.I.; Akgül, A. Analytical study of soliton solutions for an improved perturbed Schrödinger equation with Kerr law non-linearity in non-linear optics by an expansion algorithm. Part. Differ. Equ. Appl. Math. 2021, 4, 100102. [Google Scholar] [CrossRef]
- Barman, H.K.; Seadawy, A.R.; Akbar, M.A.; Baleanu, D. Competent closed form soliton solutions to the Riemann wave equation and the Novikov-Veselov equation. Results Phys. 2020, 17, 103131. [Google Scholar] [CrossRef]
- Seadawy, A.R.; Rizvi, S.T.R.; Ahmad, S.; Younis, M.; Baleanu, D. Lump, lump-one stripe, multiwave and breather solutions for the Hunter–Saxton equation. Open Phys. 2021, 19, 1–10. [Google Scholar] [CrossRef]
- Hosseini, K.; Osman, M.S.; Mirzazadeh, M.; Rabiei, F. Investigation of different wave structures to the generalized third-order nonlinear Scrödinger equation. Optik 2020, 206, 164259. [Google Scholar] [CrossRef]
- Rizvi, S.T.R.; Seadawy, A.R.; Ashraf, F.; Younis, M.; Iqbal, H.; Baleanu, D. Lump and interaction solutions of a geophysical Korteweg–de Vries equation. Results Phys. 2020, 19, 103661. [Google Scholar] [CrossRef]
- Sulaiman, T.A.; Yusuf, A.; Alquran, M. Dynamics of optical solitons and nonautonomous complex wave solutions to the nonlinear Schrodinger equation with variable coefficients. Nonlinear Dyn. 2021, 104, 639–648. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Majid, S.Z.; Faridi, W.A.; Asjad, M.I.; Abd El-Rahman, M.; Eldin, S.M. Explicit Soliton Structure Formation for the Riemann Wave Equation and a Sensitive Demonstration. Fractal Fract. 2023, 7, 102. https://doi.org/10.3390/fractalfract7020102
Majid SZ, Faridi WA, Asjad MI, Abd El-Rahman M, Eldin SM. Explicit Soliton Structure Formation for the Riemann Wave Equation and a Sensitive Demonstration. Fractal and Fractional. 2023; 7(2):102. https://doi.org/10.3390/fractalfract7020102
Chicago/Turabian StyleMajid, Sheikh Zain, Waqas Ali Faridi, Muhammad Imran Asjad, Magda Abd El-Rahman, and Sayed M. Eldin. 2023. "Explicit Soliton Structure Formation for the Riemann Wave Equation and a Sensitive Demonstration" Fractal and Fractional 7, no. 2: 102. https://doi.org/10.3390/fractalfract7020102
APA StyleMajid, S. Z., Faridi, W. A., Asjad, M. I., Abd El-Rahman, M., & Eldin, S. M. (2023). Explicit Soliton Structure Formation for the Riemann Wave Equation and a Sensitive Demonstration. Fractal and Fractional, 7(2), 102. https://doi.org/10.3390/fractalfract7020102





