A Physical Phenomenon for the Fractional Nonlinear Mixed Integro-Differential Equation Using a General Discontinuous Kernel
Abstract
:1. Introduction
2. The Solution’s Existence and Uniqueness
3. Convergence of the Solution
4. Separation of Variables Scheme
5. Convergence Investigations Based on Nonlinear Integral Model
6. Toeplitz Matrix Method (Abdou et al. [32])
7. The Nonlinear Algebraic Toeplitz Matrix System
8. The Error of the Toeplitz Matrix Method
9. Applications
10. Conclusions
- 1
- In this paper, the existence of a unique solution is proven using the Banach fixed point theorem. In addition, the reader could use the successive approximate method (Picard method) to arrive at the same conclusion. In the homogeneous case of Equation (1), the successive approximate method fails to prove the existence of a unique solution. For this, we can only use the Banach fixed point theorem.
- 2
- If the two conditions of (i) and (ii) are not satisfied, this means that we have at least one solution. In this case, we would use one of the following theorems: Brouwer fixed point theorem or Schauder fixed point theorem.
- 3
- Using TMM, we have an NAS where the coefficient of the nonlinear term is a function of time. Hence, the existence of a unique solution for the NAS is discussed in the space .
- 4
- The fractional nonlinear mixed integro-differential Equation (1), under certain relations of and v, represents the nonlinear integral equation of the fractional phase-lag termThe delaying or advancing of time reveals the natural phenomena, especially in the presence of thermoelectricity and magnetic media. Some of applications of fractional integro-differential equations are found in physics, chemistry, economics, and biology [12,29]. Equation (59) explains the physical meaning of the fractional equation of time as the first fractional approximation of the time lag equation, and this lag may be before or after real time.
- 5
- 6
- The significance of the logarithmic kernel was approved from its derivatives f with these cases:
- (a)
- Cauchy kernel.
- (b)
- Strong singular kernel
- (c)
- The Carleman function was also established as:where is a continuous function.
- 7
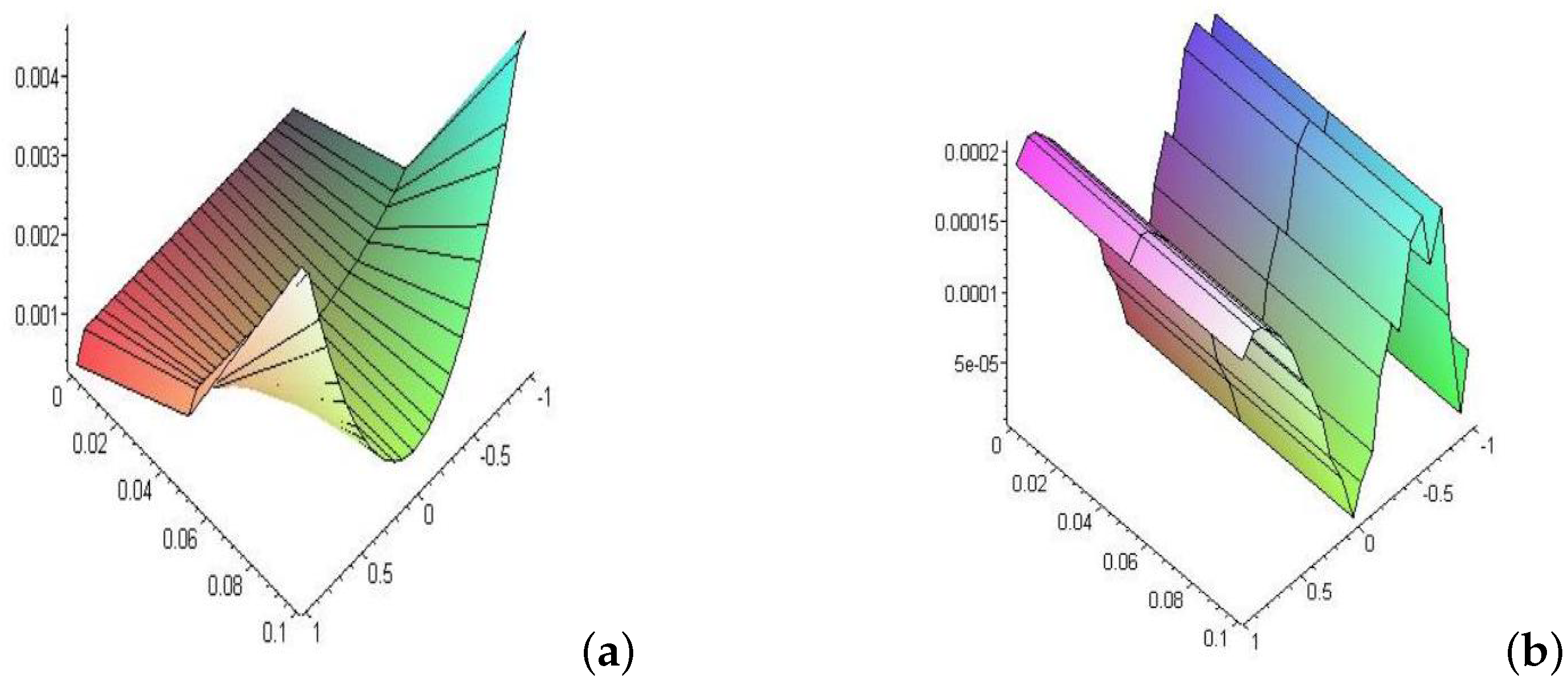
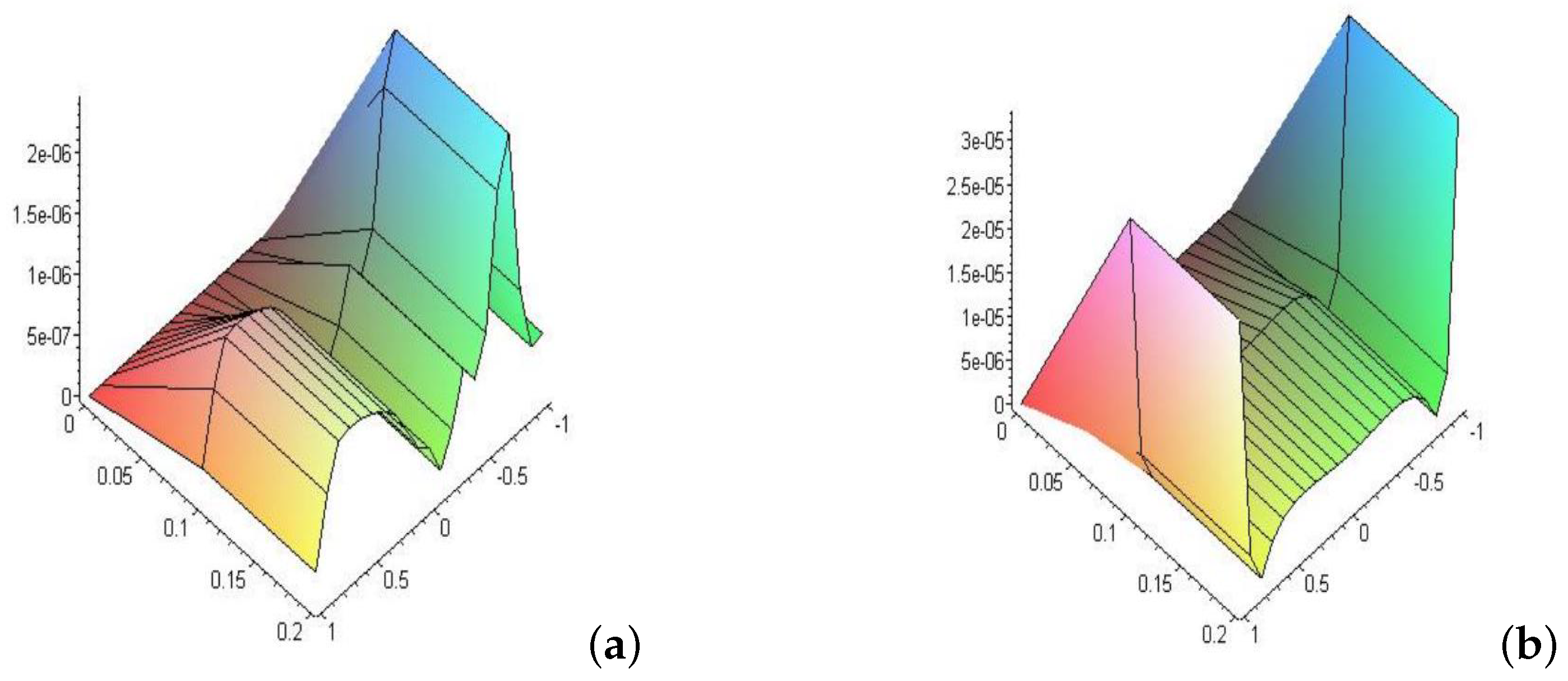
- When the kernel of the equation was in the logarithmic function form , the relative error increased with increasing time. It was also noted that the error in the non-linear case was slightly larger than in the linear case.
- 8
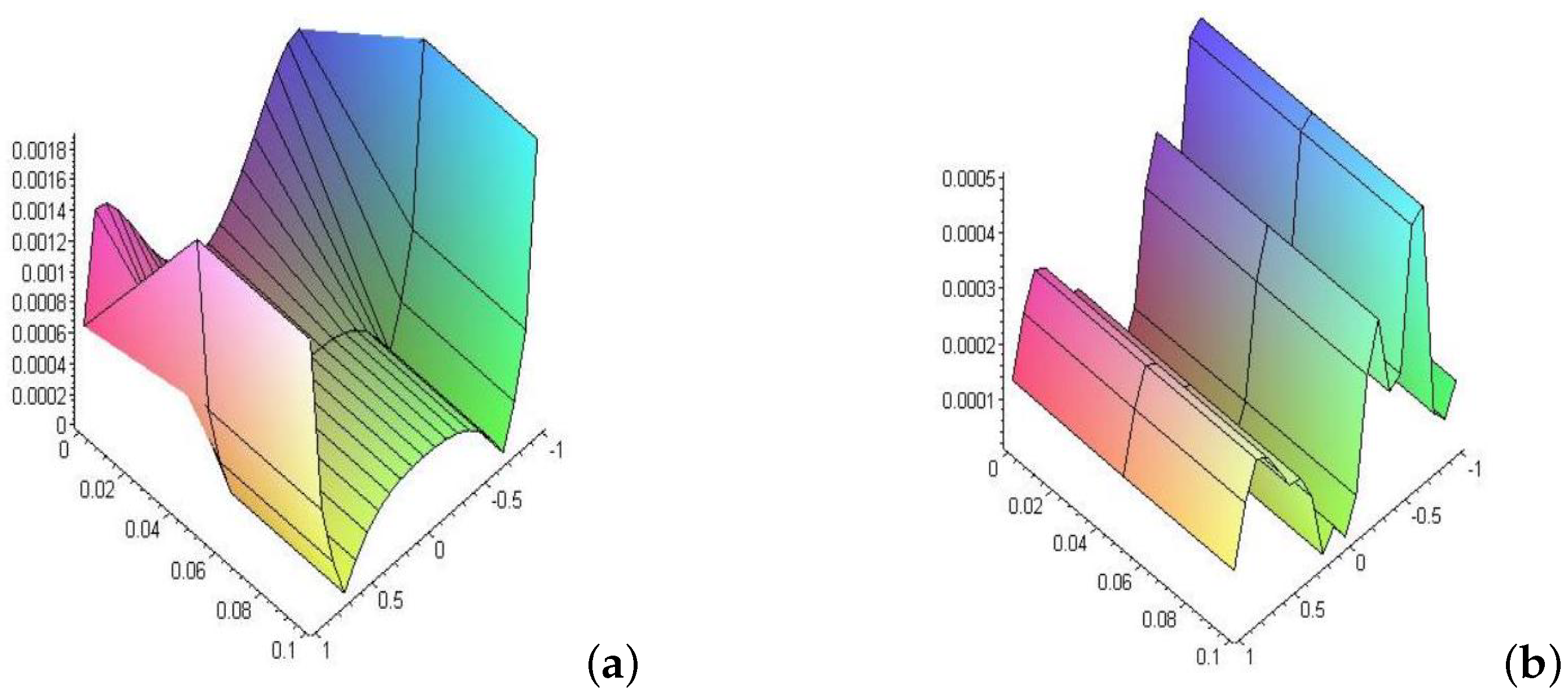
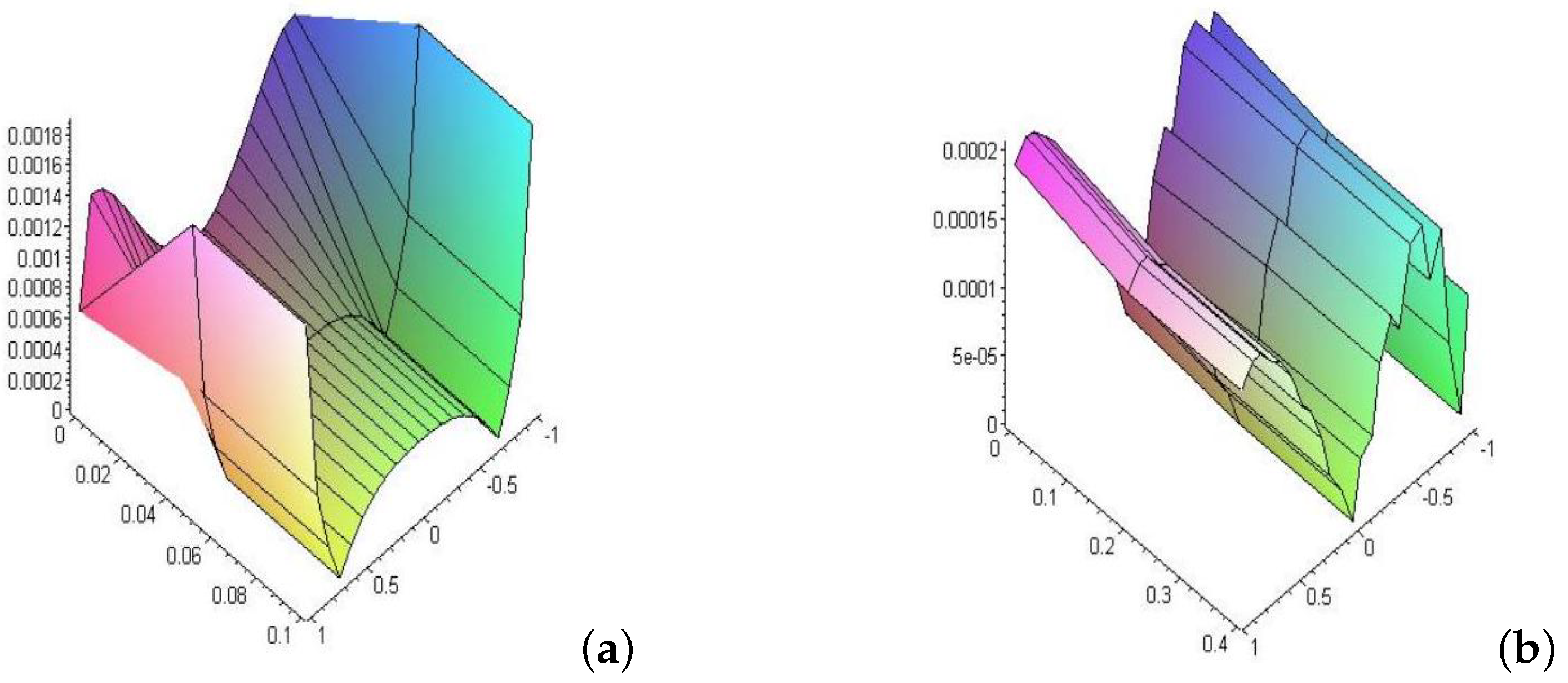
- In Example (2), when the kernel took the Carleman function , we noticed that the behavior of the error when increasing time was the same as that of the logarithmic function. However, by comparison, we found that at small times, the error in the logarithmic function was higher than in the Carleman function. With increasing time, we find that the relative error in the Carleman function is higher than its counterpart in the logarithmic function.
- 9
- In Example (3), the error behavior of the Hilbert kernel was the same as that of the logarithmic form and Carleman function.
11. Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- El-Sayed, A.M.A.; Gamal Ahmed, R. Infinite point and Riemann Stieltjes integral conditions for an integro differential equation. Nonlinear Anal. Model. Control 2019, 24, 733–754. [Google Scholar] [CrossRef]
- El-Sayed, A.M.A.; Gamal Ahmed, R. Solvability of a coupled system of functional integro-differential equations with infinite point and Riemann-Stieltjes integral conditions. Appl. Math. Comput. 2020, 370, 124918. [Google Scholar] [CrossRef]
- Mohamed, D.S. Application of Lerch polynomials to approximate solution of singular Fredholm integral equations with Cauchy kernel. Appl. Math. Inf. Sci. 2022, 16, 565–574. [Google Scholar]
- Hafez, R.M.; Youssri, Y.H. Spectral Legendre-Chebyshev Treatment of 2D linear and nonlinear mixed Volterra-Fredholm integral equation. Math. Sci. Lett. 2020, 9, 37–47. [Google Scholar]
- El-Sayed, S.M.; Abdel-Aziz, M.R. A comparison of Adomian’s decomposition method and wavelet-Galerkin method for solving integro-differential equations. Appl. Math. Comput. 2003, 136, 151–159. [Google Scholar] [CrossRef]
- Ali, M.R.; Mousa, M.M.; Ma, W.-Z. Solution of nonlinear Volterra integral equations with weakly singular kernel by using the HOBW method. Adv. Math. Phys. 2019, 2019, 1–10. [Google Scholar] [CrossRef]
- Klaseboer, E.; Sun, Q.; Chan, D.Y. Non-singular boundary integral methods for fluid mechanics applications. J. 525 Fluid Mech. 2012, 696, 468–478. [Google Scholar] [CrossRef]
- Ata, K.; Sahin, M. An integral equation approach for the solution of the Stokes flow with Hermite surfaces. Eng. Anal. Bound. Elem. 2018, 96, 14–22. [Google Scholar] [CrossRef]
- Kuzmina, K.; Marchevsky, I. The boundary integral equation solution in vortex methods with the airfoil surface line discretization into curvilinear panels. Proc. Top. Probl. Fluid Mech. 2019, 2019, 131–138. [Google Scholar]
- Lienert, M.; Tumulka, R. A new class of Volterra-type integral equations from relativistic quantum physics. J. Integral Equations Appl. 2019, 31, 535–569. [Google Scholar] [CrossRef]
- Sidorov, D. Integral Dynamical Models: Singularities, Signals and Control; World Scientific: Singapore, 2014. [Google Scholar]
- Abdou, M.A.; Basseem, M. Thermopotential function in position and time for a plate weakened by curvilinear hole. Arch. Appl. Mech. 2022, 92, 867–883. [Google Scholar] [CrossRef]
- Matoog, R.T. Treatments of probability potential function for nuclear integral equation. J. Phys. Math. 2017, 8, 2090-0902. [Google Scholar]
- Gao, J.; Condon, M.; Iserles, A. Spectral computation of highly oscillatory integral equations in laser theory. J. Comput. Phys. 2019, 395, 351–381. [Google Scholar] [CrossRef]
- Alhazmi, S.E.A. New Model for Solving Mixed Integral Equation of the First Kind with Generalized Potential Kernel. J. Math. Res. 2017, 9, 18–29. [Google Scholar] [CrossRef]
- Nemati, S.; Lima, P.M.; Ordokhani, Y. Numerical solution of a class of two-dimensional nonlinear Volterra integral equations using Legendre polynomials. J. Comput. Appl. Math. 2013, 242, 53–69. [Google Scholar] [CrossRef]
- Mirzaee, F.; Samadyar, N. Convergence of 2D-orthonormal Bernstein collocation method for solving 2D-mixed Volterra-Fredholm integral equations. Trans. A. Razmadze Math. Inst. 2018, 172, 631–641. [Google Scholar] [CrossRef]
- Basseem, M.; Alalyani, A. On the Solution of Quadratic Nonlinear Integral Equation with Different Singular Kernels. Math. Probl. Eng. 2020, 2020, 1–7. [Google Scholar] [CrossRef]
- Katani, R. Numerical solution of the Fredholm integral equations with a quadrature method. SeMA J. 2019, 76, 271276. [Google Scholar] [CrossRef]
- Al-Bugami, A.M. Numerical Treating of Mixed Integral Equation Two-Dimensional in Surface Cracks in Finite Layers of Materials. Adv. Math. Phys. 2022, 2022, 1–12. [Google Scholar] [CrossRef]
- Brezinski, C.; Redivo-Zaglia, M. Extrapolation methods for the numerical solution of nonlinear Fredholm integral equations. J. Integral Equ. Appl. 2019, 31, 29–57. [Google Scholar] [CrossRef]
- Bakhshayesh, S.J. Discontinuous Galerkin Approximations for Volterra Integral Equations of the First Kind with Convolution Kernel. Indian J. Sci. Technol. 2015, 8, 33. [Google Scholar] [CrossRef]
- Alkan, S.; Hatipoglu, V.F. Approximate solutions of Volterra-Fredholm integro-differential equations of fractional order. Tbil. Math. J. 2017, 10, 1–13. [Google Scholar]
- Mosa, G.A.; Abdou, M.A.; Gawish, F.A.; Abdalla, M.H. On the behavior solutions of fractional and partial integro differential heat equations and its numerical solutions. Math. Slovak 2022, 72, 397–410. [Google Scholar] [CrossRef]
- Jebreen, B.; Dassios, I. On the Wavelet Collocation Method for Solving Fractional Fredholm Integro-Differential Equations. Mathematics 2022, 10, 1272. [Google Scholar] [CrossRef]
- Akram, T.; Ali, Z.; Rabiei, F.; Shah, K.; Kumam, P. A Numerical Study of Nonlinear Fractional Order Partial Integro-Differential Equation with a Weakly Singular Kernel. Fractal Fract. 2021, 5, 85. [Google Scholar] [CrossRef]
- Abdelkawy, M.A.; Amin, A.Z.M.; Lopes, A.M.; Hashim, I.; Babatin, M.M. Shifted Fractional-Order Jacobi Collocation Method for Solving Variable-Order Fractional Integro-Differential. Fractal Fract. 2021, 6, 19. [Google Scholar] [CrossRef]
- Podlubny, I.; Chechkin, A.; Skovranek, T.; Chen, Y.; Jara, B.M.V. Matrix approach to discrete fractional calculus II: Partial fractional differential equations. J. Comput. Phys. 2009, 228, 3137–3153. [Google Scholar]
- Kreyszig, E. Introductory Functional Analysis with Applications; John Wiley & Sons Inc.: New York, NY, USA, 1978. [Google Scholar]
- Jan, A.R. An asymptotic model for solving mixed integral equation in position and time. J. Math. 2022, 2022, 8063971. [Google Scholar] [CrossRef]
- Jan, A.R. Solution of nonlinear mixed integral equation via collocation method basing on orthogonal polynomials. Heliyen 2022, 8, e1182. [Google Scholar] [CrossRef]
- Abdou, M.A.; El-Borai, M.M.; El-Kojok, M.M. Toeplitz matrix method and nonlinear integral equation of Hammerstein type. J. Comput. Appl. Math. 2009, 223, 765–776. [Google Scholar]
- Gu, X.M.; Huang, T.Z.; Zhao, X.L.; Xu, W.R.; Li, H.B.; Li, L. Circulant preconditioned iterative methods for peridynamic model simulation. Appl. Math. Comput. 2014, 248, 470–479. [Google Scholar] [CrossRef]
- Gradstein, I.S.; Ryzhik, I.M.; Romer, R.H. Tables of Integrals, Series, and Products; Academic Press: Cambridge, MA, USA, 1988. [Google Scholar]
- Arutiunian, N.K. Ploskaia kontaktnaia zadacha teorii polzuchesti (The plane contact problem of the theory of creep). J. Appl. Math. Mech. 1959, 23, 1283–1313. [Google Scholar] [CrossRef]

| Time | Exact Solution | Nonlinear Case m = 2, N = 20 | Linear Case m = 1, N = 20 | ||
|---|---|---|---|---|---|
| Time | Exact Solution | Nonlinear Case m = 2, N = 20 | Linear Case m = 1, N = 20 | ||
|---|---|---|---|---|---|
| Carleman Coefficients | Exact Solution at | Nonlinear Case at m = 2 | Linear Case at m = 1 | ||
|---|---|---|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alhazmi, S.E.; Abdou, M.A. A Physical Phenomenon for the Fractional Nonlinear Mixed Integro-Differential Equation Using a General Discontinuous Kernel. Fractal Fract. 2023, 7, 173. https://doi.org/10.3390/fractalfract7020173
Alhazmi SE, Abdou MA. A Physical Phenomenon for the Fractional Nonlinear Mixed Integro-Differential Equation Using a General Discontinuous Kernel. Fractal and Fractional. 2023; 7(2):173. https://doi.org/10.3390/fractalfract7020173
Chicago/Turabian StyleAlhazmi, Sharifah E., and Mohamed A. Abdou. 2023. "A Physical Phenomenon for the Fractional Nonlinear Mixed Integro-Differential Equation Using a General Discontinuous Kernel" Fractal and Fractional 7, no. 2: 173. https://doi.org/10.3390/fractalfract7020173
APA StyleAlhazmi, S. E., & Abdou, M. A. (2023). A Physical Phenomenon for the Fractional Nonlinear Mixed Integro-Differential Equation Using a General Discontinuous Kernel. Fractal and Fractional, 7(2), 173. https://doi.org/10.3390/fractalfract7020173









