Noise Spectral of GML Noise and GSR Behaviors for FGLE with Random Mass and Random Frequency
Abstract
1. Introduction
2. Three-Parameter GML Noise
3. FGLE with Multiplicative Trichotomous Noise
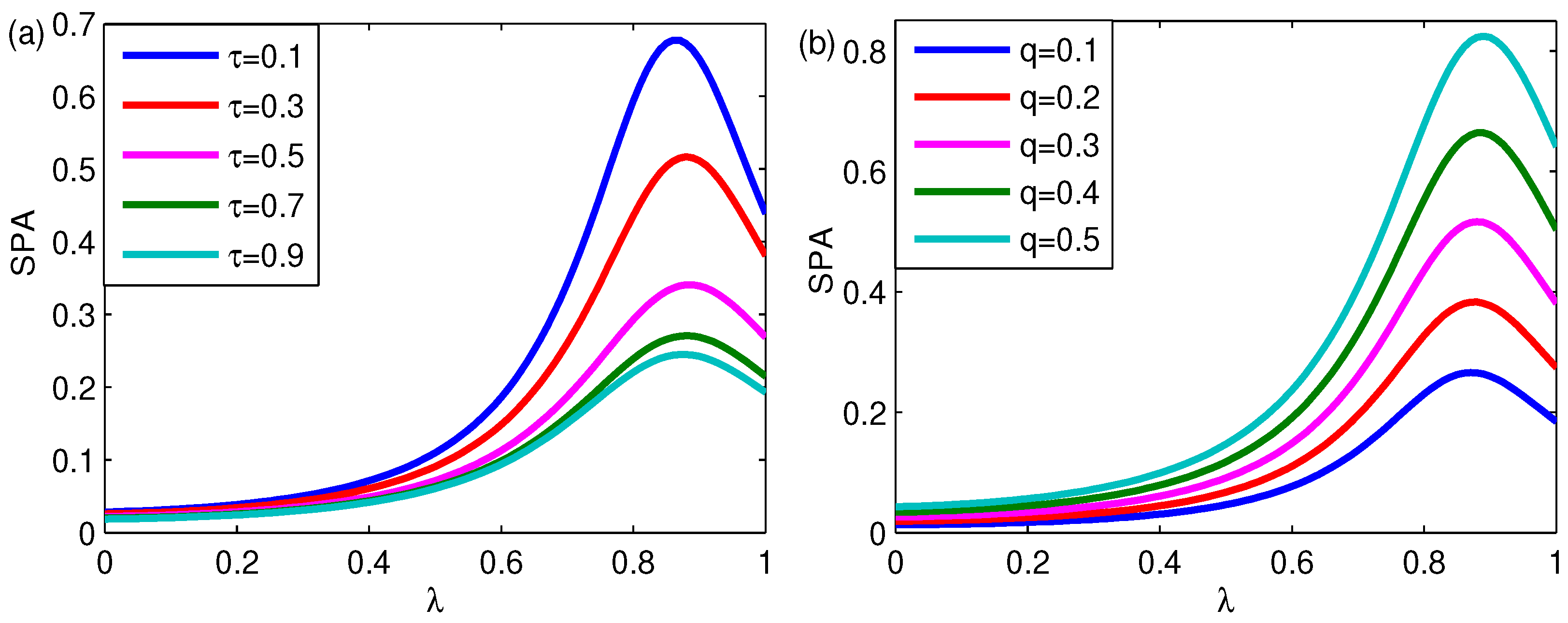
4. Spectral Amplification of FGLE
5. Resonance Behavior of FGLE
5.1. GSR for FGLE Only Influenced by GML Noise
5.2. GSR for FGLE Influenced by Two Types of Noise
6. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Benzi, R.; Sutera, A.; Vulpiani, A. The mechanism of stochastic resonance. J. Phys. A Math. Gen. 1981, 14, L453. [Google Scholar] [CrossRef]
- Benzi, R. Stochastic resonance: From climate to biology. Nonlinear Process. Geophys. 2010, 17, C431–C441. [Google Scholar] [CrossRef]
- Gammaitoni, L.; Hänggi, P.; Jung, P.; Marchesoni, F. Stochastic resonance: A remarkable idea that changed our perception of noise. Eur. Phys. J. B 2009, 69, 1–3. [Google Scholar] [CrossRef]
- Falanga, M.; De Lauro, E.; de Martino, S. Stochastic resonance observed in aerosol optical depth Time Series. Atmosphere 2020, 11, 502. [Google Scholar] [CrossRef]
- McDonnell, M.D.; Stocks, N.G.; Pearce, C.E.M.; Abbott, D. Stochastic Resonance; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Ren, R.; Yuan, G.X. Collective behaviors of star-coupled harmonic oscillators with fluctuating frequency in the presence of stochastic resonance. Fractal Fract. 2022, 6, 414. [Google Scholar] [CrossRef]
- Huang, W.; Zhang, G.; Jiao, S.; Wang, J. Bearing fault diagnosis based on stochastic resonance and improved whale optimization algorithm. Electronics 2022, 11, 2185. [Google Scholar] [CrossRef]
- Yang, Z.; Li, Z.; Zhou, F.; Ma, Y.; Yan, B. Weak fault feature extraction method based on improved stochastic resonance. Sensors 2022, 22, 6644. [Google Scholar] [CrossRef]
- Lu, S.L.; He, Q.B.; Hu, F.; Kong, F.R. Sequential multiscale noise tuning stochastic resonance for train bearing fault diagnosis in an embedded system. IEEE Trans. Instru. Meas. 2014, 63, 106. [Google Scholar] [CrossRef]
- Gitterman, M. Classical harmonic oscillator with multiplicative noise. Phys. A 2005, 352, 309. [Google Scholar] [CrossRef]
- Bobryk, R.V. Stochastic multiresonance in oscillators induced by bounded noise. Commun. Nonlin. Sci. Numer. Simul. 2021, 93, 105460. [Google Scholar] [CrossRef]
- He, G.; Tian, Y.; Luo, M. Mittag–Leffler noise induced resonance behavior in a fractional generalized Langevin equation with random trichotomous inherent frequency. J. Stat. Mech. 2018, 2018, 033201. [Google Scholar] [CrossRef]
- He, G.; Liu, H.; Tang, G.J.; Cao, J.D. Resonance behavior for a generalized Mittag–Leffler fractional Langevin equation with hydrodynamic interactions. Int. J. Mode. Phys. B 2020, 34, 2050310. [Google Scholar] [CrossRef]
- Burov, S.; Barkai, E. Fractional Langevin equation: Overdamped, underdamped, and critical behaviors. Phys. Rev. E 2008, 78, 031112. [Google Scholar] [CrossRef] [PubMed]
- Soika, E.; Mankin, R.; Ainsaar, A. Resonant behavior of a fractional oscillator with fluctuating frequency. Phys. Rev. E 2010, 81, 011141. [Google Scholar] [CrossRef]
- Ghosh, S.K.; Cherstvy, A.G.; Grebenkov, D.S.; Grebenkov, D.S.; Metzler, R. Anomalous, non-Gaussian tracer diffusion in crowded two-dimensional environments. New J. Phys. 2016, 18, 013027. [Google Scholar] [CrossRef]
- Méndez, V.D.; Campos, F. Stochastic Foundations in Movement Ecology; Springer: Berlin, Germany, 2016. [Google Scholar]
- Goychuk, I.; Kharchenko, V. Fractional Brownian motors and stochastic resonance. Phys. Rev. E 2012, 85, 051131. [Google Scholar] [CrossRef]
- Kubo, R. The fluctuation-dissipation theorem. Rep. Prog. Phys. 1966, 29, 255. [Google Scholar] [CrossRef]
- Grebenkov, D.S.; Vahabi, M. Analytical solution of the generalized Langevin equation with hydrodynamic interactions: Subdiffusion of heavy tracers. Phys. Rev. E 2014, 89, 012130. [Google Scholar] [CrossRef] [PubMed]
- Kilbas, A.A.; Sarivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: New York, NY, USA, 2006. [Google Scholar]
- Mainardi, F.; Pironi, P. The fractional Langevin equation: Brownian motion revisited. Extr. Math. 1996, 10, 140–154. [Google Scholar]
- Lim, S.C.; Teo, L.P. Modeling single-file diffusion with step fractional Brownian motion and a generalized fractional Langevin equation. J. Stat. Mech. 2009, 2009, P08015. [Google Scholar] [CrossRef]
- Eab, C.H.; Lim, S.C. Fractional generalized Langevin equation approach to single-file diffusion. Phys. A 2010, 389, 2510–2521. [Google Scholar] [CrossRef]
- Li, H.L.; He, G.T.; Peng, Y.; Cheng, H. Stochastic resonance for a Jerk oscillator with a generalized Mittag–Leffler noise. Chin. J. Phys. 2022, 77, 1997–2013. [Google Scholar] [CrossRef]
- Viñales, A.D.; Despósito, M.A. Anomalous diffusion induced by a Mittag–Leffler correlated noise. Phys. Rev. E 2007, 75, 042102. [Google Scholar] [CrossRef] [PubMed]
- Figueiredo, C.R.; Capelas de Oliveira, E.; Vaz, J.J. On anomalous diffusion and the fractional generalized Langevin equation for a harmonic oscillator. J. Math. Phys. 2009, 50, 123518. [Google Scholar] [CrossRef]
- Fa, K.S. Anomalous diffusion in a generalized Langevin equation. J. Math. Phys. 2009, 50, 083301. [Google Scholar] [CrossRef]
- Sandev, T.; Metzler, R.; Tomovski, Ž. Velocity and displacement correlation functions for fractional generalized Langevin equations. Fract. Calc. Appl. Anal. 2012, 15, 426–450. [Google Scholar] [CrossRef]
- Prabhakar, T.R. A singular integral equation with a generalized Mittag–Leffler function in the kernel. Yokohama Math. J. 1971, 19, C7–C15. [Google Scholar]
- Marchesoni, F. Comment on stochastic resonance in washboard potentials. Phys. Lett. A 1997, 231, 61–64. [Google Scholar] [CrossRef]
- Gitterman, M. Stochastic oscillator with random mass: New type of Brownian motion. Phys. A 2014, 395, 11–21. [Google Scholar] [CrossRef]
- Mankin, R.; Laas, K.; Laas, T. Stochastic multiresonance and correlation-time-controlled stability for a harmonic oscillator with fluctuating frequency. Phys. Rev. E 2008, 78, 031120. [Google Scholar] [CrossRef]
- Pottier, N. Relaxation time distributions for an anomalously diffusing particle. Phys. A 2011, 390, 2863–2879. [Google Scholar] [CrossRef]
- Shapiro, V.E.; Loginov, V.M. “Formulae of differentiation” and their use for solving stochastic equations. Phys. A 1978, 91, 563–574. [Google Scholar] [CrossRef]
- Li, J.C.; Mei, D.C. Reverse resonance in stock prices of financial system with periodic information. Phys. Rev. E 2013, 88, 012811. [Google Scholar] [CrossRef] [PubMed]
- Vilar, J.M.G.; Rubi, J.M. Stochastic multiresonance. Phys. Rev. Lett. 1997, 78, 2882. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiu, L.; He, G.; Peng, Y.; Cheng, H.; Tang, Y. Noise Spectral of GML Noise and GSR Behaviors for FGLE with Random Mass and Random Frequency. Fractal Fract. 2023, 7, 177. https://doi.org/10.3390/fractalfract7020177
Qiu L, He G, Peng Y, Cheng H, Tang Y. Noise Spectral of GML Noise and GSR Behaviors for FGLE with Random Mass and Random Frequency. Fractal and Fractional. 2023; 7(2):177. https://doi.org/10.3390/fractalfract7020177
Chicago/Turabian StyleQiu, Lini, Guitian He, Yun Peng, Hui Cheng, and Yujie Tang. 2023. "Noise Spectral of GML Noise and GSR Behaviors for FGLE with Random Mass and Random Frequency" Fractal and Fractional 7, no. 2: 177. https://doi.org/10.3390/fractalfract7020177
APA StyleQiu, L., He, G., Peng, Y., Cheng, H., & Tang, Y. (2023). Noise Spectral of GML Noise and GSR Behaviors for FGLE with Random Mass and Random Frequency. Fractal and Fractional, 7(2), 177. https://doi.org/10.3390/fractalfract7020177






