Intelligent Measurement of Void Fractions in Homogeneous Regime of Two Phase Flows Independent of the Liquid Phase Density Changes
Abstract
:1. Introduction
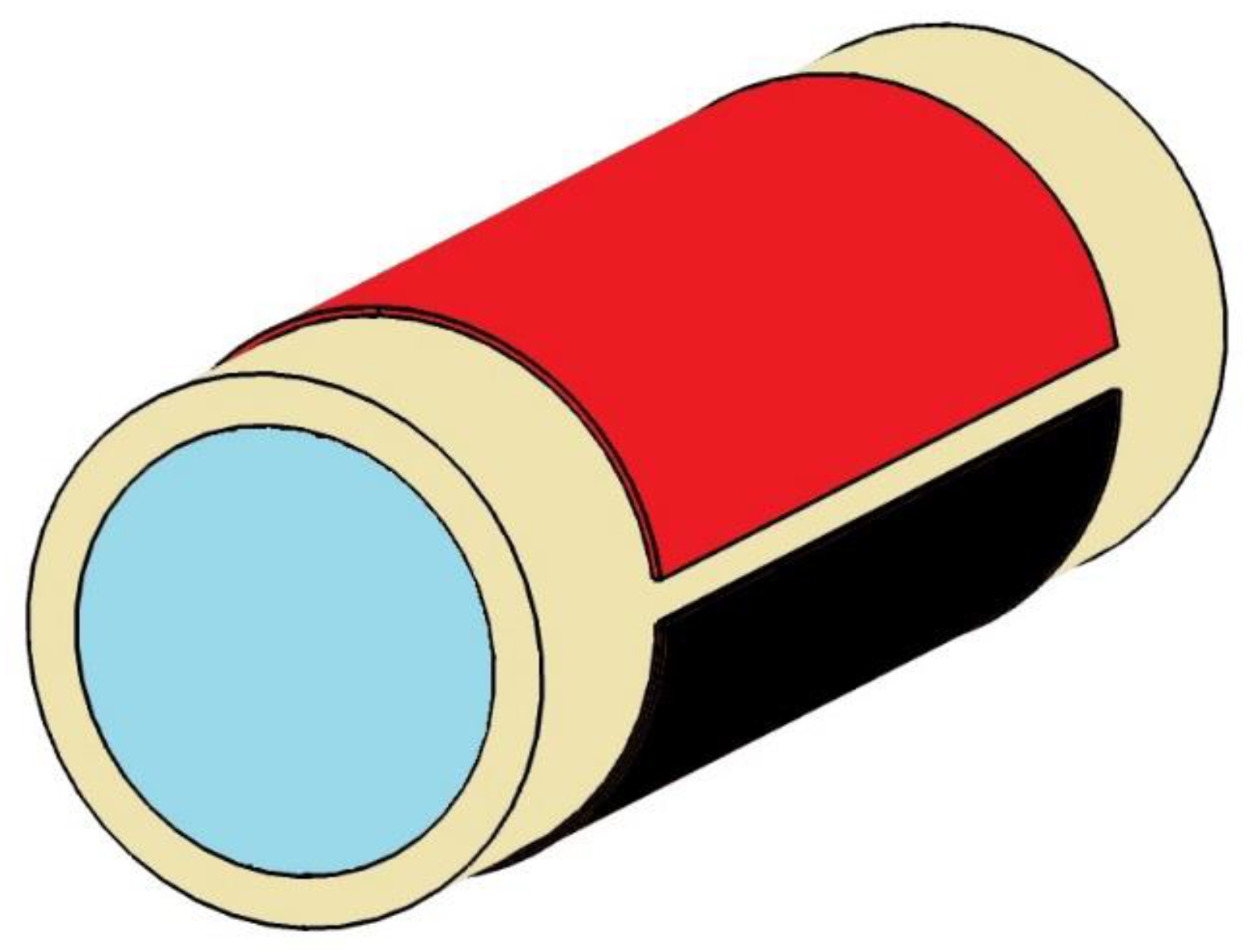
2. Experimental Setup
3. Simulation
3.1. Simulation of the Concave Sensor in a Homogeneous Regime
3.2. Simulation of the Ring Sensor in a Homogeneous Regime
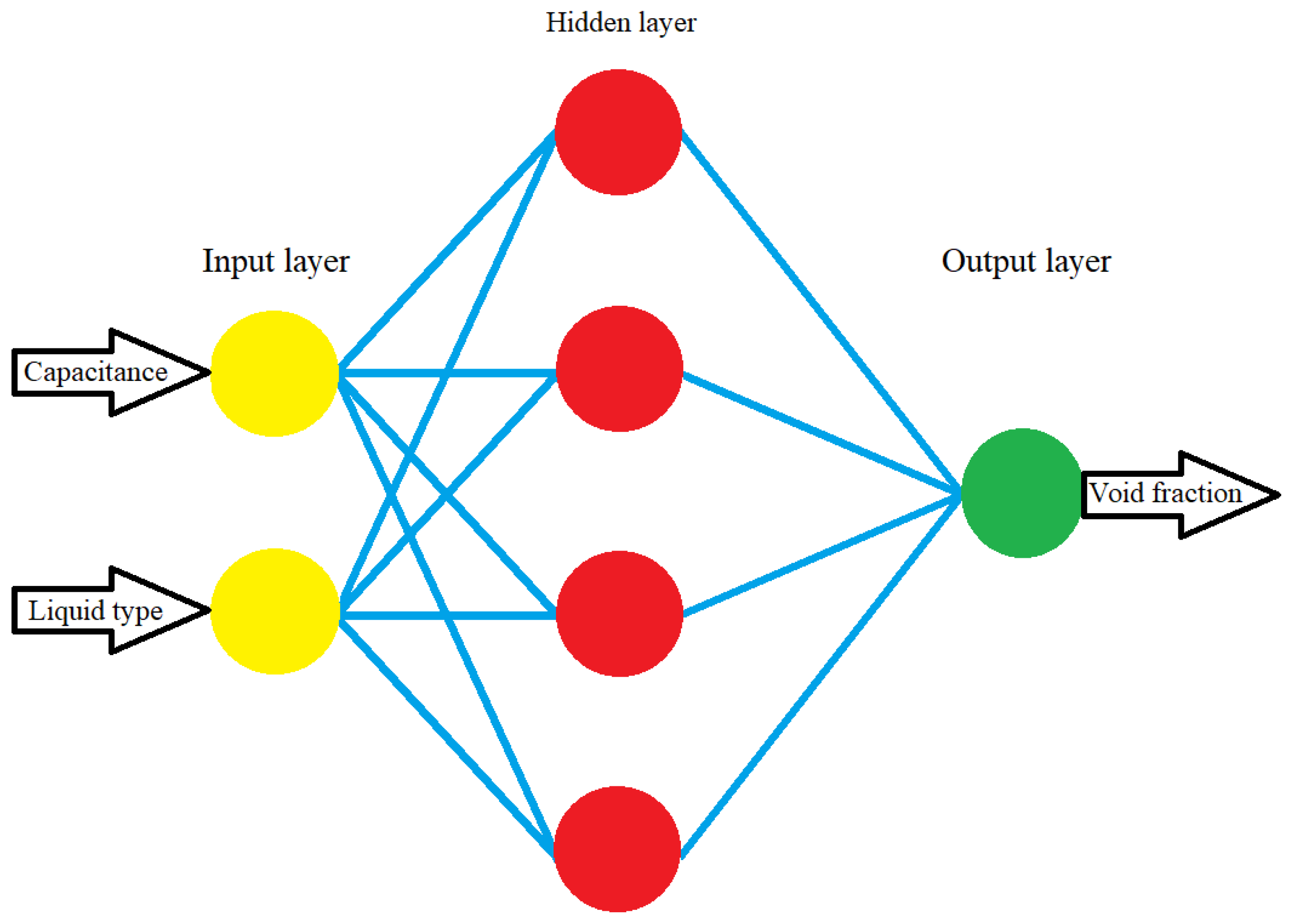
4. Artificial Neural Network
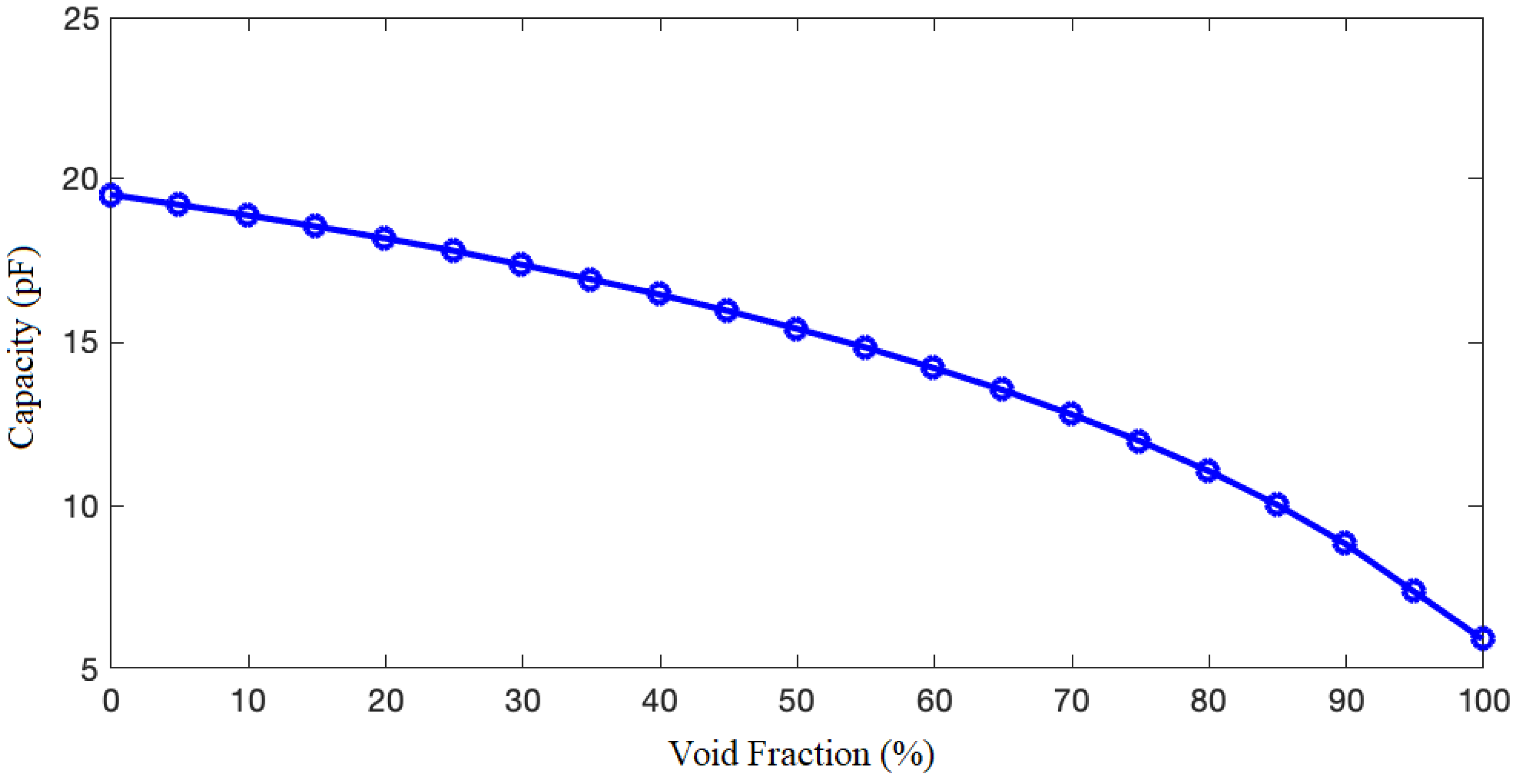
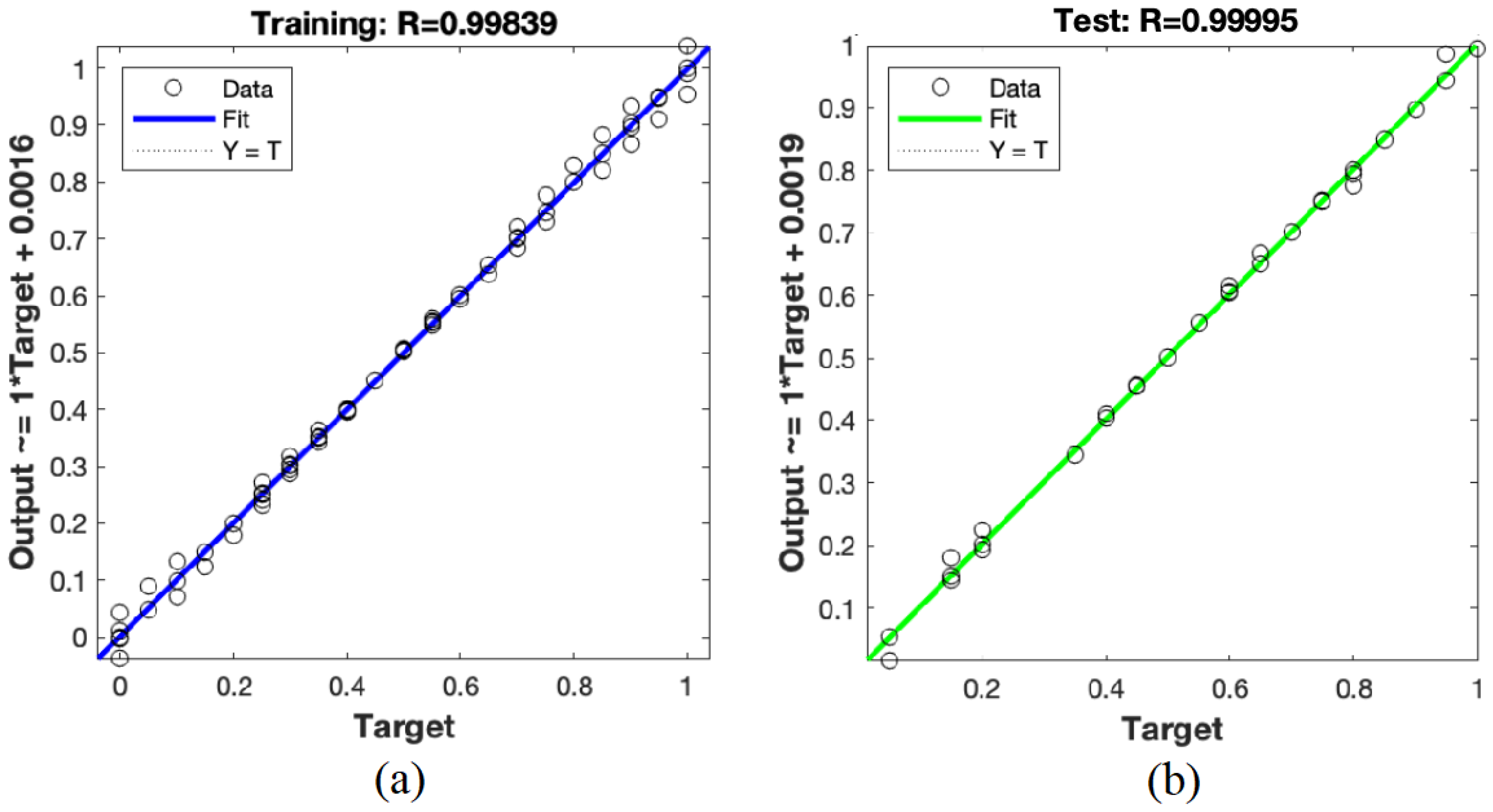
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Karimi, H.; Boostani, M. Heat transfer measurements for oil–water flow of different flow patterns in a horizontal pipe. Exp. Therm. Fluid Sci. 2016, 75, 35–42. [Google Scholar] [CrossRef]
- Steven, R.N. Wet gas metering with a horizontally mounted Venturi meter. Flow Meas. Instrum. 2002, 12, 361–372. [Google Scholar] [CrossRef]
- Wang, D.; Liang, F.; Peng, Z.; Wang, Y.; Lin, Z. Gas–liquid two-phase flow measurements by full stream batch sampling. Int. J. Multiph. Flow 2012, 40, 113–125. [Google Scholar] [CrossRef]
- Banowski, M.; Beyer, M.; Szalinski, L.; Lucas, D.; Hampel, W. Comparative study of ultrafast X-ray tomography and wire-mesh sensors for vertical gas-liquid pipe flows. Flow Meas. Instrum. 2017, 53, 95–106. [Google Scholar] [CrossRef]
- Salgado, C.M.; Dam, R.S.; Puertas, E.J.; Salgado, W.L. Calculation of volume fractions regardless scale deposition in the oil industry pipelines using feed-forward multilayer perceptron artificial neural network and MCNP6 code. Appl. Radiat. Isot. 2022, 185, 110215. [Google Scholar] [CrossRef]
- Al-Lababidi, S.; Addali, A.; Yeung, H.; Mba, D.; Khan, F. Gas void fraction measurement in two-phase gas/liquid slug flow using acoustic emission technology. J. Vib. Acoust. 2009, 131, 064501. [Google Scholar] [CrossRef]
- Xie, C.G.; Stott, A.L.; Plaskowski, A.; Beck, M.S. Design of capacitance electrodes for concentration measurement of two-phase flow. Meas. Sci. Technol. 1990, 1, 65–78. [Google Scholar] [CrossRef]
- Abdulkadir, M.; Hernandez-Perez, V.; Lowndes, I.S.; Azzopardi, B.J.; Brantson, E.T. Detailed analysis of phase distributions in a vertical riser using a wire mesh sensor (WMS). Exp. Therm. Fluid Sci. 2014, 59, 32–42. [Google Scholar] [CrossRef]
- Koyama, S.; Lee, J.; Yonemoto, R. An investigation on void fraction of vapor–liquid two-phase flow for smooth and microfin tubes with R134a at adiabatic condition. Int. J. Multiph. Flow. 2004, 30, 291–310. [Google Scholar] [CrossRef]
- Yang, H.C.; Kim, D.K.; Kim, M.H. Void fraction measurement using impedance method. Flow Meas. Instrum. 2003, 14, 151–160. [Google Scholar] [CrossRef]
- Demori, M.; Ferrari, V.; Strazza, D.; Poesio, P. A capacitive sensor system for the analysis of two-phase flows of oil and conductive water. Sens. Actuators A Phys. 2010, 163, 172–179. [Google Scholar] [CrossRef]
- Strazza, D.; Demori, M.; Ferrari, V.; Poesio, P. Capacitance sensor for hold-up measurement in high-viscous-oil/conductive-water core-annular flows. Flow Meas. Instrum. 2011, 22, 360–369. [Google Scholar] [CrossRef]
- An, Z.; Ningde, J.; Lusheng, Z.; Zhongke, G. Liquid holdup measurement in horizontal oil–water two-phase flow by using concave capacitance sensor. Measurement 2014, 49, 153–163. [Google Scholar] [CrossRef]
- Ortiz, J.; Masek, V. Cyclonic capacitive sensor for multiphase composition measurement. Sens. Transducers 2015, 191, 1. [Google Scholar]
- Zhai, L.S.; Jin, N.D.; Gao, Z.K.; Zhao, A.; Zhu, L. Cross-correlation velocity measurement of horizontal oil–water two-phase flow by using parallel–wire capacitance probe. Exp. Therm. Fluid Sci. 2014, 53, 277–289. [Google Scholar] [CrossRef]
- Zhai, L.; Jin, N.; Gao, Z.; Wang, Z. Liquid holdup measurement with double helix capacitance sensor in horizontal oil–water two-phase flow pipes. Chin. J. Chem. Eng. 2015, 23, 268–275. [Google Scholar] [CrossRef]
- Li, J.; Kong, M.; Xu, C.; Wang, S.; Fan, Y. An Integrated instrumentation system for velocity, concentration and mass flow rate measurement of solid particles based on electrostatic and capacitance sensors. Sensors 2015, 15, 31023–31035. [Google Scholar] [CrossRef]
- Elkow, K.J.; Rezkallah, K.S. Void fraction measurements in gas-liquid flows under 1-g and μ-g conditions using capacitance sensors. Int. J. Multiph. Flow 1997, 23, 815–829. [Google Scholar] [CrossRef]
- Li, H.; Yang, D.; Cheng, M.X. Sensitivity analysis of capacitance sensor with helical shaped surface plates. CIESC J. 2011, 62, 2292–2297. [Google Scholar]
- Jaworek, A.; Krupa, A. Gas/liquid ratio measurements by rf resonance capacitance sensor. Sens. Actuators A Phys. 2004, 113, 133–139. [Google Scholar] [CrossRef]
- Dos Reis, E.; da Silva Cunha, D. Experimental study on different configurations of capacitive sensors for measuring the volumetric concentration in two-phase flows. Flow Meas. Instrum. 2014, 37, 127–134. [Google Scholar] [CrossRef]
- Kendoush, A.A.; Sarkis, Z.A. Improving the accuracy of the capacitance method for void fraction measurement. Exp. Therm. Fluid Sci. 1995, 11, 321–326. [Google Scholar] [CrossRef]
- Abouelwafa, M.S.; Kendall, E.J. The use of capacitance sensors for phase percentage determination in multiphase pipelines. IEEE Trans. Instrum. Meas. 1980, 29, 24–27. [Google Scholar] [CrossRef]
- Tollefsen, J.; Hammer, E.A. Capacitance sensor design for reducing errors in phase concentration measurements. Flow Meas. Instrum. 1998, 9, 25–32. [Google Scholar] [CrossRef]
- Ahmed, H. Capacitance sensors for void-fraction measurements and flow-pattern identification in air–oil two-phase flow. IEEE Sens. J. 2006, 6, 1153–1163. [Google Scholar] [CrossRef]
- Zych, M.; Petryka, L.; Kępiński, J.; Hanus, R.; Bujak, T.; Puskarczyk, E. Radioisotope investigations of compound two-phase flows in an open channel. Flow Meas. Instrum. 2014, 35, 11–15. [Google Scholar] [CrossRef]
- Chen, X.; Zheng, J.; Jiang, J.; Peng, H.; Luo, Y.; Zhang, L. Numerical Simulation and Experimental Study of a Multistage Multiphase Separation System. Separations 2022, 9, 405. [Google Scholar] [CrossRef]
- Rushd, S.; Gazder, U.; Qureshi, H.J.; Arifuzzaman, M. Advanced Machine Learning Applications to Viscous Oil-Water Multi-Phase Flow. Appl. Sci. 2022, 12, 4871. [Google Scholar] [CrossRef]
- Veisi, A.; Shahsavari, M.H.; Roshani, G.H.; Eftekhari-Zadeh, E.; Nazemi, E. Experimental Study of Void Fraction Measurement Using a Capacitance-Based Sensor and ANN in Two-Phase Annular Regimes for Different Fluids. Axioms 2023, 12, 66. [Google Scholar] [CrossRef]
- Ssebadduka, R.; Le, N.N.; Nguele, R.; Alade, O.; Sugai, Y. Artificial Neural Network Model Prediction of Bitumen/Light Oil Mixture Viscosity under Reservoir Temperature and Pressure Conditions as a Superior Alternative to Empirical Models. Energies 2021, 14, 8520. [Google Scholar] [CrossRef]
- Mayet, A.M.; Nurgalieva, K.S.; Al-Qahtani, A.A.; Narozhnyy, I.M.; Alhashim, H.H.; Nazemi, E.; Indrupskiy, I.M. Proposing a high-precision petroleum pipeline monitoring system for identifying the type and amount of oil products using extraction of frequency characteristics and a MLP neural network. Mathematics 2022, 10, 2916. [Google Scholar] [CrossRef]
- Artyukhov, A.V.; Isaev, A.A.; Drozdov, A.N.; Gorbyleva, Y.A.; Nurgalieva, K.S. The rod string loads variation during short-term annular gas extraction. Energies 2022, 15, 5045. [Google Scholar] [CrossRef]
- Isaev, A.A.; Aliev, M.M.O.; Drozdov, A.N.; Gorbyleva, Y.A.; Nurgalieva, K.S. Improving the efficiency of curved wells’ operation by means of progressive cavity pumps. Energies 2022, 15, 4259. [Google Scholar] [CrossRef]
- Mayet, A.M.; Alizadeh, S.M.; Nurgalieva, K.S.; Hanus, R.; Nazemi, E.; Narozhnyy, I.M. Extraction of time-domain characteristics and selection of effective features using correlation analysis to increase the accuracy of petroleum fluid monitoring systems. Energies 2022, 15, 1986. [Google Scholar] [CrossRef]
- Alanazi, A.K.; Alizadeh, S.M.; Nurgalieva, K.S.; Nesic, S.; Guerrero, J.W.G.; Abo-Dief, H.M.; Narozhnyy, I.M. Application of neural network and time-domain feature extraction techniques for determining volumetric percentages and the type of two phase flow regimes independent of scale layer thickness. Appl. Sci. 2022, 12, 1336. [Google Scholar] [CrossRef]
- Hosseini, S.; Taylan, O.; Abusurrah, M.; Akilan, T.; Nazemi, E.; Eftekhari-Zadeh, E.; Bano, F.; Roshani, G.H. Application of Wavelet Feature Extraction and Artificial Neural Networks for Improving the Performance of Gas–Liquid Two-Phase Flow Meters Used in Oil and Petrochemical Industries. Polymers 2021, 13, 3647. [Google Scholar] [CrossRef]
- Roshani, G.H.; Hanus, R.; Khazaei, A.; Zych, M.; Nazemi, E.; Mosorov, V. Density and velocity determination for single-phase flow based on radiotracer technique and neural networks. Flow Meas. Instrum. 2018, 61, 9–14. [Google Scholar] [CrossRef]
- Roshani, G.H.; Nazemi, E.; Roshani, M.M. Intelligent recognition of gas-oil-water three-phase flow regime and determination of volume fraction using radial basis function. Flow Meas. Instrum. 2017, 54, 39–45. [Google Scholar] [CrossRef]
- Roshani, G.H.; Roshani, S.; Nazemi, E.; Roshani, S. Online measuring density of oil products in annular regime of gas-liquid two phase flows. Measurement 2018, 129, 296–301. [Google Scholar] [CrossRef]
- Nazemi, E.; Roshani, G.H.; Feghhi, S.A.H.; Setayeshi, S.; Zadeh, E.E.; Fatehi, A. Optimization of a method for identifying the flow regime and measuring void fraction in a broad beam gamma-ray attenuation technique. Int. J. Hydrogen Energy 2016, 41, 7438–7444. [Google Scholar] [CrossRef]
- McConn, R.J.; Gesh, C.J.; Pagh, R.T.; Rucker, R.A.; Williams, R., III. Compendium of Material Composition Data for Radiation Transport Modeling; Pacific Northwest National Lab. (PNNL): Richland, WA, USA, 2011.
- Roshani, G.H.; Nazemi, E.; Roshani, M.M. Flow regime independent volume fraction estimation in three-phase flows using dual-energy broad beam technique and artificial neural network. Neural Comput. Appl. 2017, 28, 1265–1274. [Google Scholar] [CrossRef]
- Roshani, G.H.; Feghhi, S.A.; Mahmoudi-Aznaveh, A.; Nazemi, E.; Adineh-Vand, A. Precise volume fraction prediction in oil–water–gas multiphase flows by means of gamma-ray attenuation and artificial neural networks using one detector. Measurement 2014, 51, 34–41. [Google Scholar] [CrossRef]





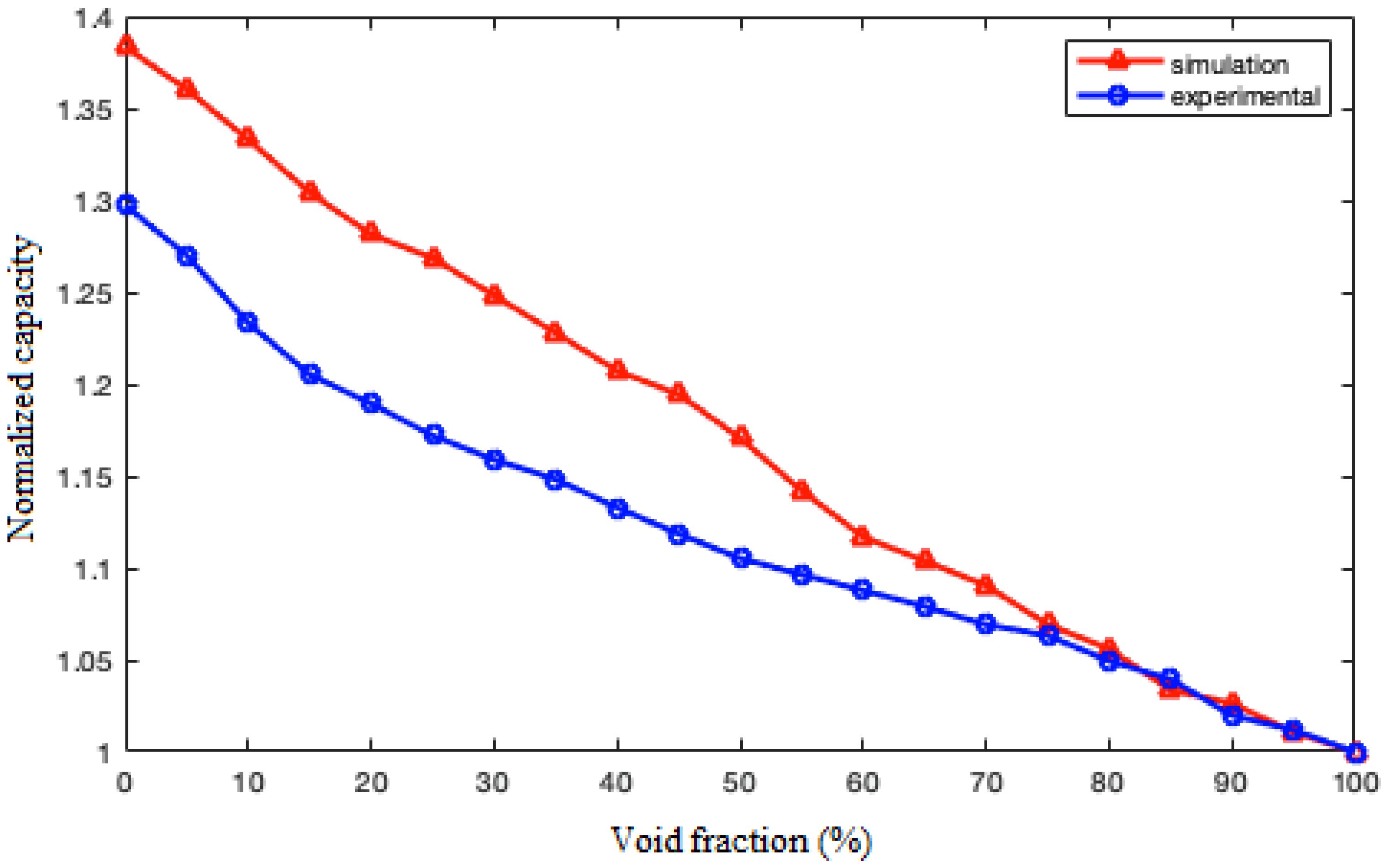

| Void Fraction | Normalized Simulation | Normalized Experimental | Relative Difference |
|---|---|---|---|
| 100 | 1.000 | 1.000 | 0.000 |
| 95 | 1.011 | 1.012 | 0.132 |
| 90 | 1.026 | 1.020 | 0.647 |
| 85 | 1.034 | 1.040 | 0.571 |
| 80 | 1.056 | 1.049 | 0.630 |
| 75 | 1.069 | 1.063 | 0.571 |
| 70 | 1.090 | 1.069 | 1.982 |
| 65 | 1.104 | 1.079 | 2.299 |
| 60 | 1.117 | 1.088 | 2.673 |
| 55 | 1.142 | 1.096 | 4.157 |
| 50 | 1.171 | 1.105 | 5.925 |
| 45 | 1.194 | 1.119 | 6.781 |
| 40 | 1.207 | 1.133 | 6.566 |
| 35 | 1.228 | 1.148 | 6.931 |
| 30 | 1.248 | 1.159 | 7.699 |
| 25 | 1.269 | 1.172 | 8.251 |
| 20 | 1.281 | 1.189 | 7.731 |
| 15 | 1.304 | 1.205 | 8.223 |
| 10 | 1.333 | 1.233 | 8.088 |
| 5 | 1.360 | 1.270 | 7.111 |
| 0 | 1.383 | 1.297 | 6.637 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iliyasu, A.M.; Fouladinia, F.; Salama, A.S.; Roshani, G.H.; Hirota, K. Intelligent Measurement of Void Fractions in Homogeneous Regime of Two Phase Flows Independent of the Liquid Phase Density Changes. Fractal Fract. 2023, 7, 179. https://doi.org/10.3390/fractalfract7020179
Iliyasu AM, Fouladinia F, Salama AS, Roshani GH, Hirota K. Intelligent Measurement of Void Fractions in Homogeneous Regime of Two Phase Flows Independent of the Liquid Phase Density Changes. Fractal and Fractional. 2023; 7(2):179. https://doi.org/10.3390/fractalfract7020179
Chicago/Turabian StyleIliyasu, Abdullah M., Farhad Fouladinia, Ahmed S. Salama, Gholam Hossein Roshani, and Kaoru Hirota. 2023. "Intelligent Measurement of Void Fractions in Homogeneous Regime of Two Phase Flows Independent of the Liquid Phase Density Changes" Fractal and Fractional 7, no. 2: 179. https://doi.org/10.3390/fractalfract7020179
APA StyleIliyasu, A. M., Fouladinia, F., Salama, A. S., Roshani, G. H., & Hirota, K. (2023). Intelligent Measurement of Void Fractions in Homogeneous Regime of Two Phase Flows Independent of the Liquid Phase Density Changes. Fractal and Fractional, 7(2), 179. https://doi.org/10.3390/fractalfract7020179






.png)


